Онлайн расчет стропил крыши — оставьте заявку InterCity
Расчет балок стропильной системы
Расчет деревянных двутавровых балок стропильной системы ведется по II предельному состоянию, по прогибам.
Сечение балок подбирается под такую нагрузку, чтобы прогиб в центе пролета был по величине не более допустимого прогиба, который определяется СНиП «Нагрузки и воздействия». В частности для стропильной системы допустимый прогиб равен L/200, где L — максимальный пролет.
Например, при максимальном пролете стропильной ноги равном 7 метров, возможен прогиб 7000/200 = 35 мм. Это прогиб, при котором возможна нормальная эксплуатация кровли.
Исходя из рекомендаций СНиП о максимальном прогибе, мы составили сводные таблицы максиманых пролетов балок в зависимости от высоты, типа, шага балок, значений нагрузки, а также от угла наклона кровли.
Примечания:
- Балки серии L изготавливаются длиной до 13,5 метров.
- Балки серии W изготавливаются длиной 6 метров.
- Рекомендуемые шаги — 0,6 и 0,8 м
- Максимальный пролет — расстояние «в свету» между соседними опорами. Например, стропильной ноги по скату провли между коньком и мауэрлатом.
- Шаг балок — межосевое расстояние двух соседних балок.
Таблица расчета балок стропильной системы
Угол наклона кровли от 12 до 25 градусов.
Расчет для нагрузки 220 кг/м2 (для III снегового региона, в т.ч. Москва и МО)
| Высота балки, мм | Тип балок / шаг балок | Максимальные пролеты, м | |||
|---|---|---|---|---|---|
| 0,4 | 0,6 | 0,8 | 1,0 | ||
| 240 | Балка ICJ-240W | 5,75 | 5,05 | 4,60 | 4,25 |
| 300 | Балка ICJ-300W | 6,00 | 5,60 | 5,45 | 5,10 |
| 360 | Балка ICJ-360W | 6,00 | 6,00 | 6,00 | 5,85 |
| 400 | Балка ICJ-400W | 6,00 | 6,00 | 6,00 | 6,00 |
| 240 | Балка ICJ-240L | 6,30 | 5,50 | 5,00 | 4,60 |
| 240 | Балка ICJ-240L с полкой 89 мм | 7,00 | 6,10 | 5,50 | 5,10 |
| 300 | Балка ICJ-300L | 7,50 | 6,50 | 5,90 | 5,50 |
| 300 | Балка ICJ-300L с полкой 89 мм | 8,40 | 7,30 | 6,60 | 6,20 |
| 360 | Балка ICJ-360L | 8,60 | 7,50 | 6,80 | 6,40 |
| 360 | Балка ICJ-360L с полкой 89 мм | 9,60 | 8,40 | 7,60 | 7,10 |
| 400 | Балка ICJ-400L | 9,40 | 8,20 | 7,40 | 6,90 |
| 400 | Балка ICJ-400L с полкой 89 мм | 10,40 | 9,10 | 8,30 | 7,70 |
| 460 | Балка ICJ-460L | 10,40 | 9,10 | 8,30 | 7,70 |
| 460 | Балка ICJ-460L с полкой 89 мм | 11,60 | 10,10 | 9,20 | 8,50 |
| 500 | Балка ICJ-500L | 11,10 | 9,70 | 8,80 | 8,20 |
| 500 | Балка ICJ-500L с полкой 89 мм | 12,50 | 10,70 | 9,80 | 9,10 |
| 600 | Балка ICJ-600L | 12,70 | 11,10 | 10,10 | 9,40 |
| 600 | Балка ICJ-600L с полкой 89 мм | 13,00 | 12,30 | 11,20 | 10,40 |
Таблица расчета балок стропильной системы
Угол наклона кровли от 25 до 35 градусов
Расчет для нагрузки 220 кг/м2 (для III снегового региона, в т.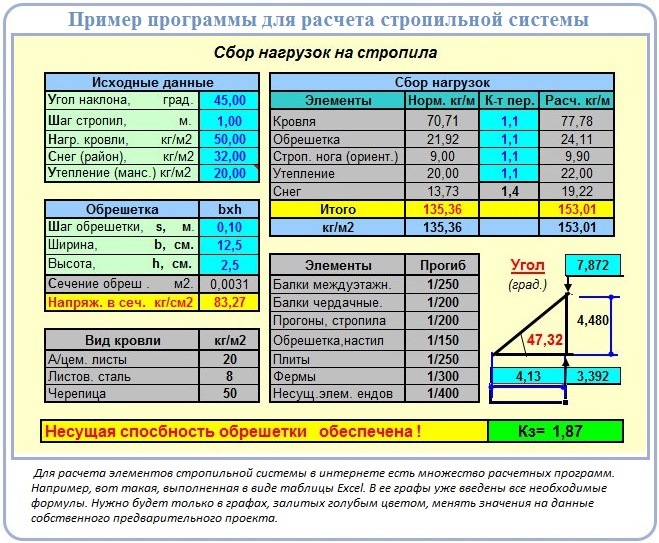
ч. Москва и МО)
| Высота балки, мм | Тип балок / шаг балок | Максимальные пролеты, м | |||
|---|---|---|---|---|---|
| 0,4 | 0,6 | 0,8 | 1,0 | ||
| 240 | Балка ICJ-240W | 5,90 | 5,10 | 4,70 | 4,30 |
| 300 | Балка ICJ-300W | 6,00 | 6,00 | 5,60 | 5,20 |
| 360 | Балка ICJ-360W | 6,00 | 6,00 | 6,00 | 6,00 |
| 400 | Балка ICJ-400W | 6,00 | 6,00 | 6,00 | 6,00 |
| 240 | Балка ICJ-240L | 6,40 | 5,60 | 5,10 | 4,70 |
| 240 | Балка ICJ-240L с полкой 89 мм | 7,20 | 6,30 | 5,70 | 5,30 |
| 300 | Балка ICJ-300L | 7,70 | 6,70 | 5,70 | |
| 300 | Балка ICJ-300L с полкой 89 мм | 8,60 | 7,50 | 6,80 | 6,30 |
| 360 | Балка ICJ-360L | 8,90 | 7,70 | 7,00 | 6,50 |
| 360 | Балка ICJ-360L с полкой 89 мм | 9,90 | 8,60 | 7,80 | 7,20 |
| 400 | Балка ICJ-400L | 9,60 | 8,40 | 7,60 | 7,10 |
| 400 | Балка ICJ-400L с полкой 89 мм | 10,70 | 9,30 | 8,50 | 7,90 |
| 460 | Балка ICJ-460L | 10,70 | 9,30 | 8,50 | 7,90 |
| 460 | Балка ICJ-460L с полкой 89 мм | 11,90 | 10,40 | 9,40 | 8,70 |
| 500 | Балка ICJ-500L | 11,40 | 9,90 | 9,00 | 8,40 |
| 500 | Балка ICJ-500L с полкой 89 мм | 12,60 | 11,00 | 10,00 | 9,30 |
| 600 | Балка ICJ-600L | 13,00 | 11,40 | 10,30 | 9,60 |
| 600 | Балка ICJ-600L с полкой 89 мм | 13,00 | 12,60 | 11,50 | 10,60 |
Таблица расчета балок стропильной системы
Угол наклона кровли от 35 до 45 градусов
Расчет для нагрузки 220 кг/м2 (для III снегового региона, в т.
ч. Москва и МО)
| Высота балки, мм | Тип балок / шаг балок | Максимальные пролеты, м | |||
|---|---|---|---|---|---|
| 0,4 | 0,6 | 0,8 | 1,0 | ||
| 240 | Балка ICJ-240W | 6,00 | 5,30 | 4,85 | 4,50 |
| 300 | Балка ICJ-300W | 6,00 | 6,00 | 5,80 | 5,30 |
| 360 | Балка ICJ-360W | 6,00 | 6,00 | 6,00 | 6,00 |
| 400 | Балка ICJ-400W | 6,00 | 6,00 | 6,00 | 6,00 |
| 240 | Балка ICJ-240L | 6,70 | 5,80 | 5,30 | 4,90 |
| 240 | Балка ICJ-240L с полкой 89 мм | 7,40 | 6,50 | 5,90 | 5,50 |
| 300 | Балка ICJ-300L | 8,00 | 6,90 | 6,30 | 5,80 |
| 300 | Балка ICJ-300L с полкой 89 мм | 8,90 | 7,80 | 7,00 | 6,50 |
| 360 | Балка ICJ-360L | 9,20 | 8,00 | 7,30 | 6,70 |
| 360 | Балка ICJ-360L с полкой 89 мм | 10,20 | 8,90 | 8,10 | 7,50 |
| 400 | Балка ICJ-400L | 9,90 | 8,70 | 7,90 | 7,30 |
| 400 | Балка ICJ-400L с полкой 89 мм | 11,00 | 9,60 | 8,80 | 8,10 |
| 460 | Балка ICJ-460L | 11,10 | 9,60 | 8,80 | 8,10 |
| 460 | Балка ICJ-460L с полкой 89 мм | 12,30 | 10,70 | 9,70 | 9,00 |
| 500 | Балка ICJ-500L | 11,80 | 10,30 | 9,30 | 8,70 |
| 500 | Балка ICJ-500L с полкой 89 мм | 13,00 | 11,40 | 10,40 | 9,60 |
| 600 | Балка ICJ-600L | 13,00 | 11,80 | 10,70 | 9,90 |
| 600 | Балка ICJ-600L с полкой 89 мм | 13,00 | 13,00 | 11,90 | 11,00 |
Расчёт стропильной системы по эскизу
Вы здесь:
by Super User
строительство домов В этой статье приведён упрощённый метод расчёта стропильной системы.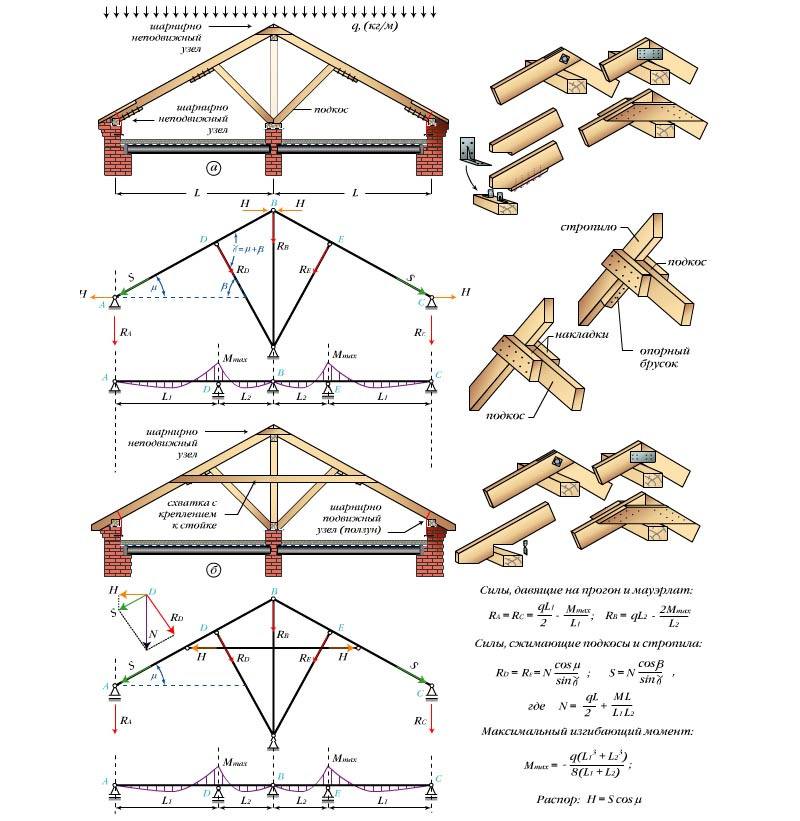
Вы узнаете, как быстро и правильно принять решение по сечению стропил и ширине пролёта. Адаптированный математический расчёт содержит минимум формул и приводит к достаточно точным результатам.
Существует стандартная методика расчёта стропильной конструкции, приведённая в соответствие со СНиП 2.01.07–85 «Нагрузки и воздействия». Она включает в себя множество довольно сложных подсчётов и справочных величин. Популярная услуга сайтов — онлайн расчет стропильной системы двускатной крыши — позволит предельно точно определить количество материала.
Примечание. В статье рассмотрена методика расчёта стропильной системы двускатной крыши с вальмой, полувальмой или фронтоном без дополнительных конструктивных элементов — козырьков, «скворечников», башен и т. д. и углом ската не менее 45°.
С чего начать
Традиционная методика предполагает следующий подход: под расчётную нагрузку подбирается конструкция кровли и сечение балок.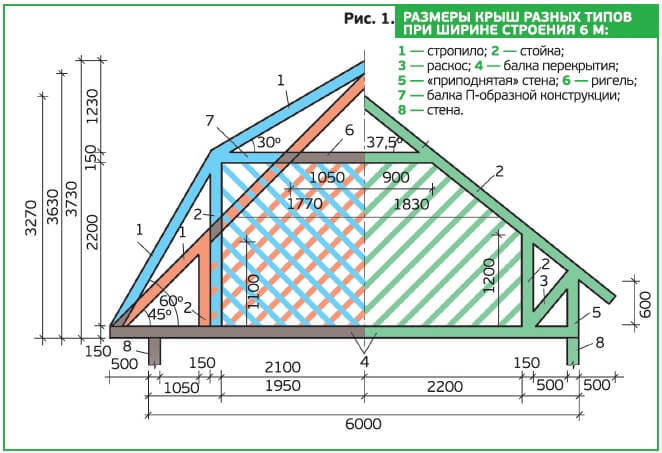
Это не в полной мере соответствует требованиям сегодняшнего дня и исходными данными в нашем случае будут следующие показатели:
1. Требования (пожелания) к конструкции крыши. В первую очередь имеется в виду наличие мансардного (жилого) этажа, расположение мансардных окон или наличие чердачного технического помещения.
2. Существующие размеры дома, либо границы постройки. 70% частных домов находятся в относительно плотной застройке, и это тоже стоит учитывать при проектировании кровли. Ограниченная площадь участка и возможные требования соседей в отношении солнечного света могут внести свои коррективы.
3. Унификация. Стропильная система — многоэлементная конструкция. Разумно постараться привести максимальное количество элементов к одному стандарту — сечению доски или бруса.
Самым сложным, как ни странно, является первый пункт. Однако, после того как получено полное представление о том, какие функции должна выполнять стропильная система (прямые или комбинированные), можно приступать к стадии проектирования.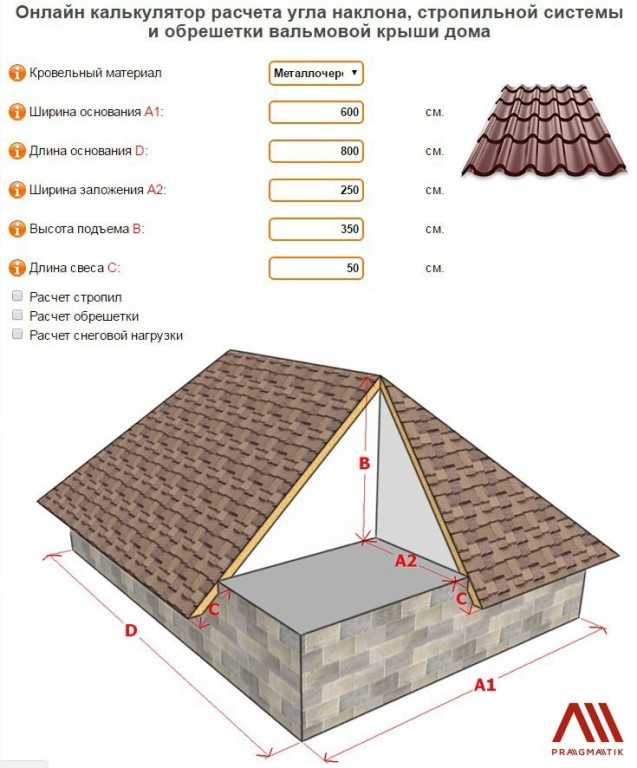
Создаём эскиз
Этот этап — один из решающих, поскольку в нём мы узнаем примерные размеры элементов. Главный из них — стропильная ферма — станет основой дальнейших расчётов. В основу самого чертежа лягут два исходных параметра:
1. Пролёт между несущими стенами. Крайне желательно, чтобы опорные точки стропильной системы, которые передают вертикальные нагрузки, располагались по осям несущих стен или опор. Расстояние от проекции конька до стены называется полупролёт.
2. Высота конька от перекрытия. Этот параметр складывается из функциональных особенностей конструкции — высота потолка мансарды, доступного чердака или «глухого» чердачного пространства.
Как известно, 75% простых стропильных систем составляют кровли с прямым и «ломаным» скатом. Это существенно влияет на расчёты, поэтому мы сразу разделим эти виды. Поскольку в основе любой стандартной кровли лежит треугольная конструкция, мы постараемся ограничиться одной формулой (теоремой Пифагора):
· с2 = a2 + b2
На этом этапе можно довольно точно подсчитать площадь скатов и расход кровельного материала вместе с обрешёткой.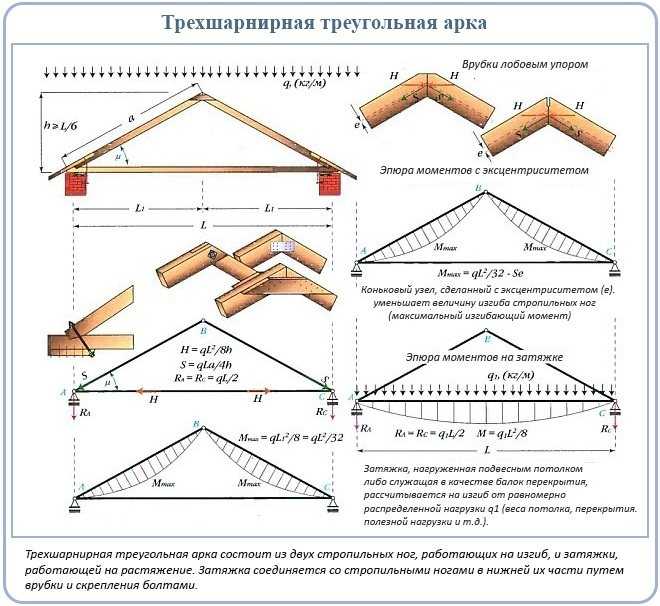
Для этого достаточно воспользоваться расчетом стропильной системы двускатной крыши онлайн, который предоставляют многие сайты.
Прямой равносторонний скат
Переносим на эскиз размеры перекрытия или расположение несущих стен (конструкция не всегда подразумевает наличие деревянного перекрытия) в масштабе. Затем отмечаем точку конька и проводим прямые к стенам с учётом принятого вылета крыши. Эти прямые уже можно замерять и умножать на масштаб — получим длину стропильной ноги.
В соответствии с выбранной структурой организации внутреннего пространства (объединённое или разделённое) располагаем подстропильную затяжку (ригель) и определяем её длину. Располагаем на чертеже упоры, откосы и вертикальные стойки, соблюдая требования правила, приведённые в статье «Стропильная система двускатной крыши своими руками». Пролёты не должны быть больше 2 м, а стропилы должны обязательно иметь промежуточный подкос. При этом достаточно придерживаться примерных рамок допусков.
Применяя формулу отношения сторон прямоугольного треугольника, можно рассчитать любой из размеров стропильной фермы. Остальные размеры можно снять с чертежа через масштаб. Главная задача — получить размеры каждого из элементов.
«Ломаный» скат
Такой вид кровли всегда принимается в связи с устройством мансарды или надстройкой жилого этажа. Он имеет одну характерную особенность — ряд вертикальных стоек в месте пересечения скатов и подстропильный ригель, который может располагаться как на уровне верха этих стоек, так и под коньком. Ряды стоек и ригелей формируют стены и потолок мансардного помещения.
Аналогичным образом переносим на чертёж основные элементы — сначала стены и перекрытие, затем ряд стоек и ригелей (на уровне потолка), затем соединяем их линиями, которые довольно точно покажут форму излома скатов.
После замеров и вычислений следует сложить длины всех элементов стропильной фермы и прибавить к полученному числу 10%.
Это будет общая длина конструктива одной фермы (ОДК1).
Подбор сечения стропил и унификация
Сечение элементов системы, особенно стропильных ног, напрямую зависит от пролёта между опорами в центральной части. Из всех пиломатериалов для стропильной системы подходят брус и доска (не считая заводских клееных ферм). При этом доска имеет гораздо лучший показатель отношения сечения к прочности на изгиб. В нашем случае речь идёт о надёжности стропил, для которых используют именно доску, т.к. есть запас глубины пазухи для закладки утеплителя.
Таблица зависимости ширины пролёта и толщины стропил
Ширина пролёта без промежуточных опор, мм | Сечение доски стропильной ноги, мм |
От 2000 до 2500 | 40х150 |
От 2500 до 3500 | 50х150 |
От 3500 до 4000 | 60х150-180 |
От 4000 до 5000 | 75х180-200 |
От 5000 до 6000 | 100х180-250 |
Устраивать пролёты стропильных ферм более 6 метров без промежуточных опор не рекомендуется.
Совет. При сращивании двух досок для создания вертикальной опоры, проложите между ними в местах крепления обрезки досок 25 мм («бобышки») с шагом 300–400 мм. Так прочность опоры будет выше по сравнению с прямым сращиванием.
После определения достаточного сечения доски можно вычислить объём одной стропильной фермы. Для этого умножаем ОДК-1 на площадь сечения доски. Полученный объём одной фермы (ОФ1) будет использован при подсчёте общего объёма.
Расчёт шага стропильных ферм
Шаг стропил мансардной стропильной системы зависит от толщины и конструкции стропильных ферм.
Таблица зависимости шага от толщины
Толщина, мм | Максимально допустимый шаг, мм |
40 | 500 |
50 | 600 |
60 | 800 |
75 | 1000 |
100 | 1200 |
Разделив длину продольной (параллельной коньку) стены на выбранный шаг мы получим количество стропильных ферм (N).
Соответственно, сможем вычислить длину доски для ферм:
· ОДК1 х N
объём доски для ферм:
· ОФ1 х N или ОДК1 х Sсечения доски х N
Расчёт мауэрлата
Если стропильная система устраивается на деревянном перекрытии, то вся горизонтальная обвязка относится к нему. Мы рассмотрим вариант с мауэрлатом по каменной стене.
Поскольку вертикальные стойки, подкосы и прогоны включены в расчёт фермы, нам осталось подсчитать горизонтальную обвязку. Здесь есть простое правило — она должна быть толщиной не менее двойной стропильной ноги. Если общая масса кровли (вместе с обрешёткой и кровельным материалом и снегом) ощутимо высока, следует применить три слоя доски.
Объём доски для мауэрлата будет равен длине несущих стен, умноженной на сечение доски и на количество слоёв. Мауэрлат, выполненный из нескольких слоёв, лучше свяжется по углам.
Общий подсчёт
Складываем все полученные объёмы вместе и прибавляем 20% на отходы и подрезку.
Количество металлических изделий и крепёжных элементов определяется индивидуально. Достоверно известно лишь то, что чем их больше, тем лучше.
Примечание. Все приведённые величины и пропорции зависимости взяты из нормативно-справочной литературы.
Заключение
Несмотря на кажущуюся простоту, данный адаптированный расчёт может соперничать в точности с онлайн-калькуляторами стропильной системы. Однако решающее слово всегда остаётся за тем, кто будет исполнять проект.
Виталий Долбинов, рмнт.ру
http://www.rmnt.ru/ — сайт RMNT.ru
Опубликовано в Новые технологииОтмечено тэгами строительство домовОнлайн-решатель 2D-ферм — FedericoBonfigli.com
С помощью этого небольшого веб-приложения вы можете решить любую плоскую ферму максимум с 30 узлами. Система рассчитывает осевые силы, смещения соединений и деформации элементов конструкции.
Он также рисует деформированную конструкцию из-за нагрузок, приложенных к суставам. Система работает, но обязательно проверяйте результаты, так как она не предназначена для профессионального использования.
| 1. | Добавить суставы | Coor X (м) | Коор Y (м) | |
| (альтернативно) Добавить соединения из списка | вставьте координаты соединений в соответствии со следующим форматом: X1/Y1(пробел)X2/Y2(пробел).  ..Xn/Yn | |||
| 2. | Добавить объект кадра | Первый стык (или нажмите на первый стык) Последний стык | Площадь сечения мм2 Модуль Юнга | |
3. | Добавить сдержанность | Соединение, подлежащее фиксации (или нажмите на нужный узел) | Тип удержания: | |
| 4. | Добавить нагрузки | Выберите сустав (или нажмите на сустав) | Загрузить X-компонент кН Y-компонент нагрузки | |
|
| Графические опции: | Деформированная форма Состав Осевые силы Ограничения Цветовая карта |
Применение метода формул рядов в оптимизации расположения перемычек
World Journal of Engineering and Technology Vol.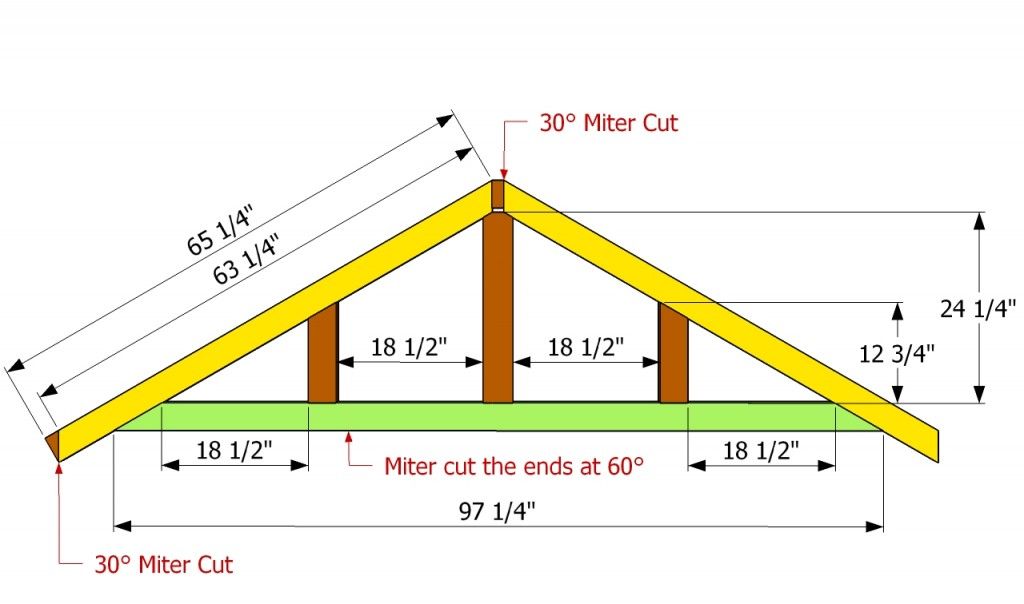
06 No.03 (2018), ID статьи: 86406, 10 страниц
10.4236/wjet.2018.63041
Применение метода формулы ряда в оптимизации расположения перемычек
Qiaozhi Sang 1 , Shuqi Li 1 Ван 2 , Дяньсюань Гонг 3*
1 Колледж Ишэн, Северо-Китайский университет науки и технологии, Таншань, Китай
2 Архитектурно-строительный колледж Северо-Китайского университета науки и технологии, Таншань, Китай
3 900 Научный колледж Северо-Китайского университета науки и технологии, Таншань, КитайАвторские права © 2018 принадлежат авторам и Scientific Research Publishing Inc.
Эта работа находится под лицензией Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/
Получено: 2 мая 2018 г.; Принято: 29 июля 2018 г.; Опубликовано: 1 августа 2018 г.
АННОТАЦИЯ
Методом математических формул исследованы выражения внутренних усилий стенок при вертикальных нагрузках свободно опертых ферм балочного типа с вертикальными и горизонтальными стенками и без вертикальных стенок.
Моделируются изменения внутренних усилий при различных углах и расстояниях между стенками. Получен закон оптимального расположения стенок параллельно-струнной однобалочной фермы: при условии, что жесткость стержня допускается, форма не вертикальной балочной фермы и уменьшение пролетного расстояния и наклона Боковой пролет рекомендуется, что может сэкономить материалы и уменьшить вес. Этот метод можно применять для расчета внутренних сил при произвольных нагрузках и формах ферм.
Ключевые слова:
Метод формул серии, балочная ферма, оптимальное расположение стенок решения и графические методы в настоящее время. Для расчета внутренней силы численным методом решения необходимо «обрезать» фермы и составить список уравнений баланса. Как правило, усеченные стержни могут быть получены, когда они не превышают 3 [1] . Этот метод широко применяется для расчета внутренних сил простой фермы, но его очень громоздко применять для сложных и многоузловых ферм. При проектировании обычно используется графический метод, но конструктор должен иметь определенный опыт и более точный чертежный уровень в построении диаграмм взаимодействия внутренних сил.
Лю Юэхуа решил внутренние силы ферм, получив две неизвестные силы в узле в сочетании с инструментами рисования AUTO CAD, основанными на графическом методе [2] . М. С. Кечум предложил экспоненциальный метод внутренних сил, в котором вертикальные составляющие силы стержня представляют его внутреннюю силу в виде тригонометрической функции, а внутренние силы элементов фермы быстро рассчитывают [3] . Для ферменной конструкции со шахматным расположением натощак Zhou Xuhong et al. ввел жесткость фермы при вращении и коэффициент передачи, чтобы получить формулу для внутренних сил элементов, которая хорошо согласовывалась с результатами анализа ANSYS [4] . Метод математической формулы — это простой и применимый метод, сочетающий метод индекса внутренней силы с традиционным методом поперечного сечения, ферма считается идеальной, которая состоит из расчетных секций между левым концом и правым концом, расположенными последовательно, Уравнение, полученное из метода сечения, содержащее только одно неизвестное на основе принципа метода виртуальной работы, используется для расчета внутренней силы простой брюшной фермы [5] .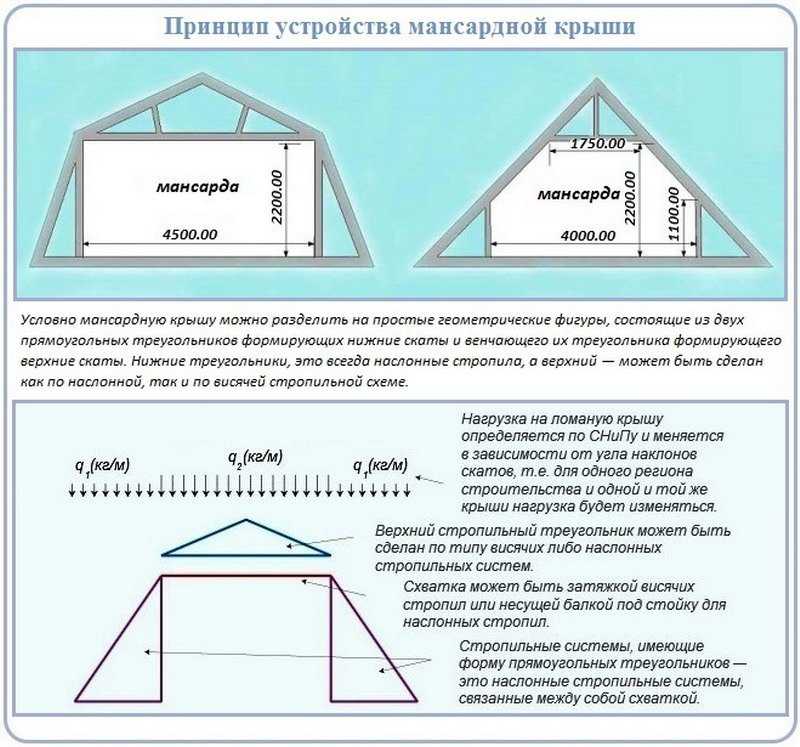
2. Классификация деталей ферм и стержней
Ферма представляет собой решетчатую конструкцию, состоящую из прямых стержней, соединенных друг с другом на концах. Простейшая форма простой брюшной фермы представляет собой треугольник, образованный тремя стержнями, шарнирно соединенными друг с другом на концах стержней. Под действием нагрузки собственная форма фермы не изменяется, за исключением незначительной упругой деформации. При каждом доступе к двум опорам можно получить различные типы стабильных ферм. Ферма, соединенная этим методом, называется простой брюшной фермой. Среди них соответствующие узлы верхнего и нижнего поясов, помимо косых стеновых элементов, имеют также вертикальную ферму-стык, называемую вертикальной стеновой фермой; ферма только с диагональной стенкой называется фермой с вертикальной стенкой. В ферме между некоторыми суставами есть вертикальная стенка, а другая ферма без вертикальной стенки называется фермой с гибридной стенкой.
Элемент фермы между двумя верхними поясами называется верхним поясом и обозначается буквой О, элемент между узлами нижнего пояса обозначается буквой U.
Стержень, соединяющий верхнюю и нижнюю струны, называется поперечным стержнем, наклонными стержнями которые наклонены вправо, называются восходящими диагональными тканями, которые представлены
Д а п
, иначе по
D в н
. Средние диагональные стержни двух соседних восходящих консольных стержней называются восходящими вертикальными стержнями стенки, обозначаемыми
В у п
соответствующие нисходящие вертикальные стержни перемычки
Вниз
; когда верхние стержни согнуты на верхнем конце одиночного вертикального стержня, один вертикальный стержень называется стержнем «个», представленным
В о
, если вертикальные и горизонтальные стержни являются диагональными стержнями, они называются
В″ о
. Когда верхний пояс пробивается на верхнем конце одиночного вертикального стержня, одиночный вертикальный стержень называется Т-образным вертикальным стержнем, обозначаемым
В т
, превращается в диагональные стержни T
В ″ т
когда вертикальные стержни наклонены.
Перевернутые вертикальные и стержни и перевернутые диагональные стержни обозначаются
В ты
и
В ″ ю
соответственно; перевернутые Т-образные вертикальные брюшные стержни и перевернутые Т-образные диагональные брюшные стержни представлены буквами V и
В″
. Определение каждого конкретного бара показано ниже (рисунок 1).
3. Введение в метод формулы ряда
3.1. Метод Описание
Определение наименований стержней и обозначения формул приведены на рисунке 1. Верхний (нижний) пояс фермы называется верхним поясом, а верхний (нижний) между х расчетными сечениями называется верхней (нижней) хордой. Наклонная паутина, которая на этом участке наклонена вправо, называется восходящим наклонным стержнем, а наклонная влево — нисходящим наклонным стержнем. Средние вертикальные и горизонтальные перемычки соседних направленных вверх наклонных стержней называются восходящими вертикальными перемычками, а средние вертикальные перемычки двух соседних направленных вниз перемычек называются нисходящими вертикальными перемычками.
Интервал между соседними тканями называется расчетным интервалом, обозначаемым x. Правило нумерации интервалов:
Фермы с вертикальным стержнем располагают в натуральном ряду (0), 1, 2, 3 и т. д., а фермы без вертикального стержня — в порядке арифметического ряда (0), 1, 1,5, 2, 2,5, 3 и т. д., когда первый стержень представляет собой восходящую косую паутину, арифметического ряда (0), 0,5, 1, 1,5, 2, 2,5 и т. д., когда первый стержень нисходящий. В таком случае при расположении последовательно слева направо в порядке арифметической прогрессии уравнение внутренней силы, выводимое методом сечений, можно упростить по формуле суммы арифметического ряда, как всем известно S п знак равно п а 1 + [ п ( п — 1 ) / 2 ] d .
Предельное выражение внутренних сил простое и имеет более широкое применение, которое способно вычислить перемещение любого стержня или узла фермы.
3.2. Вывод формулы ряда для внутренней силы
Внутренняя сила О х верхнего пояса в перекрестке Х -й : методом поперечного сечения [6] за распорку принять левую часть сечения а-а, за мавзолей нижний узел, затем ∑ М Х 0 = 0
М ты х + О х р о х = 0 (1)
О Икс знак равно — M ты Икс я о c Икс я о б Икс час Икс (2)
Нижний пояс внутренний
U x = M о x i o c x i o b x h x
сила получается так же, как показано на рис.
2:
Внутренняя сила восходящей косой стенки Д х п на перекрестке Х -й : за распорку взять левый конец участка а-а, ∑ у = 0 , затем
Q x + O x — 1 1 i o c x — 1 — U x 1 i u c x + D x u p 1 i d c x u p = 0 (3)
D x u p = — Q x i d c x u p = — Q x / cos θ d c x u p (4)
Рис. 1. Определение каждого стержня фермы.
Рис. 2. Раздел, выбранный методом сечения.
Соответствующая внутренняя сила падающего косого стержня равна D Икс d о ш п знак равно Q Икс я d c Икс d о ш п знак равно Q Икс / потому что θ d c Икс d о ш п . .
Внутренняя сила В х н п восходящей вертикальной брюшной штанги в X -й -й перекресток: за разделитель взять левую часть участка а-а [7] , ∑ у = 0
Q x + O x 1 i o c x — U x 1 i u c x — V x u p = 0 (5)
V х у р = Q х (6)
Внутренняя сила падающего вертикального стержня
V x d o w n = — Q x
рассчитывается таким же образом.
Внутренняя сила вертикального стержня «个» В о х и косой стержень V″ о х : разделитель над секцией а-а (см. рис. 3), ∑ у = 0 , то
− О Икс 1 я о c Икс — О ′ Икс 1 я ′ о c Икс + п Икс — V о Икс знак равно 0 (7)
V о Икс знак равно п Икс , V ″ о Икс знак равно п Икс / c о s θ (8)
Рис. 3. Сечение, выбранное для вертикальной полосы «个».
Внутренняя сила перевернутого вертикального стержня «个» В о х это
V u x = G x
и у наклонного V″ о х это
V ″ ты х знак равно г х я г с х я v с х
3.3. Выражения для внутренних усилий в ферме
3.3.1. Внутреннее усилие вертикальной фермы под действием единичной вертикальной узловой нагрузки (X обозначает стержень, примыкающий к левой стороне поперечного сечения)
D x u p = — 0,5 ( n — 2 x + 1 ) / cos θ
D x d o w n = 0,5 ( n — 2 x + 1 ) / cos θ
V p x u p = 0,5 ( n — 2 x — 1 )
V п Икс d о ш п знак равно — 0,5 ( п — 2 Икс + 1 )
V п о х = − 1
V p u x = 0
3.
3.2. Внутреннее усилие фермы без вертикальной стенки под действием вертикальной нагрузки на единицу
Полусекционная ферма между верхними поясами
D x u p = ( RA — x + 1,25 ) / cos θ
D x d o w n = ( RA — x + 1,25 ) / cos θ
D 1 u p = − R A / cos θ
D B x d o w n = — R B / cos θ
Ферма полусекционная между нижними поясами
D x u p = — ( RA — x + 1 ) / cos θ
D x d o w n = ( RA — x + 0,5 ) / cos θ
D 0,5 d o w n = R A / cos θ 0,5 d o w n
D B x u p = − R A / cos θ u p
4. Расположение стержней
Расположение стенок должно быть таким, чтобы конструкция фермы была простой, а сила разумной. По возможности длинные стержни растягивают, а короткие сжимают. Углы наклона стенки обычно составляют от 30˚ до 60˚. Внешняя нагрузка должна действовать на узел, чтобы избежать местного изгибающего момента пояса из-за межузловой нагрузки. В работе исследуется изменение внутренних сил одноопорной балочной фермы с вертикальными и радиальными стенками и вертикальными и горизонтальными стержнями при трехмерных вертикальных нагрузках с расположением стенок.
Среди них есть вертикальные брюшные ферменные конструкции брюшной системы, разделенные на левую половину подъема и правую половину снижения, левую половину снижения и правую половину восходящего, опускающегося и восходящего попеременного расположения, восходящий и нисходящий Формируется в виде «восьмерки»; без вертикальной перемычки балка простая балочная ферма в соответствии с брюшной компоновкой швов головки обмотки для половины шага, нижний конец пояса между половиной шага, количество междоузлий обмотки больше, чем соединение нижнего пояса Фермы с количеством и количество промежуточных хорд меньше числа промежуточных хорд показано на рис. 4 и рис. 5.
5. Применение метода формулы ряда при расположении стенок фермы
На основании формулы расчета, приведенной выше, внутренние силы стержней изменяются с наклоном стержней и расстоянием между стенками соответственно, так что угол между перемычками и вертикальным направлением изменяется от 30˚ до 60˚, а расстояние колеблется от 10 см до 50 см.
Изменение; Каждая кривая представляет определенное положение в ферме. Положение стержня меняется снизу слева направо в зависимости от расположения фермы. Она варьируется снизу вверх или сверху вниз. В качестве примера возьмем ферму с подъемом влево и падением вправо:
Левый конец брюшной стержень восходящего типа, междоузлие положение
х < п 2
, так что при положении брюшного стержня от левого конца к середине пролета давление
Д х п
постепенно снижается. В середине пролета она равна 0, т. е. конец брюшного стержня больше среднего брюшного стержня; Форма стержневых параллельных ферм не соответствует форме диаграммы изгибающих моментов, поэтому сила плохая, то есть внутренняя сила хорды неравномерна, а внутренняя сила стенки немного больше. Полотно изменяется при наклоне от 30˚ до 60˚, а внутреннее давление уменьшается. Боковая перемычка имеет тенденцию сходиться, когда угол наклона приближается к 60˚, в то время как внутренняя сила стенки промежуточного пролета наиболее чувствительно изменяется около 60˚; Под определенным углом, с увеличением числа перемычек, возрастает и внутреннее давление, так как соответствующие перемычки стыков постепенно перемещаются к пролету по расстоянию между узлами, близкому к пути передачи усилия, а внутреннее усилие и расстояние между перемычками становится линейным изменением.
Рис. 4. Ферма с межсекционным интервалом в нижней части пояса.
Рис. 5. Ферма с межсекционным интервалом на верхнем конце пояса.
нисходящий брюшной стержень меняется совершенно симметрично с восходящей тенденцией соответствующего междоузлия восходящего диагонального стержня. Внутренние силы бокового остова наиболее чувствительны к изменению угла наклона. На каждые 6° увеличения около 60° давление на стенку увеличивается примерно на 20 (см. рис. 6).
Натяжение вертикальной стенки расположено на левом пролете, а внутренняя сила постоянно меняется в зависимости от шага соединений. Тяговое усилие полотна между соединениями уменьшается с увеличением шага, потому что междоузлия увеличиваются с увеличением шага между узлами. При постепенном перемещении посередине, но от ферменной системы амплитуда его внутренней силы имела тенденцию к снижению. Правая вертикальная полоса поперечного спуска полностью перевернута симметрично восходящему изменению (см.
рис. 7).
Для фермы с параллельными струнами без вертикальной стенки восходящая стенка находится под давлением и падает, и изменение в основном такое же, как и у фермы. Количество стержней и количество узлов в вертикальной стропильной системе также невелико. Два элемента полотна в одном узле тянут одно давление и могут хорошо выдерживать нагрузку изменения.
6. Выводы
В данной статье рассматривается изменение внутренней силы в зависимости от угла наклона и шага ферменной системы двух видов ферменных систем с вертикальными и горизонтальными стенками. Во избежание местного изгибающего момента межпоясных поясов предполагается, что единичная нагрузка действует на каждый из верхних и нижних узлов. Для упрощения расчета и облегчения обсуждения на примере одноопорной балочной фермы с параллельными ветвями (левостороннее восходящее правостороннее нисходящее расположение) приведены следующие результаты:
Рис. 6. Внутренняя сила восходящего косого стержня зависит от угла наклона и количества.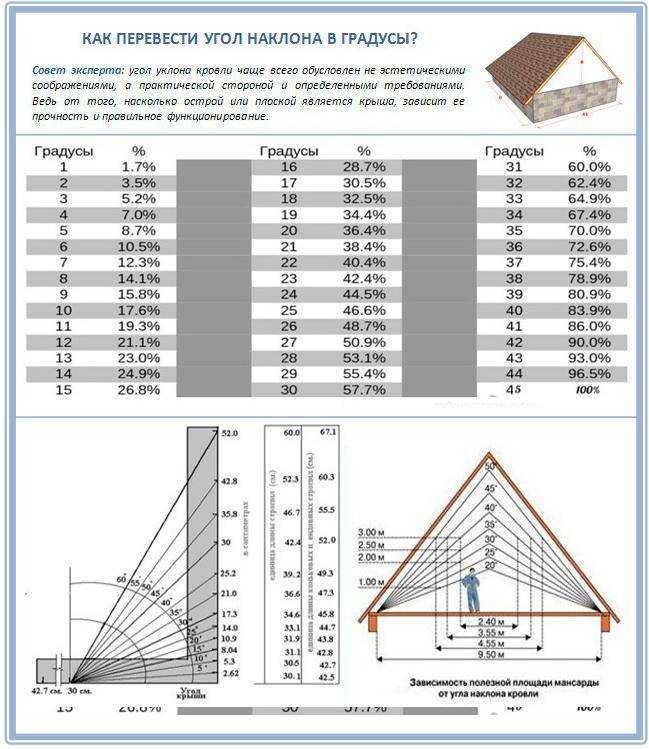
Рис. 7. Восходящая внутренняя сила вертикального стержня зависит от угла наклона и величины.
Поскольку промежуточный поперечный стержень находится далеко от пути передачи усилия, в целях экономии материала и уменьшения собственного веса можно уменьшить количество установленных поперечных средних элементов; когда угол между средним элементом перемычки и вертикальным направлением составляет около 60°, его внутренняя сила малочувствительна к углу. Сила стабильная, поэтому можно расположить полотно около 60˚ около среднего положения; внутренняя сила полотна-пролета увеличивается с углом наклона, и его чувствительность также постепенно увеличивается. Таким образом, угол наклона полотна может быть уменьшен примерно до 30˚ в боковом пролете. Это уместно.
Соответствующие стенки определенного узла будут уменьшаться по мере уменьшения шага между узлами и перемещения стержня в сторону бокового или среднего пролета, а также увеличения или уменьшения внутренней силы, воспринимаемой стержнем.
Однако с точки зрения стропильной системы величина внутренней силы в целом имела тенденцию к снижению. Следовательно, при правильном наращивании перемычек внешние нагрузки могут равномерно распределяться на стержни. Чтобы уменьшить собственный вес, разумным решением может быть уменьшение зазора между пролетами и увеличение шага между стенками.
Количество стержней и количество узлов в вертикальной стержневой системе также невелико. Два элемента полотна в одном узле тянут одно давление и могут хорошо выдерживать нагрузку изменения. Поэтому целесообразно использовать вертикальную ферму ферменного типа, когда позволяет жесткость элемента.
Благодарности
Этот проект поддерживается Национальным природным фондом Китая (11301120, 11601151), Национальным природным фондом провинции Хэбэй (A2015209189) и Проектом поддержки молодых талантов провинции Хэбэй.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в связи с публикацией данной статьи.
Процитировать эту статью
Санг, К.З., Ли, С.В., Ван, С.К. и Гонг, Д.Х. (2018) Применение метода формул ряда в оптимизации построения сетей. Всемирный журнал инженерии и технологий, 6, 651-660. https://doi.org/10.4236/wjet.2018.63041
Ссылки
- 1. Ву, М. и Дин, К.В. (2013) Обсуждение метода расчета внутренних сил фермы. Механика и практика, 35, 82-84.
- 2. Лю, Ю.Х. и Ли, Л.Ю. (1999) Использование AUTOCAD для расчета внутренних сил фермы. Сычуаньская строительная наука, № 1, 57-58.
- 3. Кечум М.С. и Фэн, С.К. (1984) Простой расчет внутренних сил элементов фермы. Железнодорожное строительство, № 3, 34-35.
- 4. Чжоу, С.Х. и Чоу, З.С. (2004) Расчет внутренней силы и поперечного смещения ферменной конструкции с шахматным расположением под действием горизонтальной нагрузки. Журнал строительных конструкций, № 4, 66-71.
- 5. Ду, К. (1987) Расчет осевой силы статически определенной фермы с плоской балкой с использованием метода формулы ряда.