Статическое давление жидкости: Гидростатическое давление: формула, свойства и особенности

Содержание

Гидростатическое давление: определение, формула и свойства.

—

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов.

Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.

В этой статье мы подготовили для Вас, всю необходимую информацию о гидростатическом давлении, начиная от закона Паскаля и определения формулы гидростатического давления и до свойств давления и применения законов гидростатики в повседневной жизни.

Содержание статьи

Закон Паскаля для гидростатики
Определение и формула гидростатического давления
Сила гидростатического давления
Измерение гидростатического давления
Свойства гидростатического давления + видеоматериалы

В 1653 году французским ученым Б.

Паскалем был открыт закон, который принято называть основным законом гидростатики.

Звучит он так:

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.

Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.

Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.

Определение и формула гидростатического давления

Из описанного выше закона Паскаля вытекает, что:

Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением

P = ρgh , где

ρ – плотность жидкости

g – ускорение свободного падения

h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.

Во всех трёх случаях давление жидкости на дно сосуда одинаково.

Полное давление жидкости в сосуде равно

P = P0 + ρgh, где

P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.

Сила гидростатического давления

Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.

Тогда гидростатическое давление формула которого выглядит как

Рср = ΔP / ΔF

представляет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.

Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.

Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.

Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м²) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:

килоньютон на квадратный метр – 1кН/м² = 1*10³ Н/м²

меганьютон на квадратный метр – 1МН/м² = 1*10⁶ Н/м²

Давление равное 1*10⁵ Н/м² называется баром (бар).

В физической системе единицей намерения давления является дина на квадратный сантиметр (дина/м²), в технической системе – килограмм-сила на квадратный метр (кгс/м²). Практически давление жидкости обычно измеряют в кгс/см², а давление равное 1 кгс/см² называется технической атмосферой (ат).

Между всеми этими единицами существует следующее соотношение:

1ат = 1 кгс/см² = 0,98 бар = 0,98 * 10⁵ Па = 0,98 * 10⁶дин = 10⁴ кгс/м²

Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см² и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.

Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).

Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.

Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.

Рман = Рабс – Ратм

и измеряют также в технических атмосферах, называемых в этом случае избыточными.

Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости

Рвак = Ратм – Рабс

и измеряется в пределах от нуля до атмосферы.

Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
Оно направлено по внутренней нормали к площади, на которую действует;
Величина давления в данной точке не зависит от направления (т. е. от ориентированности в пространстве площадки, на которой находится точка).

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.

Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.

Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.

Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.

Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.

На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.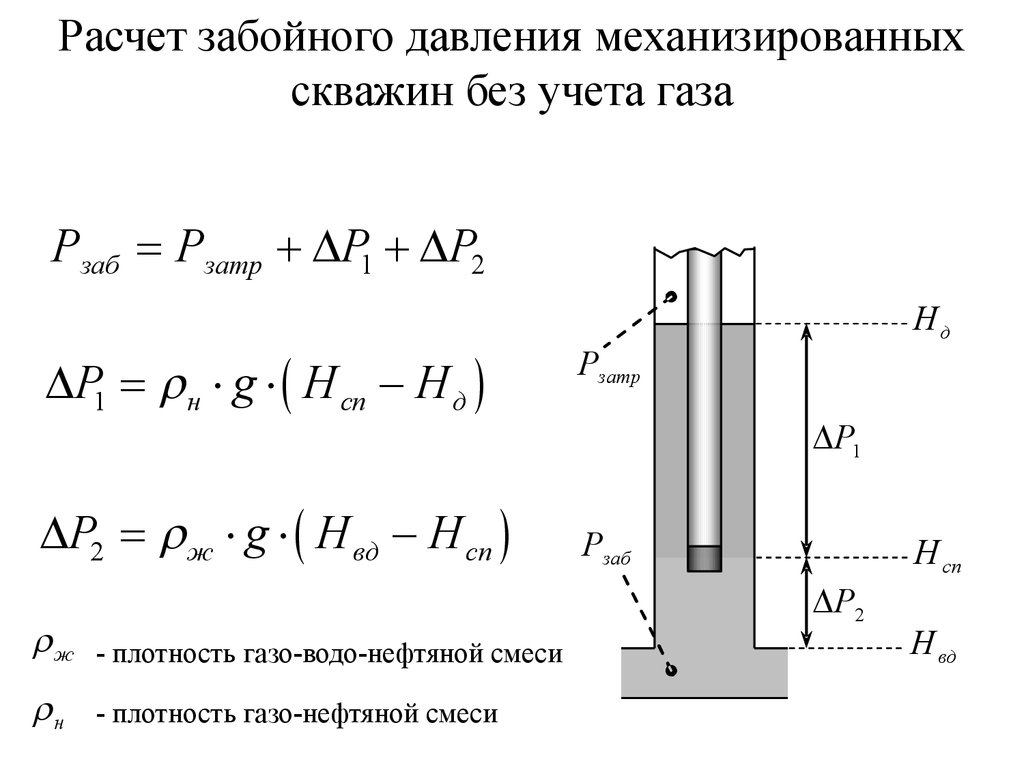

Вместе со статьей «Гидростатическое давление: определение, формула и свойства.» читают:

Гидростатическое давление, теория и онлайн калькуляторы

Определение гидростатического давления

Определение

Физическая величина, равная отношению нормальной силы ($F$), действующей со стороны жидкости на некоторую площадь, на величину этой площади ($S$) называют давлением ($p$) жидкости:

\[p=\frac{F}{S}\left(1\right).\]

Если несжимаемая жидкость находится в равновесии давление по горизонтали всегда одно и то же. Свободная поверхность жидкости всегда горизонтальна, за исключением места около стенок сосуда. У несжимаемой жидкости плотность не зависит от давления. Если поперечное сечение цилиндрического столба жидкости равно $S$, высота столба $h$, плотность жидкости $\rho $, тогда вес ($P$) этого столба равен:

\[P=\rho gSh\ \left(2\right). \]

В соответствии с (1) давление на основание столба жидкости составит величину:

\[p=\frac{P}{S}=\rho gh\left(3\right).\]

Формула (3) указывает, что давление столба несжимаемой жидкости на дно сосуда зависит от высоты и плотности жидкости. В общем случае плотность зависит от температуры жидкости. Давление, которое вычисляется при помощи формулы (3) называют гидростатическим давлением/

Определение

И так, гидростатическим давлением называют давление столба жидкости, находящейся в состоянии равновесия, над некоторым условно выбранным уровнем при действии силы тяжести. Гидростатическое давление определяется по формуле (3).

Давление внутри жидкости ($p$) на глубине $h$, будет складываться из давления атмосферы ($p_0$) и гидростатического давления:

\[p=p_0+\rho gh\left(4\right).\]

Единицей измерения гидростатического давления в Международной системе единиц (СИ) является паскаль (Па):

\[\left[p\right]=Па=\frac{кг}{с^2\cdot м}.

Закон Архимеда

В соответствии с формулой (3) давление, оказываемое на нижние слои жидкости больше, чем на верхние. Из-за этого тело, погруженное в жидкость, испытывает действие выталкивающей силы. Величину выталкивающей силы определяет закон Архимеда: На тело, находящееся в жидкости (газе) действует выталкивающая сила, которая равна весу жидкости (газа) вытесненной телом. Эта сила называется силой Архимеда ($F_A$):

\[F_A=\rho gV\ \left(4\right),\]

где $V$ — объем тела; $\rho $ — плотность жидкости; $g$ — ускорение свободного падения. Сила Архимеда направлена вверх.

Примеры задач с гидростатическим давлением

Пример 1

Задание. В чем состоит суть гидростатического парадокса?

Решение. Гидростатическим парадоксом называют явление, при котором сила весового давления жидкости, находящейся в сосуде отличается от веса находящейся там жидкости.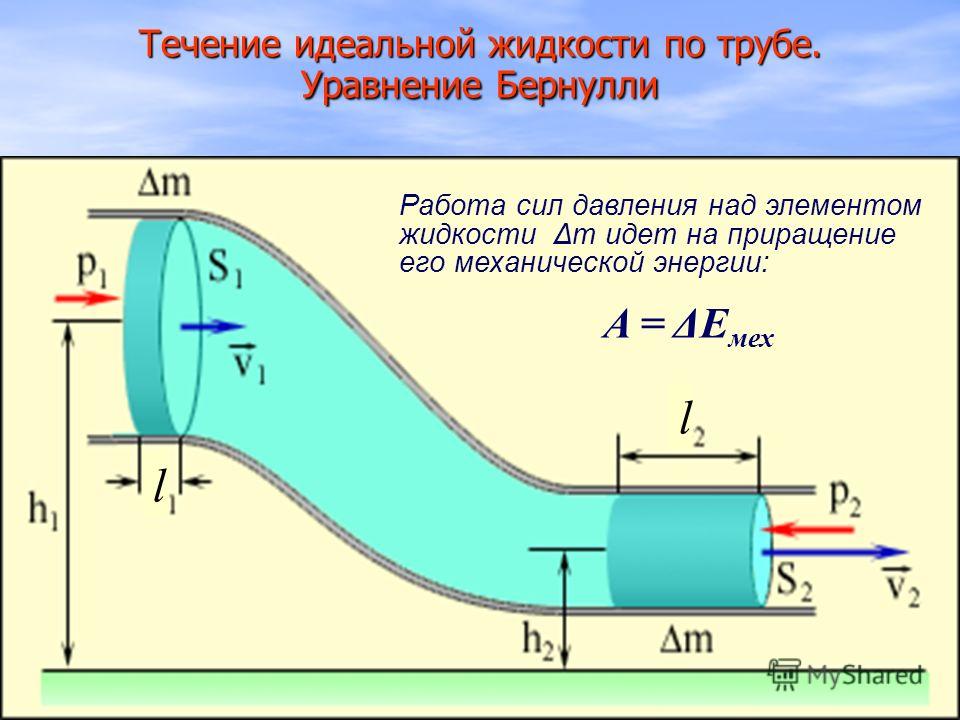 Сила давления жидкости на дно емкости равняется весу жидкости только в том случае, если сосуд имеет форму цилиндра. При такой конфигурации емкости стенки являются вертикальными, силы давления стенок на жидкость (соответственно, жидкости на стенки) направлены горизонтально, вертикальной составляющей они не имеют (рис.1).

Если сосуд имеет вверху поперечное сечение больше, чем сечение дна, то сила давления на дно меньше, чем вес жидкости. И наоборот, если сосуд с жидкостью имеет сужающееся вверху горло, то сила давления на дно сосуда больше, чем вес жидкости. Причиной возникновения гидростатического парадокса является то, что жидкость оказывает давление не только на дно сосуда, но давит и на его стенки. При этом давление на стенки сосуда, расположенные не перпендикулярно основанию имеют вертикальную составляющую. При этом в сосуде, который расширяется к верху, эта составляющая направлена вверх, а в сосуде, уменьшающем свое сечение к верху, вертикальная составляющая давления направлена вниз. 3}$.

Вычислим это давление:

\[p=1000\cdot 9,8\cdot 0,5\approx 5000\ (Па)\]

Ответ. $p\approx 5000$ Па

Читать дальше: движение по окружности.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Давление

Давление неподвижной жидкости зависит только от глубины жидкости, плотности жидкости и ускорения свободного падения.

Давление в статической жидкости зависит от веса жидкости и определяется выражением

P _{статическая жидкость} = ρgh где

ρ = м/В = плотность жидкости
g = ускорение свободного падения
h = глубина жидкости

Давление от веса столба жидкости площадью А и высотой h равно

Самое замечательное в этом выражении то, что оно включает ли не . Давление жидкости на заданной глубине не зависит от общей массы или общего объема жидкость. Приведенное выше выражение давления легко увидеть для прямая, беспрепятственная колонка, но не очевидная для показаны случаи различной геометрии.

Из-за простоты визуализации высоты столба известной жидкости стало общепринятой практикой указывать все виды давления в единицах высоты столба, таких как мм рт. с точки зрения высоты столба жидкости.

Расчет

Индекс

Расчет давления жидкости

Концепции давления

Гиперфизика***** Механика ***** Жидкости

R Ступица

Обсуждение

Высота столба жидкости в соотношении

часто используется для измерения давления.

После ввода соответствующих данных любое из выделенных ниже значений можно рассчитать, щелкнув по нему.

Перепад давления = плотность x g x высота 9м

ч = фут
тогда разница давлений
ΔP = кПа
ΔP = фунт/дюйм ²
ΔP = мм рт. ст. = дюймы рт. ст.
ΔP = атмосфер
ΔP = дюймы водяного столба = см водяного столба

Обратите внимание, что это статическое давление жидкости зависит только от плотности и глубины; он не зависит от общей массы, веса, объема и т. д. жидкости.

Индекс

обсуждение давления жидкости

Концепции давления

Гиперфизика***** Механика ***** Жидкости

R Ступица

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 18483

Том Вайдеман
Калифорнийский университет в Дэвисе

Давление в статических жидкостях

Жидкость представляет собой совокупность веществ, не являющихся твердыми. То есть частицы, из которых состоит вещество, не связаны прочно друг с другом в неподвижной решетке. Сюда входят жидкое, газообразное и даже плазменное состояния вещества. На самом деле нам нужно будет до некоторой степени ограничить свойства исследуемых нами жидкостей, чтобы мы могли получить некоторые приблизительные результаты, но полезность приложений этих моделей нельзя переоценить.

Ключевым свойством всех жидкостей является давление. Мы подробно обсуждали это в контексте газов, находящихся в термодинамическом равновесии, но в контексте жидкостей нам необходимо ослабить ограничения, которые мы ранее наложили на эту величину. Основное отличие состоит в том, что в отличие от газов в состоянии равновесия, где мы предполагали, что давление является переменной состояния, одинаковой в каждом кубическом сантиметре объема газа в состоянии равновесия, теперь мы позволим давлению изменяться от одного положения к другому. внутри жидкости. [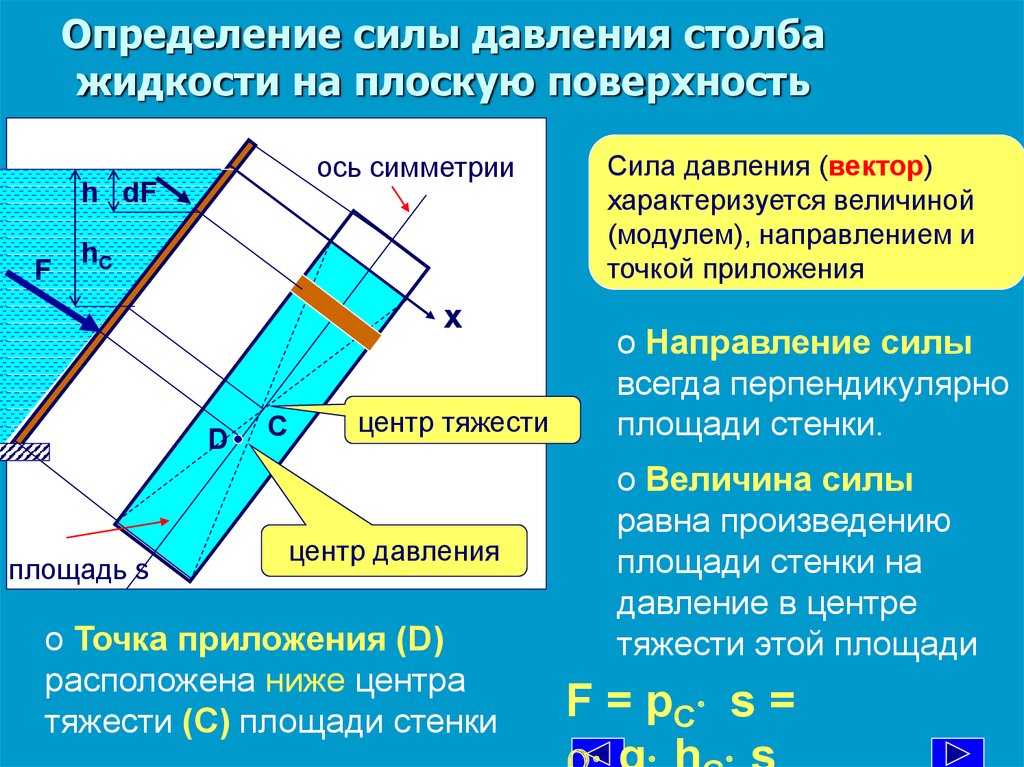

По правде говоря, наличие давления, которое изменяется в зависимости от положения внутри газа, также находится в сфере термодинамики, хотя мы не углублялись в предмет достаточно глубоко, чтобы обсуждать его. ]

Рассмотрим сосуд с жидкостью в гравитационном поле. Если мы нарисуем диаграмму свободного тела для небольшого участка этой жидкости (и исключим горизонтальные силы), то на ум приходят три силы: сила тяжести на этом участке, величина, которую жидкость над этим участком давит на него. , и количество жидкости, находящейся под этой секцией, давит на нее. Эта диаграмма на самом деле ничем не отличается от той, которую мы нарисовали бы для книги в середине стопки книг.

Рисунок 7.1.1 – Диаграмма свободного тела для сечения жидкости

Вопрос в том, как именно одна область жидкости воздействует на другую? По правде говоря, это не так. Частицы в одной области все время меняются местами с частицами в другой области. Кроме того, как мы знаем, если эта жидкость является идеальным газом, то частицы даже не взаимодействуют друг с другом. Однако если мы поместим мембрану между двумя областями, то частицы будут отражаться от мембраны дало бы силу, и результирующая физика была бы такой же — сегмент жидкости не ускоряется ни вверх, ни вниз. Поэтому мы придерживаемся мнения, что, хотя с течением времени это на самом деле не те же самые частицы, заключенные в малый объем, они ведут себя точно так же, как если бы мы могли каким-то образом ограничить их этим объемом, и наш силовой анализ верен.

Как мы впервые обсуждали в разделе 5.5, мы можем выразить эту силу отражения частиц от поверхности в терминах свойства жидкости, которое мы называем давлением. Таким образом, силы от жидкости сверху и снизу равны давлениям жидкости сверху и снизу, умноженным на площади поперечного сечения, а нулевая результирующая сила от FBD дает:

\[\слева. \begin{array}{l} F_{жидкость\;выше}=P_{выше} A \\ F_{жидкость\;ниже}=P_{ниже} A \end{массив} \right\} \;\;\ ; \Правая стрелка \;\;\; P_{ниже}A=P_{выше}A+mg\]

Как мы можем легко видеть, давление меняется в зависимости от положения в жидкости (а именно, на разной высоте) в присутствии гравитации, даже если жидкость находится в равновесие. Возможно, читатель недоумевает, как нам удалось проигнорировать этот эффект при изучении термодинамики.

3\нечисло\] 95 Па\), этой разницей легко пренебречь.

Учитывая, что нам нужны очень большие перепады высот, чтобы начать видеть значительные перепады давления в газах, с этого момента мы будем в основном иметь дело с жидкими жидкостями. Что еще более важно, рассмотрение только жидкостей устраняет еще одну неприятную сложность, которая существует для газов — жидкости в значительной степени несжимаемы . Это означает, что нам не нужно беспокоиться о влиянии повышенного давления на массовую плотность жидкости — важную величину, как мы увидим дальше.

Закон Паскаля

Мы можем переставить вещи в уравнении 7.1.1 так, чтобы разность давлений между двумя высотами в жидкости была связана с массовой плотностью $(\rho$, масса на единицу объема) жидкости :

\[P_{внизу}=P_{вверху} + \dfrac{mg\Delta y}{A\Delta y} =P_{вверху} + \dfrac{mg\Delta y}{V} = P_{вверху } + \rho g\Delta y\]

В этом результате хорошо то, что он напрямую сравнивает два давления и не зависит от выбора конкретного диска жидкости для нашей диаграммы свободного тела. Это означает, что если мы выберем диск с меньшей площадью поперечного сечения (но с той же толщиной), мы обнаружим ту же разницу в давлении. Другими словами, получается, что перепад давления на двух глубинах зависит только от плотности жидкости и разницы высот между двумя глубинами .

Насколько обоснован этот вывод? Например, предположим, что у нас есть жидкость, находящаяся в контейнере, подобном показанному на рисунке ниже. Одинакова ли разница давлений между двумя указанными высотами с обеих сторон контейнера?

Рисунок 7.1.2 – Сравнение давлений в различных частях сплошной жидкости

Ну, естественно, один и тот же анализ применим к обеим сторонам этого контейнера, поэтому разница давления одинакова с обеих сторон, но являются ли они одинаковыми двумя давлениями с обеих сторон? Здесь нам нужно сослаться на принцип, что давление не имеет направления. То есть каким бы ни было давление в нижней части $\Delta y$, это приводит к силе, толкающей вверх участок жидкости, это также приводит к силе, толкающей сегмент жидкости в сторону рассматриваемой позиции. Этот боковой сегмент статичен, как и остальная часть жидкости, поэтому давление с обеих сторон должно быть одинаковым, а это означает, что давление одинаково везде вдоль нижней пунктирной линии.

Мы уже пришли к выводу, что разница давлений между двумя пунктирными линиями одинакова в обоих столбцах жидкости, поэтому, поскольку давления в обоих столбцах в нижней строке одинаковы, они одинаковы и в верхней строке. Таким образом, мы делаем вывод Закон Паскаля :

Давления, измеренные во всех точках на одной высоте в непрерывной статической жидкости, равны.

Предупреждение

Важно отметить все квалификаторы в законе Паскаля. Кроме того, что жидкость должна быть на одинаковой высоте, она должна быть статична — позже мы получим немного более сложный результат, когда жидкость движется. Кроме того, жидкость должна быть непрерывной — если твердая преграда полностью отсекает один участок от другого, то требование одинаковости давления по горизонтали больше не выполняется. 2}\), легко приблизительно вычислить, насколько быстро давление растет с глубиной под вода – давление увеличивается на одну атмосферу с каждыми $10 м$ добавленной глубины.

Соленая вода в океанах немного плотнее пресной, поэтому давление повышается несколько быстрее, и все сертифицированные дайверы, использующие английскую систему единиц, знают, что давление в одной атмосфере увеличивается на каждую 33 фута дополнительной глубины. В самой глубокой точке океана это составляет почти 1100 атмосфер!

Верхняя поверхность жидкости может просто подвергаться воздействию атмосферы, и в этом случае $P_o$ просто $101 кПа$ (на уровне моря). Но жидкость также может быть ограничена поршнем, что приводит к интересному применению под названием 9.0173 гидравлический подъемник . Идея состоит в том, чтобы ограничить жидкость поршнями разной площади на противоположных концах сплошной жидкости, как показано на следующем рисунке.

Рисунок 7. 1.3 – Уравновешивающие силы на гидравлическом подъемнике одинаково на обеих поверхностях. Однако силы , действующие со стороны жидкости на два поршня, неодинаковы, потому что площади не равны. При одинаковом давлении на обоих концах жидкость оказывает большее усилие на поршень с большей площадью, что означает, что больший вес на большем поршне уравновешивается меньшим весом на другом поршне. Это позволяет получить механическое преимущество при подъеме тяжелого веса с гораздо меньшей силой, чем вес, определяемый соотношением площадей поршня:

\[P_1 = P_2 \;\;\;\Стрелка вправо\;\;\; \dfrac{F_1}{A_1}=\dfrac{F_2}{A_2}\;\;\;\Rightarrow\;\;\; \dfrac{F_1}{F_2}=\dfrac{A_1}{A_2}\]

Манометры

Закон Паскаля также позволяет измерять неизвестные давления путем сравнения их с известными значениями. Типовое устройство такого типа называется манометром . Существует множество специализированных устройств, предназначенных для измерения конкретных давлений, таких как барометр

(который измеряет атмосферное давление) и тонометр (который измеряет артериальное давление).
Простейшие конструкции манометров предусматривают помещение одного конца непрерывной замкнутой жидкости в область, в которой должно быть измерено давление, а другого конца в вакуум (т. е. область, где давление фактически равно нулю), а затем измерение разность высот двух столбов жидкости и использовать известную плотность жидкости для вычисления разности давлений. Например, вот простой барометр:
9Рис. 7.1.4. Простой барометр Этого легче всего добиться, наполнив трубку жидкостью, закрыв открытый конец, перевернув его в трубке, а затем открыв открытый конец так, чтобы жидкость вытекала до тех пор, пока не будет достигнуто равновесие. [ Технически это не приводит к фактическому вакууму, так как частицы в жидкости покидают поверхность и превращаются в пар, чтобы заполнить эту область, но это давление пара очень мало по сравнению с атмосферным давлением (менее 4% от атмосферного давления). при $300К$). ]
Применяя закон Паскаля, давление атмосферы на открытой поверхности такое же, как внутри колонны на той же высоте, и применяя наше уравнение для давления на глубине, мы имеем:
\[P_{atm}= P_o+\rho g d = \rho g d \]
Таким образом, мы можем измерить давление атмосферы, измерив высоту столба жидкости и зная ее плотность. Обратите внимание, что это означает, что существует максимальная высота, на которую мы можем поднять этот столбец, опустошив пространство над ним, и это указывает на важное распространенное заблуждение. Принято считать, что «всасывание» — это сила притяжения: чем сильнее насос может всасывать, тем больше он может «всасывать» жидкости. Здесь мы видим, что все «всасывание» делает удалить толкающую силу из-за одного источника давления, позволяя силе, возникающей из-за давления в другом месте, действовать неуравновешенно.
Подставив плотность воды и атмосферное давление на уровне моря, мы находим, что максимальное расстояние, которое может удержать столб воды с помощью вакуума, составляет чуть более $10 м$. Если мы хотим откачать воду из колодца (или на более высокий этаж здания), мы не можем «набрать ее», создав над ней вакуум с большей глубины. Поэтому подход, который используется вместо этого, состоит в том, чтобы накачать нижний столб воды для повышения ее давления. Единственным пределом глубины, с которой может быть извлечена вода в этом случае, является мощность двигателя, приводящего в действие насос.
Предполагая, что мы работаем с давлением, близким к атмосфере, использование воды дает довольно высокий манометр! Способ уменьшить размер этой колонки — использовать более плотную жидкость. Вещество, которое при комнатной температуре является жидкостью и имеет наибольшую плотность, — это ртуть, и много лет назад ее использование было настолько повсеместным, что на ее основе была основана единица измерения давления. Получается, что 1 атмосфера будет поддерживать только столб ртутного столба высотой $760 мм$. Таким образом, одна атмосфера давления выражается в альтернативных единицах измерения как «$760 мм рт.ст.$» или «$760 Торр$».
Вот простая конструкция простого манометра давления газа (т. е. для замкнутых газов любой разновидности, а не только атмосферы): давление измеряется таким образом, мы говорим, что измеряется абсолютное давление .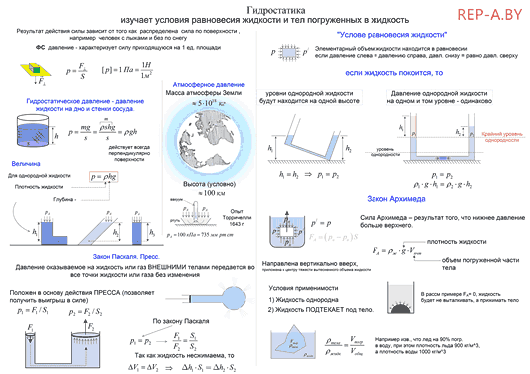 Кажется глупым добавлять лишнее лишнее слово «абсолютный», но для этого есть практическая причина. Когда дело доходит до манометров, которые измеряют давление газов в промышленных целях, оператор машины хочет знать, близко ли давление к превышению пропускной способности устройства, удерживающего газ. Что ж, любое давление, действующее снаружи устройства, помогает удержать его от взрыва, поэтому необходимо давление разница между захваченным газом и тем, что снаружи. Мы можем измерить это непосредственно с помощью устройства выше, открыв верхнюю часть трубки, чтобы там больше не было вакуума. Затем высота колонны измеряет разницу между захваченным газом и давлением окружающей среды. Это измерение давления называется манометрическим давлением . Здесь есть аналогия с температурой — абсолютная температура измеряется по шкале Кельвина, а ноль — это максимально низкая температура. Шкала Цельсия имеет ту же градацию, что и шкала Кельвина, но помещает нулевую точку в точку замерзания воды, что позволяет использовать отрицательные значения. Точно так же манометрическое давление помещает нулевую точку на давление окружающей среды (обычно атмосферное), что также допускает отрицательное значение измерения давления. 93}\) затем медленно добавляют к одной стороне трубки так, чтобы масло и вода оставались несмешанными, соприкасаясь в одной точке трубки.

Найдите расстояние от точки контакта масла и воды до центра стеклянной трубки.
Конец трубки с водой соединяется с замкнутым объемом газа неизвестного давления, а точка контакта масла и воды перемещается к центру трубки. Найдите манометрическое давление газа.
Раствор
а. Точка контакта масла и воды — это точка, в которой давление масла равно давлению воды (иначе одно вытесняло бы другое). Предполагая, что эта точка контакта находится где-то в нижней части трубы (и это должно быть, поскольку масло не может просто войти в контакт с водой, не подтолкнув ее хотя бы немного вверх с другой стороны), давление для нефти и воды каждая связана с тем, насколько высоко поднимаются их столбы с соответствующих сторон: 93}\), поэтому отношение высоты столба нефти к столбу воды равно $\frac{5}{4}$. Жидкости несжимаемы, поэтому, поскольку объемы масла и воды равны, общая длина двух столбов должна быть $36 см$, что дает нам второе уравнение, позволяющее найти высоту двух столбов:
\[\left.\begin{array}{l} h_{oil}=\frac{5}{4}h_{water} \\ h_{oil}+h_{water}=36cm \end{array} \верно\}\;\;\; \Правая стрелка \;\;\; h_{масло}=20см\;, \;\;\;h_{вода}=16см\номер\]
Если верхняя часть столба масла $4 см$ выше верхней части столба воды, точка контакта масла и воды должна быть смещена от центра на $2 см$.
б. Когда точка контакта находится в центре нижней части трубы, столбики воды и масла имеют одинаковую высоту. Опять же, давления жидкостей в точке контакта равны, а давления на вершинах колонн — нет. Манометрическое давление – это разница между давлением газа и атмосферного давления, поэтому: 92}\вправо)\влево(0,18м\вправо) = -353Па\без числа\]
Манометрическое давление отрицательное, что означает, что давление газа ниже атмосферного давления.
No related posts.