- §60. Схема соединения «звездой»
- Соединение фаз потребителей электроэнергии в звезду
- Соединение в звезду. Схема, определения
- Соединение в звезду. Схема, определения
- Соединение в звезду. Схема, определения
- Соединение в звезду. Схема, определения
- Соединение в звезду. Схема, определения
- Соединение генератора с нагрузкой
- Соединение в звезду. Фазные и линейные напряжения
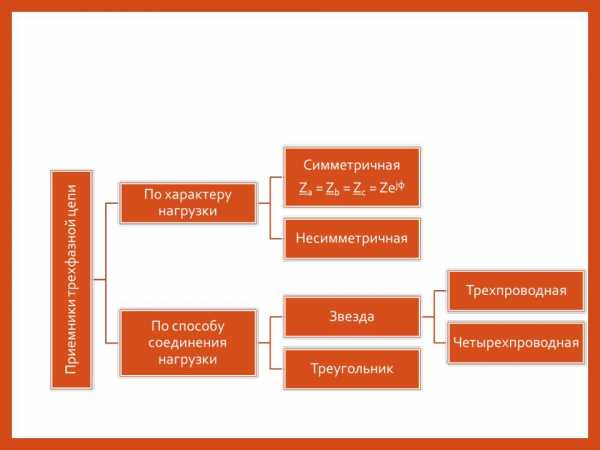
- Классификация приемников в трехфазной цепи
- Четырехпроводная звезда (звезда с нейтральным проводом)
- соединение в звезду и треугольник, особенности управления
- Расчет мощности двигателя при схеме соединения звезда-треугольник
- Схема соединения звезда — Всё о электрике в доме
- Соединение обмоток трансформатора в треугольник, звезду и зигзаг
§60. Схема соединения «звездой»
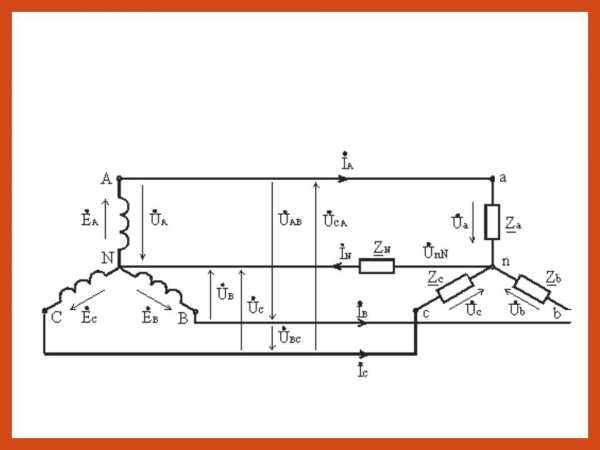
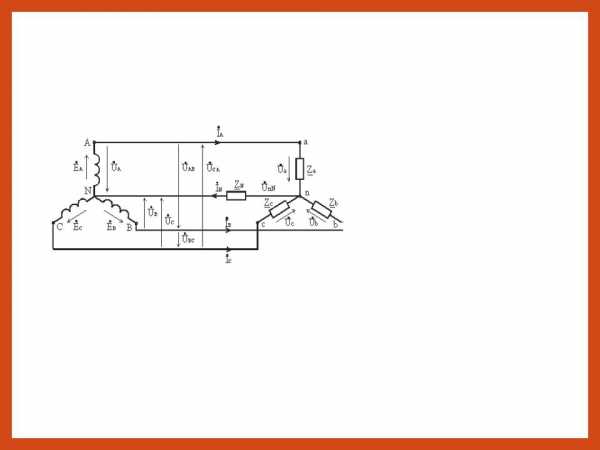
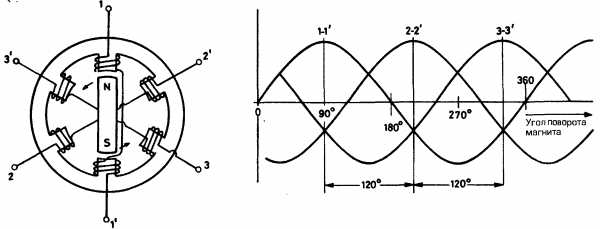
Схема «звезда с нулевым проводом». При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206). Приемники электрической энергии объединяют в три группы ZA, ZB и Zc (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным. Напряжения uА, uв и uс между началами и концами обмоток отдельных фаз источника или фаз нагрузки ZA, ZB и Zc называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках. Фазными токами i
Примем условно за положительное направление токов iA, iB и ic в фазах источника — от конца соответствующей фазы к ее началу,
Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений
Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»
в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику. Будем считать положительными напряжения uА, uB и uC в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения uАВ, uBC, uСА — если они направлены от предыдущей фазы к последующей.
Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. Iл = Iф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений. Мгновенные значения напряжений согласно второму закону Кирхгофа:
uАВ = uА – uB; uBC = uB – uС; uСА = uС – uА.
Переходя от мгновенных значений напряжений к их векторам, имеем:
?АВ = ?А – ?B
Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений. По полученным векторным уравнениям можно построить векторную диаграмму (рис. 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений ?AB, ?ВС, ?СА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений ?А, ?В, ?С. В равнобедренных треугольниках АОВ, ВОС и СОА основание равно Uл две другие стороны — Uф и острый угол между этими сторонами и основанием составляет 30°. Следовательно,
Uл = 2Uф cos 30° = 2U ?3 / 2 = ?3 Uф
Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного
в ?З раз. Величина ?З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+ic.
Переходя от мгновенных значений токов к их векторам, имеем:
?0=?A+?B+?C.
Векторы токов ?А, ?В и ?С сдвинуты относительно векторов соответствующих напряжений ?A, ?B, ?С на углы ?A, ?B, ?C (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу. На этой же диаграмме показано сложение векторов ?А
Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз
IA, 1В и IC в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.
В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное Uл (при подключении к двум линейным проводам) и фазное UФ (при подключении к нулевому и одному из линейных проводов).
Схема «звезда без нулевого провода». При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (RA =RB = RC и Х A=ХВ=ХС), фазные токи iA, iB и iC будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи iA, iB, iC будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i0 в нулевом проводе в любой момент времени равен нулю (рис. 208,б).
Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209). Такая схема называется «звезда без нулевого провода». При трехпровод-ной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210). Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207). Такими же будут и соотношения между фазными и линейными токами и напряжениями:
Iл = IФ и Uл = ?3 UФ
Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы. При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.
Рис. 209. Схема «звезда без нулевого провода»
Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз. Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом. При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в ?З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.
Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)
electrono.ru
Соединение фаз потребителей электроэнергии в звезду
Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:
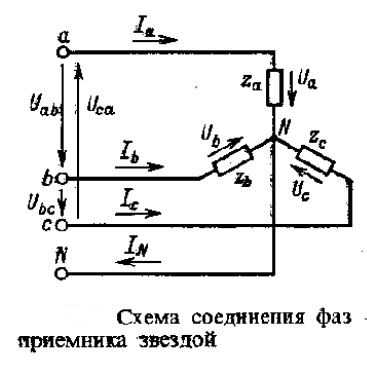
Из схемы видно, что фазные напряжения приемника Ua, Ub, Uc не равны линейным напряжениям Uab, Ubc, Uca. Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:
Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.
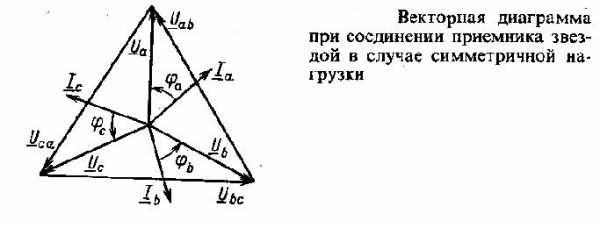
Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:
Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.
Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.
Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:
Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:
Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода IN. В случае отсутствия нейтрального провода справедливо будет выражение:
Симметричная нагрузка при соединении приемников звездой
Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:
Условие симметричности также может быть выражено через комплексные сопротивления Za = Zb = Zc.
Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.
В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:
Так как в четырехпроводной цепи Ua = Ub = Uc = Uл / , то при симметричной нагрузке:
Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше. Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен IN = Ia + Ib + Ic = 0.
Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.
Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.
Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:
Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:
Пример
К трехфазной электрической цепи с линейным напряжением Uл = Uab = Ubc = Uca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление rф = 10 Ом и индуктивное сопротивление хф = 10 Ом, которые соединены последовательно. Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.
Решение
Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.
Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:
Активная, реактивная и полная мощности приемника, а также любой фазы будут равны:
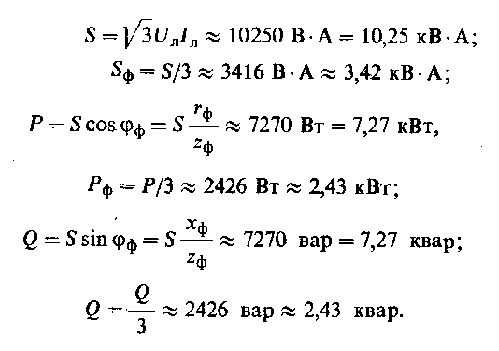
Векторная диаграмма для данной системы приводилась выше.
Несимметричная нагрузка при соединении приемников звездой
Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: ra = rb = rc, xa = xb ≠ xc. В общем случае считают, что несимметричная нагрузка возникает при отключении одной из фаз.
Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.
В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.
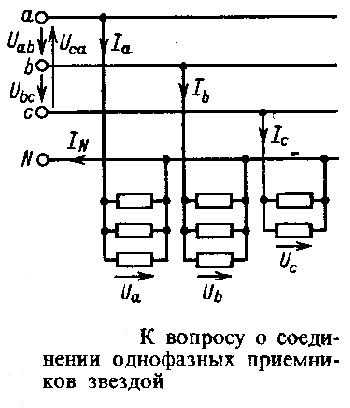
Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.
Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.
Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:
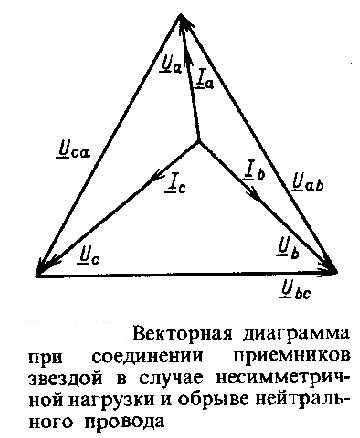
Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:
Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.
Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).
Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:
Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.
Пример
В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы Uном = 127 В, Рном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.
Решение
Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:
Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:
Для определения тока в нейтральном проводе IN решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:
Где комплексные значения фазных сопротивлений будут равны Za = 8,05 Ом, Zb = 16,1 Ом, Zс = 32,2 Ом.
Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:
elenergi.ru
Соединение в звезду. Схема, определения
Соединение в звезду. Схема, определения
провода, идущие от источника к нагрузке называют линейными проводами
провод, соединяющий нейтральные
точки источника N и приемника N’
13
называют нейтральным (нулевым)
Соединение в звезду. Схема, определения
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями
(UAB, UBC, UCA)
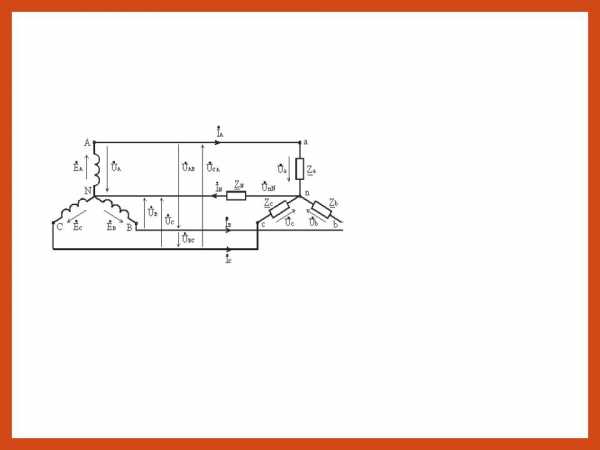
Соединение в звезду. Схема, определения
Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются
фазными напряжениями (UA, UB, UC у
источника; Ua, Ub, Uc у приемника).
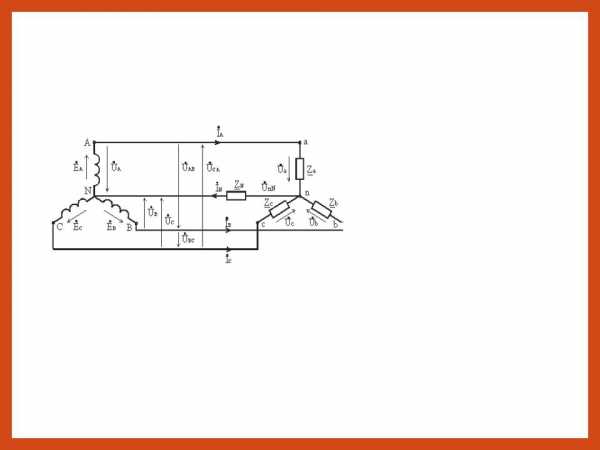
Соединение в звезду. Схема, определения
токи в фазах приемника или источника называют фазными токами,
токи в линейных проводах называются линейными токами

Соединение генератора с нагрузкой
Трехфазный генератор соединяется с нагрузкой четырьмя линейными проводами либо тремя.
Общие точки генератора О и потребителя О’ называют нулевыми (нейтральными).
Провод 00′ — нулевой (О) или нейтральный (N) провод.
Соединение в звезду. Фазные и линейные напряжения
Классификация приемников в трехфазной цепи

Четырехпроводная звезда (звезда с нейтральным проводом)
В
четырехпроводной трехфазной цепи возможно дать потребителю два различных напряжения — линейное или фазное.
studfiles.net
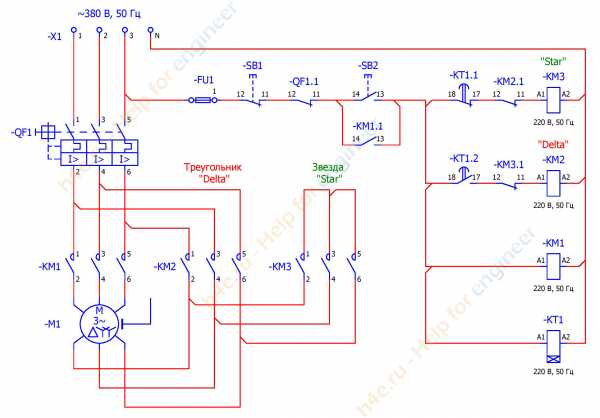
соединение в звезду и треугольник, особенности управления
 Асинхронный 3-фазный двигатель представляет собой полезное устройство, которое применяется во многих сферах деятельности человека, начиная от бытовой жизни, заканчивая промышленностью. В различных шлифовальных машинах, на конвейерах, станочных агрегатах, системах вентиляции промышленного типа и другое. Электродвигатель имеет 3 вывода, поэтому может быть выполнено соединение звезда и треугольник к трехфазной сети переменного тока или трансформатору.
Асинхронный 3-фазный двигатель представляет собой полезное устройство, которое применяется во многих сферах деятельности человека, начиная от бытовой жизни, заканчивая промышленностью. В различных шлифовальных машинах, на конвейерах, станочных агрегатах, системах вентиляции промышленного типа и другое. Электродвигатель имеет 3 вывода, поэтому может быть выполнено соединение звезда и треугольник к трехфазной сети переменного тока или трансформатору.
Конструкция двигателя
Обмотки располагаются на статоре, а ротор выполнен короткозамкнутым в виде беличьего колеса: алюминиевые или медные кольца по торцам соединены между собой параллельными перемычками. Статор намотан специальным образом с определенным количеством полюсов, что зависит от параметров мощности и питающей сети. Бытовые вентиляторы имеют всего 2 полюса, промышленные тяговые электродвигатели по 8 и более.
Преимущества использования асинхронных электродвигателей со схемой включения звезда или треугольник очевидны и заключаются в следующем:
 Повышенная выносливость – даже при превышающих номинальные нагрузки, двигатель будет работать без сбоев.
Повышенная выносливость – даже при превышающих номинальные нагрузки, двигатель будет работать без сбоев.- Возможность работы в агрессивных средах. За счет отсутствия скользящих контактов в двигателе не может возникать искрения, а, следовательно, и проблем с ним связанных. При качественной изоляции электродвигатель может работать во влажной обстановке.
- Высокая продолжительность работы на высоких нагрузках. Двигатель способен на протяжении длительного промежутка времени работать под значительной нагрузкой на валу без перегрева и сгорания обмоток.
Способы подключения к сети
Сейчас попытаемся разобраться, что такое звезда и треугольник, в чем разница между ними. Асинхронный 3-фазный электродвигатель имеет 3 обмотки, которые, соединены определенным образом. Они могут подключаться как к сети 380 В, так и к переменному напряжению 220 В. Поэтому двигатель можно считать универсальным, но его качество работы напрямую зависит от способа подключения к сети или отдельному питающему трансформатору.
Например, в режиме разгона, когда тот подключается последовательно в цепь двигателя для снижения пускового напряжения. По такому принципу действует частотный преобразователь, регулируя начальный момент посредством изменения частоты, не допуская превышение потребления мощности более, чем на 10-20%. В обычном режиме запуска асинхронный двигатель потребляет до 600% от номинала, что может стать причиной автоматического выключения вводных автоматов.
Обычно при открытии клеммной коробки на моторе можно увидеть 3 вывода и дополнительную скрутку. Это говорит о типе подключения обмоток, которым в этом случае является звезда. Раскрутив общее соединение, вы получите 6 выводов, являющиеся концами и началами каждой из 3-х обмоток. Поэтому появляется возможность выполнить подключение по схеме треугольника.
Иногда в зависимости от способа управления и алгоритма образования управляющего напряжения в приводе требуется переключение со звезды на треугольник. И делать это можно в автоматическом режиме, например, при разгоне, чтобы электродвигатель сразу обеспечивал высокий крутящий момент. Это чаще всего используется в частотных системах управления, где требуется более жестко регулировать динамику двигателя и контролировать скорость вращения.
Когда и какую схему лучше использовать, зависит от требований, но каждый из способов имеет свои особенности. Например, они заключаются в развиваемой и потребляемой мощности, разнице линейных и фазных напряжений, а, соответственно, динамических и электрических показателях.
Основные формулы
Перед тем, как ознакомиться с особенностями, как соединить электродвигатель звезда-треугольник, стоит вспомнить основные формулы расчета мощности и соотношения напряжений и токов между ними. При расчете устройств с питанием от сети переменного напряжения или отдельного трансформатора используют понятие полная мощность. Она обозначается большой буквой S и находится как произведение действующего значения напряжения и тока U × I . Также, есть возможность расчета, исходя из ЭДС, при котором S = E × I .
Кроме полной, также различают:
- активную;
- реактивную мощность.
В первом случае она обозначается буквой P = E × I × cos φ или P = U × I × cos φ . Во втором случае Q = E × I × sin φ или Q = U × I × sin φ . Где в формулах E – электродвижущая сила, I – ток, φ – угол между напряжением и током, создаваемым сдвигом фаз в обмотках.
Если обмотки двигателя одинаковы между собой по всем параметрам, то все виды мощностей определяются как произведение тока и напряжения, умноженного на 3.
Соединение двигателя в звезду
Наиболее часто используемым является именно соединение в звезду, потому что в таком режиме обеспечивается необходимая мощность и гарантируется хороший крутящий момент на валу. Но стоит понимать, что недогруженный двигатель в 3-фазной сети будет потреблять лишнюю мощность, поэтому лучше использовать менее мощный мотор или регулировать частоту питающего трансформатора или привода, в зависимости от источника напряжения.
А чтобы определить электрические параметры сети, необходимо использовать соотношение √3. Первоначально следует отметить, что при соединении в звезду линейные и фазные токи одинаковы, а напряжение определяется по формуле U = √3 × U ф. Найти из нее фазное напряжение несложно. Соответственно, мощности определяются с учетом этого соотношения:
S = √3 × U × I
Следует помнить, что если на трансформаторе кроме 3-х фаз имеется также и 4-ый вывод со средней точки, то он должен быть подключен к электродвигателю .
Особенности применения подключения в звезду
На предприятиях, да и во всех остальных сферах, основным типом соединения 3-фазных двигателей является именно звезда, а питаются они от общей подстанции или отдельного трансформатора, обеспечивая, таким образом, гальваническую развязку. Схема включения его обмоток особо не влияет на работу двигателя. Если они соединены в треугольник, то напряжение на выходе составит в 1.73 раза меньше и подключив двигатель к его обмоткам по схеме треугольника можно добиться примерного того же момента, что и в обычном режиме.
Фазные токи при соединении по схеме в звезду равны, а напряжение, подводимое к каждой из обмоток, в 1.73 раза меньше. Двигатель набирает свой момент за более длительное время, но при этом не перегревается. В таком режиме используются моторы на вентиляторах, помпах, шнеках и прочих агрегатах. Но, если необходимо увеличить момент и тяговую способность, то его кратковременно переключают в треугольник.
В таком случае к обмоткам подводится полное напряжение сети, а, следовательно, и увеличенный ток, что приводит к выделению дополнительной мощности на валу и нагреву мотора. Режим переключения на треугольник применяют для ускоренного запуска двигателя, а потому возвращают схему соединения в исходное состояние. Длительная работа в таком режиме приведет к скорому выходу из строя.
instrument.guru
Расчет мощности двигателя при схеме соединения звезда-треугольник
В этой статье я хотел бы рассказать как изменяется мощность двигателя при схеме соединения обмоток звезда – треугольник и наоборот.
В связи со спецификой своей работы я сталкиваюсь с ремонтов различных асинхронных двигателей и в большинстве случаев выход из строя двигателя происходит при неправильном переключении обмоток двигателя, так как люди не понимают, как изменяется мощность двигателя при переключении с треугольника на звезду и обратно, и как это может отразится на работоспособности самого двигателя.
Определение мощности при схеме соединения звезда
Известно [Л1. с. 34], что при соединении в звезду линейные токи Iл и фазные токи Iф равны между собой, при этом между фазным Uф и линейным напряжением Uл существует соотношение, где Uл = √3*Uф , в результате Uф = Uл/√3.
Исходя из этого, полная мощность определяется через линейные величины:
Определение мощности при схеме соединения треугольник
При схеме соединения в треугольник, фазные и линейные напряжения равны между собой Uл = Uф, при этом между токами существует соотношение: Iл = √3*Iф, в результате Iф = Iл/√3.
Исходя из этого, полная мощность определяется, как:
Для определения активной и реактивной мощности используются формулы:
Из-за того что формулы для схемы соединения звезды и треугольника имеют одинаковый вид, у мало опытных инженеров происходят недоразумения, будто вид соединения безразличен и ни на что не влияет.
Рассмотрим на примере, на сколько ошибочные данные утверждения. В данном примере будем рассматривать электродвигатель типа АИР90L2, который имеет две схемы подключения ∆/Y, технические характеристики двигателя:
- коэффициент мощности cosφ = 0,84;
- коэффициент полезного действия, η = 78,5%;
Определяем ток двигателя при напряжении 380 В и схеме соединения треугольник, мощность при таком соединении составляет 3 кВт:
Теперь соединим обмотки двигателя в звезду. В результате на фазную обмотку пришлось на 1,73 раза более низкое напряжение Uф = Uл/√3, соответственно и ток уменьшился в 1,73 раза, но так как при соединении в треугольник Uл = Uф, а линейный ток был в 1,73 раза больше фазного Iл = √3*Iф, то получается, что при соединении в звезду, мощность уменьшится в √3*√3 = 3 раза, соответственно и ток уменьшиться в 3 раза.
Из всего выше изложенного можно сделать, следующие выводы:
1. При переключении двигателя со звезды на треугольник, мощность двигателя увеличивается в 3 раза и наоборот. Использовать данные переключения, можно если схемы подключения двигателя позволяет выполнять переключения ∆/Y, в противном случае, двигатель может сгореть, когда Вы будете выполнять переключение со звезды на треугольник.
2. Как Вы уже поняли, используя схему переключения обмоток двигателя со звезды на треугольник, мы уменьшаем пусковые токи при пуске двигателя на пониженном напряжении, а затем его повышаем до номинального. Когда обмотки двигателя соединены в звезду, к каждой из них подводиться напряжение меньше номинального в 1,73 раза. В процессе пуска, двигатель увеличивает скорость вращения и ток снижается. В это время происходит переключение на треугольник.
Обращаю Ваше внимание, что двигатели, которые недогружены, работают с очень низким cosφ. Поэтому рекомендуется заменить недогруженный двигатель, на двигатель меньшей мощности. Если же у недогруженного двигателя, запас мощности велик, то cosφ можно поднять путем переключения обмоток с треугольника на звезду без риска перегреть двигатель.
Как мы видим ничего сложного нету в определении мощности при схеме звезда и треугольник.
Литература:
1. Звезда и треугольник. Е.А. Каминский, 1961 г.
Поделиться в социальных сетях
raschet.info
Схема соединения звезда — Всё о электрике в доме
Подключение звезда и треугольник – в чем разница?
Обмотки генераторов, трансформаторов, электродвигателей и других электрических приемников при их подключении к трехфазной сети соединяются двумя способами: звездой или треугольником. Эти схемы подключения сильно отличаются друг от друга и несут на себе разные токовые нагрузки. Поэтому есть необходимость разобраться в вопросе, как производится подключение звезда и треугольник – в чем разница?

Что собой представляют схемы
Подключение обмоток звездой – это их соединение в одной точке, которая носит название нулевая точка или нейтральная. Она обозначается буквой «О».
Схема подключения треугольником – это последовательное соединение концов рабочих обмоток, в которых начало одной обмотки соединяется с концом другой.
Разница очевидна. Но какую цель преследуют эти виды соединения, почему звезда треугольник применяются в разных электрических установках, в чем эффективность той и другой. Вопросов по данной теме возникает немало, с ними и надо разобраться.
Начнем с того, что при запуске того же электродвигателя ток, который называется пусковым, обладает высоким значением, который превышает номинальную его величину раз в шесть или восемь. Если это маломощный агрегат, то защита такую силу тока может выдержать, а если это электродвигатель большой мощности, то никакие защитные блоки не выдержат. И это вызовет обязательно «проседание» напряжения и выход из строя предохранителей или автоматических выключателей. Сам же двигатель начнет вращаться с небольшой скоростью, отличающуюся от паспортной. То есть, проблем с пусковым током немало.
Поэтому его надо просто снизить. Есть несколько для этого способов:
- установить в систему подключения электрического двигателя один из перечисленных приборов: трансформатор, дроссель, реостат;
- изменяется схема подключения обмоток ротора.
Именно второй вариант используется на производстве, как самый простой и эффективный. Просто производится преобразование схемы звезда в треугольник. То есть, во время пуска двигателя его обмотки соединяются по схеме звезда, затем как только мотор наберет обороты, переключается на треугольник. Процесс переключения звезды на треугольник производится автоматически.
Рекомендуется в электродвигателях, где используются одновременно два варианта соединения – звезда-треугольник, к соединению обмоток по схеме звезда, то есть, к их общей точке подключения, подсоединить нейтраль от сети питания. Для чего это необходимо делать? Все дело в том, что во время работы по данному варианту подсоединения появляется высокая вероятность асимметрии амплитуд разных фаз. Именно нейтраль будет компенсировать данную асимметрию, которая обычно появляется за счет того, что обмотки статора могут иметь разное индуктивное сопротивление.
Преимущества двух схем
У схемы звезда достаточно серьезные достоинства:
- плавный запуск электрического двигателя;
- номинальная его мощность будет соответствовать паспортным данным;
- двигатель будет работать нормально и при кратковременных высоких нагрузках, и при долгосрочных небольших перегрузов;
- в процессе работы корпус мотора не будет перегреваться.
Что касается схемы треугольник, то основное ее преимущество – это достижение электрическим двигателем в процессе его работы максимальной мощности. Но при этом рекомендуется строго придерживаться эксплуатационных режимов, которые расписаны в паспорте мотора. Тестирование электродвигателей, соединенных по схеме треугольник, показало, что его мощность в три раза больше, чем соединенных по схеме звезда.
Если говорить о генераторах, которые выдают ток в питающую сеть, то схемы соединения звезда и треугольник по своим техническим параметрам точно такие же. То есть, выдаваемое напряжение треугольником будет больше, правда, не в три раза, но не менее 1,73 раза. По сути, получается, что напряжение генератора при звезде, равное 220 вольт, преобразуется в 380 вольт, если провести переключение с одного варианта на другой. Но необходимо отметить, что мощность самого агрегата при этом остается неизменной, потому что все подчиняется закону Ома, в котором напряжение и сила тока находятся в обратной пропорциональности. То есть, увеличение напряжения в 1,73 раза, снижает ток точно на такую же величину.
Отсюда вывод: если в клеммной коробке генератора располагаются все шесть концов обмоток, то можно будет получить напряжение двух номиналов, отличающихся друг от друга коэффициентом 1,73.
Делаем выводы
Почему соединения треугольником и звездой сегодня присутствуют во всех современных мощных электродвигателях? Из всего вышесказанного становится понятным, что основное требование ситуации – это снизить токовую нагрузку, которая возникает в процессе пуска самого агрегата.
Если расписать формулы такого подключения, то они будут выглядеть вот так:
Uф=Uл/1,73=380/1,73=220, где Uф – напряжение на фазах, Uл – на питающей линии. Это соединение звездой.
После того, как электрический агрегат разгонится, то есть, скорость его вращения станет соответствовать паспортным данным, произойдет переход на треугольник со звезды. Отсюда фазное напряжение станет равным линейному.
Как правильно провести подключение электродвигателя звездой и треугольником
Схема подключения трехфазного электродвигателя к трехфазной сети
Как подключить трехфазный электродвигатель в сеть 220В – схемы и рекомендации
§60. Схема соединения «звездой»
Схема «звезда с нулевым проводом». При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой. или нейтралью источника (рис. 206). Приемники электрической энергии объединяют в три группы ZA. ZB и Zc (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым. или нейтральным. Напряжения uА. uв и uс между началами и концами обмоток отдельных фаз источника или фаз нагрузки ZA. ZB и Zc называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках. Фазными токами iA. iB. ic называют токи, протекающие по обмоткам источника или фазам нагрузки ZA. ZB и Zc. Напряжения uAB. uBC. uCA между линейными проводами и токи, проходящие по этим проводам, называют линейными.
Примем условно за положительное направление токов iA. iB и ic в фазах источника — от конца соответствующей фазы к ее началу,
Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений
Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»
в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику. Будем считать положительными напряжения uА. uB и uC в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения uАВ. uBC. uСА — если они направлены от предыдущей фазы к последующей.
Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным. т. е. Iл = Iф. так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений. Мгновенные значения напряжений согласно второму закону Кирхгофа:
Переходя от мгновенных значений напряжений к их векторам, имеем:
Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений. По полученным векторным уравнениям можно построить векторную диаграмму (рис. 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений ?AB. ВС. СА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений ?А. В. С. В равнобедренных треугольниках АОВ, ВОС и СОА основание равно Uл две другие стороны — Uф и острый угол между этими сторонами и основанием составляет 30°. Следовательно,
Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного в ?З раз. Величина ?З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.
В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+ic.
Переходя от мгновенных значений токов к их векторам, имеем:
?0 =?A +?B +?C .
Векторы токов ?А. В и ?С сдвинуты относительно векторов соответствующих напряжений ?A. B. С на углы ?A. B. C (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу. На этой же диаграмме показано сложение векторов ?А. В и ?C для определения вектора тока ?0. Обычно ток ?0 меньше токов
Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз
IA. 1В и IC в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.
В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное Uл (при подключении к двум линейным проводам) и фазное UФ (при подключении к нулевому и одному из линейных проводов).
Схема «звезда без нулевого провода». При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (RA =RB = RC и ХA =ХВ =ХС ), фазные токи iA. iB и iC будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи iA. iB. iC будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i0 в нулевом проводе в любой момент времени равен нулю (рис. 208,б).
Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209). Такая схема называется «звезда без нулевого провода». При трехпровод-ной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210). Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207). Такими же будут и соотношения между фазными и линейными токами и напряжениями:
Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы. При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.
Рис. 209. Схема «звезда без нулевого провода»
Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз. Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом. При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в ?З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.
Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)
Соединение в звезду. Схема, определения
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N’ называют нейтральным (нулевым) проводом.
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.
Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах – линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.
ZN – сопротивление нейтрального провода.
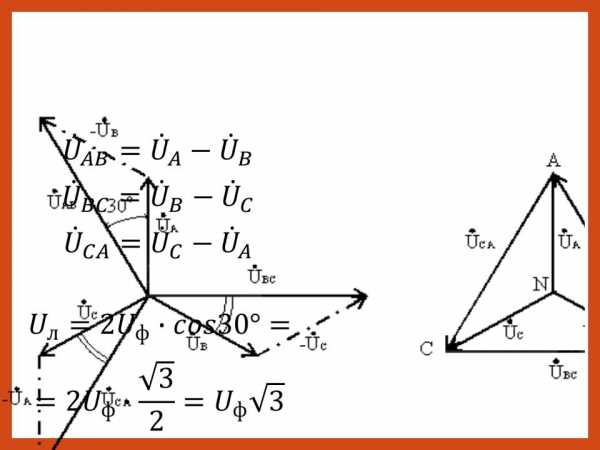
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений
На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
Из векторной диаграммы видно, что
При симметричной системе ЭДС источника линейное напряжение больше фазного
в √3 раз.
1. Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению ZA = ZB = ZC = R.
В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.
2. Нагрузка несимметричная. RA < RB = RC. но сопротивление нейтрального провода равно нулю: ZN = 0.
Фазные напряжения нагрузки и генератора одинаковы
Фазные токи определяются по формулам
Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.
На рис. 7.6 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.
3. Нагрузка несимметричная, RA < RB = RC. нейтральный провод отсутствует,
В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:
Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.
Из-за напряжения смещения нейтрали фазные напряжения нагрузки становятся неодинаковыми.
Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.
7.3. Соединение в треугольник. Схема, определения
Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.
На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно
из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.
Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.
Линейный ток равен геометрической разности соответствующих фазных токов.
На рис. 7.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.
Из векторной диаграммы видно, что
Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме «звезда». Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.
185.154.22.117 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам.
Источники: http://onlineelektrik.ru/eoborudovanie/generatori/podklyuchenie-zvezda-i-treugolnik-v-chem-raznica.html, http://electrono.ru/peremennyj-tok/60-sxema-soedineniya-zvezdoj, http://studopedia.ru/5_95473_soedinenie-v-zvezdu-shema-opredeleniya.html
electricremont.ru
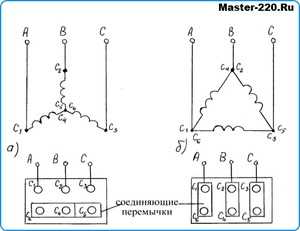
Соединение обмоток трансформатора в треугольник, звезду и зигзаг
Перед рассмотрением вопросов о группах соединений трансформаторов рассмотрим основные виды соединения обмоток силовых трансформаторов.
Соединение обмоток трансформатора в звезду
При соединении в звезду действуют следующие соотношения –
- линейные токи равны фазным,
- линейные напряжения больше фазных в √3 раз
Возможно множество вариантов соединения обмоток трансформатора в звезду, некоторые из них приведены на рисунке ниже. И, как говорится, не все из них одинаково полезны, а точнее, для разных случаев необходима разная схема соединений.
Следует отметить, что в звезду можно соединить как один трехфазный трансформатор, так и три однофазных. На рисунке обозначаются:
- А, В, С – начала обмоток высшего напряжения
- Х, Y, Z – окончания обмоток высшего напряжения
- a, b, c – начала обмоток низкого напряжения
- x, y, z – окончания обмоток низкого напряжения
Соединение обмоток трансформатора в треугольник
Соединение в треугольник так называется из-за внешнего сходства с треугольником (видно на рисунке).
При соединении в треугольник действуют следующие соотношения –
- линейные токи больше фазных в √3 раз
- линейные напряжения равны фазным
Три вторичные обмотки, при соединении в треугольник соединены последовательно, образуя тем самым замкнутую цепь. В этой цепи отсутствует ток, так-как ЭДС фаз сдвинуты на 120 градусов и их сумма в каждый момент времени равна нулю. Так же ток равен нулю при соблюдении тотчасно следующих условий – ЭДС имеют синусоидальную форму, обмотки имеют одинаковые числа витков.
Звезда и треугольник в вопросе о третьих гармониках трансформаторов
В трансформаторах схему треугольник используют кроме прочего для получения токов третьих гармоник, которые необходимы для создания синусоидальной ЭДС вторичных обмоток. Другими словами, для исключения третьей гармонической составляющей в магнитном потоке.
Чтобы ввести третьи гармоники при соединении в звезду — соединяют нейтраль звезды с нейтралью генератора, по этому пути и начинают пробегать третьи гармоники.
Соединение обмоток трансформатора в зигзаг
Соединение в зигзаг используется в случае, если на вторичных нагрузках неравномерная нагрузка. После соединения в зигзаг нагрузка распределяется более равномерно по фазам и магнитный поток трансформатора сохраняет равновесие, несмотря на неравномерную нагрузку.
Рассмотрим соединение в зигзаг-звезду трехфазного силового трансформатора. Схематично изображение приведено на рисунке.
Первичные обмотки соединяются в звезду. Далее разделяем каждую вторичную обмотку напополам. И далее соединяем, как показано на рисунке.
При соединении в зигзаг-звезду потребуется большее число витков, чем при простой звезде. Также при таком соединении возможно получение трех классов напряжения, например 380-220-127В.
Сохраните статью или поделитесь с друзьями
pomegerim.ru
