Соединение треугольником в трехфазной: Как подключить электродвигатель в схему звезда-треугольник – СамЭлектрик.ру

Соединение треугольником в трехфазной цепи при симметричной и несимметричной нагрузках

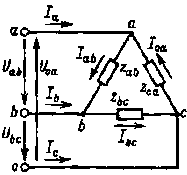
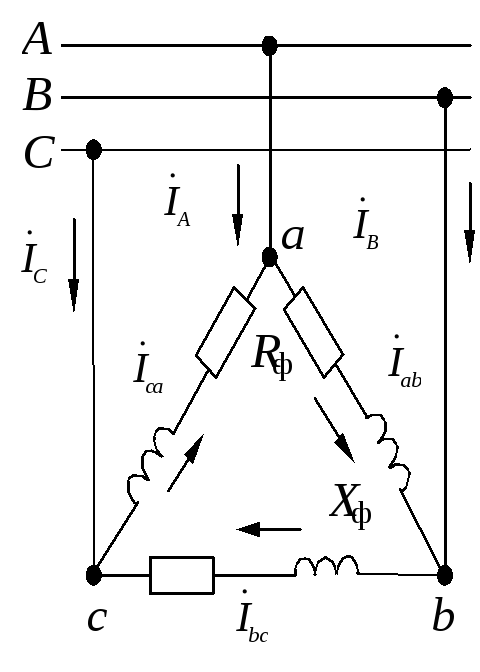
Как видно из схемы рис. 3.12, каждая фаза приемника при соединении треугольником подключена к двум линейным проводам. Поэтому независимо от значения и характера сопротивлений приемника каждое фазное напряжение равно соответствующему линейному напряжению:

Uф = Uл . (3.16)

Если не учитывать сопротивлений проводов сети, то напряжения приемника следует считать равными линейным напряжениям источника.

На основании схемы рис. 3.12 и выражения (3.16) можно сделать вывод о том, что соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника или однофазные приемники рассчитаны на напряжение, равное номинальному линейному напряжению сети.

Фазные токи Iab , Ibc и Iса в общем случае не равны линейным токам

Ia , Ib и Ic . Применяя первый закон Кирхгофа к узловым точкам а , b и с, можно получить следующие соотношения между линейными и фазными точками:

Ia = Iab — Ica , Ib = Ibc — Iab , Ic = Ica — Ibc . (3.17)

Используя указанные соотношения и имея векторы фазных токов, нетрудно построить векторы линейных токов.

Симметричная нагрузка. В отношении любой фазы справедливы все формулы, полученные ранее для однофазных цепей, например

(3.18)

Iab = Uab /zab ; φab = arcsin xab /zab ; Рab = Uab Iab cos φab = Iab2rab ; Qab = Uab Iab sin φab = Iab2xab ; Sab = Uab Iab = Iab2zab = √Pab2 + Qab2.

}

Очевидно, при симметричной нагрузке

Iab = Ibc = Ica = Iф ;
φab = φbc = φca = φф ;
Pab = Pbc = Pca = Pф ;
Qab = Qbc = Qca = Qф ;
Sab = Sbc = Sca = Sф .

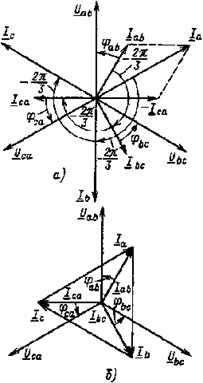
Векторная диаграмма фазных (линейных) напряжений, а также фазных токов при симметричной активно-индуктивной нагрузке приведена на рис. 3.13, а. Там же в соответствии с выражениями (3.17) построены векторы линейных токов. Следует обратить внимание на то, что при изображении векторных диаграмм в случае соединения треугольником вектор линейного напряжения Uab принято направлять вертикально вверх.

Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке существуют симметричные системы фазных и линейных токов.

Векторы линейных токов чаще изображают соединяющими векторы соответствующих фазных токов, как показано на рис. 3.13,

б. На основании векторной диаграммы рис. 3.13, б

Ia = 2Iab sin 60° = √3Iab,
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке вообще

Ia =√3Iф . (3.19)

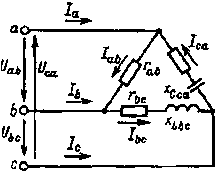
Несимметричная нагрузка. Как и при соединении звездой, в случае соединения треугольником однофазные приемники делят на три примерно равные в отношении мощности группы. Каждая группа подключается к двум проводам, между которыми имеется напряжение, отличающееся по фазе от двух других напряжений сети (рис. 3.14). В пределах каждой группы приемники соединяются параллельно.

После замены приемников каждой фазы одним приемником с эквивалентным сопротивлением и соответствующего их расположения получим схему, приведенную на рис. 3.12.

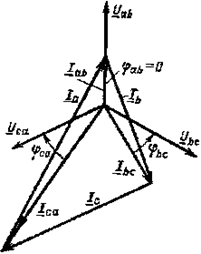
Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также фазные мощности можно определить по формулам (3.18). При несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными. Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bс — активно-индуктивная, а в фазе са — активно-емкостная (рис. 3.15), приведена на рис. 3.16. Построение векторов линейных токов произведено в соответствии с выражениями (3.17).

Для определения мощностей всех фаз следует пользоваться формулами:

P = Pab + Pbc + Pca , Q = Qab + Qbc + Qca

, (3.20)

Формулы (3.13) и (3.14), полученные ранее для симметричной нагрузки, не пригодны для определения мощностей при несимметричной нагрузке.

Если кроме фазных токов требуется определить линейные токи, задачу следует решать в комплексной форме. Для этой же цели можно воспользоваться векторной диаграммой.

При решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме фазные напряжения, а также полные сопротивления фаз. Когда это сделано, нетрудно по закону Ома определить фазные токи. Например, комплексное выражение тока Iab будет

Iab = Uab /Zab . (3.21)

Линейные токи определяются через фазные с помощью выражений (3.17).

Комплексным методом можно воспользоваться и для определения фазных мощностей. Так, мощности фазы

аb будут равны

Sab = Uab I*ab = Re Sab, (3.22)

Qab = Im Sab ; Sab = √P2ab + Q2ab .

Рассмотрим, как будут изменяться значения различных величин в электрической цепи рис. 3.15 при изменении сопротивления приемников. Например, если при xCca /rca = const увеличить вдвое сопротивление zca , то ток Ica уменьшится, а угол φca не изменится (см. рис. 3.16). Очевидно, при этом уменьшатся и токи Iа , Ic , а также мощности Рса , Qса , Sса . Токи Iаb , Ibc , Ib , углы φab , φbc , а также мощности Рab , Qab , Sab , Рbc , Qbc , Sbc останутся постоянными. При отключения фазы са сопротивление
zca = ∞, Iса = 0, токи Iаb , Ibc , Ib , а также углы φab , φbc не изменятся, а токи Iа и Ic уменьшатся

Ia = Iab , Ic = — Ibc .

23. Мощности в трехфазных цепях и способы их измерения.

Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:

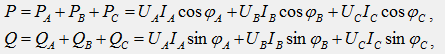
где I_A, U_A, I_B, U_B, I_C, U_C – фазные значения токов и напряжений.

В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:

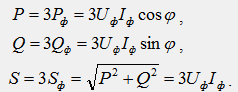
В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения Uф/Uл/√3, I_ф=I_л, тогда получим:

Для схемы треугольника верны соотношения: Uф=Uл ; Iф=Iл / √3 , тогда получим:

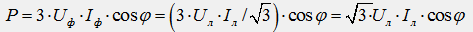
Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:

В приведенных формулах для мощностей трехфазной цепи подразумеваются линейные значения величин U и I, но индексы при их обозначениях не ставятся.

Активная мощность в электрической цепи измеряется прибором, называемым ваттметром, показания которого определяется по формуле:

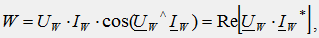
где U_w, I_w — векторы напряжения и тока, подведенные к обмоткам прибора.

Для измерения активной мощности всей трехфазной цепи в зависимости от схемы соединения фаз нагрузки и ее характера применяются различные схемы включения измерительных приборов.

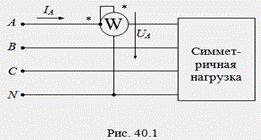
Для измерения активной мощности симметричной трехфазной цепи применяется схема с одним ваттметром, который включается в одну из фаз и измеряет активную мощность только этой фазы (рис. 40.1). Активная мощность всей цепи получается путем умножения показания ваттметра на число фаз: P=3W=3U_фI_фcos(φ). Схема с одним ваттметром может быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений.

Для измерения активной мощности в четырехпроводных трехфазных цепях (при наличии нулевого провода) применяется схема с тремя приборами (рис. 40.2), в которой производится измерение активной мощности каждой фазы в отдельности, а мощность всей цепи определяется как сумма показаний трех ваттметров:

Для измерения активной мощности в трехпроводных трехфазных цепях (при отсутствии нулевого провода) применяется схема с двумя приборами (рис. 40.3).

При отсутствии нулевого провода линейные (фазные) ток связаны между собой уравнением 1-го закона Кирхгофа: I_A+I_B+I_C=0. Сумма показаний двух ваттметров равна:

Таким образом, сумма показаний двух ваттметров равна активной трехфазной мощности, при этом показание каждого прибора в отдельности зависит не только величины нагрузки, но и от ее характера.

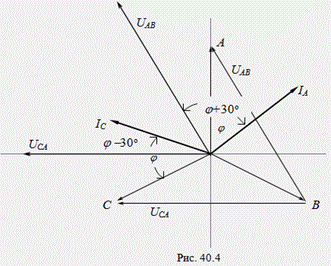
На рис. 40.4 показана векторная диаграмма токов и напряжений для симметричной нагрузки. Из диаграммы следует, что показания отдельных ваттметров могут быть определены по формулам:

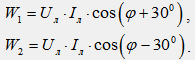
Анализ полученных выражений позволяет сделать следующие выводы. При активной нагрузке (φ = 0), показания ваттметров равны (W1 = W2).

При активно-индуктивной нагрузке(0 ≤ φ ≤ 90°) показание первого ваттметра меньше, чем второго (W1 < W2), а при φ>60° показание первого ваттметра становится отрицательным (W1<0).

При активно-емкостной нагрузке(0 ≥ φ≥ -90°) показание второго ваттметра меньше, чем первого (W1 больше W2), а при φ(меньше)-60 ° показание второго ваттметра становится отрицательным.

24) Магнитное поле и его характеристики. Магнитная цепь электромагнитного реле.
Рисунок 4. Забегая вперёд, скажу, что таков вид магнитных силовых линий, возникающих вокруг проводника с током.	Согласно теории близкодействия ток в одном из проводников не может непосредственно действовать на ток в другом проводнике. Подобно тому как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле,в пространстве, окружающем токи, возникает поле, называемое магнитным. Электрический ток в одном из проводников создаёт вокруг себя магнитное поле, которое действует на ток в другом проводнике. А поле, созданное электрическим током второго проводника, действует на первый. МАГНИТНОЕ ПОЛЕ представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.

Основные свойства магнитного поля:

1. Магнитное поле порождается электрическим током ( = движущимися зарядами).
2. Магнитное поле обнаруживается по действию на электрический ток ( = движущиеся заряды).
3. Подобно электрическому полю, магнитное поле существует реально независимо от нас, от наших знаний о нём. Экспериментальным доказательством реальности магнитного поля, как и реальности электрического поля, является факт существования электромагнитных волн (то есть посылка и приём радио- и телевизионных сигналов).

Реле? (фр. relais) — электромеханическое устройство (выключатель), предназначенное для коммутации электрических цепей при заданных изменениях электрических или неэлектрических входных величин. Различают электромагнитные, пневматические и температурные реле.

Существует класс электронных полупроводниковых приборов именуемых оптореле (твердотельное реле)

В электронной схемотехнике иногда электронные блоки с функцией переключения цепи по изменению какого-либо физического параметра также называют реле. Например, фотореле, реле контроля фаз или реле-прерыватель указателей поворота автомобиля.

Электромагнитное реле представляет собой прибор, в котором при достижении определенного значения входной величины выходная величина изменяется скачком и предназначено для применения в цепях управления, сигнализации.

Существует много разновидностей реле как по принципу действия, так и по назначению. Бывают реле механические, гидравлические, пневматические, тепловые, акустические, оптические, электрические и др.

По назначению они подразделяются на реле автоматики, реле защиты, исполнительные реле, реле промежуточные, реле связи.

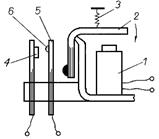
Устройство. Рассмотрим в качестве примера электромагнитное реле с поворотным якорем (рис. 1). В этом реле различают две части: воспринимающую электрический сигнал и исполнительную.

• Воспринимающая часть состоит из электромагнита 1, представляющего собой катушку, надетую на стальной сердечник, якоря 2 и пружины 3.

• Исполнительная часть состоит из неподвижных контактов 4, подвижной контактной пластины 5, посредством которой воспринимающая часть реле воздействует на исполнительную, и контактов 6.

Следует обратить внимание на то, что воспринимающая и исполнительная части реле не имеют между собой электрической связи и включаются в разные электрические цепи.

Реле приводится в действие слабым (малоточным) сигналом, и само может приводить в действие более мощную исполнительную аппаратуру (контактор, масляный выключатель, пускатель и т. д.).

Принцип действия. Когда ток в катушке электромагнита отсутствует, якорь под действием пружины удерживается в верхнем положении, при этом контакты реле разорваны.

При появлении тока в катушке электромагнита якорь притягивается к сердечнику и подвижный контакт замыкается с неподвижным. Происходит замыкание исполнительной цепи, т. е. включение того или иного подсоединенного исполнительного устройства.

В зависимости от исполнения реле комплектуются розетками под пайку, под DIN-рейку или розетками под винт.

Схема соединения «Треугольник»

Дата публикации: 17 июля 2013.
Категория: Электротехника.

Соединение в треугольник трехфазного генератора или вторичной обмотки трансформатора.

Соединим конец x обмотки ax с началом b обмотки by, конец y обмотки by с началом c обмотки cz, конец z обмотки cz с началом a обмотки ax так, как показано на рисунке 1. Такое соединение по виду напоминает треугольник, откуда и происходит его название. Линейные провода присоединены в вершинах треугольника.

Рисунок 1. Соединение в треугольник генератора.

Основные соотношения:
1. При соединении в треугольник линейные и фазные напряжения равны потому, что каждые два линейных провода (как видно из рисунка 1) присоединены к началу и концу одной из фазных обмоток, а все фазные обмотки одинаковы.
2. Линейные токи I_л больше фазных I_ф в √3 = 1,73 раза.

Как доказать, что I_л = 1,73 × I_ф? Воспользуемся для этого векторной диаграммой рисунка 2.

Рисунок 2. Определение линейных токов при соединении в треугольник.

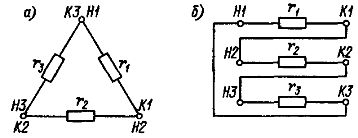
Фазные токи I_ab, I_bc, I_ca в трех электроприемниках ЭП (рисунок 2, а) изображаются векторной диаграммой (рисунок 2, б), которая получена путем перенесения параллельно самим себе векторов с рисунка 2, а. Вершины треугольника нагрузок a, b и c являются узловыми точками. Поэтому согласно первому закону Кирхгофа справедливы равенства

I_a + I_ca = I_ab, откуда I_a = I_ab – I_ca;
I_b + I_ab = I_bc, откуда I_b = I_bc – I_ab;
I_c + I_bc = I_ca, откуда I_c = I_ca – I_bc.

Понятно, что эти равенства геометрические, поэтому вычитание нужно выполнять по правилам вычитания векторов, что и сделано на рисунке 2, б. Непосредственное измерение длин векторов или вычисления по правилам геометрии показывают, что линейные токи I_a, I_b и I_c больше фазных токов I_ab, I_bc и I_ca в √3 = 1,73 раза.

На рисунке 2, б также видно, что векторная диаграмма симметричных линейных токов I_a, I_b и I_c сдвинута на 30° в сторону, обратную вращению векторов, относительно диаграммы фазных токов I_ab, I_bc и I_ca. Иными словами, ток I_a отстает на 30° от тока I_ab. Ток I_b отстает на 30° от тока I_bc, ток I_c отстает на 30° от тока I_ca.
Порядок индексов в обозначении фазных токов указывает на порядок вращения фаз. В нашем примере порядок следования (вращения) фаз: a, b, c.

На рисунке 2, в показано соединение в треугольник обмоток генератора или вторичных обмоток трансформатора. Векторы токов I_ba, I_ac, I_cb, проходящих в обмотках генератора (вторичных обмотках трансформатора), и векторы токов в нагрузке (I_ab, I_ca, I_bc) соответственно параллельны, но повернуты на 180°. Причина такого расположения векторов станет ясна, если совместить рисунок 2, в с правой частью рисунка 2, а, что и выполнено на рисунке 2, г.

Обращается внимание на то, что все три обмотки внутри генератора (трансформатора) соединены последовательно и образуют замкнутую цепь. Подобное соединение в установках постоянного тока привело бы к короткому замыканию. В установках трехфазного тока в силу того, что электродвижущие силы (э. д. с.) сдвинуты по фазе на 120°, ток в этом замкнутом контуре отсутствует, так как в каждый момент сумма э. д. с. трех обмоток равна нулю ¹.

Необходимо здесь же заметить, что для отсутствия тока в контуре обмоток генератора (трансформатора) необходимо, чтобы обмотки имели одинаковые числа витков, были сдвинуты на 120 электрических градусов и имели э. д. с. строго синусоидальные или во всяком случае не содержащие гармоник, кратных трем (смотрите статью «Понятие о магнитном равновесии трансформатора»).

Генераторы практически никогда не соединяют в треугольник. В трансформаторах такие соединения не только распространены, но иногда выполняются с целью получения внутри трансформатора токов третьих гармоник. Зачем? Понятно не затем, чтобы создавать в трансформаторе дополнительные потери. Причины здесь гораздо сложнее, смотрите статью «Понятие о магнитном равновесии трансформатора».

Соединение в треугольник обмоток трансформаторов в двух вариантах показано на рисунке 3. Подробно вопрос о соединениях обмоток трансформаторов рассмотрен в статье «Группы соединения трансформаторов».

Рисунок 3. Соединение в треугольник трансформаторов.

Соединение в треугольник электроприемников и конденсаторных батарей.

Соединение в треугольник обмоток электродвигателей показано на рисунках 4, а – в. При этом на рисунке 4, а обмотки и соединены и расположены треугольником; на рисунке 4, б обмотки соединены треугольником, но расположены произвольно; на рисунке 4, в обмотки расположены звездой, но соединены в треугольник. На рисунке 4, г обмотки расположены треугольником, но соединены в звезду.

Рисунок 4. Соединение в треугольник электроприемников.

Все эти рисунки подчеркивают, что дело отнюдь не в том, как расположены изображения электроприемников на чертежах (хотя их часто удобно располагать в соответствии с видом соединения), а в том, что с чем соединено: концы (начала) всех обмоток между собой или конец одной обмотки с началом другой. В первом случае получается соединение в звезду, во втором – в треугольник.

Соединение в треугольник конденсаторных батарей показано на рисунке 4, д.

На рисунке 4, е показано соединение в треугольник ламп. Хотя лампы территориально разбросаны по разным квартирам, но они объединены сначала в группы в пределах каждой квартиры, затем в группы по стоякам 2 и, наконец, эти группы соединены в треугольник на вводном щите 1. Заметьте: до вводного щита нагрузка трехфазная, после вводного щита (в стояках и квартирах) однофазная, хотя она и включена между двумя фазами.

На каком основании нагрузка, питающаяся от двух фаз названа однофазной? На том основании, что изменения тока в обоих проводах, к которым присоединена нагрузка, происходят одинаково, то есть в каждый момент ток проходит через одни и те же фазы.

Видео 1. Соединение треугольником

---

¹ Отсутствие тока в замкнутом контуре еще не означает, что в фазных обмотках нет тока. Токи в фазных обмотках соответствуют их нагрузкам.

Источник: Каминский Е. А., «Звезда, треугольник, зигзаг» – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.

Основные сведения о трехфазном токе. Соединение звездой и треугольником

Переменный ток, рассмотренный ранее, называется однофазным. Трехфазным называется ток, представляющий собой совокупность трех однофазных токов, сдвинутых друг относительно друга по фазе.

Простейший генератор трехфазного тока отличается от генератора однофазного тока тем, что имеет три обмотки. При вращении либо этих обмоток в поле постоянного магнита (рис.164), либо самого магнита (рис.165) в обмотках возникают переменные ЭДС  одинаковой частоты, сдвинутые друг относительно друга по фазе так, что сумма трех фазных углов составляет .

Если амплитуды ЭДС равны, а сдвиг фаз между двумя любыми смежными ЭДС равен , то трехфазная система называется симметричной. В этом случае на обмотках возникают

одинаковые по величине, но сдвинутые по фазе напряжения: , , .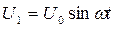

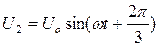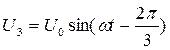Использование несвязанных между собой обмоток эквивалентно трем отдельным генераторам и требует для передачи электроэнергии потребителю три пары проводов.

Соединение обмоток между собой позволяет уменьшить количество проводов при передаче энергии и поэтому широко используется в технике.

При соединении обмоток звездой (рис.166) они имеют одну общую точку. Напряжение на каждой обмотке называется фазным. Проводник, соединенный с точкой общего потенциала, называется нулевым проводом. Проводники, соединенные со свободными концами обмоток, называются фазными проводами.

Фазные напряжения, в этом случае, это напряжения между фазными проводами и нулевым проводом. Напряжение между фазными проводами называется линейным. Ток, текущий через обмотки, называется фазным током, а ток текущий в линии, — током линии.

Из векторной диаграммы, при соединении звездой, следует, что 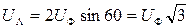. Кроме того при этом фазные токи равны токам в линии.

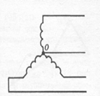
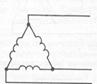
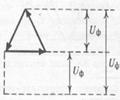
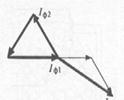
РИС.166 РИС.167 РИС.168 РИС.169 РИС.170

Если каждую обмотку замкнуть на одинаковую нагрузку R, то суммарная сила тока по нулевому проводу , так как из векторной диаграммы .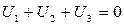

Соединение обмоток генератора звездой позволяет использовать при передаче энергии четыре провода вместо шести.

При соединении обмоток треугольником (рис.168) они образуют замкнутый контур с весьма малым сопротивлением. Линейный провод отходит от общих точек начала одной фазы и конца другой и, поэтому фазные напряжения равны линейным (рис.169).

Из векторной диаграммы токов (рис.170) следует, что

, На практике используется не только соединение обмоток генератора, но и соединение между собой нагрузок звездой или треугольником. Таких комбинаций возможного соединения генератора и нагрузок – четыре.

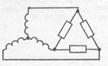
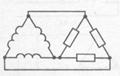
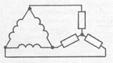
РИС.171 РИС.172 РИС.173 РИС.174

При соединении звезда – звезда (рис.171) на всех нагрузках разное напряжение, но если сопротивление нагрузок приблизительно равно, то ток по нулевому проводу практически равен нулю.

Тем не менее, нулевой провод нельзя убирать или ставить в него предохранители потому, что без него на каждую из пар нагрузок действует линейное напряжение, причем оно распределяется в соответствии с сопротивлением нагрузок. Получается, что напряжение, подаваемое на нагрузку, зависит от ее сопротивления, что неэффективно и опасно.

Если генератор и нагрузки соединены звезда – треугольник (рис.172), то на каждой нагрузке, независимо от ее сопротивления, одинаковое напряжение, равное линейному.

При соединении треугольник – треугольник (рис.173) на всех нагрузках фазное напряжение, независимо от их сопротивления.

Если генератор и нагрузки соединены треугольник – звезда (рис.174), то на каждой нагрузке напряжение равно .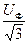

Трехфазный ток используется для получения вращающегося магнитного поля. В этом случае трехфазный ток подводится к трем обмоткам, расположенным на неподвижной станине – статоре. Внутри статора помещен стальной барабан – ротор, вдоль образующих которого в пазах уложены провода, соединенные между собой на обоих торцах кольцами.

Обмотки статора создают магнитный поток одинаковой величины, но сдвинутый по фазе, т.е. он как бы вращается относительно ротора. В обмотках ротора возникают индукционные потоки, которые, в свою очередь, взаимодействуют с вращающимся магнитным потоком, что приводит ротор во вращение, т.е. получается электродвигатель достаточно простого устройства.

При увеличении скорости ротора уменьшается относительная скорость движения его проводников относительно магнитного поля. Если бы он достиг той же скорости вращения, что и магнитный поток статора, то индукционный ток равнялся бы нулю и, соответственно, вращающий момент стал бы равным нулю.

Следовательно, при наличии тормозного момента магнитный поток и ротор не могут вращаться с той же скоростью, что и поток статора (синхронно), — скорость вращения ротора всегда несколько меньше. Поэтому двигатели такого типа называются асихронными (несинхронными).

Трехфазная система, изобретенная русским инженером М.О. Доливо-Добровольским в XIX, применяется во всем мире для передачи и распределения энергии. Доливо-Добровольский первым получил вращающееся магнитное поле с помощью трехфазного тока и построил первый асинхронный двигатель. Трехфазная система обеспечивает наиболее экономичную передачу энергии и позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы.

На практике, например, электрические лампы изготавливаются на номинальные напряжения 127 и 220В. Способ их включения в цепь трехфазного тока зависит от величины линейного напряжения трехфазной сети.

Лампы с номинальным напряжением 127 В включаются звездой с нейтральным проводом при линейном напряжении сети 220 В или треугольником при линейном напряжении сети 127 В.

Лампы с номинальным напряжением 220 В соответственно включаются звездой в сеть с линейным напряжением 380 В и треугольником в сеть с напряжением 220 В.

Обмотки трехфазных двигателей изготавливаются на номинальные фазные напряжения 127, 220 и 380 В. Каждый трехфазный двигатель может быть включен или звездой в трехфазную сеть с линейным напряжением, превышающим его фазное в 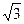раз, или треугольником, если линейное напряжение сети равно фазному напряжению его обмотки. Обычно на паспорте двигателя указано, например: треугольник -220В, звезда – 380В.

Линейные цепи. Правила Кирхгофа. Методы анализа линейных цепей. Переходные процессы в цепи с конденсатором.

Элемент электрической цепи называется линейным, если его параметры не зависят от напряжения и силы тока, т.е. вольт-амперная характеристика прямая.

Электрическая цепь называется линейной если она состоит из линейных элементов.

Применение закона Ома для расчета сложных разветвленных цепей, содержащих несколько источников довольно сложно. Для расчетов таких цепей используют два правила немецкого физика Г. Кирхгофа, первое из которых вытекает из закона сохранения заряда, а второе является обобщением закона Ома на произвольное число источников сторонних ЭДС в изолированном замкнутом контуре.

Для того чтобы использовать правила Кирхгофа необходимо ввести несколько понятий.

Электрическая схема – графическое изображение электрической цепи.

Ветвь электрической цепи – один или несколько последовательно соединенных элементов цепи, по которым течет один и тот же ток.

Узел – соединение трех или большего количества ветвей. Ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: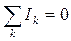

Например, для узла на рис.64 I₁-I₂+I₃-I₄-I₅=0

Контур – любой замкнутый путь, проходящий по нескольким ветвям. Положительное направление обхода контура выбирается произвольно, но одно и то же для всех контуров электрической цепи. Токи совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода – отрицательными. ЭДС считаются положительными, если они создают ток, направленный в сторону обхода контура.

Рассмотрим цепь, содержащую три источника (рис.65). Пусть R₁, R₂, R₃ общие сопротивления ветвей АВ, ВС, СА соответственно. Положительное направление обхода примем по часовой стрелке. Применим к каждой ветви закон Ома для неоднородного участка цепи.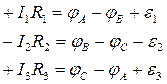

Сложив почленно эти уравнения, получим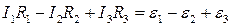

Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре: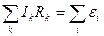

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов выяснится при решении: если искомый ток получится положительным, то его направление было выбрано правильно, а если отрицательным, то его истинное направление противоположно выбранному;

2. Выбрать направление обхода контуров и строго его придерживаться; записывая со соответствующими знаками токи и ЭДС;

3. Составить количество уравнений равное количеству искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи).

«В чем разница между подключением звезда и треугольник?» – Яндекс.Кью

Четыре провода выводятся из люстры, которую на фабрике проекировали под «раздельное включение».

Если в люстре несколько цоколей (ламп, рожков), то их, чаще всего, можно включать раздельно. Принято разделять на две группы включения. Например, одна лампа отдельно, две — отдельно на трёхламповой люстре. Или две лампы отдельно, три — отдельно — на пятиламповой.

Очень важно! Категорически нельзя сразу проверять работоспособность люстры путём подключения выходящих проводов, не убедившись, что они не подключены правильно внутри корпуса люстры.

В люстрах обычно есть специальное место, где коммутируются провода. Так в рожковых люстрах — это специальная полость в которую сходятся все рожки. Внутри неё подключение производится следующим образом: 1) все синие провода, выходящие из рожков соединяются с общим синим проводом;

2) общий жёлто-зелёный заземляющий провод соединяется с корпусом;

3) часть коричневых проводов, выходящих из рожков, соединются с коричневым общим;

4) оставшаяся часть коричневых проводов из рожков — с чёрным общим.

Иногда производители используют провода других цветов. Но этот вариант принято считать универсальным.

Второй шаг — подключение на потолке.

Обычно здесь либо три, либо четыре провода.

Варианты с тремя проводами: фаза-ноль-земля (новые проводки), фаза1-фаза2-ноль (старые проводки).

Варианты с четыремя проводами: фаза1-фаза2-ноль-земля (новые проводки), фаза1-ноль-фаза2-ноль (старые проводки). Изредка, правда, попадаются нестандартные варианты проводки в т.ч. с ошибками.

Там необходимо определить какие провода фазные, какие — ноль и заземление. Эта процедура достойна отдельной статьи

Теперь соединяем !!при отключенном напряжении!! жёлто-зелёный из люстры на заземление, синий — на ноль, коричневый — на одну фазу, чёрный — на другую. Если на потолке фаза одна, значит коричневый и чёрный из люстры соединяем вместе на неё.

Только после всего этого можно вкручивать лампы и подавать напряжение на светильник.

Но мы настоятельно рекомендуем обратиться к квалифицированному электрику, вместо самостоятельного подключения.

4.5. Расчет трехфазных цепей соединением треугольник

П

Рис. 3. 11. 3.12.

ри соединении треугольником (рис. 4.11.) каждая фаза приемника подключена к двум линейным проводам, поэтому каждое фазное напряжение равно соответствующему линейному напряжению.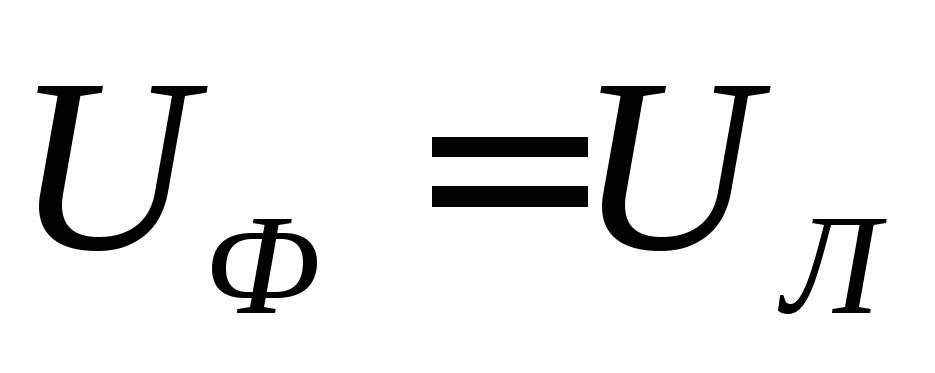

Таким образом, соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника рассчитана на напряжение, равное номинальному линейному напряжению сети.

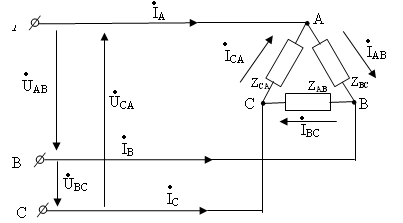
Рис. 4.11.

Фазные токи 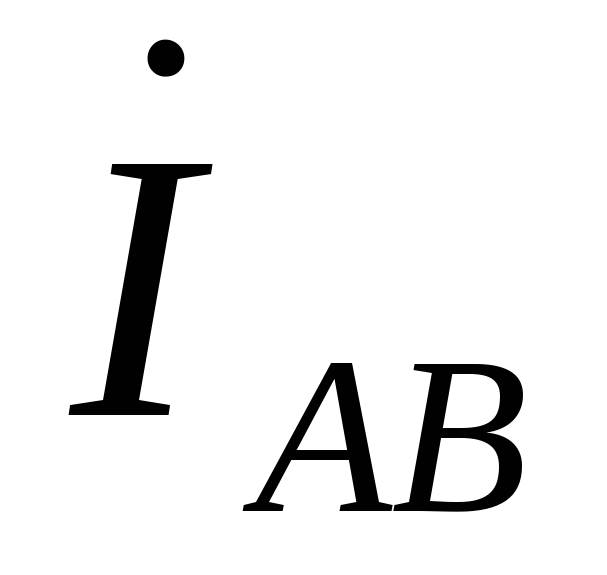,,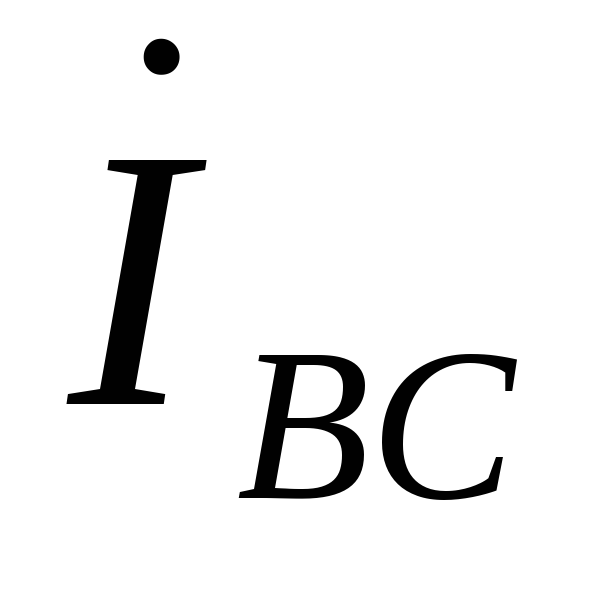в общем случае не равны линейным токам,,и могут быть найдены по следующим соотношениям:

, ,.

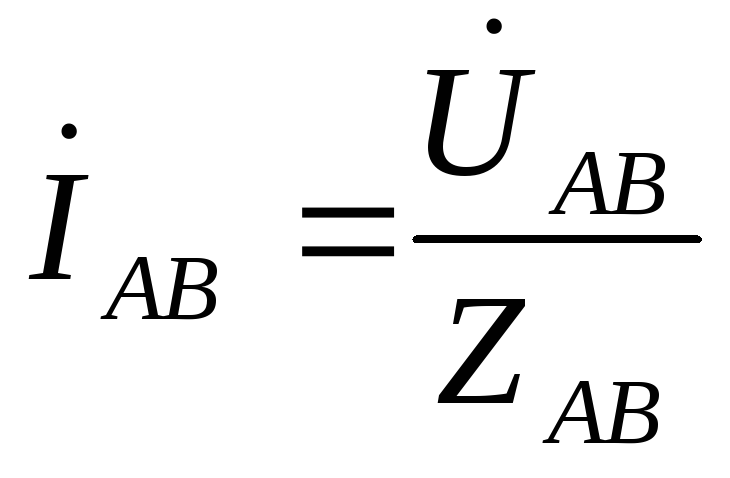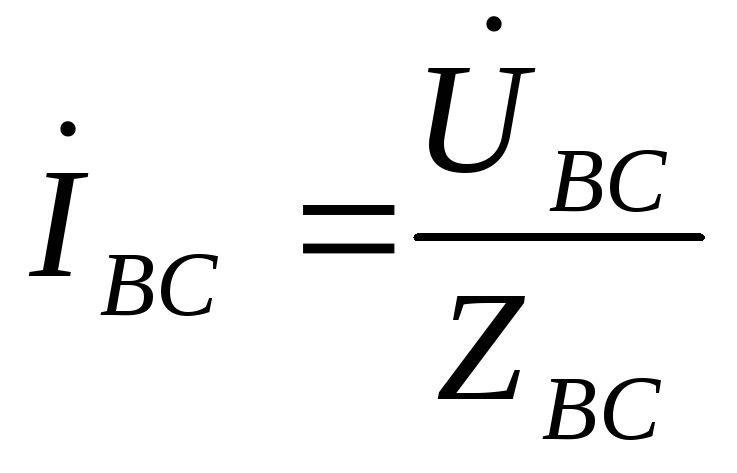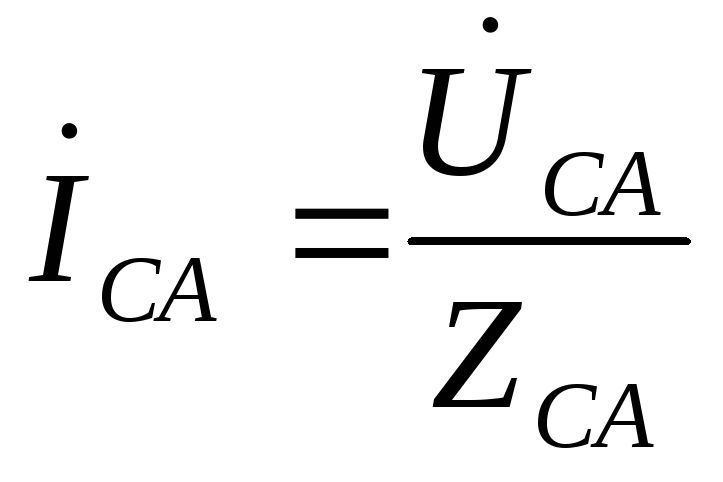Линейные токи 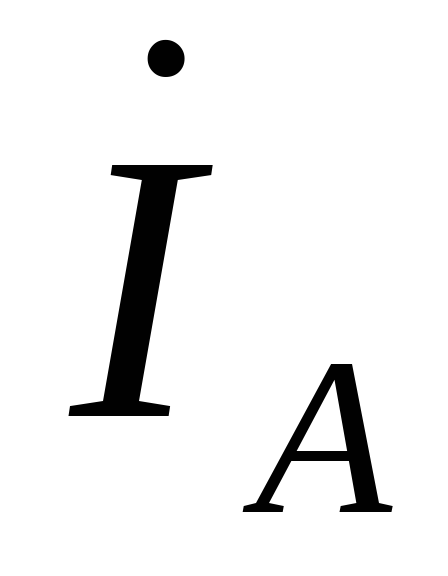,,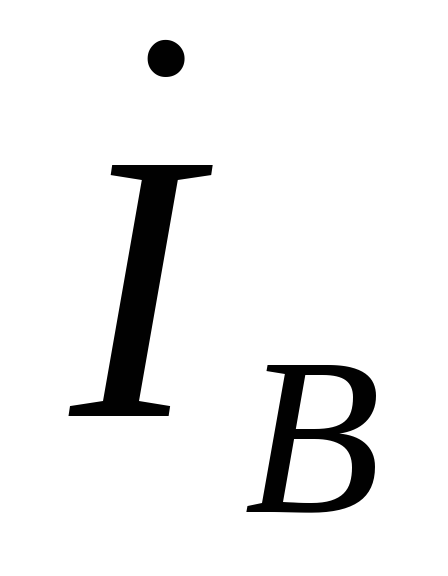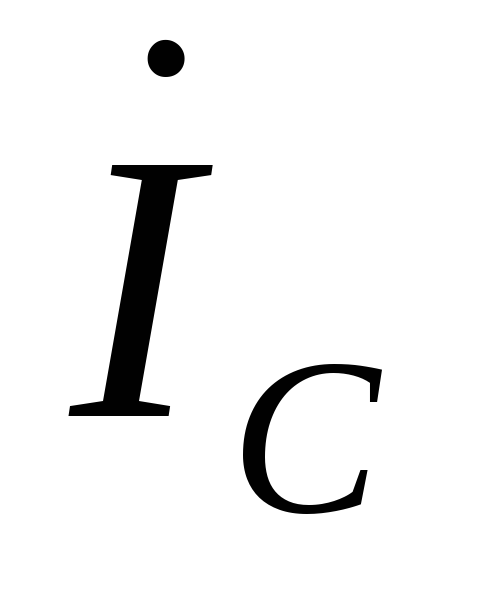могут быть определены через значения фазных токов. Из первого закона Кирхгофа запишем:

, ,.

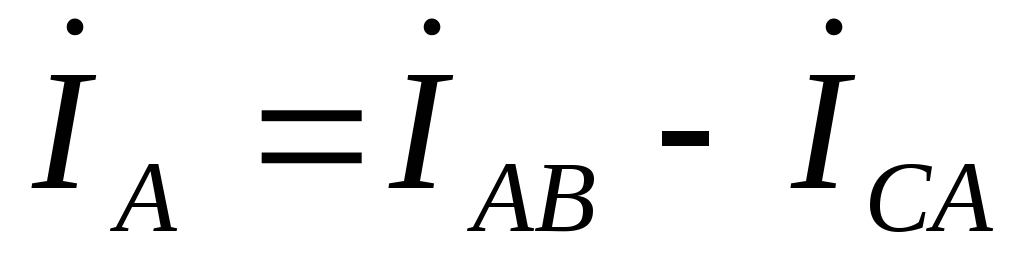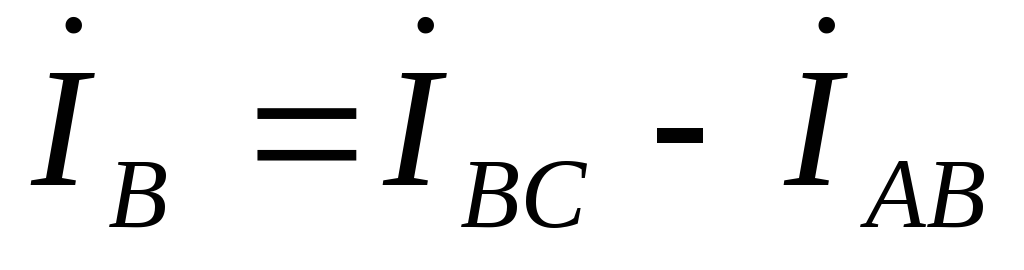Использую указанные соотношения и имея векторы фазных токов, можно построить векторную диаграмму линейных токов (рис. 4.12.).

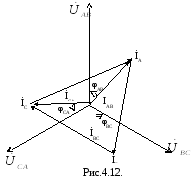
При симметричной нагрузке соединением «треугольник» равны в отдельности активные и полные реактивные сопротивления всех фаз ,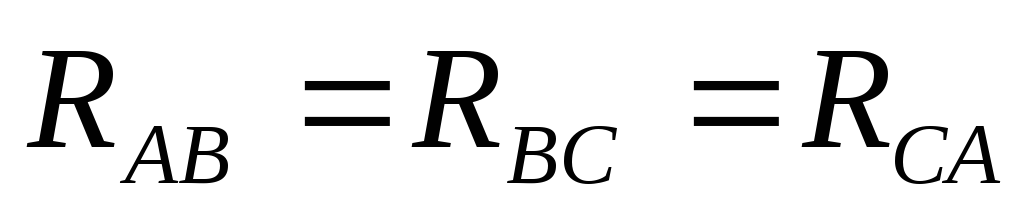

Однако, как правило, однофазные приемники подключаются не одновременно. Нагрузку можно считать симметричной лишь тогда, когда включены все приемники. Для каждой фазы могут быть использованы все методы расчета, рассмотренные ранее применительно к однофазной цепи с одним источником. Зная, например, фазные напряжения и сопротивления, можно по закону Ома найти фазные токи по формулам ,,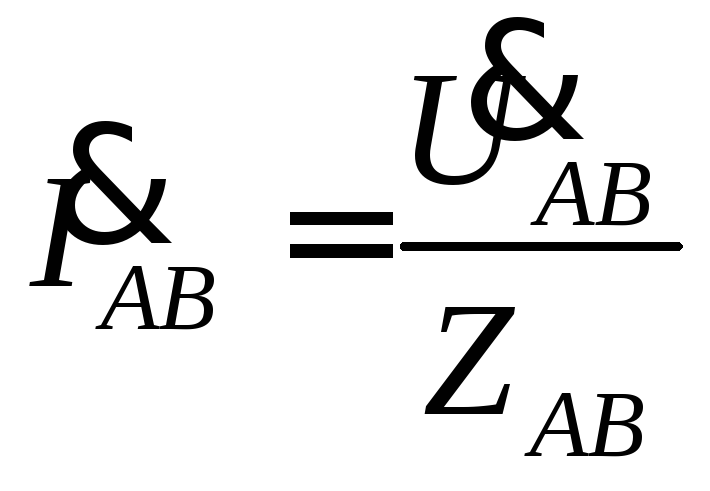

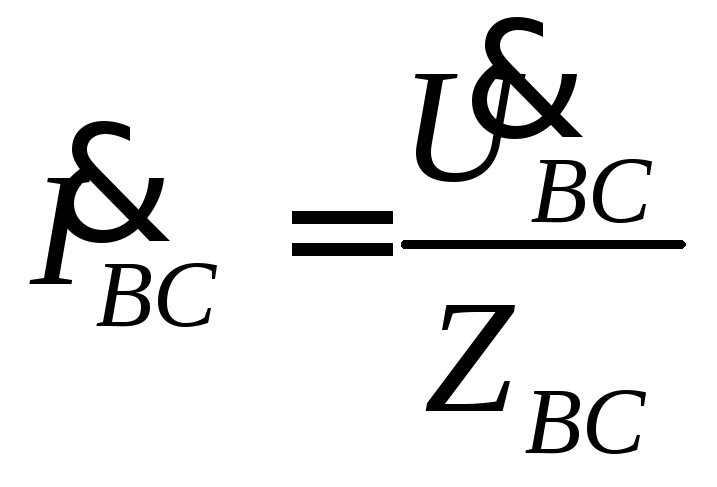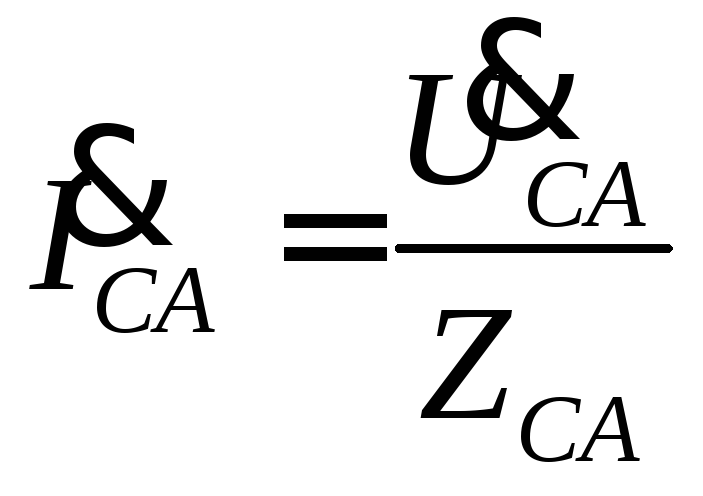
При симметричной нагрузке, ,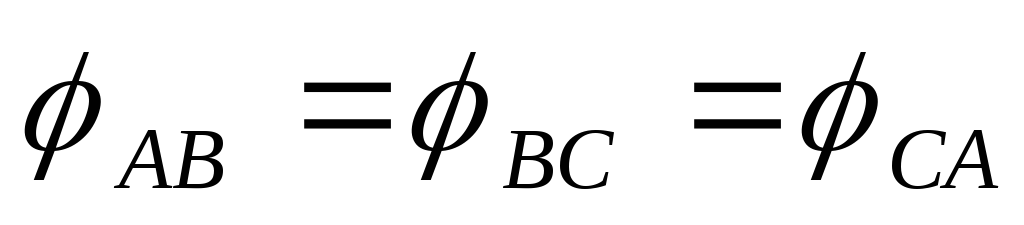-фазные токи равны друг другу и сдвинуты по фазе относительно соответствующих фазных напряжений на одинаковые углы.

В

Рис. 3. 13.

екторная диаграмма фазных напряжений и токов на рис. 4.13. показывает, что при симметричной нагрузке векторы фазных токов равны по величине и сдвинуты по фазе относительно друг друга на угол.

Векторы линейных токов изображают результирующими векторов фазных токов, как показано на рис. 4.13. Из векторной диаграммы следует, что_.

Рис. 4.13.

Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке

_.

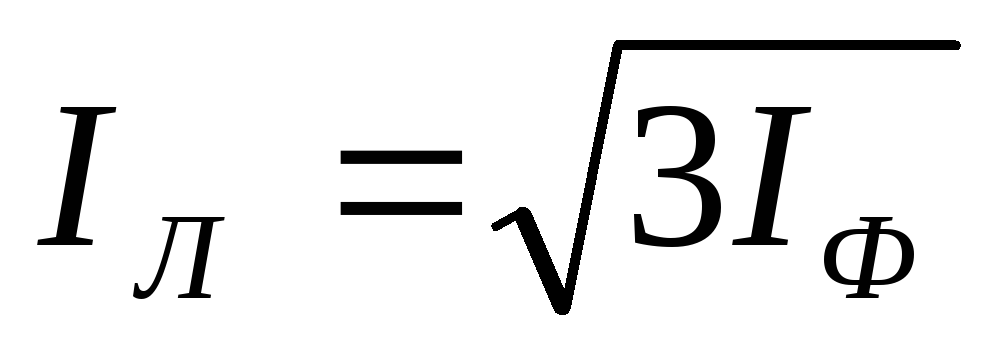Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы АВ будут равны

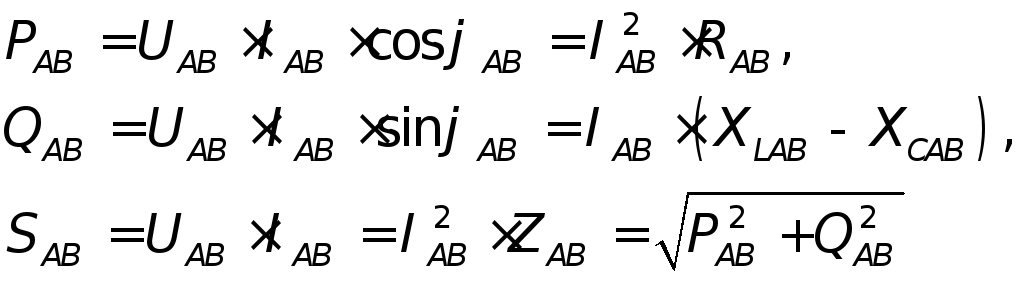
Таким же путем находим мощности фаз ВС и СА. В силу равенства напряжений, токов, углов сдвига фаз и сопротивлений при симметричной нагрузке ,,.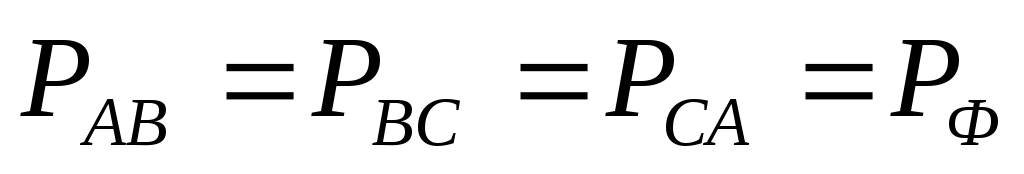

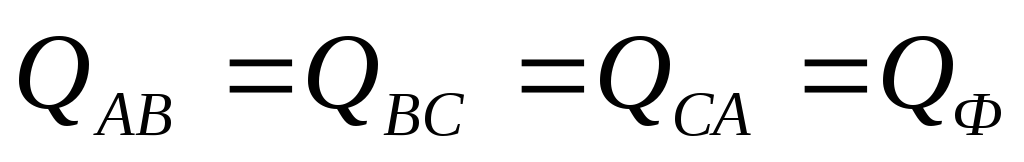При симметричной нагрузке активная Р, реактивная Q и полная S мощности трехфазного приемника ,,

.

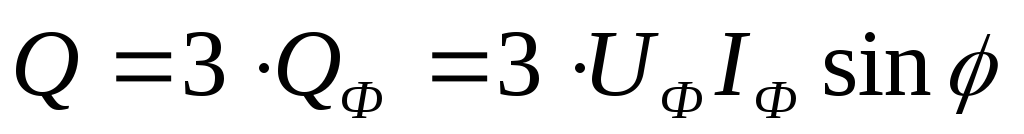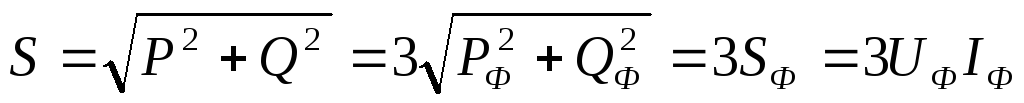В качестве номинальных напряжений и токов трехфазных приемников указываются обычно линейные напряжения и токи. Учитывая это, мощности трехфазных приемников желательно также выражать через линейные напряжения и токи ,,_.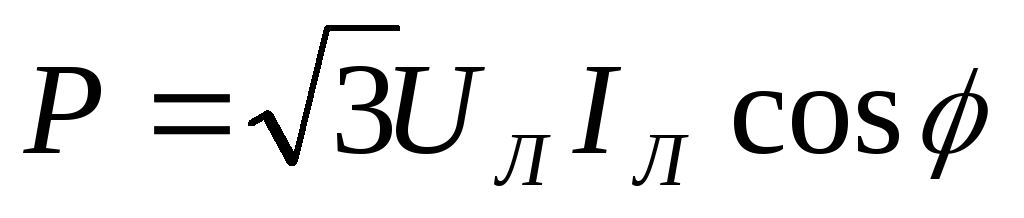

4.6. Несимметричные нагрузки при соединении треугольником

Несимметричной нагрузкой считают такую, при которой активное или реактивное сопротивление хотя бы одной из фаз не равно сопротивлениям других фаз (рис. 4.14.) r_AB = r_BC = r_C; X_AB=X_BC≠X _CA. В таком случае при несимметричной нагрузке Z_AB ≠ Z_BC ≠ Z_CA.

Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также мощности могут быть определены по формулам

, ,

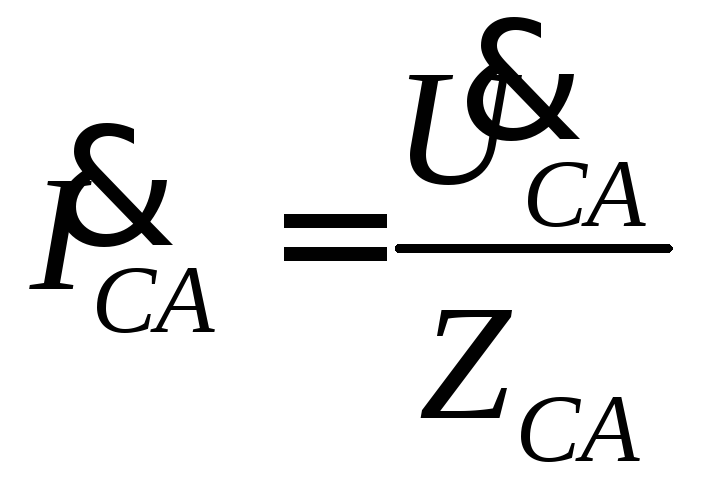
Так как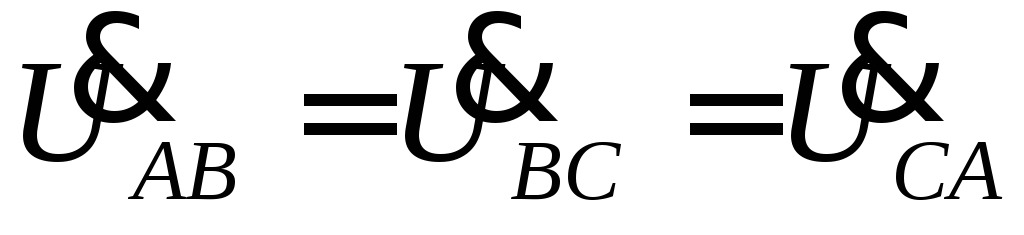, а при несимметричной нагрузкеZ_AB ≠ Z_BC ≠ Z_CA, то.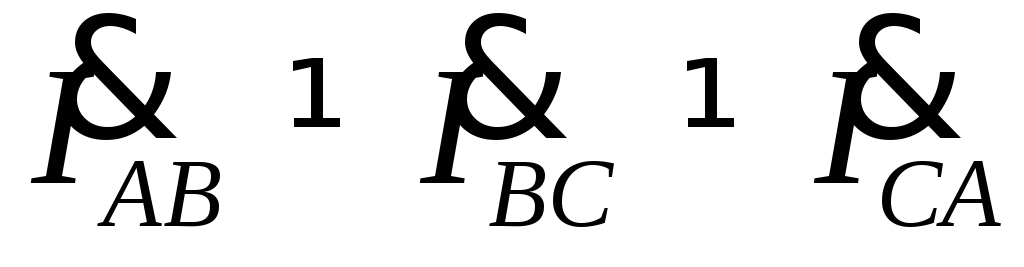

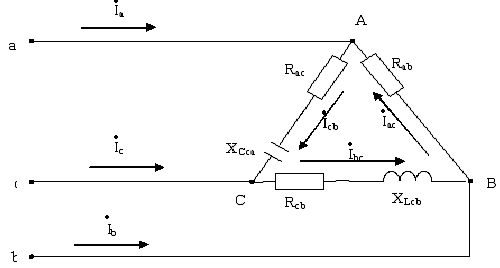
Рис. 4.14.

Углы сдвига фаз между фазными токами и напряжениями зависят от величины и характера сопротивлений фаз и могут быть определены следующим образом ;;.

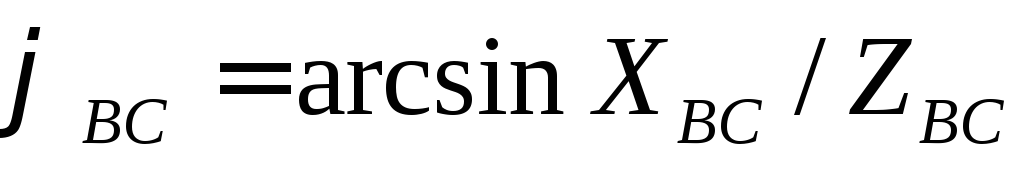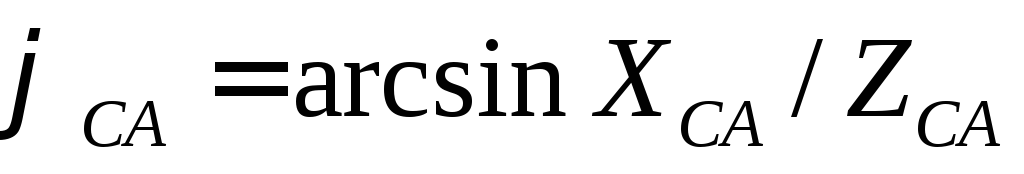Т.о., при несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности в общем случае различные.

Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы AB

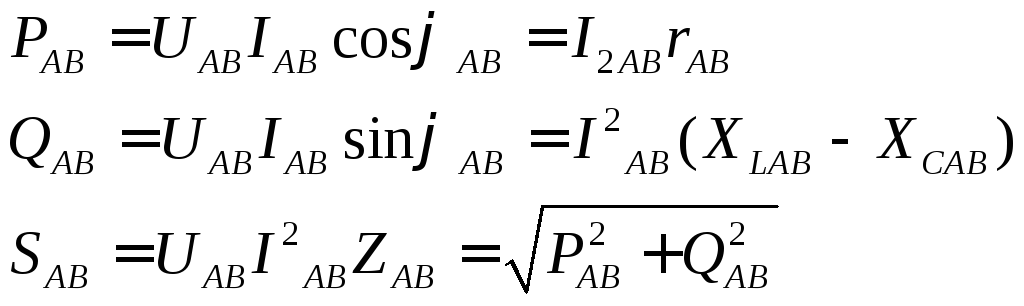
Активные и реактивные мощности приемника ; .

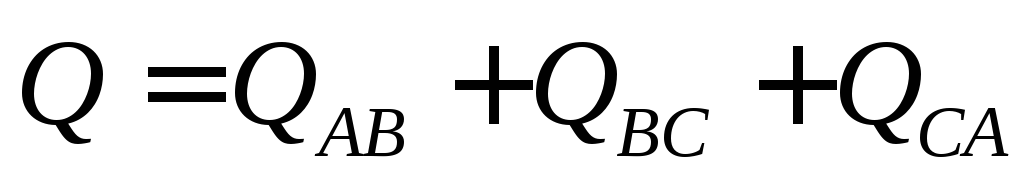Векторная диаграмма при несимметричной нагрузке для случая, когда в фазе AB имеется активное сопротивление, в фазе BC – активное и индуктивное сопротивления, фазе CA – активное и емкостное сопротивления, приведена на рис. 4.15. Построение векторов линейных токов произведено в соответствии с выражениями , ,.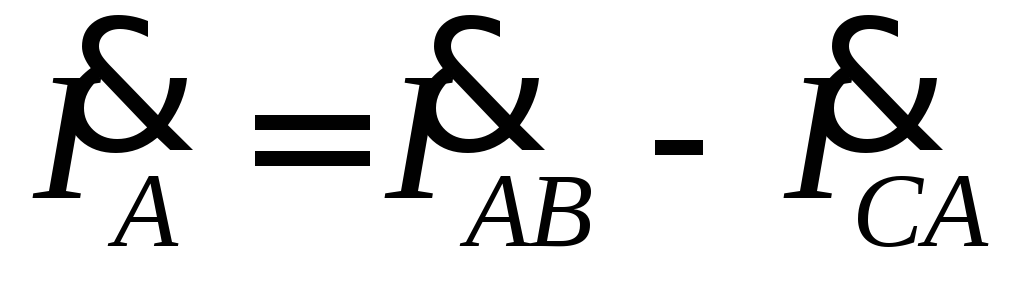

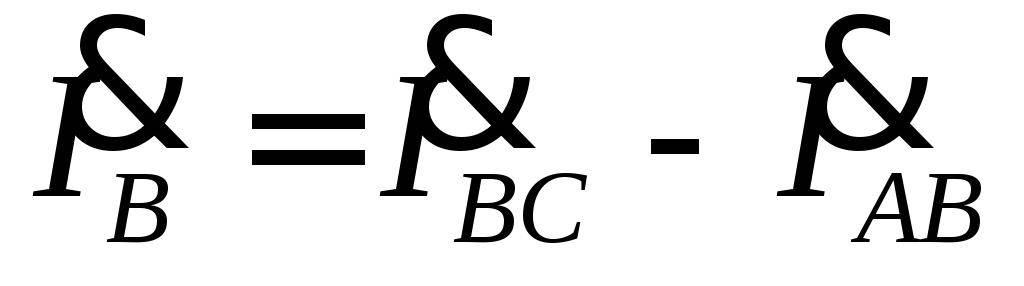Е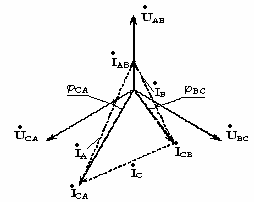сли кроме фазных токов, требуется определить линейные токи, то их можно так же определить по векторной диаграмме, не прибегая к решению задачи в комплексной форме.

Рис. 4.15.

О

Рис. 3. 15.

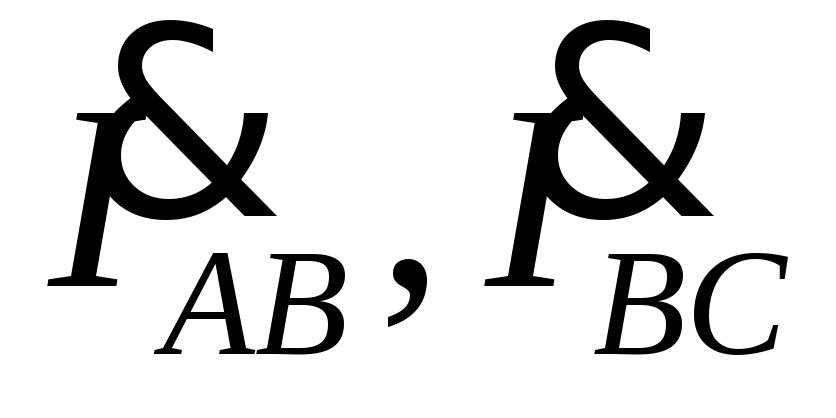тключение нагрузки одной из фаз можно считать частным случаем несимметричной нагрузки, при которой сопротивление отключенной фазы равно бесконечности. Так при отключении фазыCA сопротивление Z _CA = ∞. При этом, ток ; фазные токи, а также углыφ_AB, φ _BC не изменятся, а линейные токи 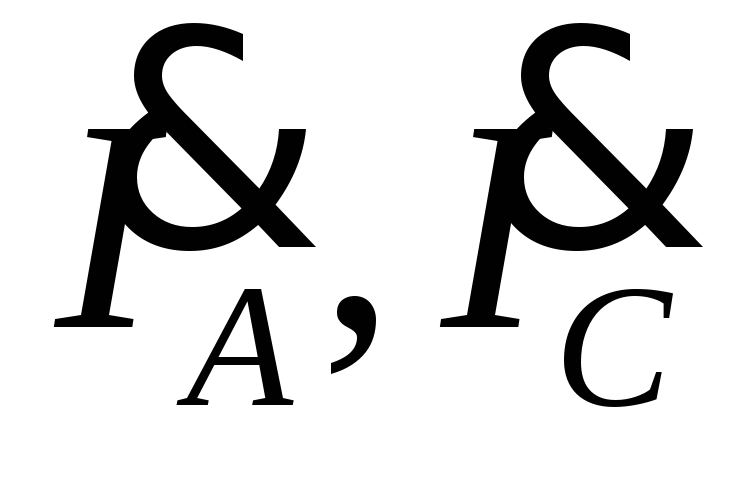уменьшатся и будут равны , _.

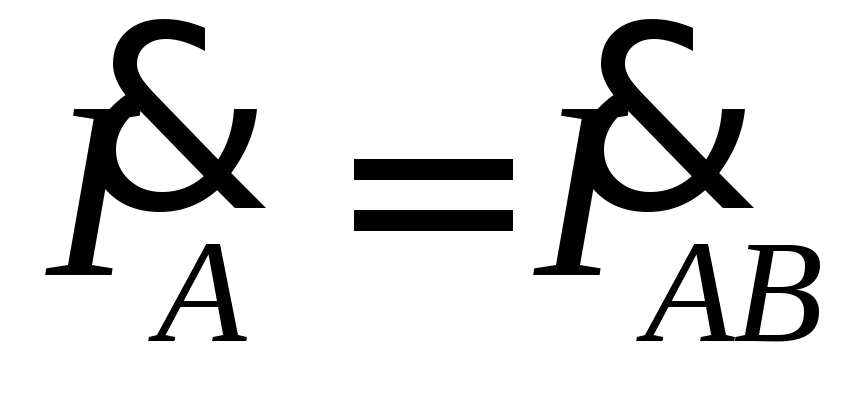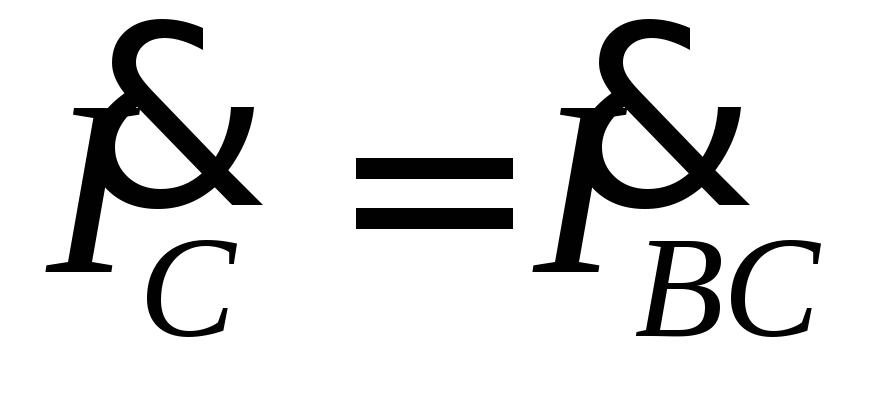Методическая разработка для дистанционного обучения «Мощность в трёхфазной цепи при соединении звездой и треугольником «

Преподаватель ___________________________________

Группа _________

Дата выдачи_________-

Тема занятия Мощность в трёхфазной цепи при соединении звездой и треугольником

Задание :

1. Прочитать учебный текст по теме «Трехфазная цепь»

2. Познакомиться с теорией по электронному ресурсу(по желанию) .

https://ru.wikipedia.org/wiki Трехфазная система электроснабжения

3. Выписать основные соотношения между фазными и линейными токами и напряжениями.

4. Выписать формулы для расчета мощности тока при соединении потребителей звездой и треугольником.

5. Решить задачу на расчет мощности (задача на второй странице задания)

Отчет представить в виде

1. Краткий перечень формул и соотношений между токами и напряжениями при соединении потребителей «звездой» и «треугольником»

2. Решенной задачи на расчет мощности в трехфазной цепи

Занятие выдано с применением электронного ресурса _. https://ru.wikipedia.org/wiki Трехфазная система электроснабжения

Срок исполнения___________________________

_________________________________подпись преподавателя

Трёхфазная цепь

 

В трехфазных цепях применяют два вида соединений генераторных обмоток – в звезду и треугольник (рис. 1). При соединении в звезду все концы фазных обмоток соединяют в один узел, называемый нейтральной или нулевой точкой, и обозначают, как правило, буквой O. При соединении в треугольник обмотки генератора соединяют так, чтобы начало одной соединялось с концом другой. ЭДС в катушках в этом случае обозначают соответственно E_BA, E_CB, E_AC. Если генератор не подключен к нагрузке, то по его обмоткам не протекают токи, т.к. сумма ЭДС равна нулю.

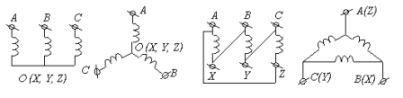
Рис. 1 Соединения генераторных обмоток – в звезду и треугольник

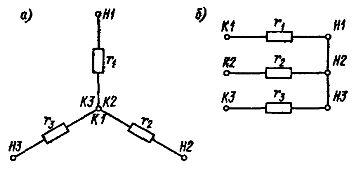
Соединение резисторов звездой: а — расположение резисторов вдоль лучей звезды, б — параллельное расположение резисторов

 Линейные и фазные величины

Напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

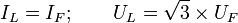
Мощность трёхфазного тока.Для соединения обмоток звездой, при симметричной нагрузке, мощность трёхфазной сети равна:

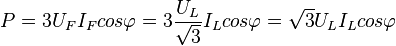
Соединение резисторов треугольником: а — расположение резисторов вдоль сторон, б — параллельное расположение резисторов

В звезду и треугольник включаются и сопротивления нагрузки так, как показано на рис. 2. Фазные сопротивления Za, Zb, Zc, Zab, Zbc, Zca, соединенные в треугольник или в звезду, называют фазами нагрузки.

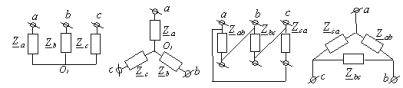
Рис. 2 Соединения нагрузки в звезду и треугольник

Существует пять видов соединения генераторов с нагрузкой: звезда – звезда с нулевым проводом, звезда – звезда без нейтрального провода, треугольник – треугольник, звезда – треугольник и т

Соотношение между линейными и фазными токами и напряжениями

Для соединения обмоток треугольником, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:

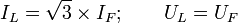
Мощность трёхфазного тока

Для соединения обмоток треугольником, при симметричной нагрузке, мощность трёхфазного тока равна:

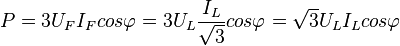
Пример задачи

Пример задачи

Трехфазный асинхронный двигатель включен в сеть 380 В по схеме «звезда». Параметры обмоток следующие: R_ф = 2 Ом(активное сопротивление обмоток двигателя),  Х_ф = 8 Ом(реактивное сопротивление катушки индуктивности )

Требуется: изобразить схему включения двигателя в сеть; определить фазные и линейные токи; определить потребляемую активную мощность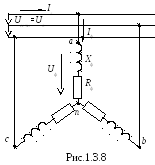

Решение:

Трехфазный асинхронный двигатель является симметричной активно-индуктивной нагрузкой, поэтому включается в сеть по схеме «звезда» без нейтрального провода. Его схема замещения представлена на рис. 1.3.8

Номинальное напряжение сети является линейным напряжением, т е. 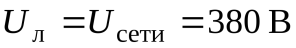, тогда фазное напряжение

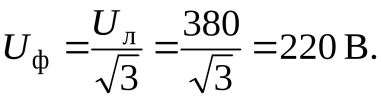 Поскольку нагрузка симметричная, то расчет можно проводить для одной фазы.

Полное сопротивление фазы

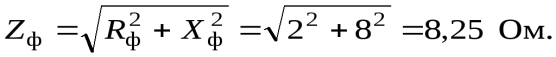
Ф

А(а)

Фазный ток

.

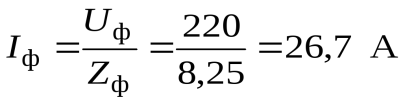Для схемы «звезда» линейный ток 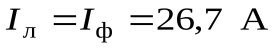. Потребляемая активная мощность

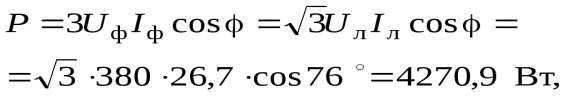
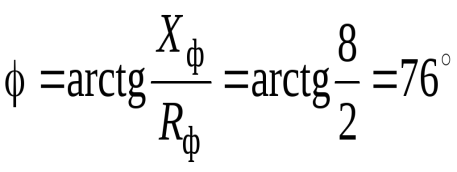
Значение угла рассчитывается по векторной диаграмме RL цепи

Решить задачи

Задача 1 .Трехфазный асинхронный двигатель включен в сеть с линейным напряжением 220 В по схеме «звезда». Параметры обмоток следующие: Rф = 8 Ом(активное сопротивление обмоток двигателя), Хф = 6 Ом(реактивное сопротивление катушки индуктивности ).

Требуется: изобразить схему включения двигателя в сеть; определить фазные и линейные токи; определить потребляемую активную мощность в одной обмотке, полную активную мощность . потребляемую двигателем и коэффициент мощности

Задача 2 .К трехфазной системе напряжением 380 В подключены три одинаковых приемника (R_Ф = 3 Ом, X_LФ = 4 Ом), соединенные по схеме “треугольник“ (рис.1.). Определить токи в фазных и линейных проводах и потребляемую мощность (активную, реактивную, полную) и коэффициент мощности

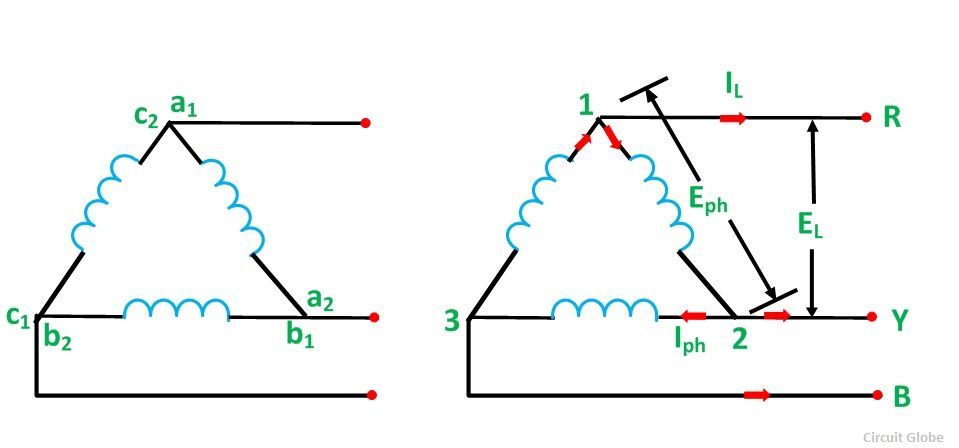
Соединение треугольником в трехфазной системе — соотношение между фазой, линейным напряжением и током

В соединении треугольник (Δ) или ячеистой сети готовый вывод одной обмотки соединяется с пусковым выводом другой фазы и так далее, что дает замкнутую цепь. Трехлинейные проводники проходят от трех соединений сетки, называемой Line Conductors .

Соединение в форме треугольника показано на рисунке ниже:

В комплекте:

Для получения соединений треугольником , a ₂ соединен с b ₁ , b ₂ соединен с c ₁ и c ₂ соединен с ₁ , как показано на рисунке выше. ,Три проводника R, Y и B проходят от трех соединений, известных как Line Conductors .

Ток, протекающий через каждую фазу, называется Phase Current (Iph) , а ток, протекающий через каждый линейный провод, называется Line Current (I _L ).

Напряжение на каждой фазе называется фазное напряжение (E _ph ) , а напряжение на двух линейных проводниках называется линейное напряжение (E _L ).

Зависимость между фазным напряжением и линейным напряжением при соединении треугольником

Чтобы понять взаимосвязь между фазным напряжением и линейным напряжением при соединении треугольником, рассмотрите рисунок A, показанный ниже:

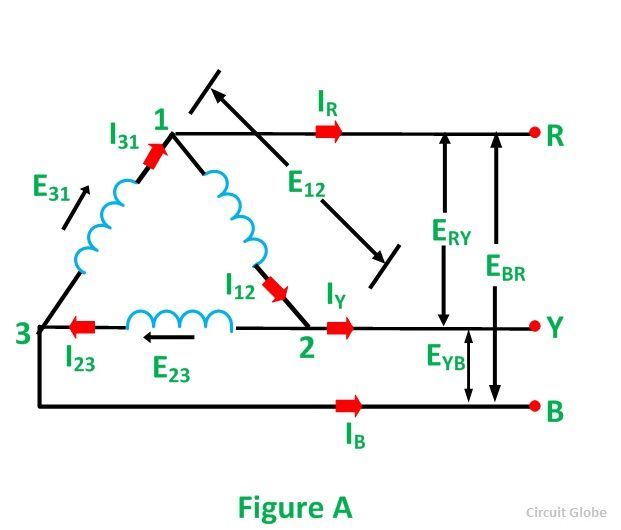Из рисунка видно, что напряжение на клеммах 1 и 2 такое же, как и на клеммах R и Y. Следовательно,

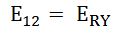
Аналогично

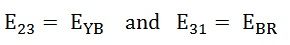
: фазные напряжения

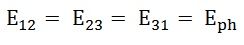
Линейные напряжения:

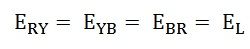
Следовательно, при соединении треугольником линейное напряжение равно фазному напряжению.

Связь между фазным током и линейным током при соединении треугольником

Как и в сбалансированной системе, трехфазный ток I ₁₂ , I ₂₃ и I ₃₁ равны по величине, но электрически смещены друг от друга на 120 °.

Векторная диаграмма показана ниже:

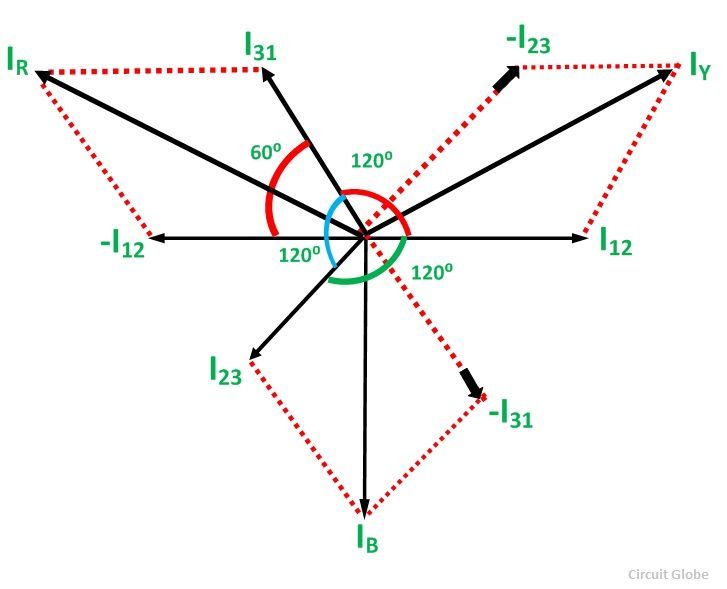Следовательно,

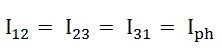
Если мы посмотрим на рисунок А, то видно, что ток делится на каждом переходе 1, 2 и 3.

Применение закона Кирхгофа на перекрестке 1,

Входящие токи равны выходным токам.

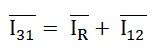
И их векторная разность будет дана как:

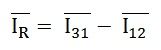
Вектор I ₁₂ переворачивается и добавляется к вектору I ₃₁ , чтобы получить векторную сумму I ₃₁ и –I ₁₂ , как показано выше на векторной диаграмме. Следовательно,

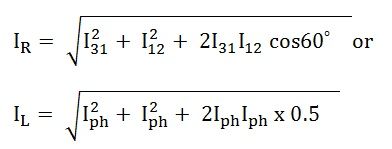
Как известно, I _R = I _L , следовательно,

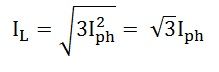
Аналогично

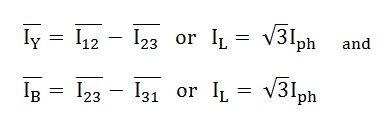
Следовательно, при соединении треугольником ток в линии в три раза больше фазного тока.

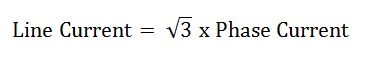
Это все о соединении треугольником в трехфазной системе.

,

Простое понимание подключения трехфазного трансформатора (треугольник – треугольник, звезда – звезда, треугольник – звезда и звезда – треугольник)

Преобразование трехфазного напряжения

Преобразование трехфазного напряжения может быть выполнено с помощью трехфазных трансформаторов, которые представляют собой отдельные устройства, все обмотки которых построены на одном железном сердечнике. Они также могут быть выполнены с помощью трех однофазных трансформаторов, подключенных извне, чтобы сформировать трехфазную батарею.

Простое понимание подключения трехфазного трансформатора — треугольник-треугольник, звезда-звезда, треугольник-звезда и звезда-треугольник (на фото: трансформатор Jefferson Electric)

В то время как трехфазные устройства обычно являются более экономичным вариантом, однофазный вариант обеспечивает большую универсальность и может быть привлекательным с точки зрения надежности и обслуживания .Если в одном месте требуется несколько идентичных трансформаторов, однофазный вариант может включать в себя покупку запасного блока, чтобы сократить время простоя в случае отказа.

Такая практика часто наблюдается с критическими батареями автотрансформаторов и повышающими трансформаторами генератора, поскольку потеря трансформатора на длительный период имеет очень серьезные последствия.

Соединения, описанные в этой статье , будут реализованы с использованием однофазных блоков .

При подключении однофазных трансформаторов в трехфазную батарею необходимо тщательно соблюдать полярность обмоток. Полярность указывается в виде точек. Ток, протекающий через точку на первичной обмотке, вызовет ток, исходящий из точки на соответствующей вторичной обмотке.

В зависимости от того, как обмотки подключены к вводам, полярности могут быть добавочными или вычитающими.

Две наиболее часто используемые конфигурации трехфазной обмотки — это треугольник и звезда , названные в честь греческой и английской буквы, на которую каждая похожа. В конфигурации треугольником три обмотки соединены встык, образуя замкнутый путь.Фаза подключена к каждому углу дельты.

Хотя обмотки треугольника часто работают без заземления, участок треугольника может быть заземлен по центру или угол треугольника может быть заземлен. В звездообразной конфигурации один конец каждой из трех обмоток соединен с нейтралью. К другому концу трех обмоток подключена фаза. Нейтраль обычно заземлена.

В следующих параграфах описываются трехфазные трансформаторы, в которых используются соединения треугольником и звездой.

1. Дельта-Дельта
2. Уай-Уай
3. Дельта-звезда
4. Уай-Дельта

В следующей части этой статьи будут обсуждаться трехфазные трансформаторы, использующие соединения «треугольник» и «звезда», где один из однофазных трансформаторов, составляющих трехфазную батарею, не используется. Ножка трансформатора с отсутствующим трансформатором называется фантомной ногой.

1. Дельта – Дельта

Трансформаторы

треугольник-треугольник, как показано на рисунке 1, часто используются для питания нагрузок, которые в основном являются трехфазными, но могут иметь небольшой однофазный компонент .

Рисунок 1 — Трансформатор треугольник-треугольник

Трехфазная нагрузка обычно представляет собой нагрузку двигателя, в то время как однофазный компонент часто представляет собой освещение и низкое напряжение. Однофазная нагрузка может быть запитана путем заземления центрального ответвления на одном из выводов вторичной обмотки треугольником, а затем подключения однофазной нагрузки между одной из фаз на заземленном плече и этой заземленной нейтралью.

На рисунке 2 показано соединение трансформатора треугольником.

Рисунок 2 — Подключение трансформатора дельта-треугольник (щелкните, чтобы развернуть диаграмму)

На схеме подключения слева показано, как может быть выполнено соединение треугольник-треугольник, либо с тремя однофазными трансформаторами, либо с одним трехфазным трансформатором .

Пунктирными линиями обозначены контуры трансформатора. Реализацию трех однофазных трансформаторов можно увидеть, не обращая внимания на внешний пунктирный контур и метки вводов, показанные на этом контуре, и сосредоточив внимание на трех меньших (однофазный трансформатор) контурах.

Проходные изоляторы однофазных трансформаторов соединяются внешними перемычками, как показано, для выполнения соединения треугольник-треугольник. В случае реализации одного трехфазного трансформатора три внутренних контура не принимаются во внимание, а перемычки между обмотками выполняются внутри бака трансформатора.Для подключения доступны шесть вводов на контуре трехфазного трансформатора.

Схематическую диаграмму в правом верхнем углу, возможно, легче анализировать, поскольку четко видны дельта-соединения.

На векторной диаграмме в правом нижнем углу показаны геометрические взаимосвязи между цепями высокого напряжения и токами цепей низкого напряжения , а уравнения в центре внизу показывают эти взаимосвязи математически.

Когда нагрузка на трансформатор треугольник-треугольник становится несимметричной, в обмотках треугольника могут циркулировать большие токи, что приводит к дисбалансу напряжений.Сбалансированная нагрузка требует выбора трех трансформаторов с равными отношениями напряжения и одинаковыми сопротивлениями .

Кроме того, величина однофазной нагрузки должна быть низкой, поскольку трансформатор с центральным отводом должен обеспечивать большую часть однофазной нагрузки. По мере увеличения однофазной нагрузки трансформатор с центральным отводом будет увеличивать свою нагрузку больше, чем два других трансформатора, и в конечном итоге приведет к перегрузке.

В случае отказа одного из однофазных трансформаторов в группе треугольник-треугольник, эта группа может работать только с двумя трансформаторами, образующими конфигурацию открытого треугольника.Номинальная мощность банка в кВА снижается, но трехфазное питание по-прежнему подается на нагрузку.

Вернуться к содержанию ↑

2. Уай – Уай

Трансформаторы

звезда-звезда, как показано на рис. 3, могут обслуживать как трехфазные, так и однофазные нагрузки. Однофазная нагрузка должна распределяться как можно более равномерно между каждой из трех фаз и нейтралью.

Рисунок 3 — Трансформатор звезда-звезда

На рис. 4 показано соединение звезда-звезда, в виде трех однофазных трансформаторов или одного трехфазного блока.Показаны метки вводов и точки полярности.

Рисунок 4 — Схема подключения трансформатора звезда-звезда (щелкните, чтобы развернуть схему)

Одной из проблем, присущих трансформаторам типа звезда-звезда, является распространение токов и напряжений третьей гармоники . Эти гармоники могут вызывать помехи в близлежащих цепях связи, а также другие проблемы с качеством электроэнергии.

Другая проблема заключается в том, что существует возможность возникновения резонанса между шунтирующей емкостью цепей, подключенных к трансформатору, и намагничивающей способностью трансформатора, особенно если цепи включают изолированный кабель.Из-за этих проблем трансформаторы «звезда-звезда» должны быть тщательно определены и реализованы.

Добавление третьей (третичной) обмотки, соединенной треугольником, снимает многие из упомянутых проблем.

Вернуться к содержанию ↑

3. Дельта-Уай

Соединение «треугольник-звезда» является наиболее часто используемым. Соединение трехфазного трансформатора . Вторичная обмотка, соединенная звездой, позволяет распределить однофазную нагрузку между тремя фазами и нейтралью вместо того, чтобы размещать все на одной обмотке, как в случае четырехпроводной вторичной обмотки треугольником.

Это помогает поддерживать балансировку фазной нагрузки на трансформаторе и особенно важно, когда величина однофазной нагрузки становится большой . Устойчивая нейтральная точка также обеспечивает хорошее заземление, чтобы обеспечить критическое демпфирование системы для предотвращения колебаний напряжения.

Если один из однофазных трансформаторов в группе треугольник-звезда выходит из строя, вся батарея выходит из строя.

Кроме того, поскольку трансформатор треугольник-звезда вводит фазовый сдвиг на 30 ° от первичной к вторичной, как видно из символов фазировки на Рисунке 5, его нельзя использовать параллельно с трансформаторами треугольник-звезда и звезда-звезда, которые не производят фазового сдвига.

Рисунок 5 — Трансформатор треугольник-звезда

На рис. 6 показано соединение треугольником и звездой в виде трех однофазных трансформаторов или одного трехфазного блока. Показаны метки вводов и точки полярности.

Рисунок 6 — Соединения трансформатора треугольником и звездочкой

Анализ трансформатора треугольник-звезда иллюстрирует многие важные концепции, касающиеся работы многофазных трансформаторов. Анализ может быть выполнен на основе напряжения или тока. Поскольку напряжение (разность потенциалов или вычитание двух векторных величин) довольно абстрактно и сложно визуализировать, ток (или поток заряда) будет использоваться в качестве основы для анализа, поскольку ток легко концептуализировать.

Токи, возникающие в обмотках трансформатора треугольник-звезда, показаны на рисунке 7. Обратите внимание, что стрелки указывают мгновенные направления переменного тока и соответствуют условным обозначениям точек.

Рисунок 7 — Обмотки треугольником и звездой

Анализ должен начинаться в одной из двух электрических цепей: цепи высокого напряжения, соединенной треугольником, или цепи низкого напряжения, соединенной звездой.

Поскольку в качестве основы для анализа используется ток, схема, соединенная звездой, выбрана в качестве отправной точки, поскольку в схеме соединения звездой линейные токи (выходящие из трансформатора) и фазные токи (возникающие в обмотках трансформатора) ) равны.Эта взаимосвязь между линейным и фазным токами упрощает анализ.

Анализ начинается с маркировки всех линейных и фазных токов. Это показано на рисунке 8.

Рисунок 8 — Трансформатор треугольник-звезда с обозначенными токами

Обратите внимание, что нижние индексы указывают линейные токи в цепи низкого напряжения, а нижние индексы верхнего регистра указывают линейные токи в цепи высокого напряжения. В цепи низкого напряжения фазные токи идентичны соответствующим линейным токам, поэтому они также обозначаются I _a , I _b и I _c .Когда обмотки трансформатора нарисованы, конкретная обмотка высокого напряжения соответствует обмотке низкого напряжения, нарисованной параллельно ей.

Другими словами, обмотка высокого напряжения и обмотка низкого напряжения, проведенные параллельно друг другу, составляют однофазный трансформатор или две обмотки на одном плече магнитопровода трехфазного трансформатора .

Фазовый ток высокого напряжения, соответствующий I _a , обозначен как I _{a ‘} .Направление I _{a ′} относительно направления I _a должно соответствовать условию точки. Величина I _{a ′} относительно I _a является обратной величиной отношения витков трансформатора «n» или

.

При анализе трансформатора на единицу, n = 1 , поэтому получается:

I _{a ′} = I _a

Итак,

I _{a ′} = I _a (на единицу)
I _{b ′} = I _b (на единицу)
I _{c ′} = I _c (на единицу) -единиц)
_(Ур.1)

Далее, текущий закон Кирхгофа может быть применен к каждому узлу дельты:

I _A = I _{a ′} — I _{b ′} = I _a — I _b
I _B = I _{b ′} — I _{c ′} = I _b — I _c
I _C = I _{c ′} — I _{a ′} = I _c — I _{a
(уравнение 2)53}

Уравнения, приведенные выше, выражают линейных токов цепи высокого напряжения через линейные токи цепи низкого напряжения.На этом этапе числовые значения могут быть заменены на I _a , I _b и I _c . Принимая во внимание, что I _a , I _b и I _c представляют сбалансированный набор векторов , произвольные значения на единицу выбираются для представления последовательности фаз a-b-c :

Ур. 3

Должна использоваться положительная последовательность фаз (a-b-c) , поскольку стандарты IEEE для силовых трансформаторов (серия IEEE C57) основаны на положительной последовательности фаз.

Подставляя уравнения. 3 в уравнения. 2:

Ур. 4

Сравнение I _a с I _A , разница величин √3 и угловая разница 30 ° очевидны .

IEEE Std. C57.12.00 определяет направление, в котором векторные углы должны изменяться от одной электрической цепи к другой. В стандартном трансформаторе треугольник-звезда (или звезда-треугольник) токи прямой последовательности и напряжения на стороне высокого напряжения опережают токи прямой последовательности и напряжения на стороне низкого напряжения на 30 °.

Когда векторы высокого напряжения отстают от векторов низкого напряжения, соединение считается нестандартным. Иногда нестандартные соединения необходимы для согласования фаз в двух разных системах, которые должны быть электрически связаны, но обычно указываются стандартные соединения.

Обратите внимание, что соглашение для определения стандартного соединения требует, чтобы векторы высокого напряжения опережали векторы низкого напряжения на 30 ° . Нет ссылок на первичный или вторичный.Первичные обмотки трансформатора — это те обмотки, на которые подается напряжение. На вторичные обмотки подается наведенное напряжение.

Обычно первичными обмотками являются обмотки высокого напряжения, но это не всегда так. Хорошим примером исключения является повышающий трансформатор генератора.

Вернуться к содержанию ↑

4. Уай – Дельта

Трансформатор звезда-треугольник, показанный на рисунке 9, иногда используется для обеспечения нейтрали в трехпроводной системе, но также может обслуживать нагрузку от вторичной обмотки .

Рисунок 9 — Трансформатор звезда-треугольник

Первичные обмотки звездой обычно заземлены. Если вторичная обмотка представляет собой четырехпроводной треугольник, четвертый провод, идущий от центрального ответвления на одном из ответвлений треугольника, заземляется.

На рисунке 10 показано соединение звезда-треугольник, либо в виде трех однофазных трансформаторов, либо в виде одного трехфазного блока. Обе метки вводов и точки полярности показаны .

Рисунок 10 — Соединения трансформатора звезда-треугольник (щелкните, чтобы развернуть диаграмму)

Вернуться к содержанию ↑

Продолжение будет…

Ссылка // Промышленное распределение электроэнергии, Ральф Э.Fehr

,

No related posts.