Силовой треугольник: Силовой треугольник — Большая Энциклопедия Нефти и Газа, статья, страница 1

Содержание

Построение — силовой треугольник — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Если требуется разложить данную силу F на две составляющие, лежащие с ней в одной плоскости, зная модули Ft и F2 этих составляющих, то задача сводится к построению силового треугольника по трем его сторонам. [16]

В первом из этих уравнений неизвестной является реакция Рм, во втором уравнении неизвестна реакция Р63 и в третьем уравнении, — реакция Рм. Эти реакции определятся построением дополнительных силовых треугольников. [17]

Сделать это невозможно, так как модуль силы RB неизвестен. Несмотря на возникшее затруднение, построение силового треугольника можно успешно завершить. Следует учесть, что при равновесии шара силовой треугольник должен быть замкнут. [18]

В первом из этих уравнений неизвестной является реакция F25, во втором уравнении неизвестна реакция F3 & и в третьем уравнении — реакция Рк. Эт / и реакции определятся

построением дополнительных силовых треугольников. Так определяются реакции во всех кинематических парах трехповодковой группы. [19]

Таким образом, на каждую из частей системы действуют по три силовых фактора. Так как при равновесии все силы должны пересекаться в одной точке, то направление действия реакции Ко, характеризуется линией, проходящей через точки 02 и Ki, из которых точка Ki получена пересечением линии IA и вертикали, проходящей через центр тяжести аппарата. Для построения силового треугольника из точки ПА ( рис. 163, б) строим вектор Ga, из концов которого проводим линии, параллельные IA и 02Ki соответственно. Замкнутый треугольник дает в соответствующем масштабе значения усилий Ког и Q. Силовой треугольник для шевра строится аналогично. [20]

При этом мы получили бы силовой треугольник, показанный на рис. 13 пунктиром. Такая возможность имеет место во всех случаях построения силовых треугольников

; это не отражается на решении задачи.

[21]

В, так как все силы, действующие на ползун, пересекаются в точке В. Часто Q2 0 или настолько мала, что ею пренебрегают. Величина RfB находится из уравнения моментов, составленного для всей группы относительно точки D, после чего RD находится построением силового треугольника для кулисы. [22]

Если линии действия всех реакций связей, наложенных на данное тело, равновесие которого рассматривается в задаче, известны, то при геометрическом способе решения задачи нужно построить замкнутый силовой многоугольник, начав построение его с известных сил. Число неизвестных сил не должно быть больше двух. В случае, когда число всех приложенных к данному телу сил, включая и реакции связей, равно трем, задача сводится к построению силового треугольника

по заданной стороне н заданным направлениям двух других его сторон. [23]

Из треугольника сил определяем величину составляющей PFC и величину равнодействующей R. R по двум направлениям AD и BE, находим величину составляющих Р0д и РЕВ — После этого реакции во всех шарнирах группы определяются построением дополнительных силовых треугольников как геометрические суммы найденных сил. Затем из уравнения равновесия сил, действующих на звено 7, могут быть определены путем построения плана сил величины составляющих PDA и РЕВ. При замене некоторых вращательных кинематических пар поступательными решение задачи несколько видоизменяется. [24]

Силовой треугольник строится следующим образом. Рядом с расчетной схемой чертится вектор известной по условию задачи силы. Через каждый из концов вектора проводится по линии, параллельной одной из неизвестных сил. В какой-то из точек эти линии обязательно пересекутся. Определив эту точку,

построение силового треугольника заканчивают нанесением стрелок, указывающих направление векторов, и обозначением векторов в соответствии с их обозначениями на расчетной схеме. Силовой треугольник должен быть замкнут. Это означает что при обходе по контуру силового треугольника в направлении вектора известной силы стрелки остальных векторов должны быть направлены в соответствии с направлением обхода. Если при этом направление вектора в силовом треугольнике не совпадет с направлением этого же вектора на расчетной схеме, то в направлении вектора на расчетной схеме допущена ошибка.

[25]

Выбираем в качестве следующей стороны силового треугольника реакцию выступа Кв. Так как направление силы Кв известно, то проведем через точку А прямую АК, параллельную линии действия реакции Кв. Сделать это невозможно, так как модуль силы Кв неизвестен. Несмотря на возникшее затруднение,

построение силового треугольника можно успешно завершить. Следует учесть, что при равновесии шара силовой треугольник должен быть замкнут. [26]

Страницы: 1 2

Система сходящихся сил

Оглавление:

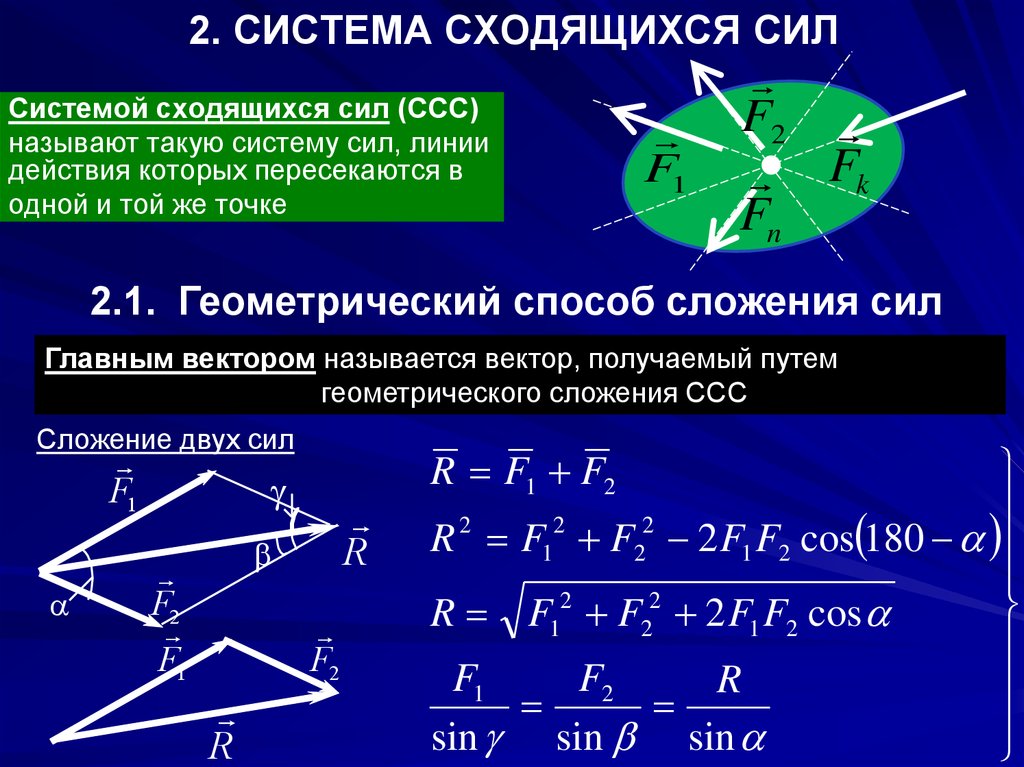
Система сил сближения 1°.Система сходящихся сил применяется к равновесию твердых тел. Называется конвергенция. Сила, при которой линия действия пересекается в 1 точке. После того, как все силы вдоль линии действия передаются в эту точку, к 1 точке прикладывается система эквивалентных сил. Рисунок 1.14. Синтез силовой системы, приложенной в 1 точке jR, приложен в той же точке и представлен силовой составляющей, состоящей из задней стороны силы Polygon. 〜 Cn、 D A’c тело, к которому применяется Ff Система сил сближения, 1.15 необходима и достаточна.

Что касается равновесия твердого тела Людмила Фирмаль
Векторная сумма этих сил равна пуле:0, то есть силовой полигон был замкнут. Это означает, что конец вектора последнего члена силы должен быть совмещен с началом вектора первого члена силы. Рисунок 1.1 замкнутый силовой полигон, построенный на 5 компонентах силы. В случае твердого равновесия, в котором приложена сила, лежащая на одной прямой, вершина замкнутого силового многоугольника оказывается на прямой, где составляющая силы рисуется в обоих направлениях, а сумма ее векторов равна пуле(рис.1.17).
Рис. 1.16. e — ’ * L и J5 Рис. 1.17. При решении задач с равновесием твердого тела, к которому приложена плоская система сил сближения, необходимо выполнить первые 4 пункта, которые обозначены x в начале книги на стр. 5) построить замкнутый силовой полигон (построение должно начинаться с известной силы, как по модулю, так и по направлению).

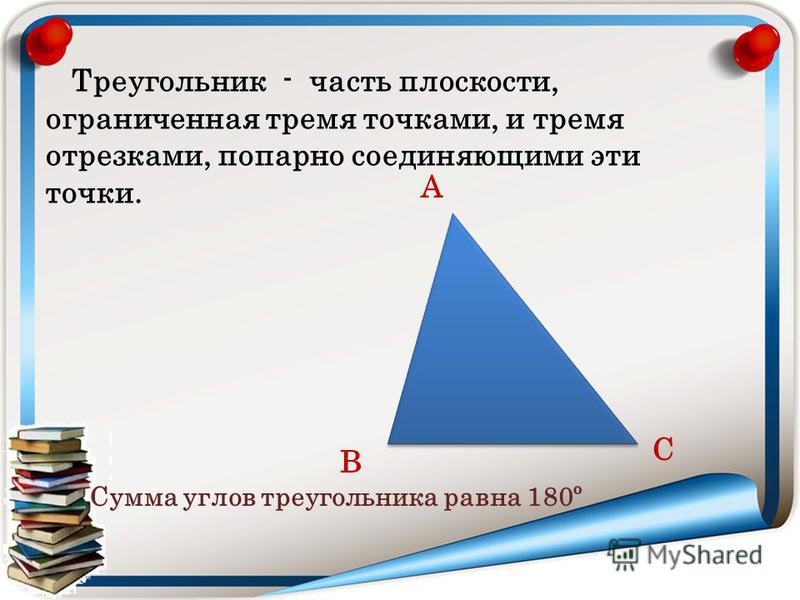
6) После того, как силовой полигон определен, определите желаемое значение.
- Если число активных сил и реакций связей, приложенных к твердому телу в равновесном состоянии, равно 3, то задача ограничивается построением и решением треугольника сил. Задача 1.1.Однородная цилиндрическая M с весом P = 20 кг лежит на гладкой горизонтальной поверхности. Вертикальная сила F = 50 к G толкает верхнюю часть цилиндра и своя линия действия проходит через центр притяжения цилиндра. о.） Определите давление цилиндра на горизонтальной поверхности. Решение.
Рассмотрим равновесие несвободного цилиндра M (рисунок A). Вес цилиндра приложен к его центроиду C и направлен вертикально вниз. Давление соответствует весу цилиндра. 1 соединение накладывается на цилиндр-ровная горизонтальная плоскость, препятствующая движению цилиндра вниз по вертикали.
К цилиндру прилагаются 2 активные силы: P-вес, F-вертикальное давление.
Людмила Фирмаль
Применяя закон невосприимчивости связывания, замените действие горизонтальной плоскости цилиндра соответствующей реакцией f (рис. 6). Давайте направим реакцию на JR. 6.） с.） М. М. р т нота Фа К задаче 1.1. В противоположность этому движению, «» ограничено горизонтальным соединением ilosx-0.»»Однако, это вертикально вверх. Здесь это несвободное твердое тело можно считать свободным объектом, в нем существует активная сила P и F, а горизонтальная плоскость f?
Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь связаться с usThese 3 силы находятся на 1 Прямой линии. Если сумма его сил находится на одной линии, то вершины силового многоугольника находятся на одной линии. Нарисуйте вектор, равный степени P, и поместите его начальную точку в любую точку. С его конца, то есть из точки А, нарисуйте вектор, равный силе F. At его конец, то есть в точке B, есть начало вектора R(рисунок C).

Когда твердое тело находится в равновесии, сумма сил P, F и R должна быть равна нулю, поэтому конечная точка вектора R должна совпадать с началом пункта 1 Силы P в точке O (на рисунке C для наглядности линии сил P и F несколько смещены друг к другу). Из рисунка c, R = P — {- F. если подставить число, то получится R = 70 кг. Давление твердого тела на горизонтальную плоскость равно коэффициенту реакции этой плоскости R и направлено в противоположную сторону, то есть вниз.
Задача 1.2. Однородный шар Р = 20 кг лежит на точке А и гладкой наклонной плоскости, образуя горизонтальную линию и угол а = 60°и находится на той же горизонтальной линии, что и точка B.4.It к услугам гостей ресторан и бар. Определите опорную реакцию выступа с наклонной плоскостью. Решение. Рассмотрим баланс мяча. 1. к шару приложена одна активная сила-его вес P направлен вертикально вниз.

Мяч Наличие 2 муфт наклонной плоскости и выступа приводит к состоянию равновесия. Примените закон освобождения, чтобы заменить действие на шар мысленно выброшенных связей соответствующей реакцией. Реакция гладкой наклонной плоскости Ra направлена вертикально. Нарисуйте касательную в точке B (рисунок B) и вызовите опорную реакцию, перпендикулярную касательной. Таким образом, линия действия проходит через центр тяжести шара С.
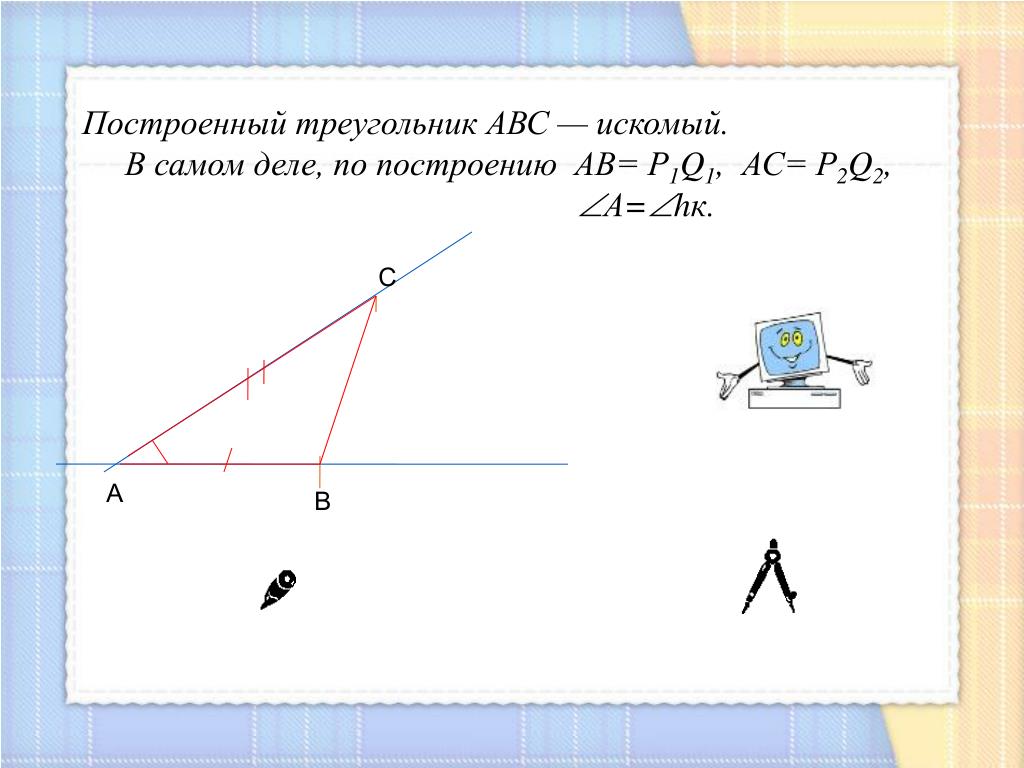
В этом случае мяч — Это P, JRa,/?Под действием плоской системы из 3 сил D можно рассматривать свободное твердое тело, находящееся в равновесии, линии действия которого пересекаются в точке C. О： Один. О б.） Один. д.） Г. К задаче 1.2. Равновесие шара необходимо и достаточно для того, чтобы сумма этих 3 сил была равна нулю. Таким образом, сила образует замкнутую улитку или треугольник. Построение силового треугольника начинается с Силы P, которая знакома как по размеру, так и по направлению.

Из любой точки O (рисунок C) нарисуйте вектор, равный силе P. At к концу силы Р необходимо добавить начало силы RA или Rl3.Выберите реакцию RB выступа как следующая сторона forstriangle. Поскольку направление силы R0 известно, проведите прямую линию AK через точку A параллельно линии действия реакции Rn. Начальная сила Ra должна быть приложена в конце Rn для последующего построения силового треугольника.
Это невозможно, поскольку коэффициент силы Rf {неизвестен. Несмотря на трудности, строительство силового треугольника может быть успешно завершено. Обратите внимание, что когда шар находится в равновесии, треугольник силы должен быть closed. In в этом случае конечная точка вектора силы реакции RA должна совпадать с начальной точкой вектора силы P. то есть, чтобы достичь точки O. таким образом, через точку O проведем линию OL, которая параллельна линии действия силы RA.
Точка B пересечения прямой AK и прямой OL, определяет расположение 3-й вершины B треугольника OAB в force. In в построенном силовом треугольнике требуется одно направление стрелки. То есть в каждой вершине треугольника только одна из 3 сил должна располагаться на 1 ребре. Для определения модулей опорных реакций RA и RD необходимо решить треугольники мощности OAW. It это легко увидеть из рисунка. c, угол, под которым образуется линия действия силы P и линия реакции Ra и Rn, равен 60°.
Таким образом, мы видим, что силовой треугольник является равносторонним, следовательно, FtA = RD = P = 20 кг. При построении треугольника сил, при приложении начала силы RA к концу силы P (а не RB, как было указано выше), треугольник силы RA (рисунок d) равен треугольнику силы OAB. 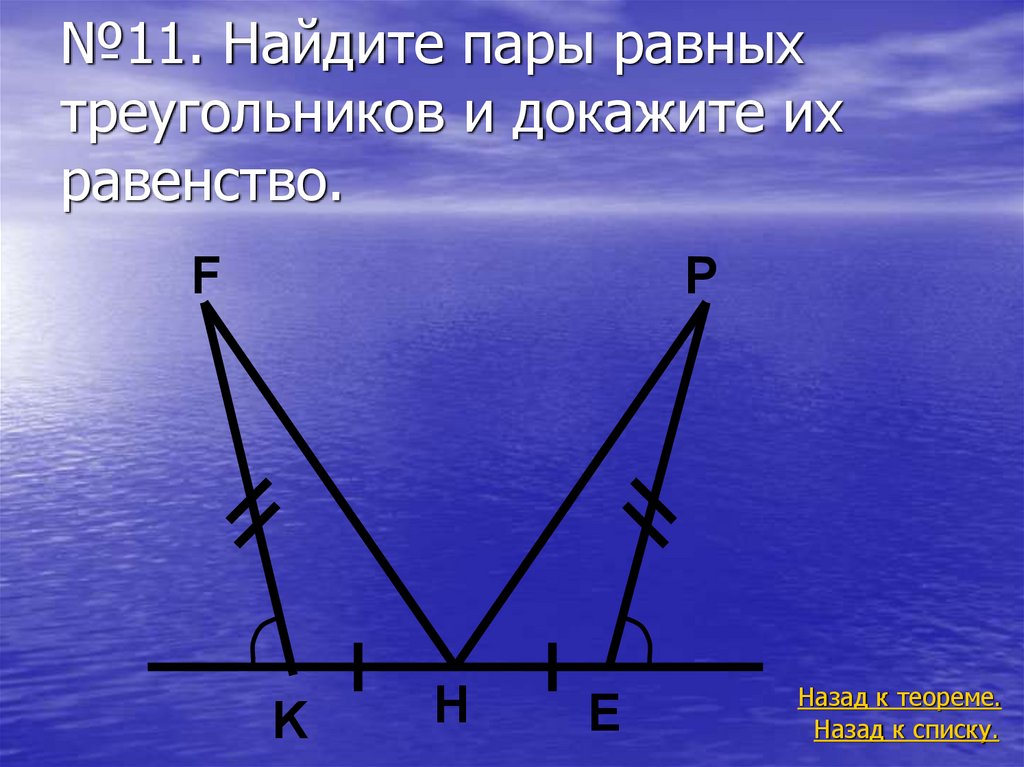Решение треугольника этой силы, конечно, приводит к тому же результату. Задача 1.3.Проденьте кабель через гвоздь, вбитый в стену (рисунок а).Один конец троса крепится к полу под углом 30°к горизонтали.
На другом конце троса свисает груз весом Р = 100 кг. Определите величину реакции стен, по которым будут забиваться гвозди. Пренебрегайте весом ногтей. Кабель вертикальный! Воздушное судно. Решение. Сначала рассмотрим баланс нагрузки(рисунок Б).Прикрепленный к нагрузке: вес P}будет вертикально вниз, и реакция кабеля Tu будет вертикально вверх. Используя 2-й закон о равновесии твердых тел под действием 2 сил, получаем следующее: T = P = 100 к G > 1 4. К задаче 1.3.
Рассмотрим равновесие ногтей. Мысленно рассеките левую и правую ветви кабеля возле гвоздя и замените действие отброшенной части кабеля его реакцией T1 и T(рисунок C).Сила T \и T *имеют тот же размер, что и сила 7\, но направление отличается: 17″.!= / Д. 2 | =(Т |.Скрепление прикрепленное к ногтю стена. Гвоздь находится в равновесии под действием активных сил T и Ti и реакции R стенки, направление которой неизвестно.
С тех пор К КОМПАКТ-ДИСК. Ф Линии действия сил этих грехов можно пересечь в 1 точке и построить силовой треугольник к силам тю-тю-а R. In треугольник этой силы, 2 силы (T1 и 71) известны как по величине, так и по направлению. После вычитания вектора равной силы из любой точки 0 к силе Th приложите вектор, равный силе 7 * 1, к его концу (рисунок D).
Поскольку силовой треугольник должен быть замкнут в равновесном состоянии гвоздя, начало силы О{определяет реакцию стенки R, соединяя конец В с концом force силы Т. Конце силы должно быть в начальной точке О. В этом случае сила треугольника ОАВ закрыт. Чтобы решить треугольник силы oaw, используйте вспомогательную структуру. Проведите горизонтальную линию от точки B вправо, продолжая ОА, но перпендикулярно вниз до пересечения с горизонтальной линией в точке D.
In треугольник ABL, угол ADD равен углу наклона левой ветви кабеля к горизонтальной линии, то есть 30 градусов. Поэтому угол плохой составляет 60°.Угол BAD находится вне силового треугольника автономной адресной книги. 173 кг.
Задача 1.4. 2 абсолютные жесткие стержни AB и AC соединены шарнирами в точке A, также закрепленными на полу шариками S и C, образующими угол 45°и 60°с IOL соответственно(рис. На шарнирном ролике а груз D подвешен на нерастягивающейся резьбе, масса которой составляет Р = 100 кг. Определяет силу, создаваемую на стержнях AB и AC. Не обращайте внимания на вес стержня. The solution.
To определяя мощность стержней AB и AC, необходимо учитывать равновесие шарнира A. Однако начинать непосредственно нельзя, так как равновесие узла A находится в равновесии под действием 3 неизвестных сил: реакции стержня AB и AC и реакции резьбы AD. Поэтому для определения реакции нити сначала рассмотрим равновесие нагрузки D. нагрузка D находится в равновесии из-за действия 2 сил (реакция массы P и нити T).
Эти силы направлены в противоположную сторону(рис. Учитывая состояние баланса нагрузки, получим T = P = = 100 для G. Теперь, когда мы знаем 1 из 3 сил, приложенных к шарниру а, мы можем посмотреть на равновесие шарнира А. 1 известная сила-противодействие винтовой резьбы T1 происходит вертикально вниз(исходя из равенства действия и закона реакции T = T).Стержень AD и AC реакции Tv и Tc направлены вдоль стержня (см. Пример 7, стр. 14 и стр. 15 в направлении реакции связи).
Рисунок 3 эти силы приложены к шарниру а(в общем случае трудно заранее указать, направлена ли мощность телевизора или нет). ТК вверх и вниз вдоль стержня; это станет ясно при последующем решении задачи). Когда шарнир а находится в равновесии, результат действия этих сил должен быть равен пуле. Таким образом, силы Tu Tn и Tc образуют замкнутый силовой треугольник. Построение треугольника сил (рисунок D)начинается с Силы T1, сила и направление которой известны.
Возьмите любую точку O и приложите силу T. Затем проведем прямые линии OL и SK параллельно стержням AC и AB соответственно через начало и конец силы T, а на пересечении получим 3-ю вершину Q силового треугольника OSQ. Нарисуйте стрелку по сторонам треугольника SQ и QO так, чтобы сумма 3 сил T \ Tn и Tc была равна нулю (в каждой из вершин силового треугольника OSQ должна располагаться только одна из 3 сил) и получите направление реакции Tr Tc. nTbU> lC-1 sin 105e’ Если вы подставите число, вы увидите следующее: ТБ = \ Б, 8 в ГУ ТС = 73.2 г Задача 1.6.На рисунке а показан механизм параллелограмма abcdy, который соединен в точках B и C и состоит из установленного абсолютно жесткого стержня ABY BC nCO.
Фиксированная связь AD \ AD = BC шарниром A и D, AB = поворачивается на CD. Горизонтальное левостороннее усилие Fc = 10 кг прикладывается к шарнирному ролику C. (Далее для краткости мы будем называть его шарнирным роликом.） Определите величину интенсивности: механизм находится в равновесии, ii. I если он находится в положении, показанном на схеме, то его прикладывают к шарниру B, причем вертикально вниз Fn. a, то есть при£BAD = 30° The solution.
To определив величину силы FB, необходимо отделить балансир от шарнира B. Однако сделать это напрямую нельзя, так как нечетного числа нет. Из 3 сил, приложенных к суставу B (реакция силы FB и стержня AB и BC), величина неизвестна. Поэтому для определения реакции стержневых везикул сначала рассмотрим равновесие сустава C. активная сила Fc и реакция стержня CD и CB приложены к суставу C. стержень соединен шарнирами, поэтому реакция осуществляется вдоль стержня x-стержня.
На рисунке показан силовой треугольник в узле C, и сила Fc рисуется из любой точки O. через начало и конец силы Fc, соответственно bar СВ и CD параллельные прямые ОК и 1: 1.it также можно использовать это приложение в качестве wallpaper. At на пересечении этих линий находим 3-ю вершину N треугольника OHN сил. Направим векторы TD и Tn так, чтобы сумма сил Fc, TD и Ti была равна пуле. OEN вернитесь к фигуре, чтобы определить угол треугольника. A. соедините точки B и D, рассмотрим треугольники ADD и DCD.
Поскольку условия на сторонах AD = BC, AB = CDy и RD являются общими, эти треугольники равны на 3 сторонах. Используя уравнение треугольника, можно увидеть, что£mDCB =£mDAB = 30°.Теперь вы можете легко доказать равенство AMD и SMV в Triangle. In факт, AD = BCt£DAM = L MCB = 30°,£AMD =£CMB = 60°.Следовательно, L CBM = L ADM-90°. 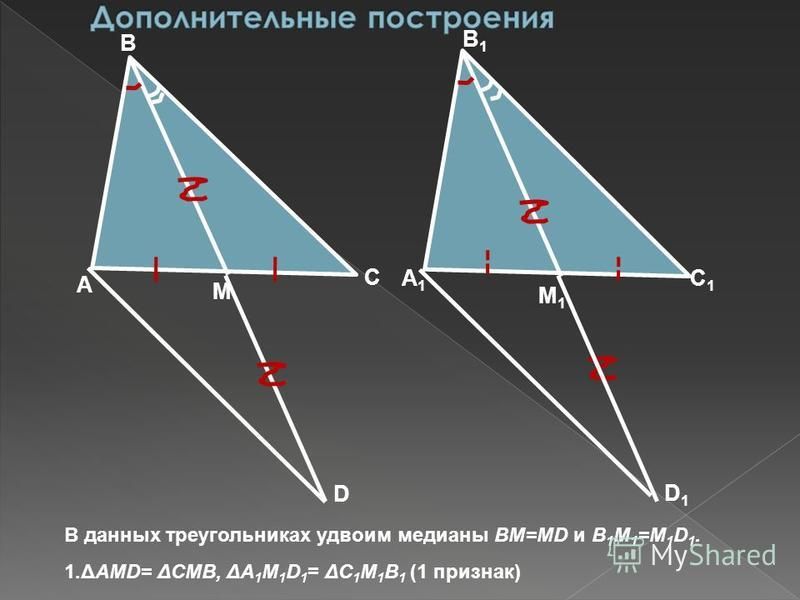.Величина силы равна Tn、 Треугольник oen силы определяется из противоположного, то есть T’N = — T [}(см. стр. 7, например, стр. 14 и стр. 15 направления реакции связывания). Затем начните строить силовой треугольник узла B с помощью react-m и T ’} V и игнорируйте любую точку P из него (рисунок E).
Затем проведем прямые линии PU и RV через начальную и конечную точки T’N соответственно параллельно линии действия искомой силы FB и стержня AB, и на пересечении получим 3-ю вершину силового треугольника PRS£.Соедините вектор TA с Fn так, чтобы силовой треугольник PRS был замкнут. Так как линии действия сил T’c и TA параллельны стержню CB и AB}, соответственно, Z. PRS = MVS = 90°. Z RPS =£BAD = 30°, и как углы сторон перпендикулярны друг другу, можно видеть из силового треугольника PRS: Ф-л-2-1 / С Т 1С05Ж-3 V6
Подставляя значение Tn из Формулы(1), получаем: Ф 2 = кт = 23.1 через Г Я… В. Мещерский рекомендует решить следующие задачи из сборника задач по теоретической механике после 1950:20, 24, 28, 31. 2°. 3 теорема о непараллельных силах. Когда твердое тело находится в равновесии под действием 3 непараллельных Если существует сила на 1 плоскости, то линии действия этих сил пересекаются в 1 точке (rx.1.18).
Имейте в виду, что пересечение рабочих линий 3-х непараллельных сил в точке является лишь необходимым условием равновесия твердого тела. Пересечение линий действия 1 из 3 сил в точке не является достаточным условием, так как результат действия этих сил может быть не равен zero. So, достаточным условием является наличие замкнутого силового треугольника, между которым в 1 точке пересекается линия действия 3 сил. 3 теоремы о непараллельных силах значительно облегчают решение задачи на рисунке 3. 1.18.
В случае твердого равновесия 3 из силы баланса, 1 направление unknown. In факт, при определении пересечения линий действия 2 сил、 Если направление известно, то можно указать направление линии действия 3-й силы, так как необходимо пройти через пересечение точки этой силы и линии действия первых 2-х сил. Задача 1.6.На рисунке показана схема опоры металлорежущего станка общего назначения с неподвижным резцом. Давление N добавляется к резцу в точке D со стороны вращаемого изделия (изделие на рисунке не показано).
Образуют угол 30°по отношению к вертикали, величина которого равна 300 кг. D-суппорты поддерживаются пружинами. Игнорируя вес суппорта, определяются реакция опоры и сила пружины пружины. Размеры показаны на рисунке. б.） Решение. рассмотрим равный выпуск 1.6. Сила приложенного веса крумциркуля: N-давление продукта, который нужно повернуть дальше на резонанс, F-восходящая сила упругости весны к vertical. By применение
В силу особенностей или законов сцепления цилиндрический шарнир а мысленно отбрасывает и корректирует свое воздействие на суппорт в соответствующей реакции РА. Обычно направление этой реакции не может быть указано заранее(с!).П. А. см. Пример 1 3 п. 14 направления реакции 4).Однако в этом случае опора находится в равновесии под действием 3-х непараллельных сил: N, F, RA. 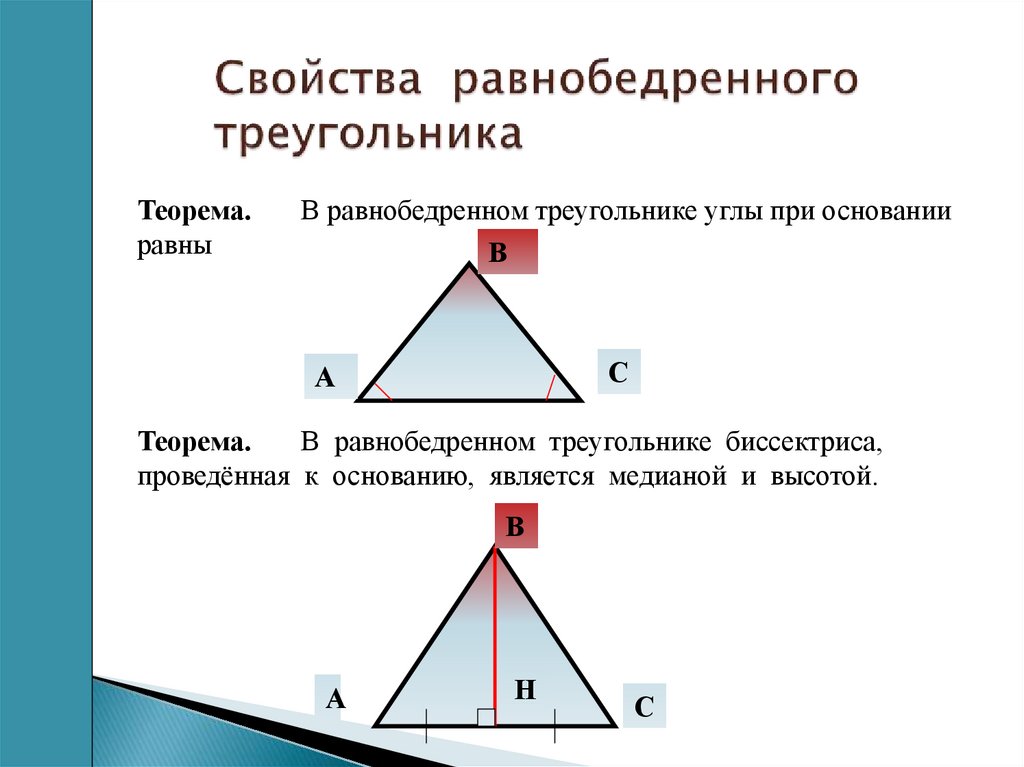So, можно использовать теорему с 3 непараллельными силами, линии действия сил N, F, RA должны пересекаться в 1 точке.
Поскольку линии действия силы N и F пересекаются в точке b, то линии действия силы RA также должны проходить через эту точку (см. Рисунок CT). Начните строить силовой треугольник (см. Рисунок C) из Силы N и добавьте его к любой точке o вне основной фигуры. Через начало O и конец Q вектора N проведите прямую линию, параллельную линии действия силы Fa RA. At на пересечении этих линий найдите 3-ю вершину силового треугольника OAIQ A1.
Направьте векторы Ra и F так, чтобы силовые треугольники были замкнуты. Работать ПА для решения силового треугольника. Вспомогательные структуры 補助: через точку D провести вертикальную линию до точки пересечения. Прямо в АЭ. Треугольники OMQ (рисунок 0)и DLE (рисунок B) имеют параллельные стороны, соответственно, поэтому легко увидеть, что они похожи. Определите длину сторон треугольника DLI:.Из прямоугольного треугольника ДКЕ, при условии、 1 см, Dl:=—r = 30 см, KE = DK ctg30°= <1р. — болен «
=1Г> 1′»: * р. Таким, бл:= BKJrKE =(20 +15УЗ) с/, То есть (Да ДЕ. 46. С. ИК-да. Средней линии с /треугольника ВАЕ равен СЛ-ть будет = 23 гл/. Следовательно, DL = CL-CD = 3 Т. В. Z. To определите е, вычислите заранее из правого треугольника Лев и:. AE = KD’Y5-p BE2 = Uz0,+ 4b5 = 55 кл. ДЕ = АС + / » Е = 2 /./: Итак, 1.Перейти к E-27.5 g l/.Таким образом, треугольник o /. Ребра / G равны (2） / ;/: = 30 см, DL = 3 g. i, LE = 27, b см. Треугольник O. используя подобие WQ и D / — E, напишите: ЛБ » дл-де」 РА = у- о компании iK>да Если подставить в Формулу(2) значения LE, DE, DL и значение N = 300 кгр, то получится: РА = 275 к г, г = 30 г
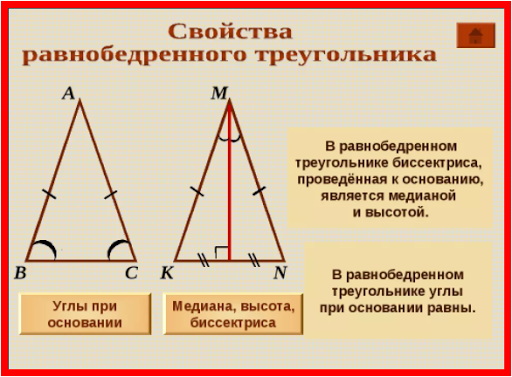
Задача 1.7.Однородный стержень массой P и длиной 2a опирается на конец а гладкой внутренней поверхности полусферической чаши радиуса R. середина B опирается на край чаши. Определите величину угла a горизонтальной линии, когда палка находится в равновесном положении и произведите опорную реакцию в точках A и B. C образует центр тяжести палки, M-центр сферы, половина ее-чаша fis. ля.) Решение.
Если опустить палку на конце а в полусферическую чашу, то палка занимает положение равновесия палки между горизонтальным и постоянным значением угла а. угол i зависит от длины палки 2А и радиуса R чаши. В случае равновесного состояния угол a должен быть таким, что он равен K. задача 1.7. Таким образом, линия действия 3 сил, приложенных к палке (P вес и реакция/?d и RB) пересекаются в 1 точке. Реакция RA направлена перпендикулярно поверхности в заданной точке, то есть вдоль радиуса AM, а реакция перпендикулярна палочке(рисунок B).
O-пересечение этих 3 сил. Такой конструкции вполне достаточно для определения величины угла a. если рассматривать равнобедренный треугольник AMB, то AM = MV = r>£BAM = = ABM. Итак, l BAM = L ABM=*.Угол ABO, вписанный в окружность с радиусом r, прост по отношению к structure. It должно быть основано на диаметре круга. Следовательно, АО = 2г. Из треугольника АОС находим а = АО•Косинус 2а-= 2Д потому, 2а. Из треугольника ОКС, это будет как = АС-COS я = а потому что. л. Итак, если вы сбрасываете отрицательное значение потому что, он будет в конечном итоге выглядеть так: потому что я = … (2） Чтобы определить реакцию опоры, создайте треугольник замкнутых сил (рисунок с).Из любой точки K нарисуем веко, равное силе P.
от начала вектора P проведем прямую линию/ C / g, параллельную силе реакции, а от конца вектора P проведем прямую линию LL), на пересечении этих линий получим 3-ю вершину N силового треугольника KLN. Из сравнения рисунков b и c, N NKL = = BOC=,,, N NLK = L QAM = go0 — > MAS = 90° — 2n, следовательно K KNL = 180°—(Z LKN — \ — £KLN) = 90° — [- I. Применяя теорему синуса треугольник сил, треугольник КЛН, мы пишем: _Tsa _ * п грех)грех з Силла(90-е-2а) ’ Эту задачу легче всего решить, применив условие равновесия рычага (11*). Мб(п)+ н(ф)=0.(1）
С тех пор mD (P)= P * BE = yP-AB sin a, tv (F)= — p. в—P-AB cos a, подставляя затем эти значения в Формулу (1), получаем: -П-АБ грех. — г-Ф•АБ соѕ а = 0、 Откуда? Я… В. Мещерский рекомендует решать следующие задачи «сборника задач теоретической механики» начиная с 1950-х годов:62, 63 и G4. Откуда? РА = Пт г,, = Здесь cos a определяется по формуле (2). Я… В. Мещерский рекомендует решать следующие задачи «сборника задач теоретической механики» начиная с 1950-х годов: 37, 38, 40, 41. 3°.Используется метод.
Как с проекцией вектора на ось, ортогональная проекция силы на ось равна произведению коэффициента силы на косинус угла, образованного положительным направлением силы, спроецированной (рис. 1.19).）： НРЛ / = * — АВ = Ф в COS(Х, ф). Проекция сил на ось является алгебраической величиной. Угол между положительным направлением оси проекции и вектором Проекция сил на ось положительна, если она заключена в диапазоне от 0°до 90°или от 270 ° до 360°.Если она находится в диапазоне около 90-270°, то проекция силы на ось будет отрицательной.
Если сила перпендикулярна оси, то проекция силы на ось равна нулю. С помощью этого метода определяется ортогональная проекция сил на координатные оси x и y(рис. 1.20） — при России Ф = АВ = /; для вида COS(Х, ф), ф = Альб [= соѕ ф(г, Ф). .Компонент силы представляет собой вектор, который может быть выражен как произведение проекции силы на единичный вектор (единичный вектор) соответствующей оси. Интернет == ФДЖ = Си, Ф = Fyj = ый. Итак, разложение сил на составляющие можно описать следующим образом: Ф = ФДЖ + ФГ] = ХВ + ый. Единичный вектор осей всегда ориентирован в положительном направлении соответствующей оси.
Знак проекции силы определяет направление ее составляющей. То есть, если проекция силы положительна, то направление составляющей силы совпадает с положительным направлением соответствующей оси, и если проекция силы отрицательна, то направление составляющей силы противоположно положительному направлению соответствующей оси. Композиция силы сходимости проективным методом требует определения плоской системы.
Дает силу FXT Fit Fn. На рабочей плоскости силы построена осевая система декартовой координаты xy. Разложение этих сил на единичные векторы этих осей имеет следующий вид: Ф \ = Flxi-Джей-Flyj, Ф3 = полон лжи, но + Fiyj,…, ФН = Fnxi Ф Разложение сходящейся плоской системы вдоль тел этих координатных осей задается следующей формулой: R = Rxi-J-Ryj, где Rx и Ry-проекции композита на соответствующие оси. 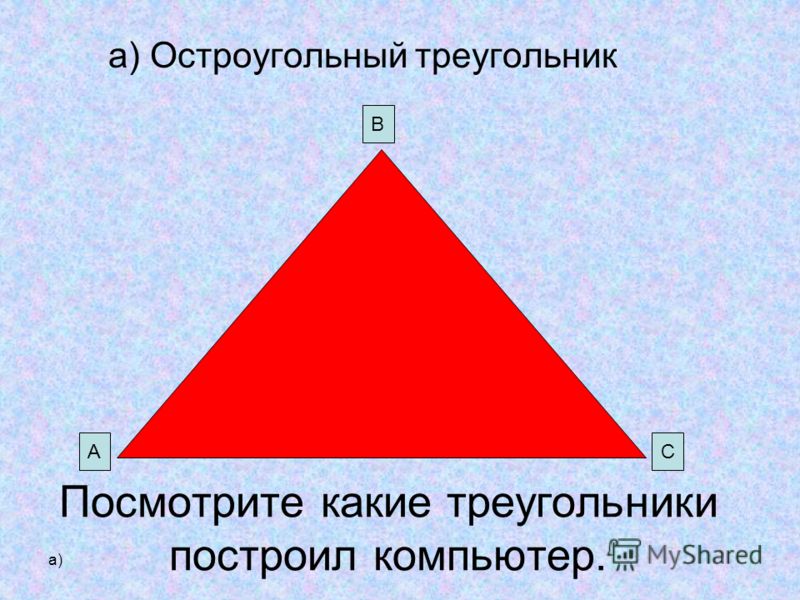в = 2 После того, как вы определили проекцию результата с помощью этих формул, вы можете рассчитать его модуль Р = УЛ + 1С(В） Направляющий ко-синус （） потому что(О)?= £, потому что(г? Я.=)
Уравнение равновесия твердого тела при наличии плоской системы сил сходимости. Для баланса、 Для тела, к которому приложена система сил сближения, необходимо, чтобы сумма проекций всех сил системы на оси декартовых координат была равна нулю и составляла 13%. Ф> Х + ч \ х -… + Fnx = 0, 1, или в краткой нотации、%Fkx = 0,£r>,=0.(7 ’） к = I к I Если неизвестное число равно числу независимых уравнений равновесия, то задача статически определена. Если число неизвестных больше числа независимых уравнений равновесия, то задача статически называется indefinite.
n последний случай, машина не может быть разрешен только мимо equations. To решая ее, необходимо использовать данное уравнение в других областях, например, сопротивление материала. Если число алгебраических неизвестных равно 2, то решается задача о равновесии твердых тел под действием плоской системы сил сходимости statically. 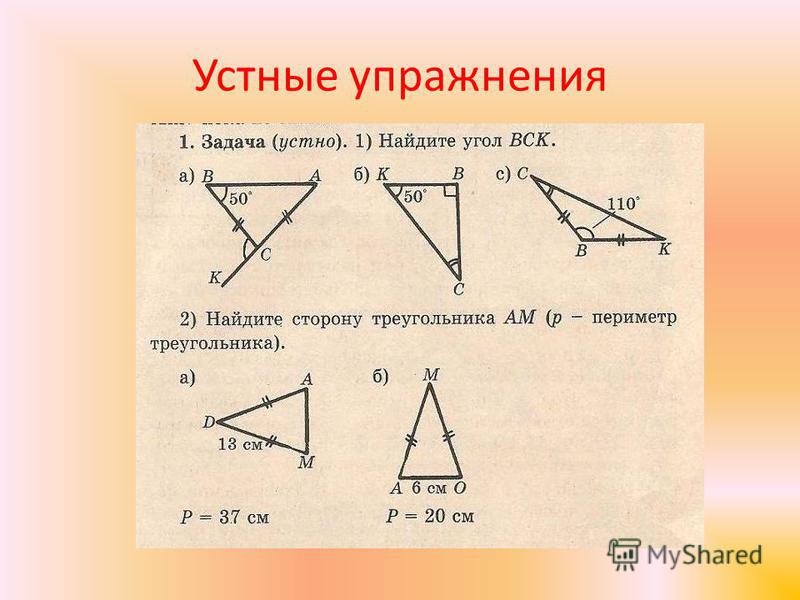So, если мы знаем направление всех составляющих сил и модуль всех сил, кроме 2, мы можем определить неизвестность 2 сил.
Если 1 силы — это не величина pi, а направление pi, то все остальные составляющие силы должны быть указаны. Преимущество аналитической проекции перед геометрическим методом силовых многоугольников особенно очевидно в задаче о равновесиях твердого тела, где имеется 3 и более сходящихся forces. In дело в том, что решение задачи мощностью 5-Гон и// — Гон указывает на определенную трудность, но решение задачи проекционным методом несколько усложняется с увеличением количества проектируемых сил.
При решении проекционных задач Метора равновесие твердых тел под действием плоской системы сил сближения должно завершиться первыми 4 пунктами (15 страниц), которые указаны в начале книги. 5) убедитесь, что эта задача определена статически, то есть алгебраические неизвестные равны до 2. 6) Выберите систему осей декартовых координат xy в рабочей плоскости силы. 7) Декартовы в проекции на координатную ось (7), создаем уравнение твердого равновесия. 8) решите систему уравнений равновесия и определите искомое значение.
Для неизвестных значений Сила будет отрицательной. Это означает, что направление силы противоположно направлению, показанному на рисунке. Если условие задачи требует определения результата, то после завершения первых 4 пунктов решения задачи необходимо рассчитать проекцию Rx и Ry результата по формуле (4) и определить модуль результата и его Косинус направления по формулам (о) и (6).
При выборе осей декартовых координат рекомендуется ориентировать их так, чтобы они были параллельны или перпендикулярны большинству составляющих силы. При определении проекции силы на ось можно использовать следующие методы: вычислить модуль проекции силы как произведение Косинуса острого угла между коэффициентом силы и линией действия силы.
Рисунок 1.22. Прямая линия, лежащая на оси projection. To определив знак проекции сил, нужно посмотреть на проецируемую силу и ось проекции так, чтобы плоскость, проходящая через них, была видна по прямой линии. 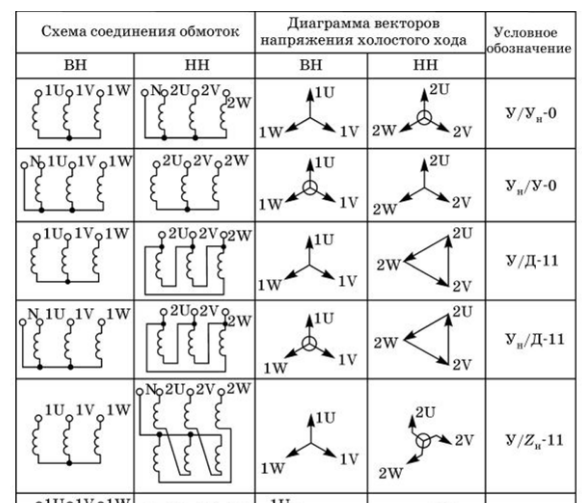Если направление силы и оси совпадает, то проекция силы положительна, а если направление силы и оси противоположно, то проекция силы отрицательна. Например, проекция сил F и Fv на ось x
1.22, а, показанный на рисунке, является положительным и может быть записан сразу： Коррекция= потому что Альф Ф, А = М, потому что АА> Вместо расчета Fu = Fi cos (360° — a. 2) = Fcos 3. Проекция Силы F3 и Fi}1.22.6 отрицательна. Потому что、 F3x = — Fa cosı3,= — сложнее вычислить прогноз FK cos официально： F3x = Ф:, соѕ(180° — Ф А3)= — Ф3 потому, А3, Я4л. = Fi cos (180°-4)= — Fi cos4. Задача 1.8.Используйте проекцию для решения задачи 1.4.
Решение: используйте изображение силы телевизора с Ту ТС, показанное в Fig. To задача 1.4.Направьте ось L. вправо по горизонтали, ось y-по вертикали. построим уравнение равновесия шарнира A на проекции осей x и Y. £Ф кДж(= ТВ соз 45°-ТС, потому что 60е = 0, 2Ф> г = т0 значение COS 45°+ + Tc cos 30° — Г= 0. Если мы решим эту систему уравнений, то получим: 7-c = 73,2 кг, Tv = 51,8 кг. 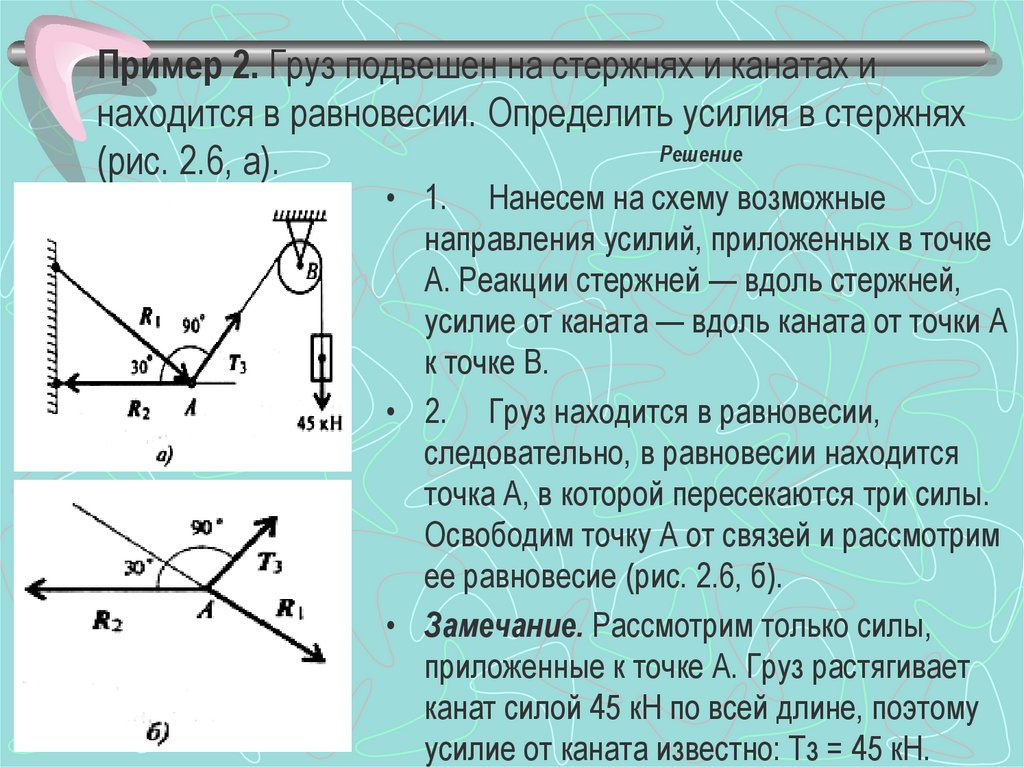Решение этой задачи аналитическими методами проще геометрического (см. Решение задачи 1.4).
Задача 1.9.На этом рисунке показано, что 4 силы Fu Fb F3 и Flf приложены к твердому телу в точке O и находятся в одной плоскости. Определите модуль и направление силы F8.Это должно быть применено к точке O так, чтобы твердое тело находилось в равновесии. Дано:= 2 n F * = G3 = 4 и Ft = 6 н. Решение. Решить задачу методом проекции, указать оси декартовой системе координат: x-ось вдоль Задача 18. 1. Л.-\ О \ \ ’ Л ’） 1 л / год / Извините. \ __ / Л. икс Горизонтально вправо, ось-выпуск 1.9. г-вертикально вверх.
уравнения равновесия твердого тела в проекциях на оси X и y имеет следующий вид: = £Fky = 0、 * = | А » = 1 Или Исправить+ + фу +исправить+ F6x = 0,(я） Fiy + Fb + Fb + Fiy + Fly = 0, (2） Вот F * x и FZy. неизвестная сила на оси v и y является проекцией Fb. Поскольку число неизвестных равно числу уравнений, задача решается статически. Приложите заданную проекцию 4 сил к F%t F3 и Ft на оси хны. 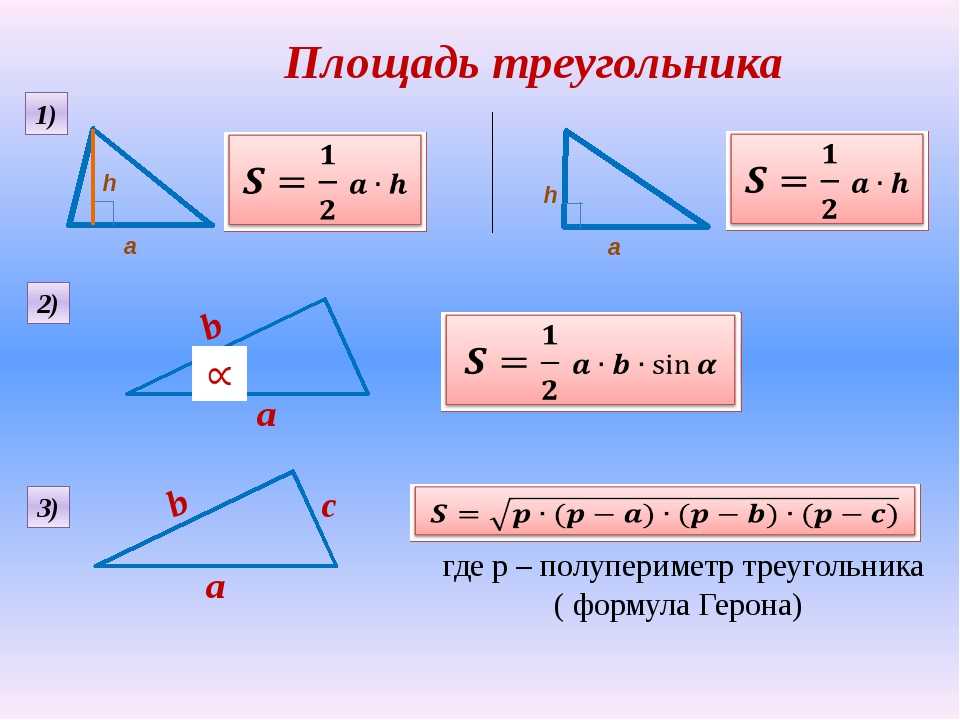13°. Мощность, требуемая проективной силой fB, не представляла труда determine. In при геометрическом подходе к решению этой задачи необходимо создать силовой пятиугольник, а затем определить модуль и направление силы, но преимущества проекционного метода нельзя отрицать.
Задача 1.10.При установке колонны MN для подъема груза весом P на вершину колонны использовали 2 моля. Груз поднимается с помощью троса BCA, который фиксирует BCA к неподвижному левому крану (кран на рисунке) и соединяет конец A с правой гусеницей крана. Когда вагонетка двигает горизонтально к праву, нагрузка будет полым цилиндром и сползает вверх вдоль колонки MN. Длина кабеля равна L. расстояние от неподвижного левого B кабеля до колонки MN равно BN = L.
Определите натяжение кабеля и давление нагрузки на колонну, предполагая, что нагрузка C является стационарной. Левая ветвь троса и угол, под которым образуется стойка, равны a. игнорируйте трение между весом троса и нагрузкой на колонну. The solution. To определим неизвестные, рассмотрим равновесие нагрузки C. 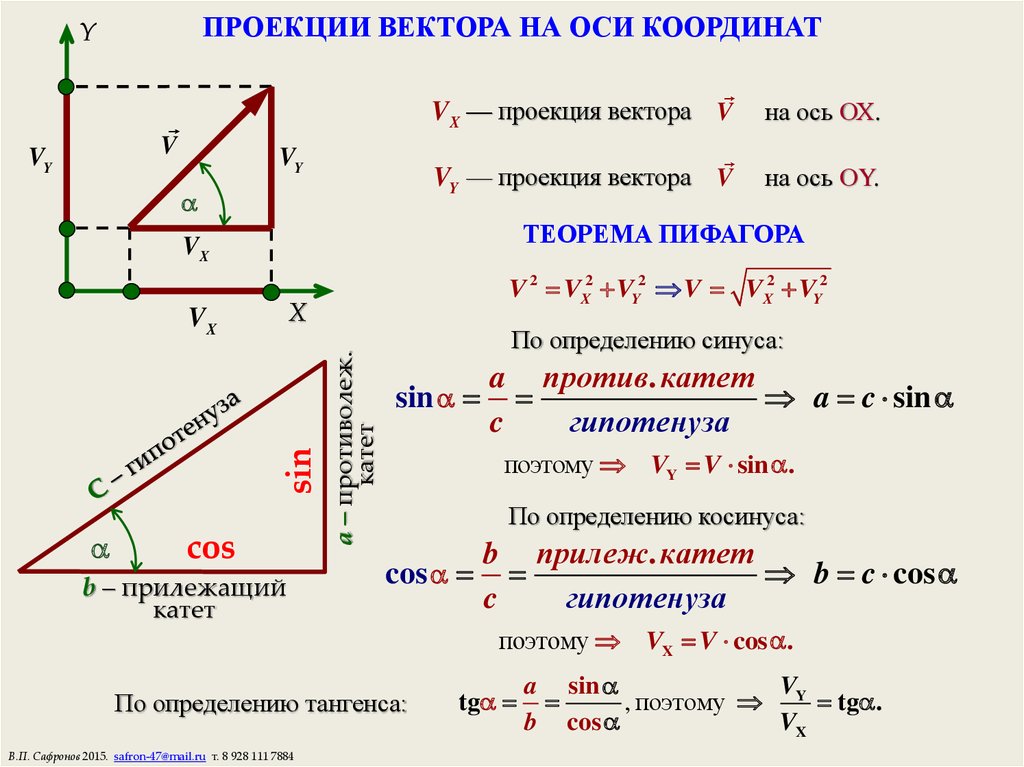потому что <? 4 ″ потому что * потому что СР и грех <? Указывает L, I, i BC-a, AC = b. В зависимости от условий а-б = л. (0） Из треугольника BCN： с. / СN = я на ктг. (Д）） Грех. Используя треугольники ACN и уравнения(5)и(6), запишем: CN я РТГ / потому что данные= — = Р Б = М — — — — (7） т б л-а /.грех i -vv
В настоящее время нетрудно вычислить sin о-У\ — cos’J <p. (7) после простого преобразования, используя результаты, вы получите следующее: В [Л * -Я — и3) грех- -/ оч Sh2w= — РХ-Р- — — — — — (8） Т / — грех — / в заменить, потому что с? Из (7), из (8) в (3) и из (4) cf, наконец, получаем следующее: Я Грех 1-Я Т = 2П. Я грех 2а ’ p_9p в(З. 2 + 12)грех-1 а-2 литий грех-(л зта -/) грех Л грех 2а
Когда нагрузка C поднимается, угол a увеличивается и становится 90°(что означает sin 2a 0). в то же время коэффициент реакции роста также grows. In в этом случае невозможно увеличить нагрузку C до горизонтального уровня AB, поскольку sin2a= sin 180°= 0 и Г значения.
Напряжение кабеля и давление нагрузки C, необходимые для колонны, равны силе T и модулю R соответственно. Решить эту задачу с помощью силовых многоугольников гораздо сложнее, так как приходится решать замкнутые силовые квадраты, построенные на основе P, R, T, G. Я… В. Мещерский рекомендует решать следующие задачи из «сборника задач теоретической механики» в издании 1950-х годов и после него:21, 26. 4°.
Момент силы находится относительно точки. Равновесие твердого тела с 1 неподвижной точкой. Момент силы F относительно точки О. Торий описывается в виде m0 (F).в системе плоских сил абсолютная величина равна модулю силы F pa, а произведение расстояния h от точки O до линии действия силы F (называется плечом). Если сила F стремится повернуть тело против часовой стрелки вокруг точки O, то момент силы положителен, а если он направлен по часовой стрелке, то отрицателен.
(В дальнейшем «сила пытается повернуть тело вокруг точки О.»).Сила будет видна вокруг точки o»).Пример (рис. 1.23), m0(F1)= FihlJ m0(F9)= -.F9h. * Размеры момента силы в технической системе агрегата-КГМУ и в системе СИ-n-m-j(Джоуль） 1 кгс = 9,81 Дж. Обратите внимание, что плечо h является частью перпендикуляра, который опускается от одной точки к линии действия силы. Иногда по ошибке отрезок представляется в виде плеча, соединяющего относительную точку, где вычисляется момент в точке приложения силы. 1 а） — уу \ а j \И М> Т \ Х Р. 6.） Проблема 1.10.Для.
Момент силы против точки равен нулю, но сила проходит через эту точку, потому что она равна нулю. Например,* о(Ф3)= 0 (рис. 1.23). Теорема бариона (теорема синтетического момента) для системы сил сходимости: момент FJ, для точки R системы сил сходимости…, Fn>находится в одной плоскости. Рис. 1.23.Равна алгебраической сумме моментов силы относительно одной и той же точки： Если линия находится на этом плече, п0(Р)= М0(а)+ 0(ф)+ … + М0(ФН)= tm0(ФК). (8 *） * =К! Здесь. * = = £ФК. ~~
Удобство применения теоремы Вариньона заключается в том, что, минуя прямое определение результата, можно рассчитать момент для точки, зная моменты всех составляющих силы на одной и той же точке. Представление силового момента F для точки A проекцией силы на ось декартовой координаты имеет вид、 Да. ма(Ф)= {Х-а)и ФГ-(г-Б)I3X! Где Fx и Fv-проекции мощности Ф па Ось декартовых координат, хна-координаты приложенных точек B силы Ft a и b-координаты точки A. (рисунок 1.24).
Целесообразно использовать эту формулу в тех случаях, когда определение величины кредитного плеча h связано с вычислительными трудностями. В частности, если силовой момент F определяется относительно начала координат O, то есть a = b = 0, то формула принимает вид m0 (F)= xFy-yF»(10 *） Так… Так… L, в Fxi 90В. Здесь. б. младший-х Рис. 1.24. Где Fx и Fy-проекции силы F на оси декартовых координат, а x и y-координаты точки действия силы F.
Рассмотрим задачу о равновесии твердого тела с 1 неподвижной точкой. Если единственной связью, наложенной на твердое тело в состоянии равновесия, является неподвижная точка (например, шарнир), то ее реакция должна быть уравновешена результирующей силой всех активных forces. As в результате, когда твердое тело находится в равновесии, линия действия равнодействующей силы всех активных сил должна проходить через неподвижную точку.
В противном случае твердое тело перевернется. Для определения условий, при которых плоская система сходящихся сил применяется для обеспечения равновесия 1 неподвижной точки и твердого тела, необходимо направить линию действия активной силы результата через пересечение линии действия активной силы и неподвижной точки. Та же проблема может быть решена с помоями: Varioma’s theorem:.
It записывается для фиксированной точки. Поскольку момент результирующей активной силы, проходящей через неподвижную точку, равен нулю, то сумма моментов всех активных сил для неподвижной точки также равна нулю. Где 0-фиксированная точка. Задача 1.11. Может тонкий однородный стержень АВ веса Р? Он вращается вокруг шарнира woo, прикрепленного к полу. Определите величину силы F. Тяги в 6） risontali право） По вопросу 11.1.
Таким образом, стержень сохраняет сбалансированное состояние, образуя вертикальную линию и угол а(рисунок а). tga, против часовой стрелки и по часовой стрелке
Смотрите также:
Предмет теоретическая механика
23 факта, которые вы должны знать
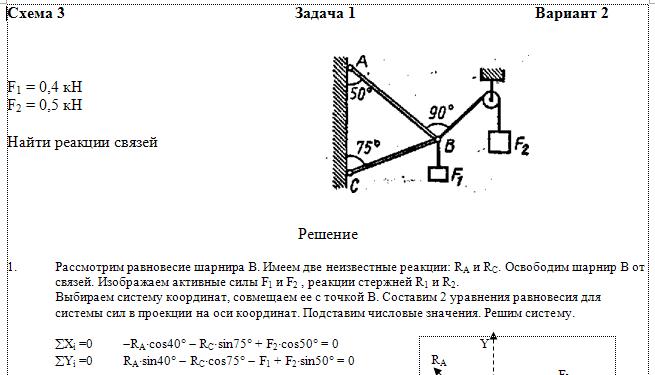
Треугольник власти | Треугольник силы тока напряженияТреугольник мощности — это просто прямоугольный треугольник, сторона которого представляет активную мощность, реактивную мощность и полную мощность. Базовая составляющая символизирует активную мощность, перпендикулярная составляющая обозначает реактивную мощность, а гипотенуза символизирует полную мощность.
Что такое треугольник власти?
Определите треугольник власти | Определение треугольника мощности Треугольник мощности — это графическое представление реальной или активной мощности, реактивной мощности и полной мощности в прямоугольном треугольнике.
Уравнение степенного треугольника | Треугольник мощности PQS
Расчет формулы треугольника мощности | Уравнение треугольника мощностиВ силовой треугольник, активная мощность P, реактивная мощность Q и полная мощность S образуют прямоугольный треугольник. Следовательно,
гипотенуза² = база² + перпендикулярный²
S² = P² + Q²
Здесь полная мощность (S) измеряется в вольт-амперах (ВА).
Активная мощность (P) измеряется в ваттах (Вт).
Реактивная мощность (Q) измеряется в вольт-амперных реактивных (VAR).
Треугольник мощности — это графическое представление реальной или активной мощности, реактивной мощности и полной мощности в прямоугольном треугольнике.
Активная или истинная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Он измеряется в ваттах (Вт) или киловаттах (кВт) и обозначается буквой P и средним значением активной мощности P..
Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. T также известен как безваттная мощность. Это мощность, получаемая от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольтах реактивной мощности (KVAR) и обозначается Q.
Полная мощность в цепи, как поглощенная, так и рассеиваемая, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без какой-либо величины фазового угла.
Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, то есть в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток не совпадают по фазе, и вводится сложная величина.
Мощность трехфазной системы равна = √3 x коэффициент мощности x напряжение x ток.
Треугольник мощности для последовательной цепи RLC | Цепи силового треугольника
Давайте рассмотрим схему RLC, включенную последовательно, как указано выше.
Где резистор с сопротивлением R.
индуктор с индуктивностью L.
конденсатор емкостью С.
Источник переменного напряжения V_msin⍵t применяется.
V — действующее значение приложенного напряжения, а I — действующее значение полного тока в цепи. В катушка индуктивности и конденсатор производят X_L и Х_C противостояния соответственно в цепи. Теперь может быть три случая:
Случай 1: X_L > X_C
Случай 2: X_L <X_C
Треугольник мощности получается из векторной диаграммы, если мы умножим каждый из векторов напряжения на I, мы получим три компонента мощности.
Из векторного треугольника мы можем быстро получить треугольник мощности путем умножения напряжений с I. Реальная мощность умножается на V_R, что равно I²R. Реактивная мощность умножается на (В_C — V_L), что равно I²(X_C — ИКС_L). Полная мощность V = I²Z рассчитывается на основе активной мощности и реактивной мощности для обоих случаев. Здесь мы принимаем во внимание другую величину, комплексную мощность. Комплексная мощность — это сумма активной мощности и реактивной мощности, представленных в комплексной форме, то есть с величиной «j».
Следовательно, комплексная мощность
S = P — jQ, когда X_L <X_C
S = P + jQ, когда X_L > X_C
Теперь, для случая 1, индуктивное сопротивление меньше, чем емкостное сопротивление. Следовательно, реактивная мощность отрицательна, и угол ϕ также отрицателен. Для случая 2 индуктивный значение реактивного сопротивления больше, чем значение емкостного сопротивления, реактивная мощность равна +ve, угол ϕ также равен +ve.
Треугольник активной реактивной полной мощности | Треугольник вольт ампер
Треугольник активной и реактивной мощности.
Треугольник истинной силы.
Активная или истинная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Она измеряется в ваттах (Вт) или киловаттах (кВт) и обозначается буквой P, а среднее значение активной мощности P равно
П = ВИ = Я²R
Треугольник реактивной мощностиРеактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. Он также известен как безваттный мощность. Это мощность, получаемая от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольтах, реактивных (KVAR) и обозначается Q.
Реактивная мощность Q = VI_{реактивный} = Я²X.
Треугольник кажущейся мощностиПолная мощность в цепи, как поглощенная, так и рассеиваемая, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без какой-либо величины фазового угла. {2} + (Реактивная\; мощность)2}[/Latex]
Для чисто резистивной схемы реактивной мощности нет. Итак, полная мощность равна активной или истинной мощности.
Силовой треугольник для цепи переменного тока | Треугольник электрической мощностиЦепи переменного тока могут иметь любую комбинацию R, L и C, и если мы хотим правильно рассчитать общую мощность, мы должны знать разницу фаз между I и V. Форма волны тока и напряжения синусоидальная. Поскольку мощность = напряжение x ток, максимальная мощность достигается, когда обе формы волны совпадают. В этой ситуации сигналы называются «синфазными» друг с другом.
В чисто резистивной схеме переменного тока I и V идеально согласованы друг с другом по фазе. Следовательно, просто умножая их, мы можем получить силу.
Если в цепи присутствует индуктивная или емкостная нагрузка, создается разность фаз. Даже если разность фаз незначительна, мощность переменного тока делится на две части — одну положительную и одну отрицательную. Отрицательная мощность не является математически отрицательной величиной; это просто означает, что питание подается в систему, но передачи энергии не происходит. Эта мощность называется реактивной мощностью. Положительная величина выполняет некоторую реальную работу, поэтому она классифицируется как реальная или активная мощность.
Другая часть питания поступает в схему от источника. Это известно как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.
Треугольник силы закона Ома | Треугольник мощности ОмаЗакон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, то есть в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток не совпадают по фазе, и вводится сложная величина. Нам нужно применить некоторые специальные формулы, чтобы рассчитать переменный ток и параметры треугольника мощности.
Треугольник мощности для емкостной нагрузкиЕмкостная нагрузка означает, что коэффициент мощности опережает напряжение, поскольку ток опережает напряжение по фазовому углу.
Треугольник мощности для индуктивной нагрузкиИндуктивная нагрузка означает, что коэффициент мощности отстает, потому что I отстает от V на фазовый угол.
Сложный треугольник властиКомплексная мощность — это не что иное, как представление власти с помощью комплексных чисел. Действительная часть представляет собой активную мощность. Мнимая часть представляет собой реактивную мощность.
Предположим, что ток и напряжение в емкостной цепи равны I и V соответственно. Мы знаем, что для емкостной нагрузки I опережает V по фазовому углу. Возьмем этот угол за ϕ.
Допустим, напряжение на нагрузке, V = ve^jƟ и ток I = iej^{(Ɵ + ϕ)}.
Мы знаем, мощность это напряжение умножается на текущее сопряжение.
Итак, комплексная мощность S = VI * = ve^jƟ х т.е.^{-j (Ɵ + ϕ)}= соперничать^-jϕ
S = vi (cosϕ — jsinϕ) = vicosϕ — jvisinϕ = P — jQ [мы знаем активную мощность P = vicosϕ и реактивную мощность Q = visinϕ]
Для емкостной нагрузки I отстает от V на фазовый угол. Итак, напряжение на нагрузке V = ve^jƟ и ток I = ie^{j (Ɵ-ϕ)}.
Такая сложная сила
S = VI * = ve^jƟ х т.е.-j^(Ɵ-ϕ)= соперничать^jϕ
S = vi (cosϕ + jsinϕ) = vicosϕ + jvisinϕ = P + jQ
Трехфазный треугольник питанияПеременный ток может быть однофазным или трехфазным. Изменение амплитуды тока приводит к генерации синусоидальных волн. Для однофазного питания есть только одна волна. Трехфазные системы разделяют ток на три части. Три компонента тока сдвинуты по фазе на треть цикла каждый. Каждый компонент тока равен по размеру, но противоположен по направлению двум другим конъюнктивам. {2}}[/латекс]
Коэффициент мощности [латекс]= \frac{R}{Z}[/латекс]
Коэффициент мощности треугольника мощностиКоэффициент мощности в треугольнике мощности называется отношением активной мощности к полной мощности, определяемой как косинус угла вектора.
Треугольник коррекции коэффициента мощностиКоррекция коэффициента мощности — это метод повышения эффективности электрической цепи за счет снижения реактивной мощности. Коррекция коэффициента мощности достигается за счет параллельно соединенных конденсаторов, которые противодействуют эффектам, вызванным индуктивными элементами, и уменьшают фазовый сдвиг.
Формула треугольника коэффициента мощностиКоэффициент мощности для емкостной или индуктивной нагрузки [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности [латекс] = \frac{Real\; мощность {Очевидная \; сила}[/латекс]
Энергетический треугольникЭлектрическая энергия определяется как мощность системы, умноженная на общее время использования мощности.
Энергия E = P x T
Как нарисовать треугольник власти?
Генератор треугольника мощностиТреугольник мощности построен на основе активной мощности в качестве основы, реактивной мощности в качестве перпендикуляра и полной мощности в качестве гипотенузы.
Металлические треугольники на линиях электропередачМы часто видим несколько треугольных петель, свисающих с линий электропередач. Они используются для обеспечения устойчивости строп при сильном ветре. Эти треугольные ребра предохраняют стропы от слишком близкого отскока друг к другу и гарантируют, что они не отсоединятся от изоляторов.
Расчет треугольников мощности | Калькулятор треугольника мощности
В. Катушка индуктивности 120 мГн и сопротивлением 70 Ом последовательно подключены к источнику питания 220 В, 50 Гц. Рассчитайте полную мощность. Индуктивное сопротивление [Latex]X_{L} = 2\pi fL = 2 \times 3. 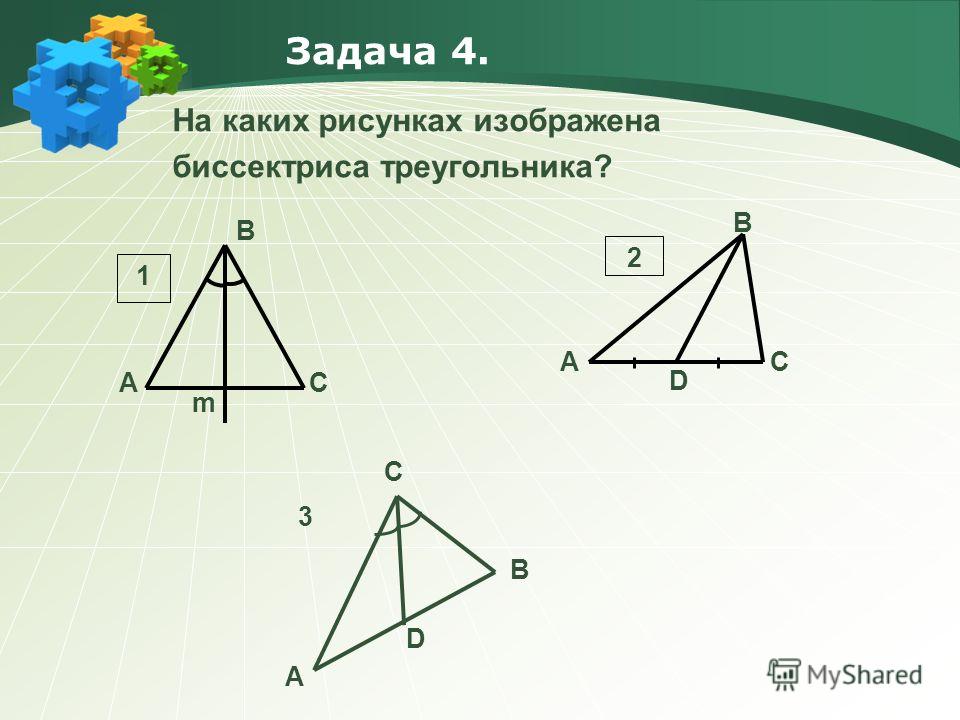{2}} = 13\:\Омега[/Латекс]
Коэффициент мощности цепи = R / Z = 12/13 = 0.92
Пример треугольника мощностиВ. Нагрузка 20 кВт имеет отстающий коэффициент мощности 0.8. Найдите такой номинал конденсатора, чтобы коэффициент мощности увеличился до 0.95.
Здесь истинная мощность P = 20 кВт.
Коэффициент мощности cosϕ₁ = 0.8
Мы знаем, что реактивная мощность должна быть уменьшена, чтобы получить повышенный коэффициент мощности. Следовательно, фазовый угол также уменьшится. Предположим, что изначально фазовый угол был ϕ₁, а после снижения реактивной мощности фазовый угол ϕ₂. Итак, треугольник мощности выглядит так:
Из диаграммы видно, что реактивная мощность снизилась на АБ с переменного тока. Итак, нам нужно вычислить разницу между переменным током и AB, и эта величина является требуемым номиналом конденсатора.
Здесь OA = 20 кВт.
cosϕ₁ = 0.8
cosϕ₂ = 0.95
Мы знаем, cosϕ₁ = OA / OC
Итак, OC = 20 / 0. 8 = 25 кВА
AC = √ (OC² — О.А.²) = 15 кВАр
Cosϕ₂ = OA / OB
Итак, ОБ = 20 / 0.95 = 21 кВА
AB = √ (OB² — О.А.²) = 6.4 кВАр
Следовательно, BC = AC — AB = (15 — 6.4) = 8.6 KVAR
Часто задаваемые вопросы
Сколько типов сил есть в треугольнике власти?
Треугольник власти состоит из трех типов власти.
— Истинная или активная мощность.
— Реактивная сила.
— полная мощность.
Что is силовой треугольник? Объясните активный,реактивная и полная мощность с образцом.Треугольник мощности — это треугольное представление отношения между истинной мощностью, реактивной мощностью и полной мощностью.
Например, в любом электрическом приборе общая генерируемая мощность складывается из активной и реактивной мощности.
Что такое силовой треугольник в цепи переменного тока?Треугольник власти Цепь переменного тока может быть резистивной, емкостной или индуктивной, а треугольник состоит из трех видов мощности, а полная мощность вычисляется с помощью активной мощности и реактивной мощности.
Что такое силовой треугольник в цепи RL?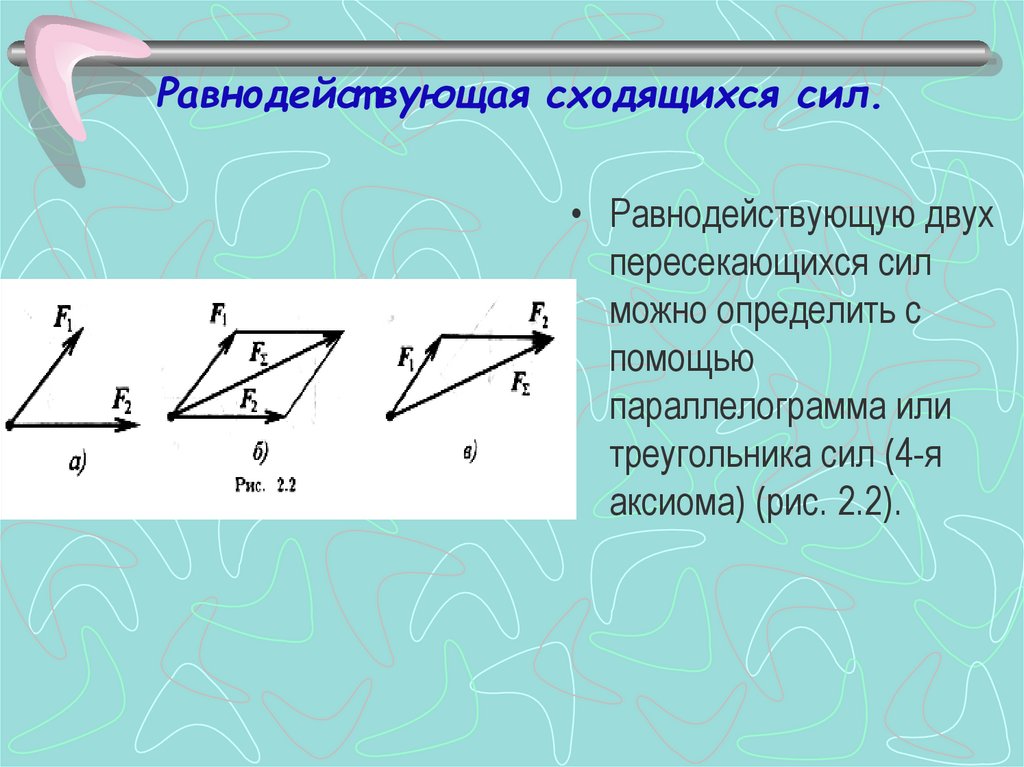Цепь RL имеет силовой треугольник с активной мощностью = I²R, реактивная мощность = I²X_L, а полная мощность = I²Z, где X_L — индуктивное реактивное сопротивление, а Z — полное сопротивление цепи.
Какая связь между кВА, кВт и кВАр?KVA — это единица измерения полной мощности, тогда как KW и KVAR — единицы истинной мощности и реактивной мощности, соответственно. Следовательно, исходя из концепции треугольника мощности, мы можем сделать вывод, что кВА² = КВт² + КВАР².
Какое значение имеет коэффициент мощности?Для индуктивных и емкостных нагрузок коэффициент мощности играет жизненно важную роль в вычислении реактивной мощности. Реактивная мощность — это часть активной мощности, которая уменьшается, а коэффициент мощности — это соотношение истинной мощности и полной мощности. Единичный коэффициент мощности указывает на то, что схема является полностью резистивной по своей природе.
Сколько ватт в 6 кВА?6 кВА = 6000 ВА
При единичном коэффициенте мощности 6 кВА = 1 x 6000 = 6000 Вт
Если коэффициент мощности другой, 6 кВА = 6 x (коэффициент мощности) ватт.
Как конвертировать KWH в KVAH?KWH = KVAH X коэффициент мощности
Следовательно, KVAH = KWH / коэффициент мощности.
Сколько ватт соответствует 1 кВА?Для чисто резистивной нагрузки реактивной мощности нет. Таким образом, коэффициент мощности равен 1. Здесь 1 кВА = 1 Вт.
Если нагрузка емкостная или индуктивная, резистивная мощность не равна 0, так как коэффициент мощности — это сопротивление / импеданс. Здесь 1 кВА = коэффициент мощности x 1 кВт.
Почему электрические башни имеют треугольную форму?По следующим причинам электрические башни имеют треугольную форму.
‌Треугольники имеют большую площадь основания, что позволяет им быть очень жесткими. Такая жесткость помогает выдерживать боковые нагрузки.
‌Треугольники имеют меньшую площадь, чем любой четырехугольник. Если бы форма была четырехугольной, то стоимость была бы больше. Треугольная форма снижает стоимость за счет устранения одной лишней стороны.
Какой коэффициент мощности у трансформатора?Коэффициент мощности трансформатор зависит от характеристик нагрузки.
‌Если нагрузка чисто резистивная, коэффициент мощности равен единице или 1.
‌Если нагрузка емкостная, т. Е. X_C > X_Lкоэффициент мощности называется опережающим.
‌Если нагрузка индуктивная, т. Е. X_L > X_Cкоэффициент мощности называется запаздывающим.
В чем разница между KVA KWH KVAH и KVAR? | Треугольник мощности KW KVA KVARKVA означает киловольт-ампер. Это единица измерения реальной или активной мощности. {2}}} [/Latex]
Какая единица измерения коэффициента мощности?Коэффициент мощности — это отношение активной мощности (кВт) к полной мощности (кВА), поскольку числитель и знаменатель являются мощностью, коэффициент мощности — это величина на единицу меньше.

23 факта, которые вы должны знать – Lambda Geeks
Треугольник власти | Треугольник мощности, напряжения, тока Треугольник мощности — это просто прямоугольный треугольник, сторона которого соответствует активной, реактивной и полной мощности. Компонент основания символизирует активную мощность, перпендикулярный компонент обозначает реактивную мощность, а гипотенуза символизирует полную мощность.
Что такое треугольник силы?
Определение треугольника власти | Определение треугольника силы Треугольник мощности — это графическое представление реальной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
Уравнение силового треугольника | Треугольник мощности PQS
Расчет формулы треугольника мощности | Уравнение треугольника мощностей В треугольнике мощностей активная мощность P, реактивная мощность Q и полная мощность S образуют прямоугольный треугольник. Следовательно,
гипотенуза ² = основание ² + перпендикуляр ²
S ² = P ² + Q ²
Здесь полная мощность (S) измеряется в вольт-амперах (ВА).
Активная мощность (P) измеряется в ваттах (Вт).
Реактивная мощность (Q) измеряется в реактивных вольт-амперах (ВАр).
Треугольник мощности — это графическое представление активной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
Активная или действительная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется как P и среднее значение активной мощности P .
Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. T также известен как мощность без ватт. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в реактивных киловольт-амперах (кВАр) и обозначается Q.
Полная мощность в цепи, как поглощаемая, так и рассеиваемая, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла.
Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т. е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина.
Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Силовой треугольник для цепи серии RLC | Цепи треугольника мощности
Рассмотрим цепь RLC, соединенную последовательно, как указано выше.
Где резистор с сопротивлением R.
индуктор с индуктивностью L.
конденсатор с емкостью C.
Источник переменного напряжения V _м sin⍵t применяется.
В — среднеквадратичное значение приложенного напряжения, а I — среднеквадратичное значение полного тока в цепи. Катушка индуктивности и конденсатор дают Х _L и X _C оппозиций соответственно в цепи. Теперь может быть три случая:
Случай 1: X _L > X _C
Случай 2: X _L < X _C
умножив каждый из векторов напряжения на I, мы получим три составляющие мощности.
Из векторного треугольника мы можем быстро получить треугольник мощности, умножив напряжения на I. Реальная мощность умножается на V _R , что равно I ² R. Реактивная мощность I умножается на (V _C – V _L ), что равно I ² (X _C – X _L). Полная мощность V = I ² Z рассчитывается из активной мощности и реактивной мощности для обоих случаев. Здесь мы принимаем во внимание другую величину, комплексную мощность. Комплексная мощность представляет собой сумму активной мощности и реактивной мощности, представленных в комплексной форме, т. е. с величиной j.
Следовательно, комплексная мощность
S = P – jQ когда X _L < X _C
S = P + jQ, когда X _L > X _C
меньше емкостного сопротивления. Следовательно, реактивная мощность отрицательна, и угол ϕ также отрицателен. Для случая 2 значение индуктивного сопротивления больше, чем значение емкостного сопротивления, реактивная мощность равна +ve, а угол ϕ также равен +ve.
Треугольник активной реактивной полной мощности | Мощность вольт ампер треугольник
Треугольник активной и реактивной мощности .
Треугольник истинной силы . Активная или действительная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется в виде P и среднего значения активной мощности P is,
P = VI = I ² R
Треугольник реактивной мощности Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. Он также известен как Вт без мощности . Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольт-амперах реактивной (кВАр) и обозначается Q.
Реактивная мощность Q = VI _{реактивная} = I ² X.
Треугольник полной мощности Полная мощность в цепи, как поглощаемой, так и рассеиваемой, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла. 9{2} + (Реактивная\; мощность)2}[/Latex]
Для чисто резистивной цепи реактивная мощность отсутствует. Итак, кажущаяся мощность равна активной или истинной мощности.
Силовой треугольник для цепи переменного тока | Треугольник электрической мощности Цепи переменного тока могут иметь любую комбинацию R, L и C, и если мы хотим правильно рассчитать общую мощность, мы должны знать разность фаз между I и V. Форма волны тока а напряжение синусоидальное. Поскольку мощность = напряжение x ток, максимальная мощность достигается, когда обе формы волны совпадают. В этой ситуации формы волны называются «синфазными» друг с другом.
В чисто резистивной цепи переменного тока I и V идеально совпадают по фазе. Следовательно, просто умножая их, мы можем получить мощность.
Если в цепи имеется индуктивная или емкостная нагрузка, создается разность фаз. Даже если разница фаз незначительна, мощность переменного тока делится на две части: одну положительную и одну отрицательную. Отрицательная мощность не является математически отрицательной величиной; это просто означает, что в систему подается питание, но передачи энергии не происходит. Эта мощность известна как реактивная мощность. Положительная величина совершает некоторую реальную работу, поэтому ее классифицируют как реальную или активную мощность.
Другая часть питания подается в цепь от источника. Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.
Треугольник силы по закону Ома | Треугольник силы Ома Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т. е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина. Нам нужно применить некоторые специальные формулы, чтобы рассчитать переменный ток и параметры силового треугольника.
Треугольник мощности для емкостной нагрузки Емкостная нагрузка означает, что коэффициент мощности опережает ток по фазовому углу относительно напряжения.
Треугольник мощности для индуктивной нагрузки Индуктивная нагрузка показывает, что коэффициент мощности отстает, поскольку I отстает от V на фазовый угол.
Треугольник комплексной мощности Комплексная мощность есть не что иное, как представление мощности с использованием комплексных чисел. Действительная часть представляет собой активную мощность. Мнимая часть представляет собой реактивную мощность.
Предположим, что ток и напряжение в емкостной цепи равны I и V соответственно. Мы знаем, что для емкостной нагрузки I опережает V на фазовый угол. Примем этот угол за ϕ.
Допустим, напряжение на нагрузке V= ve ^jƟ и ток I = iej ^(Ɵ+ϕ) .
Мы знаем, мощность — это напряжение, умноженное на сопряженный ток.
Итак, комплексная мощность S = VI* = ve ^jƟ x ie ^-j(Ɵ+ϕ) = vie ^-jϕ
S = vi(cosϕ – jsinϕ) = vicosϕ – jvisinϕ = P – jQ [мы знаем активную мощность P = vicosϕ и реактивную мощность Q = visinϕ]
Для емкостной нагрузки I отстает от V на фазовый угол. Итак, напряжение на нагрузке V= ve ^jƟ и ток I = ie ^j(Ɵ-ϕ) .
So комплексная мощность
S = VI* = ve ^jƟ x ie-j ^(Ɵ-ϕ) = vie ^jϕ
S = vi(cosϕ + jsinϕ) = P vicosϕ + jvisinϕ
Трехфазный силовой треугольник Переменный ток может быть однофазным или трехфазным. Изменение амплитуды тока приводит к генерации синусоидальных волн. Для однофазного питания есть только одна волна. Трехфазные системы разделяют ток на три части. Три составляющие тока не совпадают по фазе на одну треть цикла каждая. Каждая текущая составляющая равна по величине, но противоположна по направлению двум другим конъюнктивным.
Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Треугольник импеданса и треугольник мощности
Коэффициент мощности треугольника импеданса В цепях постоянного тока только сопротивление отвечает за противодействие току. Но в цепях переменного тока величина, называемая реактивным сопротивлением, также противодействует току. Реактивное сопротивление может быть любой комбинацией индуктивности и емкости. Но и индуктивность, и емкость отличаются от сопротивления фазовым углом (отстающим или опережающим). Таким образом, мы не можем сложить их арифметически. Итак, мы строим треугольник импеданса с гипотенузой Z (импеданс), основанием R (сопротивление) и реактивным сопротивлением X (индуктивное или емкостное реактивное сопротивление или оба). 9{2}}[/Latex]
Коэффициент мощности [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности треугольника мощности Коэффициент мощности в треугольнике мощности обозначается как отношение активной мощности к полной мощности, определяемое как косинус угла вектора.
Треугольник коррекции коэффициента мощности Коррекция коэффициента мощности — это метод повышения эффективности электрической цепи за счет снижения реактивной мощности. Коррекция коэффициента мощности достигается за счет параллельно соединенных конденсаторов, которые противодействуют эффектам, вызванным индуктивными элементами, и уменьшают фазовый сдвиг.
Формула треугольника коэффициента мощности Коэффициент мощности для емкостной или индуктивной нагрузки [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности [Latex]= \frac{Real\; мощность {Очевидная \; power}[/Latex]
Треугольник энергии мощности Электрическая энергия определяется как мощность системы, умноженная на общее время использования энергии.
Энергия E = P x T
Как нарисовать треугольник мощности?
Генератор треугольника мощностей Треугольник мощностей строится с использованием активной мощности в качестве основания, реактивной мощности в качестве перпендикуляра и полной мощности в качестве гипотенузы.
Металлические треугольники на линиях электропередач Мы часто видим несколько треугольных петель, свисающих с линий электропередач. Они используются для обеспечения устойчивости строп при сильном ветре. Эти треугольные ребра предотвращают подпрыгивание строп слишком близко друг к другу и гарантируют, что они не оторвутся от изоляторов. 9{2}} = 13\: \Omega[/Latex]
Коэффициент мощности цепи = R/Z = 12/13 = 0,92
Пример треугольника мощностей Q. Нагрузка 20 кВт при коэффициент мощности 0,8 отстает. Найдите номинал конденсатора, чтобы он мог поднять значение коэффициента мощности до 0,95.
Здесь реальная мощность P = 20 кВт
Коэффициент мощности cosϕ ₁ = 0,8
Мы знаем, что реактивная мощность должна быть уменьшена, чтобы получить увеличенный коэффициент мощности. Следовательно, фазовый угол также уменьшится. Предположим, что изначально фазовый угол был ϕ ₁ , а после снижения реактивной мощности фазовый угол равен ϕ ₂ . Итак, треугольник мощностей выглядит так-
Из диаграммы видно, что реактивная мощность уменьшилась до AB от переменного тока. Итак, нам нужно вычислить разницу AC и AB, и эта величина является требуемым номиналом конденсатора.
Здесь, OA = 20 кВт
COS Вотство ₁ = 0,8
COS Вотство ₂ = 0,95
Мы знаем, COSЦ ₁ = OA/OC
SO, OC = 20/0,8 = 25 KVA 9009 = OA
SO, OC = 20/0,8 = 25 KVA 9008
SO, OC = 20/0,8 = 25 KVA 9008
SO, OC = 20/0,8 = 25 KVA 9008
SO, OC = 20/0,8 = 25 KVA0008
AC = √ (OC ² — OA ²) = 15 KVAR
COSЦ ₂ = OA/OB
SO, OB = 20/0,95 = 21 KVA
AB = √ (OB ^2. – OA ² ) = 6,4 квар
Следовательно, BC = AC – AB = (15 – 6,4) = 8,6 квар
Часто задаваемые вопросы
Сколько типов треугольника в степени степеней?
Треугольник мощности состоит из трех типов мощности
– Истинная или активная мощность.
– реактивная мощность.
– полная мощность.
Что такое силовой треугольник? Объясните активную , реактивную и полную мощность на примере. Треугольник мощности представляет собой треугольное представление отношения между активной мощностью, реактивной мощностью и полной мощностью.
Например, в любом электроприборе общая вырабатываемая мощность представляет собой части активной и реактивной мощности.
Что такое треугольник мощности цепи переменного тока? Треугольник мощности цепи переменного тока может быть резистивным, емкостным или индуктивным, и треугольник состоит из трех видов мощностей, а полная мощность рассчитывается с помощью активной мощности и реактивной мощности.
Что такое треугольник мощности цепи RL? Цепь RL имеет треугольник мощности с активной мощностью = I ² R, реактивной мощностью = I ² X _L , а полная мощность = I ² Z, где X _L — индуктивное реактивное сопротивление, а Z — полное сопротивление цепи.
Какая связь между KVA, KW и KVAr? КВА — это единица измерения полной мощности, а кВт и кВАр — это единицы активной мощности и реактивной мощности соответственно. Таким образом, из концепции треугольника мощностей можно сделать вывод, что ^{кВА 2} = ² кВт + кВАр.0034 2 .
Какое значение имеет коэффициент мощности? Для индуктивных и емкостных нагрузок коэффициент мощности играет жизненно важную роль при расчете реактивной мощности. Реактивная мощность — это часть активной мощности, которая уменьшается, а коэффициент мощности — это отношение истинной мощности к полной мощности. Коэффициент мощности, равный единице, указывает на то, что цепь имеет полностью резистивный характер.
Сколько ватт составляет 6 кВА? 6 кВА = 6000 ВА
При единичном коэффициенте мощности 6 кВА = 1 x 6000 = 6000 Вт
Если коэффициент мощности другой, 6 кВА = 6 x (коэффициент мощности) Вт
Как преобразовать кВтч в кВАч? кВтч = кВАч X коэффициент мощности
Следовательно, кВАч = кВтч/коэффициент мощности
Сколько ватт составляет 1 кВА? Для чисто резистивной нагрузки реактивная мощность отсутствует. Таким образом, коэффициент мощности равен 1. Здесь 1 кВА = 1 Вт
. Если нагрузка емкостная или индуктивная, резистивная мощность не равна 0, поскольку коэффициент мощности представляет собой сопротивление/импеданс. Здесь 1 кВА = коэффициент мощности x 1 кВт
Почему электрические опоры имеют треугольную форму? По следующим причинам электрические опоры имеют треугольную форму.
‌Треугольники имеют большую площадь основания, что делает их очень жесткими. Эта жесткость помогает выдерживать боковые нагрузки.
‌Треугольники имеют меньшую площадь, чем любой четырехугольник. Если бы форма была четырехугольной, то стоимость была бы больше. Треугольная форма снижает стоимость за счет исключения одной лишней стороны.
Каков коэффициент мощности трансформатора? Коэффициент мощности трансформатора зависит от характеристик нагрузки.
‌Если нагрузка чисто резистивная, коэффициент мощности равен единице или 1.
‌Если нагрузка емкостная, т. е. X _C > X _L , коэффициент мощности называется опережающим.
‌Если нагрузка индуктивная, т. е. X _L > X _C , коэффициент мощности называется отстающим.
В чем разница между KVA KWH KVAH и KVAR? | Треугольник мощности кВт КВА КВАР КВА означает киловольт-ампер. Это единица реальной или активной мощности.
KWH означает киловатт-час. Это используется для измерения того, сколько энергии (в киловаттах) потребляется за час.
KVAH означает киловольт-ампер-час. KVAH — это полная мощность, а KWH — это активная мощность. KVAH = кВтч/коэффициент мощности
KVAR означает реактивный киловольт-ампер. Используется для измерения реактивной мощности. 9{2}}}[/Latex]
Какова единица коэффициента мощности? Коэффициент мощности – это отношение активной мощности (кВт) к полной мощности (кВА), поскольку и числитель, и знаменатель являются мощностями, коэффициент мощности – это величина без единицы.

Формула, треугольник импеданса и его работа
В общем, мощность — это способность выполнять работу. В области электричества электрическая мощность — это количество энергии, переданной в какую-либо другую форму в единицу времени, такую как свет, тепло и т. д. Математически ее можно определить как произведение напряжения и силы тока. Рассмотрим цепи постоянного тока, которые имеют только один источник напряжения либо источник напряжения, либо источник тока, поэтому конденсаторы работают как разомкнутая цепь в установившемся режиме, тогда как катушки индуктивности работают как короткое замыкание. Здесь цепь постоянного тока работает как резистивная цепь, поэтому вся электрическая мощность может рассеиваться в виде тепла. Здесь напряжение и ток находятся в одной фазе, и вся электрическая мощность может быть представлена как P = V * I. Итак, в этой статье дается краткая информация о треугольнике власти.
Три элемента, составляющие мощность переменного тока, а именно активная мощность, реактивная мощность и полная мощность, могут быть выражены графически на трех сторонах прямоугольного треугольника, такого как треугольник импеданса, обсуждаемый ниже. 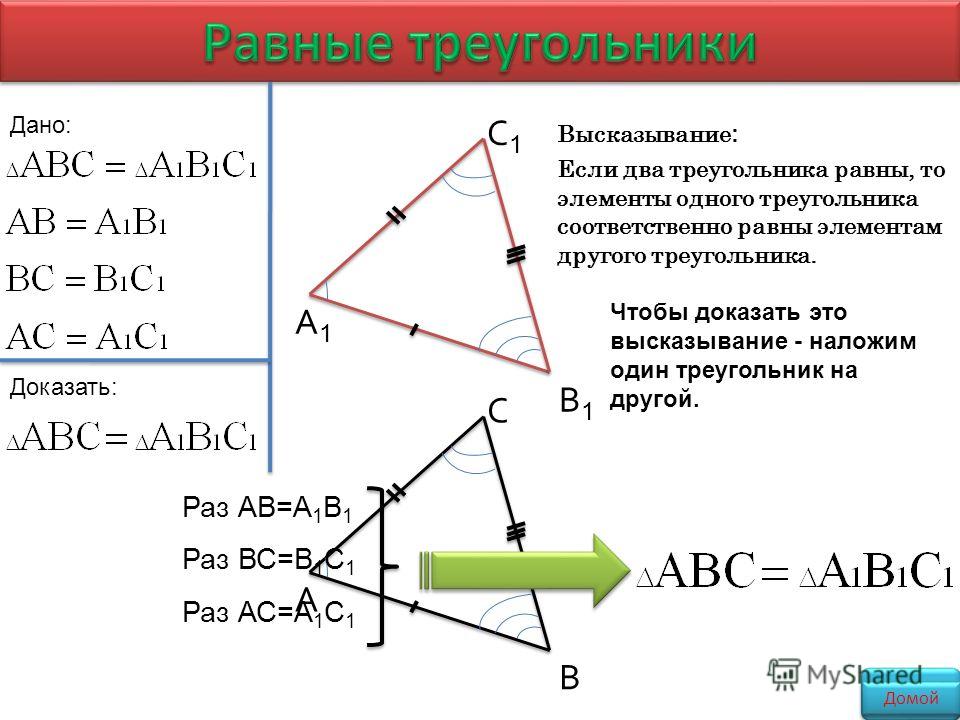Как показано на рисунке ниже, фактическая мощность P цепи представляет собой горизонтальную (прилегающую) сторону, реактивная мощность Q представляет собой вертикальную (противоположную) сторону, а гипотенуза представляет собой полную мощность (S), генерируемую из мощности. треугольник.
Силовой треугольник 92 в омах
Φ = фазовый угол в градусах. Больший фазовый угол дает большую реактивную мощность
Коэффициент мощности Cos(Φ) = P/S = R/Z W/VA =
Sin(Φ) = Q/S = X/Z = ВАр/ВА
Tan(Φ) = Q/P = X/R =VAr/W
полная мощность и разность фаз будут равны 0. Это называется единичным коэффициентом мощности.
Коэффициент мощности = Cos 0° = 1
Когда кривые напряжения и тока чисто реактивной цепи противофазны друг другу на угол 90 градусов, тогда разность фаз будет 90 градусов.
Коэффициент мощности = cos 90° =0
Соотношение между полной мощностью, активной мощностью и коэффициентом мощности цепи определяется как
Активная мощность P = Полная мощность (S) x коэффициент мощности
Коэффициент мощности = Вт/Вольт-ампер
В индуктивной цепи отстающий коэффициент мощности получается, потому что ток отстает от напряжения. В емкостной цепи получается опережающий коэффициент мощности, потому что ток опережает напряжение. Концепция треугольника мощности — это просто схематическое изображение фазовой диаграммы индуктивной/емкостной нагрузки, подключенной к источнику. Он получается путем умножения тока I в цепи, активного тока (IcosØ) и реактивного тока (IsinØ) на напряжение V.
Напряжение «V» и ток «I» в цепи, активный ток IcosØ и реактивный ток IsinØ дают полную мощность (S), активную мощность (P) и реактивную мощность (Q) соответственно.
Формула треугольника мощности
Графическое изображение прямоугольного треугольника, показывающее взаимосвязь между реактивной мощностью, реальной/активной мощностью и полной мощностью, известно как треугольник мощности. Умножая каждую составляющую тока, т.е. активную составляющую (Icosϕ) или реактивную составляющую (Isinϕ) на напряжение V, мы получаем треугольник мощности, как показано на рисунке ниже.
Прямоугольный треугольник
Фактическая мощность, потребляемая или используемая в цепи переменного тока, называется истинной мощностью, реальной мощностью или активной мощностью. Измеряется в киловаттах (кВт) или МВт. Мощность, которая течет туда и обратно, то есть мощность, которая перемещается или реагирует в обоих направлениях в цепи, называется реактивной мощностью.
Реактивная мощность измеряется в реактивной мощности киловольт-ампер (кВАр) или реактивной мощности МВАР.
Произведение квадратного корня (RMS) из напряжения и тока (RMS) называется полной мощностью. Эта мощность измеряется в кВА или МВА. Следующая точка представляет взаимосвязь между следующими величинами и иллюстрируется графиком, называемым треугольником мощности, показанным выше. Умножение активной составляющей тока на напряжение цепи V дает активную мощность. Эта мощность создает крутящий момент в двигателе, тепло в нагревателе и т. д. Эта мощность измеряется с помощью устройства, называемого ваттметром. Умножьте реактивный ток на напряжение в цепи, чтобы получить реактивную мощность. Эта мощность дает коэффициент мощности, который перемещается взад и вперед по цепи.
Умножьте ток цепи на напряжение цепи, чтобы получить полную мощность. Отношение можно определить из перевернутого треугольника, изображенного на графике выше, т. е. мощность, взяв отношение активной мощности к кажущейся мощности. Коэффициент мощности рассчитывается из приведенного выше треугольника мощности, который представляет собой угол косинуса между векторами напряжения и тока, заданный как
Коэффициент мощности Cosφ = Активная мощность / Полная мощность = кВт/кВА
Как мы знаем, мощность просто известен как произведение напряжения и тока, но в цепях переменного тока, за исключением чисто резистивных цепей, обычно существует разность фаз между напряжением и током, поэтому VI не представляет фактическую мощность цепи. Соотношение между активной, реактивной и полной мощностью определяется как 92
Треугольник импеданса
Прямоугольный треугольник, основание, перпендикуляр и гипотенуза которого представляют соответственно электрическое сопротивление, реактивное сопротивление и импеданс, называется треугольником импеданса.
Это основное геометрическое представление импеданса цепи.
Импеданс состоит из двух компонентов. одно сопротивление, а другое реактивное сопротивление. Таким образом, это может быть выражено этими двумя факторами. Полное сопротивление цепи переменного тока Z = R+jX
Где «R» — сопротивление
«X» — реактивное сопротивление.
Из приведенного выше выражения Z является комплексным числом и, следовательно, может быть выражено геометрически так же, как и комплексное число. Геометрическое представление показано ниже.
Геометрическое представление
Полученный треугольник OAB называется треугольником импеданса. Значение импеданса Z можно легко определить по этому треугольнику, используя теорему Пифагора. Значение импеданса Z равно OB и может быть найдено как 92)
Угол Z с R — это угол, образованный между OA и OB, как показано на рисунке выше.
tanƟ = (X/R)
Следовательно, треугольник импеданса используется для определения величины и угла импеданса, а также коэффициента мощности данной цепи. 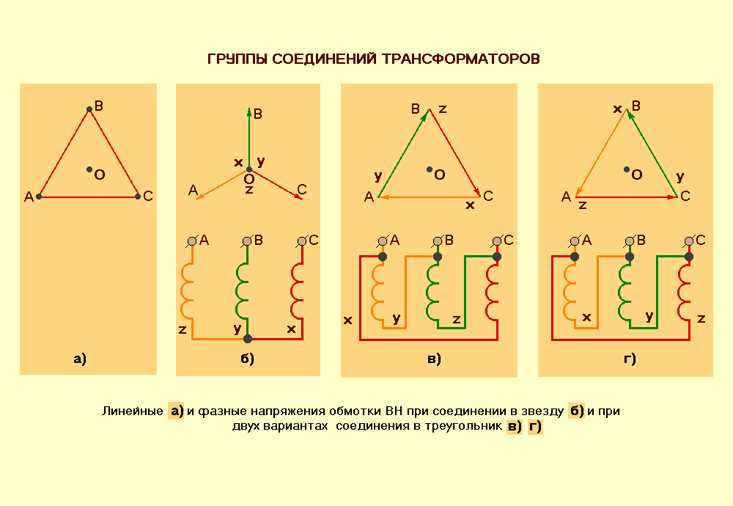2 * R.
, где R — общая резистивная составляющая цепи.
Поскольку резисторы не создают разности фаз (фазового сдвига) между напряжением и током, вся полезная мощность передается непосредственно на резистор и преобразуется в тепло, свет и работу. Тогда мощность, потребляемая резистором, является фактической мощностью, которая в основном представляет собой среднюю мощность схемы. Умножьте среднеквадратичное значение напряжения и тока на косинус фазового угла (φ), как показано на рисунке, чтобы найти соответствующее фактическое значение мощности. 92*R = V*I*Cosφ в ваттах (Вт)
Поскольку в резистивной цепи нет разности фаз между напряжением и током, фазовый сдвиг между осциллограммами напряжения и тока также равен нулю.
Следовательно,
P = Vrms x Irms x Cosφ
Cos (0°) = 1
Следовательно, P = Vrms x Irms Ваттах
или киловатты или мегаватты
В = среднеквадратичное значение напряжения в вольтах
I= среднеквадратичное значение тока в амперах
Реактивная мощность (S)
Мощность, потребляемая в цепи переменного тока, которая не выполняет полезной задачи, но оказывает значительное влияние на фазовый сдвиг между напряжением и током, называется реактивной мощностью. . Реактивная мощность связана с реактивным сопротивлением, создаваемым катушкой и конденсатором, и противодействует действию активной мощности. В цепях постоянного тока нет реактивной мощности.
В отличие от реальной мощности (P), которая выполняет всю работу, реактивная мощность (Q) создает и ослабляет наведенное магнитное поле и емкостное электростатическое поле для извлечения или удаления мощности из цепи, что затрудняет передачу реальной мощности напрямую подавать реальную мощность на нагрузку или цепь.
В магнитном поле энергия, накопленная катушкой индуктивности, пытается управлять током, а энергия, накопленная конденсаторами в электростатическом поле, пытается контролировать напряжение. В результате конденсатор вырабатывает реактивную мощность, а дроссель потребляет реактивную мощность. Это означает, что реальная мощность не потребляется, поскольку они одновременно потребляют энергию и отправляют ее обратно к источнику. Чтобы найти реактивную мощность, умножьте среднеквадратичное значение напряжения и тока на синус фазового угла (φ), как показано на рисунке. 92X = VIsinφ Вольт-Ампер реактивный (VAr)
Разность фаз в 90 градусов между формами тока и напряжения в чистом реактивном сопротивлении (емкостном или индуктивном), умножение VIsinφ дает перпендикулярную составляющую, которая на 90 градусов не совпадает по фазе друг с другом.
Следовательно,
Q = VRMS X IRMS X SINφ
SIN (90 °) = 1
Q = VRMS X IRMS (VAR)
Где Q = Реактивная мощность в VRM-AMPER (ВАр) или киловольт-ампер реактивный (кВАр) или мегавольт-ампер реактивный (МВАр)
Vrms = среднеквадратичное значение напряжения в вольтах
Irms = среднеквадратичное значение тока в амперах
Произведение вольт и ампер, сдвинутых по фазе друг относительно друга на 90 градусов, представляет собой реактивную мощность. В общем случае между током и напряжением может быть любой фазовый угол.
Полная мощность (S)
Мы знаем, что активная мощность рассеивается через резистор, а реактивная мощность поступает на реактивное сопротивление. Это приводит к тому, что волны тока и напряжения не совпадают по фазе из-за разницы между резистивной и реактивной составляющими цепи. Тогда математическое соотношение между реальной мощностью (P) и реактивной мощностью (Q) называется комплексным числом. Произведение среднеквадратичного напряжения V, приложенного к цепи переменного тока, и среднеквадратичного значения тока, протекающего по этой цепи, называется произведением вольт-ампер (ВА), обозначаемым буквой «S», известным как полная мощность.
Эта комплексная мощность не равна алгебраической сумме объединенных активной и реактивной мощностей, а выражается векторной суммой P и Q в вольт-амперах (ВА), которая представляет собой комплексную мощность, представленную треугольником мощности. Среднеквадратичное значение произведения вольт-ампер обычно называют полной мощностью. Потому что «очевидно», что фактическая мощность, совершающая работу, намного меньше, но это общая мощность, потребляемая схемой.
Полная мощность вырабатывается двумя частями: резистивная мощность, которая представляет собой фактическую мощность или мощность в фазе или в ваттах, и другая часть — реактивная мощность, которая представляет собой фазную мощность (в противофазе) в вольт-амперах, поэтому мы можем представить векторную сумму этих двух компонентов мощности в виде треугольника мощности. Треугольник сил P, Q, S и θ.
Что такое импеданс силового треугольника?
Импеданс треугольника мощности представляет собой геометрическую зависимость между реактивным сопротивлением, сопротивлением и импедансом. Это треугольник, образованный добавлением сопротивления к реактивному сопротивлению.
Как найти настоящую силу?
В электрической цепи активная мощность также называется активной мощностью или реальной мощностью, измеряемой в ваттах. Это полная мощность, потребляемая резистивной частью цепи. Эта мощность в цепях постоянного тока такая же, как мощность в цепях переменного тока, которую можно рассчитать по приведенной ниже формуле 9.2*R
Где «I» — ток в амперах
R — резистивная составляющая.
Или Активная мощность = VIcosφ
По какой формуле рассчитывается мощность?
Максимальная мощность, возникающая в цепи переменного тока, возникает, когда кривые тока и напряжения находятся в фазе друг с другом. Формула для расчета мощности дается как
P = V * I
Таким образом, это все, что касается обзора треугольника мощности. Вот вопрос к вам: «Какие различия между активной мощностью, полной мощностью и реактивной мощностью?
7.3: Треугольник силы — Инженерные тексты LibreTexts
Последнее обновление
Сохранить как PDF
Идентификатор страницы
25281

Джеймс М. Фиоре
Колледж Mohawk Valley Community College

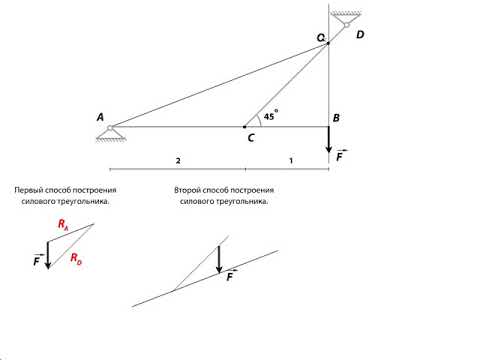
В предыдущем разделе было показано, что фазовый угол между током и напряжением нельзя игнорировать при расчете мощности. Например, если источник RMS на 120 вольт выдает ток 2 ампера, кажется, что он выдает 240 ватт. Это верно только в том случае, если нагрузка чисто резистивная. При комплексной нагрузке истинная мощность несколько меньше. На самом деле, как мы только что видели, если нагрузка является чисто реактивной, реальной мощности нагрузки вообще не будет.

Хотя построение кривых тока, напряжения и мощности является поучительным, оно может быть несколько громоздким. Вместо этого мы используем треугольник мощности, как показано на рисунке \(\PageIndex{1}\). Горизонтальная ось представляет реальную мощность, \(P\), в ваттах. Вертикальная ось представляет реактивную мощность \(Q\) в ВАр. Комбинация векторов \(P\) и \(Q\) дает полную мощность, \(S\), в ВА. Помните, что кажущаяся мощность является произведением величин тока и напряжения. Это то, чем «кажется» мощность на основе простых измерений тока и напряжения с помощью цифрового мультиметра по сравнению с надлежащим измерителем мощности. В резистивном случае реактивной мощности нет, поэтому \(S\) и \(P\) одинаковы. Следовательно, вектор \(S\) коллапсирует на вектор \(P\). В чисто реактивном случае истинной мощности нет и \(S\) и \(Q\) одинаковы; оба вектора идентичны и вертикальны. Для сложного случая \(S\) является векторной суммой \(P\) и \(Q\). Этот простой график хорошо иллюстрирует взаимосвязь между тремя векторами. Кроме того, имея любые две из четырех частей (три величины вектора и \(\тета\)) и немного тригонометрии, можно найти две другие части.

Рисунок \(\PageIndex{1}\): треугольник власти.
Например, зная активную и реактивную мощности, можно найти полную мощность по теореме Пифагора. Точно так же, если известны кажущаяся мощность и угол, действительную и реактивную мощности можно найти с помощью синуса и косинуса. Помните, что кажущаяся мощность может быть найдена из произведения среднеквадратичных величин напряжения и тока для любого комплексного импеданса, а \(\theta\) совпадает с углом импеданса (т. е. угол напряжения минус угол тока). Для вашего удобства ниже перечислены некоторые полезные отношения треугольника мощности. 92} \метка{7.10} \]
Power Factor
Поскольку нас часто интересует истинная мощность, стоит отметить, что преобразование уравнения \ref{7.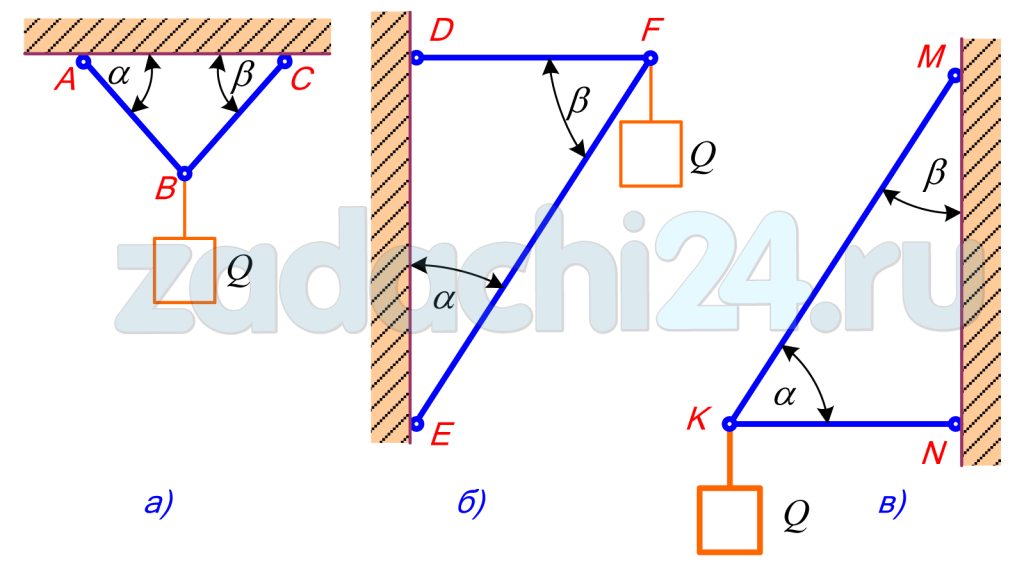 {\ circ}) = 86,6 \) Вт.
\[PF = \frac{P}{S} = \cos \theta \text{ (положительное значение запаздывает и является индуктивным)} \label{7.11} \]
Пример \(\PageIndex{1}\)
Найдите \(S\), \(P\) и \(Q\) в схеме на рисунке \(\PageIndex{2}\). \(E = 120\) вольт среднеквадратичное значение. Частота источника 60 Гц.
Рисунок \(\PageIndex{2}\): Схема для примера \(\PageIndex{1}\).
Первым шагом является определение индуктивного сопротивления.
\[X_L = 2\pi f L \без номера \]
\[X_L = 2\pi 60 Гц 150 мГн \без номера \] 92}{160 \Omega} \nonumber \]
\[P = 90 Вт \nonumber \]
Треугольник мощности для этой схемы показан на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\): треугольник мощности для схемы на рисунке \(\PageIndex{2}\).
Коррекция коэффициента мощности
Одна проблема с реактивной нагрузкой заключается в том, что ток выше, чем необходимо для достижения определенной фактической мощности нагрузки. Это расточительно и потребует более крупных проводников.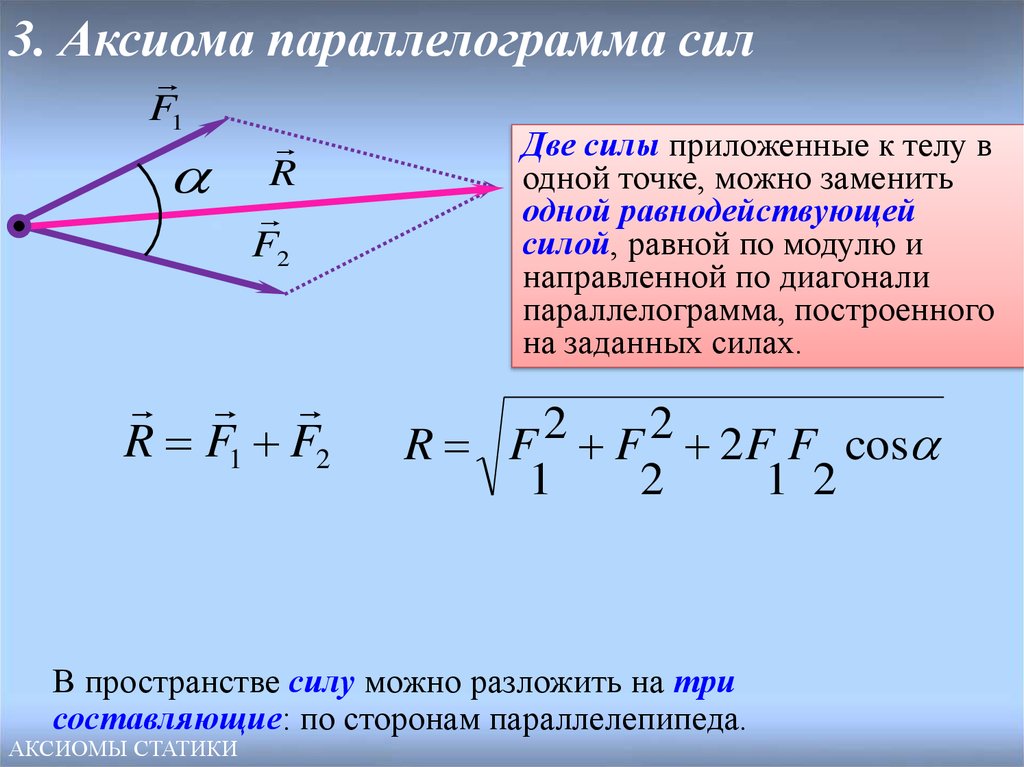 Чтобы решить эти проблемы, к нагрузке можно добавить противоположное реактивное сопротивление, чтобы результирующая нагрузка была чисто резистивной. Это можно реализовать, определив первоначальное значение \(Q\), а затем добавив реактивное сопротивление, достаточное для получения дополнительного \(Q\) противоположного знака, что приведет к нейтрализации. Оттуда, это короткий шаг, чтобы определить требуемый импеданс. Затем, зная частоту, можно найти требуемую емкость или индуктивность, используя соответствующую формулу реактивного сопротивления. Это показано в следующем примере. 9{\circ}\) пика вольт на частоте 10 кГц. Также найдите соответствующий компонент, который при размещении из узла \(a\) на землю приводит \(PF\) к единице.
Рисунок \(\PageIndex{4}\): Схема для примера \(\PageIndex{2}\).
Индуктивное сопротивление 1 мГн на частоте 10 кГц равно \(j62,83 \Омега\). Это параллельно резистору 100 Ом, который затем последовательно с резистором 20 Ом.
\[Z = 20\Омега +(100\Омега || j 62,83\Омега ) \без числа \]
\[Z = 20\Омега +(28,3+j 45\Омега ) \без числа \] 9{\circ} \nonumber \]
\[Q = 2,07 \text{ вар, индуктивная} \nonumber \]
Треугольник мощности для этой схемы показан на рисунке \(\PageIndex{5}\).
Рисунок \(\PageIndex{5}\): треугольник мощности для схемы на рисунке \(\PageIndex{4}\).
Для второй части, связанной с коррекцией коэффициента мощности, нам необходимо добавить реактивную мощность, равную по величине существующему значению, но противоположного знака. Это означает, что нам нужно добавить емкостное напряжение 2,07 ВАР. Новый треугольник мощности показан на рисунке \(\PageIndex{6}\). Вертикальные компоненты сокращаются, в результате чего кажущаяся мощность равна истинной мощности с \(PF = 1\).
Рисунок \(\PageIndex{6}\): треугольник мощности для схемы на рисунке \(\PageIndex{4}\) с коррекцией коэффициента мощности.
Мы можем разместить корректирующий конденсатор там, где это удобно с физической точки зрения, если мы добавим емкость 2,07 ВАР. У нас нет физической цепи, так что это здесь не рассматривается. Удобным расположением было бы разместить его на существующей комбинации резистор-индуктор. Наша цель состоит в том, чтобы сначала найти требуемое реактивное сопротивление и, исходя из этого, определить требуемую емкость.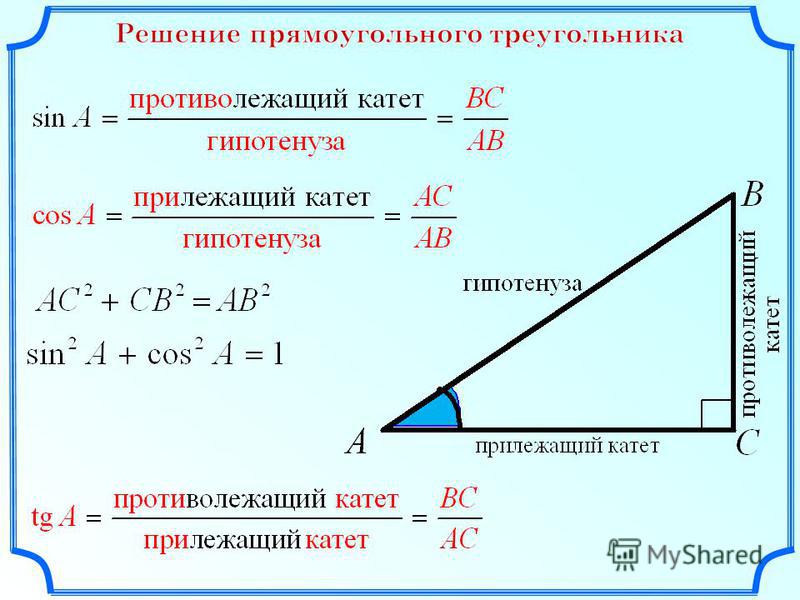 Мы сделаем это двумя разными способами. В первом случае заметим, что конденсатор появляется на единственном другом реактивном элементе в цепи. Следовательно, для того, чтобы они компенсировались, они должны иметь одинаковую величину реактивного сопротивления, и, таким образом, \(X_C\) должно равняться \(-j62,8 \Omega\). Но что, если в схеме было несколько реактивных элементов или если было бы нецелесообразно размещать компонент там, например, из-за нехватки места? В этом случае мы просто проработали бы соотношение сил в обратном порядке. Для сравнения предположим, что мы разместили конденсатор в том же месте; от узла \(a\) до земли. Делитель напряжения можно использовать для определения текущего значения \(v_a\). Это работает до 11,4 вольт RMS. Используя форму напряжения правила мощности: 92}{2.07VAR} \nonumber \]
\[X = 62.8\Omega \nonumber \]
В любом случае мы получим \(X_C\), теперь мы просто решим формулу емкостного реактивного сопротивления, чтобы найти \(C\) .
\[C = \frac{1}{2\pi f X_C} \nonumber \]
\[ C = \frac{1}{2\pi 10 kHz62. 8\Omega} \nonumber \]
\[C = 253,3 нФ \номер \]
Результирующая схема показана на рисунке \(\PageIndex{7}\).
Рисунок \(\PageIndex{7}\): Схема на рисунке \(\PageIndex{4}\) с коррекцией коэффициента мощности.
Компьютерное моделирование
Полезно видеть снижение потребляемой мощности, вызванное использованием коррекции коэффициента мощности. Таким образом, схема на рисунке \(\PageIndex{7}\) захвачена в симуляторе, как показано на рисунке \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\): Схема рисунка \(\PageIndex{7}\) в симуляторе.
Мы проведем два анализа переходных процессов, чтобы определить ток источника. Первая версия будет работать с оригинальной схемой без конденсатора. Второй запуск будет включать конденсатор. Для построения токов воспользуемся законом Ома. Сначала мы получаем напряжения в узлах 1 и 2. Затем, используя постпроцессор симулятора, мы вычитаем \(v_1\) из \(v_2\), что дает напряжение на резисторе 20 \(\Омега\). Эта величина затем делится на 20 \(\Омега\), чтобы получить входной ток. Это похоже на метод резистора измерения тока, использованный в предыдущих главах.
Результирующий ток для исходной цепи показан на рисунке \(\PageIndex{9}\). Обратите внимание, что пиковый ток составляет чуть более 300 миллиампер, рассчитанный на втором шаге примера.
Рисунок \(\PageIndex{9}\): результаты моделирования схемы на рисунке \(\PageIndex{8}\) без коррекции коэффициента мощности.
Второе моделирование показано на рисунке \(\PageIndex{10}\), теперь с коррекцией коэффициента мощности.
Рисунок \(\PageIndex{10}\): результаты моделирования схемы на рисунке \(\PageIndex{8}\) с коррекцией коэффициента мощности.
Амплитуда здесь сильно уменьшена, в диапазоне от 160 до 170 мА пик. При добавлении конденсатора два реактивных тока компенсируются, оставляя параллельное сопротивление всего 100 Ом. Это последовательно с резистором 20 \(\Омега\). Разделение 120 \(\Omega \) на пиковое напряжение источника 20 вольт дает пиковый ток приблизительно 167 мА, что соответствует моделированию. На компенсацию реактивных токов также указывает тот факт, что ток источника больше не находится в противофазе. На рисунке \(\PageIndex{10}\) текущий сигнал находится в фазе и начинается с нуля, как и ожидалось. Это подразумевает нагрузку, эквивалентную чистому сопротивлению. Напротив, график рисунка \(\PageIndex{9}\) показывает ток, который отстает примерно на половину деления, или примерно на 45 градусов, что неудивительно, что это приблизительное значение угла импеданса цепи. Очевидно, что этот комбинированный импеданс должен быть индуктивным.
Подводя итог, можно сказать, что коррекция коэффициента мощности используется для снижения потребления тока при сохранении постоянной мощности нагрузки. Если нагрузка фиксированная, этого можно добиться за счет использования конденсатора (для индуктивных нагрузок) или катушки индуктивности (для емкостных нагрузок). Если нагрузка является динамической, то требуется более сложная система, например, переключение через батарею конденсаторов для получения значения, близкого к точному значению, необходимому для этой конкретной нагрузки. Дополнительные примеры коррекции коэффициента мощности приведены в следующем разделе.
Ссылки
¹ Гипербола, похоже, работает в киноиндустрии.
Эта страница под названием 7.3: Power Triangle распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
Джеймс М.
No related posts.