Сбор нагрузок на балку перекрытия пример: Пример 1.3 Сбор нагрузок на балку перекрытия

Пример 1.3 Сбор нагрузок на балку перекрытия

 

 

Требуется собрать нагрузки на монолитную балку перекрытия жилого дома (балка по оси «2» в осях «Б-В» на рис.1). Размеры сечения балки: h = 0,5 м, b = 0,4 м. Конструкцию пола принять по рисунку в Пример 1.1 Сбор нагрузок на плиту перекрытия жилого здания.

Решение

Данный тип здания относится ко II классу ответственности. Коэффициент надежности по ответственности γн = 1,0.

Состав пола и значения постоянных нагрузок примем из примера 1.1.

Нагрузки, действующие на балку, принимаются линейно распределенными (кН/м). Для этого равномерно распределенные нагрузки на перекрытие умножаются на ширину грузового участка, равному для средних балок шагу рам. В нашем примере см. рис. 1 ширина грузового участка составляет В = 6,6 м. Остается умножить постоянную нагрузку, вычисленную в примере 1.1, на данную величину и записать в таблицу 1:

q1 = 5,89*В = 5,89*6,6 = 38,87 кН/м;

q1p = 6,63*В = 6,63*6,6 = 43,76 кН/м.

Таблица 1

Сбор нагрузок на балку перекрытия

Вид нагрузки	Норм. кН/м	Коэф. γt	Расч. кН/м
Постоянная нагрузка
1. Ж.б. плита + пол	38,87		43,76
2. Собственный вес балки	5,0	1,1	5,5
Всего:	43,87		49,26
Временная нагрузка
1. Полезная нагрузка: кратковременная ν1 длительная р1	6,53 2,29	1,3 1,3	8,49 2,98
2. Перегородки (длительная) р2	3,3	1,3	4,29

 

Вычислим нагрузку от собственного веса балки.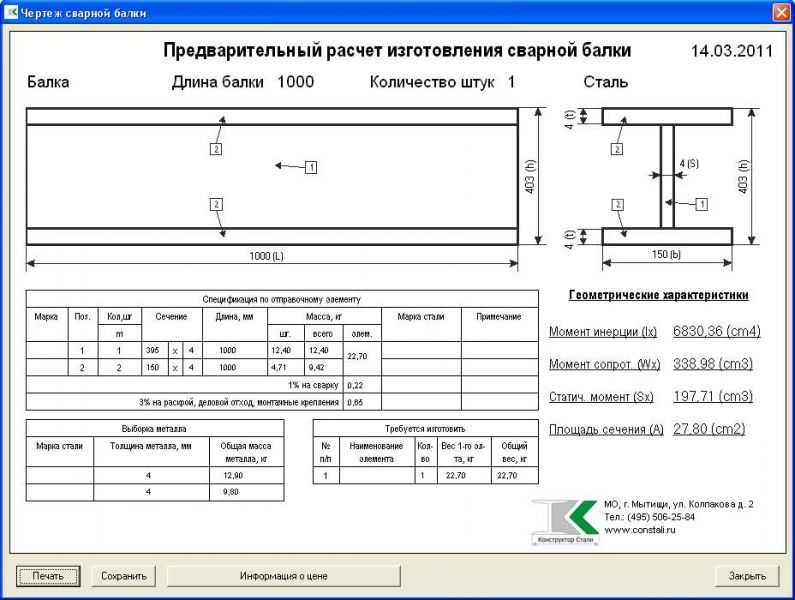

Объемный вес железобетона равен 2500 кг/м3 (25 кН/м3). При высоте балки h = 0,5 м и ее ширине b = 0,4 м нормативное значение нагрузки от собственного веса составляет

q2 = 25*h*b*γн =25*0,5*0,4*1,0 =5,0 кН/м.

Коэффициент надежности по нагрузке γt = 1,1,  тогда расчетное значение составит:

q2р = q2*γt =5*1,1 =5,5 кН/м.

Суммарная нормативная постоянная нагрузка составляет

q = q1 + q2 = 38,87 + 5,0 = 43,87 кН/м;

расчетная:

qр = q1р + q2р = 43,76 + 5,5 = 49,26 кН/м.

Понижающие коэффициенты φ1, φ2, φ3 или φ4, при расчете балок нормативные значения нагрузок, допускается снижать в зависимости от грузовой площади А, м2, рассчитываемого элемента умножением на коэффициент сочетания φ. При грузовой площади А = 6,6*7,2 = 47,52 м2 и при А = 47,52 м2 > А1 = 9,0 м2 для помещений коэффициент сочетания φ1 определяется по формуле:

 

φ1 = 0,4 + 0,6/ √(А/А1) = 0,4 + 0,6/√(47,52/9,0) = 0,66.

Полное (кратковременное) нормативное значение нагрузки от людей и мебели для квартир жилых зданий составляет 1,5 кПа (1,5 кН/м2). Учитывая коэффициент надежности по ответственности здания γн = 1,0 и коэффициент сочетания φ1 = 0,66, итоговая нормативная кратковременная полезная нагрузка составляет:

ν1 = 1,5*В*γн*φ1 = 1,5*6,6*1,0*0,66 = 6,53 кН/м.

При нормативном значении временной нагрузки менее 2,0 кПа коэффициент надежности по нагрузке  γt принимается равным γt = 1,3. Тогда расчетное значение составляет:

ν1р = ν1*γt = 6,53*1,3 = 8,49 кН/м.

Длительную полезную нагрузку получаем путем умножения ее полного значения на коэффициент 0,35 т.е:

р1 = 0,35*ν1 = 0,35*6,53 = 2,29 кН/м;

р1р = р1*γt = 2,29*1,3 = 2,98 кН/м.

Нормативное значение равномерно распределенной нагрузки от перегородок составляет не менее 0,5 кН/м2. Приводим ее к линейно распределенной нагрузке на балку путем умножения на ширину грузового участка В=6,6 м:

р2 = 0,5*В*γн = 0,5*6,6*1,0 = 3,3 кН/м.

Расчетное значение нагрузки тогда:

р2р = р2*γt = 3,3*1,3 = 4,29 кН/м.

I сочетание: постоянная нагрузка (собственный вес перекрытия и балки) + полезная (кратковременная).

При учете основных сочетаний, включающих постоянные нагрузки и одну временную нагрузку (длительную или кратковременную), коэффициент Ψl, Ψt вводить не следует.

q1 = q + ν1 = 43,87 + 6,53 = 50,4 кН/м;

q1р = qр + ν1р = 49,26 + 8,49 = 57,75 кН/м.

II сочетание: постоянная нагрузка (собственный вес перекрытия и балки) + полезная (кратковременная) + нагрузка от перегородок (длительная).

Для основных сочетаний коэффициент сочетаний длительных нагрузок Ψ1 принимается: для первой (по степени влияния) длительной нагрузки — 1,0, для остальных — 0,95. Коэффициент Ψ2 для кратковременных нагрузок принимается: для первой (по степени влияния) кратковременной нагрузки — 1,0, для второй — 0,9, для остальных — 0,7.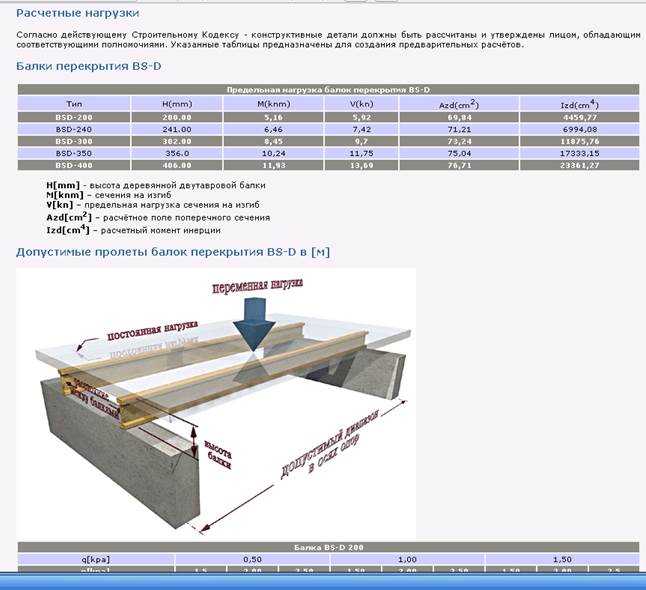

Поскольку во II сочетании присутствует одна кратковременная и одна длительная нагрузка, то коэффициент Ψl и Ψt = 1,0.

qII = q + ν1 + р2 = 43,87 + 6,53 + 3,3 = 53,7 кН/м;

qIIр = qр+ ν1р + р2р = 49,26 + 8,49 + 4,29 = 62,04 кН/м.

Примеры:

 

Пример 2. Сбор и расчет нагрузок на отдельные конструктивные элементы (колонны, балки, плиты перекрытий и покрытий). — Студопедия

Поделись  

После того, как был выполнен общий сбор нагрузок, переходим к сбору нагрузок на отдельные конструктивные элементы.

Для дальнейших расчетов в качестве примера примем участок перекрытия типа 2 в зоне парковки (основное сочетание нагрузок выделено в п. 5.3.4),перекрытие типа 2 для стоянок в зоне парковки:

нормативная С_m1 = 226,8 + 400,0 = 626,8(630,0) кг/м²;

расчетная С_m1 = 250,0 + 485,0 = 735,0 кг/м².

Плиты перекрытий и покрытий.

Нагрузки на плиты перекрытий и покрытий представляются в зависимости от предполагаемых методов расчета: на единицу площади 1 м

2 плиты, погонные на 1 погонный метр участка плиты шириной 1 метр, сосредоточенными силами, различными сочетаниями нагрузок. Для расчета и проверки плоских плит, как правило, используется погонная нагрузка на участок плиты шириной 1 м. Для подбора сборных плит используется та нагрузка, которая указана в паспорте на плиты.

В нашем примере полная нормативная равномерно распределенная нагрузка на 1 м² плиты перекрытия в зоне парковки составит 630,0 кг/м²; полная нормативная равномерно распределенная погоннаянагрузка на участок плиты шириной 1 м составит 630,0 кг/м²*1 м =630,0 кг/пог.м.

Балки.

Нагрузки на балки представляются сосредоточенными силами, моментами, погонными равномерными или неравномерными силами и моментами, различными сочетаниями этих нагрузок.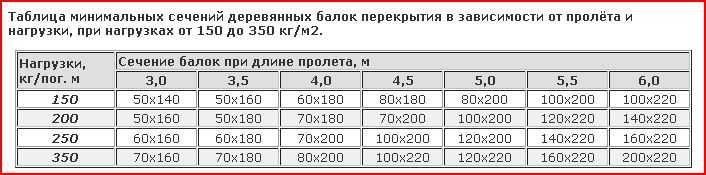

Как правило, для подбора и проверки балок принимается нагрузка с грузовой площади, приходящейся на балку (рис. 3).

Определим полную расчетнуюи нормативную равномерно распределеннуюпогонную нагрузку на второстепенную балку по оси Б в осях 2-3 (считаем, что это зона стоянки автомобилей).

Расчетная q = Р*а = 735,0*3,0 = 2200кг/м.

Нормативнаяq_n = 630,0*3,0 = 1890~1900 кг/м

гдеа =3 м -шаг второстепенных балок;

Р — полная равномерно распределенная нагрузка на 1 м² плиты перекрытия в соответствующей зоне, в нашем случае – зона стоянки автомобилей, расчетная Р = 735,0 кг/м², нормативная Р_n = 630 кг/м².

Колонны.

Нагрузки на колонны представляются сосредоточенными силами, моментами, горизонтальными равномерно распределенными и сосредоточенными силами, различными сочетаниями этих нагрузок. Как правило, для подбора и проверки колонн принимается нагрузка с грузовой площади, приходящейся на колонну (рис.

2) или нагрузка, полученная из расчета балок (рис. 3).

Определим расчетную вертикальную нагрузку на центральную колонну из грузовой площади. Нагрузка определяется от перекрытия и покрытиядля сечения колонны у обреза фундамента.

N = А_гр*Р_пер+А_гр*Р_покр= 36 м²*735,0 кг/м²+36*875,0= 57960,0 кг.

где А_гр–грузовая площадь, которая определяется как произведение шага колонн по цифровым осямL₁=6 м на шаг колонн по буквенным осямL₂ =6 м, А_гр=6*6=36 м²;Р_пер= 735,0 кг/м²; Р

покр=875,0 кг/м² (см. п. 5.3.4).

 

 

 

Рис. 2. Схема балочной клетки. Грузовые площади балок и колонн

для второстепенной балкиА_гр=6*3=18 м²;

для колонны А_гр=6*6=36 м²;

Рис. 3. Нагрузка на центральную колонну от балок



Назначить нагрузки на пол

Имя группы нагрузки Выберите нужную группу нагрузок, которая будет включать введенные данные о нагрузках на перекрытия. Выберите «По умолчанию», если групповое назначение не требуется. Нажмите справа, чтобы добавить, изменить или удалить группы нагрузки. Нагрузка на пол не может быть удалена, если она была загружена на стадии строительства. Любая временная нагрузка должна быть определена в другой группе нагрузок при анализе стадии строительства.  Тип нагрузки на пол Тип нагрузки: выберите тип нагрузки на пол, определенный параметром «Определить тип нагрузки на пол». Нажмите справа, чтобы определить, добавить, изменить или удалить новые или существующие типы нагрузки на пол, если это необходимо. Тип распределения     : Одностороннее распределение         : Двустороннее распределение       : Многоугольник-центроид Распределение нагрузки на основе площадей треугольных сегментов, созданных путем деления многоугольника относительно центроида     : Длина полигона Распределение нагрузки пропорционально длинам сторон многоугольника

Исключить внутренний элемент. площади: используется, чтобы не нагружать элементы в пределах площади назначенной нагрузки на пол. Это становится полезным, например, когда мы хотим не рассматривать раскосы пола как часть каркаса пола.

Разрешить площадь блока типа многоугольника: используется для приложения нагрузки на пол в области вогнутого многоугольника с внутренним углом, превышающим 1800 . Если в разделе «Распределение» выбрано значение «Двустороннее», можно установить флажок «Разрешить единицу площади полигонального типа».

Примечание 1

Области притока отмечены, если в  Отображении установлен флажок Нагрузка >Площадь нагрузки на пол.

 

Примечание 2

Цвета могут быть назначены вспомогательным областям с помощью параметра «Цвет» > «Нагрузка» > «Область нагрузки на пол» в «Параметры отображения».

 

Угол нагрузки (A1): угол, определяющий направление распределяемой нагрузки.

Угол нагрузки применим только для одностороннего распределения. Это угол, образованный линией, соединяющей 1-й узел со 2-м узлом, определяющим нагруженную область и направление распределения нагрузки. Соглашение о знаках для угла следует правилу правой руки. Положительный угол (+) определяется угловым направлением последовательности присваивания угловых узлов, определяющих нагруженную область. (См. рис. 2,3)

 

Немодулированная вспомогательная балка

Типичная система перекрытий может включать в себя односторонние плиты, опирающиеся на балки, опирающиеся на фермы.

Элементы балок (называемые вспомогательными балками), опирающиеся на балки в типичной конструктивной системе, не влияют на поведение конструкции. Они просто действуют как средство передачи нагрузки на пол. В результате элементы балки обычно исключаются из расчетной модели.

Следуя концепции гравитационной системы, MIDAS/Civil позволяет пользователю задавать фиктивные балки для правильного учета гравитационных нагрузок на пол. Воображаемые (несмоделированные) балки учитывают пути распределения нагрузки.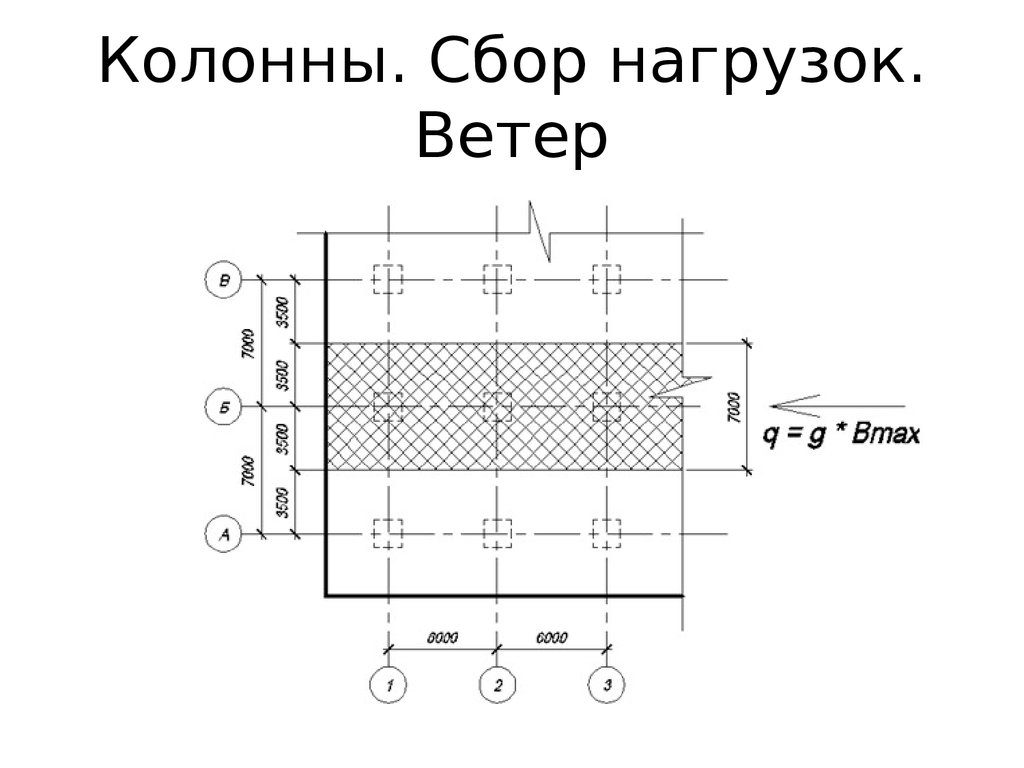

Загружаемая область определяется угловыми узлами, введенными в «Узлы, определяющие загрузочную область».

Форма поднагруженной зоны, образованной балками и фермами в пределах нагруженной зоны, должна быть треугольником или четырехугольником.

Количество вспомогательных балок: количество элементов вспомогательной балки, размещенных в подобласти (см. примечание и рис. 4 и 5)

Угол вспомогательной балки (A2): Угол размещения элементов вспомогательной балки (см. рис. 4, 5)

Собственный вес блока: собственный вес на единицу длины элемента подбалки (нагрузка/длина)

Примечание

Собственный вес вспомогательной балки всегда применяется в глобальном направлении Z, независимо от направления нагрузки. В случае, если направление собственного веса подбалки (глобальная Z) совпадает с направлением нагрузки, собственный вес подбалки интегрируется в нагрузку на перекрытие. В противном случае создаются отдельные нагрузки.

Направление нагрузки и проекция

Выберите направление нагрузки и параметры проекции нагрузок на пол.

Система координат для загруженной области определяется при назначении загружаемой области. Направление от 1-го углового узла ко 2-му угловому узлу соответствует локальному x-направлению плоскости. Используя направление вращения в соответствии с последовательностью присвоения угловых узлов и правилом правой руки, ось вращения становится локальным направлением z. Направление, перпендикулярное направлениям x и z в первом узле, является локальным направлением y. (См. рис.3)

Local x: нагрузка на пол, приложенная в направлении x локальной системы координат плиты пола (см. рис. 3)

Local y: Нагрузка на перекрытие, приложенная в направлении y локальной системы координат плиты пола (см. рис. 3)

Локальная z: нагрузка на пол, приложенная в направлении z локальной системы координат плиты пола (см. рис. 3)

Global X: нагрузка на пол, приложенная в направлении X GCS

Global Y: нагрузка на пол, приложенная в направлении Y GCS

Global Z: нагрузка на пол, приложенная в направлении Z GCS

Концепция распределения нагрузки для перекрытий

Выступ
Когда направление нагрузки на пол соответствует «Глобальным X, Y или Z», выберите параметр, независимо от того, следует ли проецировать нагрузку на пол.

Да: когда нагрузка на пол приложена к площади, проецируемой на плоскость, перпендикулярную направлению нагрузки

Нет: при приложении нагрузки к полу вдоль плоскости конструкции

Например, выберите «Да» для снеговой нагрузки и выберите «Нет» для постоянной нагрузки, приложенной к наклонной крыше.

Описание
Введите краткое описание.

Узлы, определяющие область загрузки
Назначьте угловые узлы, определяющие загруженную область последовательно в выбранном направлении вращения. Вы можете напрямую ввести номера узлов или щелкнуть поле ввода и узлы в окне модели, используя Node Snap. Локальная система координат плиты перекрытия и знаки нагрузки определяются последовательностью присвоения угловых узлов. (См. рис. 3)

Угловые узлы можно вводить последовательно, как показано на <Рис. 6>. Неугловые узлы, такие как N9 и N11, определять не нужно.

Узлы выбраны в углах непрямых граничных ребер.

Все балочные элементы (или элементы стен) в границах нагруженной области должны сохранять поднагруженные области в виде треугольников и четырехугольников.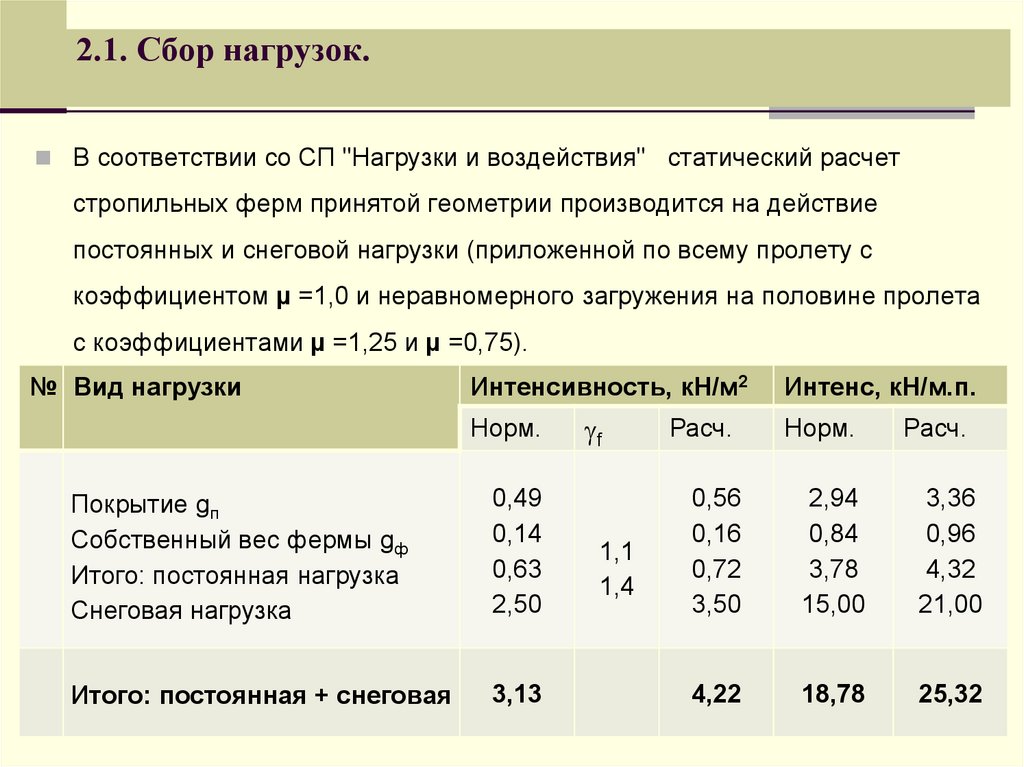 Если элементы балки (или стены) перекрываются на одной линии или точки пересечения не соединены узлами, будут допущены ошибки.

При использовании курсора мыши в окне модели последовательно назначайте угловые узлы и переназначайте первый узел для завершения полигона.

 

<Рисунок 6> Ввод данных угловых узлов для определения нагруженной области, подверженной нагрузкам пола

Копирование нагрузки на пол

Скопируйте введенную нагрузку на перекрытие на другие плиты перекрытия такой же формы (размеров).

Ось: Назначить направление копирования

x: ПСК, направление x

г: UCS направление Y

z: z-направление ПСК

Расстояния: Множественные расстояния копирования

Укажите относительные расстояния столько раз, сколько необходимо для копирования нагрузки на пол.

Примечание
Используя понятие подбалки, метод преобразования нагрузки перекрытия в нагрузки, приложенные к элементам балки или фермы в виде распределенных нагрузок или сосредоточенных нагрузок в пролете, выглядит следующим образом:

Площадь, на которую воздействует нагрузка на пол, определяется угловыми узлами, как показано на <Рис. 7(а)>. Поднагруженные области, состоящие из многоугольных единиц, образованных треугольниками или четырехугольниками, создаются балочными элементами, размещенными внутри границ, как показано на <Рис. 7(б)>.

После того, как ‘No. Вспомогательных балок определено, поднагруженные области далее делятся, как показано на <Рис. 7(с)>. (Количество вспомогательных лучей = 1 на <Рис. 7(c)>)

В соответствии с концепцией распределения, показанной на <Рис. 7> на основе повторно разделенных областей поднагружения распределенные нагрузки применяются к элементам балки и подбалкам, как показано на <Рис. 7(г)>. Распределенные нагрузки, приложенные к вспомогательным балкам, преобразуются (предположим, что оба конца закреплены) в реакции на обоих концах.

Реакции, передаваемые от вспомогательных балок, и распределенные нагрузки, действующие на элементы балки, наконец применяются к элементам балки, как показано на <Рис. 7(д)>.

Подбалки размещаются так, чтобы образовать угол «A2» с локальной осью x плиты пола, как показано на <Рис. 4(а)>. Вспомогательные балки размещаются на равном расстоянии ‘No. дополнительных лучей +1. Промежутки создаются путем разделения фиктивной линии, перпендикулярной вспомогательным балкам.

Длина фиктивной линии определяется двумя проекционными линиями, проходящими через самые дальние угловые узлы параллельно подбалкам.

Многоугольные формы поднагруженных областей, образованных вспомогательными балками и существующими балочными элементами, могут быть только треугольниками или четырехугольниками.

<Рис. 4(b)> представлены пятиугольники (заштрихованная область), которые отклоняются от основных требований к форме. Результатом будет ошибка.

<Рисунок 7> Преобразование нагрузки на плиту перекрытия в распределенные нагрузки, действующие на балочные элементы

 

Преобразование в тип нагрузки на балку

Если элементы балки впоследствии добавляются к существующей загруженной плоскости, нагрузка на перекрытие автоматически перераспределяется в соответствии с добавленными элементами.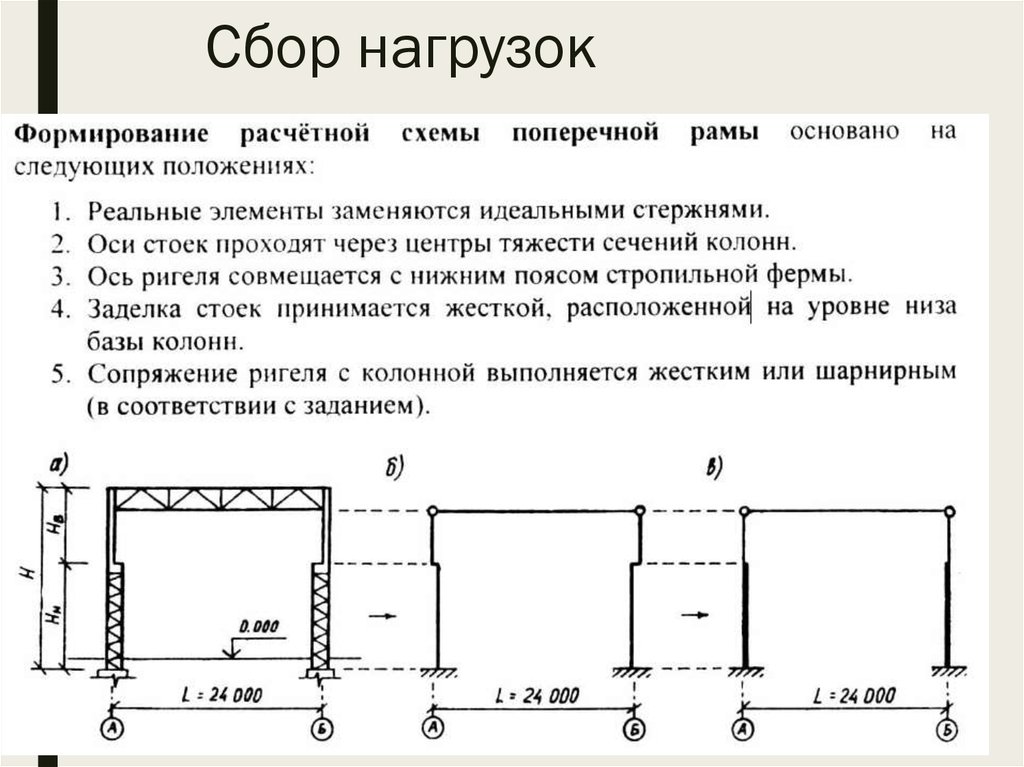 Используйте эту функцию для преобразования нагрузки на пол в нагрузки на балки, когда нагрузка на пол не должна применяться к добавленным элементам.

Примечание 1
Если необходимо изменить величину нагрузки на пол, измените только значение типа нагрузки на пол. Затем к модели прикладывается модифицированная нагрузка. Однако, если выбран параметр «Преобразовать в тип нагрузки на балку» и изменена нагрузка на перекрытие, изменение не имеет смысла. Нагрузки, прикладываемые к элементам балки, должны изменяться напрямую.

Примечание 2
Предупреждение о применении нагрузки на пол

1. 1. • Нагрузка на перекрытие применяется к треугольным или четырехугольным областям, ограниченным элементами балки или стены. При использовании вспомогательных балок требования к форме должны оставаться неизменными.

      • Когда элементы балки перекрываются, нагрузка на перекрытие не может быть применена. В таком случае удалите повторяющиеся записи с помощью «Удалить элементы» или «Проверить и удалить повторяющиеся элементы».

Beams — Поддерживается на обоих концах

. Напряжение в изгибающем луче может быть выражено как

σ = y m / i (1)

, где

σ = напряжение (N / M

σ = стресс (N / M

σ = стресс (N / M

9

σ = стресс (N / M

σ = стресс (N / M

σ = стресс (N / M. ² ), Н/мм ² , фунтов/кв.0265

I = момент инерции (M ⁴ , MM ⁴ , в ⁴ )

• BEAM — на обоих концах — непрерывный и точечный нагруз и поддерживаемые с другой стороны — непрерывные и точечные нагрузки
• Балки — закрепленные на обоих концах — непрерывные и точечные нагрузки

Приведенный ниже калькулятор можно использовать для расчета максимальных напряжений и прогибов балок с одной одинарной или равномерно распределенной нагрузкой.

Балка с опорой на обоих концах — равномерная непрерывная распределенная нагрузка

Момент в балке с равномерной нагрузкой на обоих концах в положении x может быть выражен как

M _x = q x (L — x) / 2 (2)

, где

M _x = момент в положении x (нм, фунт в)

x = расстояние от конца (мм, мм, в)

. 0338 moment is at the center of the beam at distance L/2 and can be expressed as

M _max = q L ² / 8                                          (2a)

where

M _max = максимальный момент ( Нм, фунт·дюйм)

q = равномерная нагрузка на единицу длины балки (Н/м, Н/мм, фунт/дюйм)

6 8 L = длина балки (м, мм, дюйм)

Максимальное напряжение

Уравнение 1 и 2A можно объединить для выражения максимума напряжения в луче с однородной нагрузкой, поддерживаемым на обоих концах на расстоянии L/2 AS

666. _{. = Y MAX Q L ² /(8 I) (2B)}

, где

σ _MAX = Максимум стресс (PA (N/M 9027 2 2 44444444444444444444444444444444444 2 . ² , psi)

y _max  = distance to extreme point from neutral axis (m, mm, in)

• 1 N/m ² = 1×10 ^-6 N /мм ² = 1 PA = 1,4504×10 ^-4 PSI
• 1 PSI/LB/в ² ) = 144 PSF (LB _F /FT ^{2 2 74). 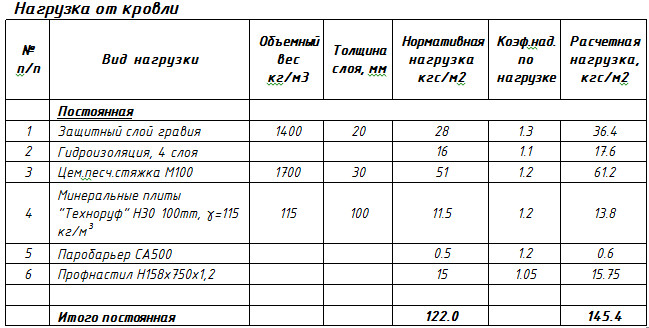м 2 ) = 6,895×10 -3 Н/мм 2}

• Максимальная прочность на растяжение для некоторых распространенных материалов

Максимум отклонение :

Δ _MAX = 5 Q L ⁴ / (384 E I) (2C)

, где

9999999967

, где

. , in)

E =  Modulus of Elasticity (Pa (N/m ² ), N/mm ² , psi)

Deflection in position x:

δ _x = Q x ( L ³ — 2 L x ² + x ³ ) ^{/ (24 E I) (2d)}

Примечание! — прогиб часто является ограничивающим фактором в конструкции балки. В некоторых случаях балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимых прогибов.

Силы, действующие на концах:

R ₁ = R ₂

     = q L / 2                    0265

где 

R = сила реакции (Н, фунты)   

Пример — Балка с равномерной нагрузкой, метрические единицы из

6 Н/мм . Момент инерции балки равен 8196 см ⁴ (81960000 мм ⁴ ) , а модуль упругости стали, используемой в балке, равен 200 ГПа (200000 Н/мм 2 9263)0265 . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).

Максимальное напряжение в балке может быть рассчитано   = 34,3 Н/мм ²

  = 34,3 10 ⁶ Н/м ² (Па)

7

6 МПа

,

Максимальное отклонение в луче может быть рассчитано

Δ _MAX = 5 (6 Н/мм) (5000 мм) ⁴ /( 200000 N/ММ) ⁴ /( 200000 N/ММ) ⁴ /( 200000 N/ММ) /( 200000 N/ММ) /( 200000 N/ММ) ⁴ /( 200000 N/ММ) ⁴ /( 200000 N/ММ) ⁴ /( 200000 N/мМ) ( 81960000 мм ⁴ ) 384)

= 2,98 мм

Универс.

— Длина балки (мм)

I — Moment of Inertia (mm ⁴ )

E — Modulus of Elasticity (N/mm ² )

y —  Distance of extreme point off neutral axis (mm)

• 1 мм ⁴ = 10 ^-4 CM ⁴ = 10 ^-12 M ⁴
• 42 ⁴
• 42 ⁴
• 42429273 ⁴
• 42 ⁴
• 42 ⁴
M ⁴
• 42424242793 9027 мм
• 1 дюйм ⁴ = 4.16×10 ⁵ mm ⁴ = 41.6 cm ⁴
• 1 N/mm ² = 10 ⁶ N/m ² (Pa)

Uniform Load Калькулятор балки — британские единицы

q — нагрузка (фунт/дюйм)

L — длина балки (дюйм)

I — момент инерции (в ⁴

9 модуль 08 08

упругости (psi)

г — Расстояние от крайней точки до нейтральной оси (дюймы)

Пример — балка с равномерной нагрузкой, британские единицы Инерция

285 в ⁴ , модуль эластичности 2

00 PSI

, с равномерной нагрузкой 100 фунтов / в .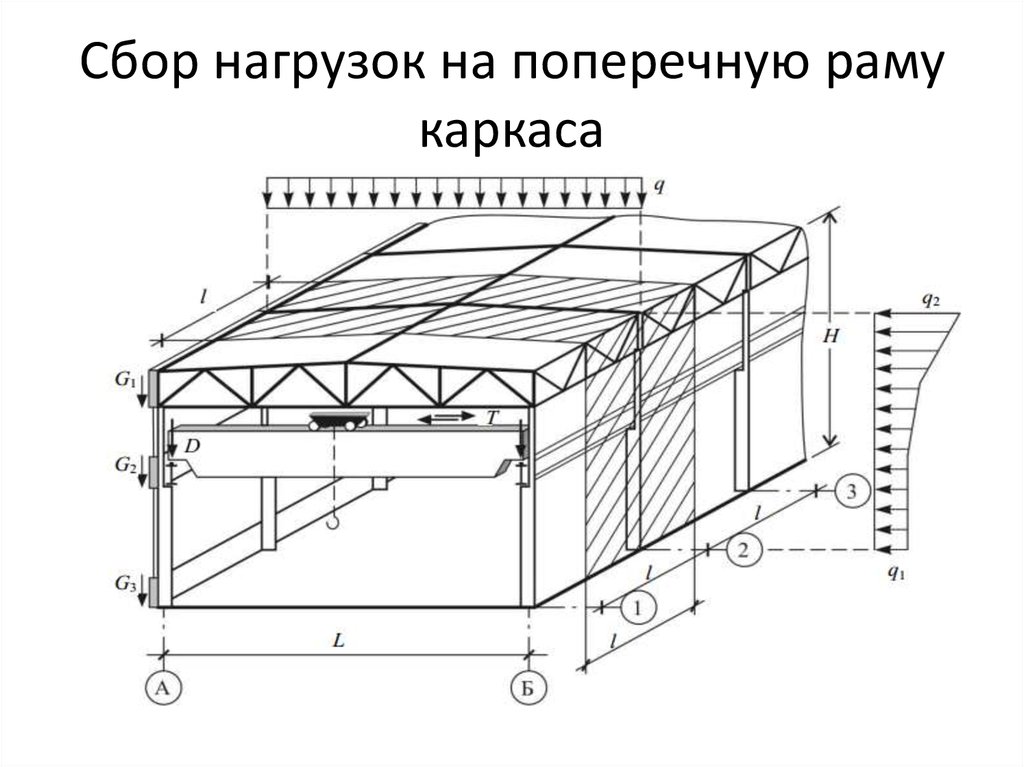 я)

    = (6.25 in) (100 lb/in) (100 in) ² / (8 (285 in ⁴ ))

    = 2741 (lb/in ² , psi)

Максимальное отклонение может быть рассчитано как

Δ _MAX = 5 Q L ⁴ / (E I 384)

= 5 (100 фунтов/ дюйм) (100 дюймов) ^{4 9024/ (2}

000000000000 (2

00000000000000 (2

000000000000 (2

00000000 (2

000000 (2

0000 (2

0000/ in) (100 дюймов). фунт/дюйм

² ) (285 дюймов ⁴ ) 384)

    = 0,016 дюйма

Луч, поддерживаемый на обоих концах — нагрузка в центре

Максимум Момент в балке с центральной нагрузкой, поддерживаемой на обоих концах:

M _{Максимальный} = F L / 4 (3A)

9

7777770 = F L / 4 (3A)

99

7777777777770 = F L / 4 (3A)

77777777777777777777 гг. (3b)0367

where

F = load (N, lb)

Maximum deflection can be expressed as

δ _max = F L ³ / (48 E I)                                  (3c)

Силы, действующие на концах:

R ₁ = R ₂

= f / 2 (3d)

Калькулятор балки с одной центральной нагрузкой — метрические единицы

.

0007

F — Load (N)

L — Length of Beam (mm)

I — Moment of Inertia (mm ⁴ )

E — Modulus of Elasticity (N/mm ² )

y —  Расстояние от крайней точки до нейтральной оси (мм)

Расчет нагрузки на балку с одним центром — британские единицы измерения

F — нагрузка (фунты) — длина балки (в)

I — Момент инерции (в ⁴ )

E — Модуль упругости (psi)

y —  Расстояние от крайней точки до нейтральной оси a Одноцентровая нагрузка

Максимальное напряжение в стальной широкополочной балке «W 12 x 35», 100 дюймов в длину , момент инерции 285 дюймов ⁴ , модуль упругости 2

00 psi

, с центром загрузить 10000 фунтов можно рассчитать как

σ _макс. = y _макс. F L / (4 I)

4 ))

= 5482 (фунт / в ² , PSI)

Максимальное отклонение может быть рассчитано как

Δ _MAX = F L ^{666 / E.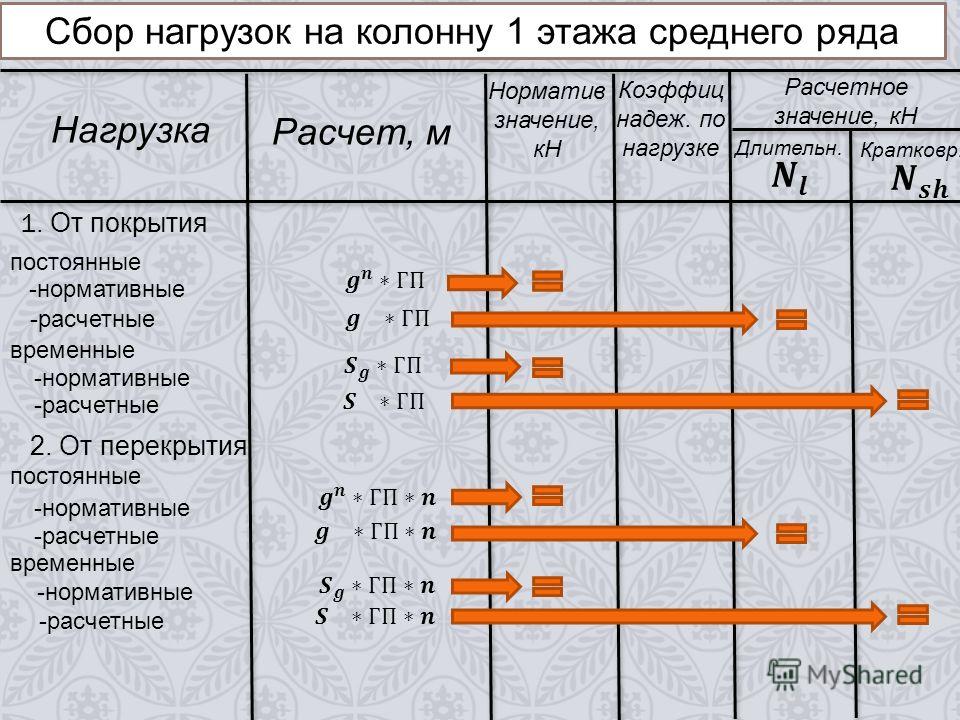 6666666666666666666666666666666666666666666666666666666666666666666666666666689н. (10000 фунтов/дюйм) (100 дюймов) 3 / ((2}

00 фунтов/дюйм

² ) (285 в ⁴ ) 48)

= 0,025 в

. пролёт/180

деревянные балки перекрытий: пролёт/330 (макс. 14 мм)

хрупкие элементы: пролёт/500

крановые балки: пролёт/600

Балка, поддерживаемая с обоих концов – внецентренная нагрузка

220009

Максимум Момент в луче с единственной эксцентричной нагрузкой в ​​точке нагрузки:

M _MAX = F A B / L (4A)

Максимальный напряжение

Максимум Пресс в луче с однократным центром

. нагрузка, поддерживаемая с обоих концов:

σ _max = y _max F a b / (LI)                                                 0009

δ _F = F A ² B ² / (3 E I L) (4C)

Силы, действующие на концах:

R ₁ = F B / L (4d) R ₁ = F B / L (4d) R ₁ = F B / L (4d) R ₁ = F B / L (4d)

R ₂ = F A / L (4E)

Луч, поддерживаемый на обоих концах — две эксцентричные нагрузки

Максимум Момент (между нагрузками) в луче с двумя экцентрическими нагрузками: Момент (между нагрузками) в луче с двумя экцентрическими нагрузками: Момент (между нагрузками). 0009

M _MAX = F A (5A)

Максимальное напряжение

Максимум Frails в луче с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:

σ _MAX = Y

σ _MAX = Y

σ _{. / I (5B)}

Максимум отклонение в точке нагрузки может быть выражено как

Δ _F = F A (3L ² — 4 A ² ) / (24 E I) (5C)

Силы, действующие на концах:

R ₁ = R ₂

= F (5d)

= F (5d)

= F (5d)

= F (5d)

модель с расширением Sketchup Engineering ToolBox

Балка с опорой на обоих концах — трехточечная нагрузка

Максимальный момент (между нагрузками) в балке с трехточечной нагрузкой:

M _MAX = F L / 2 (6A)

Максимальный напряжение

Максимум Пресс в луче с тремя точками, поддерживаемыми на обоих концах:

σ _Max = Y

σ _Max = Y

σ _.

No related posts.