Расчет треугольной фермы пример: Металлические конструкции расчет фермы. Пример расчета треугольной фермы

Содержание

Проектирование и расчет металлических ферм всех разновидностей

Проектирование металлической фермы (систем) со всеми расчетами (сбор нагрузок, точная расчётная модель и сочетания нагрузок). Именно за счёт этого получаются лёгкие конструкции. В реальности небольшая вероятность что вам, как заказчику, будут просчитывать ферму полностью -«это ни кому не нужно (недоплачивают)»! Чаще всего, берется стропильная ферма по серии и интуитивно увеличиваются сечения элементов. Если повезет то сделают расчет элементов и будет точнее к совершенной.

Итак субъективно: на первом месте почти все фермы тяжелее чем должны быть (более 15%), на втором месте с недостающей несущей способностью — со слабым местом (1-10%) и на третьем месте это идеальные — стальные Легкие (5%). Все проектируют как умеют не более, подобно врачам — лечат как умеют.

Содержание

Расчет металлических ферм любой формы и габаритов

Каждый проект уникальный — соответственно индивидуальный подход. Проектирование и расчет металлических ферм без применений типовых серийных решений:
а) определение оптимальной геометрии стропильной конструкции;
б) проектирование системы связей — задание расчётных длин элементов
в) Определение сечений элементов
г) Расчёт узлов ферм (узел примыкания элементов решётки, фланцевый узел, опорный узел)
д) Проверка сечений элементов связей
е) расчет прогонов, с учётом наклона и промежуточных связей
Легкость (экономичность). Обеспечивается достаточным опытом всех требуемых расчетов
Быстрота выполнения проекта. Определяется профессиональным подходом, как правило до 5 дней
Доступная цена ообеспечивается работой без посредников, а так же нет необходимости платить за печать (СРО)
Проектирование стропильных (подстропильных) ферм любой конфигурации и сложности!
Пример расчета фермы и чертежей

Стоимость расчета и чертежей фермы

Цена проекта КМ (КМД) зависит главным образом от её ширины! А именно 75% её габарита, пример если стропильная конструкция имеет ширину 20м, то купить документацию за 15тр:

Некоторые показательные примеры

Виды проектируемых стальных ферм

Фермы профильной трубы

На мой взгляд это самые оптимальные вид стропильных систем, которые и просты в изготовлении.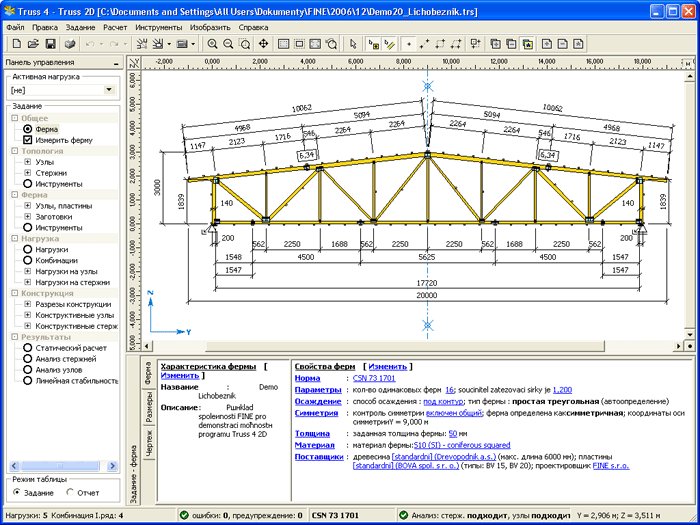 При пролётках 15-35м независимо от нагрузок, если округлить, получаются стропильные фермы стальные легкие. При расчёте данной фермы обычно возникает трудность, от лени проектировщиков, с расчётом узла примыкания решётки к поясу. Есть в СП 294.1325800.2017СП 16.3330.2011 точный алгоритм расчёта, но он весьма ёмкий. Обычная лень проектировщика копаться и разбираться с формулами. Есть программы которые это дело считают, но могу сказать что между ними есть отличия, хотя в том что они разработаны по разным рекомендациям.

Проектировщики пользуются серией по типу Молодечно и стараются применять серийные фермы в проектах. Но бывает часто что необходимо сконструировать ферму с нестандартной геометрией и здесь включается у проектировщиков интуиция и творчество…

Фермы из круглой трубы

Не приходилось проектировать. да они чуть легче чем из серии Молодечно, но изготовление трудоёмкое. Изготавливать качественно их могут только мощные обеспеченные автоматикой заводы

Фермы из ЛСТК

Как-то поступило мне предложение спроектировать покрытие (пролет 18,0м) из ЛСТК. Заказчику промыли уши что мол легкие конструкции и тд. Я согласился — и мне пришлось поднимать материал на эту тему. начал делать расчеты и выходи что физически не хватает сечения самого тяжелого профиля. Плюс ко всему, сейчас можно скачать рекомендации НИИ по проектированию конструкций из ЛСТК. В разделе ферм, там найдете что рекомендации применять фермы до 15,0м. Да ещё оптимальная геометрия — треугольная.

Вывод: фермы стальные легкие самые из ЛСТК, когда у них оптимальный пролёт и есть возможность устанавливать с частным шагом. Такое применение возможно если такие фермы монтируются на существующие стены, или в летних сооружениях, где не нужно делать фундаментов. Основной эффект экономический это снижение массы на прогонах, так же на самом деле стропильная система легкая, просто потому, что если делать сварную конструкцию то по рекомендациям нужно брать стенку не менее 3мм (нормы), а здесь можно на болтах брать стенку 1,5мм.

Проектирование фермы из гнутых тонкостенных сечений имеет подводный камень — сложность расчётов. Вышло только недавно официальный российский документ по расчёту. И выходит что сам расчёт по объему раз в 5-10 может быть объемный. Автоматизированных программ халявных нет — проектируют интуитивно. Мне уже дважды предлагали посредники с предложением проектировать (заводы изготовители ищут исполнителей которые будут строго делать расчёты по СП 260.1325800.2016 Конструкции стальные тонкостенные )

Фермы из парных уголков

Классические фермы. Трудоёмкие в изготовлении, да тяжеловатые получаются. Если сейчас и вводят в проект, то только потому, что на них есть готовые серийные проекты. Суть чем проще тем лучше для проектировщика. Их применяются проектировщики старой закалки, которые сидят как правило в проектных организациях советского времени.

Фермы из двутавров

Проектировать пока не было возможности, но можно сказать, применяются при больших пролётах или с огромными нагрузками.

Фермы с поясами из двутавров и решёткой из профильной трубы

При высоких нагрузках, можно спроектировать ферму из двутавров, но элементы решётки которые менее нагруженные, можно заменить на профильную трубу, для облегчения конструкции.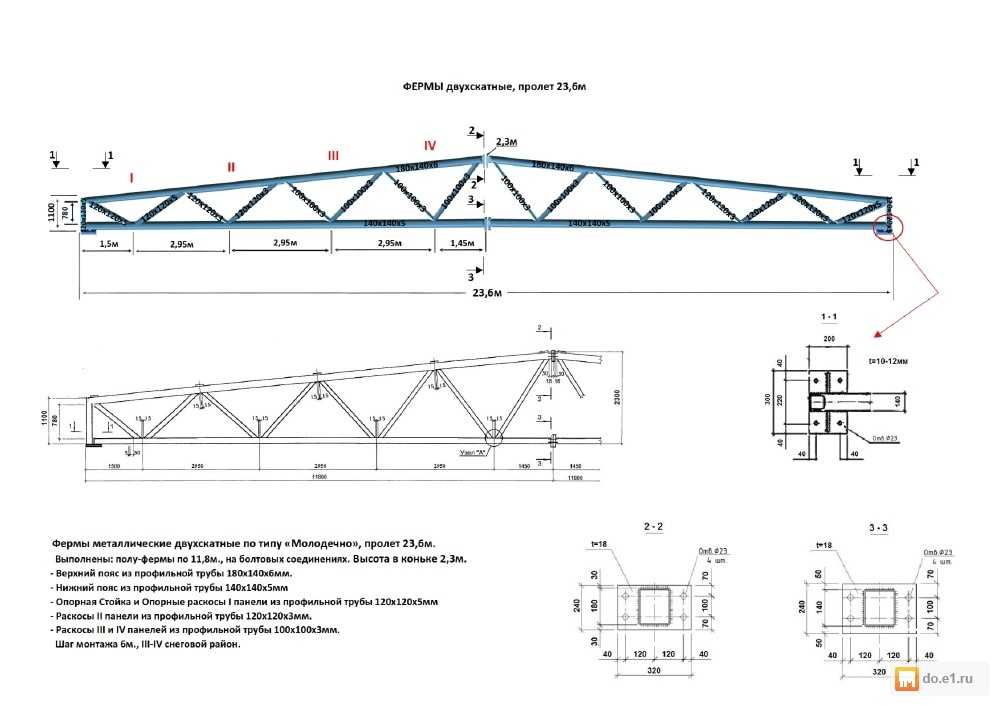

Геометрические типы

Схема стропильный конструкции	Описание
	Можно сказать что трапецевидная самая оптимальная геометрия фермы, при малых уклонах. Такая ферма (из профильной) трубы получается легче чем другие типы
	С параллельными поясами применяется при плоских рулонных кровлях
	Односкатная (возможно консольная) При применение кровельных сэндвич панелей, необходимо соблюдать требование по уклону верхнего пояса , а также более частый шаг прогонов. и как не крути при больших пролётах получается такая односкатная ферма.
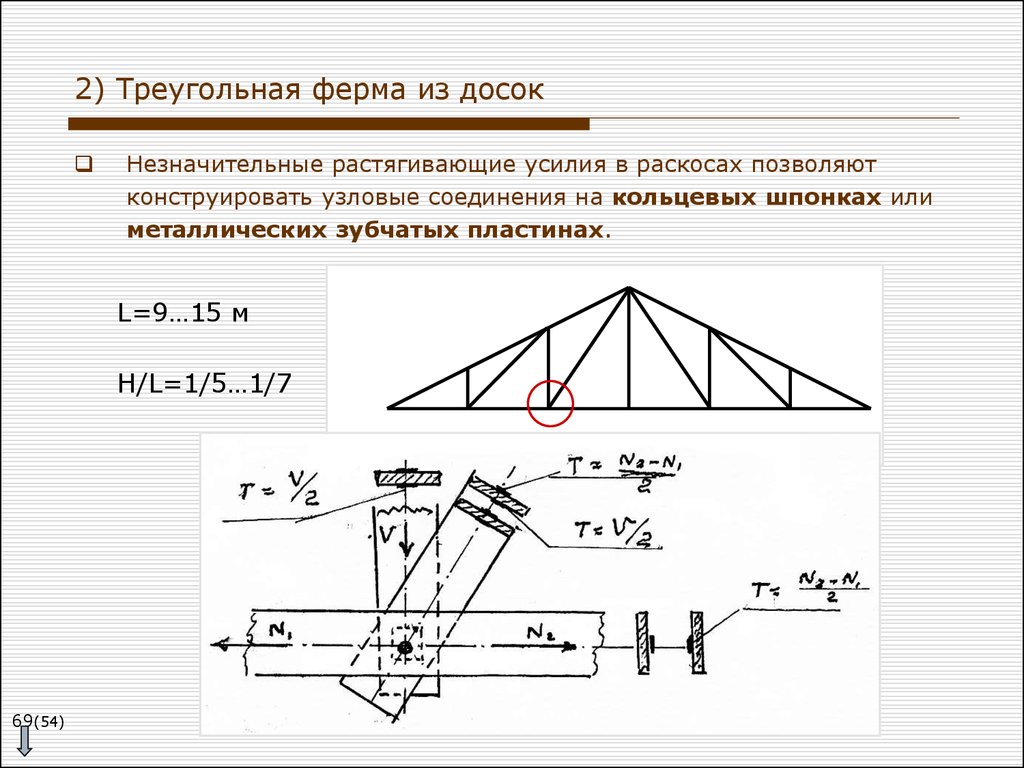
	Треугольная ферма с классическим уклоном скатов. Проектируют видимо при холодных кровлях. Хотя тут увеличенное пространство которое нужно отапливать. Это ферма к тому же обещает быть тяжелее чем трапециевидная Особенность расчёт металлической фермы, в том что на опорах пояса загибаются при малых уклонах, и верхний пояс здесь перенапряжён.
	Такие арочные фермы не встречал. видимо из-за сложности материала покрытия, напрашивается тент — ПВХ ткань. Затруднительно видимо гнуть проф. настил, что бы потом сделать мембранное покрытие. Минус дополнительный распор на оголовок колонны.
	Арка — распространённый вид основных несущих конструкций ангаров в сельском хозяйстве — покрытие тентовое.
	Полигональная — Применяется в качестве при строительстве ангарных сооружений с профнастилом
	Хорошо работает при больших высотах и пролётов, при условии что ветровые нагрузки (эстрадное здание на открытой местности или на берегу). Особенность сильный распор на фундамент Отличительная черта — хитрая связевая система и интересный узел примыкания рамной фермы с «колонной»

Как рассчитать ферму онлайн?

Продолжаем серию статей о расчетах сопромата онлайн. В этой статье я хочу поделиться онлайн-сервисом, который позволяет рассчитывать фермы. С помощью этого сайта вы узнаете, как произвести расчет фермы онлайн: определить реакции в опорах и узнать усилия, возникающие в стержнях.

В такой отрасли, как строительство, ферма — элемент, который ничем нельзя заменить. Ее используют для построения мостов, ангаров, стадионов. Без нее не обойдется строительство павильонов, сцен, подиумов. Кузов автомобиля, корпус корабля, самолета также считают фермой. Что немаловажно, при создании проекта корабля или самолета расчеты на прочность производят так же, как и при расчете стержневой системы. Ферма — это огромное количество стержней, соединенных в одну систему. Нагрузки приходится на места, в которых соединяются детали. На сегодняшний день в строительной отрасли отдают предпочтение жесткому скреплению, а не шарнирному.

Данный сервис расположен по адресу — skyciv.com/free-truss-calculator

Авторы данного проекта позиционируют свой онлайн-калькулятор как инструмент для проектирования ферм, который позволяет рассчитывать продольные усилия в стержнях, определить реакции, возникающие в опорах фермы и д. р.

Создатели также отмечают, что данный софт особенно полезен для проектирования мостовых ферм и стропильных систем деревянных крыш.

Сразу оговорюсь, бесплатная функциональность программы имеет определенные ограничения: можно добавить не более 12-ти стержней, 2-ух опор и 5-ти сосредоточенных внешних сил. В платной версии ограничений нет. Для расчета простых ферменных конструкций бесплатных возможностей вполне хватает.

Пример расчета фермы онлайн

В этом разделе я покажу, как создать расчетную схему простейшей фермы и получить результаты расчета.

Задаем узлы фермы

Первым делом необходимо задать узлы будущей фермы, которые дальше будут учитываться в расчете как простые шарниры. Для создания нового узла нужно выбрать кнопку – «Nodes».

Каждый задаваемый узел имеет свой уникальный идентификатор, к которому по ходу формирования расчетной схемы будем обращаться: при создании стержней фермы и приложении нагрузок. Для того чтобы создать новый узел, нужно задать его координаты по X и Y:

Примечание: рекомендуется первый узел задавать с координатами (0;0), так легче будет высчитывать координаты всех последующих узлов.

Создаем стержни фермы

Стержни задаются достаточно просто. Для создания нового стержня нужно выбрать кнопку — «Members». Далее нужно будет указать идентификатор узла, с которым будет соединяться стержень в начале и в конце. Вот что получилось у меня:

Назначаем опоры

Для того чтобы задать связи (опоры) фермы нужно выбрать кнопку – «Support». Эта программа имеет в своем функционале 6 видов связей. Я выберу классическую шарнирно-подвижную и неподвижную опору. Для того чтобы установить опору, нужно выбрать вид опоры и указать узел, где ее нужно установить.

Прикладываем нагрузку

В данной программе на ферму можно накладывать все виды нагрузок: сосредоточенные силы (Point Loads) и моменты (Moments), распределенную нагрузку (Distributed Loads). Например, для приложения сосредоточенной силы, нужно выбрать узел и задать ее численное значение.

Получаем результаты расчета

После выполнения всех вышеописанных шагов можно получить результаты расчета. Для этого нужно нажать кнопку – «Solve». Бесплатно можно вывести реакции в опорах фермы, значения продольных усилий. Также для каждого стержня указывается растянут он или сжат:

Вот такая есть полезная программа для расчета фермы онлайн!

Также для расчета фермы можно воспользоваться программой, описываемой на этой страничке.

3 метода анализа ферм | Engineersdaily

Перед обсуждением различных методов анализа ферм уместно сделать краткое введение.

Конструкция, состоящая из нескольких стержней, соединенных штифтами на концах и образующих устойчивый каркас, называется фермой. Обычно предполагается, что нагрузки и реакции действуют на ферму только в узлах. Ферма обычно состоит из треугольных элементов со стержнями на верхнем поясе, находящимися под сжатием, и стержнями вдоль нижнего пояса, находящимися под напряжением. Фермы широко используются для мостов, длинных пролетных крыш, электрических мачт и космических конструкций.

Фермы статически определимы, когда все усилия на стержнях могут быть определены только из уравнений статики.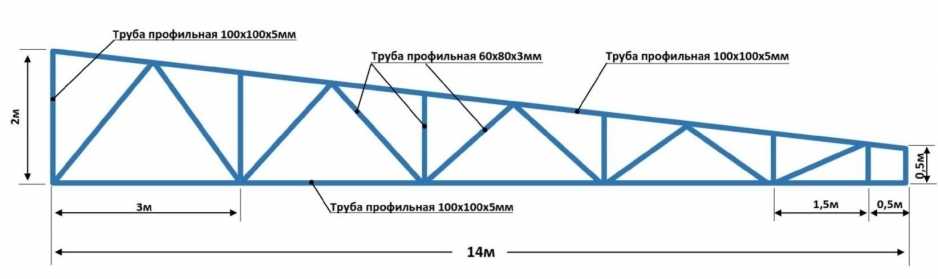 В противном случае ферма статически неопределима. Ферма может быть статически (внешне) определимой или неопределенной по реакциям (более 3 или 6 реакций в 2D или 3D задачах соответственно).

Правила знаков

Для анализа ферм предполагается, что:

Стержни соединены штифтами.
Соединения представляют собой шарниры без трения.
Нагрузки действуют только на соединения.
Напряжение в каждом стержне постоянно по его длине.

Целью анализа фермы является определение реакций и усилий на стержнях. Методы, используемые для проведения анализа с помощью уравнений равновесия и путем рассмотрения только частей конструкции путем анализа ее диаграммы свободного тела для решения неизвестных.

1. Метод соединений для анализа фермы

Начнем с предположения, что все элементы испытывают реакцию растяжения. Натяжной элемент испытывает тяговые усилия на обоих концах стержня и обычно обозначается положительным знаком (+ve). Когда на элемент действует толкающее усилие с обоих концов, говорят, что стержень находится в режиме сжатия и обозначается знаком минус (-ve).

В методе суставов вокруг сустава делается виртуальный разрез, а часть разреза изолируется в виде диаграммы свободного тела (FBD). Используя уравнения равновесия ∑ Fx = 0 и ∑ Fy = 0, можно решить неизвестные силы-члены. Предполагается, что все элементы соединены вместе в виде идеального штифта и что все силы находятся в напряжении (положительные реакции).

Воображаемое сечение может полностью проходить вокруг соединения в ферме. Сустав стал свободным телом, находящимся в равновесии под действием приложенных к нему сил. Уравнения ∑ H = 0 и ∑ V = 0 могут быть применены к соединению для определения неизвестных сил в элементах, встречающихся в нем. Очевидно, что на стыке этих двух уравнений можно определить не более двух неизвестных.

Простая модель фермы, опирающаяся на шарнирную и роликовую опору на конце. Каждый треугольник имеет одинаковую длину L и является равносторонним, где градус угла θ равен 60 ° на каждом угле. Опорные реакции Ra и Rc можно определить, взяв точку момента либо в точке A, либо в точке C, тогда как Ha = 0 (другая горизонтальная сила отсутствует).

Вот несколько простых рекомендаций по этому методу:

Сначала нарисуйте диаграмму свободного тела (FBD),
Решите реакции данной структуры,
Выберите соединение с минимальным количеством неизвестных (не более 2) и проанализируйте его с ∑ Fx = 0 и ∑ Fy = 0,
Перейдите к остальным суставам и снова сосредоточьтесь на суставах, которые имеют минимальное количество неизвестных,
Проверить усилия на стержнях в неиспользуемых соединениях с ∑ Fx = 0 и ∑ Fy = 0,
Занесите в таблицу усилия на стержень независимо от того, находится ли он в реакции растяжения (+ve) или сжатия (-ve).

На рисунке показаны 3 выбранных соединения в точках B, C и E. Силы в каждом элементе можно определить по любому соединению или точке. Лучше всего начать с выбора самого простого соединения, такого как соединение C, где реакция Rc уже получена и только с двумя неизвестными силами FCB и FCD. Оба могут быть оценены с помощью правил ∑ Fx = 0 и ∑ Fy = 0. В соединении E действуют 3 неизвестные силы FEA, FEB и FED, что может привести к более сложному решению по сравнению с 2 неизвестными значениями. В целях проверки соединение B выбирается так, чтобы показать, что уравнение ∑ Fx равно ∑ Fy, что приводит к нулевому значению, ∑ Fx = ∑ Fy = 0. Состояние каждого стержня должно быть четко указано, например, находится ли он в напряжении (+ ve) или в сжатом (-ve) состоянии.

Тригонометрические функции:

Определение угла между стержнями x и z…

Cos θ = x / z
Sin θ = y / z
Тан θ = у / х

2. Метод сечений для расчета ферм

Метод сечения является эффективным методом, когда необходимо определить силы во всех элементах фермы. Если требуется только несколько сил, действующих на ферму, то самый быстрый способ найти эти силы — метод сечений. В этом методе воображаемая линия разреза, называемая сечением, проводится через устойчивую и определенную ферму. Таким образом, сечение делит ферму на две отдельные части. Поскольку вся ферма находится в равновесии, любая ее часть также должна находиться в равновесии. Можно рассмотреть любую из двух частей фермы и применить три уравнения равновесия ∑ Fx = 0, ∑ Fy = 0 и ∑ M = 0 для расчета сил стержней.

Используя ту же модель простой фермы, детали будут такими же, как на предыдущем рисунке, с двумя разными профилями опор. В отличие от совместного метода, здесь нас интересует только нахождение значения сил для элементов BC, EC и ED.
Несколько простых указаний:

Пропустите секцию через максимум 3 элемента фермы, 1 из которых является нужным элементом, разделяющим ферму на 2 совершенно отдельные части,
В 1 части фермы определите моменты относительно точки (в стыке), где пересекаются 2 стержня, и определите силу стержня, используя ∑ M = 0,
Решите два других неизвестных, используя уравнение равновесия для сил, используя ∑ Fx = 0 и ∑ Fy = 0.

Примечание: 3 силы не могут быть одновременными, иначе их нельзя решить.

Виртуальный разрез вводится через единственные обязательные элементы, расположенные вдоль элементов BC, EC и ED. Во-первых, следует определить опорные реакции Ra и Rd. Опять же, для решения этой проблемы требуется здравый смысл, где проще всего было бы рассмотреть либо левую, либо правую сторону. Измерить момент в соединении E (виртуальная точка) по часовой стрелке для всей правой части будет намного проще, чем в соединении C (левая часть). Затем либо сустав D, либо C можно рассматривать как точку момента, либо же, используя метод соединения, найти силы стержня для FCB, FCE и FDE. Примечание. Каждое значение состояния элемента должно быть четко указано, находится ли он в состоянии растяжения (+ve) или в состоянии сжатия (-ve).

3. Графический метод анализа ферм (диаграмма Максвелла)

Метод соединений может быть использован в качестве основы для графического анализа ферм.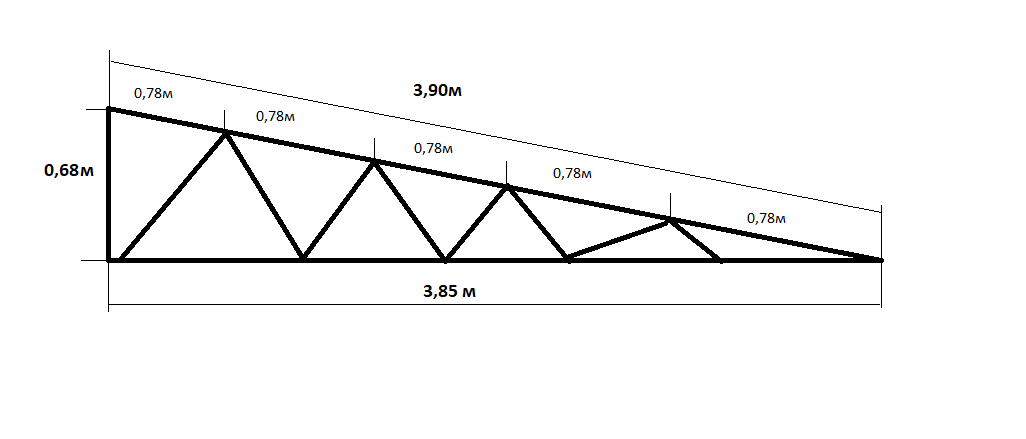 Графический анализ был разработан с помощью полигонов сил, начерченных в масштабе для каждого соединения, а затем усилия в каждом элементе были измерены по одному из этих полигонов сил. Однако количество линий, которые необходимо нарисовать, можно значительно сократить, если различные силовые полигоны накладываются друг на друга. Полученная диаграмма фермы известна как диаграмма Максвелла.

Чтобы напрямую нарисовать диаграмму Максвелла, вот простые рекомендации:

Решите реакции на опорах, решив уравнения равновесия для всей фермы,
Двигайтесь по часовой стрелке вокруг внешней стороны фермы; нарисуйте многоугольник силы в масштабе для всей фермы,
Возьмите каждый сустав по очереди (один за другим), затем нарисуйте многоугольник сил, рассматривая последовательные суставы, на которые действуют только две неизвестные силы,
Измерьте величину силы в каждом элементе по диаграмме,
Наконец, обратите внимание, что работа велась от одного конца фермы к другому, так как это используется для проверки баланса и соединения с другим концом.

Простая треугольная ферма с углом наклона θ составляет 60° на каждом угле (равносторонний) и такой же длиной элемента L на 2 типах опор. Опять же, оценка реакции опоры играет важную роль в решении любых структурных задач. В этом случае значение Hb равно нулю, так как на него не влияют никакие горизонтальные силы. Процедура решения этой задачи может быть довольно сложной и требует воображения. Он начинается с маркировки промежутков между силами и стержнями с помощью примера, показанного выше; реакцию Ra и приложенную силу P, обозначенную пробелом 1, и продолжайте движение по часовой стрелке вокруг фермы. Для каждого члена, например, между пробелами 1 и 5 будет член AC и так далее. Примечание. Выберите подходящий масштаб для рисования диаграммы Максвелла.

В заключение, внутренние реакции фермы, а также силы, действующие на ее элементы, можно определить любым из этих трех методов. Тем не менее, метод соединений становится наиболее предпочтительным методом, когда речь идет о более сложных конструкциях.

Для получения дополнительной информации по теме:

☞ Статически определяемые фермы
☞ Решенные примеры для метода соединений для расчета ферм

☞ Анализ ферм

Поставьте лайк и поделитесь этой статьей на facebook:

3 метода анализа ферм Оставьте свои комментарии ниже для любых улучшений или предложений. Мы будем рады разместить ваш ценный вклад.
Опубликовано Engineers Daily в понедельник, 6 июня 2016 г.

5.6: Методы анализа ферм

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 42966

Рене Альдерлистен
Делфтский технологический университет через TU Delft Open

Существует несколько методов анализа ферм, но наиболее распространенными являются метод соединения и метод сечения (или момента).

5.6.1 Соглашение о знаках

При расчете ферм отрицательная осевая сила на стержне означает, что элемент или соединения на обоих концах элемента испытывают сжатие, тогда как положительное значение осевой силы на стержне указывает на то, что элемент или соединения на обоих концах элемента находятся в состоянии растяжения.

5.6.2 Анализ ферм методом соединения

Этот метод основан на том принципе, что если структурная система представляет собой тело, находящееся в равновесии, то любое соединение в этой системе также находится в равновесии и, таким образом, может быть выделено из всей системы и проанализировано с использованием условий равновесия. Метод соединения включает в себя последовательную изоляцию каждого соединения в системе ферм и определение осевых усилий в элементах, встречающихся в соединении, с помощью уравнений равновесия. Подробная процедура анализа этим методом изложена ниже.

Процедура анализа

• Проверить устойчивость и определенность конструкции.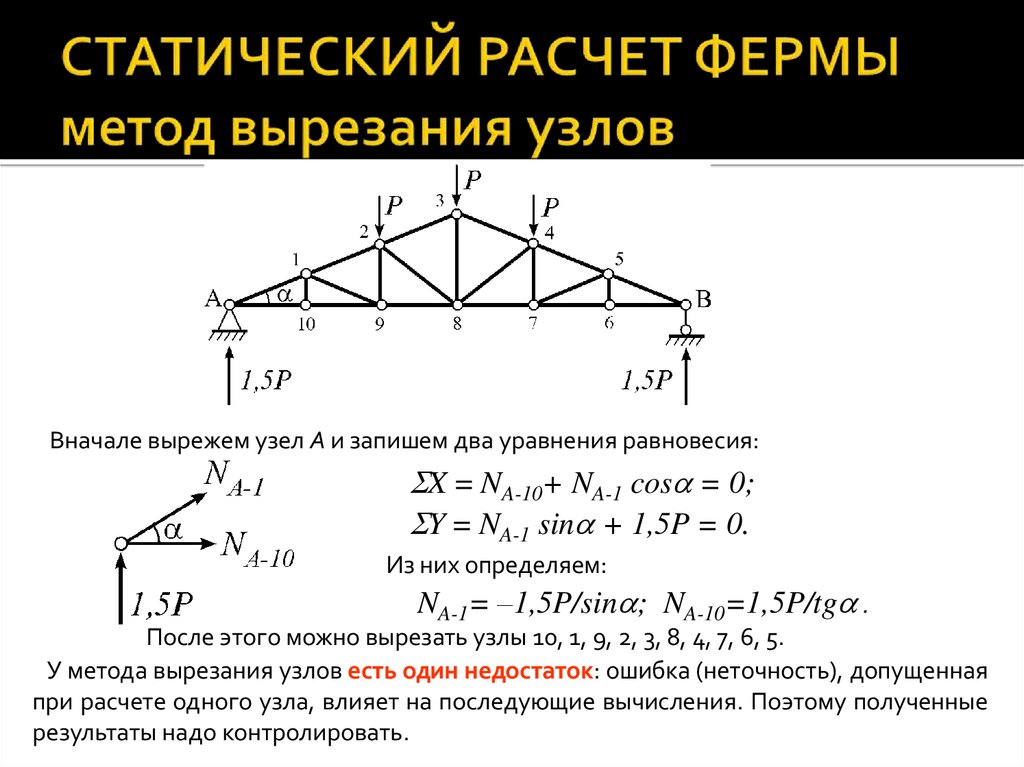 Если ферма устойчива и детерминирована, переходите к следующему шагу.

•Определить опорные реакции в ферме.

• Определить элементы нулевой силы в системе. Это неизмеримо сократит вычислительные усилия, связанные с анализом.

•Выберите соединение для анализа. Ни в коем случае в анализируемом соединении не должно быть более двух неизвестных сил стержня.

• Начертите изолированную диаграмму свободного тела выбранного соединения и обозначьте осевые силы во всех элементах, встречающихся в соединении, как растягивающие (т.е. отрывающие от соединения). Если это первоначальное допущение неверно, определенная осевая сила стержня при анализе будет отрицательной, что означает, что стержень находится в состоянии сжатия, а не растяжения.

• Примените два уравнения \(\Sigma F_{X}=0\) и \(\Sigma F_{Y}=0\) для определения осевых усилий стержня.

•Продолжить анализ, перейдя к следующему соединению с двумя или меньшим числом неизвестных сил-членов.

Пример 5.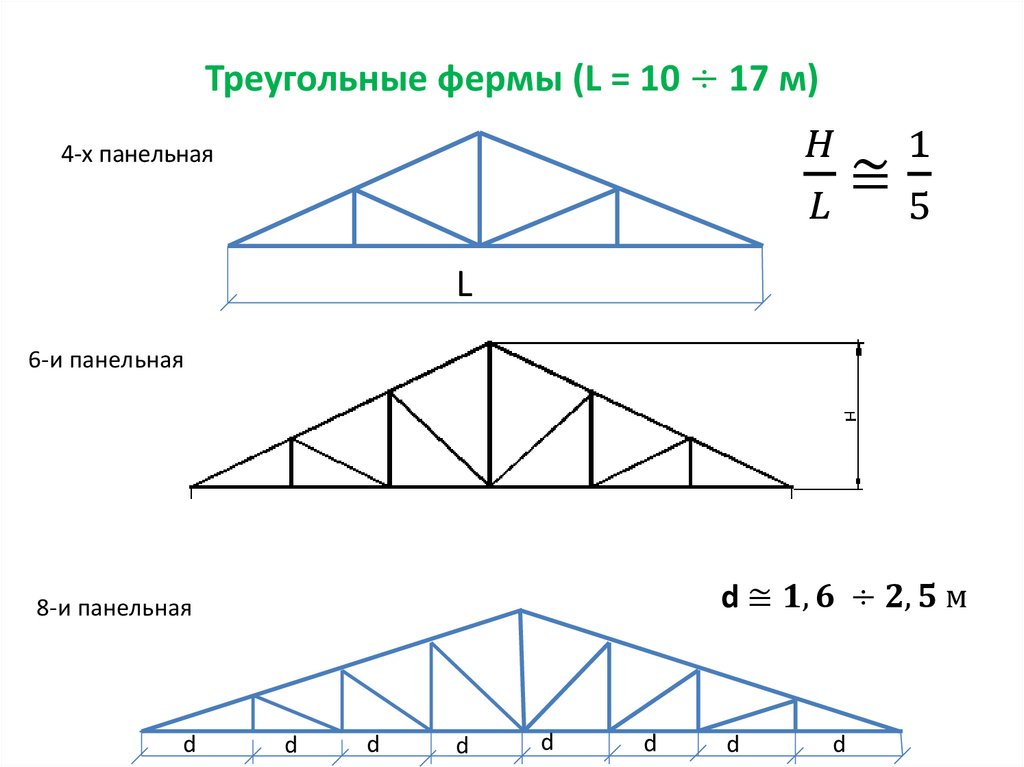 2

Используя метод соединения, определите осевую силу в каждом элементе фермы, показанной на рис. 5.10а.

\(рис. 5.10\). Ферма.

Решение

Реакции поддержки. Применяя уравнения статического равновесия к диаграмме свободного тела, показанной на рис. 5.10б, опорные реакции можно определить следующим образом:

\(\begin{array}{ll}
+\curvearrowleft \sum M_{A} =0 \\
20(4)-12(3)+(8) C_{y}=0 \\
C_{y}=-5,5 \mathrm{кН} & C_{y}=5,5 \mathrm{кН } \стрелка вниз\\
+\стрелка вверх \сумма F_{y}=0 \\
A_{y}-5,5+20=0 \\
A_{y}=-14,5 \mathrm{кН} & A_{y}=14,5 \mathrm{ кН} \downarrow \\
+\rightarrow \sum F_{x}=0 \\
-A_{x}+12=0 \\
A_{x}=12 \mathrm{kN} & A_{x}= 12 \mathrm{кН} \leftarrow \\
\end{array}\)

Анализ соединений. Анализ начинается с выбора соединения, которое имеет две или меньше неизвестных сил стержня. Диаграмма свободного тела фермы покажет, что соединения \(A\) и \(B\) удовлетворяют этому требованию. Чтобы определить осевые усилия в элементах, встречающихся в стыке \(A\), сначала изолируйте соединение от фермы и обозначьте осевые усилия элементов как \(F_{A B}\) и \(F_{A D}\) 9{\circ}=-7,34 \mathrm{кН}
\end{массив}\)

После завершения анализа соединения \(A\) , соединения \(B\) или \(D\) можно проанализировать, так как есть только две неизвестные силы.

Анализ соединения \(D\).

\(\begin{array}{l}
+\стрелка вверх \sum F_{y}=0 \\
F_{DB}=0 \\
+\стрелка вправо \sum F_{x}=0 \\
-F_{D A}+F_{D C}=0 \\
F_{D C}=F_{D A}=-7,34 \mathrm{кН}
\end{массив}\)

Анализ соединения \(B \).

\(\begin{array}{l}
+\rightarrow \sum F_{x}=0 \\
-F_{BA} \sin 53.13+F_{BC} \sin 53.13+15=0 \\
F_{B C} \sin 53.13=-15+24.17 \sin 53.13= \\
F_{BC}=5.42 \mathrm{кН}
\end{массив}\)

5.6.3 Члены Zero Force

Анализ сложной фермы можно значительно упростить, если сначала определить «элементы с нулевой силой». Элемент с нулевой силой — это элемент, который не подвергается какой-либо осевой нагрузке. Иногда такие элементы вводят в систему ферм, чтобы предотвратить коробление и вибрацию других элементов. Конструкции ферменных элементов, приводящие к элементам нулевой силы, перечислены ниже:

1. Если существует неколлинеарность между двумя элементами, встречающимися в стыке, на который не действует никакая внешняя сила, то эти два элемента являются элементами с нулевой силой (см. рис. 5.11а).

2. Если три элемента встречаются в стыке без внешней силы, а два из них коллинеарны, третий элемент является элементом с нулевой силой (см. рис. 5.11b).

3. Если два элемента встречаются в стыке, и сила, приложенная к стыку, параллельна одному элементу и перпендикулярна другому, то элемент, перпендикулярный приложенной силе, является элементом с нулевой силой (см. рис. 5.11c).

\(рис. 5.11\). Члены нулевой силы.

5.6.4 Анализ ферм методом раздела

Иногда определение осевой силы в конкретных элементах ферменной системы методом соединения может быть очень трудоемким и громоздким, особенно когда система состоит из нескольких элементов. В таких случаях использование метода сечения может сэкономить время и поэтому предпочтительнее. Этот метод включает в себя прохождение воображаемого сечения через ферму так, чтобы оно делило систему на две части и прорезало элементы, осевые усилия которых желательны. Осевые силы стержня затем определяются с использованием условий равновесия. Подробная процедура анализа этим методом представлена ниже.

Процедура анализа ферм методом раздела

•Проверьте устойчивость и определенность конструкции. Если ферма устойчива и детерминирована, переходите к следующему шагу.

•Определить опорные реакции в ферме.

• Сделайте воображаемый разрез в конструкции так, чтобы он включал в себя элементы, осевые усилия которых нужны. Воображаемый разрез делит ферму на две части.

• Прилагайте усилия к каждой части фермы, чтобы удерживать ее в равновесии.

• Выберите любую часть фермы для определения сил стержня.

• Применить условия равновесия для определения осевых усилий стержня.

Пример 5.3

Методом сечения определите осевые усилия в элементах \(CD\), \(CG\) и \(HG\) фермы, показанной на рис. 5.12а.

\(рис. 5.12\). Ферма.

Решение

Реакции поддержки. Применяя уравнения статического равновесия к диаграмме свободного тела на рис. 5.12b, опорные реакции можно определить следующим образом:

\(\begin{array}{l}
A_{y}=F_{y}=\frac{160}{2}=80 \mathrm{кН} \\
+\стрелка вправо \Sigma F_{x} =0 \quad A_{x}=0
\end{array}\)

Анализ методом сечения. Во-первых, воображаемое сечение проходит через ферму так, чтобы оно пересекало элементы \(CD\), \(CG\) и \(HG\) и делило ферму на две части, как показано на рис. 5.12c и рис. 5.12г. Все силы, воздействующие на стержень, обозначаются как силы растяжения (т. е. отрыв от соединения). Если это первоначальное предположение неверно, расчетные силы на стержнях будут отрицательными, что указывает на то, что они сжимаются. Любая из двух частей может быть использована для анализа. Левая часть будет использоваться для определения сил стержня в этом примере. Применяя уравнение равновесия к левому сегменту фермы, осевые силы в элементах можно определить следующим образом:

Осевая сила в стержне \(CD\). Чтобы определить осевую силу в элементе \(CD\) , , найдите момент относительно соединения фермы, при котором только \(CD\) будет иметь момент относительно этого соединения, а все остальные разрезанные элементы не будут иметь момента. Внимательное рассмотрение покажет, что соединение, удовлетворяющее этому требованию, является соединением \(G\). Таким образом, взятие момента около \(G\) предполагает следующее:

\(\begin{array}{l}
+\curvearrowleft \sum M_{G}=0 \\
-80(6)+80( 3)-F_{C D}(3)=0 \\
F_{C D}=-80 \mathrm{кН} и 80 \mathrm{кН} (C)
\end{массив}\)

Осевая сила в стержне \(HG\).

\(\begin{array}{l}
+\curvearrowleft \sum M_{C}=0 \\
-80(3)+F_{H G}(3)=0 \\
F_{H G}= 80 \mathrm{kN} & 80 \mathrm{kN} (T)
\end{array}\)

Осевая сила в стержне \(CG\). Осевая сила в стержне \(CG\) определяется с учетом вертикального равновесия левой части. Таким образом,

\(\begin{array}{l}
+\uparrow \sum F_{y}=0 \\ 9{\circ}=0 \\
F_{C G}=0
\end{массив}\)

Краткое изложение главы

Внутренние силы в плоских фермах: Фермы представляют собой конструктивные системы, состоящие из прямых и гибких элементов, соединенных на концах. Допущения при расчете плоских ферм включают следующее:

1.Элементы ферм соединены на концах безфрикционными штифтами.

2. Стержни прямые и подвергаются осевым нагрузкам.

3. Деформации элементов малы и пренебрежимо малы.

4. Нагрузки в фермах действуют только на их соединения.

Элементы фермы могут подвергаться осевому сжатию или осевому растяжению. Осевое сжатие элементов всегда считается отрицательным, а осевое растяжение всегда считается положительным.

Фермы могут быть внешне или внутренне определенными или неопределенными. Внешне детерминированные фермы — это фермы, неизвестные внешние реакции которых можно определить, используя только уравнение статического равновесия. Внешне неопределенными называют фермы, внешняя неизвестная реакция которых не может быть полностью определена с помощью уравнений равновесия. Для определения числа неизвестных реакций, превышающих уравнение равновесия неопределенных ферм, необходимо составить дополнительные уравнения, исходя из совместимости частей системы. Внутренне определенные фермы — это фермы, элементы которых расположены таким образом, что образуется ровно столько треугольных ячеек, чтобы предотвратить геометрическую нестабильность системы.

Формулировка устойчивости и определенности в фермах следующая:

\(\begin{array}{l}
m+r<2 j \quad \text { конструкция статически неустойчива } \\
m+r=2 j \quad \text { конструкция детерминирована } \\
m +r>2 j \quad \text { структура не определена }
\end{массив}\)

Методы анализа ферм: Двумя распространенными методами расчета ферм являются метод соединения и метод сечения (или момента).

Метод соединения : Этот метод включает изоляцию каждого соединения фермы и учет равновесия соединения при определении осевой силы элемента. Два уравнения, используемые для определения осевых сил стержня, это \(\Sigma F_{X}=0\) и \(\Sigma F_{y}=0\). Соединения изолируют последовательно для анализа, исходя из того принципа, что количество осевых сил неизвестного стержня никогда не должно быть больше двух в рассматриваемом соединении в плоском доверии.

Метод сечения: Этот метод включает в себя прохождение воображаемого сечения через ферму, чтобы разделить ее на две части. Силы стержня определяются с учетом равновесия части фермы по обе стороны от сечения. Этот метод удобен, когда требуются осевые усилия в определенных элементах в ферме с несколькими элементами.

Практические задачи

5.1 Классифицируйте фермы, показанные на рис. P5.1a–рис. P5.1r.

\(Рис. П5.1\). Классификация ферм.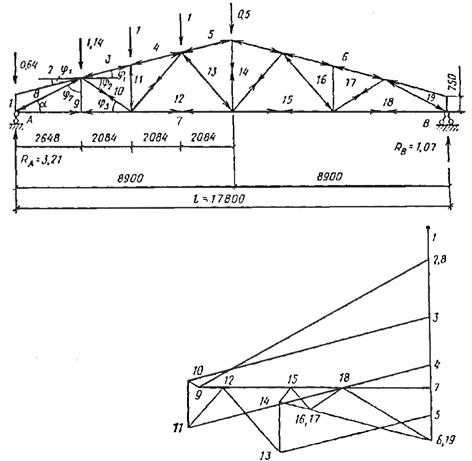

5.2 Определите усилие в каждом элементе ферм, показанных на рис. P5.2–рис. P5.12, используя метод соединения.

\(Рис. П5.2\). Ферма.

\(Рис. П5.3\). Ферма.

\(Рис. П5.4\). Ферма.

\(Рис. П5.5\). Ферма.

\(Рис. П5.6\). Ферма.

\(Рис. П5.7\). Ферма.

\(Рис. П5.8\). Ферма.

\(Рис. П5.9\). Ферма.

\(Рис. П5.10\). Ферма.

\(Рис. П5.11\). Ферма.