Как посчитать определитель матрицы: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.

Содержание

Определитель матрицы 2×2, 3×3, 4×4…

Определитель (детерминант) квадратной матрицы A — это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.

Обозначения

Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$

Свойства определителя

Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)
или
$\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны)
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или
$ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 16
В определителе
$\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:
$3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:
$6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$
При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.
Пример 17
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
Пример 18
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.
Пример 19
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$
Пример 20
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$
Определитель матрицы равен определителю транспонированной матрицы.
Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.

Минор матрицы

Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.

Пример 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

Один из миноров матрицы A есть $\begin{vmatrix} 1 & 4\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)

Другим минором является $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)

Пример 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $

Один из миноров матрицы B есть $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)

Другим минором является $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)

Пусть $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{pmatrix}$

Можно определить минор $\Delta_{i,j}$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_{i,j}$ квадратной матрицы A. Такой минор называется дополнительным.

Пример 23
$ A = \begin{pmatrix} 4 & 7\\ 2 & 9 \end{pmatrix}$

Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_{2,1}$.

Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем

Минор, дополнительный к элементу 2, есть $\Delta_{2,1} = 7$.

Пример 24
$B=\begin{pmatrix} 1 & 4 & 2\\ 5 & 3 & 7\\ 6 & 2 & 1\\ \end{pmatrix}$

Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_{2,3}$.

Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем

Минор, дополнительный к элементу 7, — это $\Delta_{2,3}= \begin{vmatrix} 1 & 4\\ 6 & 2 \end{vmatrix}$

Пример 25
$C=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix}$

Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_{1,2}$.

Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем

Минор, дополнительный к элементу 5, — это $\Delta_{1,2}= \begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$

Алгебраическое дополнение элемента матрицы

Пусть $A=\begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . {7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $a_{2,5}$.

Порядок определителя

Порядок определителя матрицы равен числу ее строк и столбцов.

Пример 26
$\begin{vmatrix} 1 & 4\\ 6 & 2\\ \end{vmatrix}$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)

Пример 27
$\begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)

Вычисление определителя матрицы

Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.

$\left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & .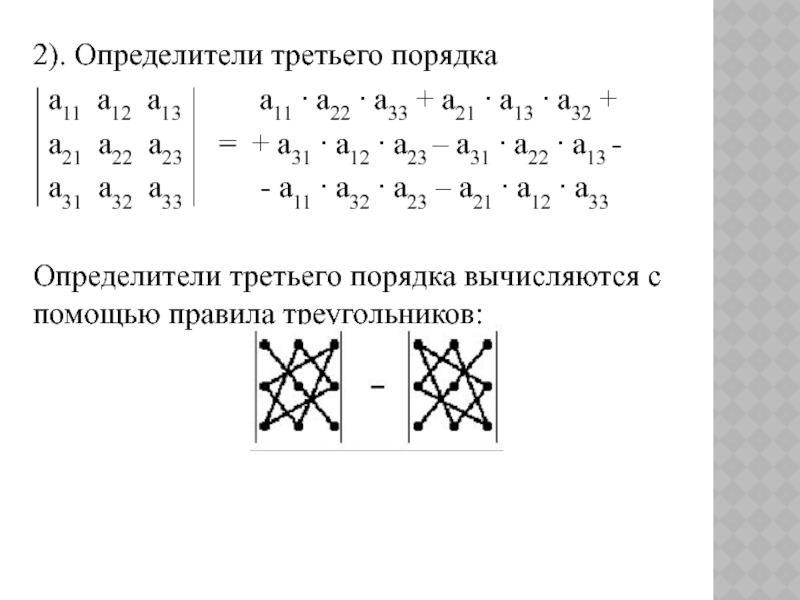 {4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$

$\Delta_{1,1}= \begin{vmatrix} a_{2,2} & a_{2,3}\\ a_{3,2} & a_{3,3} \end{vmatrix} = a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2}$

$\Delta_{1,2}= \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3} \end{vmatrix} = a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1}$

$\Delta_{1,3}= \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{vmatrix} = a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1}$

$\left| A\right| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot(a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1,2}\cdot a_{2.1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$

Упростить получение последней формулы можно следующим образом.

Начнем с того, что перепишем первые две строки под определителем как показано ниже.

$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\ a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\ \end{array}$

Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}}$

$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm} \begin{array}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{array}$

Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:

$\color{blue}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$

Вычитая вторую сумму из первой, получаем формулу определителя:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$

Пример 30
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{pmatrix}$

$\begin{vmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 1 & 4 & 3\\ 2 & 1 & 5\\ \end{array}$

$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 -(3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $ 1 + 12 + 60 -(9 + 10 + 8)=73-27=46$

Пример 31
$A=\begin{pmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{pmatrix}$

$\begin{vmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 3 & 5 & 1\\ 1 & 4 & 2\\ \end{array} $

$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 -(1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$

Элементы матрицы могут быть обозначены буквами.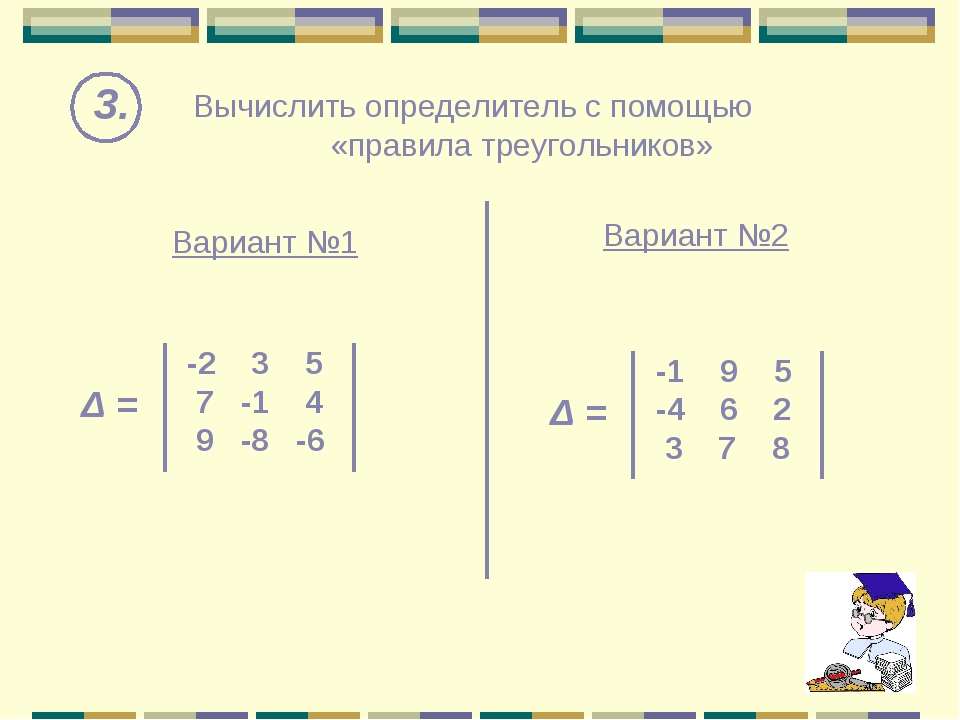 {2} \end{vmatrix}= $

$\begin{vmatrix} a-c & b-c \\ (a-c)(a+c) & (b-c)(b+c) \end{vmatrix}=$ $(a-c)(b-c)\begin{vmatrix} 1 & 1\\ a+c & b+c \end{vmatrix}=$

$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$

Вычисление определителя матрицы 4×4

Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.

Но сначала надо использовать свойства определителей:

Проверим, не выполняется ли одно из условий того, что определитель равен 0.
Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.

В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение — это определитель матрицы 3×3, который считается по уже известной формуле.

Пример 33
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 0 & 0 & 0 & 0\\ 2 & 3 & 1 & 8 \end{vmatrix}$

Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.

Пример 34
$\begin{vmatrix} 1 & 3 & 1 & 2\\ 5 & 8 & 5 & 3\\ 0 & 4 & 0 & 0\\ 2 & 3 & 2 & 8 \end{vmatrix}$
Замечаем, что $C_{1}$ равно $C_{3}$, следовательно, определитель равен 0.

Пример 35
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 10 & 16 & 18 & 4\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.

Пример 36
$\begin{vmatrix} \color{red}{4} & 3 & 2 & 2\\ 0 & 1 & -3 & 3\\ 0 & -1 & 3 & 3\\ 0 & 3 & 1 & 1 \end{vmatrix}$

Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец. Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.

=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot(-3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$

Пример 37
$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix}$

Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением. {2+2}\cdot \begin{vmatrix} 4 & 2 & 8\\ 1 & 3 & 1\\ 2 & 1 & 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$

Пример 38
$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 3 & 3 & 3 & 3\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Можно вынести множитель 3 из строки 3:
$3\cdot \begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Поскольку в строке 3 все элементы равны 1, легко обратить получить нули.

$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1 \end{vmatrix}$ $ \xlongequal{C_{1} — C_{4},C_{2}-C_{4},C_{3}-C_{4}} \begin{vmatrix} -1 & -4 & 1 & 2\\ 3 & 4 & 2 & -1\\ 0 & 0 & 0 & \color{red}{1}\\ -2 & 3 & 1 & 1 \end{vmatrix}$ $=1\cdot(-1)^{3+4}\cdot$ $=(-1)\cdot \begin{vmatrix} -1 & -4 & 1\\ 3 & 4 & 2 \\ -2 & 3 & 1\\ \end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4\cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47$

Пример 39
$\begin{vmatrix} 2 & 5 & 1 & 4\\ 4 & 1 & 6 & 3\\ 5 & 3 & 7 & 2\\ 1 & 0 & 2 & 4 \end{vmatrix}$

Здесь мы можем использовать единицу из последней строки и обратить остальные элементы первого столбца в нули. {4+1}\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}$

Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 — (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3\cdot 1)]=$ $-(180+12+117-24-195-54)=36$

Пример 40
$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$

Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули.

$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 & 1 & 2 & -1\\ 0 & 0 & \color{red}{1} & 0 \\ -1 & -4 & 3 & -2\\ -1 & -2 & 2 & -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 & 1 & -1\\ -1 & -4 & -2\\ -1 & -2 & -1 \end{vmatrix}$

Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $-[2\cdot 4\cdot 1 + 1\cdot 2\cdot (-1)+ 1\cdot 1\cdot 2 — ((-1)\cdot 4\cdot 1 + 2\cdot 2\cdot 2 + 1\cdot 1\cdot 1)]=$ $-(8-2+2+4-8-1)=-3$

Пример 41
$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3\\ \end{vmatrix}$

Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы.

$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{L_{1}+L_{2}+L_{3}+L_{4}} \begin{vmatrix} 10 & 10 & 10 & 10\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix} =$ $10\cdot \begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{C_{1} — C_{4},C_{2}-C_{4},C_{3}-C_{4}}10\cdot \begin{vmatrix} 0 & 0 & 0 & \color{red}{1}\\ -1 & 1 & 2 & 2\\ 2 & 3 & 1 & 1\\ 1 & -1 & -2 & 3 \end{vmatrix}=$

$=10\cdot1\cdot(-1)^{1+4}$

$ = (-10)\cdot \begin{vmatrix} -1 & 1 & 2\\ 2 & 3 & 1\\ 1 & -1 & -2 \end{vmatrix}=$ $(-10)\cdot((-1)\cdot 3\cdot (-2) +2 \cdot (-1)\cdot2 + 1\cdot 1\cdot 1$ $-(2\cdot 3\cdot 1 + 1\cdot (-1)\cdot (-1) + (-2)\cdot1\cdot2))$ $= -10\cdot(6 -4 +1 -6 — 1 + 4) =0$

Определитель 4 порядка.

Калькулятор

Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.

Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.

Пример 1. Вычислить определитель методом разложения.

Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются — выделено красным)

В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников

Найденные значения подставляем в выходной детерминант

Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.

Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных

Результаты совпадают, следовательно вычисления проведены верно.

Пример 2. Вычислить определитель матрицы четвертого порядка.

Решение.

Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде

Далее переходим к отысканию определителей по правилу треугольников

Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем

Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком

Метод возведения определителя к треугольному виду

Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.

Пример 3. Найти определитель матрицы сведением к треугольному виду

Решение.

Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим

Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем

Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид

Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе

По свойству, определитель треугольной матрицы равен произведению диагональных элементов.

По желанию можно проверить результат матричным калькулятором.

В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.

Рассмотрим более сложный.

Пример 4.

Найти определитель матрицы 4-го порядка

Решение.

Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант

Для удобства вычислений, меняем третью строчку со вторым местами..

По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.

От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим

Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.

Результат будет следующим

От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.

Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления

Проверка матричным калькулятором подтверждает правильность производимых вычислений.

Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.

Определитель матрицы: алгоритм, примеры вычисления, правила

Определение 1

Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.

|А|, ∆, det A — символы, которыми обозначают определитель матрицы.

Способ вычисления определителя выбирают в зависимости от порядка матрицы.

Пример 1

Определитель матрицы 2-го порядка вычисляют по формуле:

А=1-231.

Решение:

det A=1-231=1×1-3×(-2)=1+6=7

Определитель матрицы 3-го порядка: правило треугольника

Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:

правило треугольника;
правило Саррюса.

Как найти определитель матрицы 3-го порядка по методу треугольника?

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 2

А=13402115-1

Решение:

det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

дописать слева от определителя два первых столбца;
перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 3

А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:

разложением по элементам строки;
разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Пример 4

Разложение матрицы по элементам строки:

det A=ai1×Ai1+ai2×Ai2+…+аin×Аin

Разложение матрицы по элементам столбца:

det A=а1i×А1i+а2i×А2i+…+аni×Аni

Замечание

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Пример 5

А=01-132100-24513210

Решение:

раскладываем по 2-ой строке:

А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310

раскладываем по 4-му столбцу:

А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321

Свойства определителя

Свойства определителя:

если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
если поменять местами строки и столбцы, то знак поменяется на противоположный;
определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Пример 6

А=134021005

Решение:

det А=134021005=1×5×2=10

Замечание

Определитель матрицы, который содержит нулевой столбец, равняется нулю.

Определитель матрицы онлайн

Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6. 7 и т.д.

Примеры вычисления определителя матрицы

Пример 1. Найти определитель матрицы

Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:

Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):

Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:

Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:

Определитель матрицы 3 на 3

Определение 1

Детерминант матрицы (не путайте с дискриминантом для квадратных уравнений) — это определённая матричная характеристика. Иногда вместо термина «детерминант» также используется понятие «определитель».

Детерминант можно посчитать только для квадратных матриц, поэтому при постановке вопроса о нахождении детерминанта для матрицы с размерностью 3 имеют в виду именно квадратную матрицу.

Ниже мы рассмотрим различные способы нахождения определителя 3х3.

Разложение определителя матрицы по строчке

Этот метод сложнее на словах, чем на деле.

Суть его в том, что определитель записывается как сумма произведений элементов первой или любой другой строчки и соответствующих им определителей размером 2 на 2.

Определитель для каждого произведения состоит из элементов, записанных без элементов той строчки и столбца, в которых стоит единичный элемент-множитель.

Также можно осуществлять разложение не только по первой строчке, но и по любой другой или даже столбцу.

Чтобы определить знак, который записывается перед очередным произведением, необходимо помнить, что знаки при элементах чередуются, у первого элемента первой строки — плюс.

То есть произведение при первом элементе первой строчки будет записываться положительным.

Пример 1

Вычислите определитель для $M$ разложением по любой строчке:

$M = \begin{pmatrix} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -5 & 0 & 10 \\ \end{pmatrix}$

Решение:

Рисунок 1. Пример матрицы 3х3. Автор24 — интернет-биржа студенческих работ

В последней строчке присутствует нуль, поэтому удобно будет сделать разложение именно по ней:

$Δ= (-5) \cdot \begin{array}{|cc|} 2 & 5 \\ -4 & 3 \\ \end{array} – 0 \cdot \begin{array} {|cc|} — 1 & 5 \\ 7 & 3 \\ \end{array} + 10 \cdot \begin{array}{|cc|} -1 & 2 \\ 7 & -4 \\ \end{array} = ( — 5 \cdot (6 + 20) – 0 + 10 \cdot (4 – 14) = (-5) \cdot 26 – 0 – 100 = -230$.

Способ «по-французски»: правило Саррюса

Самый легко запоминаемый способ.

Первые два столбика матрицы переписываются рядом справа с исходной матрицей, а дальше рассматриваются левые и правые образуемые диагонали.

Тройки произведений чисел с розовых диагоналей записываются с плюсом, а с синих – с минусом.

Рисунок 2. Как посчитать матрицу 3 на 3. Автор24 — интернет-биржа студенческих работ

Пример 2

Посчитайте определитель $М$ этим методом.

Решение:

$Δ = (-1) \cdot (-4) \cdot 10 + 2 \cdot 3 \cdot (-5) + 5 \cdot 7 \cdot 0 – 2 \cdot 7 \cdot 10 — (-1) \cdot 3 \cdot 0 – 5 \cdot (-4) \cdot (-5) = 40 – 30 + 0 -140 – 0 – 100 = 230$.

Мнемоническое правило с треугольниками

Несколько более сложный способ для запоминания в отличие от предыдущего.

Суть его в том, что произведения троек значений с главной диагонали и с двух треугольников, одна из сторон для каждого параллельна главной диагонали, записываются с плюсом, а с минусом записываются те произведения, что на побочной диагонали и двух треугольниках с параллельными ей сторонами (смотрите рисунок).

Рисунок 3. Как найти детерминант матрицы 3 на 3. Автор24 — интернет-биржа студенческих работ

Приведение матричной таблицы к треугольной

В этом методе нужно получить матрицу, элементы которой сверху или снизу от главной диагонали равны нулю.

Пример 3

Найти определитель для М с помощью получения треугольной матрицы.

Решение:

Вспомним свойство определителя: из любой строки или столбца можно вынести общий для этой строчки или столбца множитель.

Поэтому:

$\begin{array} {|ccc|} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -5 & 0 & 10 \\ \end{array} = \begin{array} {|ccc|} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -1 \cdot 5 & 0 \cdot 5 & 2 \cdot 5 \\ \end{array}= 5 \cdot \begin{array} {|ccc|} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -1 & 0 & 2 \\ \end{array} = 5 \cdot \begin{array} {|ccc|} -1 & 1 \cdot 2 & 5 \\ 7 & -2 \cdot 2 & 3 \\ -1 & 0 \cdot 2 & 2 \\ \end{array}= 10 \cdot \begin{array} {|ccc|} -1 & 1 & 5 \\ 7 & -2 & 3 \\ -1 & 0 & 2 \\ \end{array}$.

Теперь преобразуем полученную таблицу, для этого начинаем приводить к нулям элементы крайнего левого столбца. Строчки для удобства будем записывать как (n), где n — это номер строчки.

1) (2) $\cdot \frac17$ + (3), результат запишем в третьей строчке:

$ \begin{array} {|ccc|} -1 & 1 & 5 \\ 7 & -2 & 3 \\ 0 & -\frac27 & \frac{17}{7} \\ \end{array}$ ;

2) (1) $ \cdot 7$ + (2), полученное запишем во второй строчке:

$ \begin{array} {|ccc|} -1 & 1 & 5 \\ 0 & 5 & 38 \\ 0 & -\frac27 & \frac{17}{7} \\ \end{array}$ ;

3) (2) $\cdot \frac{2}{35}$ + (3)$, пишем в 3-ью:, пишем в 3-ью:

$ \begin{array} {|ccc|} -1 & 1 & 5 \\ 0 & 5 & 38 \\ 0 & 0 & \frac{23}{5} \\ \end{array}$ ;

Получили матрицу нужного типа. Посчитаем $D$:

$Δ = 10 \cdot (-1) \cdot 5 \cdot \frac{23}{5} = -230$.

Во время использования данного способа внимательно следите за знаками, а также за порядком вычислений.

Теперь вы умеете решать определители матриц наиболее распространёнными способами.

Вычисление определителей. Миноры, алгебраические дополнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$

Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$

— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число

$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}. 2+5x+4=0:$

$D=25-16=9$

$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$

Ответ: $x_1=-4;\,\,\, x_2=-1.$

{jumi[*4]}

3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$

Решение.

$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$

$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$

Ответ: $0.$

3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$

Решение.

$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$

$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$

$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha). T=\det A.$

2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.

3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.

4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.

5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.

6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).

Примеры:

3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. $

Доказательство.

$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$

$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$

$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$

$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$

$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$

$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$

$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$

$=8a+15b+12c-19d.$

Ответ: $8a+15b+12c-19d.$

{jumi[*4]}

3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$

Решение.

Вычислим этот определитель с помощью приведения определителя к треугольному виду:

$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два

$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394. 2.$

Вычислить определители, используя подходящее разложение по строке или столбцу.

3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$

Ответ: $-14.$

3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$

Ответ: $4.$

3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$

Ответ: $2a-8b+c+5d.$

3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$

Ответ: $665.$

{jumi[*4]}

Определитель, детерминант матрицы

Способы вычисления определителя матрицы

Определителем матрицы второго порядка называется число, равное

Определитель матрицы третьего порядка

Определитель матрицы третьего порядка можно вычислить, используя правило треугольника или правило Саррюса.

Правило треугольника. Определителем матрицы третьего порядка можно вычислить по формуле

Схематически это правило можно изобразить следующим образом

Правило Саррюса. Для вычисления определителя третьего порядка, допишем два первых столбца и перемножим диагональные элементы, взяв произведение со знаком «плюс», если диагональ является главной или параллельна её и, взяв произведение со знаком «минус», если диагональ является побочной или параллельной ей, получим

Вычисление определителей высших порядков

Для вычисления определителей высших порядков, используется способ разложения определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения. При этом вычисление определителя -го порядка сводится к вычислению определителей -го порядка.

Свойства определителя матрицы

Определитель любого порядка может быть вычислен с использованием свойств определителя:

определитель не изменяется при элементарных преобразованиях строк или столбцов;
при перестановке строк или столбцов знак определителя меняется на противоположный;
определитель треугольной матрицы равен произведению элементов расположенных на диагонали. Например, для верхнетреугольной матрицы

определитель равен

Понравился сайт? Расскажи друзьям!

Определитель матрицы

Определитель матрицы — это специальное число , которое можно вычислить из квадратной матрицы.

Матрица — это массив чисел:

Матрица
(в ней 2 строки и 2 столбца)

Определитель этой матрицы (расчеты объяснены позже):

3 × 6 — 8 × 4 = 18 — 32 = −14

Для чего это нужно?

Определитель помогает нам найти обратную матрицу, говорит нам о матрице, которая полезна в системах линейных уравнений, исчислении и многом другом.

Символ

Символ для определителя — это две вертикальные линии с каждой стороны.

Пример:

| A | означает определитель матрицы A

(точно такой же символ, что и абсолютное значение.)

Вычисление определителя

Прежде всего, матрица должна быть квадратной (т.е. иметь такое же количество строк, как и столбцов). Тогда это просто арифметика. Вот как:

Для матрицы 2 × 2

Для матрицы 2 × 2 (2 строки и 2 столбца):

Определитель:

| A | = ad — bc
«Определитель A равен умножению на d минус b, умноженному на c»

Легко вспомнить, когда вы думаете о кресте:

Синий положительный (+ объявление),
Красный отрицательный (-bc)

Пример:

| B | = 4 × 8 — 6 × 3

= 32–18

= 14

Для матрицы 3 × 3

Для матрицы 3 × 3 (3 строки и 3 столбца):

Определитель:

| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
«Определитель A равен. .. etc »

Может показаться сложным, но есть шаблон :

Для определения определителя матрицы 3 × 3 :

Умножьте на на определитель матрицы 2 × 2 , то есть не в строке или столбце .
Аналогично для b и для c
Суммируйте, но помните минус перед цифрой b

В виде формулы (помните, что вертикальные полосы || означают «определитель») :

«Определитель A равен умноженному на определитель… etc »

Пример:

| C | = 6 × (−2 × 7 — 5 × 8) — 1 × (4 × 7 — 5 × 2) + 1 × (4 × 8 — (−2 × 2))

= 6 × (−54) — 1 × (18) + 1 × (36)

= −306

Для матриц 4 × 4 и выше

Шаблон продолжается для матриц 4 × 4:

плюс a -кратный определитель матрицы, который равен , а не в строке или столбце ,
минус b , умноженное на определитель матрицы, которая равна , а не в строке или столбце b ,
плюс c , умноженное на определитель матрицы, которая равна , а не в строке или столбце c ,
минус d , умноженное на определитель матрицы, которая равна , а не в строке или столбце d ,

В виде формулы:

Обратите внимание на шаблон + — + — (+ a. .. −b … + c … −d …). Это важно помнить.

Шаблон продолжается для матриц 5 × 5 и выше. Обычно для таких случаев лучше всего использовать Матричный калькулятор!

Не единственный путь

Этот метод расчета называется «разложением Лапласа», и мне он нравится, потому что его легко запомнить. Но есть и другие методы (чтобы вы знали).

Сводка

Для матрицы 2 × 2 определитель равен ad — bc
Для матрицы 3 × 3 умножьте на на определитель матрицы 2 × 2 , то есть , а не в строке или столбце , аналогично для b и c , но помните, что b имеет отрицательный знак!
Шаблон продолжается для больших матриц: умножьте на на определитель матрицы , то есть на , а не на на , строку или столбец , продолжайте таким же образом по всей строке, но помните + — + — шаблон.

Определители 2 на 2

Детерминанты: 22 Детерминанты (стр. 1 из 2)

Разделы: 22 определителя, 33 детерминанты

Детерминанты подобны матрицам, но заключены в столбцы абсолютных значений вместо квадратных скобок.Там есть многое, что вы можете сделать с детерминантами (и поучиться на них), но вам понадобится дождаться продвинутого курса, чтобы узнать о них. На этом уроке я просто покажу вам, как вычислить 22 и 33 детерминанты. (Это возможно для вычисления более крупных детерминант, но процесс намного сложнее.)

Если у вас квадратная матрица, его определитель записывается, взяв ту же самую сетку чисел и положив их внутри столбцов абсолютных значений вместо квадратных скобок:

Если это «матрица A » (или « A »). ..	… тогда это «определитель из A » (или « дет. A «).

Как абсолютные значения можно оценить и упростить, чтобы получить одно число, как и определители.Процесс оценки детерминант довольно запутан, поэтому давайте начнем простой, с корпусом 22.

Для матрицы 22 определитель находится путем вычитания произведений его диагоналей, что является причудливым способ выразить словами то, что следующее говорит в картинках:

г. матрица A	г. определитель A («дет. A «)

г. матрица A	г. определитель A («дет. A «)

В другими словами, чтобы взять определитель матрицы 22, вы умножаете диагональ сверху-слева-снизу-справа, и из нее вы вычитаете произведение диагонали снизу-слева-вверх-вправо.

«Но погоди!» я слышу, как ты плачешь; «Разве абсолютные ценности не всегда должны быть положительными? Вы показываете, что вторая матрица выше имеет отрицательный определитель. Что такое с этим? «Вы хорошо замечаете. Детерминанты похожи на абсолютные значения и используют те же обозначения, но они не идентичны, и одно из различий состоит в том, что детерминанты действительно могут быть отрицательными.

Оцените следующее определитель:

Найти определитель следующей матрицы:

конвертирую из матрицы до определителя, умножить по диагоналям, вычесть и упростить:

Верх | 1 | 2 | Возвращаться к указателю Вперед >>

Цитируйте эту статью как:

Стапель, Елизавета. «Детерминанты: детерминанты 2×2». Purplemath . Имеется в наличии с
https://www.purplemath.com/modules/determs.htm . Дата обращения [Дата] [Месяц] 2016 г.

Определитель матрицы 3 x 3 (общий и сокращенный метод)

Определитель матрицы 3×3 (общий и сокращенный метод)

Как мы видели в прошлых уроках, чтобы определить, что является определителем матрицы, нам нужно вернуться к нашему определению матрицы.Помните, что мы узнали, что матрица — это упорядоченный список чисел, заключенный в прямоугольную скобку. Этот список также можно назвать прямоугольным массивом, и он обеспечивает упорядоченный способ отображения «списка» информационных элементов. Если вы хотите более подробно ознакомиться с определением матрицы, вы можете вернуться к нашему уроку о нотации матриц.

Матрица описывает линейное преобразование или линейную карту, которая является своего рода транскрипцией между двумя типами алгебраических структур, такими как векторные поля. Таким образом, мы можем разрешить системы линейных уравнений, представив линейную систему в виде матрицы. Матричное представление линейной системы создается с использованием всех переменных коэффициентов, найденных в системе, и использования их в качестве элементов для построения прямоугольного массива расширенной матрицы соответствующего размера. В такой матрице результаты каждого уравнения из системы будут помещены справа от вертикальной линии, которая представляет знак равенства.

Зная это, в этом уроке основное внимание будет уделено процессу оценки определителя матрицы 3×3 и двум возможным методам, которые можно использовать.

Какой определитель матрицы

Используя знание того, что матрица представляет собой массив, содержащий информацию о линейном преобразовании, и что этот массив может быть согласован с коэффициентами каждой переменной в системе уравнений, мы можем описать функцию определителя: определитель будет масштабироваться линейное преобразование из матрицы, это позволит нам получить обратную матрицу (если таковая имеется) и поможет в решении систем линейных уравнений, создав условия, при которых мы можем ожидать определенных результатов или характеристик от система (в зависимости от определителя и типа линейной системы, мы можем знать, можем ли мы ожидать уникального решения, более одного решения или вообще ни одного решения для системы).

Но есть условие для получения определителя матрицы, матрица должна быть квадратной матрицей, чтобы ее можно было вычислить. Следовательно, упрощенное определение состоит в том, что определитель — это значение, которое может быть вычислено из квадратной матрицы, чтобы помочь в разрешении систем линейных уравнений, связанных с такой матрицей. Определителя неквадратной матрицы не существует, математически определяются только определители квадратных матриц.

Определитель матрицы можно обозначить просто как det A, det (A) или | A |.Это последнее обозначение происходит от обозначения, которое мы непосредственно применяем к матрице, определитель которой мы получаем. Другими словами, мы обычно записываем матрицы и их определители очень похожим образом:

Уравнение 1: Разница между обозначениями матрицы и определителя

Обратите внимание на разницу: матрица записана в прямоугольных скобках, а компоненты определителя матрицы окружены двумя прямыми линиями.

Сегодняшний урок будет сосредоточен на процессе вычисления определителя матрицы 3×3, используя подход свойств определителя матрицы, которые были кратко рассмотрены на прошлых уроках. Помните, что мы рассмотрим эту полную тему на следующем уроке, который называется: свойства детерминантов. Тем не менее, важно помнить об этих свойствах при выполнении расчетов упражнений в последнем разделе этого урока.

Как найти определитель матрицы 3×3

Существует два метода нахождения определителя матрицы 3×3: общий метод и сокращенный метод. Так же, как звучат названия каждого из них, общий метод — это «формальный» метод, который можно использовать математически, следуя всем правилам и производя некоторые второстепенные вычисления определителя матрицы по пути нахождения окончательного решения.Хотя метод быстрого доступа — это более хитрый прием, который мы можем использовать для упрощения вычислений, при этом стараясь не забыть числа, порядок, в котором они должны быть умножены, и некоторые перестановки элементов в матрице.

После того, как вы взглянете на оба метода, чтобы найти определитель матрицы 3×3, вы всегда можете выбрать тот, который вам больше всего подходит, и использовать его для своих исследований, но помните, что важно знать оба из них, на случай, если вас когда-нибудь спросят сравнить результаты с ними.

Итак, без дальнейших задержек, давайте определим определитель матрицы 3×3 A, как показано ниже, чтобы мы могли наблюдать, как его можно вычислить обоими методами:

Уравнение 2: Определитель матрицы A

Общий метод
Общий метод получения определителя матрицы 3×3 состоит в разбиении матрицы на вторичные матрицы меньших размеров в процессе, называемом «расширением первой строки». Этот процесс использует элементы из первой строки матрицы 3×3 и использует их как множители в сумме умножений, при которой большая матрица перераспределяется.
Давайте шаг за шагом рассмотрим, как вычислить определитель матрицы 3×3:
1. Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому принадлежит ваш первый выбранный элемент.
  Взяв в качестве ссылки определитель матрицы 3×3, показанный в уравнении 2, мы строим первую часть результата этой операции, выбирая первый элемент первой строки и столбца (который является константой «a»), а затем умножаем его на матрица, созданная из четырех элементов, которые не принадлежат ни одной строке столбца, в котором находится «a». Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения.
2. Второй член начинается со второго элемента в верхней строке (константа «b»), сопровождаемого отрицательным знаком, который теперь умножает вторичную матрицу 2×2, которая снова получается из четырех элементов в матрице, которые не принадлежат в любой столбец строки, в которой находится «b».
3. Повторяем первый шаг, но уже с третьим элементом из верхней строки матрицы.
Итак, определитель матричной формулы 3×3 для общего метода:
Уравнение 3: Уравнение для определителя матрицы 3×3 посредством общего метода
Процесс называется расширением первой строки, потому что, как вы можете видеть в уравнении 3, все элементы из первой строки исходной матрицы 3×3 остаются основными факторами в расширении, для которого необходимо решить. Все матрицы 2×2 в раскрытии — это то, что мы называем «вторичными матрицами», и их можно легко разрешить, используя уравнение, изученное на определителе на уроке по матрице 2×2.
Итак, принимая во внимание формулу для определителя квадратной матрицы размером 2×2, мы видим, что уравнение 3 дает:
Уравнение 4: Уравнение для определителя матрицы 3×3 посредством общего метода (часть 2)
На этом этапе вы, возможно, заметили, что поиск определителя матрицы, превышающей 2×2, становится долгим испытанием, но логика процесса остается той же, и поэтому сложность аналогична, единственный ключевой момент — отслеживать операции вы прорабатываете даже больше с матрицами даже большего размера, чем 3×3.
Сокращенный метод
Определитель быстрого метода матрицы 3×3 — это хитрый трюк, который упрощает вычисление определителя большой матрицы путем прямого умножения и добавления (или вычитания) всех элементов в их необходимом виде, без необходимости пройти через матричное расширение первой строки и без необходимости оценивать детерминанты вторичных матриц.
Весь процесс того, как оценить определитель матрицы 3×3, используя сокращенный метод, можно увидеть в уравнении ниже:
Уравнение 5: Быстрый метод получения определителя матрицы 3×3
Теперь давайте четко объясним метод быстрого доступа:
При вычислении определителя матрицы размера nxn (в данном случае матрицы 3×3), как показано выше, обратите внимание, что мы сначала переписываем матрицу, сопровождаемую повторением двух первых столбцов, которые теперь записываются снаружи с правой стороны.
Тогда значение определителя будет результатом вычитания между сложением произведений всех умножений вниз-вправо и умножений вниз-влево. Сказано более ясно, в общей сложности будет три полных диагонали, идущих от верхнего левого угла до нижнего правого, и еще один набор из трех полных диагоналей, идущих от верхнего правого угла до нижнего левого угла.
Мы умножим элементы каждой диагонали вместе, а затем сложим их с результатами, полученными на других диагоналях.Есть кое-что, что нужно иметь в виду, все умножения диагоналей, идущие от верхнего левого угла к нижнему правому, имеют внутренний положительный знак, умноженный на них, в то время как все умножения диагоналей, идущие сверху справа вниз слева, имеют внутренний отрицательный знак к ним, и поэтому при сложении результатов всех умножений будет получено вычитание, подобное тому, которое показано в уравнении 5.
Хотя этот метод проще в применении, чем общий метод, его немного сложно объяснить из-за того, что все операции умножения и сложения выполняются одновременно, поэтому мы рекомендуем вам использовать уравнение 5 в качестве руководства и уделять пристальное внимание к видео, где демонстрируются примеры этого метода.
В последнем разделе этого урока мы проработаем набор из трех различных матриц 3×3 и их детерминанты. Мы рекомендуем вам сравнить процессы для обоих методов, чтобы лучше понять их.

Определитель большой матрицы

Процесс вычисления определителя матрицы большей размерности, чем 3×3, следует той же логике, что и то, что мы видели до сих пор. Используя общий метод на матрице A 4×4, где ее первая (верхняя) строка соответствует элементам a, b, c и d, мы вычисляем определитель матрицы следующим образом:

Уравнение 6: Определитель матрицы 4×4

Мы еще раз расширили определитель на его первую строку и получили вторичные матрицы, которые в данном случае являются матрицами 3×3, каждая из которых может быть расширена и разбита на матрицы 2×2.Шаблон в процессе повторяется, вы можете продолжать работать таким образом с еще более крупными квадратными матрицами, и он всегда будет работать, но если вам больше нравится метод ярлыков, то вас ждет удовольствие, поскольку метод работает точно так же как и в случае с матрицами 3×3, он просто увеличивает количество элементов, с которыми вы работаете, но логика и перестановка точно такие же (умножение сверху слева вниз справа имеет положительный знак, умножения из верхнего правого угла в нижний левый имеют внутренний отрицательный знак).

Вы взволнованы, увидев, как сокращенный метод работает с матрицами большего размера? Мы рекомендуем вам попробовать это самостоятельно, чтобы вы могли увидеть весь процесс. Вы всегда можете вернуться и решить ту же матрицу, используя общий метод, и доказать, что ваш результат верен.

Упражнения по вычислению определителя матрицы 3×3

В следующих упражнениях мы решим определитель матрицы 3×3, предоставленной в каждом случае, с помощью соответствующего метода, а в конце мы сравним полученные результаты.

Обратите внимание, что матрицы A, B и C, представленные в обоих разделах упражнений выше, абсолютно одинаковы. Это было сделано специально, чтобы вы могли сравнить результаты обоих методов и посмотреть, как они дают одинаковые значения.

Чтобы завершить этот урок, мы хотели бы порекомендовать вам эту статью о том, как вычислить определители, и другую статью о определителе квадратной матрицы, где вы найдете гораздо больше примеров, чем приведенные здесь.

Надеемся, этот урок был интересным и полезным, до встречи в следующем!

Определитель квадратной матрицы

6.4 — Определитель квадратной матрицы

Определитель — это действительное число, связанное с каждой квадратной матрицей. Я еще не нашел хорошего Английское определение детерминанта. Все, что я могу найти, определяет это с точки зрения математическая формула или предлагает некоторые из ее использования. Есть даже определение определитель, который определяет его в терминах самого себя.

Определитель квадратной матрицы A обозначается как «det A» или | А |, Теперь последний выглядит как абсолютное значение A, но вам придется применить контекст.Если вертикальные линии находятся вокруг матрица, то есть определитель.

В строке ниже показаны два способа записи определителя.

3	1	=	дет		3	1
5	2	=	дет		5	2

Определитель матрицы 2 × 2

Определитель матрицы 2 × 2 находится во многом как операция поворота. Это произведение элементов на главной диагонали за вычетом произведение элементов от главной диагонали.

Свойства детерминантов

Определитель — действительное число, а не матрица.
Определитель может быть отрицательным числом.
Он вообще не связан с абсолютным значением, за исключением того, что они оба используют вертикальные линии.
Определитель существует только для квадратных матриц (2 × 2, 3 × 3, … n × n). Определитель матрицы 1 × 1 — это единственное значение в определителе.
Обратная матрица будет существовать, только если определитель не равен нулю.

Расширение с использованием младших и сомножителей

Определение определителя, которое у нас есть до сих пор, относится только к матрице 2 × 2. Есть ярлык для матрица 3 × 3, но я твердо верю, что вам следует изучить способ, который будет работать для всех размеров, а не только для частный случай для матрицы 3 × 3.

Метод называется расширением с использованием миноров и сомножителей.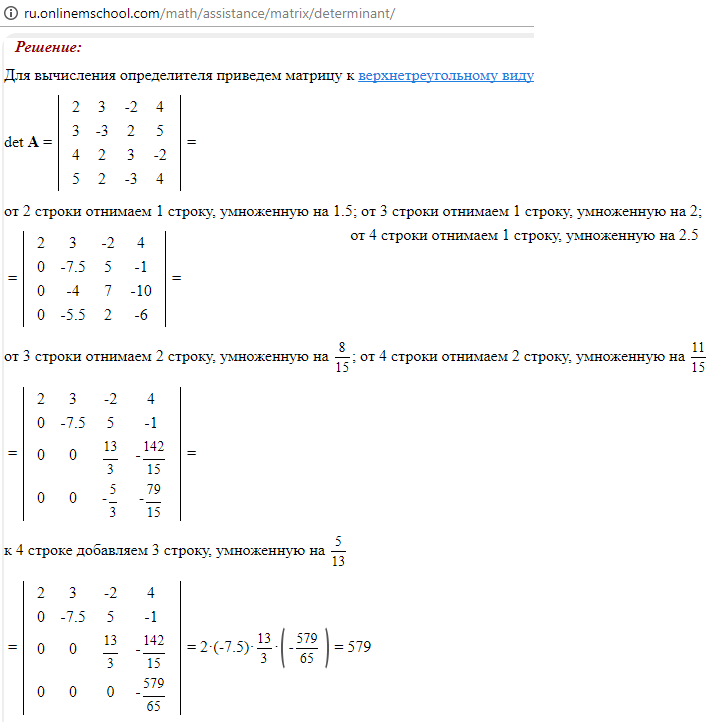 Прежде чем мы сможем использовать их, нам нужно их определить.

Несовершеннолетние

Второстепенным для любого элемента является определитель, который получается, когда строка и столбец что элементы удалены.

Обозначение M _ij используется для обозначения минорной части элемента. в строке i и столбце j. Таким образом, M ₂₁ будет означать второстепенное значение для элемента. в строке 2, столбце 1.

Рассмотрим определитель 3 × 3, показанный ниже. Я включил заголовки, чтобы вы можете держать строки и столбцы ровными, но обычно вы не включаете те.Мы собираемся найти нескольких несовершеннолетних.

	С ₁	С ₂	С ₃
R ₁	1	3	2
R ₂	4	1	3
R ₃	2	5	2

Поиск второстепенного для R

₂ C ₁

Младший — это определитель, который остается при удалении строки и столбца. элемента, для которого вы пытаетесь найти второстепенное.Это означает, что мы должны удалить строка 2 и столбец 1, а затем найдите определитель.

	С ₂	С ₃
R ₁	3	2	= 3 (2) — 5 (2) = 6-10 = -4
R ₃	5	2	= 3 (2) — 5 (2) = 6-10 = -4

Как видите, второстепенное значение для строки 2 и столбца 1 — M ₂₁ = -4.

Попробуем еще.

В поисках второстепенного для R

₃ C ₂

На этот раз мы удалим строку 3 и столбец 2.

	С ₁	С ₃
R ₁	1	2	= 1 (3) — 4 (2) = 3-8 = -5
R ₂	4	3	= 1 (3) — 4 (2) = 3-8 = -5

Таким образом, второстепенное значение для строки 3, столбца 2 — M ₃₂ = -5.

Матрица несовершеннолетних

Когда вы просто пытаетесь найти определитель матрицы, это перебор. Но для него есть одно чрезвычайно полезное приложение, которое даст нам практику. поиск несовершеннолетних.

Матрица миноров — это квадратная матрица, в которой каждый элемент является минорным. для номера в этой позиции.

Вот общая матрица миноров для определителя 3 × 3.

	С ₁	С ₂	С ₃
R ₁	M ₁₁	M ₁₂	M ₁₃
R ₂	M ₂₁	M ₂₂	M ₂₃
R ₃	M ₃₁	M ₃₂	M ₃₃

Найдем матрицу миноров для нашего исходного определителя. Здесь определитель.

	С ₁	С ₂	С ₃
R ₁	1	3	2
R ₂	4	1	3
R ₃	2	5	2

Вот работа по поиску каждого несовершеннолетнего в матрице несовершеннолетних.

	С ₁	С ₂	С ₃
R ₁	= 2-15 = -13	= 8–6 = 2	= 20 — 2 = 18
R ₂	= 6-10 = -4	= 2–4 = -2	= 5-6 = -1
R ₃	= 9 — 2 = 7	= 3-8 = -5	= 1–12 = -11

И, наконец, матрица миноров. Опять же, метки ставить не нужно для строки и столбцов, но это может вам помочь.

	С ₁	С ₂	С ₃
R ₁	-13	2	18
R ₂	-4	-2	-1
R ₃	7	-5	-11

Кофакторы

Кофактор для любого элемента является второстепенным или противоположным второстепенным, в зависимости от того, где находится элемент в исходном определителе.Если строка и столбец элемента суммируется до четного числа, тогда сомножитель — это так же, как и несовершеннолетний. Если сумма строки и столбца элемента получается нечетной число, то сомножитель — это противоположность несовершеннолетнему.

О, ты понял? Нечетное меняет знаки, четное — тот же знак. Дежавю. Мы говорим об этом с момента раздела 3.2 о многочленах.

Знаковая диаграмма

Вместо того, чтобы складывать строку и столбец элемента, чтобы проверить, является четным или нечетным, многие люди предпочитают использовать знаковую диаграмму.Знаковая диаграмма — это либо a + или — для каждого элемента в матрице. Первый элемент (строка 1, столбец 1) является всегда а + и чередуется оттуда.

Примечание. Знак «+» не означает «положительный», а «-» — отрицательный. + Означает то же самое знак как несовершеннолетний и — означает противоположность несовершеннолетнему. Подумайте об этом дополнении и вычитание, а не положительное или отрицательное.

Вот знаковая диаграмма для определителя 2 × 2.

Вот знаковая диаграмма для определителя 3 × 3.

	С ₁	С ₂	С ₃
R ₁	+	–	+
R ₂	–	+	–
R ₃	+	–	+

Матрица сомножителей

Опять же, если все, что вы пытаетесь сделать, это найти определитель, вам не нужно проделать такую большую работу.

Матрица сомножителей — это матрица, найденная заменой каждого элемента матрицу ее сомножителем. Это матрица несовершеннолетних с измененными знаками по элементам в позициях -.

	С ₁	С ₂	С ₃
R ₁	-13	-2	18
R ₂	4	-2	1
R ₃	7	5	-11

Расширение для поиска определителя

Вот шаги, которые необходимо выполнить, чтобы найти определитель.

Выберите любую строку или столбец в матрице. Неважно, какая строка или какая столбец, который вы используете, ответ будет одинаковым для любой строки. Есть несколько строк или столбцы, которые проще, чем другие, но мы вернемся к этому позже.
Умножить каждые элемент в этой строке или столбце по его кофактору и добавьте. В результате определитель.

Разложим нашу матрицу по первой строке.

Из диаграммы знаков мы видим, что 1 находится в положительном положении, 3 — в отрицательном положение, а 2 находится в положительном положении.Поставив + или — перед элемент, он заботится о корректировке знака при переходе от второстепенного к кофактору.

+ 1	1	3	— 3	4	3	+ 2	4	1
+ 1	5	2	— 3	2	2	+ 2	2	5

= 1 (2-15) — 3 (8-6) + 2 (20-2)
= 1 (-13) — 3 (2) + 2 (18)
= -13-6 + 36
= 17

Определитель этой матрицы равен 17.

Как я сказал ранее, на самом деле не имеет значения, какую строку или столбец вы используете.

Давайте попробуем еще раз, но на этот раз расширим вторые столбцы. Как усилие для экономии времени миноры для этого столбца (из матрицы миноров) были 2, -2 и -5. Исходные элементы были 3, 1 и 5. 3 и 5 отрицательны. позиции.

Определитель

= — 3 (2) + 1 (-2) — 5 (-5) = -6-2 + 25 = 17

Разверните любую строку или любой столбец, вы получите 17.

Но диагонали делать нельзя.Если попробовать по главной диагонали, получится

+ 1 (-13) + 1 (-2) + 2 (-11) = -13-2-22 = -37

Некоторые строки или столбцы лучше других

Выберите строку или столбец с наибольшим количеством нулей.
Поскольку каждый младший или сомножитель умножается на элемент в матрице, выбор строки или столбца с большим количеством нулей означает, что вы будете умножение на множество нулей. Умножение на ноль совсем не занимает много времени. Фактически, если элемент равен нулю, вы не нужно даже найти несовершеннолетнего или кофактор.
Выберите строку или столбец с наибольшими числами (или переменными) в нем.
Элементы в строке или столбце, по которым вы разворачиваете, не используются для поиска несовершеннолетние. Единственное место, где они умножаются, — это один раз в расширении. Если вы выберете строку или столбец с наименьшие числа, то каждое младшее число будет произведением большего числа.
Если вы выберете строку или столбец, в котором есть переменные, то вы только имеют умножить на переменные один раз во время раскрытия.

Обратная матрица (пересмотрено)

Давайте на этот раз рассмотрим наш исходный определитель как матрицу.

1	3	2
4	1	3
2	5	2

Найдите матрицу миноров , как описано выше.

-13	2	18
-4	-2	-1
7	-5	-11

Превратите его в матрицу сомножителей , изменив знаки на соответствующих элементы на основе знаковой диаграммы.

-13	-2	18
4	-2	1
7	5	-11

Найдите сопряженное , переставив матрицу сомножителей.

Чтобы транспонировать матрицу, вы переключаете строки и столбцы. То есть строки стать столбцами и столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82. или калькулятор TI-83, введя имя матрицы и затем выбрав Матрица, Math, а затем вариант 2, буква T с надстрочным индексом, например [A] ^T.

-13	4	7
-2	-2	5
18	1	-11

Наконец разделите сопряженную матрицу на определитель матрицы.В этой задаче определитель равен 17, поэтому мы разделим каждый элемент на 17. Результирующая матрица — , обратная исходной матрицы.

-13/17	4/17	7/17
-2/17	-2/17	5/17
18/17	1/17	-11/17

Матрица, обратная матрице, находится делением сопряженной матрица по определителю матрицы.Не пытайтесь это сделать на своем калькулятор, поскольку калькулятор не позволяет разделить матрицу на скаляр. Вместо этого вам придется умножить на обратное значение определителя.

Если вы проверите это с помощью своего калькулятора, вы можете убедиться, что обратное фактически является сопряженным, деленным на определитель.

Поскольку обратная величина — это присоединенный элемент, деленный на детерминант, мы можем понять, почему обратное не существует, если определитель равен нулю. Это приведет к делению на ноль, что не определено.

Детерминанты более крупного порядка

Найдем определитель системы 4х4.

	С ₁	С ₂	С ₃	С ₄
R ₁	3	2	0	1
R ₂	4	0	1	2
R ₃	3	0	2	1
R ₄	9	2	3	1

Выберите строку или столбец с наибольшим количеством нулей.В данном случае это второй столбец.

Для каждого элемента исходной матрицы свой минор будет определителем 3 × 3. Придется расширить каждый из них на с использованием трех определителей 2 × 2.

Вот почему мы хотим развернуть второй столбец. Несовершеннолетние умножаются по их элементам, поэтому, если элемент в исходной матрице равен 0, он не действительно имеет значение, что такое несовершеннолетний, и мы можем сэкономить много времени, не имея найти это. Во втором столбце вам не нужно будет искать двух несовершеннолетних. потому что их соответствующий элемент во втором столбце равен нулю.

— 2	4	1	2	+ 0		— 0		+ 2	3	0	1
	3	2	1		?		?		4	1	2
	9	3	1						3	2	1

Мы действительно могли бы заполнить эти два средних младших, но поскольку они умножаются на 0, неважно, какие они.Фактически, вы могли бы так же легко пропустить их.

Теперь осталось найти два определителя 3×3.

В первом определителе 3×3 нулей нет, поэтому выберите строку или столбец с наибольшими числами. Что будет столбцом 1, поэтому разверните его по первому столбцу.

Уведомление 4 находится в положительном положении. Таблицы знаков начинаются заново с каждого новый определитель. Положение числа в исходной матрице не имеет значение, только его положение в текущей матрице.

4	1	2
3	2	1	=	+ 4	2	1	— 3	1	2	+ 9	1	2
9	3	1			3	1		3	1		2	1

= 4 (2-3) — 3 (1-6) + 9 (1-4) = 4 (-1) — 3 (-5) + 9 (-3 ) = -4 + 15 — 27 = -16

Рассмотрим другую матрицу 3 × 3.В этом в строке стоит 0 1 и столбец 2. Любой из них будет хорошим выбором для расширения, но поскольку в строке 1 числа немного больше, мы расширим первую строку.

3	0	1
4	1	2	=	+ 3	1	2	–0	?	?	+ 1	4	1
3	2	1			2	1		?	?		3	2

= 3 (1-4) — 0 (не имеет значения) + 1 (8-3) = 3 (-3) + 1 (5) = -9 + 5 = -4

Когда вы идете искать определитель, помните, что были элементы из исходная матрица 4 × 4, умноженная на каждый из этих определителей 3 × 3.Первый — -2, второй — +2.

Определитель = -2 (-16) + 2 (-4) = 32 — 8 = 24

Худший сценарий

Чтобы найти определитель 3×3 без нулей, вам нужно найти три определителя 2×2.

Чтобы найти определитель 4×4 без нулей, вам нужно найти четыре определителя 3×3, каждый из которых затем становится тремя определителями 2×2, что в сумме дает двенадцать определителей 2×2.

Чтобы найти определитель 5×5 без нулей, вам нужно найти пять определителей 4×4, каждый из которых затем становится четырьмя детерминантами 3×3, каждый из которых становится тремя детерминантами 2×2, в сумме шестидесяти определителей 2×2.

Использование калькулятора

После этой последней проблемы вы должны спросить себя, нет ли более простого пути. Ну да, есть, если в определителе нет никаких переменных. Вы можете воспользоваться калькулятором.

Обозначение, которое использует калькулятор TI-82 или TI-83, — это обозначение Det A. Итак, после входа в матрицу в одну из доступных матриц на калькуляторе, введите DET, выбрав Матрица, Математика и выбор варианта 1. Затем введите название матрицы, которую вы используете.

Вам не нужно использовать круглые скобки (если у вас нет TI-83), но вы можете, если ты хочешь найти определитель продукта «det ([A] * [B])» или определитель транспонирования «det ([A] ^T) «как в отличие от транспонирования определителя «(det [A]) ^T». Кстати, калькулятор не найдет транспонирование определителя, потому что в детерминант — скаляр (действительное число), а калькулятор знает только, как найти транспонирование матрицы. Транспонирование скаляр — это то, что скаляр.

Треугольные матрицы

Вам действительно понравится находить определители этих матриц.

Верхняя треугольная матрица: Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо над ней. То есть все ненулевые значения находятся в верхнем треугольнике. Все, что ниже диагонали это ноль.
Нижняя треугольная матрица: Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо ниже нее.; То есть все ненулевые значения находятся в нижнем треугольнике. Все выше диагонали равно нулю.
Диагональная матрица: Матрица, в которой все ненулевые элементы находятся на главной диагонали. Все выключено главная диагональ — ноль.

Определителем треугольной или диагональной матрицы является произведение элементов по главной диагонали.

Операции с элементарными строками

Существовали три элементарные операции со строками, которые могли быть выполнены, которые возвращали бы эквивалентная система.С определителями, поскольку определитель транспонирования такой же, как и у Определитель матрицы, элементарные операции со строками также могут применяться к столбцам.

Выполняя сокращение строк (используя поворот на 1, если хотите), вы можете поместить матрицу в треугольная форма. Как только он приобретет треугольную форму, все, что вам нужно сделать, это умножить на элементы на главной диагонали, и у вас есть определитель.

Давайте рассмотрим каждую из трех элементарных операций со строками.

Если вы поменяете местами две строки или два столбца в определителе, результирующий определитель будет отличаются только знаком.То есть, если вы меняете местами строки или столбцы, результирующий определитель будет противоположно исходному определителю.
Если вы умножаете строку или столбец на ненулевую константу, определитель умножается на эту та же ненулевая константа.
Если вы умножите строку или столбец на ненулевую константу и добавите ее к другой строке или столбцу, при замене этой строки или столбца определитель не изменяется.

Последняя операция эквивалентна повороту на единицу!

Предупреждение, если ваша точка поворота — это число, отличное от единицы, то вы умножаете каждую строку, которую вы изменение поворотным элементом.Итак, если вы повернетесь к 3 и измените две строки, то полученный определитель будет в 3 * 3 = 9 раз больше, чем исходный определитель.

Пока вы выбираете единицу, все будет в порядке.

Вам не нужно преобразовывать матрицу в сокращенную форму строки-эшелон или даже форму строки-эшелона. Вы можете в любой момент остановить сокращение и расширить, используя миноры и кофакторы. Что я Предлагаю это стержень там, где он есть, а затем разверните.

Нулевые детерминанты

Определитель матрицы будет равен нулю, если

Вся строка нулевая.
Две строки или столбцы равны.
Строка или столбец является постоянным кратным другой строке или столбцу.

Помните, что матрица обратима и невырождена тогда и только тогда, когда определитель не равен нулю. Итак, если определитель равен нулю, матрица сингулярна и не имеет обратной.

Определитель матрицы — 2×2, 3×3, 4×4 …

Автор Каталин Давид

Определение

Определитель квадратной матрицы A — это целое число, полученное с помощью ряда методов, использующих элементы матрицы.

Обозначение

Пусть $ A = \ begin {pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {pmatrix} $

$ det (A) = \ left | A \ right | знак равно \ begin {vmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {vmatrix} $

Свойства определителя

Если матрица имеет строку или столбец со всеми элементами, равными 0 , то ее определитель равен 0 .
Пример 12
$ \ begin {vmatrix} 1 и 4 и 2 \\ 0 & 0 & 0 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ или же $ \ begin {vmatrix} 1 и 4 и 0 \\ 4 и 2 и 0 \\ 3 и 9 и 0 \ end {vmatrix} = 0 $
Если матрица имеет две равные строки или два равных столбца , тогда ее определитель равен 0 .
Пример 13
$ \ begin {vmatrix} 1 и 4 и 2 \\ 1 и 4 и 2 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ или же $ \ begin {vmatrix} 1 и 4 и 1 \\ 4 и 2 и 4 \\ 3 и 9 и 3 \ end {vmatrix} = 0 $
Если матрица имеет две пропорциональные строки или два пропорциональных столбца , тогда ее определитель равен 0 .
Пример 14
$ \ begin {vmatrix} 1 и 4 и 2 \\ 2 и 8 и 4 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ (первые две строки пропорциональны)
или
$ \ begin {vmatrix} 8 и 4 и 7 \\ 4 и 2 и 3 \\ 18 и 9 и 8 \ end {vmatrix} = 0 $ (первые два столбца пропорциональны)
Если строка или столбец является суммой или разностью других строк, соответственно столбцов , тогда определитель равен 0 .
Пример 15
$ \ begin {vmatrix} 1 и 4 и 2 \\ 7 и 2 и 3 \\ 8 и 6 и 5 \ end {vmatrix} = 0 $ $ R_ {1} + R_ {2} = R_ {3} $ или
$ \ begin {vmatrix} 9 и 12 и 3 \\ 1 и 8 и 7 \\ 5 и 7 и 2 \ end {vmatrix} = 0 $ $ C_ {1} + C_ {3} = C_ {2} $
В определителе мы можем индивидуально выделить целые числа из строк и столбцов.
Пример 16
В определителе
$ \ begin {vmatrix} 3 и 9 и 12 \\ 5 и 1 и 8 \\ 7 и 4 и 2 \ end {vmatrix} $, мы вынимаем 3 из строки 1 $ (R_ {1}) $ и получаем:
$ 3 \ cdot \ begin {vmatrix} 1 и 3 и 4 \\ 5 и 1 и 8 \\ 7 и 4 и 2 \ end {vmatrix} $, затем мы выносим 2 из столбца 3 $ (C_ {3}) $:
$ 6 \ cdot \ begin {vmatrix} 1 и 3 и 2 \\ 5 и 1 и 4 \\ 7 и 4 и 1 \ end {vmatrix} $
В определителе мы можем добавлять или вычитать строки или столбцы из других строк, соответственно столбцов, и значение определителя остается прежним.
Пример 17
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {R_ {1} + R_ {2}} \ begin {vmatrix} 4 и 13 \\ 3 и 8 \ end {vmatrix} $
Пример 18
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {C_ {1} + C_ {2}} \ begin {vmatrix} 6 и 5 \\ 11 и 8 \ end {vmatrix} $
В определителе мы можем складывать или вычитать несколько строк или столбцов.
Пример 19
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {2R_ {1} + 3R_ {2}} \ begin {vmatrix} 11 и 34 \\ 3 и 8 \ end {vmatrix} $
Пример 20
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {5C_ {1} -C_ {2}} \ begin {vmatrix} 0 и 5 \\ 7 и 8 \ end {vmatrix} $
Определитель матрицы равен определителю ее транспонирования.
Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.

Минор матрицы

Определитель, полученный путем исключения некоторых строк и столбцов в квадратной матрице, называется минором этой матрицы.

Пример 21
$ A = \ begin {pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {pmatrix} $

Одним из миноров матрицы A является $ \ begin {vmatrix} 1 и 4 \\ 5 и 3 \ end {vmatrix} $ (получается путем исключения строки 3 и столбца 3 из матрицы A)

Другой минор — $ \ begin {vmatrix} 1 и 2 \\ 6 и 1 \ end {vmatrix} $ (получается путем исключения строки 2 и столбца 2 из матрицы A)

Пример 22
$ B = \ begin {pmatrix} 2 и 5 и 1 и 3 \\ 4 и 1 и 7 и 9 \\ 6 и 8 и 3 и 2 \\ 7 и 8 и 1 и 4 \ end {pmatrix} $

Одним из миноров матрицы B является $ \ begin {vmatrix} 1 и 7 и 9 \\ 8 и 3 и 2 \\ 8 и 1 и 4 \ end {vmatrix} $ (получается путем исключения строки 1 и столбца 1 из матрицы B)

Другой несовершеннолетний $ \ begin {vmatrix} 1 и 7 \\ 8 и 3 \ end {vmatrix} $ (получается путем исключения строк 1 и 4 и столбцов 1 и 4 из матрицы B)

Позволять $ A = \ begin {pmatrix} a_ {1,1} и a_ {1,2} и a_ {1,3} &.&. & a_ {1, n} \\ a_ {2,1} и a_ {2,2} и a_ {2,3} &. &. & a_ {2, n} \\ а_ {3,1} и а_ {3,2} и а_ {3,3} &. &. & a_ {3, n} \\ . &. &. &. &. &. \\ a_ {n, 1} и a_ {n, 2} и a_ {n, 3} &. &. & Аня} \ end {pmatrix} $

Мы можем связать минор $ \ Delta_ {i, j} $ (полученный путем исключения строки i и столбца j) с любым элементом $ a_ {i, j} $ матрицы A.

Пример 23
$ A = \ begin {pmatrix} 4 и 7 \\ 2 и 9 \ end {pmatrix} $

Мы должны определить минор, связанный с 2.Поскольку этот элемент находится в строке 2, столбце 1, то 2 — это $ a_ {2,1} $.

Мы должны удалить строку 2 и столбец 1 из матрицы A, в результате получим

Младший из 2 равен $ \ Delta_ {2,1} = 7 $.

Пример 24
$ B = \ begin {pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {pmatrix} $

Мы должны определить младший, связанный с 7. Поскольку этот элемент находится в строке 2, столбце 3, то 7 — это $ a_ {2,3} $.

Мы должны удалить строку 2 и столбец 3 из матрицы B, в результате чего получится

Минор 7 равен $ \ Delta_ {2,3} = \ begin {vmatrix} 1 и 4 \\ 6 и 2 \ end {vmatrix} $

Пример 25
$ C = \ begin {pmatrix} 2 и 5 и 1 и 3 \\ 4 и 1 и 7 и 9 \\ 6 и 8 и 3 и 2 \\ 7 и 8 и 1 и 4 \ end {pmatrix} $

Мы должны определить минор, связанный с 5.Поскольку этот элемент находится в строке 1, столбце 2, то 5 — это $ a_ {1,2} $.

Мы должны удалить строку 1 и столбец 2 из матрицы C, в результате чего получится

Минор из 5 равен $ \ Delta_ {1,2} = \ begin {vmatrix} 4 и 7 и 9 \\ 6 и 3 и 2 \\ 7 и 1 и 4 \\ \ end {vmatrix} $

Кофактор элемента матрицы

Пусть $ A = \ begin {pmatrix} a_ {1,1} и a_ {1,2} и a_ {1,3} &. &. & a_ {1, n} \\ a_ {2,1} и a_ {2,2} и a_ {2,3} &. &.{7} \ cdot \ Delta_ {2,5} = — \ Delta_ {2,5} $ соответствует элементу $ a_ {2.5} $

Порядок определения определителя

Порядок определителя равен количеству строк и столбцов в нем.

Пример 26
$ \ begin {vmatrix} 1 и 4 \\ 6 и 2 \\ \ end {vmatrix} $ (в нем 2 строки и 2 столбца, поэтому порядок равен 2)

Пример 27
$ \ begin {vmatrix} 4 и 7 и 9 \\ 6 и 3 и 2 \\ 7 и 1 и 4 \\ \ end {vmatrix} $ (в нем 3 строки и 3 столбца, поэтому порядок равен 3)

Вычисление определителя матрицы

Определитель матрицы равен сумме произведений элементов любой строки или столбца и их сомножителей. {i + 3} \ cdot \ Delta_ {i, 3} +.{3} \ cdot \ Delta_ {1,2} = a_ {1,1} \ cdot \ Delta_ {1,1} -a_ {1.2} \ cdot \ Delta_ {1,2}

долларов США

Однако $ \ Delta_ {1,1} = a_ {2,2} $ и $ \ Delta_ {1,2} = a_ {2,1} $

$ \ left | А \ право | = a_ {1.1} \ cdot a_ {2,2} — a_ {1.2} \ cdot a_ {2,1} $

$ \ color {красный} { \ begin {vmatrix} а & б \\ CD \ end {vmatrix} = a \ cdot d — b \ cdot c} $

Пример 28
$ \ begin {vmatrix} 2 и 5 \\ 3 и 8 \ end {vmatrix} = 2 \ cdot 8 — 3 \ cdot 5 = 16-15 = 1 $

Пример 29
$ \ begin {vmatrix} -4 & 7 \\ -2 и 9 \ end {vmatrix} = -4 \ cdot 9 — 7 \ cdot (-2) = -36 — (- 14) = -36 + 14 = — 22 $

Расчет определителя 3×3

Мы используем строку 1 для вычисления определителя.{4} \ cdot \ Delta_ {1,3} = $ $ a_ {1,1} \ cdot \ Delta_ {1,1} -a_ {1.2} \ cdot \ Delta_ {1,2} + a_ {1.3} \ cdot \ Delta_ {1,3} $

$ \ Delta_ {1,1} = \ begin {vmatrix} а_ {2,2} и а_ {2,3} \\ а_ {3,2} и а_ {3,3} \ end {vmatrix} = a_ {2,2} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,2} $

$ \ Delta_ {1,2} = \ begin {vmatrix} а_ {2,1} и а_ {2,3} \\ а_ {3,1} и а_ {3,3} \ end {vmatrix} = a_ {2,1} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,1} $

$ \ Delta_ {1,3} = \ begin {vmatrix} а_ {2,1} и а_ {2,2} \\ а_ {3,1} и а_ {3,2} \ end {vmatrix} = a_ {2,1} \ cdot a_ {3,2} -a_ {2,2} \ cdot a_ {3,1} $

$ \ left | А \ право | = a_ {1,1} \ cdot (a_ {2,2} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,2}) — a_ {1,2} \ cdot ( a_ {2,1} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,1}) + $ $ a_ {1,3} \ cdot (a_ {2,1} \ cdot a_ {3,2} -a_ {2,2} \ cdot a_ {3,1}) = $ $ a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} -a_ {1,1} \ cdot a_ {2,3} \ cdot a_ {3,2} -a_ {1 , 2} \ cdot a_ {2.1} \ cdot a_ {3,3} + a_ {1,2} \ cdot a_ {2,3} \ cdot a_ {3,1} + $ $ a_ {1,3} \ cdot a_ {2,1} \ cdot a_ {3,2} -a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} = $ $ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {1,2} \ cdot a_ {2,3} \ cdot a_ {3, 1} + a_ {1,3} \ cdot a_ {2,1} \ cdot a_ {3,2} -} $ $ \ color {красный} {(a_ {1,1} \ cdot a_ {2,3} \ cdot a_ {3,2} + a_ {1,2} \ cdot a_ {2,1} \ cdot a_ {3 , 3} + a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1})} $

Чтобы быстрее достичь последнего отношения, мы можем использовать следующий метод.

Сначала перепишем первые две строки под определитель следующим образом.

$ \ begin {vmatrix} \ color {красный} {a_ {1,1}} & a_ {1,2} & a_ {1,3} \\ \ color {red} {a_ {2,1}} & \ color {red} {a_ {2,2}} & a_ {2,3} \\ \ color {красный} {a_ {3,1}} & \ color {красный} {a_ {3,2}} & \ color {красный} {a_ {3,3}} \ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc} a_ {1,1} & \ color {красный} {a_ {1,2}} & \ color {красный} {a_ {1,3}} \\ a_ {2,1} & a_ {2,2} & \ color {красный} {a_ {2,3}} \\ \ end {array} $

Мы умножаем элементы на каждой из трех красных диагоналей (главной диагонали и тех, что под ней), и складываем результаты:
$ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {2,1} \ cdot a_ {3,2} \ cdot a_ {1,3} + a_ {3,1} \ cdot a_ {1,2} \ cdot a_ {2 , 3}} $

$ \ begin {vmatrix} \ color {red} {a_ {1,1}} & \ color {red} {a_ {1,2}} & \ color {blue} {a_ {1,3}} \\ \ color {red} {a_ {2,1}} & \ color {blue} {a_ {2,2}} & \ color {blue} {a_ {2,3}} \\ \ color {blue} {a_ {3,1}} & \ color {blue} {a_ {3,2}} & \ color {blue} {a_ {3,3}} \ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc} \ color {blue} {a_ {1,1}} & \ color {blue} {a_ {1,2}} & \ color {red} {a_ {1,3}} \\ \ color {blue} {a_ {2,1}} & \ color {red} {a_ {2,2}} & \ color {red} {a_ {2,3}} \\ \ end {array} $

Мы умножаем элементы на каждой из трех синих диагоналей (вторичная диагональ и те, что под ней), и складываем результаты:

$ \ color {blue} {a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} + a_ {2,3} \ cdot a_ {3,2} \ cdot a_ {1, 1} + a_ {3,3} \ cdot a_ {1,2} \ cdot a_ {2,1}} $

Если вычесть два отношения, мы получим формулу определителя:

$ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {2,1} \ cdot a_ {3,2} \ cdot a_ {1, 3} + a_ {3,1} \ cdot a_ {1,2} \ cdot a_ {2,3} -} $ $ \ color {красный} {(a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} + a_ {2,3} \ cdot a_ {3,2} \ cdot a_ {1 , 1} + a_ {3,3} \ cdot a_ {1,2} \ cdot a_ {2,1})} $

Пример 30
$ A = \ begin {pmatrix} 1 и 4 и 3 \\ 2 и 1 и 5 \\ 3 и 2 и 1 \\ \ end {pmatrix} $

$ \ begin {vmatrix} 1 и 4 и 3 \\ 2 и 1 и 5 \\ 3 и 2 и 1 \\ \ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc} 1 и 4 и 3 \\ 2 и 1 и 5 \\ \ end {array} $

$ = 1 \ cdot1 \ cdot1 + 2 \ cdot2 \ cdot3 + 3 \ cdot4 \ cdot5 — (3 \ cdot1 \ cdot3 + 5 \ cdot2 \ cdot1 + 1 \ cdot4 \ cdot2) = $ 1 $ + 12 + 60 — (9 + 10 + 8) = 73-27 = 46 $

Пример 31
$ A = \ begin {pmatrix} 3 и 5 и 1 \\ 1 и 4 и 2 \\ 7 и 1 и 9 \\ \ end {pmatrix} $

$ \ begin {vmatrix} 3 и 5 и 1 \\ 1 и 4 и 2 \\ 7 и 1 и 9 \\ \ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc} 3 и 5 и 1 \\ 1 и 4 и 2 \\ \ end {array} $

$ = 3 \ cdot4 \ cdot9 + 1 \ cdot1 \ cdot1 + 7 \ cdot5 \ cdot2 — (1 \ cdot4 \ cdot7 + 2 \ cdot1 \ cdot3 + 9 \ cdot5 \ cdot1) = $ 108 $ + 1 + 70 — (28 + 6 + 45) = 79-79 = 100 $

Есть определители, элементами которых являются буквы. {2 }] $

Пример 32
Вычисляем определитель матрицы Вандермонда.{2} \ end {vmatrix} = $

$ \ begin {vmatrix} а-с и б-с \\ (a-c) (a + c) и (b-c) (b + c) \ end {vmatrix} = $ $ (a-c) (b-c) \ begin {vmatrix} 1 и 1 \\ а + с и б + с \ end {vmatrix} = $

$ = (a-c) (b-c) [(b + c) — (a + c)] = $ $ (a-c) (b-c) (b + c-a-c) = (a-c) (b-c) (b-a) $

Расчет определителя 4×4

Для вычисления определителей 4×4 воспользуемся общей формулой.

Перед применением формулы, используя свойства определителей:

Мы проверяем, выполняется ли какое-либо из условий, при которых значение определителя равно 0.
Мы проверяем, можем ли мы исключить какую-либо строку или столбец.
Мы проверяем, является ли определитель матрицей Вандермонда или он имеет те же элементы, но переупорядоченные, в любой строке или столбце.

В любом из этих случаев мы используем соответствующие методы вычисления определителей 3×3. Мы модифицируем строку или столбец, чтобы заполнить их 0, за исключением одного элемента. Определитель будет равен произведению этого элемента и его сомножителя. В этом случае сомножитель — это определитель 3×3, который вычисляется по его специальной формуле.

Пример 33
$ \ begin {vmatrix} 1 и 3 и 9 и 2 \\ 5 и 8 и 4 и 3 \\ 0 & 0 & 0 & 0 \\ 2 и 3 и 1 и 8 \ end {vmatrix} $

Мы замечаем, что все элементы в строке 3 равны 0, поэтому определитель равен 0.

Пример 34
$ \ begin {vmatrix} 1 и 3 и 1 и 2 \\ 5 и 8 и 5 и 3 \\ 0 & 4 & 0 & 0 \\ 2 и 3 и 2 и 8 \ end {vmatrix} $
Мы замечаем, что $ C_ {1} $ и $ C_ {3} $ равны, поэтому определитель равен 0.

Пример 35
$ \ begin {vmatrix} 1 и 3 и 9 и 2 \\ 5 и 8 и 4 и 3 \\ 10 и 16 и 18 и 4 \\ 2 и 3 и 1 и 8 \ end {vmatrix} $
Мы замечаем, что строки 2 и 3 пропорциональны, поэтому определитель равен 0.

Пример 36
$ \ begin {vmatrix} \ color {красный} {4} & 3 & 2 & 2 \\ 0 & 1 & -3 & 3 \\ 0 и -1 и 3 и 3 \\ 0 и 3 и 1 и 1 \ end {vmatrix} $

Поскольку в столбце 1 есть только один элемент, отличный от 0, мы применяем общую формулу, используя этот столбец.Кофакторы, соответствующие элементам, равным 0, не нужно вычислять, потому что их произведение на эти элементы будет равно 0.

=
$ = 4 (1 \ cdot3 \ cdot1 + (- 1) \ cdot1 \ cdot3 + 3 \ cdot (-3) \ cdot3 $ $ — (3 \ cdot3 \ cdot3 + 3 \ cdot1 \ cdot1 +1 \ cdot ( -3) \ cdot (-1))) $ $ = 4 (3-3-27- (27 + 3 + 3)) = 4 \ cdot (-60) = — 240 $

Пример 37
$ \ begin {vmatrix} 4 и 3 и 2 и 2 \\ 0 & 1 & 0 & -2 \\ 1 и -1 и 3 и 3 \\ 2 и 3 и 1 и 1 \ end {vmatrix} $

Чтобы изменить строки, чтобы в них было больше нулей, мы работаем со столбцами и наоборот.Мы выбираем строку или столбец, содержащие элемент 1, потому что мы можем получить любое число путем умножения.

Мы замечаем, что уже есть два элемента, равных 0 в строке 2. Мы делаем только один другой 0, чтобы вычислить только кофактор 1.

$ \ begin {vmatrix} 4 и 3 и 2 и 2 \\ 0 & 1 & 0 & -2 \\ 1 и -1 и 3 и 3 \\ 2 и 3 и 1 и 1 \ end {vmatrix} \ xlongequal {C_ {4} + 2C_ {2}} $ $ \ begin {vmatrix} 4 и 3 и 2 и 8 \\ 0 & \ color {красный} {1} & 0 & 0 \\ 1 и -1 и 3 и 1 \\ 2 и 3 и 1 и 7 \ end {vmatrix} = $ $ =
$

$ = 1 \ cdot (-1) ^ {2 + 2} \ cdot \ begin {vmatrix} 4 и 2 и 8 \\ 1 и 3 и 1 \\ 2 и 1 и 7 \ end {vmatrix} = $
$ = 4 \ cdot3 \ cdot7 + 1 \ cdot1 \ cdot8 + 2 \ cdot2 \ cdot1 $ $ — (8 \ cdot3 \ cdot2 + 1 \ cdot1 \ cdot4 + 7 \ cdot2 \ cdot1) = $ 84 $ + 8 + 4- 48-4-14 = 30 $

Пример 38
$ \ begin {vmatrix} 1 и -2 и 3 и 2 \\ 2 и 3 и 1 и -1 \\ 3 и 3 и 3 и 3 \\ -1 и 4 и 2 и 1 \\ \ end {vmatrix} $

Мы можем вынести 3 из строки 3:
$ 3 \ cdot \ begin {vmatrix} 1 и -2 и 3 и 2 \\ 2 и 3 и 1 и -1 \\ 1 и 1 и 1 и 1 \\ -1 и 4 и 2 и 1 \\ \ end {vmatrix} $

Поскольку в строке 3 есть только элементы, равные 1, мы можем легко сделать нули.{3 + 4} \ cdot $ $ = (- 1) \ cdot \ begin {vmatrix} -1 & -4 & 1 \\ 3 и 4 и 2 \\ -2 и 3 и 1 \\ \ end {vmatrix} $
$ = — ((- 1) \ cdot 4 \ cdot 1 +3 \ cdot 3 \ cdot1 + (-2) \ cdot (-4) \ cdot 2 $ $ — (1 \ cdot 4 \ cdot (-2) + 2 \ cdot 3 \ cdot (-1) + 1 \ cdot (-4) \ cdot3)) $ $ = — (- 4 + 9 + 16 + 8 + 6 + 12) = -47 $

Пример 39
$ \ begin {vmatrix} 2 и 5 и 1 и 4 \\ 4 и 1 и 6 и 3 \\ 5 и 3 и 7 и 2 \\ 1 и 0, 2 и 4 \ end {vmatrix} $

В этом примере мы можем использовать последнюю строку (которая содержит 1) и сделать нули в первом столбце.{4 + 1} \ cdot \ begin {vmatrix} 5 & -3 & -4 \\ 1 и -2 и -13 \\ 3 и -3 и -18 \ end {vmatrix} = $ $ (- 1) \ cdot \ begin {vmatrix} 5 & -3 & -4 \\ 1 и -2 и -13 \\ 3 и -3 и -18 \ end {vmatrix} $

Мы вычитаем -1 из столбца 2 и -1 из столбца 3.
$ (-1) \ cdot (-1) \ cdot (-1) \ cdot \ begin {vmatrix} 5 и 3 и 4 \\ 1 и 2 и 13 \\ 3 и 3 и 18 \ end {vmatrix} = $ $ (- 1) \ cdot \ begin {vmatrix} 5 и 3 и 4 \\ 1 и 2 и 13 \\ 3 и 3 и 18 \ end {vmatrix} = $ $ — [5 \ cdot 2 \ cdot 18 + 1 \ cdot 3 \ cdot 4+ 3 \ cdot 3 \ cdot 13 — (4 \ cdot 2 \ cdot 3 \ cdot + 13 \ cdot 3 \ cdot 5 + 18 \ cdot 3 \ cdot 1)] = $ $ — (180 + 12 + 117-24-195-54) = 36 $

Пример 40
$ \ begin {vmatrix} 4 и 7 и 2 и 3 \\ 1 и 3 и 1 и 2 \\ 2 и 5 и 3 и 4 \\ 1 и 4, 2 и 3 \ end {vmatrix} $

В столбце 3 стоит 1, поэтому мы сделаем нули в строке 2.{2 + 5} \ cdot \ begin {vmatrix} 2 и 1 и -1 \\ -1 & -4 & -2 \\ -1 и -2 и -1 \ end {vmatrix} $

Мы вычитаем -1 из строки 2 и -1 из строки 3.
$ (-1) \ cdot (-1) \ cdot (-1) \ cdot \ begin {vmatrix} 2 и 1 и -1 \\ 1 и 4 и 2 \\ 1 и 2 и 1 \ end {vmatrix} = $ $ (- 1) \ cdot \ begin {vmatrix} 2 и 1 и -1 \\ 1 и 4 и 2 \\ 1 и 2 и 1 \ end {vmatrix} = $ $ — [2 \ cdot 4 \ cdot 1 + 1 \ cdot 2 \ cdot (-1) + 1 \ cdot 1 \ cdot 2 — ((-1) \ cdot 4 \ cdot 1 + 2 \ cdot 2 \ cdot 2 + 1 \ cdot 1 \ cdot 1)] = $ $ — (8-2 + 2 + 4-8-1) = — 3 $

Пример 41
$ \ begin {vmatrix} 2 и 1 и 3 и 4 \\ 1 и 3 и 4 и 2 \\ 3 и 4 и 2 и 1 \\ 4 и 2 и 1 и 3 \\ \ end {vmatrix} $

Мы замечаем, что любая строка или столбец имеет одинаковые элементы, но переупорядочены.В этом случае мы складываем все строки или все столбцы.

$ \ begin {vmatrix} 2 и 1 и 3 и 4 \\ 1 и 3 и 4 и 2 \\ 3 и 4 и 2 и 1 \\ 4 и 2 и 1 и 3 \ end {vmatrix} $ $ \ xlongequal {L_ {1} + L_ {2} + L_ {3} + L_ {4}} \ begin {vmatrix} 10 и 10 и 10 и 10 \\ 1 и 3 и 4 и 2 \\ 3 и 4 и 2 и 1 \\ 4 и 2 и 1 и 3 \ end {vmatrix} = $ 10 \ cdot \ begin {vmatrix} 1 и 1 и 1 и 1 \\ 1 и 3 и 4 и 2 \\ 3 и 4 и 2 и 1 \\ 4 и 2 и 1 и 3 \ end {vmatrix} $ $ \ xlongequal {C_ {1} — C_ {4}, C_ {2} -C_ {4}, C_ {3} -C_ {4}} 10 \ cdot \ begin {vmatrix} 0 & 0 & 0 & \ color {красный} {1} \\ -1 и 1 и 2 и 2 \\ 2 и 3 и 1 и 1 \\ 1 и -1 и -2 и 3 \ end {vmatrix} = $

$ = 10 \ cdot1 \ cdot (-1) ^ {1 + 4} $

$ = (-10) \ cdot \ begin {vmatrix} -1 и 1 и 2 \\ 2 и 3 и 1 \\ 1 и -1 и -2 \ end {vmatrix} = $ $ (- 10) \ cdot ((- 1) \ cdot 3 \ cdot (-2) +2 \ cdot (-1) \ cdot2 + 1 \ cdot 1 \ cdot 1 $ $ — (2 \ cdot 3 \ cdot 1 + 1 \ cdot (-1) \ cdot (-1) + (-2) \ cdot1 \ cdot2)) $ $ = -10 \ cdot (6-4 +1-6-1 + 4) = 0 $

Детерминанты и правило Крамера | Безграничная алгебра

Определители квадратных матриц 2 на 2

Определитель квадратной матрицы [латекс] 2 \ умножить на 2 [/ латекс] — это математическая конструкция, используемая при решении задач, которая находится по специальной формуле.

Цели обучения

Попрактикуйтесь в нахождении определителя матрицы [латекс] 2 \ умножить на 2 [/ латекс]

Основные выводы

Ключевые моменты

Определитель [latex] 2 \ times 2 [/ latex] матрицы [latex] \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} [/ latex] определяется как [latex] ad-bc [ /латекс].
Матрица часто используется для представления коэффициентов в системе линейных уравнений, а определитель может использоваться для решения этих уравнений.
Любая матрица имеет уникальную обратную, если ее определитель не равен нулю.

Ключевые термины

определитель : Уникальная скалярная функция над квадратными матрицами, которая является распределительной по матричному умножению, полилинейной по строкам и столбцам и принимает значение 1 для единичной матрицы. Его аббревиатура — «[латекс] \ det [/ latex]».

Что такое определитель?

Матрица часто используется для представления коэффициентов в системе линейных уравнений, а определитель может использоваться для решения этих уравнений.Использование определителей в исчислении включает определитель Якоби в правило замены переменных для интегралов от функций нескольких переменных. Определители также используются для определения характеристического полинома матрицы, что важно для задач на собственные значения в линейной алгебре. В аналитической геометрии детерминанты выражают подписанные [латекс] n [/ латекс] -мерные объемы [латекс] n [/ латекс] -мерных параллелепипедов. Иногда детерминанты используются просто как компактная запись для выражений, которые в противном случае было бы неудобно записывать.

Можно доказать, что любая матрица имеет единственную обратную матрицу, если ее определитель отличен от нуля. Также могут быть доказаны различные другие теоремы, в том числе то, что определитель произведения матриц всегда равен произведению определителей; и определитель эрмитовой матрицы всегда действительный.

Определитель матрицы [латекс] [A] [/ латекс] обозначается [латекс] \ det (A) [/ latex], [латекс] \ det \ A [/ latex] или [латекс] \ left | А \ правый | [/ латекс]. В случае, когда элементы матрицы записаны полностью, определитель обозначается путем окружения элементов матрицы вертикальными чертами вместо скобок или круглых скобок матрицы.

Например, определитель матрицы [latex] \ begin {bmatrix} a & b \\ d & e \ end {bmatrix} [/ latex] записывается [latex] \ begin {vmatrix} a & b \\ d & e \ end {vmatrix} [/ латекс].

Определитель матрицы 2 на 2

В линейной алгебре определитель — это значение, связанное с квадратной матрицей. Его можно вычислить из элементов матрицы с помощью определенного арифметического выражения, показанного ниже:

Для матрицы [latex] 2 \ times 2 [/ latex], [latex] \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} [/ latex],

определитель [латекс] \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} [/ latex] определяется как [latex] ad-bc [/ latex].

Пример 1: Найдите определитель следующей матрицы:

[латекс] \ displaystyle \ begin {bmatrix} 4 & -2 \\ 7 & 5 \ end {bmatrix} [/ latex]

Определитель [латекс] \ begin {vmatrix} 4 & -2 \\ 7 & 5 \ end {vmatrix} [/ latex]:

[латекс] \ displaystyle \ begin {align} (4 \ cdot 5) — (-2 \ cdot 7) & = 20 — (-14) \\ & = 34 \ end {align} [/ latex]

Кофакторы, второстепенные и другие детерминанты

Кофактор записи [latex] (i, j) [/ latex] матрицы [latex] A [/ latex] является минорным знаком этой матрицы.

Цели обучения

Объясните, как использовать вспомогательные матрицы и матрицы сомножителей для вычисления определителей

Основные выводы

Ключевые моменты

Пусть [latex] A [/ latex] представляет собой матрицу [latex] m \ times n [/ latex], а [latex] k [/ latex] — целое число с [latex] 0

Ключевые термины

кофактор : минор со знаком записи матрицы.
второстепенный : определитель некоторой меньшей квадратной матрицы, вырезанной из матрицы [latex] A [/ latex] путем удаления одной или нескольких ее строк или столбцов.

Кофактор и младший: определения

Кофактор

В линейной алгебре кофактор (иногда называемый дополнительным) описывает особую конструкцию, которая полезна для вычисления как определителя, так и обратного значения квадратных матриц.{i + j} M_ {ij} [/ латекс]

Незначительный

Чтобы знать, что такое минор со знаком, нам нужно знать, что такое минор матрицы. В линейной алгебре минор матрицы [latex] A [/ latex] является определителем некоторой меньшей квадратной матрицы, вырезанной из [latex] A [/ latex] путем удаления одной или нескольких ее строк или столбцов. Миноры, полученные путем удаления только одной строки и одного столбца из квадратных матриц (первые миноры), необходимы для вычисления сомножителей матрицы .

Пусть [latex] A [/ latex] представляет собой матрицу [latex] m \ times n [/ latex], а [latex] k [/ latex] — целое число с [latex] 0

Вычислить определитель

Определитель любой матрицы можно найти с помощью миноров со знаком. Определитель — это сумма минорных значений со знаком любой строки или столбца матрицы, масштабируемая элементами в этой строке или столбце.

Вычисление несовершеннолетних

Для нахождения определителя заданного минора матрицы A используются следующие шаги:

Выберите запись [latex] a_ {ij} [/ latex] из матрицы.
Вычеркните записи, которые лежат в соответствующей строке [latex] i [/ latex] и столбце [latex] j [/ latex].
Перепишите матрицу без отмеченных записей.
Получите определитель этой новой матрицы.

[латекс] M_ {ij} [/ latex] называется второстепенным для входа [latex] a_ {ij} [/ latex].

Примечание. Если [latex] i + j [/ latex] — четное число, кофактор совпадает со своим младшим числом: [latex] C_ {ij} = M_ {ij} [/ latex]. В противном случае он равен аддитивной инверсии своего минорного значения: [latex] C_ {ij} = — M_ {ij} [/ latex]

Расчет определителя

Мы найдем определитель следующей матрицы A, вычислив определители ее сомножителей для третьего, крайнего правого столбца, а затем умножив их на элементы этого столбца.

[латекс] \ displaystyle \ begin {bmatrix} 1 & 4 & 7 \\ 3 & 0 & 5 \\ -1 & 9 & 11 \\ \ end {bmatrix} [/ latex]

В качестве примера мы вычислим определитель второстепенного [латекса] M_ {23} [/ latex], который является определителем матрицы [латекс] 2 \ times 2 [/ latex], образованной удалением [латекса] 2 [/ latex] -й ряд и [latex] 3 [/ latex] -й столбец. Черная точка представляет собой удаляемый элемент.

[латекс] \ displaystyle \ begin {align} \ begin {vmatrix} 1 & 4 & \ bullet \\ \ bullet & \ bullet & \ bullet \\ -1 & 9 & \ bullet \ end {vmatrix} & = \ begin {vmatrix} 1 & 4 \\ -1 & 9 \ end {vmatrix} \\ & = (9 — (- 4)) \\ & = 13 \ end {align} [/ latex]

Поскольку [latex] i + j = 5 [/ latex] является нечетным числом, кофактор является аддитивным, обратным его второстепенному значению: [latex] — (13) = — 13 [/ latex]

Умножаем это число на [latex] a_ {23} = 5 [/ latex], что дает [latex] -65 [/ latex].

Тот же самый процесс выполняется для нахождения детерминантов [латекса] C_ {13} [/ latex] и [latex] C_ {33} [/ latex], которые затем умножаются на [latex] a_ {13} [/ латекс] и [латекс] а_ {33} [/ латекс] соответственно. Затем определитель находится путем суммирования всех этих величин:

[латекс] \ begin {align} \ det {A} & = a_ {13} \ det {C_ {13}} + a_ {23} \ det {C_ {23}} + a_ {33} \ det {C_ {33}} \\ & = 7 \ cdot27-5 \ cdot13 + 11 \ cdot-12 \\ & = — 8 \ end {align} [/ latex]

Правило Крамера

Правило Крамера использует определители для решения уравнения [латекс] Ax = b [/ latex], когда [latex] A [/ latex] представляет собой квадратную матрицу.

Цели обучения

Используйте правило Крамера, чтобы найти единственную переменную в системе линейных уравнений

Основные выводы

Ключевые моменты

Правило Крамера работает только с квадратными матрицами, которые имеют ненулевой определитель и уникальное решение.
Рассмотрим линейную систему [латекс] \ left \ {\ begin {matrix} ax + by & = {\ color {Red} e} \\ cx + dy & = {\ color {Red} f} \ end {matrix} \ right. [/ latex], который в формате матрицы имеет вид [latex] \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \ begin {bmatrix} x \\ y \ end {bmatrix} = \ begin {bmatrix} {\ color {Red} e} \\ {\ color {Red} f} \ end {bmatrix} [/ latex].Предположим, что определитель не равен нулю. Затем [latex] x [/ latex] и [latex] y [/ latex] можно найти по правилу Крамера: [latex] x = \ frac {\ begin {vmatrix} {\ color {Red} e} & b \\ {\ color {Red} f} & d \ end {vmatrix}} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix}} = \ frac {{\ color {Red} e} db {\ color {Red} f}} {ad-bc} [/ latex] и [latex] y = \ frac {\ begin {vmatrix} a & {\ color {Red} e} \\ c & {\ color {Red} f} \ end {vmatrix }} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix}} = \ frac {a {\ color {Red} f} — {\ color {Red} e} c} {ad-bc} [/ латекс ].
Правило Крамера эффективно для решения небольших систем и может быть вычислено довольно быстро; однако по мере роста системы вычисление новых детерминантов может быть утомительным.

Ключевые термины

определитель : Уникальная скалярная функция над квадратными матрицами, которая является распределительной по умножению матриц, полилинейной по строкам и столбцам и принимает значение [latex] 1 [/ latex] для единичной матрицы. Его аббревиатура — «[латекс] \ det [/ latex]».
квадратная матрица : матрица, имеющая такое же количество строк, как и столбцов.

«Правило Крамера» — это еще один способ решения системы линейных уравнений с матрицами.Он использует формулу для вычисления решения системы с использованием определения определителей.

Правило Крамера: определение

Правило Крамера — это явная формула для решения системы линейных уравнений с таким же количеством уравнений, сколько и неизвестных, то есть квадратная матрица, действительная во всех случаях, когда система имеет уникальное решение. Он выражает решение в терминах определителей (квадратной) матрицы коэффициентов и матриц, полученных из нее путем замены одного столбца вектором правых частей уравнений.

Правило Крамера: формула

Правила для матрицы [латекс] 2 \ times 2 [/ latex]

Рассмотрим линейную систему:

[латекс] \ displaystyle \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \ begin {bmatrix} x \\ y \ end {bmatrix} = \ begin {bmatrix} {\ color {Red} e} \\ {\ color {Red} f} \ end {bmatrix} [/ latex]

Предположим, что определитель не равен нулю. Тогда [latex] x [/ latex] и [latex] y [/ latex] можно найти по правилу Крамера:

[латекс] \ displaystyle x = \ frac {\ begin {vmatrix} {\ color {Red} e} & b \\ {\ color {Red} f} & d \ end {vmatrix}} {\ begin {vmatrix} a & b \ \ c & d \ end {vmatrix}} = \ frac {{\ color {Red} e} db {\ color {Red} f}} {ad-bc} [/ latex]

А:

[латекс] \ displaystyle y = \ frac {\ begin {vmatrix} a & {\ color {Red} e} \\ c & {\ color {Red} f} \ end {vmatrix}} {\ begin {vmatrix} a & b \ \ c & d \ end {vmatrix}} = \ frac {a {\ color {Red} f} — {\ color {Red} e} c} {ad-bc} [/ latex]

Правила для [латексной] 3 \ times 3 [/ latex] матрицы

Дано:

[латекс] \ displaystyle \ begin {bmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {bmatrix} \ begin {bmatrix} x \\ y \\ z \ end {bmatrix} = \ begin {bmatrix} {\ color { Красный} j} \\ {\ color {Red} k} \\ {\ color {Red} l} \ end {bmatrix} [/ latex]

Тогда значения [latex] x [/ latex], [latex] y [/ latex] и [latex] z [/ latex] могут быть найдены следующим образом:

[латекс] \ displaystyle x = \ frac {\ begin {vmatrix} {\ color {Red} j} & b & c \\ {\ color {Red} k} & e & f \\ {\ color {Red} l} & h & i \ end { vmatrix}} {\ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix}} \ quad y = \ frac {\ begin {vmatrix} a & {\ color {Red} j} & c \\ d & {\ color {Red} k} & f \\ g & {\ color {Red} l} & i \ end {vmatrix}} {\ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix}} \ quad z = \ frac { \ begin {vmatrix} a & b & {\ color {Red} j} \\ d & e & {\ color {Red} k} \\ g & h & {\ color {Red} l} \ end {vmatrix}} {\ begin {vmatrix} a & b & c \ \ d & e & f \\ g & h & i \ end {vmatrix}} [/ латекс]

Использование правила Крамера

Пример 1. Решите систему, используя правило Крамера:

[латекс] \ displaystyle \ left \ {\ begin {matrix} 3x + 2y & = 10 \\ -6x + 4y & = 4 \ end {matrix} \ right.[/ латекс]

В матричном формате:

[латекс] \ displaystyle \ begin {bmatrix} 3 & 2 \\ — 6 & 4 \ end {bmatrix} \ begin {bmatrix} x \\ y \ end {bmatrix} = \ begin {bmatrix} 10 \\ 4 \ end {bmatrix} [/ латекс]

[латекс] \ displaystyle \ begin {align} x & = \ frac {\ begin {vmatrix} {\ color {Red} e} & b \\ {\ color {Red} f} & d \ end {vmatrix}} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix}} \\ & = \ frac {{\ color {Red} e} db {\ color {Red} f}} {ad-bc} \ end {align} [/ латекс]

[латекс] \ displaystyle \ begin {align} x & = \ frac {\ begin {vmatrix} 10 & 2 \\ 4 & 4 \ end {vmatrix}} {\ begin {vmatrix} 3 & 2 \\ — 6 & 4 \ end {vmatrix}} \\ & = \ frac {10 \ cdot 4-2 \ cdot 4} {(3 \ cdot 4) — [2 \ cdot (-6)]} \\ & = \ frac {32} {24} = \ frac {4 } {3} \ end {align} [/ latex]

[латекс] \ displaystyle \ begin {align} y & = \ frac {\ begin {vmatrix} a & {\ color {Red} e} \\ c & {\ color {Red} f} \ end {vmatrix}} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix}} \\ & = \ frac {a {\ color {Red} f} — {\ color {Red} e} c} {ad-bc} \ end {align} [/ латекс]

[латекс] \ displaystyle \ begin {align} y & = \ frac {\ begin {vmatrix} 3 & 10 \\ — 6 & 4 \ end {vmatrix}} {\ begin {vmatrix} 3 & 2 \\ — 6 & 4 \ end {vmatrix}} \ \ & = \ frac {(3 \ cdot 4) — [10 \ cdot (-6)]} {(3 \ cdot 4) — [2 \ cdot (-6)]} \\ & = \ frac {72} {24} = 3 \ end {align} [/ латекс]

Решение системы — [latex] (\ frac {4} {3}, 3) [/ latex].

Калькулятор определяющей матрицы 2×2 3×3 4×4 NxN

Поиск инструмента

Определитель матрицы

Инструмент для вычисления определителя матрицы. Определитель квадратной матрицы M — это полезное значение, вычисляемое из ее внутренних элементов и обозначаемое det (M) или | M |.

Результаты

Определитель матрицы — dCode

Тэги: Matrix

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Вычислитель определителя матрицы 2×2

Погрузка…
(если это сообщение не исчезает, попробуйте обновить страницу)

Рассчитать

Калькулятор определителя матрицы 3×3

Загрузка …
(если это сообщение не исчезает, попробуйте обновить страницу)

Рассчитать

Вычислитель определителя Matrix 4×4

Загрузка …
(если это сообщение не исчезает, попробуйте обновить страницу)

Рассчитать

Калькулятор определителя матрицы NxN

Ответы на вопросы (FAQ)

Как вычислить определитель матрицы?

Для квадратной матрицы 2×2 (порядок 2) вычисление выглядит следующим образом:

$$ \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} = ad — bc $$

Пример: $$ \ begin {vmatrix} 1 & 2 \\ 3 & 4 \ end {vmatrix} = 1 \ times 4 — 2 \ times 3 = -2 $$

Для матрицы большего размера, такой как порядок 3 (3×3), вычислите:

$$ \ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} = a \ begin {vmatrix} e & f \\ h & i \ end {vmatrix} — b \ begin {vmatrix} d & f \\ g & i \ end {vmatrix} + c \ begin {vmatrix} d & e \\ g & h \ end {vmatrix} \\ = aei-afh + bfg-bdi + cdh-ceg $$

Вычисленные подматрицы называются минорами исходной матрицы.

Идея та же для матриц большего размера:

Для определителя порядка 4 матрицы 4×4 :

$$ \ begin {vmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \ end {vmatrix} = a \ begin {vmatrix} f & g & h \\ j & k & l \\ n & o & p \ end {vmatrix} — b \ begin {vmatrix} e & g & h \\ i & k & l \\ m & o & p \ end {vmatrix} + c \ begin {vmatrix} e & f & h \\ i & j & l \\ m & n & p \ end {vmatrix} — d \ begin {vmatrix} e & f & g \\ i & j & k \\ m & n & o \ end {vmatrix} \\ = \\ a (fkp — flo — gjp + gln + hjo — hkn) — b (ekp — elo — gip + glm + hio — hkm) + c (ejp — eln — fip + flm + hin — hjm) — d (ejo — ekn — fio + fkm + gin — gjm) \\ = \\ afkp — aflo — agjp + agln + ahjo — ahkn — bekp + belo + bgip — bglm — bhio + bhkm + cejp — celn — cfip + cflm + chin — chjm — dejo + dekn + dfio — dfkm — dgin + dgjm $$

Как вычислить определитель для неквадратной матрицы?

Определитель неквадратной матрицы не определен, он не существует согласно определению определителя.

По какой формуле вычисляется определитель матрицы порядка n?

Нет другой формулы, кроме приведенного выше объяснения для общего случая матрицы порядка n.

Как вычислить определитель матрицы 1х1?

Для матрицы 1×1 определитель является единственным элементом матрицы.

Пример: $$ | 1 | = 1 $$

Что такое определитель единичной матрицы?

Определитель единичной матрицы равен 1.

Пример: $$ \ begin {vmatrix} 1 & 0 \\ 0 & 1 \ end {vmatrix} = 1 \ times 1 — 0 \ times 0 $$

Пример: $$ \ begin {vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {vmatrix} = (1 \ times 1 \ times 1) — (1 \ раз 0 \ раз 0) + (0 \ раз 0 \ раз 0) — (0 \ раз 0 \ раз 1) + (0 \ раз 0 \ раз 0) — (0 \ раз 1 \ раз 0) = 1 $ $

Только член, соответствующий умножению диагонали, будет равен 1, а остальные члены будут нулевыми.

Как найти определитель матрицы по ее собственным значениям?

Определитель матрицы является произведением ее собственных значений (включая комплексные значения и потенциальную кратность).

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Определитель матрицы». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любых алгоритмов, апплетов или фрагментов «Определителя матрицы» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любые другие. Определитель функции Матрицы (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанную на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копирование-вставка или доступ к API для «Определителя матрицы» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

определитель, матрица, дет, квадрат, тождество

Ссылки

Источник: https: // www.