Как определить угол наклона в градусах: Как в градусах определить уклон крыши

Как определить уклон кровли своими руками

Сложно представить себе любое здание без крыши. Кровля должна защищать здание от воздействия природных осадков, обладать огнестойкими и водонепроницаемыми свойствами, обеспечивать эффективный отвод атмосферных осадков. Долговечность эксплуатации здания и его отдельных элементов во многом зависит от качественной крыши. Для достижения лучших результатов стоит использовать более простые виды скатных крыш: односкатные, двухскатные, вальмовые, полувальмовые, мансардные.

Минимальный угол наклона крыши из металлочерепицы должен составлять 14 градусов.

Основные данные

График выбора кровельного материала в зависимости от уклона крыши.

Допустимый угол наклона металлической крыши обычно измеряют своими руками исходя из климатических условий того района, в котором ведется строительство, и кровельного материала. Минимально угол наклона должен составлять 110°, максимальный угол наклона можно определить путем анализа погодных условий, его значение может быть 45°.

и больше. Для более теплого и сухого климата используется менее пологая крыша. Более крутой угол наклона дает возможность минимально скапливать снег и, соответственно, снижать снеговую нагрузку. Например, уклон 45° позволяет почти не учитывать вес снежного покрова.

Наряду с этим, увеличенный угол наклона резко повышает давление ветра на крышу. При уклоне в 45° давление ветра больше в 5 раз по сравнению с показателем в 11°. Следовательно, для большего угла наклона возникает необходимость в большем количестве реек для усиления обрешетки и стропил. От угла уклона крыши прямо зависит и ее стоимость.

Для кровли с углом наклона около 40-45° необходимо больше материалов (примерно в 1,5 раза), нежели для плоской крыши, а для 60° требуется в 2 раза больше кровельных материалов. При выборе конфигурации важно помнить, что от угла наклона напрямую зависит выбор кровельных материалов. Учет угла наклона позволяет определить материалы для кровли, а также произвести расчет слоев крыши и ее площади.

Зависимость полезной площади мансарды от уклона крыши.

Материалы для кровли по своим свойствам (технические, экономические, физические) объединились в группе 1-11.

На графике они показаны дугообразными стрелками. Линии наклона показывают уклон ската. Выделенная (жирным) линия на графике обозначает отношение полной высоты данного конька h к половине его обычного заложения ½. Отношение 1/2 указывает, что вертикальный отрезок h располагается на горизонтальном отрезке ½ два раза. Наклонная линия на полукруглой шкале обозначает угол наклона в градусах, а шкала, расположенная вертикально, – уклон крыши в %.

Так рассчитывают минимальный уклон для тех или иных кровельных материалов. В качестве примера, с помощью данного графика проведем расчет нужного угла наклона для данной крыши с использованием металлической черепицы.

Вернуться к оглавлению

Как измерить уклон

Таблица соотношения градус/процент уклона кровли.

На графике ищем наклонную линию, с которой стыкуется дугообразная стрела 2.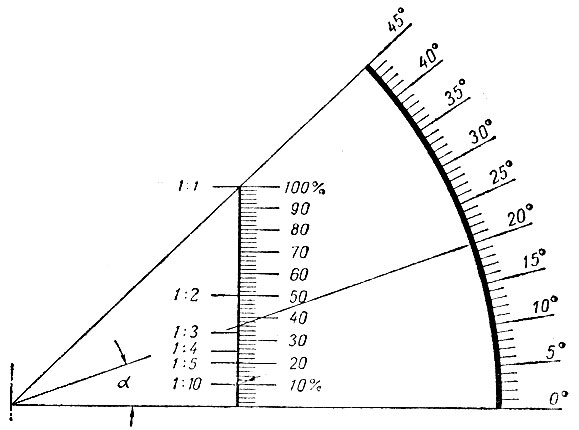 Пересечение наклонной линии c вертикальной шкалой определяет уклон, минимально допустимый для данной крыши, который равен 50%. Нам известно, что уклон ската определяется отношением высоты конька к половине его заложения. Произведем расчет таким образом:

i = 10 метров (заложение)

h = 4 метра (высота конька)

получаем

i= h / (1/2) = 4 / (10/2) = 0,8

Для того чтобы измерить уклон в %, это отношение умножают на 100

0,8х100 = 80.

Схема расчета угла кровли.

Таким образом, уклон в 80% при соблюдении норм строительства обеспечит достаточный сброс дождевой воды со всей площади. Для кровли из рулонных полимерно-битумных, битумных и мастичных материалов с уклоном 10° необходим защитный слой для основного водоизоляционного покрова из гравия либо каменной крошки, у которой марка морозостойкости не меньше 100. Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки – 0,3-0,5 см.

Причем на крышах с уклоном примерно до 2,5% с использованием эластомерных пленочных материалов в рулонах, выполненных свободной кладкой, необходим утяжеляющий слой гравия из расчета 50 кгс/кв.м.

На крышах из битумно-полимерных или битумных покрытий в рулонах с углом наклона выше 10% верхний слой гидроизоляционного покрова выполняется из крупнозернистой посыпки. На крышах из мастичных материалов с углом больше 10% предусматривается защитный слой из красочных составов.

При создании крыши из асбестоцементных листов, а также профнастила и металлической черепицы с наклоном до 20% по всей площади необходимо производить герметизацию стыков. Не более чем на 5% можно допустить отклонение уклона кровли из мелкоштучных материалов. Производя эти расчеты, можно узнать площадь помещения мансарды или чердака.

Вернуться к оглавлению

Единицы измерения и инструменты

В основание металлической конструкции встроены цифровой дисплей с элементами управления.  

Величина уклона на всех чертежах может обозначаться в градусах или в процентах, а сам он обозначается буквой «i». В настоящий момент нет строгих правил, как обозначать данную величину. Единицей измерения считают градусы или проценты (%).

Угол уклона измеряется двумя способами:

1. Специальным уклономером.
2. Математическим способом, с помощью вычислений.

Уклономер – это специальная рейка с рамкой, у которой между планками есть ось, на которой закреплен маятник, и своя шкала деления. Когда эта рейка расположена в горизонтальном положении, то маятник на ее шкале отклонен на ноль градусов. Для произведения измерения уклона ската рейку прибора располагают перпендикулярно коньку, в вертикальном положении.

По шкале определяют угол отклонения маятника, который указывает уклон этого ската данной крыши в градусах. Этот метод определения применяется очень и очень редко. На данный момент разработано множество геодезических приборов для определения этих величин и специальные уровни-уклономеры, как капельные, так и электронные.

Математический расчет

Расчет уклона кровли.

Можно спокойно рассчитать наклон данной крыши, не прибегая к использованию специальных геодезических, механических и других видов приборов для замеров уклона. Необходимо просто измерить некоторые параметры крыши:

1. Вертикальная высота (обозначается как H) – высота от верхней точки данного ската (обычно считают от конька) до самой нижней точки (так называемого карниза).
2. Заложение – горизонтальный промежуток от самой нижней точки данного ската до самой верхней его точки.

Уклон крыши (его величину) с применением математического расчета находят так.

Угол наклона отдельного ската i выражается через отношение измеренной высоты крыши Н к расстоянию заложения L. Таким образом

i = Н:L

Для точного определения этого значения в процентах отношение i умножают на 100. Затем, для определения его значения в градусах, мы производим перевод процентов в градусы.

Для полного понимания этого метода приведем наглядный расчет:

высота равна 3,0 м,

длина заложения равна 5 м.

По формуле вычисляем i:

i = 3:5 = 0,6

Проводим расчет процентов

i × 100 = 60%.

Переводим в градусы. Получаем 31 градус.

Уклон плоских крыш — База знаний ТЕХНОНИКОЛЬ

Уклон крыши необходим для эффективного отвода воды с поверхности ската.

При нарушении уклона крыши образуются застойные зоны, которые способствуют сокращению срока службы водоизоляционного ковра.

Крыша с большим уклоном «прощает» мелкие ошибки при монтаже и увеличивает срок службы конструкции.

В чем измеряется уклон крыши

Уклоном называют величину крутизны ската крыши.

Если представить крышу в разрезе, то получится прямоугольный треугольник. Уклоном будет считаться тангенс угла α, который равен отношению противолежащего катета к прилежащему.

Уклон может измеряться в градусах – °, процентах – %, а также может быть выражен коэффициентом уклона i.

Крыши с уклоном до 12° принято считать плоскими, а с уклоном 12° и более — скатными.

Перевод уклона из градусов в проценты

Для перевода уклона из градусов в проценты следует тангенс угла в градусах умножить на 100:

Для перевода уклона из процентов в градусы следует вычислить функцию арктангенса угла в процентах, умноженного на 0,01:

Сводная таблица с уклонами в различных величинах

Коэффициент уклона, i	Угол наклона, °	Наклон, %
0,008	0,5	0,8
0,01	0,6	1,0
0,015	0,9	1,5
0,02	1,1	2,0
0,03	1,7	3,0
0,05	2,9	5,0
0,10	5,7	10,0
0,12	6,8	12,0
0,15	8,5	15,0
0,20	11,3	20,0
0,25	14	25,0
0,30	16,7	30,0
0,45	24,2	45,0
0,60	31	60,0
1,00	45	100,0

Минимальный уклон крыши

В соответствии с действующими нормативными документами в строительстве, устройство скатов крыши необходимо выполнять с уклоном не менее 1,5% (i=0,015, 0,9°), т. е. 1,5 см подъема ската крыши на 100 см длины.

 

Угол наклона и наклон линии

Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный в направлении против часовой стрелки, называется углом наклона прямая л.

На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.

(i) 0° ≤ θ ≤ 180°

(ii)  Для горизонтальных линий θ = 0° или 180° и для вертикальных линий θ = 90°

(iii)  Если прямая линия первоначально лежит вдоль оси х и начинает вращаться вокруг неподвижной точки А на оси х против часовой стрелки и, наконец, совпадает с осью х, то угол наклона прямой линии в начальном положении равно 0°, а линии в конечном положении равно 0°.

(iv)  Линии, перпендикулярные оси x, называются вертикальными линиями.

(v)  Линии, перпендикулярные оси Y, называются горизонтальными линиями.

(vi)  Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.

Угол наклона и наклон линии – приложение

Основное применение угла наклона прямой линии – определение уклона.

Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».

Следовательно, наклон прямой равен

м  = tan θ 

для 0° ≤ θ ≤ 180°

Найдем наклон прямой по приведенной выше формуле

(i)  Для горизонтальных линий угол наклона равен 0° или 180°.

То есть

θ = 0° или 180°

Следовательно, наклон прямой линии равен

м  = tan0° или tan 180°  = 0

(ii) Для вертикальных линий угол наклона равен 90°.

То есть

θ = 90°

Следовательно, наклон прямой равен

м  =  tan90°  =  Не определено

(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.

Наклон линии — положительный или отрицательный, нулевой или неопределенный

Когда мы смотрим на прямую линию визуально, мы можем легко определить знак наклона.

Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.

Это иллюстрируют приведенные ниже рисунки.

Решенные задачи

Задача 1 :

Найдите угол наклона прямой, наклон которой равен 1/√3.

Решение :

Пусть θ — угол наклона линии.

Тогда наклон линии составляет

M = tanθ

Дано: наклон = 1/√3

Затем,

1/√3 = tanθ

θ = 30 °

Итак, угол угла наклон 30°.

Задача 2 :

Если угол наклона прямой равен 45°, найдите ее наклон.

Решение :

Пусть θ — угол наклона линии.

Тогда, наклон линии,

M = TANθ

Дано: θ = 45 °

Затем,

M = TAN 45 °

M = 1

Итак, склон — 1.

40002 M = 1

Итак, склон — 1.

4

Задача 3 :

Если угол наклона прямой равен 30°, найдите ее наклон.

Решение :

Пусть θ — угол наклона линии.

Затем, наклон линии,

м = tanθ

Дано: θ = 30°

Тогда

м = tan30°

м = 1/√3

Итак, уклон равен √3

.

Задача 4 :

Найдите угол наклона прямой, наклон которой равен √3.

Решение :

Пусть θ — угол наклона линии.

Затем, наклон линии,  

м  = tanθ

Дано: Уклон  =  √3

Тогда, 

√3  =  tanθ  

θ  = 60°

Итак, угол наклона равен 60°.

Задача 5 :

Найдите угол наклона прямой, уравнение которой y = x + 32.

Решение :

Пусть θ — угол наклона линии.

Данное уравнение находится в форме пересечения наклона.

То есть

y = mx + b

Сравнивая

y = x + 32

и

y = mx + b,

получаем наклон 1. m = 9.0004

Мы знаем, что наклон линии равен

м  =  tanθ

Тогда

1  =  tanθ

θ  = 45°

Итак, угол наклона равен 45°.

Пожалуйста, отправьте свой отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

4.3 Наклон линии | Аналитическая геометрия

4.

3 Наклон линии (EMBGD)

На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется угол наклона прямой.

Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения \(y\)-направление на изменение \(x\)-направления:

\[m=\frac{\Delta y}{\Delta x}\]

Из тригонометрии мы знаем, что функция тангенса определяется как отношение:

\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]

А из схемы мы видим, что

\начать{выровнять*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \конец{выравнивание*}

Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и положительное направление оси \(х\).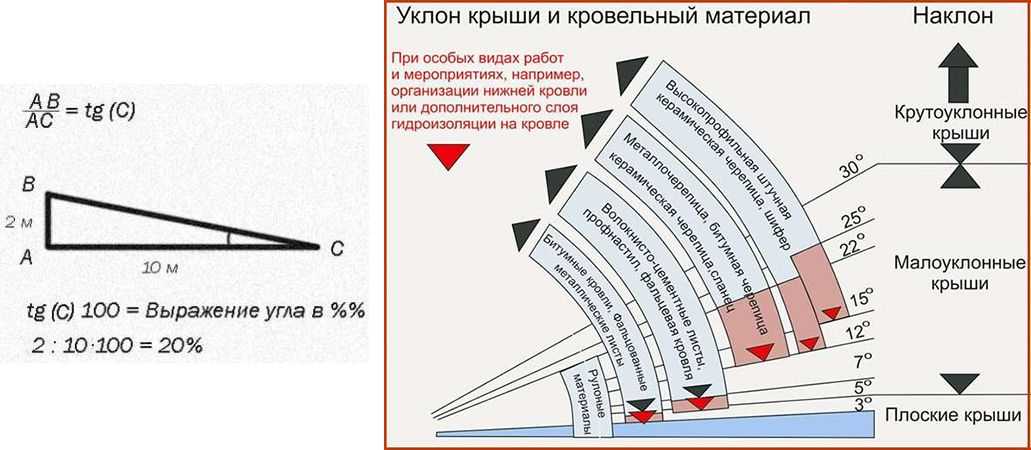

Вертикальные линии

• \(\тета = \текст{90}\текст{°}\)
• Градиент не определен, так как значения \(x\) не изменились (\(\Delta x = 0\)).
• Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta = \text{90}\text{°}\)).

Горизонтальные линии

• \(\тета = \текст{0}\текст{°}\)
• Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
• Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через происхождение \((\text{0}\text{°};0))\).

Линии с отрицательным уклоном

Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный между прямой и положительным направлением оси \(х\) тупая.

Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в второй квадрант:

Если нам дана прямая с градиентом \(m = -\text{0,7}\), то мы можем определить угол наклон с помощью калькулятора: 9{-1}(-\текст{0,7}) \\ &= -\текст{35,0}\текст{°} \конец{выравнивание*}

Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой угол во втором квадранте:

\начать{выровнять*} \тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\ &= \текст{145}\текст{°} \конец{выравнивание*}

И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\) дает градиент \(m = -\text{0,7}\).

Угол наклона

Учебник Упражнение 4.5

\(\text{60}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \tan \text{60}\text{°} \\ \поэтому m &= \text{1,7} \end{align*}

\(\text{135}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -\text{1} \end{выравнивание*}

\(\text{0}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \tan \text{0}\text{°} \\ \поэтому m &= \text{0} \end{align*}

\(\text{54}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \загар \текст{54}\текст{°} \\ \поэтому m &= \text{1,4} \end{выравнивание*}

\(\text{90}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \загар \текст{90}\текст{°} \\ \поэтому m & \text{ не определено} \end{align*}

\(\text{45}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \tan \text{45}\text{°} \\ \поэтому m &= \text{1} \end{выравнивание*}

\(\text{140}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \tan \text{140}\text{°} \\ \поэтому m &= -\text{0,8} \end{align*}

\(\text{180}\text{°}\)

\begin{align*} м &= \загар \тета\\ &= \tan \text{180}\text{°} \\ \поэтому m &= \text{0} \end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\ \поэтому \тета &= \text{36,8}\text{°} \end{align*}

\(2y — x = 6\)

\begin{align*} 2у — х&=6\ 2у &= х + 6 \\ y &= \frac{1}{2}x + 3 \\ \загар \тета &= м \\ &= \фракция{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \поэтому \тета &= \текст{26,6}\текст{°} \end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\ \поэтому \тета &= \text{45}\text{°} \end{align*}

\(y=4\)

Горизонтальная линия

\(x = 3y + \frac{1}{2}\)

\begin{align*} х &= 3y + \frac{1}{2} \\ x — \frac{1}{2} &= 3y \\ \frac{1}{3}x — \frac{1}{6} &= y \\ \поэтому m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \поэтому \тета &= \text{18,4}\text{°} \end{выравнивание*} 9{-1} \влево( \текст{0,577} \вправо) \\ \поэтому \тета &= \text{30}\text{°} \конец{выравнивание*}

Рабочий пример 8: Наклон прямой линии

Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии проходящей через точки \((2;1)\) и \((-3;-9)\).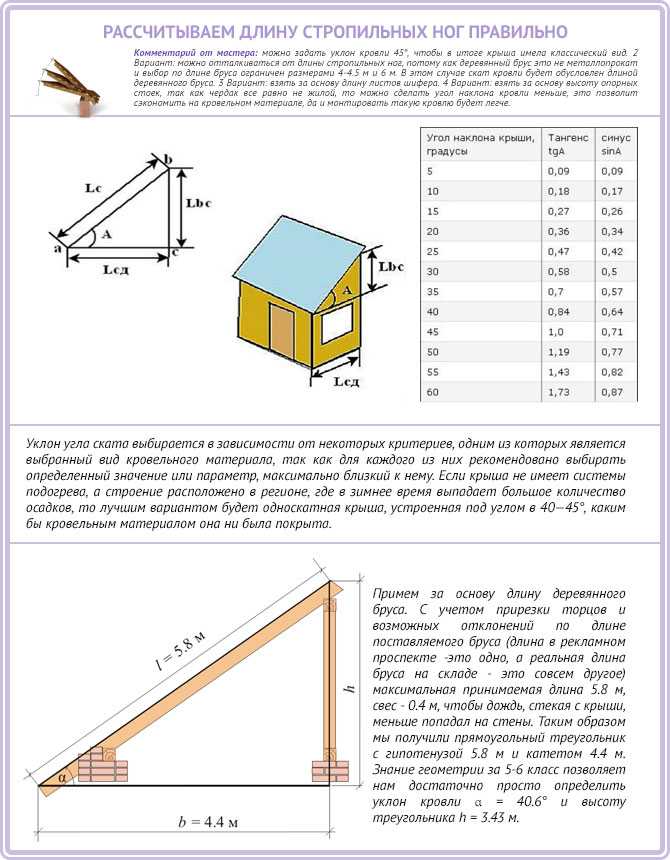 {-1}2\\ &= \текст{63,4}\текст{°} \end{выравнивание*}

Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).

Напишите окончательный ответ

Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).

temp text

Рабочий пример 9: Наклон прямой линии

Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом наклон \(\text{135}\text{°}\).

Используйте угол наклона для определения градиента линии

\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -1 \конец{выравнивание*}

Запишите уравнение прямой линии в форме точки градиента. x — x_1)\]

Подставить заданную точку \((3;1)\)

\begin{выравнивание*} у — 1 & = -(х — 3) \\ у&=-х+3+1\ &= -х + 4 \конец{выравнивание*}

Напишите окончательный ответ

Уравнение прямой линии \(y = -x + 4\).

temp text

Рабочий пример 10: Наклон прямой линии

Определить острый угол (с точностью до \(\text{1}\) десятичного знака) между прямой, проходящей через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = — \frac{3}{2}x + 4\).

Нарисуйте эскиз

Проведите прямую через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямую \(y = — \ дробь{3}{2}x + 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона две строки. Обозначьте \(\theta\) острый угол между двумя прямыми.

Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.

\[\begin{массив}{rll} \hat{B}_1 &= \text{180}\text{°} — \beta & (\angle \text{на строке}) \\ \text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle = \text{ сумма внутр. опп}) \\ \поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\ &= \text{180}\text{°} + \alpha — \beta \конец{массив}\] 9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°} \конец{выравнивание*}

Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен тупой угол лежит во второй четверти, поэтому

\начать{выравнивать*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \текст{123,7}\текст{°} \конец{выравнивание*}

Определить градиент и угол наклона линии через \(M\) и \(N\)

Определение градиента \начать{выравнивать*} m & = \frac{y_2 — y_1}{x_2 — x_1} \\ & = \dfrac{3 — \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \фракция{1}{4} \end{align*}

Определить угол наклона \начать{выравнивать*} \загар \альфа & = м\\ & = \фракция{1}{4} \\ \поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \текст{14,0}\текст{°} \end{выравнивание*}

Напишите окончательный ответ

\begin{align*} \тета & = \текст{180}\текст{°} + \альфа — \бета\\ & = \text{180}\text{°} + \text{14,0}\text{°} — \text{123,7}\text{°} \\ & = \текст{70,3}\текст{°} \end{align*}

Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\). {-1} \left( -\text{2} \right) \\ &= -\текст{63,4}\текст{°} \\ \поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\ \поэтому \тета &= \text{80}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\ &= -\текст{77,5}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\ \поэтому \тета &= \текст{102,5}\текст{°} \end{align*}

линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)

\begin{выравнивание*} m &= \frac{y_2 -y_1}{x_2 — x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\ \поэтому m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \поэтому \тета &= \text{45}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\ \поэтому \тета &= -\текст{18,4}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} — \text{18,4}\text{°} \\ \поэтому \тета &= \текст{161,6}\текст{°} \end{align*}

Градиент undefined

Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\) и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\).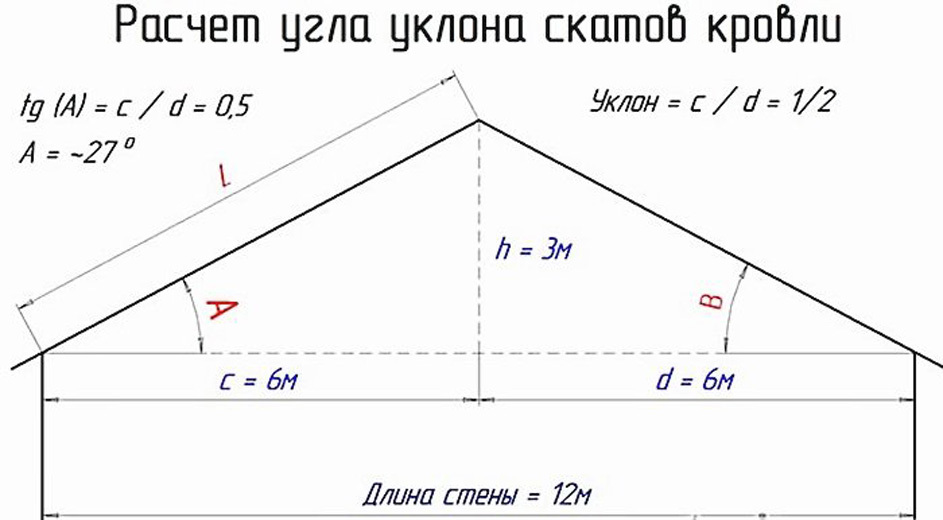 {-1} \left(-2 \right) \\ \поэтому \alpha &= -\text{63,4}\text{°} \\ \поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\ \поэтому \alpha &= \text{116,6}\text{°} \\ \text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle \треугольник)\\ \поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} — \text{116,6}\text{°} ) \\ &= \текст{85,2}\текст{°} \конец{выравнивание*}

Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).

Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя строки будут \(\тета\):

\начать{выравнивать*} у &= — х + 3 \\ \поэтому m &= — 1 \\ \alpha &= \tan^{-1} \left(-1\right) \\ \поэтому \alpha &= -\text{45}\text{°} \\ \поэтому \alpha &= \text{180}\text{°} — \text{45}\text{°} \\ \поэтому \alpha &= \text{135}\text{°} \\ х &= у + \ гидроразрыва {1} {2} \\ х — \фракция{1}{2} &= у \\ \поэтому m &= 1 \\ \beta &= \tan^{-1} \left(1 \right) \\ \поэтому \бета &= \text{45}\text{°} \\ \text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext.