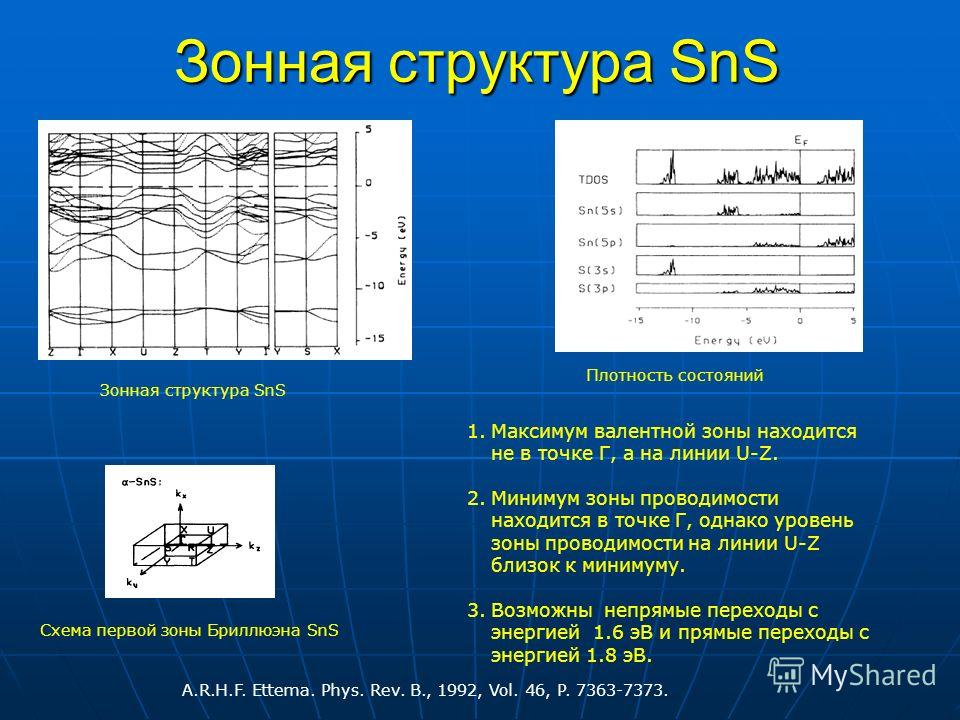
5.4. Плотность состояний для электронов и дырок в полупроводниках.
При анализе работы различных приборов одной из важнейших характеристик является число электронов dnв некотором интервале энергий, например в интервалеdE. Для того, чтобы определить это число, необходимо знать число энергетических состояний в этом интервале энергийdZи вероятность заполнения этих состояний электронами, или функцию распределения электронов по энергиям.
(5.13)
Число состояний можно получить через плотность энергетических состояний N(E), которую определим как число состояний в единичном интервале энергий в единице объёма полупроводника
(5.14).
С учётом (5.14) выражение (5.13) запишется как
(5.15).
Множитель 2 в (5.15) отражает
принцип Паули, в соответствии с которым
в каждом квантовом состоянии может
находиться 2 электрона с противоположно
направленными спинами.
dГ =V4p2dp(5.16).
В этом объёме будет dZ квантових состояний, которое определяется как
(5.17),
а на единицу объёма таких состояний будет
(5.18).
Начало отсчёта энергии совместим с минимумом энергии в зоне проводимости.
Тогда, в
соответствии с (4.15)(5.19).
Подставляем выражения (5.19) в (5.18) и получим
(5.20),
откуда следует, что
(5.21)
Аналогичное выражение может быть получено для плотности состояний вблизи потолка валентной зоны.
Лекция 6.
Мы определили плотность состояний как число состояний в единичном интервале энергий в единице объёма. Тогда концентрация электронов будет определяться как
(6.1)
Здесь пределами интегрирования являются
минимальная и максимальная энергии
электронов в первой зоне Бриллюэна зоны
проводимости. Если начало отсчёта
энергии совместить с минимумом энергии
в зоне проводимости, то нижний предел
в интеграле (6.1) будет равным нулю, а
верхний предел можно положить равным
бесконечности, поскольку электроны
занимают состояния вблизи дна зоны
проводимости и функция распределения,
как мы увидим ниже, резко спадает с
увеличением энергии.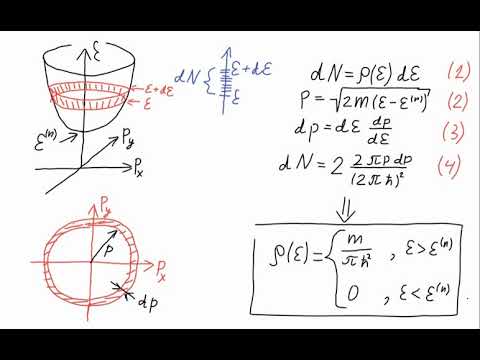
(6.2).
Как мы помним из общего курса физики, электроны являются фермионами12, и для них необходимо использовать функцию распределения Ферми-Дирака
(6.3)
ЗдесьkT– тепловая энергия,F– энергия Ферми. На рис. 6.1 показана зависимостьf(E)при разных температурах. Из этого рисунка видно, что энергию (уровень) Ферми можно определить двояко. Во-первых, это есть максимальная энергия электронов при0 Ки, во-вторых – это есть уровень, вероятность заполнения которого при всех температурах равна ½. Из (6.3) видно, что функция распределения Ферми-Дирака, а следовательно, и концентрация электронов в зоне проводимости, зависят от температуры и энергии.
Для полупроводников различают два крайних случая. 1. Если уровень Ферми находится в запрещённой зоне, так что , то в этом случае показатель степени в (6.3) больше 1 и функция распределения Ферми-Дирака переходит в классическую функцию Максвелла-Больцмана
(6.
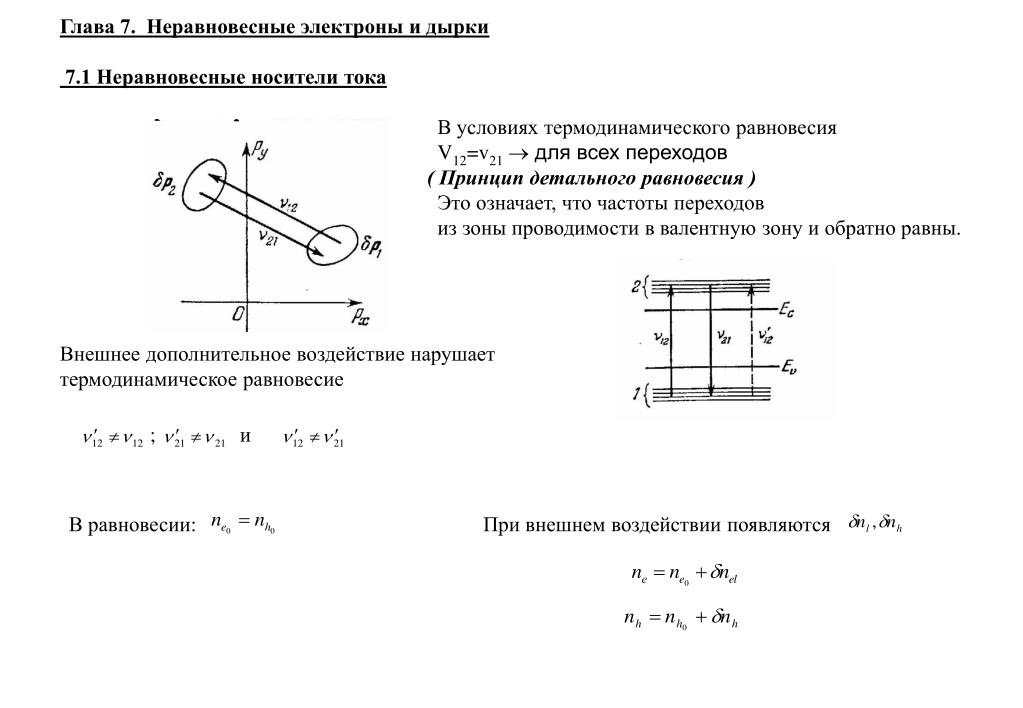4).
Полупроводник при этом называется невырожденными концентрация электронов (6.2) с функцией распределения (6.3) при этом определяется выражением
(6.5).
Здесь — так называемая эффективная плотность состояний для зоны проводимости.
В противоположном случае, когда уровень
Ферми находится в зоне проводимости,
причём
,
полупроводник называется вырожденным
и для нахождения концентрации необходимо
использовать функцию Ферми-Дирака
(6.3). При этом, с хорошей точностью
получается
(6.6)
Аналогичные выражения можно получить и для дырочного полупроводника. На рис. 6.2 схематично показаны плотность состояний Nc, функция распределенияf(E)и произведение этих величиндля невырожденного и вырожденного полупроводников.
Физические процессы в p-n переходах. Физический смысл понятия “Эффективная плотность состояний”
Министерство образования РФ
ВлГУ
Кафедра КТРЭС
Лабораторная работа№1
Физические процессы в p-n переходах
Выполнил:
студент гр.
РЭ-100
Проверил:
Владимир, 2002
1. Вопрос №7
Физический смысл понятия “Эффективная плотность состояний”
Физический смысл понятия “Эффективная плотность состояний” определяется в зоне проводимости и в валентной зоне. В зоне проводимости эффективная плотность состояний определяется формулой:
где NC – эффективная плотность состояний в зоне проводимости;
mn – эффективная масса электрона;
q – элементарный заряд;
φt– температурный потенциал;
h – постоянная Планка;
m – масса свободного электрона;
T – термодинамическая температура.
Из формулы (1) следует,
что эффективная плотность состояний в зоне проводимости представляет собой
максимально возможную концентрацию электронов в невырожденном полупроводнике.
Понятие “эффективная плотность состояний” применимо в тех случаях, когда
выполняется условие: энергия уровня Ферми стремиться быть равной энергии дна
зоны проводимости.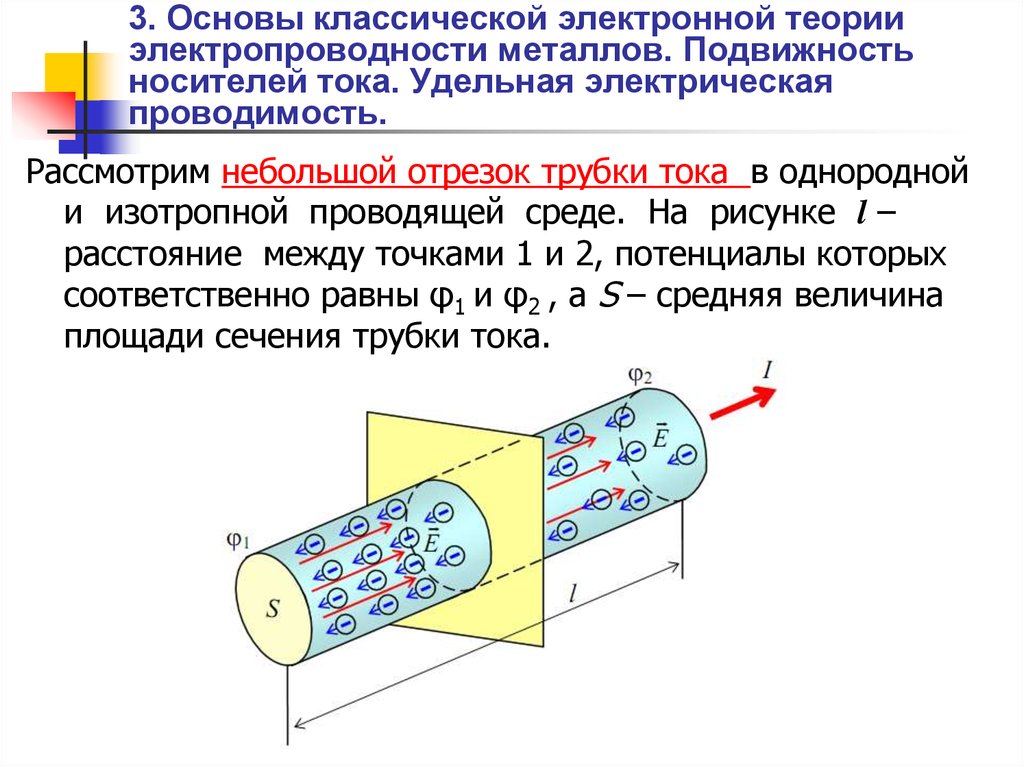
По физическому смыслу величина NCблизка к плотности энергитических уровней в зоне
проводимости в полосе энергий от φ
В валентной зоне эффективная плотность состояний определяется формулой:
где NV – эффективная плотность состояний в валентной зоне;
mp – эффективная масса “дырки”;
q – элементарный заряд;
φt– температурный потенциал;
h – постоянная Планка;
m – масса свободного электрона;
T – термодинамическая температура.
Из формулы (2) следует,
что эффективная плотность состояний в валентной зоне представляет собой
максимально возможную концентрацию “дырок” в невырожденном полупроводнике.
Понятие “эффективная плотность состояний” применимо в тех случаях, когда
выполняется условие: энергия уровня Ферми стремиться быть равной энергии
потолка валентной зоны.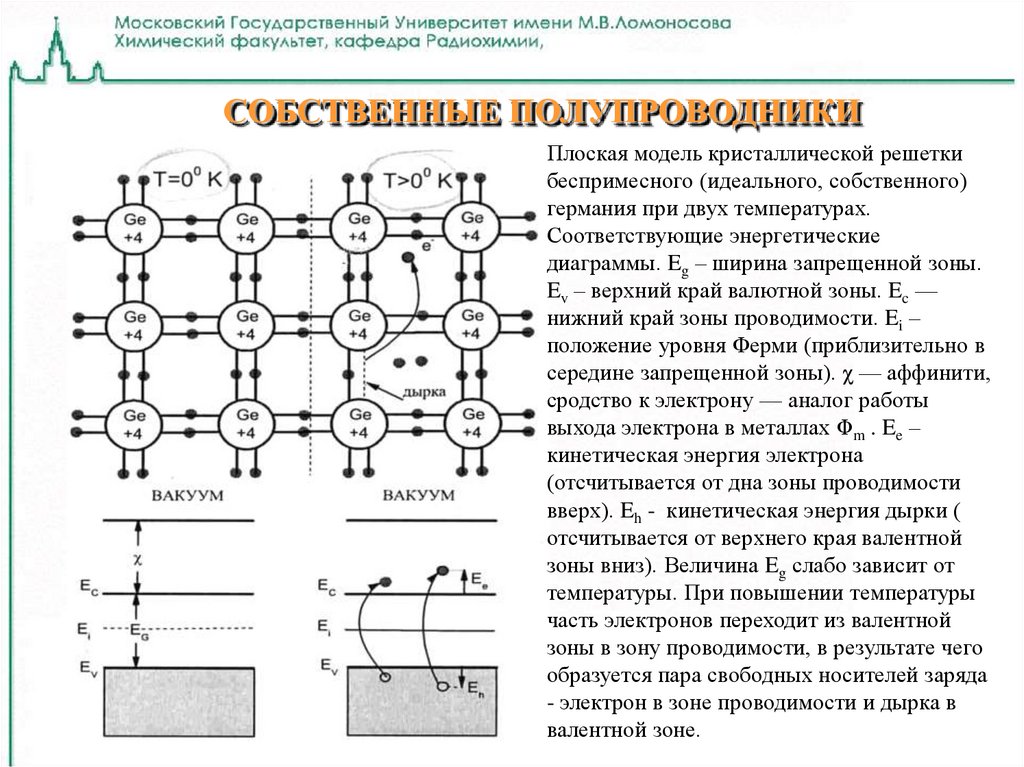
2. Задача № 7
Условие:
Используя распределение Ферми-Дирака для примесного полупроводника
где Ndn – концентрация нейтральных атомов донорной примеси; Ed– энергия донорного уровня, определить относительную долю ионизированных атомов фосфора с энергией активации Ec-Ed=0.044 эВ при температурах 50, 100, 300 К.
Решение:
Относительная доля ионизированных атомов фосфора определяется распределением Ферми-Дирака:
где Ndn– концентрация нейтральных атомов донорной примеси;
Nd– концентрация ионизированных атомов донорной примеси;
Ec-Ed – энергиея активации;
k – коэффициент Больцмана;
T – термодинамическая температура.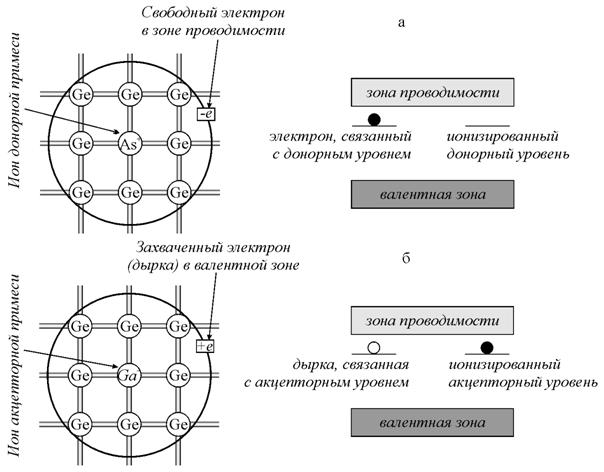
При температуре, равной 300 К, уровень Ферми размещается в середине примесной зоны, поэтому разность между энергией донорного уровня и энергией уровня Ферми равна половине энергии активации:
Относительная доля ионизированных атомов фосфора при температуре — 300 К, равна:
При более низких температурах (T=50 К; T=100 К) уровень Ферми располагается несколько ближе к дну зоны проводимости и дальше от донорного уровня, т.к. энергия электронов прямо пропорциональна kT, и им необходимо затратить большую энергию для достижения энергии уровня Ферми. Разность между энергией донорного уровня и энергией уровня Ферми изменяется не значительно, поэтому берётся такое же значение энергии активации как при температуре 300 К для 100 К:
, для 50 К:
Ответ: для значений
температур T=300 К, T=100 К и T=50 К полученны соответственно следующие результаты
относительной доли ионизированных атомов фосфора: 0.
459, 0.13, 0.1.
3.3.5 Эффективная плотность состояний
3.3.5 Эффективная плотность состоянийДалее: 3.4 Мобильность оператора связи Up: 3.3 Ленточная структура Предыдущий: 3.3.4 Эффективная масса носителя
Эффективная плотность состояний (DOS) в зоне проводимости и валентной зоне выражаются следующими теоретическими выражениями [86]:
| (3.91) | |||
| (3.92) |
представляет собой количество эквивалентных минимумов энергии в зоне проводимости.
|
Для альтернативной модели, основанной на данных после Зеленый [120] реализован,
который основан на полиномиальной подгонке второго порядка.
| (3.93) |
|
В модели для материалов сплава используются эффективные несущие массы компонентов .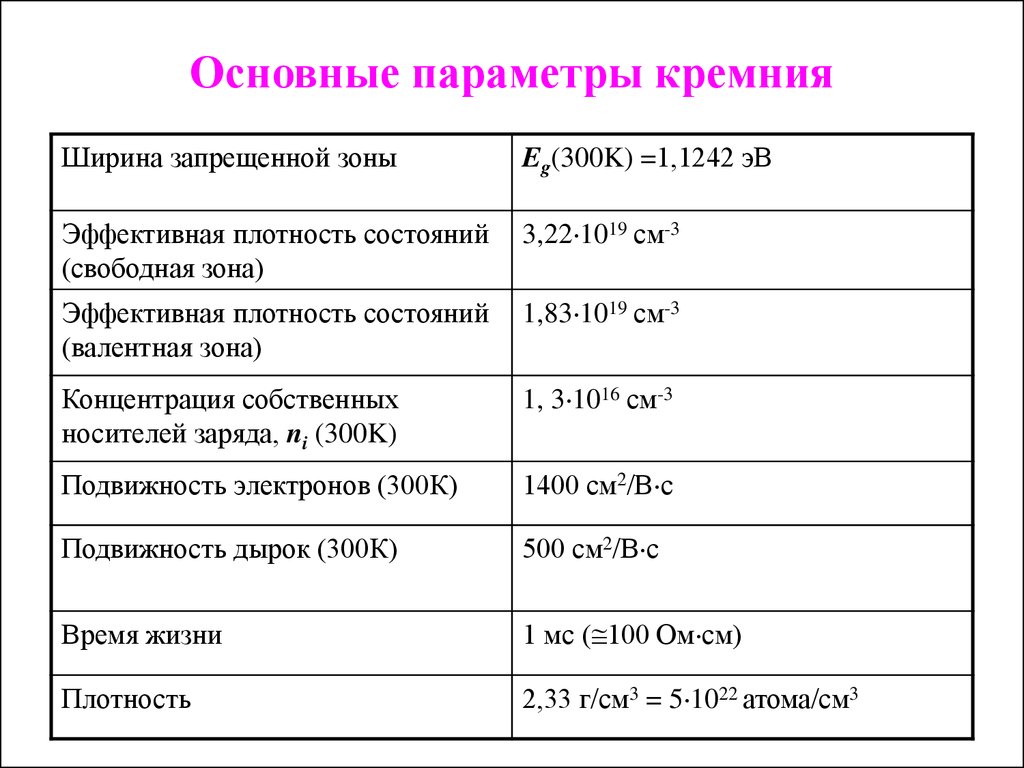
в выражениях (3.91) и (3.92).
В случае перехода между прямой и непрямой запрещенной зоной в III-V
тройных соединений фактор долинного вырождения моделируется
выражение, эквивалентное предложенному в [157].
| (3.94) |
Верхние индексы и обозначают прямое и косвенное соответственно.
В случае SiGe расщепление долинного вырождения из-за
деформация моделируется соответственно, как в [158].
| (3,95) |
Здесь обозначает разность энергий между долинами, сдвинутыми вниз и вверх по энергии соответственно. Оно установлено равным 0,6 эВ, как указано в [158].
Далее: 3.4 Мобильность оператора связи Up: 3.3 Ленточная структура Предыдущий: 3.3.4 Эффективная масса носителя Васил Паланковски
28 февраля 2001 г.
Общие свойства кремния | ПВЕОбучение
| Собственность | Значение |
|---|---|
| Атомная плотность | 5 x 10 22 см -3 5 x 10 28 м -3 |
| Атомный вес | 28.09 |
| Плотность (ρ) | 2,328 г см -3 2328 кг м -3 |
| Ширина запрещенной зоны (E G ) | 1,1242 эВ |
| Концентрация внутреннего носителя (n и ) при 300K* | 1 x 10 10 см -3 1 x 10 16 м -3 |
| Концентрация внутреннего носителя (n i ) при 25°C* | 8,6 x 10 9 см -3 8,6 x 10 15 м -3 |
| Постоянная решетки | 0,543095 нм |
| Точка плавления | 1415 °С |
| Теплопроводность | 1,5 Вт·см -1 K -1 150 Вт·м -1 K -1 |
| Коэффициент теплового расширения | 2,6 x 10 -6 К -1 |
| Эффективная плотность состояний в зоне проводимости (N C ) | 3 x 10 19 см -3 3 x 10 25 м -3 |
| Эффективная плотность состояний в валентной зоне (N V ) | 1 x 10 19 см -3 1 x 10 25 м -3 |
| Относительная диэлектрическая проницаемость (ε r ) | 11,7 |
| Электронное сродство | 4,05 эВ |
| Коэффициент электронной диффузии (D e ) | кТл/кв мкм e |
| Коэффициент диффузии отверстия (D h ) | кТ/кв мкм ч |
* обновленные значения приведены в 1 2.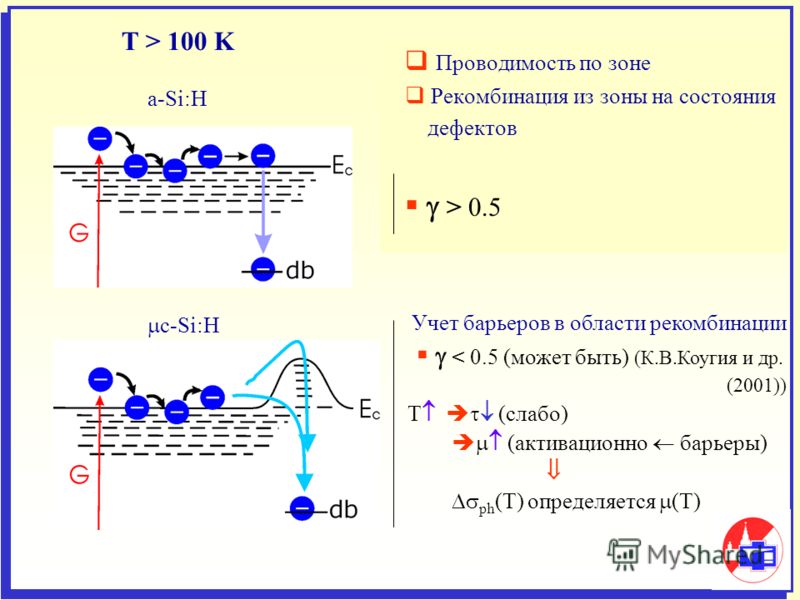
Свойства кремния в зависимости от легирования (300 K)
Подвижность носителей зависит от типа носителей и уровня легирования. Значения, рассчитанные здесь, используют ту же формулу, что и PC1D, чтобы соответствовать значениям, приведенным в 3 и 45 6. Срок службы как функция легирования дается на объемном сроке службы.
- 1. A.B. Sproul, Green, M.A., y Zhao, J., «Улучшенное значение концентрации собственных носителей кремния при 300 K», Applied Physics Letters, vol. 57, с. 255, 1990.
- 2. A.B. Sprouly Green, M.A., «Улучшенное значение концентрации собственных носителей кремния от 275 до 375 K», Journal of Applied Physics, vol. 70, стр. 846-854, 1991.
- 3. CH Wang, Misiakos, K., y Neugroschel, A., «Параметры транспортировки неосновных носителей в кремнии n-типа», IEEE Transactions on Electron Devices, vol. 37, стр. 1314 — 1322, 1990.
- 4. Тербер В.Р., Мэттис Р.Л., Лю Ю.М., Филлибен Дж.Дж., «Взаимосвязь удельного сопротивления и плотности легирующей примеси для кремния, легированного бором», Журнал Электрохимического общества, том.
