|
Random converter |
Калькулятор остановочного пути автомобиляКалькулятор определяет остановочный путь автомобиля с момента обнаружения водителем опасности до момента полной остановки автомобиля, а также другие параметры, связанные с этим событием, в частности, время восприятия водителем сигнала о необходимости торможения, время реакции водителя, а также расстояние, которое прошел автомобиль во время этих событий. Калькулятор также определяет начальную скорость (скорость до начала торможения) по известной длине торможения (длины тормозного пути) с учетом дорожных условий. Как и все остальные калькуляторы, этот калькулятор не следует использовать в судебных процессах и при необходимости получения высокой точности. Пример 1: Рассчитать расстояние, необходимое для остановки автомобиля, движущегося со скоростью 90 км/ч по мокрой горизонтальной дороге с асфальтобетонным покрытием (коэффициент трения μ = 0,4) если время восприятия водителя 0,5 с и время реакции водителя 0,7 с. Пример 2: Рассчитать начальную скорость автомобиля, движущегося по дороге с мокрым асфальтобетонным покрытием (μ = 0.4), если длина тормозного пути равна 100 м. Автомобиль движется на спуске с уклоном 10%. Калькулятор остановочного путиВходные данные Начальная скорость v0м/скм/чфут/смиля/ч Время восприятия опасности водителем thp с Время реакции водителя thr с Уклон σградус% Движение вверх Движение вниз Состояние дороги —Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальт или Коэффициент трения μ Тип привода тормозов —ПневматическийГидравлический или Время срабатывания тормозной системы tbrl с Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Угол крутизны уклона θ= ° Замедление a= м/с² Время торможения tbr= с Расстояние, которое проедет автомобиль во время восприятия водителем опасности Shp= м Расстояние, которое проедет автомобиль во время реакции водителя на опасность Shr= м Расстояние, которое проедет автомобиль за время задержки срабатывания тормоза Sbrl= м Тормозной путь Sbr= м Остановочный путь Sstop= м Критический угол наклона для заданного коэффициента трения θcrit= ° Критический уклон для заданного коэффициента трения σcrit= % Калькулятор определения скорости по тормозному путиВходные данные Длина тормозного следа Sbrметр (м)футярд Уклон σградус% Движение вверх Движение вниз Состояние дороги —Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальт или Коэффициент трения μ Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Скорость перед началом торможения v0 м/с км/ч Определения и формулы Остановочный путь Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуации Расстояние, которое пройдет автомобиль во время реакции водителя Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы Замедление Тормозной путь автомобиля Вывод зависимости тормозного пути от скорости и трения с использованием второго закона Ньютона Вывод зависимости тормозного пути от скорости и трения с помощью энергетического метода Время торможения Движение вверх и вниз по уклону Уклон Критический угол Определения и формулыОстановочный путьОстановочный путь — это расстояние, которое проходит автомобиль с момента, когда водитель видит опасность, оценивает ее, принимает решение остановиться и нажимает на педаль тормоза и до момента полной остановки автомобиля. где shr — расстояние, которое проедет автомобиль во время восприятия и оценки водителем ситуации, shr — расстояние, которое проедет автомобиль во время во время реакции водителя на ситуацию, sbrl — расстояние, которое проедет автомобиль во время задержки срабатывания тормозов, и sbr — тормозной путь. Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуацииРасстояние человеческого восприятия ситуации — это расстояние, которое пройдет автомобиль в то время, пока водитель оценивает опасность и принимает решение уменьшить скорость и остановиться. Оно определяется по формуле где shp расстояние человеческого восприятия в метрах, v скорость автомобиля в км/ч, thp — время человеческого восприятия в секундах и 1000/3600 — коэффициент преобразования километров в час в метры в секунду (1 километр равен 1000 метров и 1 час равен 3600 секундам). Расстояние, которое пройдет автомобиль во время реакции водителяРасстояние реакции водителя — это расстояние, которое пройдет автомобиль пока водитель выполняет решение остановить автомобиль после оценки опасности и принятия решения об остановке. Оно определяется по формуле где shp — расстояние реакции водителя с метрах, v — скорость автомобиля в км/ч и thr — время реакции водителя в секундах. Расстояние, которое пройдет автомобиль во время срабатывания тормозной системыРасстояние, которое пройдет автомобиль во время срабатывания тормозной системы, зависит от типа тормозной системы, установленной на автомобиле. Почти на всех легковых автомобилях и малотоннажных грузовых автомобилях используются гидравлическая тормозная система. На большинстве большегрузных автомобилей используются тормоза с пневматическим приводом. Задержка срабатывания пневматических тормозов приблизительно равна 0,4 с, а гидравлических (жидкость несжимаема!) 0,1–0,2 с. Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, определяется по формуле где sbrl — расстояние в метрах, которое пройдет автомобиль во время срабатывания тормозной системы, v — скорость движения автомобиля в км/ч, tbrl — время срабатывания тормозной системы в секундах. ЗамедлениеДля упрощения расчетов предположим, что автомобиль движется с постоянным ускорением или замедлением, которое определяется по известной из курса элементарной физики формуле равноускоренного или равнозамедленного движения где a — ускорение, v — начальная скорость, v0 — конечная скорость и t — время. Тормозной путь автомобиляТормозной путь автомобиля — это расстояние, которое проходит автомобиль с момента полного нажатия на педаль тормоза до момента полной остановки. Это расстояние зависит от скорости автомобиля перед началом торможения и от коэффициента трения между шинами и дорожным покрытием. В этом калькуляторе мы не учитываем другие факторы, влияющие на тормозной путь, например, сопротивление качению шин или лобовое сопротивление воздуха В результатах исследования1, в котором коэффициент трения определялся путем измерения замедления, определено, что антиблокировочная тормозная система (АБС) влияла на коэффициент трения таким образом: он увеличивается с увеличением скорости при использовании АБС и уменьшается, если АБС не используется. В этом исследовании также подтверждается, что на коэффициент трения между шинами и дорожным покрытием влияет температура и интенсивность дождя. Вывод зависимости тормозного пути от скорости и трения с использованием второго закона НьютонаКоэффициент трения определяется как отношения силы трения к силе нормального давления, прижимающей тело к опоре: или где Ffr — сила трения, μ коэффициент трения и Fnorm — сила реакции опоры. Действующая на тело нормальная сила реакции опоры определяется как составляющая силы реакции, перпендикулярная к поверхности опоры тела. В простейшем случае, когда тело находится на плоской горизонтальной поверхности, нормальная сила равна весу этого тела: где m — масса тела и g — ускорение свободного падения. Эта формула выведена из второго закона Ньютона: В более сложном случае, если тело расположено на наклонной плоскости, нормальная сила рассчитывается как где θ — угол наклона между плоскостью поверхности и горизонтальной плоскостью. В этом случае нормальная сила меньше веса тела. Случай наклонной поверхности мы рассмотрим чуть позже. В случае же горизонтальной поверхности, если коэффициент трения между телом и поверхностью равен μ, то сила трения равна В соответствии со вторым законом Ньютона, эта сила трения, приложенная к движущемуся телу (автомобилю) приводит к возникновению пропорционального ей замедления: или Теперь, в соответствии с уравнением ускоренного (замедленного) движения имеем Из курса элементарной физики известно, что при равнозамедленном движении с постоянным замедлением, если конечная скорость равна нулю, то тормозной путь определяется уравнением Это уравнение можно переписать в более удобной форме с использованием преобразования скорости в км/час в м/с: Подставляя в это уравнение a = μg, получаем формулу тормозного пути: где скорость v задается в км/час, а ускорение силы тяжести g в м/с². Решая это уравнение относительно v, получаем: Аналогичную формулу для определения тормозного пути можно получить с помощью энергетического метода. Вывод зависимости тормозного пути от скорости и трения с помощью энергетического методаТеоретическое значение тормозного пути можно найти, если определить работу по рассеиванию кинетической энергии автомобиля. Если автомобиль, движущийся со скоростью v, замедляет движение до полной остановки, работа тормозной системы Wb, требуемая для полного рассеяния кинетической энергии автомобиля Ek, равна этой энергии: Кинетическая энергия движущегося автомобиля Ek определяется формулой где m — масса автомобиля и v — скорость движения автомобиля перед началом торможения. Работа Wb, выполненная тормозной системой, определяется как где m — масса автомобиля, μ — коэффициент трения между шинами и дорожным покрытием, g — ускорение силы тяжести и sbr — тормозной путь, то есть расстояние, которое прошел автомобиль от начала торможения до полной остановки. Теперь, с учетом того, что Ek = Wb, имеем: или Скорость автомобиля до начала торможения является наиболее важным фактором, влияющим на величину остановочного пути. Другими, менее важными, факторами, влияющими на остановочный путь, являются время оценки водителем ситуации, время реакции водителя, скорость работы тормозной системы автомобиля и состояние дороги. Время торможенияИз курса элементарной физики известно, что средняя скорость при равноускоренном движении равна полусумме начальной и конечной скорости: С учетом, что конечная скорость равна нулю, время торможения определяется в калькуляторе как Движение вверх и вниз по уклонуСилы, действующие на автомобиль на уклоне: Fg — сила тяжести (вес автомобиля), Fgd — скатывающая вниз составляющая веса автомобиля, Ffr — сила трения, действующая параллельно поверхности дорожного полотна с уклоном, Fgn — нормальная составляющая веса автомобиля, направленная перпендикулярно поверхности дороги, и Fnr — сила реакции опоры, равная нормальной составляющей веса автомобиля. Когда водитель нажимает на педаль тормоза, замедляющий движение автомобиль может быть представлен в виде тела на поверхности с углом наклона θ (см. рисунок выше). Для простоты мы будем рассматривать только две силы, действующие на автомобиль, находящийся на уклоне. Это вес автомобиля и сила трения. Автомобиль, движущийся с начальной скоростью, замедляет движение, если сила трения, действующая параллельно дорожному полотну, больше, чем скатывающая сила, являющаяся составляющей силы тяжести, которая также параллельна дорожному полотну. Если начальная скорость автомобиля равна нулю, он в этой ситуации остается на месте при условии, что угол уклона меньше критического (об этом — ниже). В то время, как сила тяжести Fg стремится скатывать автомобиль вниз, сила трения Ffr сопротивляется этому движению. Чтобы автомобиль мог в этой ситуации остановиться, сила трения должна превышать скатывающую составляющую силы тяжести Fgd. В то же время, если сила трения превышает скатывающую составляющую силы тяжести, автомобиль будет двигаться вниз с постоянным ускорением и его тормозная система будет неспособна его остановить. Это может произойти, если угол наклона (уклон) дорожного полотна слишком велик или коэффициент трения слишком мал (вспомним как ведет себя автомобиль с обычными шинами на уклоне, если он покрыт коркой льда!). По определению коэффициента трения, можно записать уравнение для силы трения: или Скатывающая составляющая силы тяжести: Результирующая сила Ftotal, действующая на автомобиль на уклоне: или Как мы уже отмечали, сила Ftotal должна быть направлена вверх, иначе автомобиль при движении вниз остановить невозможно. В соответствии со вторым законом Ньютона, ускорение (точнее, замедление) автомобиля, движущегося под действием силы Ftotal, определяется как Подставляя ускорение в выведенную выше формулу тормозного пути, получаем: Решая это уравнение для vpre-braking, получим: Отметим еще раз, что в этих формулах g задается в м/с, v в км/ч и s в метрах. Припаркованные и движущиеся по ул. Дивисадеро в Сан-Франциско (Калифорния) автомобили. Уклон дорожного полотна в этом месте равен 31% или 17°. УклонВеличина уклона дороги (показателя крутизны склона) равна тангенсу угла плоскости дорожного покрытия к горизонтали. Он рассчитывается как отношение перпендикуляра, опущенного из точки на поверхность (превышения местности) к длине горизонтальной поверхности от начала склона до перпендикуляра (горизонтальному расстоянию). По определению уклона считается, что при движении вверх уклон является положительным, а при движении вниз уклон является отрицательным, когда превышение в действительности является понижением дороги. Уклон дороги σ выражают как угол наклона к горизонтали в градусах или как отношение в процентах. Например, подъёму 15 метров на 100 метров перемещения по горизонтали соответствует уклон, равный 0,15 или 15%. В этом калькуляторе мы используем уклон в процентах, определяемый по формуле где Δh — превышение местности и d — проекция уклона на горизонталь (см. Критический уголПри увеличении угла наклона дорожного полотна выше определенного значения, называемого критическим углом, движущийся вниз автомобиль затормозить невозможно, так как действующая на него сила трения становится меньше скатывающей силы. Этот критический угол находится из условия или или Из этой формулы можно найти критический угол для данного коэффициента трения, при котором автомобиль не сможет затормозить: Уклон, выраженный в процентах, определяется по известному углу наклона таким образом: ПримерВ этом примере мы покажем, как использовать формулу для определения тормозного пути. Пусть автомобиль движется с начальной скоростью vpre-braking = 90 км/ч вниз по уклону σ = 5% по мокрому асфальту (коэффициент трения μ = 0,4). Нужно определить тормозной путь. Для расчетов используем выведенные выше формулы. Особые случаиНажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:
Литература
Автор статьи: Анатолий Золотков Вас могут заинтересовать и другие калькуляторы из группы «Механика»:Калькулятор скорости, времени и расстояния при свободном падении Калькулятор выигрыша в силе Калькуляторы рычага Калькулятор выигрыша в силе, даваемого воротом Калькулятор выигрыша в силе, даваемого полиспастом Калькулятор выигрыша в силе наклонной плоскости Калькулятор выигрыша в силе винта Калькулятор выигрыша в силе, даваемого клином Калькулятор давления Калькулятор импульса (количества движения) и импульса силы Калькуляторы Механика |
Как считать уклон в процентах — Строй Обзор
Содержание
- Рисунок
- Описание
- Калькулятор уклонов
- Как посчитать уклон в процентах
- Методы вычислений уклона в процентах
- Определение уклона при строительных работах
- Что означает уклон в процентах, и как перевести его в градусы
- От чего зависит уклон кровли
- В чем измеряется угол уклона крыши
- Уклон крыши соотношение градусы-проценты
- Конвертер уклона — онлайн калькулятор
- Замер уклона крыши
- Математический расчёт уклона
Рисунок
Описание
С помощью кальулятора перевода из процентов в градусы можно визуально измерить и оценить необходимый угол (уклон). Данные расчеты очень часто требуются при проектировании и устройстве скатных крыш (наклон), строительстве автомобильных дорог, проектирование пандусов и .п. Многие инженеры допускают ошибки при данных расчетах, т.к. считают что зависимость перевода из процентов в градусы линейная, но это не так.
Данные расчеты очень часто требуются при проектировании и устройстве скатных крыш (наклон), строительстве автомобильных дорог, проектирование пандусов и .п. Многие инженеры допускают ошибки при данных расчетах, т.к. считают что зависимость перевода из процентов в градусы линейная, но это не так.
Перевод из процентов в градусы
Проценты = tg (Градусы) * 100
Перевод из градусов в проценты
Градусы = arctg (Проценты / 100)
Калькулятор уклонов
Калькулятор уклонов поможет Вам в нужный момент рассчитать уклон, превышение либо расстояние без всяких проблем.
Калькулятор способен рассчитать уклон крыши. уклон трубопровода. уклон лестницы. уклон дороги и тд. Также есть возможность рассчитать превышение между точками или расстояние от точки до точки (полезно в геодезии).
Порядок работы:
1. Выбрать ту величину, которую Вам нужно рассчитать
2. Выбрать в какой единице измерения вы хотите задать/рассчитать уклон (на выбор 3 вида: градусы, промилле, проценты)
3. Задать 1-ую неизвестную
Задать 1-ую неизвестную
4. Задать 2-ую неизвестную
5. Нажать кнопку «Расчет»
Для справки:
— уклон в градусах считается через тангенс угла: tgx = h / L
— уклон в промилле считается по следующей формуле: x = 1000 * h / L
— уклон в процентах считается по следующей формуле: x = 100 * h / L
Калькулятор уклонов создан как дополнение к основным онлайн расчетам на сайте, и если он Вам понравился, то не забывайте рассказывать про него своим друзьям и коллегам.
Как посчитать уклон в процентах
При создании проектной документации очень часто уклон обозначается не в градусах, а в процентах. Это позволяет избежать проблем с монтажом готовой конструкции.
Уклон в градусах рассчитывается для крутых скатов крыш, так будет удобнее. Но когда речь идет о небольшом угле, то использование процентов для обозначения значения уклона поможет избежать ошибок при расчете и монтаже.
Методы вычислений уклона в процентах
Чтобы узнать процентное значение уклона на земельном участке, можно воспользоваться следующими методами:
- самым простым и точным способом определения угла склона будет нивелирование.
 При помощи специального прибора измеряются все необходимые величины и путем простого соотношения производятся несложные вычисления. Разность высот делится на расстояние, затем результат умножается на 100%. Современные нивелиры оснащены встроенной памятью, которая значительно облегчает работу замерщиков;
При помощи специального прибора измеряются все необходимые величины и путем простого соотношения производятся несложные вычисления. Разность высот делится на расстояние, затем результат умножается на 100%. Современные нивелиры оснащены встроенной памятью, которая значительно облегчает работу замерщиков; - измерить уклон можно и на своем участке без использования дорогостоящего оборудования. На плане участка или топографических картах часто обозначаются высоты. На земельном участке эти места намечаются, можно использовать для этой цели колышки, затем расстояние между ними измеряется землемерным циркулем. Математические расчеты производятся по той же схеме, что и при работе с нивелиром;
- используя метод интерполирования, значение уклона в процентах, можно вычислить по топографической карте. Для этого также определяется разность отметок, которая делится на расстояние и умножается на 100%.
Определение уклона при строительных работах
Специалисты, производящие кровельные работы, очень часто сталкиваются с необходимостью измерять уклоны крыш. Знание этих параметров позволяет выбрать тип материалов, которые будут использоваться, свериться с рекомендуемыми значениями для строений, выбрать метод ведения кровельных работ.
Знание этих параметров позволяет выбрать тип материалов, которые будут использоваться, свериться с рекомендуемыми значениями для строений, выбрать метод ведения кровельных работ.
Чтобы не производить сложные математические расчеты каждый раз, был разработан специальный инструмент, который называется уклономер. Это приспособление устроено довольно просто. На рейку крепится специальная рамка, внутри которой закрепляется маятник, он имеет грузик и указатель. Рейку устанавливают в горизонтальном положении на измеряемом участке кровли и по указателю определяют на шкале численное значение уклона.
В случае, когда известно значение уклона крыши в градусах, перевести его в проценты можно воспользовавшись специальными таблицами. В них уже прописаны процентные значения для каждого угла от одного до сорока пяти градусов.
Советы в статье «Виды укладки ламината» здесь .
Как запилить стропила под нужным углом и нужных размеров смотрим в видео:
Что означает уклон в процентах, и как перевести его в градусы
December 13, 2013
Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.
В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.
Расчет уклона в процентах
Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.
Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.
Как понимать угол уклона в процентах?
Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.
Почему не в градусах?
Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами. Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.
Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.
Применение на практике
Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам. Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan -1 (0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.
Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.
11 странных признаков, указывающих, что вы хороши в постели Вам тоже хочется верить в то, что вы доставляете своему романтическому партнеру удовольствие в постели? По крайней мере, вы не хотите краснеть и извин.
Чарли Гард умер за неделю до своего первого дня рождения Чарли Гард, неизлечимо больной младенец, о котором говорит весь мир, умер 28 июля, за неделю до своего первого дня рождения.
13 признаков, что у вас самый лучший муж Мужья – это воистину великие люди. Как жаль, что хорошие супруги не растут на деревьях. Если ваша вторая половинка делает эти 13 вещей, то вы можете с.
Никогда не делайте этого в церкви! Если вы не уверены относительно того, правильно ведете себя в церкви или нет, то, вероятно, поступаете все же не так, как положено.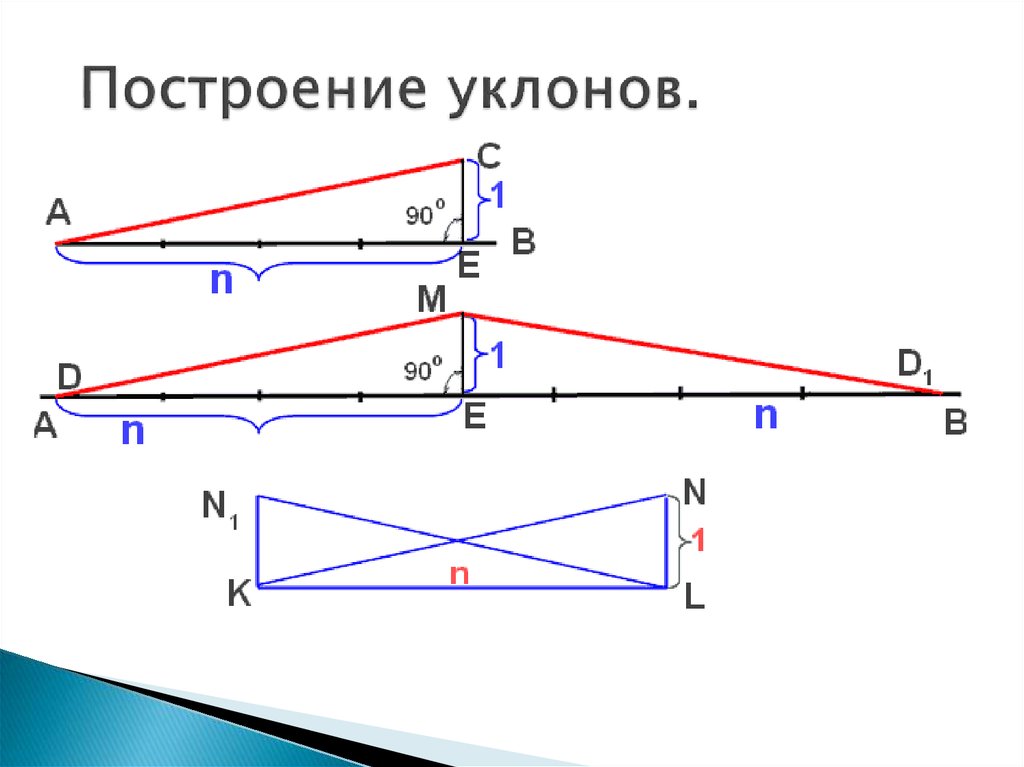 Вот список ужасных.
Вот список ужасных.
20 фото кошек, сделанных в правильный момент Кошки — удивительные создания, и об этом, пожалуй, знает каждый. А еще они невероятно фотогеничны и всегда умеют оказаться в правильное время в правил.
Непростительные ошибки в фильмах, которых вы, вероятно, никогда не замечали Наверное, найдется очень мало людей, которые бы не любили смотреть фильмы. Однако даже в лучшем кино встречаются ошибки, которые могут заметить зрител.
Уклон скатов крыши — от чего зависит и в чём он измеряется.
Такой немаловажный для крыши факт — её уклон. Уклон крыши — это угол наклона кровли относительно горизонтального уровня. По углу наклона скатов крыши бывают малоуклонные (пологие), средней наклонности и крыши с крутыми (сильноуклонными) скатами.
Малоуклонная крыша та крыша, монтаж которой осуществляется из расчёта наименьшего, рекомендованного угла наклона скатов. Так для каждого кровельного покрытия есть свой рекомендуемый минимальный уклон.
Так для каждого кровельного покрытия есть свой рекомендуемый минимальный уклон.
От чего зависит уклон кровли
- От способности крыши защищать строение от внешних факторов и воздействий.
- От ветра — чем больше уклон крыши, тем больше значение приходящихся ветровых нагрузок. При крутых уклонах уменьшается сопротивляемость ветру, повышается парусность. В регионах и местах с сильными ветрами рекомендуется применять минимальный уклон крыши, чтоб уменьшить нагрузки на несущие конструкции крыши.
- Откровельного покрытия (материала) — Для каждого кровельного материала существует свой минимальный угол наклона, при котором можно использовать данный материал.
- От архитектурных задумок, решений, местных традиций — так в разных регионах отдаётся предпочтение для той или иной конструкции крыши.
- От атмосферных осадков: снеговых нагрузок и дождей в регионе. На крышах с большим уклоном не будет скапливаться в огромных количествах снег, грязь и листья.

В чем измеряется угол уклона крыши
Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i .
В СНиПе II-26-76, данная величина указывается в процентах ( % ). В данный момент не существует строгих правил по обозначению размера уклона крыши.
Единицей измерения уклона крыши считают градусы или проценты ( %). Их соотношение указаны ниже в таблице.
Уклон крыши соотношение градусы-проценты
| градусы | % | градусы | % | градусы | % |
| 1° | 1,75% | 16° | 28,68% | 31° | 60,09% |
| 2° | 3,50% | 17° | 30,58% | 32° | 62,48% |
| 3° | 5,24% | 18° | 32,50% | 33° | 64,93% |
| 4° | 7,00% | 19° | 34,43% | 34° | 67,45% |
| 5° | 8,75% | 20° | 36,39% | 35° | 70,01% |
| 6° | 10,51% | 21° | 38,38% | 36° | 72,65% |
| 7° | 12,28% | 22° | 40,40% | 37° | 75,35% |
| 8° | 14,05% | 23° | 42,45% | 38° | 78,13% |
| 9° | 15,84% | 24° | 44,52% | 39° | 80,98% |
| 10° | 17,64% | 25° | 46,64% | 40° | 83,90% |
| 11° | 19,44% | 26° | 48,78% | 41° | 86,92% |
| 12° | 21,25% | 27° | 50,95% | 42° | 90,04% |
| 13° | 23,09% | 28° | 53,18% | 43° | 93,25% |
| 14° | 24,94% | 29° | 55,42% | 44° | 96,58% |
| 15° | 26,80% | 30° | 57,73% | 45° | 100% |
Перевести уклон из процентов в градусы и наоборот из градусов в проценты можно при помощи онлайн конвертера:
Конвертер уклона — онлайн калькулятор
из градусов в проценты и из процентов в грудусы Перейти
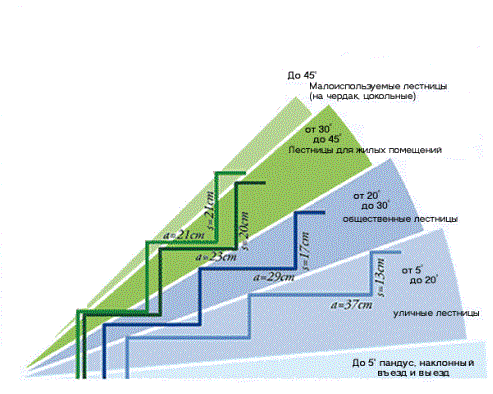
Замер уклона крыши
Измеряют угол уклона при помощи уклономера или же математическим способом.
Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.
Математический расчёт уклона
Можно рассчитать уклон крыши не используя геодезические и другие приборы для замеров уклона. Для этого необходимо знать два размера:
- Вертикальная высота ( H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
- Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней
При помощи математического расчёта величину уклона крыши находит следующим образом:
Для того, чтобы значение уклона выразить в процентах, это отношение умножают на 100. Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.
Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.
Чтобы было понятней рассмотрим на примере:
Длина заложения 4,5 м, высота крыши 2,0 м.
Уклон равен: i = 2.0 : 4,5 = 0,44 теперь умножим на × 100 = 44 %. Переводим данное значение по таблице в градусы и получаем — 24°.
Быстрый обзор использования Алгебры карт в Spatial Analyst—ArcMap
Доступно с лицензией Spatial Analyst.
- Основы работы с Алгеброй карт
- Работа с инструментами
- Работа с операторами
- Создание сложных выражений
- Использование классов
- Функции Алгебры карт, создающие пространственные объекты, таблицы или файлы
- Рекомендации по выполнению выражений Алгебры карт
- Дополнительная литература
 В базовом варианте выходной растр указывается слева от знака равенства (=), а инструменты, операторы и их параметры – справа. Пример:
В базовом варианте выходной растр указывается слева от знака равенства (=), а инструменты, операторы и их параметры – справа. Пример:from arcpy.sa import *
outShade = Hillshade("inelevation", 99, 33)
Приведенное выше выражение вычисляет отмывку рельефа, определяя освещенность при азимуте солнца 99 градусов и высоте 33 градуса, и создает объект типа Raster с именем outShade для сохранения результатов.
Алгебра карт может выполнять простые выражения, но вся мощь языка проявляется при создании сложных выражений и моделей. Поскольку Алгебра карт интегрирована в Python, разработчику модели доступна вся функциональность Python, ArcPy и расширений (модули, классы, функции и свойства).
Научиться работать с Алгеброй карт несложно, и по мере роста ваших запросов вы будете открывать для себя все новые возможности. Ниже даны основные сведения для начала работы.
Основы работы с Алгеброй карт
Три способа применения Алгебры карт:
- Инструмент Калькулятор растра
- Окно Python
- Интегрированная среда разработки (IDE) Python, которой вы пользуетесь
Калькулятор растра
Инструмент Калькулятор растра выполняет выражения Алгебры карт. Инструмент имеет легкий в использовании интерфейс калькулятора, в котором с помощью кнопок можно создать большинство выражений Алгебры карт. Инструмент Калькулятор растра можно использовать автономно или в ModelBuilder. Тем самым инструмент позволяет интегрировать богатые возможности Алгебры карт в ModelBuilder.
Инструмент имеет легкий в использовании интерфейс калькулятора, в котором с помощью кнопок можно создать большинство выражений Алгебры карт. Инструмент Калькулятор растра можно использовать автономно или в ModelBuilder. Тем самым инструмент позволяет интегрировать богатые возможности Алгебры карт в ModelBuilder.
Пользовательский интерфейс инструмента Калькулятор растра
В приведенном выше выражении суммируются три растра. Обратите внимание на то, что операторы были указаны в определенном порядке очередности.
Инструмент Калькулятор растра не служит для замены других инструментов дополнительного модуля Spatial Analyst. Используйте другие инструменты для соответствующих вычислений. Например, для вычисления уклона используйте инструмент Уклон. Инструмент Калькулятор растра предназначен для выполнения однострочных алгебраических выражений.
Инструмент Калькулятор растра – это инструмент геообработки и, как все инструменты, может быть интегрирован в ModelBuilder. Более подробную информацию см. в разделах:
Более подробную информацию см. в разделах:
- Что такое ModelBuilder?
- Словарь основных терминов ModelBuilder
- Из чего состоит модель
Окно Python
Окно Python – это эффективное и удобное средство для использования инструментов геообработки и функциональных возможностей Python при работе в ArcGIS. Команды Python, доступные для выполнения в этом окне, могут состоять из одной строки кода или представлять собой сложные блоки кода с использованием логики. Окно Python также предоставляет место для доступа к дополнительным функциональным возможностям с помощью пользовательских или сторонних модулей и библиотек Python.
Чтобы вызвать окно Python, нажмите кнопку Окно Python на панели инструментов Стандартные или выберите окно Python в ниспадающем меню Геообработка.
В вышеприведенной последовательности выражений сначала импортируются пакет сайта ArcPy, параметры среды геообработки и модули из дополнительного модуля Spatial Analyst; задается рабочая область; запускается инструмент Уклон; затем сохраняется результат. После ввода символа возврата каретки в конце выражения оно немедленно выполняется.
После ввода символа возврата каретки в конце выражения оно немедленно выполняется.
Окно Python имеет встроенную функцию автозаполнения строки, позволяет использовать переменные и обеспечивает доступ к функциональности Python и ArcPy.
Интегрированная среда разработки Python
Хотя в окне Python нет ограничения на число вводимых выражений, оно может оказаться неудобным для создания сложных моделей. Вы также можете работать с инструментами, операторами, функциями и классами дополнительного модуля Spatial Analyst в интегрированной среде разработчика, которой вы пользуетесь, например, в PythonWin. Откройте вашу интегрированную среду разработки (ИСР) и введите нужные выражения.
В приведенном ниже скрипте ArcPy импортируются параметры среды геообработки и модуль из Spatial Analyst; задаются переменные; проверяется дополнительный модуль; запускается инструмент Уклон и сохраняется результат.
# Name: Slope # Description: Identifies the rate of maximum change # in z-value from each cell.# Requirements: Spatial Analyst Extension # Import system modules import arcpy from arcpy import env from arcpy.sa import * # Set environment settings env.workspace = "C:/data" # Set local variables inRaster = "elevation" outMeasurement = "DEGREE" zFactor = 0.3043 # Check out the ArcGIS Spatial Analyst extension license arcpy.CheckOutExtension("Spatial") # Execute Slope outSlope = Slope(inRaster, outMeasurement, zFactor) # Save the output outSlope.save("C:/output/outslope02")
Как и окно Python, ИСР обеспечивает доступ ко всей имеющейся функциональности Python и ArcPy.
- Более подробно о создании нового модуля скрипта Python
- Более подробно о написании скриптов Python
Работа с инструментами
Все инструменты дополнительного модуля Spatial Analyst, дающие на выходе растр, доступны в алгебраическом формате. Имя набора данных можно использовать, если он находится в окне Таблица содержания или в текущей рабочей области; в противном случае необходимо ввести полный путь.
# In the following statement, indem is either
# in the TOC or in the current workspace
outRas = Aspect("indem")
# In the following statement the full path is specified
outRas2 = Aspect("C:/Data/indem2")
Результат одного выражения можно вводить в другое, последующее выражение.
outRas = Select("inras", "Value > 105")
# outRas is variable defined by the previous statement and is not quoted
outdist = EucDistance(outRas)
Работа с операторами
Алгебра карт поддерживает ряд операторов (например, +, – и *). Эти же операторы имеются и в Python, но в Алгебре карт они модифицированы для работы с растровыми объектами. Например, в следующем выражении сложение двух чисел дает значение переменной:
# set outVar to 14 using the Python + operator outVar = 5 + 9
Чтобы использовать выражение для растров (то есть, чтобы использовать оператор дополнительного модуля Spatial Analyst), вы должны квалифицировать набор данных как Растр. В приведенном ниже примере оператор + дополнительного модуля Spatial Analyst используется для сложения двух растров:
outRas = Raster("inras1") + Raster("inras2")
Операторы допускают совместное использование растров и чисел. Например, в следующем выражении ко всем ячейкам входного растра прибавляется число 8:
Например, в следующем выражении ко всем ячейкам входного растра прибавляется число 8:
outRas = Raster("inras1") + 8
Создание сложных выражений
В одном выражении можно связать инструменты и операторы. В приведенном ниже примере в каждом выражении выполняется несколько инструментов и операторов:
outRas = Slope("indem" * 2) / 57
outdist = EucDistance(ExtractByAttributes("inras", "Value > 105"))
Для определения последовательности выполнения можно использовать скобки. В двух примерах ниже используются одинаковые операторы, однако результат получается разным из-за добавления в первом примере скобок:
outRas1 = (Raster("inras1") + Raster("inras2")) / Raster("inras3")
and
outRas2 = Raster("inras1") + Raster("inras2") / Raster("inras3")
В первом выражении inras1 складывается с inras2 и сумма делится на inras3. Во втором выражении (без скобок) inras2 делится на inras3, а затем результат деления складывается с inras1.
Если в одном выражении последовательно используются несколько булевых операторов (~, &, ^, |) и/или операторов отношений (<, <=, >, >=, ==, !=), необходимо использовать скобки. Например, скобки необходимы в выражении: (a>2) & (a<5). Если в выражении не использовать скобки, оно приведет к ошибке: a>2 & a<5 . Следующее выражение будет выполнено, потому что есть скобки:
Например, скобки необходимы в выражении: (a>2) & (a<5). Если в выражении не использовать скобки, оно приведет к ошибке: a>2 & a<5 . Следующее выражение будет выполнено, потому что есть скобки:
outRas = (Raster("a") > 2) & (Raster("a") < 5)
Более подробно:
Для некоторых выражений требуются не скобки, а другая форма записи. Например, выражение вида a < b < c не будет выполнено, а добавление скобок изменит его смысл. Поэтому для успешного выполнения это выражение необходимо переписать в виде (a < b) & (b < c).
Использование классов
Классы используются в инструментах Алгебры карт для параметров с несколькими аргументами. Использование классов для входных параметров обеспечивает легкий доступ к отдельным аргументам параметра для запроса, изменения и добавления аргументов. Ниже приведен пример использования класса:
outRas = FocalStatistics("inRaster", NbrCircle(5, "CELL"), "SUM")
В вышеприведенном выражении для каждой ячейки вычисляется сумма пятиячеечной круговой окрестности. NbrCircle – это класс, который создает объект NbrCircle.
NbrCircle – это класс, который создает объект NbrCircle.
Ниже приведен пример класса таблицы перекодировки. В класс перекодировки можно ввести любое число значений.
outReclass = Reclassify("inRaster", "VALUE", RemapRange([[0, 1], [3, 10], [4, 8]]))
В вышеприведенном выражении класс RemapRange используется для переклассификации входных значений. Ячейкам со значениями 0, 3 и 4 в inRaster будут присвоены в outReclass значения 1, 10 и 8 соответственно.
Более подробно об использовании классов в Алгебре карт см. Обзор классов дополнительного модуля ArcGIS Spatial Analyst extension.
Функции Алгебры карт, создающие пространственные объекты, таблицы или файлы
В алгебраическом формате реализованы только те инструменты дополнительного модуля Spatial Analyst, которые дают на выходе растр. Для тех инструментов дополнительного модуля Spatial Analyst, которые дают на выходе результат, отличный от растра (например, пространственные объекты, таблицы или текстовые файлы), результат их выполнения указывается в виде параметра инструмента в скобках.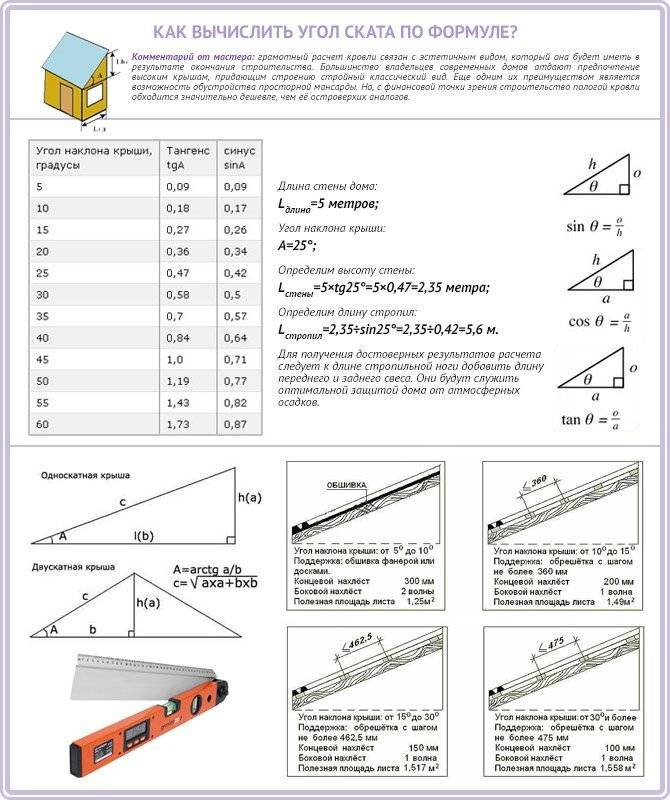 Обратите внимание на синтаксис в следующем примере создания изолиний как выходного набора классов полилинейных объектов:
Обратите внимание на синтаксис в следующем примере создания изолиний как выходного набора классов полилинейных объектов:
indem = "C:/Data/indem" Contour(indem, "C:/output/outcontours")
Рекомендации по выполнению выражений Алгебры карт
Во всех примерах Алгебры карт, приведенных ниже, результатом является Растровый объект. Растровый объект указывает на временный набор растровых данных, который будет удален, если только он не сохранен явно, по окончании сеанса ArcGIS. Чтобы сохранить временный набор данных, для Растрового объекта необходимо вызвать метод save (см. два примера ниже).
Перед использованием инструмента или оператора Алгебры карт рекомендуется задать соответствующие параметры среды анализа, в частности Текущую рабочую область, Экстент, Размер ячейки, Метод проекции размера ячейки и Маску.
- Более подробно о параметрах среды геообработки
Пример параметра среды Рабочая область:
import arcpy from arcpy import env from arcpy.sa import * env.workspace = "C:/sapyexamples/data" outHillshade = Hillshade("elevation", 180, 75, "SHADOWS", 1) outHillshade.save("outhillshd01")
В вышеприведенном выражении задана рабочая область, поэтому outhillshd01 будет сохранен в C:/sapyexamples/data.
Рекомендуется задавать классы для сложных данных на входе инструмента Алгебры карт в виде переменной и использовать в выражении эту переменную. В выражении ниже объект класса RemapRange задан в виде переменной myRemapRange и используется как входные данные для инструмента Переклассификация.
import arcpy
from arcpy import env
from arcpy.sa import *
env.workspace = "C:/sapyexamples/data"
myRemapRange = RemapRange([[-3, 0, 0], [0, 1.75, 25], [1.75, 3.5, 50],
[3.5, 5.25, 75], [5.25, 7, 100]])
outReclassRR = Reclassify("inreclass", "VALUE", myRemapRange)
outReclassRR.save("rclassremran")
Дополнительная литература
Более подробные сведения об ArcPy можно найти в следующих темах:
- Что такое ArcPy?
- Python.
 Краткий обзор
Краткий обзор - Словарь основных терминов Python
Более подробно о геообработке в Python см.
- Как использовать инструменты в Python
- Доступ к лицензированию и дополнительным модулям
- Как использовать классы в Python
- Использование параметров среды
Ссылки на другие источники информации о Python см. на следующей странице:
- Изучение Python
Связанные разделы
Калькулятор уклона
Калькулятор Использование
Наклон линии представляет собой ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как подъем относительно пробега. Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Наклон линии является мерой ее крутизны.
Решения для калькулятора уклона
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби.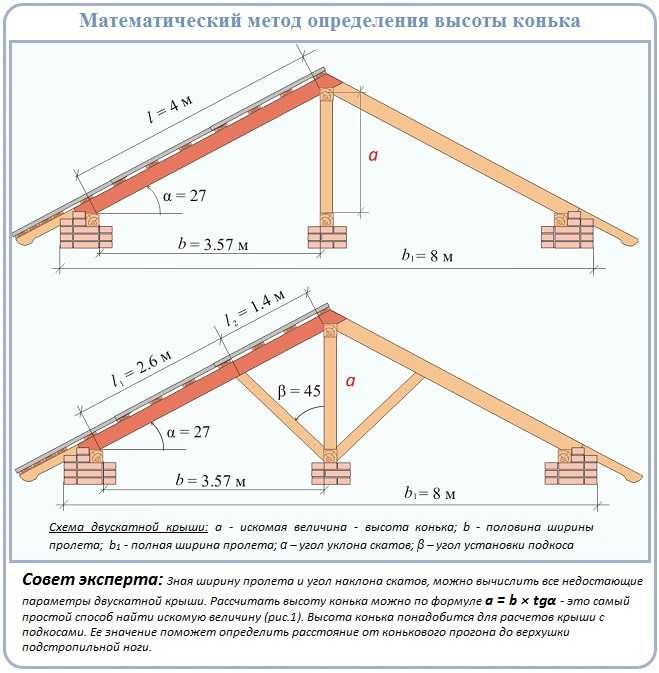 Калькулятор уклона показывает работу и дает следующие решения для уклона:
Калькулятор уклона показывает работу и дает следующие решения для уклона:
- Уклон м с двумя точками
- График линии для y = mx + b
- Форма уклона точки y — y 1 = m(x — x 1 )
- Форма пересечения уклона y = mx + b
- Стандартная форма Ax + By = C
- y-отрезок, когда x = 0
- x-пересечение, когда y = 0
Вам также будет предоставлена настраиваемая ссылка на Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Как рассчитать уклон линии
Рассчитать уклон, м , используя формулу для уклона:
Формула уклона
\[ m = \dfrac {(y_{2} — y_{1})} {(x_{2} — x_{1})} \] \[ m = \dfrac{rise}{run} = \dfrac{ \Delta y}{\Delta x} = \dfrac{y_2 — y_1}{x_2 — x_1} \]
Здесь вам нужно знать координаты 2-х точек на прямой, (x 1 , y 1 ) и (x 2 , y 2 ).
Как найти наклон линии
- Найти разницу между координатами y, Δy — изменение y
- Найдите разницу между координатами x, Δx — это изменение x
- Разделите Δy на Δx, чтобы найти наклон
Δу = у 2 — у 1
Δх = х 2 — х 1
м = Δy/Δx
Пример: Найдите уклон
Допустим, вы знаете две точки на прямой, и их координаты (2, 5) и (9, 19). Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
- Разница между координатами y Δy равна
- Разница между координатами x Δx равна
- Разделите Δy на Δx, чтобы найти уклон м
Δу = у 2 — у 1
Δу = 19 — 5
Δy = 14
Δх = х 2 — х 1
Δx = 9 — 2
Δx = 7
\( m = \dfrac {14} {2} \)
\(m = 7 \)
Уравнения линии с наклоном
Существует 3 распространенных способа записи уравнений линии с наклоном:
- Точечный наклон форма
- Форма пересечения уклона
- Стандартная форма
Точечный уклон формы записывается как
y — y 1 = м (x — x 1 )
Используя координаты одной из точек на линии, вставьте значения в x1 и y1 точек, чтобы получить уравнение линии в форме точечного наклона.
Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы вычислили как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
y — 5 = 7(x — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения уклона записывается как
y = м x + b
Возьмите уравнение формы уклона точки и умножьте его на 7 x и 7 на 2.
y — 5 = 7(x — 2) )
y — 5 = 7x — 14
Продолжайте работать над уравнением так, чтобы y было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме точки пересечения:
y = 7x — 9
Стандартная форма уравнения для линии записывается как
Ax + By = C
Вы также можете увидеть стандартную форму, записанную как Ax + By + C = 0 в некоторых ссылках.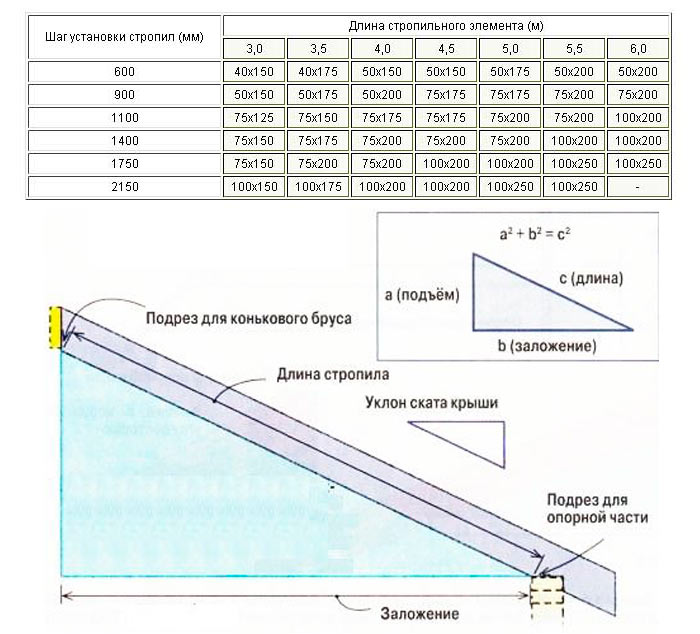
Используйте либо формулу формы точки наклона, либо формулу пересечения наклона и выполните математические вычисления, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Наклон форма перехвата y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Найти наклон по уравнению
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
Пример
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.
Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
- Начните с уравнения 6x — 2y = 12
- Добавьте 2y к обеим сторонам, чтобы получить 6x = 12 + 2y
- Вычтите 12 из обеих частей уравнения, чтобы получить 6x — 12 = 2y
- Вы хотите получить y в одной части уравнения, поэтому вам нужно разделить обе части на 2, чтобы получить y = 3x — 6
- Это форма пересечения наклона, y = 3x — 6.
 Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Как найти точку пересечения с осью y
Точка пересечения с осью y представляет собой значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
y = 3(0) — 6
y = -6
Точка пересечения с осью y равна -6
Как найти точку пересечения с осью x =0. Это точка пересечения прямой с осью x.
Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
x = 2
Пересечение по оси X равно 2
Наклон параллельных прямых
одинаковый наклон, и эти линии никогда не пересекутся.
Наклон перпендикулярных линий
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикуляр означает, что линии образуют угол 90° при пересечении.
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
- Сначала возьмите отрицательный наклон вашей линии
-(-4) = 4 - Во-вторых, возьмите обратное число. 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
- Отрицательная инверсия наклона -4 равна наклону 1/4.
- Линия, перпендикулярная исходной линии, имеет наклон 1/4.
Дальнейшее исследование
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
Калькулятор уклона
В вашем веб-браузере должен быть включен JavaScript
для того, чтобы калькулятор наклона работал.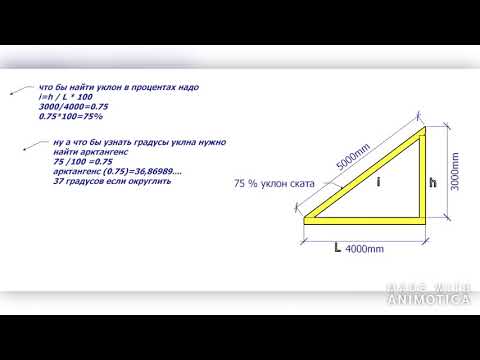
Использование калькулятора уклона
Этот калькулятор наклона берет две точки, а затем использует формулу наклона для вычисления наклона линии, определяемой этими двумя точками, а затем точку пересечения по оси y. Затем наклон и точка пересечения объединяются, чтобы получить уравнение линии в форме точки пересечения наклона («y=mx+b»). График линии рисуется на координатной плоскости вместе с уравнением пересечения наклона.
Калькулятор уклона автоматически обновляет график и уравнение при вводе новых значений точек. Калькулятор также позволяет напрямую вводить значения роста или пробега или десятичное значение m. Калькулятор автоматически создаст правильные десятичные или дробные компоненты для всего, что вы вводите.
Вы также можете рассчитать уравнение для линии, независимо изменив наклон (либо в виде дроби наклона, либо в виде десятичной дроби) или введя новую точку пересечения по оси y. Если введен новый уклон, калькулятор уклона переместит одну из точек, чтобы уравнение соответствовало новой линии. Если введена новая точка пересечения по оси y, наклон останется прежним, но калькулятор переместит две точки, чтобы сместить линию, чтобы она соответствовала новой точке пересечения по оси y.
Если введена новая точка пересечения по оси y, наклон останется прежним, но калькулятор переместит две точки, чтобы сместить линию, чтобы она соответствовала новой точке пересечения по оси y.
Что такое наклон линии?
Наклон линии представляет собой математическое измерение того, насколько крутой выглядит линия, нарисованная на графике, и это значение обычно отображается как переменная m в уравнении в форме пересечения наклона, y=mx+b.
Наклон определяется как отношение изменения по вертикали (по оси Y) к заданной величине изменения по горизонтали (по оси X), часто более просто запоминается как дробь, описывающая подъем по отношению к пробегу или скорость изменения . Этот калькулятор наклона предоставляет это отношение как в виде дроби, так и в виде десятичной дроби, но показывает наклон в виде дроби на графике калькулятора.
Если линия наклонена вверх и вправо, она поднимается, когда вы смотрите слева направо по оси x. Подъем в этом случае положительный, и такая линия будет иметь положительный наклон .
Подъем в этом случае положительный, и такая линия будет иметь положительный наклон .
Если линия наклонена вниз и вправо, она падает, если смотреть слева направо по оси x. Подъем в данном случае отрицательный (линия «падает»), и такая линия будет иметь отрицательный наклон .
Форма пересечения наклона
Когда мы имеем дело с уравнением, описывающим линии (т. е. линейное уравнение ), мы обычно помещаем уравнения в форму, называемую формой пересечения наклона , которая выглядит так…
y = mx + b
Уравнение в этой форме описывает, как координата y для точки на линии вычисляется по координате x. Калькулятор наклона берет указанные вами точки, а затем вычисляет наклон и точку пересечения по оси y, как описано ниже. Эти значения объединяются, и уравнение линии отображается в области графика калькулятора.
Как найти наклон линии
Если у вас есть две точки, они определяют линию в декартовой координатной плоскости, и вы можете использовать эти точки для вычисления наклона линии. Этот калькулятор наклона делает именно то, что использует формулу ниже…
Этот калькулятор наклона делает именно то, что использует формулу ниже…
M =
Rise
Run
=
Y 2 -Y 1
x 2 -x 1
2 -x 1
2 -x 1
x . с двумя точками (x 1 ,y 1 ) и (x 2 ,y 2 ), калькулятор уклона подставляет значения в это уравнение, чтобы рассчитать «подъем» вверху и «пробег» внизу. При выборе между двумя точками не имеет значения, какая точка используется как (x 1 ,y 1 ) или (x 2 ,y 2 ), но очень важно, чтобы вы последовательно использовать соответствующие индивидуальные координаты в пределах каждой точки. Например, если вы выбираете одну точку, такую как (5, 6), обязательно используйте 6 (координата y) в качестве первого члена вычитания «подъема» в верхней части уравнения и 6 в качестве первого члена вычитание «бег» в нижней части уравнения.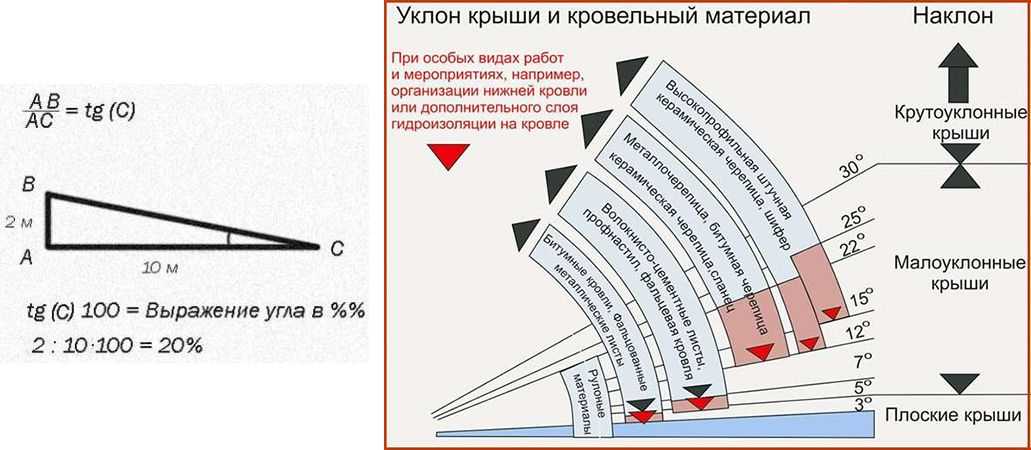 Смешивая отдельные координаты между точками или думая, что есть какая-то конкретная причина выбрать одну точку как (x 1 ,y 1 ) являются распространенными ошибками при расчете уклона. Если вы сомневаетесь, проверьте свой ответ с помощью этого калькулятора наклона, и вы увидите, что это намного проще, чем кажется.
Смешивая отдельные координаты между точками или думая, что есть какая-то конкретная причина выбрать одну точку как (x 1 ,y 1 ) являются распространенными ошибками при расчете уклона. Если вы сомневаетесь, проверьте свой ответ с помощью этого калькулятора наклона, и вы увидите, что это намного проще, чем кажется.
Что такое наклон горизонтальной линии?
Наклон горизонтальной линии равен нулю. В приведенной выше формуле наклона верхний компонент коэффициента наклона показывает вертикальное изменение между двумя точками на линии. Поскольку каждая точка на горизонтальной линии будет иметь одну и ту же координату по оси Y, числитель этой доли наклона всегда будет равен нулю, и, следовательно, вычисленный наклон также всегда будет равен нулю.
Калькулятор наклона рассчитает уравнение прямой без первого члена, эффективно приведя уравнение y=mx+b к форме y=b, отражая, что вычисленная координата y постоянна для любой заданной координаты x.
Каков наклон вертикальной линии?
Как и наклон горизонтальной линии, наклон вертикальной линии особенный. Опять же, обращаясь к уравнению наклона, рассмотрим, как меняются координаты при движении вверх и вниз по вертикальной линии. В случае вертикальной линии координата оси x никогда не изменится для любой заданной координаты оси y. Из-за этого изменение по оси x, представленное как нижний компонент коэффициента наклона, равно нулю.
Опять же, обращаясь к уравнению наклона, рассмотрим, как меняются координаты при движении вверх и вниз по вертикальной линии. В случае вертикальной линии координата оси x никогда не изменится для любой заданной координаты оси y. Из-за этого изменение по оси x, представленное как нижний компонент коэффициента наклона, равно нулю.
Здесь проблема. Уравнение наклона делится на это изменение результата значения x, и деление на ноль не допускается. В результате наклон вертикальной линии не определен, и вы можете легко видеть, что вы не можете вычислить значения y через значения x, используя уравнение в форме пересечения наклона y=mx+b, потому что значение m для наклона не определено, делая все уравнение неопределенным.
Проще говоря, не существует эквивалентного уравнения формы пересечения наклона для вертикальной линии, поэтому нам нужно что-то еще.
Уравнение для вертикальной линии преобразуется калькулятором наклона в форму x=c, где c представляет постоянное значение x, определяющее линию для каждой возможной координаты y.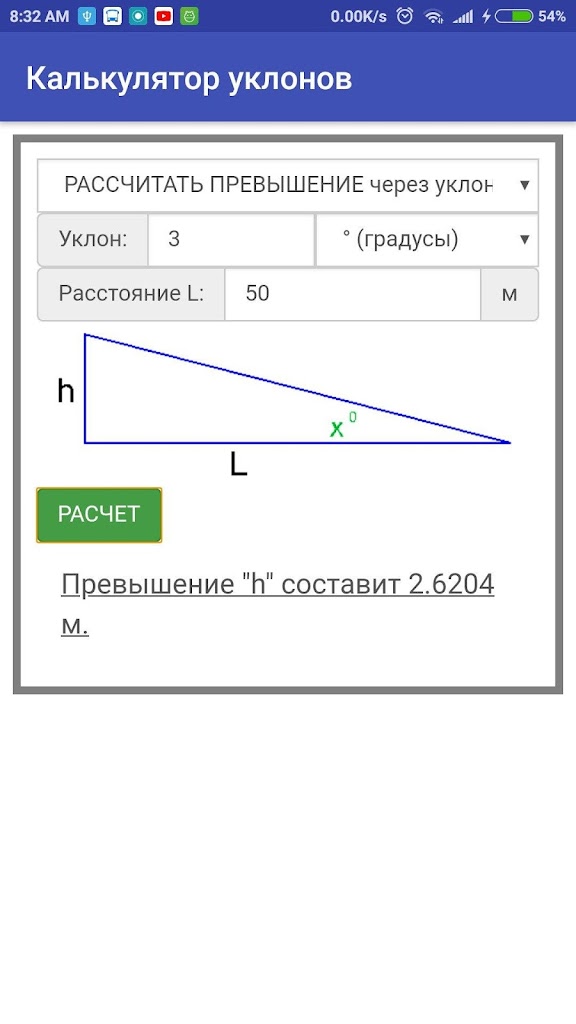
Как найти точку пересечения линии по оси Y
Если у вас есть уравнение линии в форме точки пересечения наклона, найти точку пересечения по оси Y несложно, но понимание того, почему уравнение выделяет точку пересечения, так же важно, как и умение читать это из последнего члена уравнения.
Точка пересечения y — это точка пересечения прямой с осью y. Поскольку каждая точка на оси Y имеет нулевое значение координаты x, уравнение пересечения наклона линии можно использовать для решения для y при нулевом значении x. Это рассчитает значение, в котором линия пересекает ось Y.
Точка пересечения y формально представляет собой пару координат, но поскольку координата x по определению равна нулю, точка пересечения y часто идентифицируется только одним значением (координатой y).
Кроме того, это значение по оси Y является единственным в качестве переменной b в уравнении пересечения наклона y=mx+b. На самом деле, когда линия описывается как уравнение пересечения наклона, значение пересечения y можно считать из последнего члена уравнения.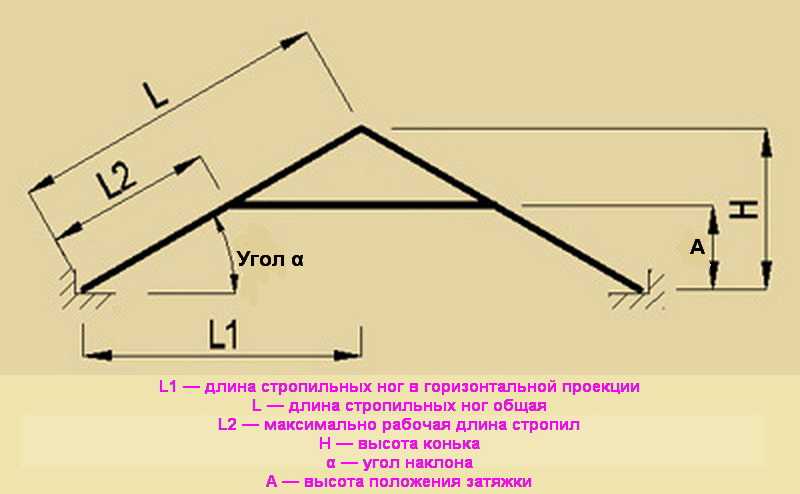
Но что, если у вас нет уравнения прямой и вы только начинаете с точек? Вы можете перетасовать уравнение пересечения наклона, чтобы оно приняло следующую форму:
b = y — mx
Эта формула вычисляет пересечение от наклона и одной точки на линии. Калькулятор уклона использует эту же формулу для нахождения точки пересечения после определения фактического уклона, как описано выше.
Как найти уравнение прямой
Существует два сценария поиска уравнения прямой, оба из которых используются внутри этого калькулятора наклона в зависимости от того, какие значения вы изменяете.
Вышеприведенное обсуждение показывает, как калькулятор находит уклон, используя две точки, используя формулу уклона (расчет «подъем над пробегом»).
Учитывая наклон и хотя бы одну точку, уравнение b=y-mx используется для нахождения точки пересечения.
После вычисления точки пересечения и наклона имеются все части, необходимые для создания уравнения в форме точки пересечения наклона. Уравнение пересечения наклона для линии показано на графике калькулятора в одном из квадрантов, не пересекаемых линией.
Уравнение пересечения наклона для линии показано на графике калькулятора в одном из квадрантов, не пересекаемых линией.
Координатная плоскость для печати
Обновления калькулятора уклона
| Дата | Описание |
|---|---|
| 16.04.2019 | Начальная версия калькулятора уклона. |
| 21.04.2019 | Исправлены сообщения об ошибках в графике калькулятора уклона. |
| 22.04.2019 | Расширенные инструкции калькулятора. |
| 24.04.2019 | В график калькулятора уклона добавлена шкала превышения пробега. |
| 29.04.2019 | В описание калькулятора добавлены изображения. |
| 14.04.2021 | Исправлены мобильные поля в уравнении пересечения y. |
Калькулятор уклона / Поиск уклона — [100% бесплатно]
Используйте калькулятор уклона, чтобы узнать формулу линии для любых двух заданных точек, через которые проходит линия. Вы также используете искатель наклона для определения коэффициентов наклона, точки пересечения по оси Y и точки пересечения по оси X с помощью формул наклона. Давайте рассмотрим, как использовать этот калькулятор, определение уклона и многое другое.
Вы также используете искатель наклона для определения коэффициентов наклона, точки пересечения по оси Y и точки пересечения по оси X с помощью формул наклона. Давайте рассмотрим, как использовать этот калькулятор, определение уклона и многое другое.
Загрузка калькулятора…
Содержание
Как пользоваться калькулятором уклона?
Хотя формула уклона может вызвать у вас чувство ошеломления или замешательства, этот калькулятор уклона является полной противоположностью. Это простой онлайн-инструмент, который вы можете использовать для определения наклона путем ввода определенных значений. Вот шаги, которые нужно выполнить для этого калькулятора уклона точки:
- Сначала введите значение X1 .
- Затем введите значение У1 .
- Далее введите значение X2 .
- Наконец, введите значение Y2 .
- После ввода всех необходимых значений этот калькулятор линейного уклона автоматически генерирует нужные вам значения, включая наклон, угол, расстояние и значения Δx и Δy .

Что такое уклон?
Прежде чем использовать этот калькулятор уклона или определитель уклона, важно понять, что такое уклон. Вы можете математически описать любую заданную линию на плоской плоскости как отношение между ось х (горизонтальная) и ось у (вертикальная) положения каждой из точек, составляющих линию.
Вы можете записать эту связь как y = [что-то с x] . Конкретная форма «[что-то с x]» определяет тип линии, которая у вас есть. Например:
- Если у вас есть y = x² + x , это означает, что у вас есть парабола, которая также известна как квадратичная функция.
- Если у вас y = mx + b где m и b представляют любые заданные числа, это означает, что у вас есть прямая линия.
Этот калькулятор наклона линии выполняет вычисления только для прямых линий. Но если вы хотите узнать больше о параболе и параболической функции, вы можете использовать онлайн-калькуляторы и изучить квадратичную формулу, чтобы лучше понять ее.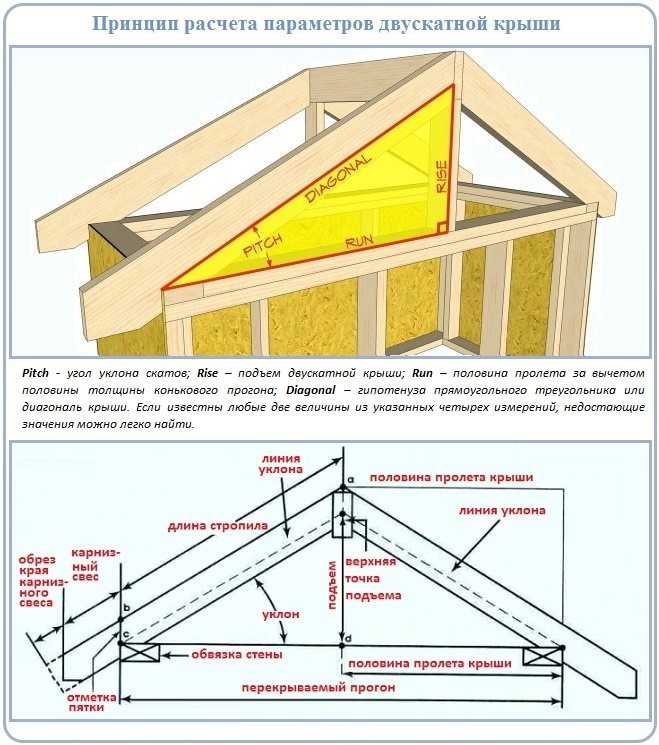
Возвращаясь к прямым линиям, вы можете легко распознать прямые или линейные уравнения, поскольку они не имеют членов с показателями степени. Например, вы можете найти y терм или x терм , но вы никогда не найдете ни y2 , ни x2 терма.
Каждая линейная формула описывает прямые линии, и вы можете выразить их с помощью уравнения формы пересечения наклона. Как мы уже говорили в предыдущем примере, вы можете записать формулу любой заданной строки в виде:
y = mx + b.
Это то, что известно как «форма пересечения наклона». Это очень важная формула, потому что она предоставляет вам две важные части информации, а именно точку пересечения линии по оси y и наклон m. Позже вы можете использовать эти значения, когда вам нужно выполнить линейную интерполяцию.
Слово «наклон» относится к градиенту или наклону любой заданной линии.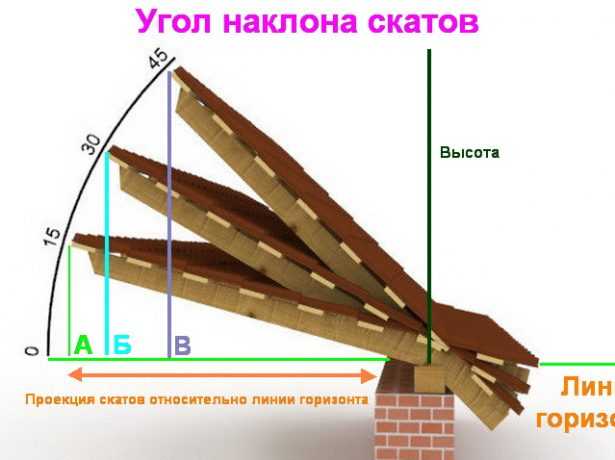 Он говорит вам, сколько изменений вы можете ожидать от y , когда фиксированное изменение происходит в x . Если есть положительное изменение, значения у увеличиваются вместе с значениями х. Если есть отрицательное изменение, значения y уменьшаются вместе с значениями x .
Он говорит вам, сколько изменений вы можете ожидать от y , когда фиксированное изменение происходит в x . Если есть положительное изменение, значения у увеличиваются вместе с значениями х. Если есть отрицательное изменение, значения y уменьшаются вместе с значениями x .
Пересечение с осью y относится к значению y, при котором данная линия пересекает ось y. Чтобы вычислить его, вы должны заменить x на ноль в своем линейном уравнении.
Как найти уклон?
Итак, как найти уклон без использования калькулятора уклона? Для этого предположим, что вы уже знаете точки, через которые проходит заданная вами линия. Первая точка имеет координаты (x₁, y₁) , а вторая точка имеет координаты (x₂, y₂) . В этом примере вы решаете точку пересечения по оси Y и наклон.
Первым шагом является подстановка координат обеих точек в уравнение для пересечения наклона:
для первой точки: y₁ = mx₁ + b
для второй точки: y₂ = mx₂ + b
Следующим шагом является вычитание вашего первого уравнения из второго уравнения y₂ – y₁ = m(x₂ – x₁) На последнем шаге найдите наклон, разделив обе части уравнения на (x₂ – x₁): )/(x₂ – x₁) После решения для наклона вы можете подставить значение в первое или второе уравнение. y₁ = x₁(y₂ – y₁)/(x₂ – x₁) + b С помощью этого калькулятора уклона точки вы можете найти уравнение любой заданной линии в форме пересечения уклона. Просто введите требуемые значения точек, через которые проходит линия. Конечно, вы также можете выполнить расчет вручную без использования калькулятора уклона. Вот шаги:  Сделайте это, чтобы найти точку пересечения y:
Сделайте это, чтобы найти точку пересечения y:
b = y₁ – x₁(y₂ – y₁) –/ x(y₂ – y₁) ) Как найти наклон линии?
м = (y₂ – y₁)/(x₂ – x₁) = (3-1)/(2-1) = 2/ 1 = 2.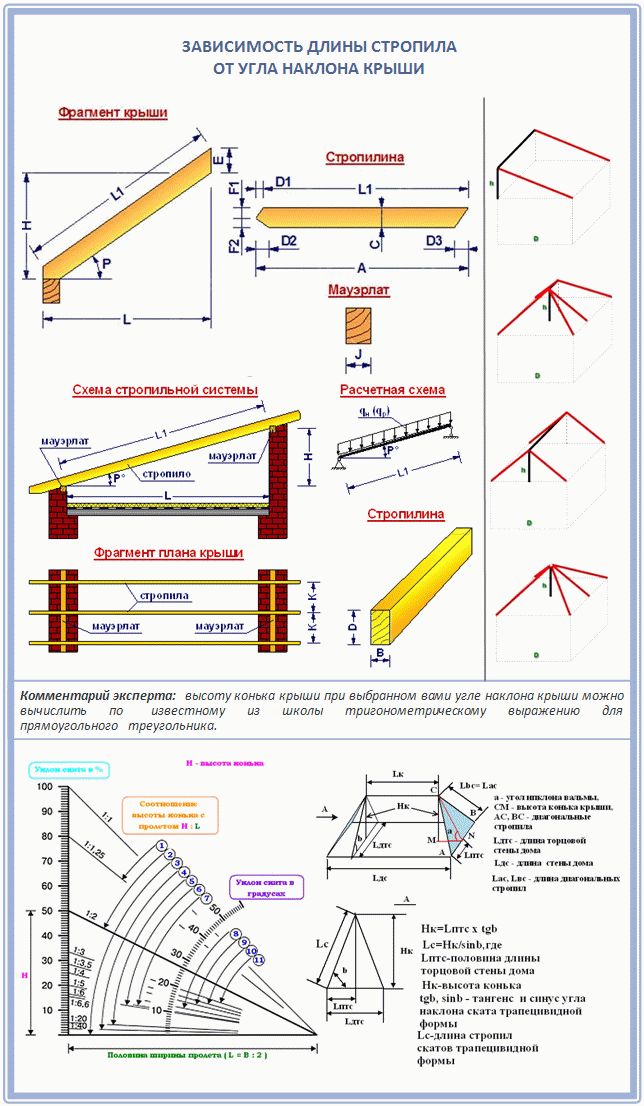

 Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
 Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.
Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.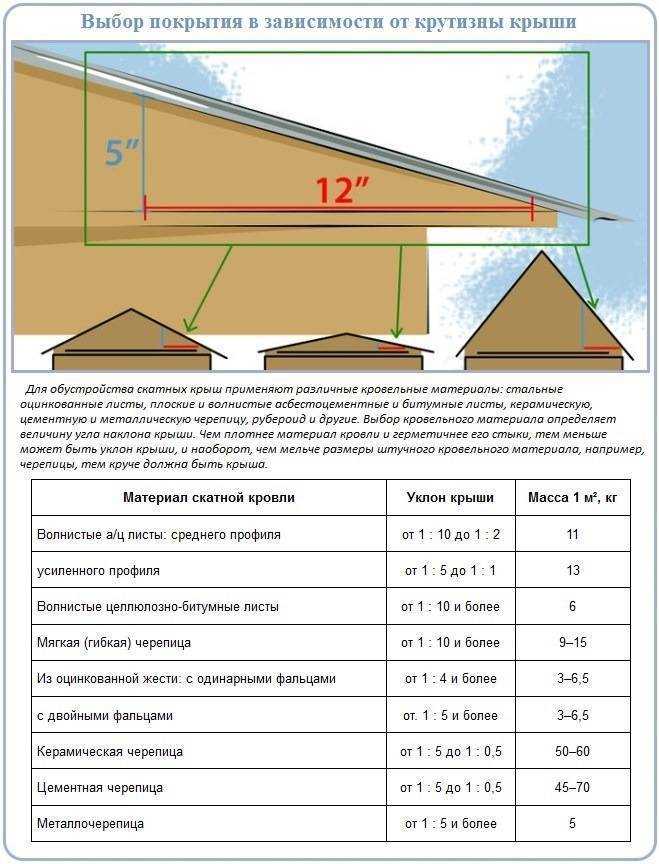




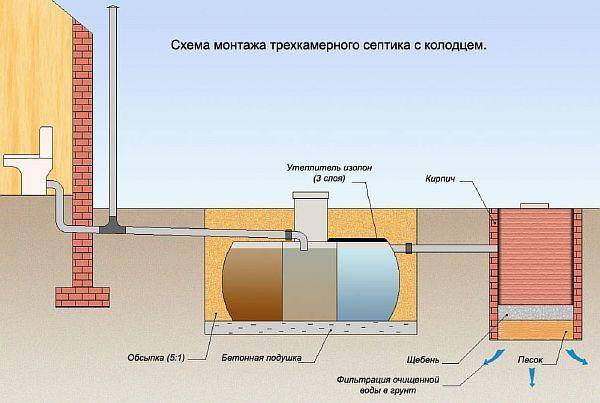 В нашем калькуляторе используются две последние формулы.
В нашем калькуляторе используются две последние формулы. рисунок выше). Если известен уклон, то угол наклона можно определить по формуле
рисунок выше). Если известен уклон, то угол наклона можно определить по формуле
 Движущийся вниз автомобиль не может быть остановлен и будет двигаться вниз с постоянным ускорением.
Движущийся вниз автомобиль не может быть остановлен и будет двигаться вниз с постоянным ускорением.