Трехфазные электрические цепи (Лекция №16)
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
- фаза как аргумент синусоидально изменяющейся величины;
- фаза как составная часть многофазной электрической системы.
Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений.
Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.
Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на рад. (см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
— экономичность передачи электроэнергии на большие расстояния;
— самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
— возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
— уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
Система ЭДС (напряжений, токов и т.д.) называется симметричной, если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3.
| Рис.3 | Рис.4 |
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4).
Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются
Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.
Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.
Схемы соединения трехфазных систем
Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 120°. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике.
Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных, к линии — линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; — фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
| ; | (1) |
| (2) |
| . | (3) |
Отметим, что всегда — как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае
| (4) |
Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фаз фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; .
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
.
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| . | (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой принцип действия у трехфазного генератора?
- В чем заключаются основные преимущества трехфазных систем?
- Какие системы обладают свойством уравновешенности, в чем оно выражается?
- Какие существуют схемы соединения в трехфазных цепях?
- Какие соотношения между фазными и линейными величинами имеют место при соединении в звезду и в треугольник?
- Что будет, если поменять местами начало и конец одной из фаз генератора при соединении в треугольник, и почему?
- Определите комплексы линейных напряжений, если при соединении фаз генератора в звезду начало и конец обмотки фазы С поменяли местами.
- На диаграмме на рис. 10 (трехфазная система токов симметрична) . Определить комплексы остальных фазных и линейных токов.
- Какие схемы соединения обеспечивают автономность работы фаз нагрузки?
Соединение в треугольник. Схема, определения
Соединение в звезду. Схема, определения
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.
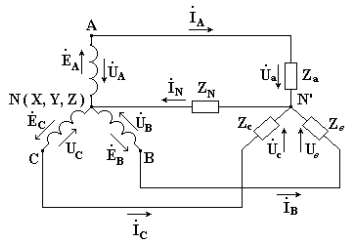
Рис. 7.1
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N’ называют нейтральным (нулевым) проводом.
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.
Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах — линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.
Iл = Iф.
ZN — сопротивление нейтрального провода.
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений
 (7.1)
(7.1)
На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
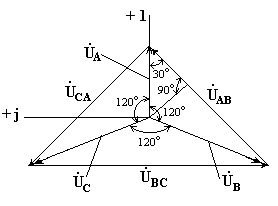
Рис. 7.2
Из векторной диаграммы видно, что
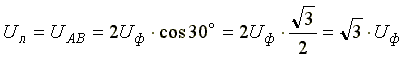
При симметричной системе ЭДС источника линейное напряжение больше фазного
в √3 раз.
Uл = √3 Uф
Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.
На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно
из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.
Uл = Uф
IA, IB, IC — линейные токи;
Iab, Ibc, Ica— фазные токи.
Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.


Рис. 7.3
Линейный ток равен геометрической разности соответствующих фазных токов.
На рис. 7.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.
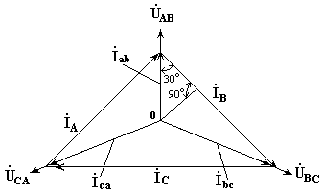
Рис. 7.4
Из векторной диаграммы видно, что
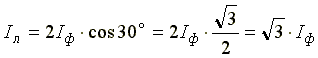 ,
,
Iл = √3 Iф при симметричной нагрузке.
Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме «звезда». Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.
Трехфазную цепь, соединенную звездой, удобнее всего рассчитать методом двух узлов.
На рис. 7.5 изображена трехфазная цепь при соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы (ZA ≠ ZB ≠ ZC )
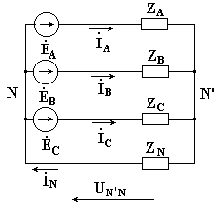 Нейтральный провод имеет конечное сопротивление ZN .
Нейтральный провод имеет конечное сопротивление ZN .
В схеме между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали.
Это напряжение определяется по формуле (7.2).
Рис.7.5
 (7.2)
(7.2)
Фазные токи определяются по формулам (в соответствии с законом Ома для активной ветви):
 (7.3)
(7.3)
Ток в нейтральном проводе
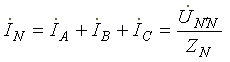 (7.4)
(7.4)
Частные случаи.
1. Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению ZA = ZB = ZC = R.
Узловое напряжение
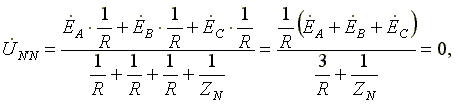 ,
,
потому что трехфазная система ЭДС симметрична, 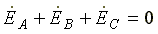 .
.
Напряжения фаз нагрузки и генератора одинаковы:
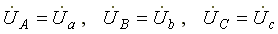
Фазные токи одинаковы по величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует
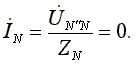
В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.
На рис. 7.6 изображена векторная диаграмма трехфазной цепи для симметричной нагрузки.
2. Нагрузка несимметричная, RA< RB = RC, но сопротивление нейтрального провода равно нулю: ZN = 0. Напряжение смещения нейтрали
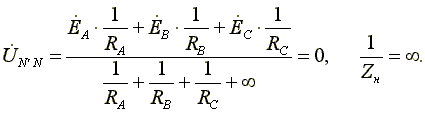
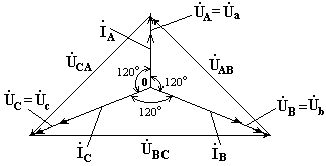
рис. 7.6
Фазные напряжения нагрузки и генератора одинаковы
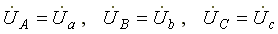
Фазные токи определяются по формулам
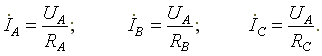
Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.
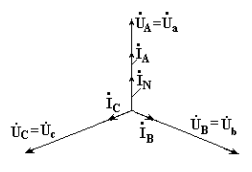 На рис. 7.7 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.
На рис. 7.7 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.
Рис. 7.7
3. Нагрузка несимметричная, RA< RB = RC, нейтральный провод отсутствует,
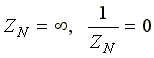
В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:
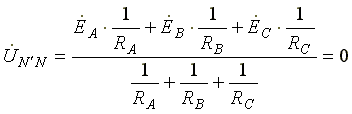
Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.
Из-за напряжения смещения нейтрали фазные напряжения нагрузки становятся неодинаковыми.
Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.
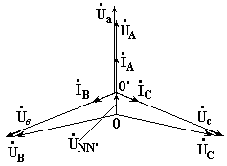 На рис. 7.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми.
На рис. 7.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми.
Рис. 7.8
Цель работы. Исследовать электрическую цепь трехфазного переменного тока, содержащую приемник электрической энергии, соединенный по схеме «звезда» с нулевым (нейтральным) проводом и без него.
Краткие теоретические сведения
Трехфазная симметричная система ЭДС состоит из трех ЭДС, одинаковых по амплитуде и частоте, но сдвинутых друг относительно друга на 120º.
При соединении «звездой» концы обмоток фаз генератора X, Y, Z соединяют в одну общую точку N , называемую нейтральной или нулевой. К началам фаз генератора А, В, С подключают провода, с помощью которых источник питания (генератор) соединяется с приемником. Эти провода называются линейными, а трехфазная система – трехпроводной (рис.20).
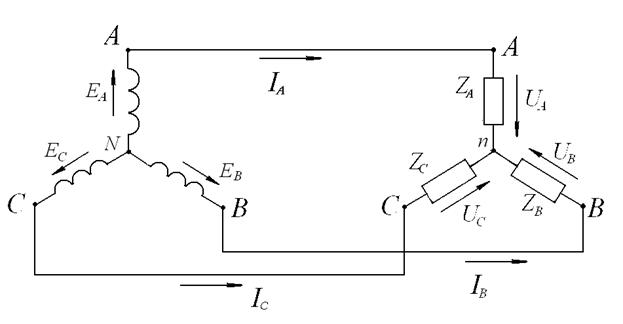
Рис.20. Трехпроводная система трехфазного переменного тока (соединение по схеме «звезда»).
Если нейтральная (нулевая) точка N генератора соединена проводом с нейтральной (нулевой) точкой n приемника, то система называется четырехпроводной с нулевым (нейтральным) проводом (рис.19).

Рис.21. Четырехпроводная система трехфазного переменного тока с нулевым (нейтральным) проводом (соединение по схеме «звезда»).
При соединении «звездой» каждая фаза генератора, линейный провод и фаза нагрузки соединены между собой последовательно и через них проходит один и тот же ток. Следовательно, при соединении «звездой» линейный ток равен фазному, т.е.
IЛ = IФ . (36)
Напряжения между началом и концом каждой фазы нагрузки  А,
А, 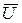 В,
В,  С, равные (при пренебрежении падением напряжения в проводах) напряжениям на фазах генератора, называются фазными напряжениями. Напряжения между линейными проводами
С, равные (при пренебрежении падением напряжения в проводах) напряжениям на фазах генератора, называются фазными напряжениями. Напряжения между линейными проводами  AB,
AB,  BC,
BC, 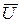 CA называются линейными напряжениями. Токи, протекающие в фазах нагрузки
CA называются линейными напряжениями. Токи, протекающие в фазах нагрузки  A,
A,  B,
B,  C, называются фазными токами. Для системы «звезда» линейные токи одни и те же с фазными
C, называются фазными токами. Для системы «звезда» линейные токи одни и те же с фазными  Л =
Л =  Ф.
Ф.
По второму закону Кирхгофа можно определить соотношения между фазными и линейными напряжениями
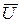 AB =
AB = 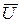 A −
A − 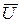 B
B
 BC =
BC =  B −
B −  C (37)
C (37)
 CA =
CA =  C −
C −  A
A
Так как трехфазная система генератора симметрична, то действующие значения ЭДС генератора равны между собой и равны действующим значениям на нагрузке при пренебрежении падением напряжения в линии  A =
A =  B =
B =  C =
C =  A =
A =  B =
B =  C =
C =  Ф .
Ф .
ЕA = ЕB = ЕC = UA = U B = U C = U Ф .
Исходя из равенства угла сдвига между фазами 120 на генераторе и нагрузке и выведенных из второго закона Кирхгофа уравнений (37), равны между собой и действующие значения линейных напряжений
UAB = UBC = UCA = UЛ .
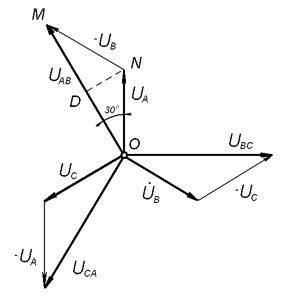
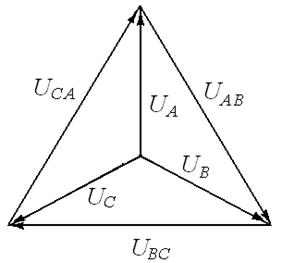
Векторная диаграмма фазных и линейных напряжений (рис.20) будет для симметричного генератора и четырехпроводной системы «звезда» неизменна при любой нагрузке. На рис.20а приведена полярная, а на рис. 20б – топографичекая векторная диаграмма.
| 
|
| а) | б) |
Рис.22. Полярная и топографическая векторные диаграммы напряжений в четырехпроводной системе «звезда»
Из векторной диаграммы (рис.20а) получим соотношение между линейными и фазными напряжениями.
UAB = 2UА ∙ cos 30º =  UА =
UА = 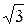 UФ.
UФ.
В общем случае для четырехпроводной системы «звезда» при любой нагрузке
UЛ =  UФ . (38)
UФ . (38)
К симметричному трехфазному генератору с нейтральным проводом может быть присоединена любая симметричная и несимметричная нагрузка. Нагрузка называется симметричной, если сопротивления и углы сдвига фаз между напряжением и током всех ее фаз одинаковы
ZA = ZB = ZC , φA = φB = φC. (39)
Несоблюдение любого из условий (39) приведет к нарушению симметричности нагрузки трехфазной системы.
Рассмотрим четырехпроводную трехфазную систему с нагрузкой, соединенной по схеме «звезда».
1) Симметричная активная нагрузка: ZA = ZB = ZC = RA = RB = RC
IA = 
IB = 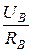
IC = 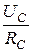
Так как UA = UB = UC = UФ =  , то
, то
IA = IB = IC = IФ =  =
=  (40)
(40)
Топографическая векторная диаграмма токов и напряжений при симметричной активной нагрузке представлена на рис.21.
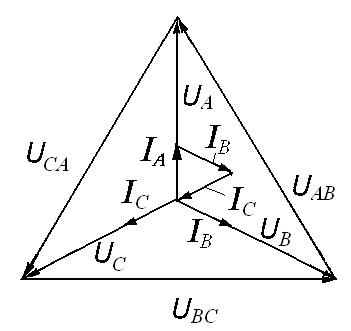
Рис.23. Топографическая векторная диаграмма четырехпроводной трехфазной системы «звезда» при симметричной активной нагрузке
По первому закону Кирхгофа
 A +
A +  B +
B +  C =
C =  N .
N .
Для симметричной нагрузки
 N = 0.
N = 0.
2) Несимметричная активная нагрузка: ZA = RA ; ZB = RB ; ZC = RC ; RA ≠ RB ≠ RC ; IA ≠ IB ≠ IC
 A =
A =  IA =
IA =  =
= 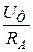 =
=  ;
;
 B =
B =  IB =
IB =  =
=  =
= 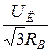 ; (41)
; (41)
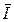 C =
C = 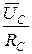 IC =
IC =  =
=  =
=  ;
;
 N =
N =  A +
A +  B +
B +  C . (42)
C . (42)
Топографическая векторная диаграмма токов и напряжений при несимметричной нагрузке представлена на рис.22

Рис.24. Топографическая векторная диаграмма четырехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке
Для нахождения значения тока IN по выражению (42) необходимо найти геометрическую сумму векторов  A ,
A ,  B и
B и  C (рис.22). В результате получаем
C (рис.22). В результате получаем
IN =  (43)
(43)
Общая мощность трехфазной цепи в этом случае будет равна
P =  (44)
(44)
Трехпроводная трехфазная система с соединением нагрузки по схеме «звезда» без нулевого (нейтрального) провода (рис.20).
Рассмотрим, что произойдет с токами и напряжениями при отключении нейтрального провода (рис.20).
В трехпроводной системе, соединенной по схеме «звезда» между нулевой точкой нагрузки и нулевой точкой генератора возникает напряжение UnN , величина и направление которого зависят от величины и характера нагрузки.
Согласно методу двух узлов в случае активной нагрузки напряжение UnN, можно выразить следующим образом
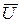 nN =
nN = 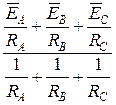 . (45)
. (45)
Составим уравнения по второму закону Кирхгофа
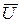 nN =
nN =  −
− 
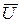 nN =
nN =  −
− 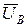 (46)
(46)
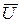 nN =
nN = 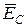 −
− 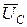
Откуда
 =
=  −
− 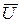 nN
nN
 =
= 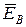 −
− 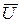 nN (47)
nN (47)
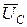 =
=  −
− 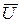 nN .
nN .
Токи в фазах нагрузки определяются
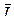 A =
A = 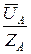 =
= 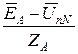
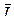 B =
B = 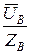 =
= 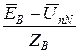 (48)
(48)
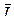 C =
C = 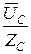 =
= 
Проанализируем электрическое состояние трехпроводной трехфазной системы, соединенной по схеме «звезда», при различных значениях нагрузки.
1) Симметричная активная нагрузка: ZA = ZB = ZC = RA = RB = RC
 =
= 
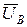 =
= 
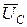 =
= 
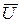 nN = 0
nN = 0
 =
=  =
= 
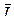 A =
A =  IA =
IA = 
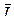 B =
B =  IB =
IB = 
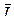 C =
C = 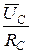 IC =
IC = 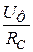
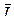 A +
A + 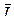 B +
B + 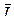 C =
C = 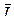 N = 0
N = 0
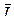 A =
A = 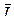 B =
B = 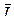 C =
C = 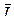 Ф .
Ф .
Векторная диаграмма токов и напряжений приведена на рис.25.
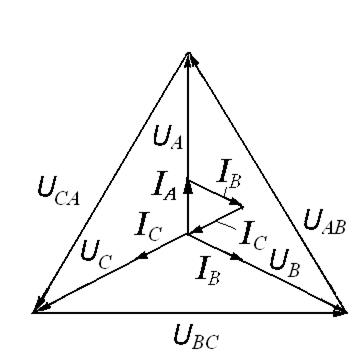
Рис.25. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при симметричной активной нагрузке
Векторная диаграмма аналогична диаграмме, построенной для четырехпроводной системы с симметричной активной нагрузкой. Подобным образом аналогична диаграмма для симметричной активно-реактивной нагрузки, поэтому при симметричной нагрузке отпадает необходимость нулевого провода, т.к. ток в нем равен нулю.
2) Несимметричная активная нагрузка: ZA = RA ; ZB = RB ; ZC = RC ; RA ≠ RB ≠ RC ; IA ≠ IB ≠ IC
При отключении нейтрального провода ток I0 становится равным нулю, следовательно, при несимметричной нагрузке должны измениться и токи IA , IB , IC. изменение же этих токов может произойти только при условии, что изменились напряжения на фазах нагрузки. Следовательно, фазные напряжения нагрузки теперь не будут представлять симметричную систему векторов, т.к. действующие значения этих напряжений не будут равны между собой, а их фазовый сдвиг относительно друг друга будет отличаться от 120º (рис.26).

Рис.26. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке
Нулевая точка нагрузки n смещена относительно нулевой точки генератора N.
Из рис.25 видно, что напряжения на фазах нагрузки определяются как
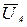 =
=  −
−  nN
nN
 =
=  −
− 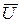 nN
nN
 =
=  −
− 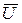 nN .
nN .
что соответствует выражению (47)
Проведя геометрическое сложение векторов  ,
, 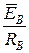 ,
,  и разделив полученный результат на значение проводимости Y =
и разделив полученный результат на значение проводимости Y = 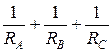 , в соответствии с выражением (45), получаем вектор
, в соответствии с выражением (45), получаем вектор 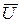 nN.
nN.
Вычитая полученный результат из векторов  ,
, 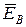 , и
, и  , находим соответственно
, находим соответственно 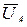 ,
,  и
и  .
.
В результате получаем выражения для расчета действующих значений фазных напряжений UA, UВ, UС и токов IA, IВ, IС.
UА = UЛ ∙  ; IA =
; IA = 
UВ = UЛ ∙ 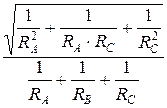 ; IВ =
; IВ = 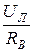
UС = UЛ ∙  ; IС =
; IС =  (49)
(49)
Для измерения мощности в работе используется метод двух ваттметров W1 и W2 (рис.27).

Рис.27. Схема измерения мощности методом двух ваттметров
Поясним принцип работы этого метода.
Приборы для измерения активной мощности (ваттметры), включенные в цепь однофазного переменного тока, измеряют величину
Р = U ∙ I ∙ cos (U ^ I) , (50)
где U — напряжение, приложенное к обмотке напряжения ваттметра;
I — ток, протекающий по токовой обмотке ваттметра;
U ^ I = φ — угол сдвига между напряжением и током.
Активная мощность трехфазной цепи при симметричной нагрузке фаз может быть выражена двумя равноценными формулами
Р = 3∙UФ ∙ IФ ∙ cos φ или
Р = 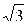 ∙UЛ ∙ IФ ∙ cos φ . (51)
∙UЛ ∙ IФ ∙ cos φ . (51)
Для измерения активной мощности в трехпроводных цепях трехфазного тока как при симметричной, так и при несимметричной нагрузке фаз (независимо от способа соединения нагрузки «звездой» или «треугольником»), широкое практическое применение получил метод двух ваттметров, включенных как показано на рис.14.
Показания ваттметров W1 и W2 можно записать следующим образом
Р1 = UАВ ∙ IA ∙ cos (UAB ^ IA)
Р2 = UСВ ∙ IC ∙ cos (UCB ^ IC) (52)
Обозначим через α и β соответственно углы (UAB ^ IA) и (UCB ^ IC) . Для определения α и β построим векторную диаграмму для случая симметричной активно-индуктивной нагрузки (рис.27). Согласно построению α = 30º + φ, β = 30º – φ.
Учитывая, что при симметричной нагрузке UАВ = UСВ = UЛ и IА = IС = IЛ, показания ваттметров можно записать следующим образом:
Р = Р1 + Р2 = UЛ ∙ IЛ ∙ [cos (30º + φ) + cos (30º – φ)] = 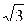 UЛ ∙ IЛ ∙ cos φ. (53)
UЛ ∙ IЛ ∙ cos φ. (53)
Полученное выражение совпадает с выражением (45). Таким образом доказано, что сумма показаний двух ваттметров будет равна активной мощности трехфазной цепи.

Рис.28. Векторная диаграмма трехпроводной системы трехфазного переменного тока с симметричной активно-индуктивной нагрузкой
Разность показаний двух ваттметров, умноженная на  , будет равна реактивной мощности цепи Q.
, будет равна реактивной мощности цепи Q.
Q = 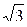 ( Р1 – Р2) =
( Р1 – Р2) = 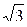 UЛ ∙ IЛ ∙ [cos (30º + φ) – cos (30º – φ)] =
UЛ ∙ IЛ ∙ [cos (30º + φ) – cos (30º – φ)] =  UЛ ∙ IЛ ∙sin φ. (54)
UЛ ∙ IЛ ∙sin φ. (54)
Показания каждого из ваттметров в отдельности не имеют никакого физического смысла, за исключением случая симметричной и чисто активной нагрузки, при которой Р1 = Р2 и составляет половину измеряемой мощности трехфазной цепи.
ПЛАН РАБОТЫ
Задание 1. Определить электрические параметры четырехпроводной трехфазной цепи при симметричной и несимметричной нагрузке, соединенной по схеме «звезда» с нулевым (нейтральным) проводом.
1. Собрать электрическую схему (рис.29).
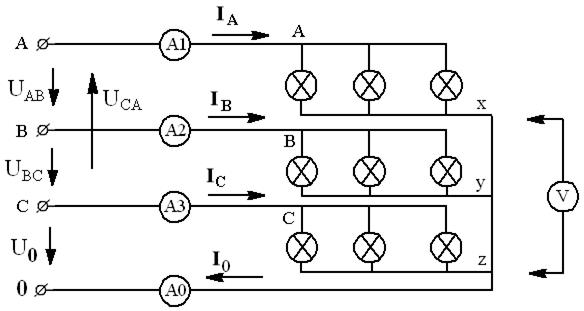
Рис.29. Схема лабораторной установки: А-х, В-y, C-z — трехфазный ламповый реостат, установленный на стенде; А1 — амперметр на ток 1–2 А; А2, А3, А0 — амперметры на ток 0,25–0,5–1 А; V – вольтметр на 75-150-300-600 В.
2. Установить симметричную нагрузку фаз, включив по пять ламп в каждой фазе, и измерить IA, IB, IC, IN, UA, UB, UC, UAB, UBC, UCA.
3. Установить несимметричную нагрузку фаз, включив 5 ламп в фазе А, 4 лампы в фазе «В» и 3 лампы в фазе «С» и осуществить измерения электрических параметров, указанных в п.2.
4. Вычислить электрические параметры, указанные в табл.7.
5. занести результаты измерений и вычислений в табл.7.
Задание 2. Определить электрические параметры трехпроводной трехфазной цепи при симметричной и несимметричной нагрузке, соединенной по схеме «звезда» без нулевого (нейтрального) провода.
1. Собрать электрическую схему (рис.30).

Рис.30. Схема лабораторной установки: А-х, В-y, C-z — трехфазный ламповый реостат, установленный на стенде; А1 — амперметр на ток 1–2 А; А2, А3 — амперметры на ток 0,25–0,5–1 А; V – вольтметр на 75-150-300-600 В; W1 и W2 — ваттметры на напряжение 75−150−300−600 В и ток 1−2,5−5 А.
2. Установить симметричную нагрузку, включив по пять ламп в каждой фазе, и измерить линейные и фазные напряжения, фазные токи, активные мощности.
3. Установить несимметричную нагрузку фаз, включив 5 ламп в фазе А, 4 лампы в фазе «В» и 3 лампы в фазе «С» и измерить электрические параметры, указанные в п.2.
4. Вычислить электрические параметры, указанные в табл.8.
5. Занести результаты измерений и вычислений в табл.8.
Содержание отчета.
1. Схемы измерений (рис.29 и 30) с обозначениями используемых приборов.
2. Расчет электрических параметров.
3. Таблицы 7 и 8 с результатами измерений и вычислений.
4. Построенные в масштабе топографические векторные диаграммы (две к заданию 1 по данным п.1-2 табл.7 в соответствии с рис. 21 и 22 и две к заданию 2 по данным пп.1-2 табл.8 в соответствии с рис. 24 и 25.
Таблица 7
Измеренные величины | Вычисленные величины | |||||||||||||
| IA | IВ | IС | I0 | UA | UВ | UС | UAВ | UВС | UСА | UЛ/ UФ | РА | РВ | РС | Р |
| А | А | А | А | В | В | В | В | В | В | В | Вт | Вт | Вт | Вт |
| 0,6 | 0,6 | 0,6 | 0 | 228 | 220 | 220 | 380 | 380 | 380 | |||||
| 0,6 | 0,45 | 0,35 | 0,21 | 228 | 220 | 220 | 380 | 380 | 380 | |||||
Таблица 8
Измеренные величины
| Вычисленные величины | |||||||||||||||
| IA | IВ | IС | UA | UВ | UС | UAВ | UВС | UСА | Р1(W1) | Р2(W2) | UЛ/ UФ | РА | РВ | РС | Ррасч | Р(W1+W2) |
| А | А | А | В | В | В | В | В | В | Вт | Вт | В | Вт | Вт | Вт | Вт | Вт |
| 0,6 | 0,6 | 0,6 | 220 | 220 | 220 | 380 | 380 | 380 | 200 | 200 | ||||||
| 0,525 | 0,475 | 0,375 | 193 | 226 | 260 | 380 | 380 | 380 | 190 | 120 | ||||||
Контрольные вопросы
1. Как относятся друг с другом ЭДС, составляющие трехфазную систему?
2. Как соединяются обмотки генератора при соединении «звездой»?
3. Чем отличается схема четырехпроводной системы трехфазного тока от схемы трехпроводной системы?
4. Что соединяет нулевой (нейтральный) провод?
5. Что такое линейные и фазные токи и напряжения и каковы соотношения между ними при соединении звездой в векторной форме?
6. Как связаны линейные и фазные напряжения в четырехпроводной системе трехфазного тока?
7. Что такое симметричная и несимметричная нагрузка?
8. Чему равна геометрическая сумма токов в четырехпроводной трехфазной системе при симметричной нагрузке?
9. Чему равен ток в нулевом проводе при симметричной нагрузке?
10. отличаются ли токи и напряжения в четырехпроводной и трехпроводной системах трехфазного тока при одинаковой симметричной нагрузке?
11. При какой нагрузке необходимо включить в трехфазную систему нулевой провод и зачем?
12. Как определить ток в нулевом проводе четырехпроводной системы при несимметричной нагрузке, зная линейные токи?
13. При каких условиях будут равны напряжения на всех фазах нагрузки в трехпроводной трехфазной системе?
14. Каков характер нагрузки в осветительных сетях?
15. Какую систему трехфазного тока нужно использовать в осветительных сетях и почему?
16. какую мощность можно определить методом двух ваттметров?
17. Чему равна активная мощность цепи при применении метода двух ваттметров?
18. В каких системах трехфазного тока может быть применен метод двух ваттметров?
19. Можно ли определить полную мощность трехфазной системы, используя метод двух ваттметров?
20. Можно ли определить коэффициент мощности трехфазной системы, используя метод двух ваттметров?
Выбор статьи по меткам 03 (1) 5 марта 2020 (1) 5 мая Статград (2) 9 класс (3) 10 класс (1) 11 класс (2) 12 (1) 13 (С1) (3) 14 ноября (2) 14 февраля (1) 15 задание ЕГЭ (2) 16 задача профиль (1) 16 профильного ЕГЭ (1) 16 января Статград (2) 18 (С5) (2) 18 задача ЕГЭ (2) 18 мая 2020 физика (1) 23 марта (1) 31 января (1) 2016 (2) 140319 (1) 14032019 (1) C5 (1) RC-цепь (1) А9 (1) Александрова (2) Ампера (2) Архимед (2) Бернулли (1) Бойля-Мариотта (1) В8 (1) В12 (1) В13 (1) В15 (1) ВК (1) ВШЭ (2) ГИА физика задания 5 (1) Герона (1) Герцшпрунга-Рассела (1) Гринвич (1) ДВИ (1) ДПТ (1) Деление отрезка (1) Десятичные приставки (1) Дж (1) Диэлектрические проницаемости веществ (1) ЕГЭ 11 (2) ЕГЭ 14 (1) ЕГЭ 15 (2) ЕГЭ 18 (1) ЕГЭ С1 (1) ЕГЭ по математике (25) ЕГЭ по физике (49) ЕГЭ профиль (6) Европа (1) Задача 17 ЕГЭ (7) Задачи на движение (1) Закон Архимеда (2) Законы Ньютона (1) Земля (1) Ио (1) КПД (9) Каллисто (1) Кельвин (1) Кирхгоф (1) Кирхгофа (1) Койпера (1) Колебания (1) Коши (1) Коэффициенты поверхностного натяжения жидкостей (1) Кулона-Амонтона (1) Ломоносов (2) Лоренца (1) Луна (1) МГУ (1) МКТ (7) МФТИ олимпиада (1) Максвелл (2) Максвелла (1) Максимальное удаление тела от точки бросания (1) Менделеева-Клапейрона (3) Менелая (4) Метод наложения (2) Метод узловых потенциалов (1) Метод эквивалентных преобразований (1) НОД (1) Нансен (1) НеИСО (1) ОГЭ (11) ОГЭ (ГИА) по математике (27) ОГЭ 3 (ГИА В1) (1) ОГЭ 21 (3) ОГЭ 21 (ГИА С1) (4) ОГЭ 22 (2) ОГЭ 25 (3) ОГЭ 26 (1) ОГЭ 26 (ГИА С6) (1) ОГЭ по физике 5 (1) ОДЗ (13) Обыкновенная дробь (1) Оорта (1) Основные физические константы (1) Отношение объемов (1) Плюк (1) Показатели преломления (1) Показательные неравенства (1) Противо-эдс (1) Работа выхода электронов (1) Радиус кривизны траектории (1) Расстояние между скрещивающимися (1) Релятивистское замедление времени (1) Релятивистское изменение массы (1) С1 (1) С1 ЕГЭ (1) С2 (2) С3 (1) С4 (3) С6 (5) СУНЦ МГУ (2) Савченко (1) Сиена (1) Синхронная машина (1) Снеллиуса (2) Солнечной системы (1) Солнце (2) СпБ ГУ вступительный (1) Средняя кинетическая энергия молекул (1) Статград физика (6) Таблица Менделеева (1) Текстовые задачи (8) Тьерри Даксу (1) ФИПИ (1) Фазовые переходы (1) Фаренгейт (1) Фобос (1) Френеля (1) Цельсий (1) ЭДС (6) ЭДС индукции (2) Эйлера (1) Электрохимические эквиваленты (1) Эрастофен (1) абсолютная (1) абсолютная влажность (2) абсолютная звездная величина (3) абсолютная температура (1) абсолютный ноль (1) адиабаты (1) аксиомы (1) алгоритм Евклида (2) алгоритм Робертса (1) аморфное (1) амплитуда (3) аналитическое решение (1) анекдоты (1) апериодический переходной процесс (2) аргумент (1) арифметическая прогрессия (5) арифметической прогрессии (1) арки (1) арккосинус (1) арккотангенс (1) арксинус (1) арктангенс (1) архимеда (3) асинхронный (1) атмосферное (2) атмосферном (1) атомная масса (2) афелий (2) база (1) балка (1) банк (1) без калькулятора (1) без отрыва (1) белого карлика (1) бензин (1) бесконечная периодическая дробь (1) бесконечный предел (1) биквадратные уравнения (1) бипризма (1) биссектриса (4) биссектрисы (2) благоприятный исход (1) блеск (4) блок (2) блоки (2) боковой поверхности (1) большая полуось (1) большем давлении (1) бревно (2) бригада (2) бросили вертикально (1) бросили под углом (3) бросили со скоростью (2) броуновское движение (1) брошенного горизонтально (2) бруски (1) брусок (4) брусок распилили (1) бусинка (1) быстрый способ извлечения (1) вариант (3) вариант ЕГЭ (12) вариант ЕГЭ по физике (18) вариант по физике (1) варианты ЕГЭ (6) вариент по физике (1) введение дополнительного угла (1) вектор (5) векторное произведение (2) велосипедисты (1) вероятность (3) вертикальная составляющая (1) вертикально вверх (1) вертикальные углы (1) вес (3) весов (1) вес тела (1) ветви (1) ветвь (2) ветер (1) взаимодействие зарядов (1) видеоразбор (2) видеоразбор варианта (1) видимая звездная величина (2) виртуальная работа (1) виртуальный банк (1) виртуальных перемещений (1) витка (1) витков (1) виток (1) вклад (1) влажность (3) влажность воздуха (1) влетает (2) вневписанная окружность (2) внутреннее сопротивление (1) внутреннее сопротивление источника (1) внутреннюю энергию (1) внутренняя энергия (8) вода (1) вода течет (1) воды (1) возведение в квадрат (1) возвратное уравнение (1) возвратность (1) возвратные уравнения (2) воздушный шар (1) возрастающая (1) возрастет (1) волны (1) вписанная (1) вписанная окружность (3) вписанной окружности (1) вписанный угол (4) в правильной пирамиде (1) вращается (1) вращение (1) времени (2) время (24) время в минутах (1) время выполнения (1) время движения (2) время минимально (1) время падения (1) все значения а (1) всесибирская олимпиада (1) в стоячей воде (1) встретились (1) встретятся (1) вступительный (1) вступительный экзамен (1) вторая половина пути (1) вторая экваториальная система координат (1) вторичная (1) вторичная обмотка (1) вторичные изображения (1) второй закон (1) второй закон Ньютона (4) выбор двигателя (1) выборка корней (4) выколотая точка (1) выплаты (2) выразить вектор (1) высота (5) высота Солнца (1) высота столба (1) высота столба жидкости (1) высота столбика (1) высоте (3) высоту (1) высоты (3) выталкивающая сила (2) вычисления (2) газ (3) газа (1) газов (1) газовая атмосфера (1) галочка (1) гамма-лучей (1) гармоника (2) гвоздя (1) геометрическая вероятность (1) геометрическая прогрессия (4) геометрические высказывания (1) геометрический смысл (2) геометрическую прогрессию (1) геометрия (7) гигрометр (1) гидродинамика (1) гидростатика (3) гимназия при ВШЭ (1) гипербола (2) гипотенуза (3) гистерезисный двигатель (1) главный период (1) глубина (1) глухозаземленная нейтраль (1) гомотетия (2) гонщик (1) горизонтальная сила (1) горизонтальной спицы (1) горизонтальную силу (1) горка (1) гравитационная постоянная (1) градус (1) грани (2) график (2) графики функций (5) графически (1) графический способ (1) графическое решение (3) груз (2) грузик (2) грузовик (1) грузы (1) группа (1) давление (28) давление жидкости (3) давление пара (1) дальность полета (1) двигатель с активным ротором (1) движение под углом (1) движение под углом к горизонту (4) движение по кругу (1) движение по течению (1) движение с постоянной скоростью (2) движется груз (1) двойное неравенство (1) двойной фокус (1) двойным неравенством (1) двугранный угол при вершине (1) девальвация (1) действительная часть (1) действующее значение (2) деление (1) деление многочленов (2) деление уголком (1) делимость (23) делимость чисел (1) делители (1) делитель (2) делится (3) демонстрационный варант (1) деталей в час (1) диаграмма (1) диаметр (2) диаметру (1) динамика (4) диод (1) диск (2) дискриминант (5) дифракционная решетка (2) дифференцированный платеж (3) диффузия (1) диэлектрик (1) диэлектрическая проницаемость (1) длина (4) длина вектора (1) длина волны (7) длина медианы (1) длина отрезка (2) длина пружины (1) длина тени (1) длиной волны (2) длину нити (1) длины поездов (1) длительность разгона (1) длительный режим (1) добротность (1) догнал (1) догоняет (1) докажите (1) долг (1) доля (1) дополнительный угол (2) досок (1) досрочный (2) досрочный вариант (1) дптр (1) дуга (1) единицы продукции (1) единичный источник (1) единичных кубов (1) единмтвенное решение (1) единственный корень (1) ежесекундно (1) емкость (7) емкость заряженного шара (1) естественная область определения (1) желоб (2) жесткость (6) жеткость (1) живая математика (2) жидкости (1) жидкость (1) завод (1) загадка (2) задание 13 (2) задание 15 (3) задание 23 (1) задания 1-14 ЕГЭ (1) задача 4 ЕГЭ (2) задача 9 (1) задача 13 ЕГЭ (1) задача 13 профиль (1) задача 14 профиль (3) задача 15 профиль (1) задача 16 (1) задача 16 ЕГЭ (1) задача 16 профиль (4) задача 17 (1) задача 18 (1) задача 19 (2) задача 26 ОГЭ (2) задача с параметром (7) задачи (1) задачи на доказательство (4) задачи на разрезание (4) задачи на совместную работу (3) задачи про часы (1) задачи с фантазией (1) задерживающее напряжение (1) заземление (1) заказ (1) закон Бернулли (1) закон Гука (1) закон Ома (3) закон Снеллиуса (1) закона сохранения (1) закон движения (1) закон кулона (7) закон палочки (3) закон сложения классических скоростей (1) закон сохранения импульса (7) закон сохранения энергии (4) законы Кирхгофа (6) законы коммутации (1) законы сохранения (1) закрытым концом (1) замена переменной (2) замкнутая система (2) зануление (1) запаянная (2) заряд (9) заряда (1) заряд конденсатора (1) заряженная сфера (1) заряженный шар (1) защитная характеристика (1) звездочка (1) звезды (1) зенит (1) зенитное расстояние (1) зеркало (2) знак неравенства (1) знаменатель (1) знаменатель прогрессии (4) значение выражения (1) идеальный блок (1) идеальный газ (5) извлечение в столбик (1) излом (1) излучение (2) изменение длины (2) изменение импульса (2) изобара (1) изобаричесикй (1) изобарический (2) изобарный (1) изобарный процесс (1) изображение (3) изолированная нейтраль (1) изопроцессы (1) изотерма (2) изотермически (1) изотермический (2) изотермический процесс (1) изотоп (1) изохора (1) изохорический (1) изохорный процесс (1) импульс (11) импульса (1) импульс силы (2) импульс системы (1) импульс системы тел (4) импульс тела (4) импульс частицы (1) инвариантность (1) индуктивно-связанные цепи (1) индуктивное сопротивление (1) индуктивность (1) индукцией (1) индукция (8) интеграл Дюамеля (1) интервал (1) интересное (3) интерференционных полос (1) иррациональность (2) испарение (2) исследование функции (4) источник (1) источник света (1) исход (1) камень (1) камешек (1) капилляр (1) карлик (2) касательная (4) касательного (1) касательные (1) касаются (1) катер (2) катет (3) катится (2) катушка (6) качаний (2) квадлратичная зависимость (1) квадрант (1) квадрат (3) квадратичная функция (3) квадратное (1) квадратное уравнение (4) квадратную рамку (1) квазар (1) квант (1) квантов (1) кинематика (2) кинематическая связь (1) кинематические связи (5) кинетическая (12) кинетическая энергия (5) кинетической (1) кинетической энергии (1) кинетическую энегрию (1) кинетическую энергию (1) классический метод (3) классический метод расчета (1) клин (3) ключ (1) кодификатор (1) колебаний (1) колене (1) колесо (1) количество вещества (1) количество теплоты (9) коллектор (1) кольцо (2) комбинаторика (1) комбинированное (1) коммутация (1) комплексное сопротивление (1) комплексное число (1) комплексные числа (1) компонент (1) конвекция (3) конденсатор (10) конденсаторы (1) конденсации (1) конечная скорость (1) конечная температура (1) конечная температура смеси (1) конечный предел (1) консервативные (1) консоль (1) контрольная (1) контрольные (1) контур (5) конус (4) концентрация (7) концентрически (1) концентрическим (1) координата (5) координатный метод (2) координаты (3) координаты вектора (2) координаты середины отрезка (1) координаты точки (1) корабля (1) корень (4) корень квадратный (1) корень кубический (2) корни (3) корни иррациональные (1) корни квадратного уравнения (3) корни уравнения (1) корпоративных (1) косинус (2) косинус разности (1) косинусы (1) котангенс (1) коэффициент (1) коэффициент жесткости (1) коэффициент наклона (3) коэффициент поверхностного натяжения (3) коэффициент подобия (5) коэффициент трансформации (1) коэффициент трения (6) коэффициенты (1) красное смещение (1) красной границы (1) красный (1) кратковременный режим (1) кратные звезды (1) кредит (11) кредитная ставка (4) кредиты (1) криволинейная трапеция (2) кристаллизация (1) критерии оценки (1) круговая частота (1) круговой контур (1) кружок (1) кубическая парабола (1) кулонова сила (1) кульминация (1) кусочная функция (1) левом колене (1) лед (2) лет (1) линейная скорость (2) линейное напряжение (1) линейное уравнение (2) линейный размер (1) линза (2) линзы (2) линии излома (1) линиями поля (1) линия отвеса (1) литров (1) лифт (1) лифта (1) лифте (1) логарифм (10) логарифмические неравенства (3) логарифмические уравнения (1) логарифмическое неравенство (3) логарифмическое с переменным основанием (1) логарифмы (1) лунка (1) лучевая (1) льда (1) магнитное поле (2) магнитном поле (2) магнитные цепи (1) максимальная высота (1) максимальная скорость (1) максимум (1) малых колебаний (1) масса (24) масса воздуха (1) массе (1) массивная звезда (1) массовое содержание (1) массой (1) массу (1) математика (4) математический маятник (1) математического маятника (2) маятник (4) мгновенный центр вращения (1) медиана (2) меридиан (1) мертвая вода (1) мертвая петля (1) металлическая оболочка (1) метод виртуальных (1) метод внутреннего проецирования (1) метод замены переменной (4) метод интервалов (3) метод комплексных амплитуд (3) метод контурных токов (1) метод координат (1) метод линий (1) методом внутреннего проецирования (1) метод переброски (1) метод переменных состояния (1) метод подстановки (4) метод рационализации (4) метод решетки (1) метод следов (5) метод сложения (4) метод телескопирования (1) метод узловых напряжений (1) методы расчета цепей (2) методы расчета цепей постоянного тока (1) метод эквивалентного генератора (2) механика (1) механическая характеристика (1) механическое напряжение (1) миля (1) минимальная скорость (1) минимальное (1) минимальной высоты (1) минимальной скоростью (1) минимум (2) мишени (1) мнимая единица (1) мнимая часть (1) многоугольник (1) многочлены (1) мода (2) модули (1) модуль (13) модуль Юнга (1) модуль средней скорости (1) молекулярно-кинетическая теория (2) моль (2) молярная масса (5) момент (7) момент инерции (2) момент инерции двигателя (1) момент нагрузки (1) момент сил (1) монета (1) монотонная (1) монотонность функции (1) монохроматического (1) московская олимпиада (1) мощности силы тяжести (1) мощность (9) мощностью (1) мяч (1) наблюдатель (1) нагревание (1) нагреватель (1) нагревателя (1) нагрели (1) наибольшее (1) наивысшая точка (1) наименьшая работа (1) наименьшее (1) наименьшее общее кратное (1) наклон (1) наклонная плоскость (2) налог (1) на направление (2) на отрезке (2) на подумать (2) направление (1) направление обхода (3) направлении (1) направляющий вектор (1) напряжение (9) напряжение на зажимах (1) напряжение смещения нейтрали (2) напряженность (4) напряженность поля (6) нарушенная схема (5) насос (2) насоса (1) насыщенный пар (4) натуральное (9) натуральные (10) натуральных (1) натяжение нити (5) натяжения (1) находился в полете (2) начальная температура (1) начальной скоростью (1) недовозбуждение (1) незамкнутая система (2) нелинейное сопротивление (1) неопределенность типа бесконечность на бесконечность (1) неопределенность типа ноль на ноль (1) непериодическая дробь (1) неравенства (8) неравенство (22) неравенство профиль (1) неразрывности струи (1) нерастяжима (3) нерастяжимой (1) нерастяжимой нити (1) нерастянутой резинки (1) несимметричная нагрузка (1) несинусоидальный ток (3) нестандартные задачи (1) нестрогое (1) неупругим (1) нецентральный (1) нечетная функция (2) нечетное (1) нечетность (1) неявнополюсный (1) нити (3) нити паутины (1) нитку (1) нить (2) нить нерастяжима (1) новости (1) нормаль (1) нормальное ускорение (11) нормальной реакции опоры (1) нулевой ток (2) обкладками (1) обкладках (1) обкладки (1) область допустимых значений (9) область значений (1) область определения (8) область определения функции (4) оборот (1) обратные тригонометрические функции (1) обратные функции (1) общая хорда (1) общее сопротивление (1) общее сопротивление цепи (1) объем (37) объемный расход (1) объемом (1) объем пара (1) объем параллелепипеда (1) объем пирамиды (1) одинаковые части (1) одновременно (1) одновременно из одной точки (1) однозначное (1) окружность (13) окружность описанная (1) олимпиада (2) олимпиады по физике (2) они встретятся (1) операторный метод (4) описанная (1) оптика (1) оптимальный выбор (1) оптимизация (1) оптическая разность хода (1) оптический центр (1) орбитам (1) орбитой (1) оригинал (1) осевое сечение (1) оси (1) основание (2) основание логарифма (2) основания трапеции (1) основное тригонометрическое тождество (1) основное уравнение МКТ (2) основной газовый закон (1) основной период (1) основной уровень (1) основные углы (1) остаток (1) ось (1) отбор корней (6) ответ (1) отданное (1) отличная (1) относительная (2) относительная влажность (3) относительная скорость (1) относительно (4) относительность движениия (1) относительность движения (2) относительность скоростей (1) отношение (6) отношение времен (1) отношение длин (3) отношение площадей (4) отношение скоростей (2) отрезке (1) отрезок (1) отсечение невидимых граней (1) очки (1) падает (1) падает луч (1) падает под углом (1) падение (3) падение напряжения (2) падения (1) пар (3) парабола (5) параболы (1) параллакс (5) параллелепепед (2) параллелепипед (3) параллелограмм (4) параллелограмм Виньера (1) параллельно (2) параллельно двум векторам (1) параллельное соединение (3) параллельные прямые (1) параллельными граням (1) параметр (32) параметры (1) парообразование (1) парсек (1) парциальное (1) парциальное давление (1) пары (1) паскаль (1) первая треть (1) первичная (1) переброски (1) перевозбуждение (1) перегородка (1) перегрузок (1) перелетит (1) переливания (1) переменное магнитное поле (1) переменное основание (2) перемещение (6) перемычка (5) перемычке (1) перемычку (1) переносная (1) переносная скорость (1) пересекает (1) пересечение (1) пересечения (1) переходная проводимость (1) переходное сопротивление (1) переходной процесс (1) переходные процессы (9) перигелий (2) периметр (3) период (15) периодическая дробь (1) период колебаний (3) период малых колебаний (1) период обращения (2) период функции (1) периоды (1) перпендикулярно (1) песок (1) пион (1) пипетка (1) пирамида (7) пирамида шестиугольная (1) пирамиды (2) пирсона (1) плавание (1) плавкие предохранители (1) плавление (1) план (1) планете (1) планеты (3) планиметрия (14) планиметрия профиль (1) пластинами (1) пластинка (1) платеж (8) плечо (2) плоского зеркала (1) плоскопараллельная (1) плоскость (4) плоскость сечения (1) плотности веществ (1) плотность (23) плотность пара (3) плотность сосуда (1) плотность энергии (1) площади (2) площади фигур на клетчатой бумаге (1) площадь (30) площадь круга (1) площадь пластин (1) площадь поверхности (1) площадь под кривой (2) площадь проекции (1) площадь проекции сечения (1) площадь сектора (1) площадь сечения (5) площадь треугольника (3) поверхностная плотность заряда (1) поворот (1) повторно-кратковременный режим (1) по гладкому стержню (1) погрешность (1) погружено (1) подвесили (1) подготовка к контрольным (3) под каким углом (1) подмодульное (1) подмодульных выражений (1) подобен (1) подобие (8) подобия треугольников (1) подобны (1) подпереть (1) под углом (2) под углом к горизонту (3) показателем преломления (1) показательное (1) показатель преломления (4) поле (1) полезной работы (1) полезную мощность (1) полигон частот (1) по линиям сетки (1) полное ускорение (1) половина времени (1) половинный угол (1) положение равновесия (1) положительный знаменатель (1) полония (1) полость (1) полуокружность (1) полупроводник (1) полученное (1) понижение горизонта (1) по окружности (1) по переменному основанию (1) поправка часов (1) по прямой (1) поршень (4) поршня (1) порядок решетки (2) последовательно (1) последовательное соединение (3) последовательность (4) по сторонам клеток (1) посторонние корни (4) постоянная Авогадро (1) постоянная Хаббла (1) постоянная времени (1) постоянная скорость (1) постоянная составляющая (2) постоянный ток (5) построение (2) построение графика функции (1) потенциал (6) потенциал сферы (1) потенциал шара (2) потенциальная (13) потенциальная энергия (3) потенциальной (1) потери в стали (2) потеря корней (4) поток (5) по физике (1) правило левой (1) правило моментов (5) правильная пирамида (1) правильной пирамиде (1) правильную пирамиду (1) правильный многоугольник (1) правом колене (1) предел функции (1) преломляющий угол (1) преобразование графиков функций (1) преобразования (3) преподаватели (2) пресс (2) призма (7) призмы (3) признаки подобия (4) признаки равенства треугольников (3) пробн (1) пробник (206) пробник по физике (12) пробниук (1) пробный (1) пробный ЕГЭ (2) пробный ЕГЭ по физике (4) пробный вариант (25) пробный вариант ЕГЭ (17) пробный вариант ЕГЭ по физике (148) пробный вариант по физике (2) провода (1) проводник (1) проводник с током (1) проводящая оболочка (1) проводящего шара (1) проволока (1) проволоки (1) прогрессия (5) проекции (1) проекции скоростей (1) проекции ускорения (2) проекция (7) проекция перемещения (1) проекция скорости (6) проекция ускорения (2) производительность (2) производная (3) промежутка времени (1) промежуток (1) промежуток знакопостоянства (1) пропорциональны (1) проскальзывает (1) проскальзывания (1) противоположное событие (1) противостояние (1) протона (1) прототипы (1) профиль (2) профильный ЕГЭ (1) процент (5) процентная ставка (6) процентное отношение (1) процентное содержание (2) проценты (3) пружин (1) пружина (6) пружинный маятник (1) пружины (1) прямая (7) прямое восхождение (3) прямой (1) прямой АВ (1) прямолинейные разрезы (1) прямоугольник (1) пузырек (1) пульсар (1) пуля (1) пути (1) путь (27) пушка (1) пять корней (1) работа (16) работа газа (5) работа тока (1) работу выхода (2) рабочее тело (1) рабочие (1) равнобедренный (1) равновеликий (1) равновесие (4) равновесия (2) равновесное (1) равнодействующая (1) равномерно (1) равноускоренно (2) равноускоренное (3) равные (1) равные фигуры (1) радиальную ось (1) радикал (1) радикалы (1) радиус (11) радиус колеса (1) радиус кривизны (2) радиус описанной сферы (1) радиус темного кольца в отраженном свете (1) разбор (1) разбор Статграда по физике (4) разложение на множители (2) размах (1) разности температур (1) разность (2) разность потенциалов (2) разность прогрессии (3) разность хода (1) разрежьте (2) разрезание (6) разрешающая сила (1) разрыв функции (1) рамка (8) рамка с током (1) раскрытие модуля (1) расписание (1) расположение корней квадратного трехчлена (1) распределение частот (1) рассеивающая (1) расстояние (21) расстояние между зарядами (1) расстояние между прямыми (1) расстояние между скрещивающимися прямыми (1) расстояние на карте (1) расстояние от точки (1) расстояния (2) раствор (2) растяжение (2) расходуется (1) расцепители (1) расчеты по формулам (1) рационализация (4) рациональное (1) рациональные неравенства (1) реактивные элементы (1) реактивный двигатель (1) реакция опоры (4) реакция якоря (1) реальные 17 задачи (5) ребра (1) ребус (2) резервуар (1) резистор (1) рейки (2) рельс (1) рельса (1) рентгеновскую трубку (1) репетитор (1) решебник (1) решение тригонометрических уравнений (1) решение уравнений (2) решение уравнений больших степеней (1) решить в натуральных (1) решить в целых (1) ровно один (1) розетка (1) ромб (1) ряд Фурье (1) сарай с покатой крышей (1) сближаются (1) сближения (1) сбрасывают с высоты (1) сверхгигант (2) сверхновая (1) светимость (3) свободно (1) свободного падения (1) свободно падает (2) свойства (2) свойства отрезков (1) свойства степени (1) свойства функции (1) свойства функций (2) свойства чисел (1) свойство биссектрисы (2) свойству биссектрисы (1) сдвинуть (1) сегмент (1) сектор (1) секущая (2) серия решений (1) сертификация (6) сессия (1) сечение (14) сечение наклонной плоскостью (1) сидерический (1) сила (7) сила Архимеда (5) сила Лоренца (4) сила ампера (9) сила взаимодействия (4) сила давления (1) сила на дно (1) сила натяжения (8) сила натяжения нити (4) сила поверхностного натяжения (3) сила реакции опоры (1) сила трения (3) сила тяготения (1) сила тяжести (7) сила упругости (2) силой (2) силу (1) силу натяжения (1) силы (1) силы от перемещения (1) силы трения (2) символический метод (3) симметричная нагрузка (1) симметрия (3) синодический (1) синус (4) синусоида (1) синусоидальный закон (1) синусоидальный ток (5) синус половинного аргумента (1) синусы (1) синхронный компенсатор (1) система (5) система неравенств (7) система отсчета (3) система счисления (1) система уравнений (3) системы уравнений (3) скалярное произведение (3) склонение (2) скольжение (2) скользит (1) скользит равномерно (1) скоросмть (1) скоростей (1) скорости (3) скорости течения (1) скорость (45) скорость реки (1) скорость сближения (3) скорость света (1) скорость теплохода (1) скорость удаления (1) скорость частицы (1) скоростью (1) скрещивающиеся прямые (1) с лестницы (1) сложение векторов (1) сложная задача на разрезание (1) сложная функция (1) сложные экономические задачи (6) смежные углы (1) смекалка (2) смеси (1) смешанное число (1) смещение (2) с нарушенной схемой (1) снаряд (2) собирающая (2) событие (1) соединение звездой (1) соединение треугольником (1) сокращение (1) сокращение дробей (1) соленоид (1) солнечная постоянная (3) солнечная система (1)
Для расчета токов должна быть задана схема цепи, значение и тип сопротивлений, напряжение источника энергии. Расчеты обычно проводят для комплексных значений.
Симметричная нагрузка в схеме соединением «звезда – звезда» с нулевым проводом представлена на рис. 4.8.
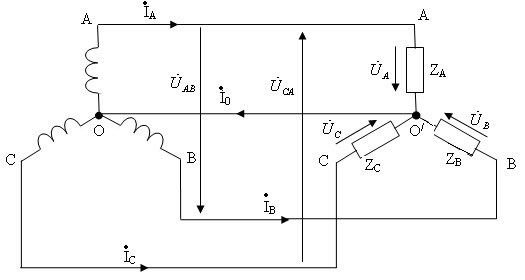
Рис. 4.8.
Если нулевой провод
в схеме симметричного приемника (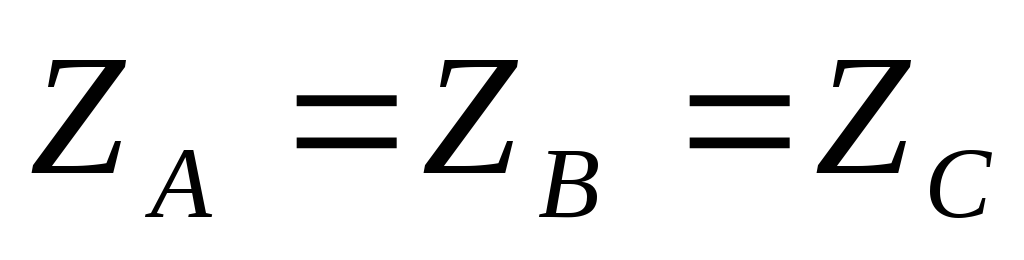 )
обладает весьма малым сопротивлением
(Z0 = 0), то потенциал точки О/ практически равен потенциалу точки О,
и точки сливаются в одну. В схеме
образуются три обособленных контура,
комплексные значения токов в каждом из
которых определяются как в однофазной
цепи
)
обладает весьма малым сопротивлением
(Z0 = 0), то потенциал точки О/ практически равен потенциалу точки О,
и точки сливаются в одну. В схеме
образуются три обособленных контура,
комплексные значения токов в каждом из
которых определяются как в однофазной
цепи 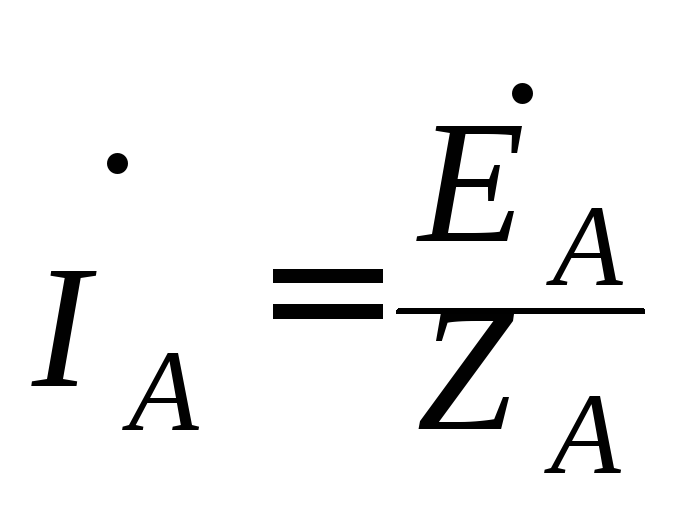 ;
; 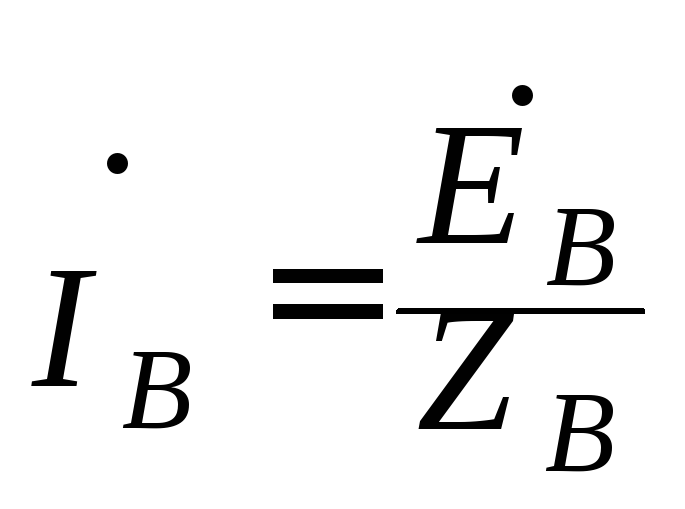 ;
; 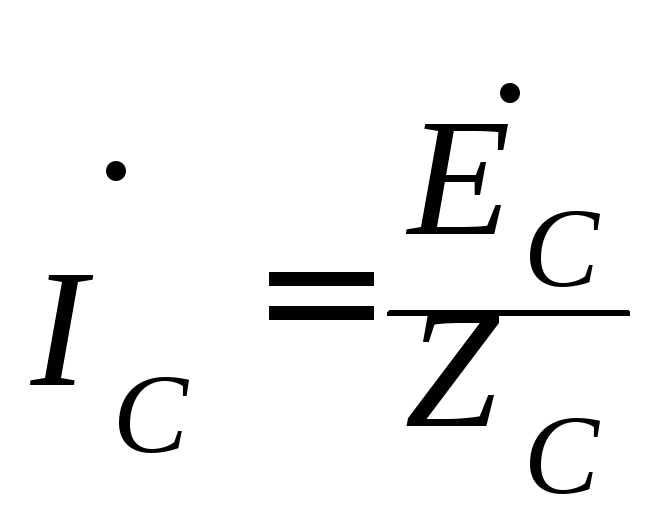
где ĖА, ĖВ, ĖС – фазные напряжения на зажимах генератора.
По первому закону
Кирхгофа ток в нулевом проводе 4-х
проводной системы равен геометрической
сумме фазных токов 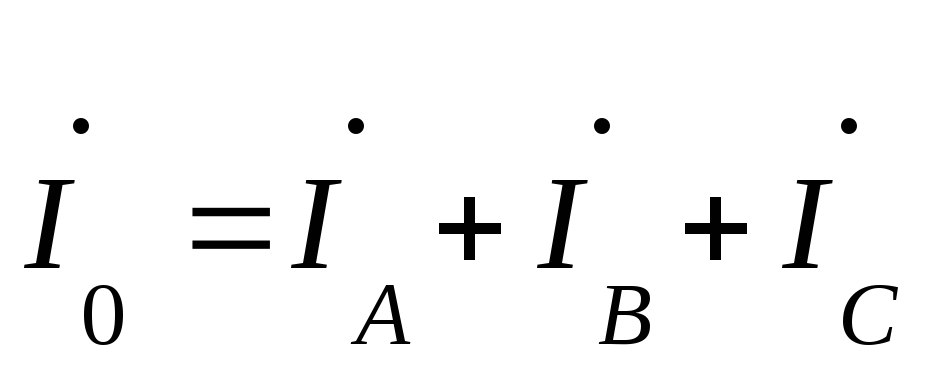 .
.
В общем случае
комплексное напряжение между нулевыми
точками 0 –
0` при наличии
нейтрального провода 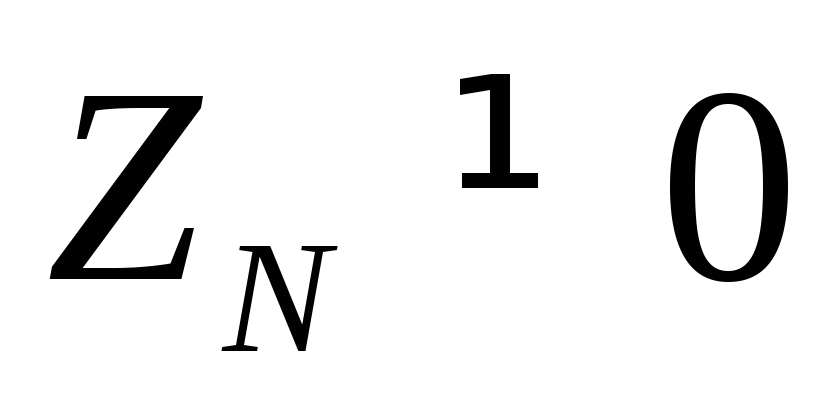
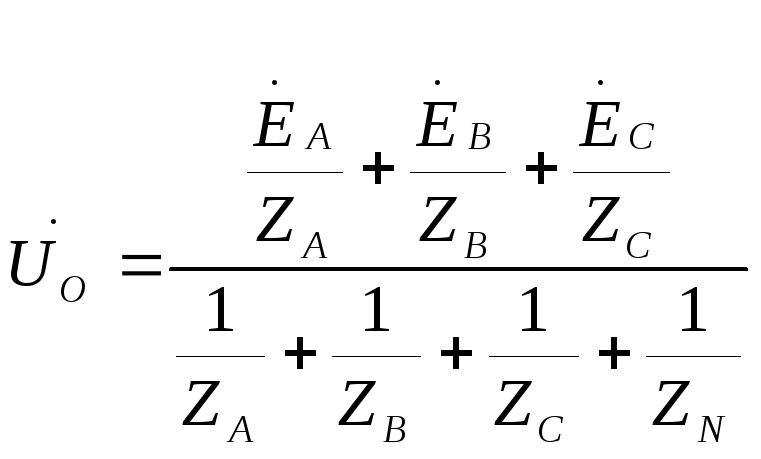 .
.
При равномерной симметричной нагрузке ток I0=0, и нулевой провод может быть изъят из схемы без изменения ее режима работы. Для 3-х проводной системы, т.е. не содержащей нейтральный провод (ZN = ∞) слагаемое 1/ ZN в знаменателе будет отсутствовать.
При определении
напряжения фаз приемника если не
учитывать сопротивления источника, то 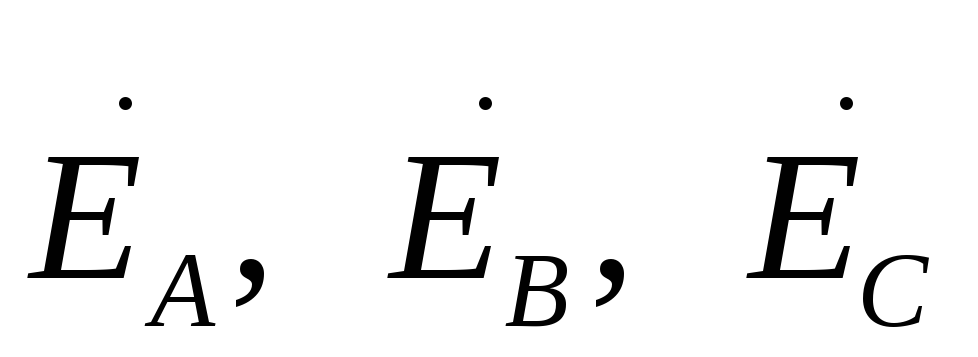 можно заменить
на
можно заменить
на 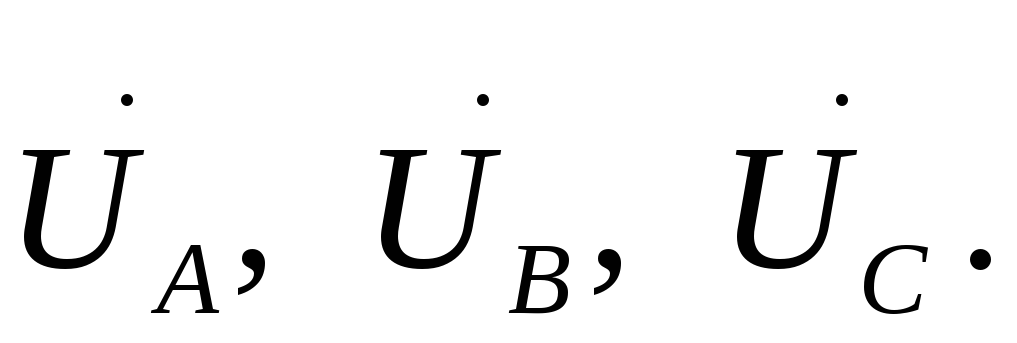
Переходя к
действующим значениям величин в случае,
когда нагрузки во всех фазах равны и
имеют активный характер 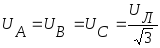 ,
,
где 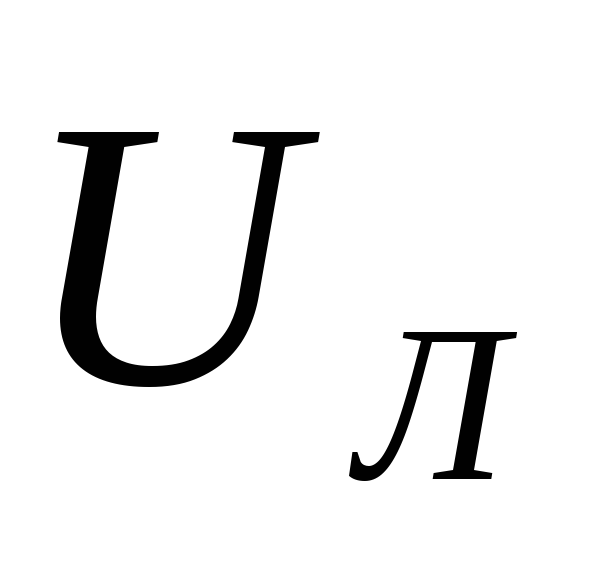 − значение линейного напряжения, токи
соответственно принимают значения
− значение линейного напряжения, токи
соответственно принимают значения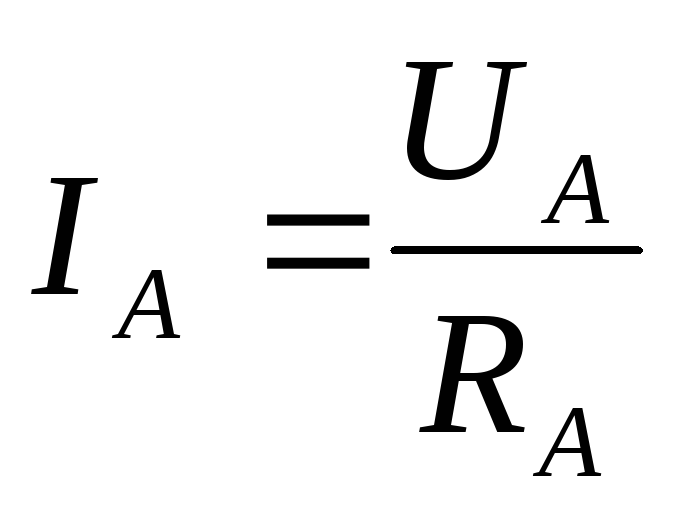 ,
,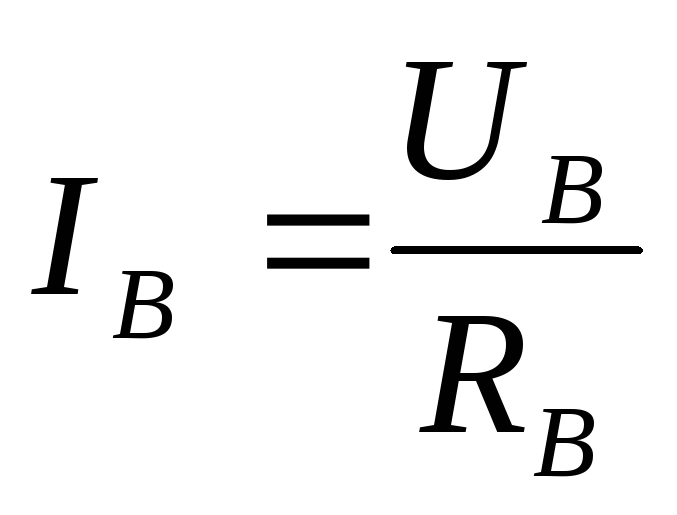 ,
,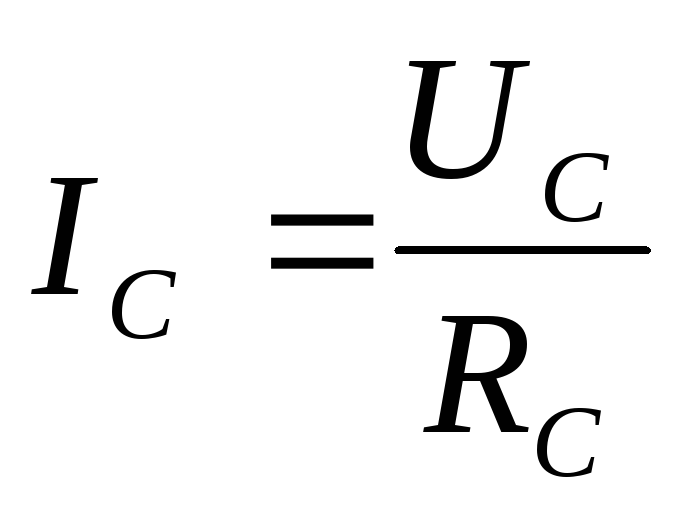 .
.
Общая мощность трехфазной цепи с активной нагрузкой равна
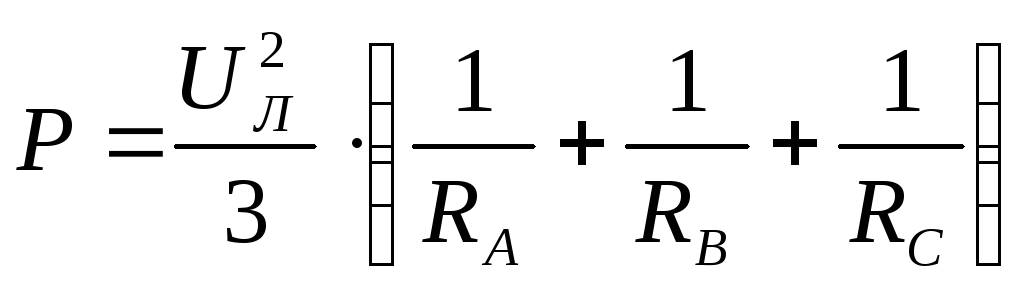 .
.
4.4. Несимметричная нагрузка при соединении звездой
При несимметричной
нагрузке и отсутствии нулевого провода
между нулевыми точками генератора О и
приемника О/ появляется
напряжение  ,
в результате чего фазные напряжения
приемника оказываются различными.
Расчетные соотношение
,
в результате чего фазные напряжения
приемника оказываются различными.
Расчетные соотношение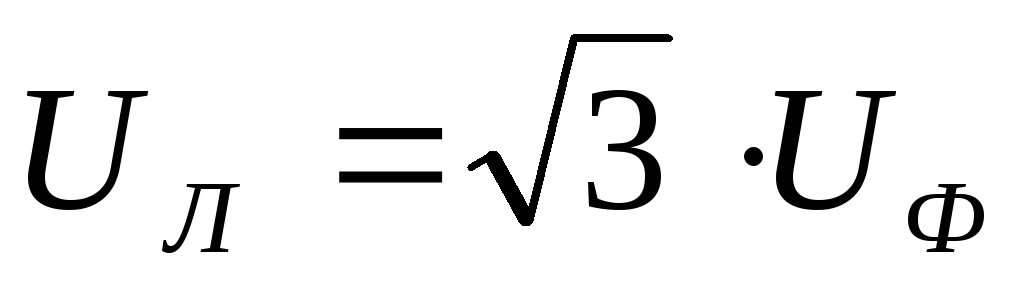 между фазными и линейными напряжениями
при этом нарушается. Для определения
напряжения между нулевыми точками, а
также фазных напряжений приемника
предположим, что в электрической цепи
имеется нейтральный (нулевой) провод,
сопротивление которого
между фазными и линейными напряжениями
при этом нарушается. Для определения
напряжения между нулевыми точками, а
также фазных напряжений приемника
предположим, что в электрической цепи
имеется нейтральный (нулевой) провод,
сопротивление которого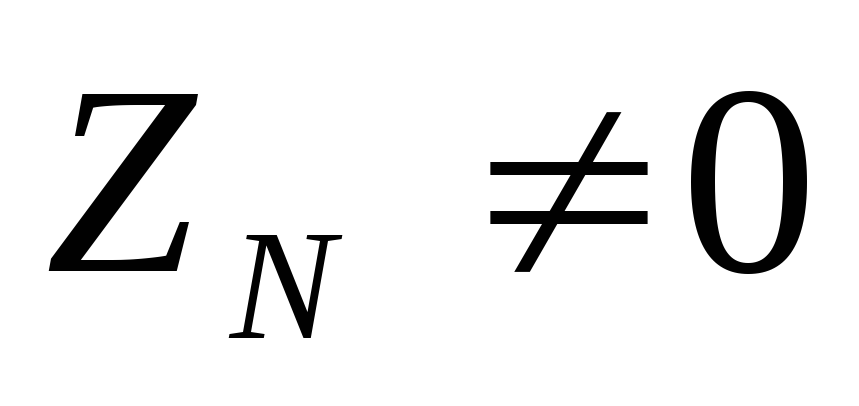 .
Тогда напряжение между нулевыми точками
источника и приемника
.
Тогда напряжение между нулевыми точками
источника и приемника
 ,
,
где g A, g B, g C, g N – проводимости фазных и нулевого проводов,
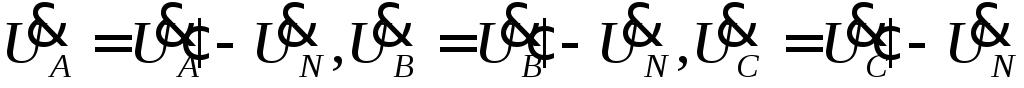
т
Рис. 3. 9. 3.10.
.е. для несимметричной системы при определении в знаменателе учитывается
проводимость нейтрального провода gN..
в знаменателе учитывается
проводимость нейтрального провода gN.. На рис. 4.9. приведена
векторная диаграмма без нейтрального
провода, на которой 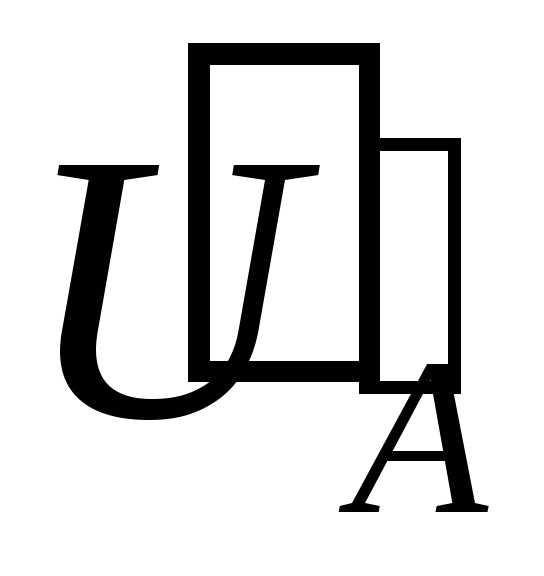 ,
,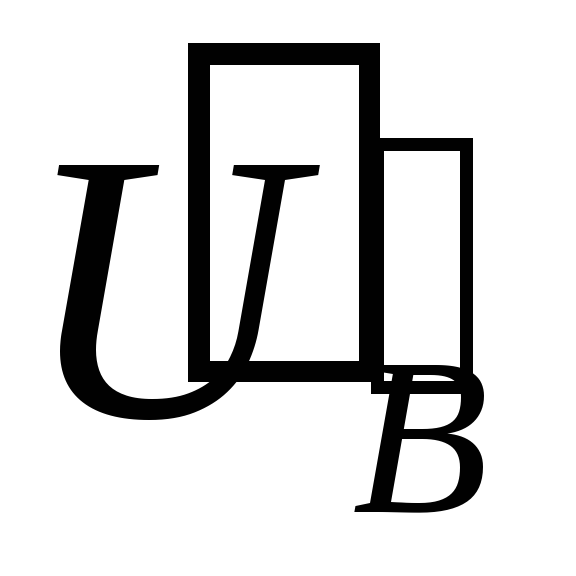 ,
, −
векторы фазных напряжений источника,
а
−
векторы фазных напряжений источника,
а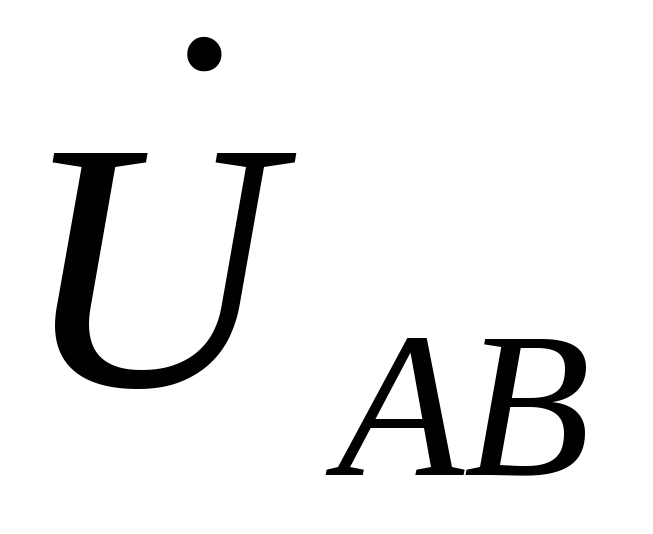 ,
, ,
, −
векторы линейных напряжений источника,
а также линейных напряжений приемника.
Для построения вектора напряжения
−
векторы линейных напряжений источника,
а также линейных напряжений приемника.
Для построения вектора напряжения 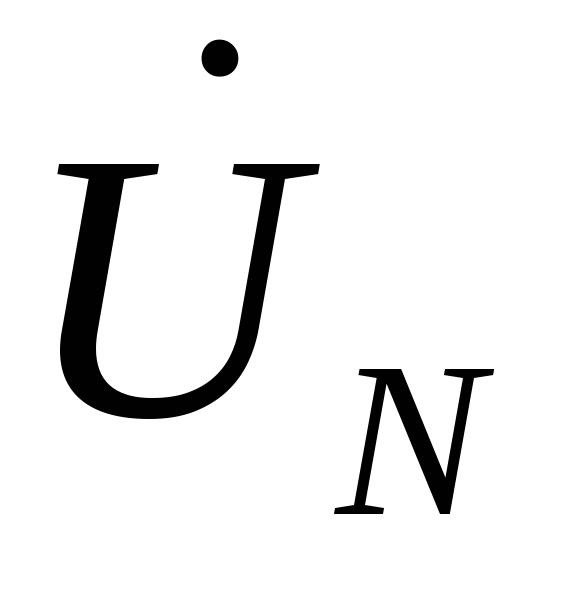 и векторов фазных напряжений приемника
и векторов фазных напряжений приемника  ,
,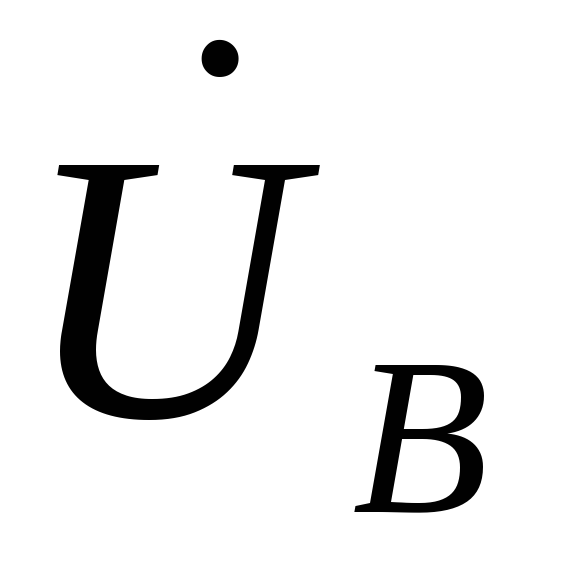 ,
,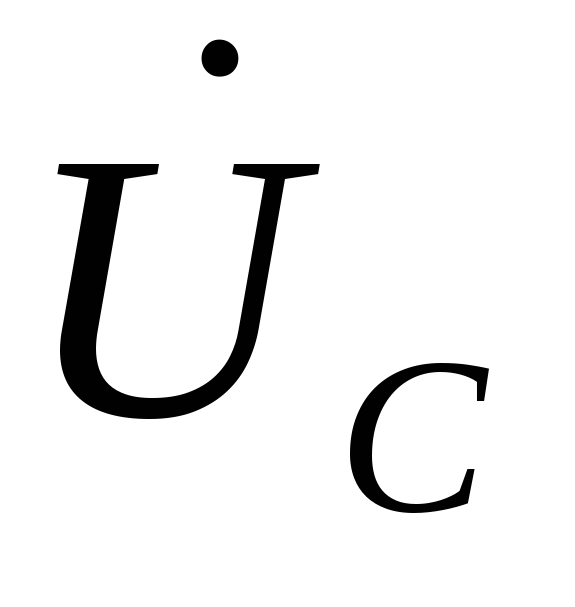 используем их значения, полученные
выше.
используем их значения, полученные
выше.
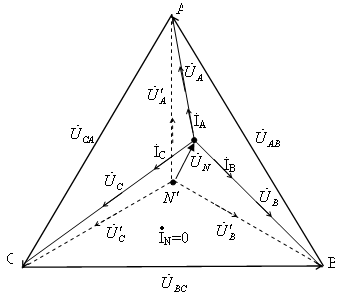
Рис. 4.9.
Связь между фазными
и линейными векторами 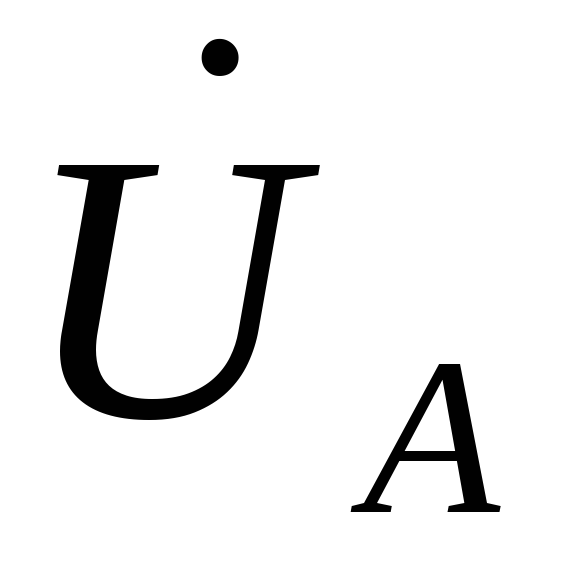 ,
,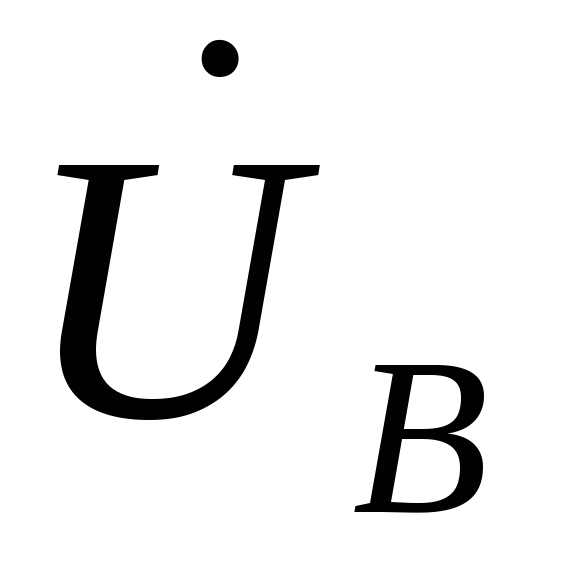 ,
,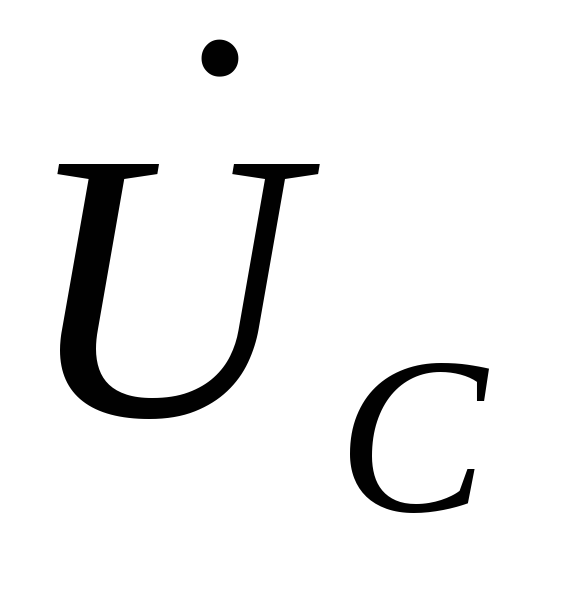 и
и ,
,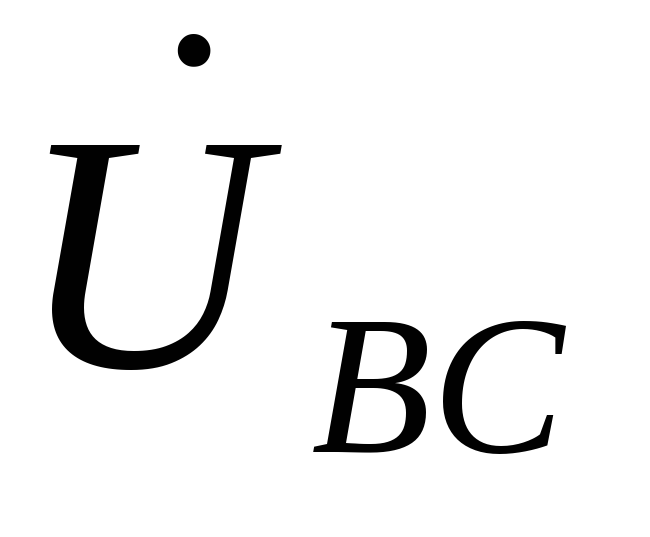 ,
, , определяем выражениями
, определяем выражениями  ,
,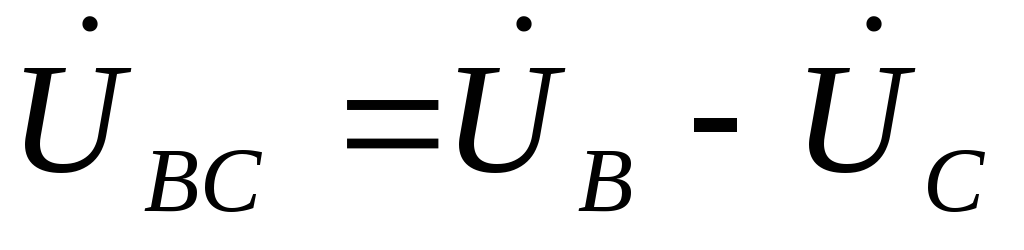 ,
,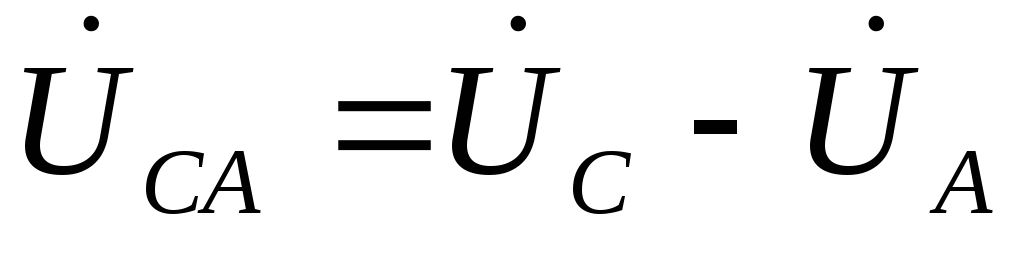 .
.
Векторная диаграмма
построена для активной несимметричной
нагрузки фаз (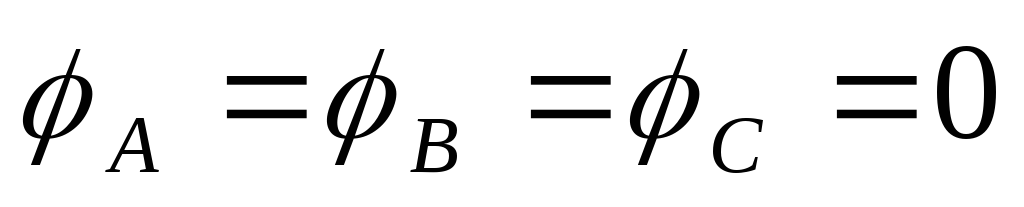 ).
).
При изменении
величины фазных активных сопротивлений
напряжение 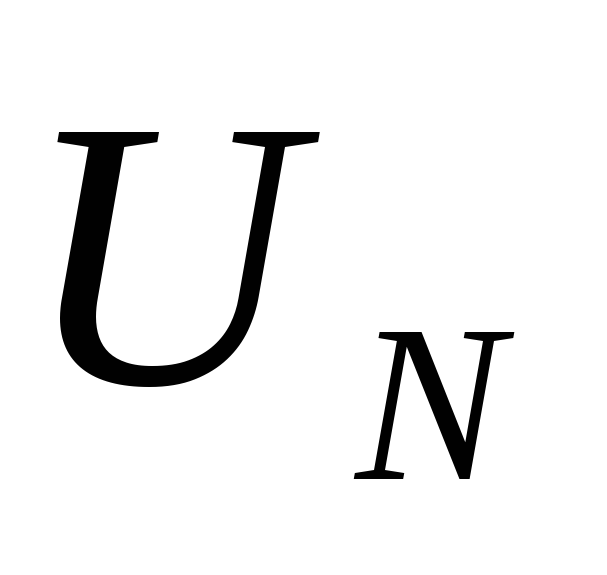 может изменяться в широких пределах. В
соответствии с этим точкаN
на диаграмме может занимать различные
положения, а фазовые напряжения приемника
могут отличаться друг от друга весьма
существенно.
может изменяться в широких пределах. В
соответствии с этим точкаN
на диаграмме может занимать различные
положения, а фазовые напряжения приемника
могут отличаться друг от друга весьма
существенно.
Рассмотрим, частный
случай несимметричной нагрузки, когда 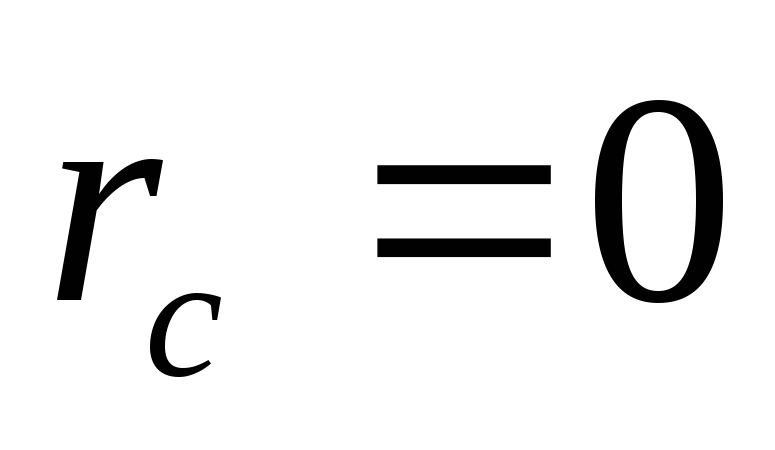 .
Поскольку
.
Поскольку ,
то и
,
то и ,
получим
,
получим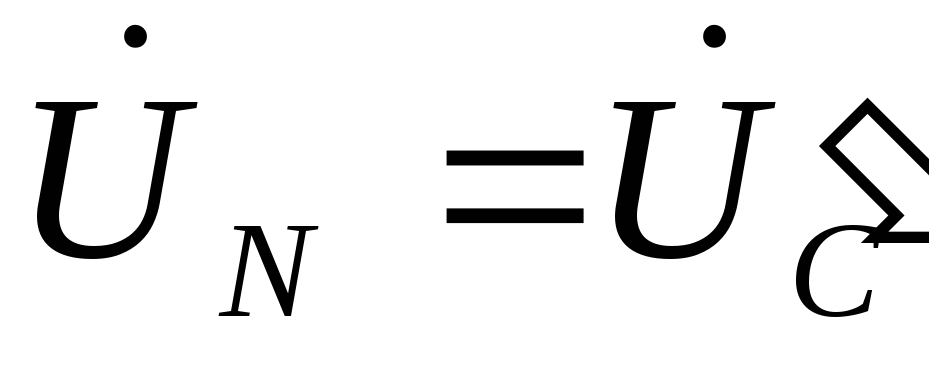 ,
,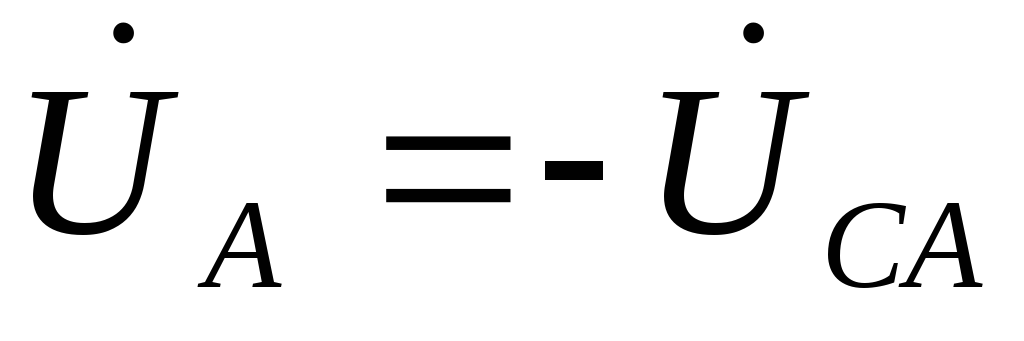 и
и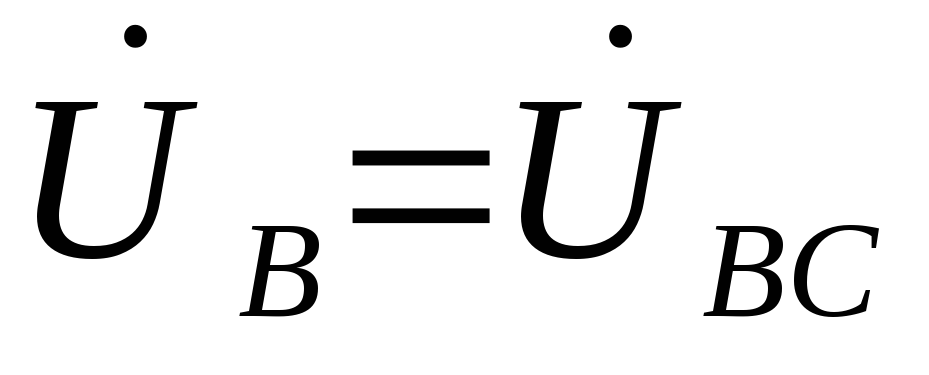 .
ТочкаN на диаграмме переместится в точку С,
напряжение
.
ТочкаN на диаграмме переместится в точку С,
напряжение  возрастет до фазного напряжения
источника, а напряжения
возрастет до фазного напряжения
источника, а напряжения  ,
, − до линейных напряжений.
− до линейных напряжений.

Рис. 4.10.
При изменении фазных напряжений происходит изменение фазных токов и мощностей − «перекос фаз».
Если при несимметричной
нагрузке нулевые точки источника и
приемника соединить нулевым проводом,
то поскольку сопротивление нулевого
провода мало, (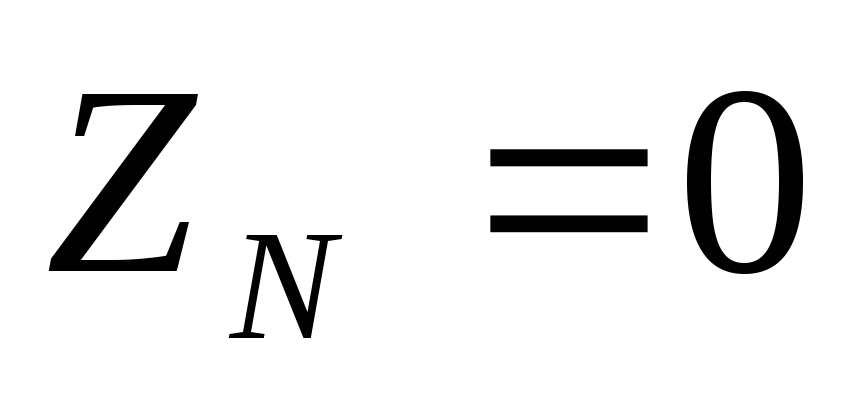 и
и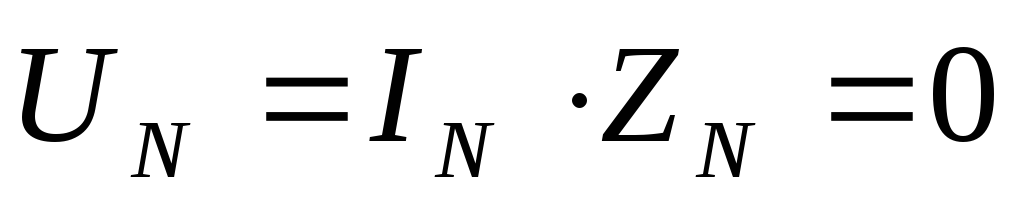 ),
то фазные напряжения приемника получаются
одинаковыми и сдвинутыми по фазе
относительно друг друга на угол
),
то фазные напряжения приемника получаются
одинаковыми и сдвинутыми по фазе
относительно друг друга на угол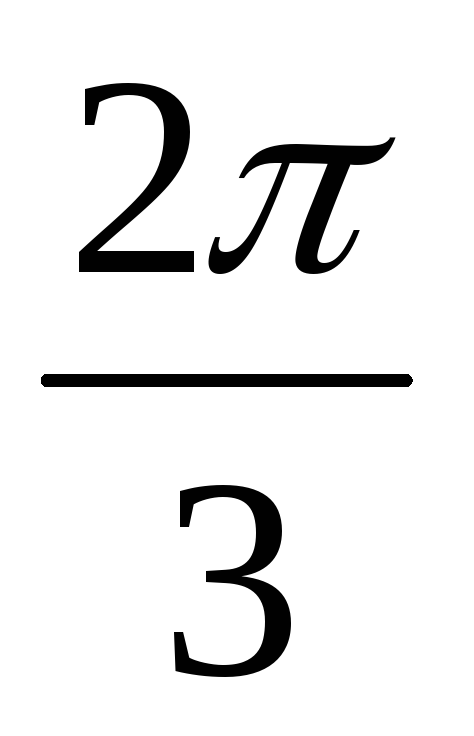 .
Включение нулевого провода приводит к
соответствующим изменениям векторной
диаграммы электрической цепи. Так, если
электрической цепи без нулевого провода
соответствует векторная диаграмма,
изображенная на рис.3.9. сплошной линией,
то той же цепи при включении нулевого
провода соответствует диаграмма,
изображенная на том же рисунке пунктиром.
.
Включение нулевого провода приводит к
соответствующим изменениям векторной
диаграммы электрической цепи. Так, если
электрической цепи без нулевого провода
соответствует векторная диаграмма,
изображенная на рис.3.9. сплошной линией,
то той же цепи при включении нулевого
провода соответствует диаграмма,
изображенная на том же рисунке пунктиром.
Вектор  построен
в соответствии с выражением.
построен
в соответствии с выражением. 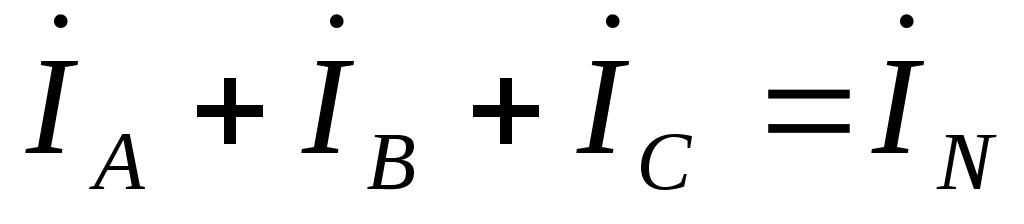 .
.
При наличии нулевого провода в схемах с несимметричной нагрузкой, так же как и в случае с симметричной нагрузкой остается в силе соотношение
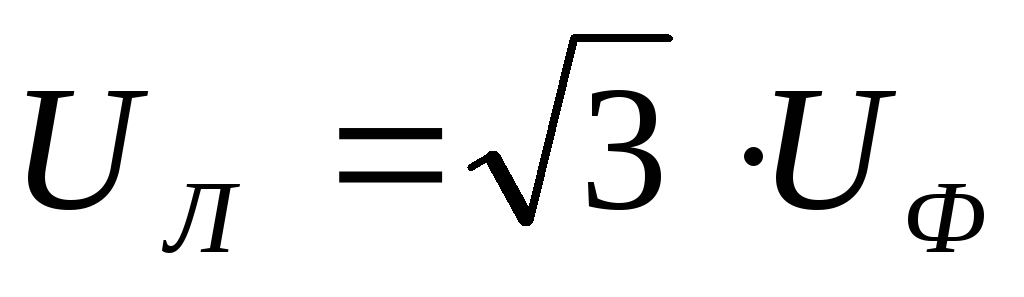 .
.
На основании
изложенного можно сделать вывод, что
нулевой провод необходим для того, чтобы
при несимметричной нагрузке выравнивать
фазные напряжения приемника, т.е. получать
во всех фазах приемника одинаковые
напряжения, равные 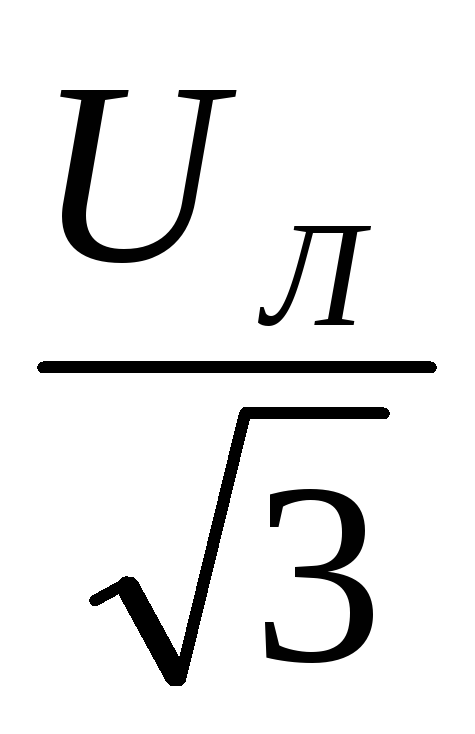 .
.
Фазные токи, углы
сдвига фаз между фазовыми напряжениями
и токами, а также фазные мощности при
несимметричной нагрузке в цепи с нулевым
проводом будут в общем случае различными.
Они могут быть определены по следующим
формулам:  ,
, ,
,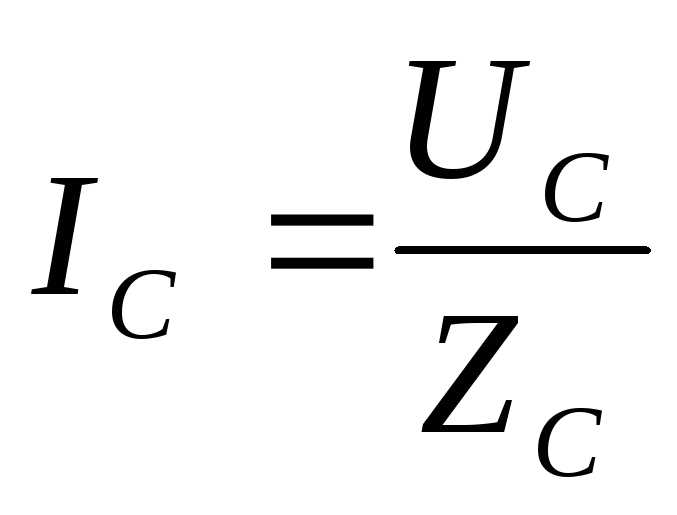 .
.
Углы сдвига фаз между фазными токами и напряжениями зависят от величины и характера сопротивлений фаз приемника и равны
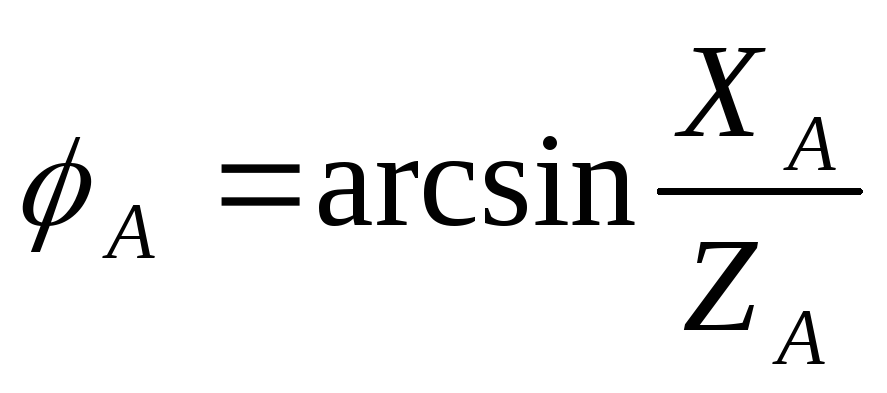 ,
,  ,
,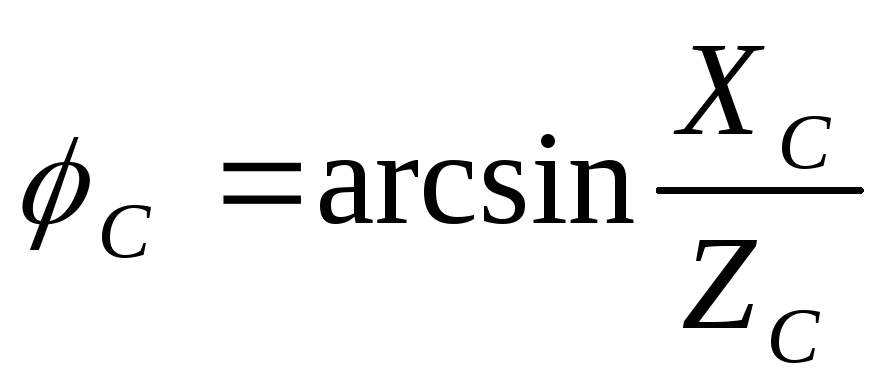 .
.
Мощности для фазы «А» равны
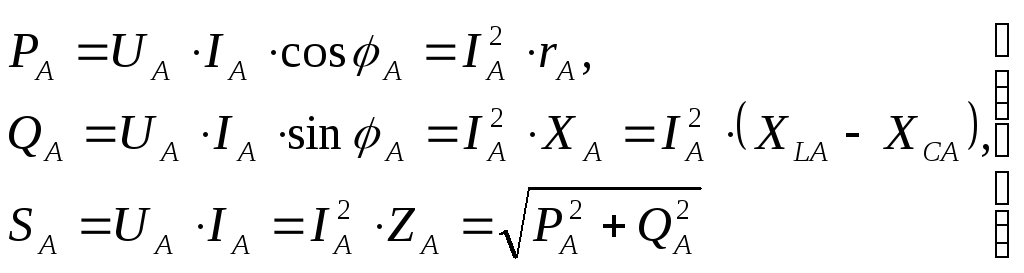
Активная и реактивная
мощности трехфазного приемника при
соединении звездой 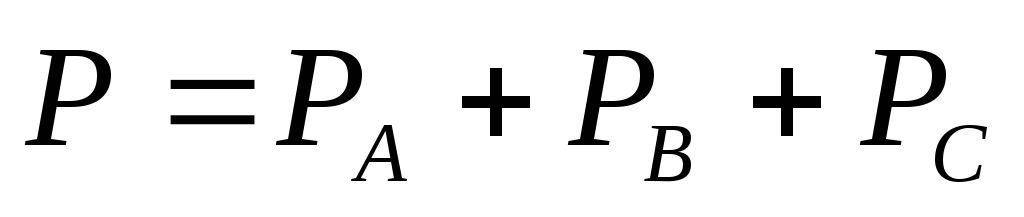 ,
, .
.
Если кроме фазных
токов требуется найти ток в нулевом
проводе, то задачу следует решать в
комплексной форме. При этом необходимо
прежде всего выразить в комплексной
форме то 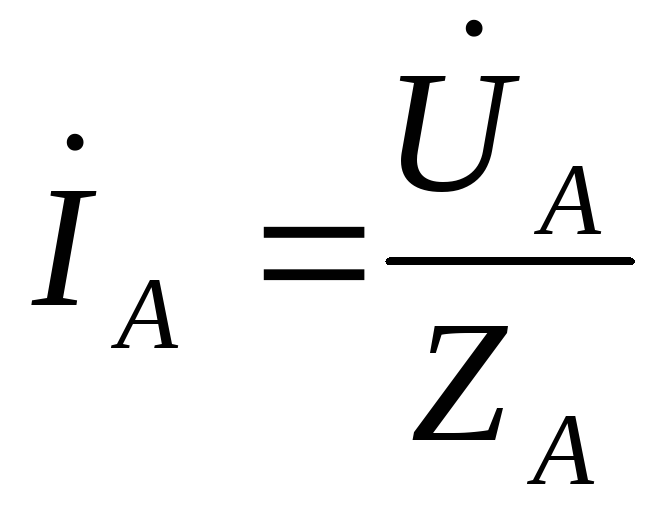 ,
,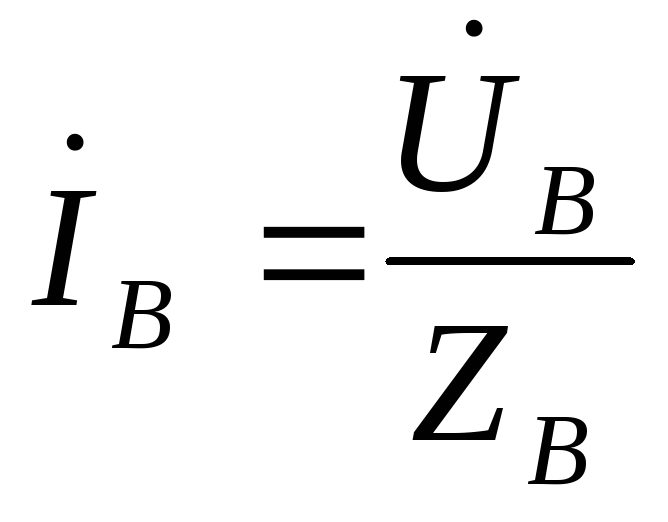 ,
,
Ток в нулевом проводе можно определить также по векторной диаграмме, не прибегая к решению задачи в комплексной форме.
Соединение в звезду. Схема, определения
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.
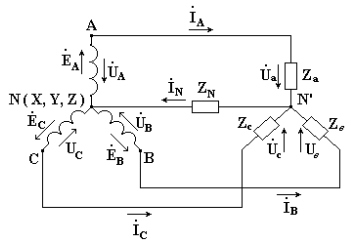
Рис. 6.1
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N’ называют нейтральным (нулевым) проводом.
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.
Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах — линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.
Iл = Iф.
ZN — сопротивление нейтрального провода.
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений
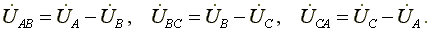 (7.1)
(7.1)
На рис. 6.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
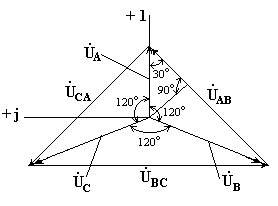
Рис. 6.2
Из векторной диаграммы видно, что
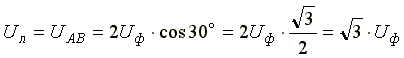
При симметричной системе ЭДС источника линейное напряжение больше фазного
в √3 раз.
Uл = √3 Uф
Расчет трехфазной цепи, соединенной звездой
Трехфазную цепь, соединенную звездой, удобнее всего рассчитать методом двух узлов.
На рис. 7.5 изображена трехфазная цепь при соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы (ZA ≠ ZB ≠ ZC )
Нейтральный провод имеет конечное сопротивление ZN .
В схеме между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали.
Это напряжение определяется по формуле (6.2).
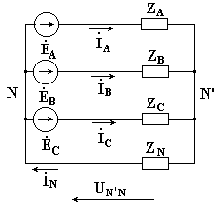
Рис.6. 5
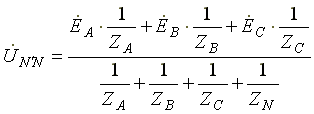 (6.2)
(6.2)
Фазные токи определяются по формулам (в соответствии с законом Ома для активной ветви):
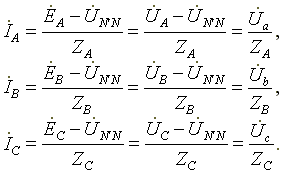 (6.3)
(6.3)
Ток в нейтральном проводе
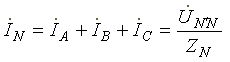 (6.4)
(6.4)
Частные случаи.
1. Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению ZA = ZB = ZC = R.
Узловое напряжение
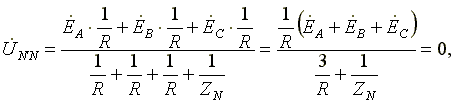 ,
,
потому что трехфазная система ЭДС симметрична, 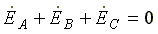 .
.
Напряжения фаз нагрузки и генератора одинаковы:
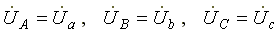
Фазные токи одинаковы по величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует
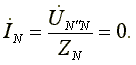
В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.
На рис. 6.6 изображена векторная диаграмма трехфазной цепи для симметричной нагрузки.
2. Нагрузка несимметричная, RA< RB = RC, но сопротивление нейтрального провода равно нулю: ZN = 0. Напряжение смещения нейтрали
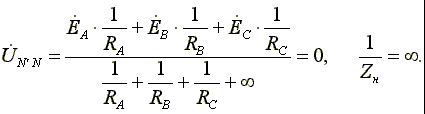
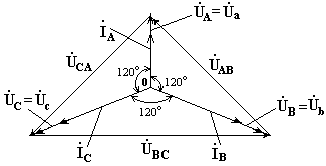
рис. 6.6
Фазные напряжения нагрузки и генератора одинаковы
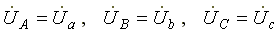
Фазные токи определяются по формулам
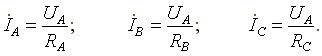
Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.
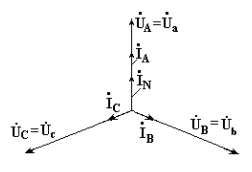 На рис. 6.7 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.
На рис. 6.7 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.
Рис. 6.7
3. Нагрузка несимметричная, RA< RB = RC, нейтральный провод отсутствует,
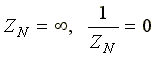
В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:
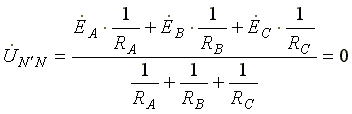
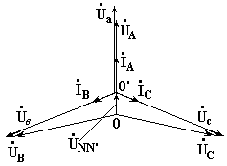 Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.
Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.
Из-за напряжения смещения нейтрали фазные напряжения нагрузки становятся неодинаковыми.
Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.
На рис. 6.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми.
Рис. 6.8
Симметричным режимом трехфазной цепи называют режим, при котором трехфазные системы токов и напряжений в этой цепи одновременно симметричны. Для реализации такого режима необходимо, чтобы сопротивления всех фаз были одинаковы.
На рис. 11.3 приведены векторные диаграммы, характерные для цепи при симметричном режиме в случае соединения нагрузки звездой (рис. 11.3а) и треугольником (рис. 11.3б).

Из приведенных диаграмм следуют простые соотношения, связывающие фазные и линейные токи и напряжения в симметричных режимах.
Вектора  ,
,  и
и  на рис. 11.3а образуют равнобедренный треугольник с углом 30 градусов при основании, следовательно
на рис. 11.3а образуют равнобедренный треугольник с углом 30 градусов при основании, следовательно
 или
или 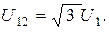
Аналогичные соотношения связывают другие линейные и фазные напряжения, а также фазные токи с линейными в случае соединения треугольником, поэтому
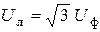 — при соединении звездой,
— при соединении звездой,
 — при соединении треугольником .
— при соединении треугольником .
Активная мощность в случае симметричной трехфазной нагрузки определяется в виде:
 или
или 
где 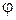 — угол сдвига между фазным напряжением и фазным током.
— угол сдвига между фазным напряжением и фазным током.
Аналогичный вид имеют выражения для реактивной и полной мощностей:
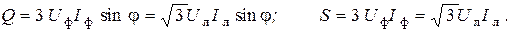
В симметричной трехфазной цепи токи и напряжения различных фаз одинаковы по амплитуде и отличаются только начальными фазами. Поэтому информации об этих параметрах в одной из фаз достаточно, чтобы определить состояние всей трехфазной цепи. Следовательно, расчет трехфазной цепи может быть выполнен по схеме замещения, составленной для одной фазы.
У источника энергии, выполненного по схеме «звезда», концы фазных обмоток X, Y, Z генератора соединяются в общий узел в N (рис. 4.2).
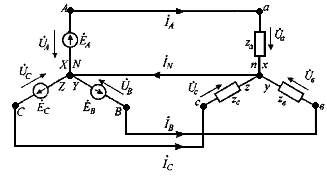
Рис. 4.2. Схема электрической цепи при соединении источника и приемника
по схеме «звезда» с нулевым проводом
Аналогичный узел п образует соединение концов x, y, z трех фаз приемника, а точки Nun соединяет нейтральный провод, в результате чего потенциалы этих точек равны. Остальные три провода, соединяющие выводы генератора А, В, С с выводами приемника а, в, с, называются линейными.
Таким образом, вместо шести проводов (в случае раздельного питания фаз приемника однофазными источниками) трехфазная система, выполненная по схеме «звезда» с нулевым проводом, содержит четыре провода.
Следовательно, трехфазная электрическая цепь обеспечивает передачу электрической энергии с меньшими потерями и с меньшим расходом материала проводов при передаче одинаковой мощности. В этом состоит преимущество трехфазных электрических цепей перед однофазными.
Линейные токи  в линиях (проводах) А – а, В – в, С – с определяются по закону Ома в комплексной форме:
в линиях (проводах) А – а, В – в, С – с определяются по закону Ома в комплексной форме:

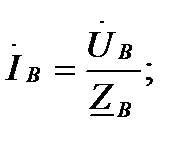
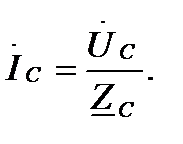 (4.4)
(4.4)
Ток  в нейтральном проводе связан с линейными токами законом Кирхгофа в комплексной форме:
в нейтральном проводе связан с линейными токами законом Кирхгофа в комплексной форме:
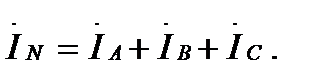 (4.5)
(4.5)
Очевидно, что в схеме (рис. 4.2) линейные токи  являются одновременно и фазными, т.е. они протекают одновременно в фазах источника и приемника и в соединяющих их проводах (линиях).
являются одновременно и фазными, т.е. они протекают одновременно в фазах источника и приемника и в соединяющих их проводах (линиях).
Соединение приемника по схеме «треугольник»
В этом случае к фазным выводам источника электрической энергии А, В, С подсоединяются выводы приемника а, в, с (рис. 4.4)
Таким образом, к фазам приемника приложена симметричная система линейных напряжений трехфазного источника электрической энергии.
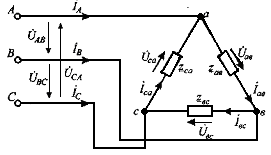
Рис. 4.4. Схема трехфазной электрической цепи при соединении приемника
«треугольником»
В линейных проводах А — а, В – в, С – с протекают линейные токи  В фазах приемника протекают фазные токи
В фазах приемника протекают фазные токи  , определяемые по закону Ома в комплексной форме:
, определяемые по закону Ома в комплексной форме:
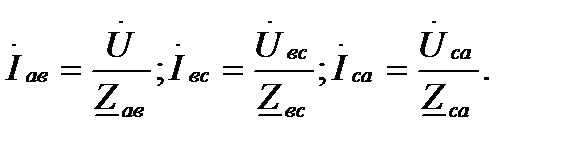 (4.9)
(4.9)
Линейные токи 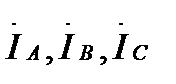 при известных фазных токах находятся по первому закону Кирхгофа в комплексной форме:
при известных фазных токах находятся по первому закону Кирхгофа в комплексной форме:
 (4.10)
(4.10)
Из уравнений (4.9) и (4.10) следует, что при симметричном приемнике ( 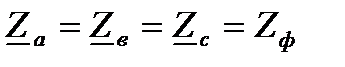 ) системы фазных (
) системы фазных ( 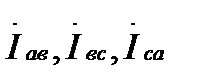 ) и линейных (
) и линейных (  ) токов симметричны, а модули фазных
) токов симметричны, а модули фазных 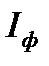 и линейных
и линейных 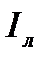 токов находятся в соотношении:
токов находятся в соотношении:
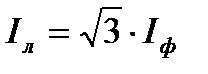 . (4.11)
. (4.11)
В случае несимметричного приемника токи не будут представлять собой симметричные системы и соотношение (4.11) не выполняется.
Что такое звезда и треугольник
Соединение в звезду подразумевает под собой такое соединение, в котором все рабочие концы фазных обмоток объединяются в один узел, называемый нулевой или нейтральной точкой и обозначается буквой O.
Соединение в треугольник представляет собой схему, при которой фазные обмотки генератора соединяются таким образом, что начало одной из них соединяется с концом другой.
к содержанию ↑
Разница между звездой и треугольником
В чем же разница между соединением звездой и треугольником? Различие в указанных схемах состоит в соединении концов обмоток генератора электродвигателя. В схеме «звезда», все концы обмоток соединяются вместе, тогда как в схеме «треугольник»конец одной фазной обмотки монтируется с началом следующей.

Кроме принципиальной схемы сборки, электродвигатели с фазными обмотками, соединенными звездой, функционируют значительно мягче, чем двигатели, имеющие соединение фазных обмоток в треугольник. Но при соединении звездой электродвигатель не имеет возможности развивать свою полную паспортную мощность. Тогда как, при соединении фазных обмоток в треугольник двигатель всегда работает на полную заявленную мощность, которая почти в полтора раза выше, чем при соединении в звезду. Большим недостатком соединения треугольником являются очень большие величины пусковых токов.
СоединениеВ соединении звезда аналогичные концы (либо начало, либо конец) трех обмоток соединены с общей точкой, называемой звездой или нейтральной точкой. Трехпроводные проводники проходят от остальных трех свободных клемм, называемых линейных проводников .
Провода передаются во внешнюю цепь, давая трехфазные, трехпроводные системы, соединенные звездой. Однако иногда четвертый провод переносится от точки звезды к внешней цепи, называемой , нейтральный провод , образуя трехфазные четырехпроводные системы, соединенные звездой.
Содержание:
Звездообразное соединение показано на диаграмме ниже:
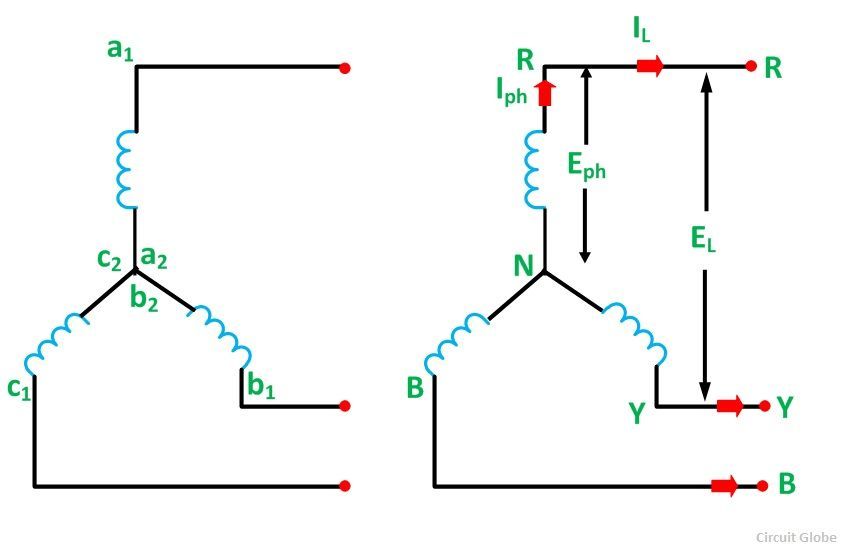 Учитывая приведенный выше рисунок, финишные клеммы a 2 , b 2 и c 2 из трех обмоток соединены в звезду или нейтральную точку. Три проводника, обозначенные как R, Y и B, проходят от оставшихся трех свободных клемм, как показано на рисунке выше.
Учитывая приведенный выше рисунок, финишные клеммы a 2 , b 2 и c 2 из трех обмоток соединены в звезду или нейтральную точку. Три проводника, обозначенные как R, Y и B, проходят от оставшихся трех свободных клемм, как показано на рисунке выше.
Ток, протекающий через каждую фазу, называется Фазовый ток I ph , а ток, протекающий через каждый линейный провод, называется Линейный ток I L .Аналогично, напряжение на каждой фазе называется фазным напряжением E ph , а напряжение на двух линейных проводниках называется линейным напряжением E L .
Соотношение между фазным напряжением и линейным напряжением в соединении звезды
Звездное соединение показано на рисунке ниже:
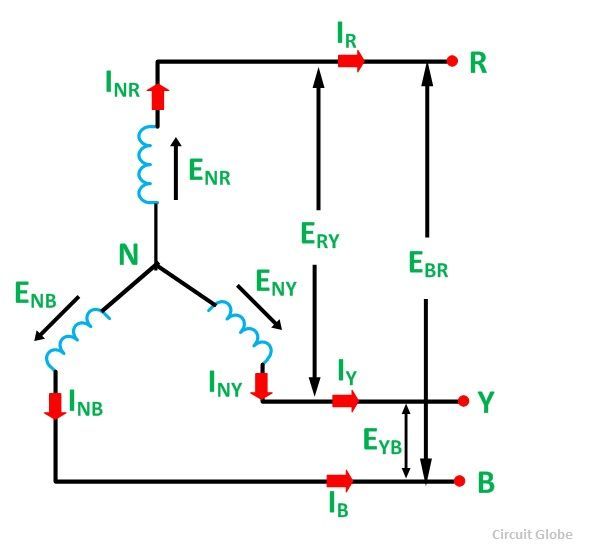 Поскольку система сбалансирована, сбалансированная система означает, что во всех трех фазах, то есть R, Y и B, через них протекает одинаковое количество тока.Следовательно, три напряжения E NR , E NY и E NB равны по величине, но смещены относительно друг друга на 120 °.
Поскольку система сбалансирована, сбалансированная система означает, что во всех трех фазах, то есть R, Y и B, через них протекает одинаковое количество тока.Следовательно, три напряжения E NR , E NY и E NB равны по величине, но смещены относительно друг друга на 120 °.
Диаграмма Phasor соединения звезды показана ниже:
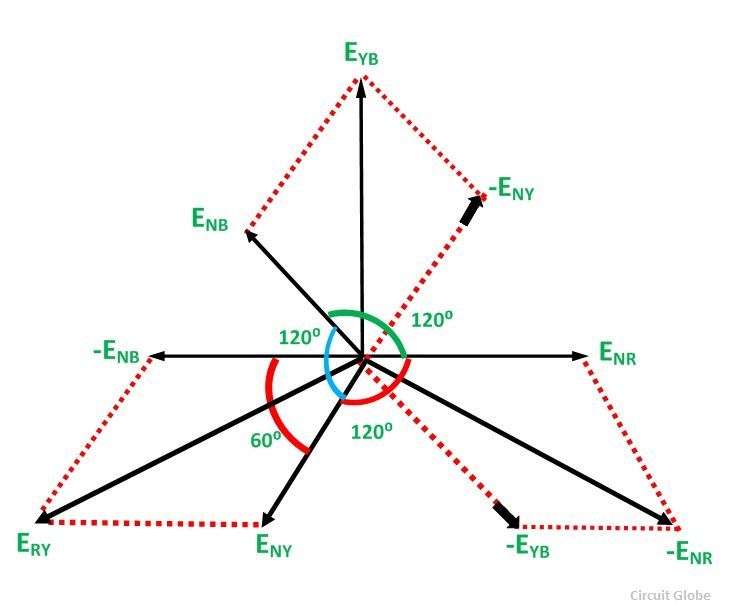 Стрелки на ЭДС и токе указывают направление, а не их фактическое направление в любой момент.
Стрелки на ЭДС и токе указывают направление, а не их фактическое направление в любой момент.
Сейчас
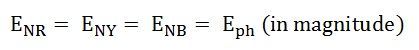
Между любыми двумя линиями имеется двухфазное напряжение.
Трассировка петли NRYN
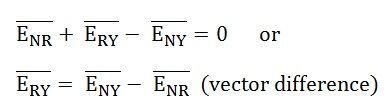
Чтобы найти векторную сумму ENY и –ENR, мы должны обратить вектор ENR и добавить его с помощью ENY, как показано на векторной диаграмме выше.
Следовательно,
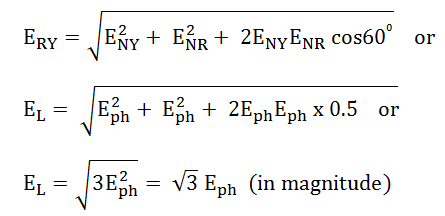
Аналогично,

Следовательно, в соединительной линии звездное напряжение в корне в 3 раза больше фазового напряжения.
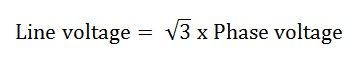
Соотношение между фазным током и линейным током в соединении звезды
Ток такой же силы течет через фазовую обмотку, а также через линейный провод, поскольку он соединен последовательно с фазовой обмоткой.
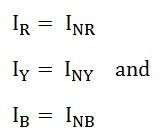
Где фазовый ток будет:
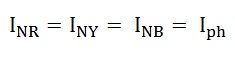
Ток линии будет:
Следовательно, в 3-фазной системе звездных соединений ток в линии равен фазному току.
,3-фазные значения мощности, напряжения и тока
Подключение трехфазной звезды: линия, ток фазы, напряжения и мощность в конфигурации Y
Что такое подключение звезды (Y)?
Звездное соединение ( Y ) Система также известна как Трехфазная четырехпроводная система (3000-фазный провод ), и она является наиболее предпочтительной системой для распределения электроэнергии переменного тока при передаче, Delta. соединение обычно используется.
В системе взаимосвязи Star (также обозначаемой Y ) начальные концы или конечные концы (аналогичные концы) трех катушек соединяются вместе, образуя нейтральную точку. Или
Звездное соединение получается путем соединения вместе одинаковых концов трех катушек: «Старт» или «Финиш». Другие концы соединены с проводами линии. Общая точка называется нейтральной или звездной точкой , которая представлена N .(Как показано на рис. 1)
Звездное соединениетакже называется трехфазной 4-проводной (3-фазной, 4-проводной) системой.
Также читайте:
Если симметричная нагрузка баланса подключена параллельно к трехфазной системе напряжения, то в нейтральном проводе будут течь три тока, величины которых будут одинаковыми, но они будут отличаться на 120 ° (не в фазе) следовательно, векторная сумма этих трех токов = 0. т.е.
I R + I Y + I B = 0 …………….Викториально
Напряжение между любыми двумя клеммами или напряжение между линией и нейтралью (точка звезды) называется фазным напряжением или напряжением звезды, обозначаемым V Ph . А напряжение между двумя линиями называется линейным напряжением или линейным напряжением, обозначаемым V L .
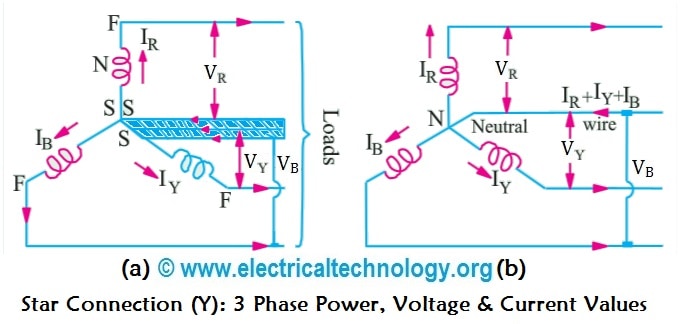
 Звездное соединение (Y) Трехфазные значения мощности, напряжения и тока
Звездное соединение (Y) Трехфазные значения мощности, напряжения и токаЗначения напряжения, тока и мощности в соединении звезды (Y)
Теперь мы найдем значения линейного тока, линейного напряжения, фазного тока , Фазовые напряжения и мощность в трехфазной системе переменного тока Star.
Напряжение в линии и фазное напряжение в соединении звезда
Мы знаем, что линейное напряжение между линией 1 и линией 2 (из рисунка 3а) составляет
В RY = V R — V Y …. (Разница в векторах)
Таким образом, чтобы найти вектор V RY , увеличьте Вектор V Y в обратном направлении, как показано в пунктирной форме на рисунке 2 ниже. Аналогично, на обоих концах вектора V R и Vector V Y делают перпендикулярные пунктирные линии, которые выглядят как параллелограмм, как показано на рис. (2).Диагональная линия, которая делит параллелограмм на две части, показывает значение V RY . Угол между векторами V Y и V R составляет 60 °.
Следовательно, если
V R = V Y = V B = V PH
, то
V RY = 2 x V PH x Cos (60 ° / 2)
= 2 x В PH x Cos 30 °
= 2 x V PH x (√3 / 2) …… Поскольку Cos 30 ° = √3 / 2
V RY = √3 В PH
Аналогично,
В YB = V Y — V B
В YB = √3 В PH
И
В BR = V B — V R
V BR = √3 V PH
Таким образом, доказано, что V RY = V YB = V BR линейные напряжения (V L ) в соединении звезда , поэтому в соединении звезда;
В L = √3 В PH или V L = √3 E PH
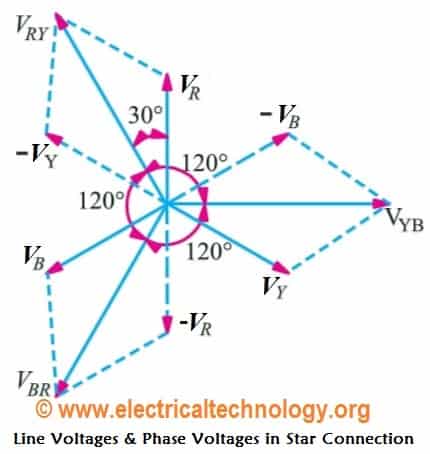
 Линейные и фазные напряжения при подключении звезды
Линейные и фазные напряжения при подключении звездыИз рисунка 2 видно, что;
- Линейные напряжения находятся на расстоянии 120 ° друг от друга
- Линейные напряжения на 30 ° идут выше соответствующих фазных напряжений
- Угол Ф между линейными токами и соответствующими линейными напряжениями составляет (30 ° + Ф), т.е.е. ток каждой линии отстает (30 ° + Ф) от соответствующего напряжения сети.
Связанный пост: нагрузка освещения со звездой и треугольником
Токи линии и фазные токи в соединении звезды
Из рисунка (3а) видно, что каждая линия последовательно с отдельной фазовой обмоткой, поэтому значение ток в линии такой же, как в фазных обмотках, к которым подключена линия. т.е. .;
- Ток в линии 1 = I R
- Ток в линии 2 = I Y
- Ток в линии 3 = I B
Поскольку текущие токи во всех трех линиях одинаковы, и следовательно, отдельный ток в каждой линии равен соответствующему фазному току;
I R = I Y = I B = I PH ….Фазовый ток
Линейный ток = Фазный ток
I L = I PH
Проще говоря, значения линейных токов и фазных токов одинаковы в соединении звездой .
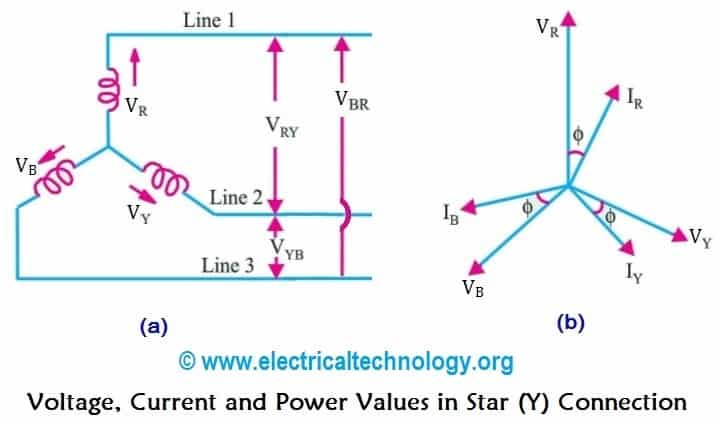
 Звездное соединение (Y): Значения линейных токов и напряжений и фазных токов и напряжений
Звездное соединение (Y): Значения линейных токов и напряжений и фазных токов и напряженийМощность в звездообразном соединении
В трехфазной цепи переменного тока полная Истинная или Активная мощность представляет собой сумму трехфазной мощности. ,Или сумма всех трех фазовых мощностей — Полная Активная или Истинная Мощность.
Следовательно, общая активная или истинная мощность в трехфазной системе переменного тока;
Полная истинная или активная мощность = 3-фазная мощность
или
P = 3 х В PH x I PH x CosФ … .. Уравнение (1)
Мы знаем, что значения фазного тока и фазного напряжения в соединении звезды;
I L = I PH
V PH = V L / √3 …., (От В L = √3 В PH )
Приведение этих значений в уравнение мощности ……. (1)
P = 3 x (V L / √3) x I L x CosФ …….…. (V PH = V L / √3)
P = √3 x√3 x (V L / √3) x I L x CosФ….… {3 = √3x√3 }
P = √3 x V L x I L x CosФ
Следовательно доказано;
Мощность в соединении звезда ,
P = 3 x В PH x I PH x CosФ или
P = √3 x V L x I L x CosF
То же самое объясняется в MCQ с 3 фазами с пояснительным ответом (MCQ No.1)
Аналогичным образом,
Общая реактивная мощность = Q = √3 x В L x I L x SinФ
Где Cos Φ = Коэффициент мощности = фазовый угол между фазным напряжением и фазным током, а не между линейным током и линейным напряжением.
Полезно знать : Реактивная мощность индуктивной катушки принимается за положительную (+), а за конденсаторную — за отрицательную (-).
Кроме того, общая кажущаяся мощность трех фаз;
Общая кажущаяся мощность = S = √3 x В L x I L Или
S = √ (P 2 + Q 2 )
Читайте также:
.Разница между соединением звезда и треугольник
Разница между соединением звезда и треугольник объясняется с учетом различных факторов, таких как базовое определение соединений, наличие нейтральной точки, соединение клемм, соотношение между линейным током и фазным током, а также между линейным напряжением и фазным напряжением, скорость, уровень изоляции, количество оборотов, тип системы, использование сети и т. д.
Разница между соединением звезда и треугольник приведена ниже в виде таблицы и формы .
| ОСНОВАНИЕ | СОЕДИНЕНИЕ ЗВЕЗД | ПОДКЛЮЧЕНИЕ DELTA |
|---|---|---|
| Базовое определение | Клеммы трех ответвлений подключены к общей точке. Сформированная сеть известна как Star Connection | Три ветви сети соединены таким образом, что она образует замкнутый контур, известный как Delta Connection | .
| Соединение клемм | Начальная и конечная точки, которые являются одинаковыми концами трех катушек, соединены вместе | Конец каждой катушки соединен с начальной точкой другой катушки, что означает, что противоположные клеммы катушек связаны друг с другом. |
| Нейтральная точка | Нейтральная или звездная точка существует в соединении звезды. | Нейтральная точка не существует в соединении треугольником. |
| Соотношение между током линии и фазы | Ток линии равен фазному току. | Ток линии равен корню в три раза больше тока фазы. |
| Соотношение между линейным и фазным напряжением | Напряжение в линии равно корню, в три раза превышающему фазное напряжение | Напряжение в линии равно фазному напряжению. |
| Скорость | Скорость двигателей, подключенных к звезде, мала, поскольку они получают 1 / √3 напряжения. | Скорость подключенных треугольником двигателей высока, потому что каждая фаза получает общее напряжение сети. |
| Фазовое напряжение | Фазовое напряжение в 1 / √3 раз превышает линейное напряжение. | Фазовое напряжение равно линейному напряжению. |
| Число витков | Требуется меньшее количество витков | Требуется большое количество витков. |
| Уровень изоляции | Требуется низкая изоляция. | Требуется высокая изоляция. |
| Тип сети | В основном используется в сетях передачи электроэнергии. | Используется в распределительных сетях. |
| Полученное напряжение | В соединении звездой каждая обмотка получает 230 вольт | В соединении треугольником каждая обмотка получает 414 вольт. |
| Тип системы | Как трехфазная четырехпроводная, так и трехфазная трехпроводная система может быть получена при соединении звездой. | Трехфазная четырехпроводная система может быть получена из соединения Delta. |
В этой статье объясняется разница между звездой и треугольником. В трехфазной цепи есть два типа соединений. Один из них называется Star Connection, а другой — Delta Connection. Звездное соединение имеет общую или звездную точку, к которой подключены все три клеммы, образуя форму звезды, как показано ниже.
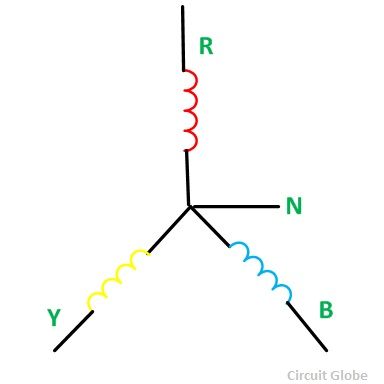
В соединении треугольником все три клеммы соединены вместе, образуя замкнутый контур.При этом нет общей или нейтральной точки, и она используется для передачи энергии на короткие расстояния. Схема подключения показана ниже.
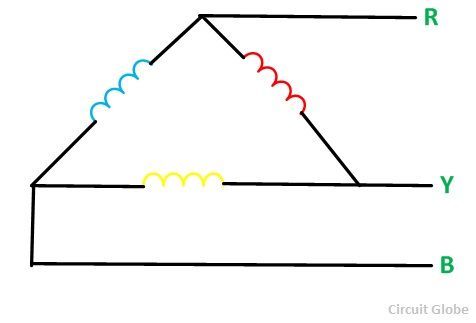
Разница между соединением звезда и треугольник заключается в следующем: —
- Клеммы трех ответвлений связаны с общей точкой. Сформированная сеть известна как Star Connection . Три ветви сети связаны таким образом, что она образует замкнутый контур, известный как Delta Connection .
- В соединении звездой концы начальной и конечной точек трех катушек соединены вместе в общую точку, известную как нейтральная точка . Но в соединении Delta нет нейтральной точки. Конец каждой катушки соединен с начальной точкой другой катушки, что означает, что противоположные выводы катушек соединены вместе.
- В соединении «звезда» ток в линии равен фазному току, тогда как в соединении «треугольник» ток в линии равен корню, в три раза превышающему фазный ток.
- В соединении «звезда» линейное напряжение равно корневому значению в три раза от напряжения фазы, тогда как в соединении «треугольник» напряжение линии равно напряжению фазы.
- Скорость соединенных звездой двигателей является низкой, поскольку они получают 1 / √3 напряжения, но Скорость соединенных треугольником двигателей высока, потому что каждая фаза получает суммарное напряжение линии.
- В соединении «звезда» фазовое напряжение в 1 / √3 раз меньше напряжения сети, тогда как в соединении «треугольник» напряжение фазы равно напряжению сети. Соединения типа «звезда»
- в основном требуются для сети электропередачи на большие расстояния, тогда как в соединении «треугольник» главным образом в распределительных сетях и используются на более короткие расстояния.
- В соединении «звезда» каждая обмотка получает 230 вольт, а в соединении «треугольник» каждая обмотка получает 415 вольт.
- Как трехфазная 4-проводная, так и 3-фазная 3-проводная системы могут быть получены в звездообразном соединении, тогда как в Delta Connection может быть получена только 3-фазная 4-проводная система.
- Количество требуемой изоляции в соединении «звезда» низкое, а в соединении «треугольник» требуется высокий уровень изоляции.
Соединение трехфазного двигателя Звезда / треугольник (Y-Δ) Реверс и Вперед с диаграммой питания и управления таймера
Как мы имеем уже поделился метод запуска трехфазного двигателя от Star Delta Starter с цепью таймера (цепи питания и управления). Теперь на следующих рисунках трехфазный двигатель будет вращаться в двух направлениях, а именно вперед и назад. Но мы контролировали направление вращения этого трехфазного двигателя с помощью цепи таймера.
Сокращения:
O / L = реле перегрузки
NO = нормально разомкнутый
NC = нормально замкнутый
FOR = вперед
REV = назад
T = таймер
3-фазное подключение двигателя звезда / треугольник (Y-Δ) Реверс / Вперед с таймером Питание Диаграмма
Схема питания:
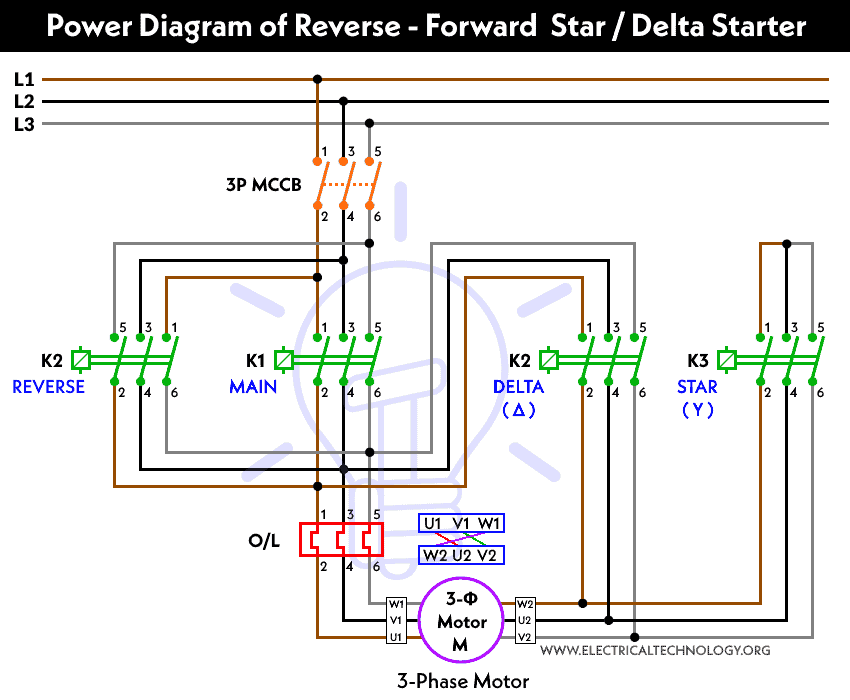

3-фазное подключение двигателя Звезда / Дельта (Y-Δ) Реверс / Вперед с таймером Управление Диаграмма
Схема управления :
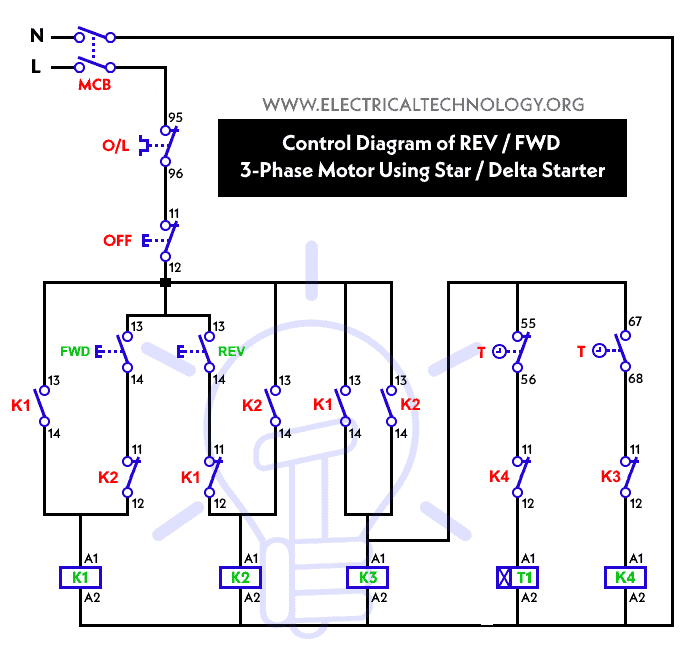
 ,
,