Треугольник мощности – Треугольник мощностей

Треугольник мощностей

Дата публикации: 17 апреля 2015.
Категория: Электротехника.

Если величины треугольника напряжений (рисунок 1, а) умножить на ток I (рисунок 1, б), то получим треугольник мощностей (рисунок 1, в). Все стороны треугольника мощностей, показанного отдельно на рисунке 2, представляют собой мощности.

Рисунок 1. Получение треугольника мощностей

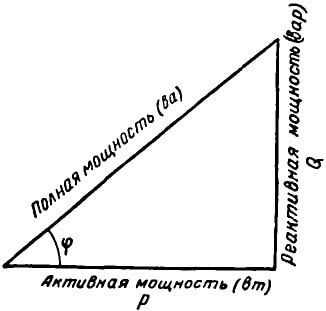Рисунок 2. Треугольник мощностей

Гипотенуза треугольника мощностей есть полная мощность S.

S = U × I .

Она измеряется в вольт-амперах (ВА) или киловольт-амперах (кВА) по показаниям вольтметра и амперметра. Величина полной мощности характеризует основные габариты (наибольшие размеры) генераторов и трансформаторов. В самом деле, изоляция обмоток генераторов и трансформаторов рассчитывается на определенное напряжение, а величина тока определяет нагрев их обмоток (I² × r).

Катет, прилегающий к углу φ, представляет собой известную нам активную мощность P.

P = U_а × I .

Так как U_а = I × r, то

P = I² × r .

Активная мощность в цепях переменного тока расходуется на нагрев. В двигателях переменного тока большая часть активной мощности превращается в механическую мощность.

Активная мощность измеряется ваттметром и выражается в ваттах (Вт) или киловаттах (кВт). Из треугольника мощностей имеем:

P = S × cos φ = U × I × cos φ .

Активная мощность характеризует степень нагрузки первичного двигателя, вращающего генератор.

Катет, лежащий против угла φ, есть реактивная мощность Q.

Q = U_r ×I .

Так как U_r = I × x (где x – реактивное сопротивление), то

Q = I² × x .

Реактивная мощность обусловлена наличием магнитных и электрических полей в индуктивностях и емкостях цепей. Из треугольника мощностей имеем:

Q = S × sin φ = U × I × sin φ .

Реактивная мощность измеряется в вольт-амперах реактивных (вар) или киловольт-амперах реактивных (квар). Применяя к треугольнику мощностей теорему Пифагора, получим:

S² = P² + Q²

или

Рассмотрим электрическую цепь, показанную на рисунке 3, в которую входят индуктивное и активное сопротивления и измерительные приборы – амперметр, вольтметр и ваттметр.

1. Если подключить эту цепь к постоянному напряжению, то, поскольку индуктивное сопротивление xL при постоянном токе будет равно нулю, в цепи остается одно активное сопротивление r и тогда

Амперметр покажет ток 5 А.

Мощность

P = I × U = 5 × 120 = 600 Вт

или

P = I² × r = 25 × 24 = 600 Вт .

Следовательно, ваттметр покажет 600 Вт. Таким образом, ваттметр, включенный в цепь постоянного тока, показывает мощность в ваттах, потребляемую цепью. Показание ваттметра равно произведению показаний вольтметра и амперметра.

2. Подключим ту же цепь к переменному напряжению.

В этом случае:

Ток в цепи

Амперметр покажет ток 4 А.

Подсчитаем мощность, идущую на нагрев:

P = I² × r = 4² × 24 = 384 Вт .

Показание ваттметра в этом случае будет 384 Вт.

Полная мощность, забираемая цепью от источника переменного тока,

S = I × U = 4 × 120 = 480 Вт .

Следовательно, генератор, питающий эту цепь, отдает полную мощность S = 480 ВА. Но в самой цепи только активная мощность P = 384 Вт безвозвратно теряется в виде тепла.

Отсюда видно, что цепь переменного тока, содержащая наряду с активным сопротивлением индуктивное, из всей получаемой ею полной энергии только часть расходует на тепло. Остальная часть – реактивная энергия – то забирается цепью от генератора и запасается в магнитном поле катушки, то возвращается обратно генератору.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

www.electromechanics.ru

2.2. Виды мощности. Треугольник мощностей

В цепях переменного тока различают три понятия мощности: активная Р, реактивная Q, полная S.

Соотношения между мощностями могут быть получены из треугольника мощностей, который образуется путем умножения всех сторон треугольника напряжений на значение тока I.

Рис.2.3. Треугольник мощностей

Здесь:

Q_L— реактивная индуктивная мощность,

Q_C — реактивная емкостная мощность.

Активная мощность [Вт] — характеризует необратимый процесс преобразования электромагнитной энергии источника в другие виды энергии: механическую, тепловую, световую и т.д.

Реактивная мощность [Вар] (вольт-ампер реактивный) — характеризует обратимый процесс преобразования электромагнитной энергии источника в энергию магнитного поля катушки и энергию электрического поля конденсатора.

Полная мощность [ВА] (вольт-ампер) — характеризует наибольшее значение активной мощности при заданных действующих значениях тока и напряжения.

Как видно из выражения активной мощности, если мощность, потребляемая приемником в данной цепи, является вполне определенной величиной, то при неизменном напряжении на зажимах цепи и с уменьшением ток нагрузки источника будет увеличиваться при одной и той же отдаваемой мощности.

.

(2.11.)

Поэтому даже при полной загрузке током источника, но при низком источник по мощности будет недогружен. Значениехарактеризует использование полной или установленной мощности источника и называется коэффициентом мощности.

Наибольшего значения активная мощность достигает при = 1, т.е. когда = 0, или, как следует из выражения (2.10), когда . Такой режим работы называется резонансом напряжений. Явление резонанса напряжений как положительный эффект используется в технике слабых токов (в радиотехнике). В технике сильных токов резонанс напряжений является аварийным режимом, т.к. в этом случае напряжения на реактивных элементах могут достигать значений, намного превышающих приложенное напряжение, что может привести к пробою изоляции конденсаторов и катушек индуктивности.

2.3. Параметры цепи и характер нагрузки

Работа электрической цепи может быть описана, по крайней мере, тремя основными параметрами: напряжением (U), током (I) и активной мощностью (P). Произведение напряжения и тока в цепи дает нам полную мощность цепи (S = UI), а реактивную мощность (Q) можно найти из треугольника мощностей, зная полную и активную мощности.

Если активная мощность равна полной (P = S), то реактивная мощность обращается в ноль (Q = 0), тогда характер нагрузки является активным, а схема замещения цепи содержит только активное сопротивление.

Если активная мощность в цепи равна нулю (P = 0), то полная мощность равна реактивной (Q = S), тогда характер нагрузки становится реактивным: или индуктивным (если в цепи содержится реактивное индуктивное сопротивление), или емкостным (если в цепи содержится реактивное емкостное сопротивление), а схема замещения содержит или индуктивность, или емкость.

Если активная мощность имеет значение отличное от нуля, но при этом меньше полной (0 < P < S), то мы имеем случай, когда характер нагрузки смешанный. Какой конкретно характер нагрузки будет, — зависит от разницы между реактивными сопротивлениями Х_L — Х_C. Если разница положительная (X_L > X_C ), то характер нагрузки активно-индуктивный, если отрицательная (X

L < X_C ) – активно-емкостной.

Таким образом характер нагрузки может быть определен, если известна структура цепи. Это легко сделать для простых электрических цепей. Для более сложных электрических цепей, содержащих большое количество электротехнических устройств, обычно используют фазометр, позволяющий определить угол сдвига фаз между напряжением и током и его характер: емкостной или индуктивный.

studfile.net

как найти, формула расчёта, в чем измеряется

Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.

Мощность в цепи переменного электрического тока

Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.

Мощность – физическая величина, отражающая скорость преобразования или передачи электрической энергии.

В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.

Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.

При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.

Понятие активной мощности

Активная “полезная” мощность – это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).

Рассчитывается по формуле: P = U⋅I⋅cosφ,

где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.

ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73

Понятие реактивной мощности

Реактивная “вредная” мощность – это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.

Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.

Обозначается эта величина латинской буквой Q.

ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).

Рассчитывается по формуле:

Q = U⋅I⋅sinφ,

где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.

ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.

Емкостные и индуктивные нагрузки

Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.

Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.

ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.

Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.

ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.

Коэффициент мощности cosφ

Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.

Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.

ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.

Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.

Понятие полной мощности. Треугольник мощностей

Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.

Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.

S = U⋅I

ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).

Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.

Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.

Как найти активную, реактивную и полную мощности. Пример расчета

Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.

Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.

Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.

Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.

Как измеряют cosφ на практике

Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.

Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.

1. Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
2. Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.

Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.

odinelectric.ru

Электрическая мощность. Треугольник мощностей. — Теоретические основы электротехники — Каталог статей

Электрическая мощность. Треугольник мощностей.  Сегодня мы поговорим об электрической мощности, о том, что это такое, о её видах и о том, чем они отличаются.Начнем с определения. Электрическая мощность – величина, характеризующая скорость передачи (преобразования) электроэнергии. Соответственно, если мощность это скорость преобразования электроэнергии, то по аналогии с расчетом обычной скорости (например автомобиля), для её расчета необходимо в знаменатель поставить время, а в числитель электроэнергию. Пример — электрочайник включили, чтобы вскипятить воду, за 6 минут счетчик «накрутил» 0,2 кВт*ч, найдем мощность чайника: Р = W / t (Р – активная мощность, W – электроэнергия, t – время), Р = 0,2 / (6/60) = 2 кВт. Если то же количество электроэнергии фен «потребил» за время 9 мин, то по той же формуле Р2 = W2 / t = 0,2 / (9/60) = 1,33 кВт. Обратите внимание, чайник потребил одинаковое количество электроэнергии, но за меньшее время, именно поэтому он мощнее, то есть он обладает большей мощностью. То? о чем мы говорили в предыдущем абзаце, отражает физический смысл понятия «электрическая мощность». Теперь поговорим о мощности в энергетическом ракурсе. В зависимости от вида мощности измеряться она может в ВА (Вольт-Амперах) – полная мощность, Вт (ваттах) – активная мощность  или вар (Вольт-Ампер реактивный) – реактивная мощность. Кстати, несмотря на присутствие имен собственных в единице вар, в международной системе единиц (СИ) принято решение обозначать единицы реактивной мощности с маленькой буквы– вар. Итак, полная мощность, судя по названию, выражает всю мощность переданную или преобразованную электроустановкой. Она обозначается буквой S и измеряется в Вольт-Амперах (ВА). Полная мощность однофазной цепи S = U*I, ВА, 3-хфазной цепи S = √3*U*I, где U – линейное напряжение, I – фазный ток (данная формула применима для симметричной нагрузки, при нессиметричной нагрузке необходимо суммировать мощность каждой фазы). Активная мощность является частью полной и характеризует электрическую энергию, преобразуемую в любой другой вид энергии. Например, вентилятор преобразовывает электрическую энергию в механическую, а печка в тепловую и т.п. Активная мощность обозначается Р и измеряется в Вт. Формула активной мощности Р = S*cos φ, для однофазной цепи Р = U*I* cos φ, для 3-хфазной Р = √3*U*I*cos φ, где U – линейное напряжение, I – фазный ток. Угол φ – так называемый угол сдвига фаз (между током и напряжением цепи) или коэффициент мощности, он может изменяться в пределах от 0 до 1. В случае, когда cos φ = 1, активную мощность можно выразить как Р = I2*R (вспоминаем правило Джоуля-Ленца), в этом случае Р = I2*R = S. Есть ещё реактивная мощность, характеризующая циклические режимы в электротехнических устройствах, или можно сказать, что реактивная мощность учитывает нагрузки, создаваемые в электроустановках колебаниями энергии в цепях переменного тока. Довольно непонятно, не правда ли? Попробуйте выучить любое из понравившихся Вам определений, чтобы блеснуть им в каком-нибудь умном разговоре. На этом его польза и закончится. Итак, реактивная мощность – обозначается Q, измеряется в вар. Она численно равна Q = S*sinφ (1-нофазные цепи) и Q = √3*U*I* sin φ. Для понимания связи всех видов электрической мощности удобно воспользоваться графическим их изображением (рис. 1). Это так называемый, треугольник мощностей. Как мы видим S = √(Р2 + Q2). Приведем пример: Полная мощность цепи S = 100 кВА, cos φ = 0,9. Найти активную и реактивную мощность. Решение: если косинус φ равен 0,9 , то синус равен sin φ = 1-0.92 (основное тригонометрическое тождество) = 0,436. Тогда Р = 100*0,9, а Q = 100*0,436. Находим Р = 90 кВт, а Q = 43.6 квар. Пример2: 3-хфазный асинхронный двигатель (номинальное напряжение 380 В) имеет номинальную электрическую мощность 15 кВт, cos φ = 0,85. КПД принять 100 %. Рассчитать номинальный ток двигателя для последующего выбора кабельной линии. Решение I = P/(√3*U* cos φ) = 15/(1,73*0,38*0,85) = 26,8 А. 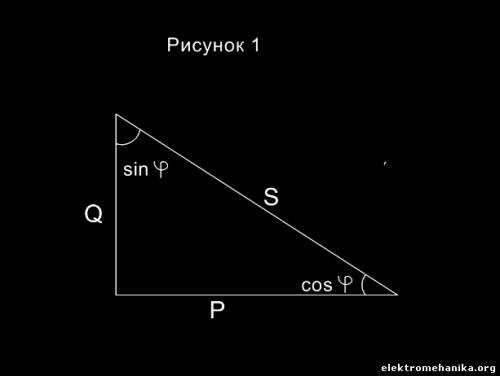Вадим Д. г.Волгодонск Ростовская обл.

elektromehanika.org

2.2.2. Виды мощности. Треугольник мощностей

В цепях переменного тока различают три понятия мощности: активная Р, реактивная Q, полная S.

Соотношения между мощностями могут быть получены из треугольника мощностей, который образуется путем умножения всех сторон треугольника напряжений на значение тока I.

Рис.2.4. Треугольник мощностей

Здесь Q_L— реактивная индуктив­ная мощность, Q_C — реактивная емкостная мощность.

Активная мощность P=U∙I∙Cosφ [Вт] — характеризует необратимый процесс преобразования электромагнитной энергии источника в другие виды энергии: механическую, тепловую, световую и т.д.

Реактивная мощность Q=U∙I∙Sinφ [Вар] (вольт-ампер реактивный) — характеризует обратимый процесс преобразования электромагнитной энергии источника в энергию магнитного поля катушки и энергию электрического поля конденсатора.

Полная мощность S=U∙I[ВА] (вольт-ампер) — характеризует наибольшее значение активной мощности при заданных действующих значениях тока и напряжения.

Как видно из выражения активной мощности, при неизменном напряжении на зажимах цепи и с уменьшением Cosφ ток нагрузки источника будет увеличиваться при одной и той же отдаваемой мощности:

I = . (2.10)

Поэтому даже при полной загрузке источника током , но при низком Cosφ источник по мощности будет недогружен.

Значение Cosφ характеризует использование полной мощности источника и называется коэффициентом мощности. Он показывает, какая доля полной мощности источника необратимо превращается в другой вид.

Наибольшего значения активная мощность достигает при Cosφ = 1, т.е. когда  = 0, или, как следует из выражения (2.9), когда X_L=X_C. Такой режим работы называется резонансом напряжений. Явление резонанса напряжений как положительный эффект используется в технике слабых токов (в радиотехнике). В технике больших токов резонанс напряжений является аварийным режимом, т.к. в этом случае напряжения на реактивных элементах могут достигать значений, намного превышающих приложенное напряжение, что может привести к пробою изоляции конденсаторов и катушек индуктивности.

2.2.3. Параметры цепи и характер нагрузки

Работа электрической цепи может быть охарактеризована тремя основными параметрами: напряжением (U), током (I) и активной мощностью (P). Произведение напряжения и тока дает полную мощность цепи (S = UI), а реактивную мощность (Q) можно найти из треугольника мощностей, зная полную и активную мощности.

При идеальной активной нагрузке вся энергия источника необратимо превращается в другой вид. Активная мощность равна полной (P = S=U∙I), а реактивная равна нулю (Q = 0).Схема замещения цепи с идеальной активной нагрузкой содержит только активное сопротивление R.

При идеальной реактивной нагрузке (индуктивной или емкостной) активная мощность равна нулю (P = 0), а реактивная мощность равна полной (Q = S=U∙I). Схема замещения будет содержать только индуктивность, или только емкость.

При смешанной нагрузке активная мощность отлична от нуля, но при этом она меньше полной (0 < P < S). Какой конкретно характер нагрузки будет, — зависит от разности между реактивными сопротивлениями Х_L — Х_C. Если разность положительная (X_L > X_C ), то нагрузка активно-индуктивная, если отрицательна (X_L < X_C ) — активно-емкостная.

Таким образом, характер нагрузки может быть определен, если известна структура цепи. Это легко сделать для простых электрических цепей. Для более сложных электрических цепей, содержащих большое количество электротехнических устройств, обычно используют фазометр, позволяющий определить угол сдвига фаз между напряжением и током и характер нагрузки: емкостной или индуктивный.

studfiles.net

Полная мощность. Треугольник мощностей — КиберПедия

 

Сделаем некоторые выводы.

Существует два типа элементов: активные элементы, всегда только потребляющие мощность и реактивные, средняя мощность потребления у которых равна нулю.

 

При синусоидальных напряжениях и токах все мгновенные мощности также являются синусоидальными функциями, частота их при этом в два раза больше, чем у тока и напряжения.

Активная мощность Р измеряется в Ваттах – Вт.

Реактивная мощность Q измеряется в варах (Вольт-Ампер реактивный, ВАр).

Q = Q_L— Q_C  (При последовательном соединении).

Полная мощность S измеряется в Вольт-Амперах (ВА).    

‌‌S = P + jQ =

 

Для записи комплекса мощности через ток и напря-жение, необходимо использовать понятие комплексно сопряжённого числа.

Для тока – İ = I₁ + jI₂ = I e^jψi

Комплексно сопряжённый ток: = I₁ — jI₂ = I e^—jψi

Обозначается со знаком звёздочки.

 

Комплекс мощности:

S = Ù

S = U e^jψu I e^-jψi = U I e^{j(ψu — ψi)} = S e^jφ

Основные соотношения такие же, как для сопротивлений.

φ = arctg Q/P P = S cos φ Q = S sin φ

 

 

Pисунок 2.27 — Треугольник мощностей

Для наглядности можно это представить в виде треугольника мощностей, который подобен треугольнику сопротивлений, с таким же углом φ (рисунок 2.27).

 

 

Важную роль в промышленном потреблении энергии играет угол сдвига фаз φ. Большинство потребителей энергии имеют индуктивный характер нагрузки (электродвигатели и пр.), в связи с чем увеличивается cos φ. Увеличение реактивной мощности за счёт активной означает бесполезное расходование мощности электрогенераторов и, зачастую, огромные материальные затраты – например при работе крупных промышленных предприятий.

Для предотвращения этого, на предприятиях, параллельно основной, подключается дополнительная ёмкостная нагрузка – для компенсации. Косинус φ должен соответствовать определённым нормам и не превосходить 0,9 — 0,95.

 

Резонанс

 

Резонанс напряжений

 

Рассмотрим цепь с последовательным соединением резистора, катушки и конденсатора (рисунок 2.28).

Рисунок 2.28 — Последовательное соединение R, L, C

 

Полное сопротивление цепи:

Z = R+ jX = R+ j( X_L— X_C)

 

Соотношения для определения токов и напряжений уже рассмотрены неоднократно, поэтому детально приводить их не имеет смысла. Векторные диаграммы показаны на рисунках 2.29 и 2.30.

 

Рисунок 2.29 — Сопротивления при последовательном соединении R, L, С: a – XL<XC, φ < 0, b — XL>XC, φ > 0

 

 

Рисунок 2.30 — Векторные диаграммы при последовательном соединении R, L, С: a – XL<XC, b — XL>XC

 

На рисунках показаны варианты при X_L< X_C и X_L> X_C. Возможен вариант, когда X_L= X_C и φ = 0. Такое явление в электрической цепи, содержащей L и C, при котором сдвиг фаз между током и напряжением равен нулю, называется резонансом. При резонансе цепь, несмотря на наличие реактивных элементов, ведёт себя как активное сопротивление (рисунок 2.31).

Электрическая цепь, в которой возможен резонанс, называется колебательным контуром. В данном случае, при последовательном соединении, схема называется последовательным колебательным контуром. Резонанс в такой цепи называется резонансом напряжений.

 

Условие резонанса: X_L= X_C => ω L=1/ω C

Рисунок 2.31 — Векторная диаграмма при последовательном резонансе

 

 

При заданных L и C резонанс возможен на одной частоте, называемой резонансной частотой ω₀:

 

 

Свойства схемы на частоте резонанса:

 

— φ = 0, напряжение и ток совпадают по фазе;

 

— Полное сопротивление Z = R;

 

— Ток в цепи максимальный I = I_max= U/ I;

 

— реактивные сопротивления равны. Подставив из формулы частоту резонанса, получим:

 

 

 

ρ называется волновым или характеристическим сопротивлением;

 

— Напряжения на L и C равны: U_L= U_C= X_LI = ρ I

 

— Общее напряжение цепи: U = U_R= RI

 

Важный момент: напряжения на реактивных элементах могут быть больше общего напряжения цепи, если ρ> R.

 

— Величина Q = ρ/ R = U_L/ U = U_C/ U называется добротностью колебательного контура Q (не путать с реактивной мощностью) показывает во сколько раз напряжение на реактивных элементах больше напряжения на резисторе;

 

— Полная мощность равна активной мощности:

S = P, Q = 0

Частотная характеристика колебательного контура показана на рисунке 2.32. С ростом частоты X_L линейно возрастает, X_С обратно пропорционально убывает, а Z имеет минимум на частоте резонанса ω₀.

Рисунок 2.32 — Частотные характеристики последовательного колебательного контура

.

 

 

Рисунок 2.33 — Частотная характеристика тока I = f (ω)

Зависимость тока от частоты I = f (ω)  — показана на рисунке 2.33. При постоянном напряжении ток максима-лен на частоте ω₀.

 

На рисунке 2.34 показана фазо-частотная характе-ристика – зависимость сдвига фаз между током и напря-жением от частоты φ( ω). На частоте резонанса ω₀ сдвиг фаз равен нулю. При ω < ω₀ цепь носит индуктивный характер и φ < 0, при φ > ω₀ – ёмкостной и φ > 0.

 

 

Рисунок 2.34 – Фазо-частотная характеристика последовательного колебательного контура

Резонанс токов

 

Аналогично рассмотрим цепь с параллельным соединением резистора, катушки и конденсатора (рисунок 2.35).

Рисунок 2.35 — Параллельное соединение R, L, C

↓iR(t)   ↓iC(t)   ↓iL(t)

 

 

Как обычно, при параллельном соединении, удобно использовать проводимости, а не сопротивления.

 

Полная проводимость цепи:

Y = G — jB = G — j( B_L— B_C)

 

Векторные диаграммы при B_C< B_L и B_C>B_L показаны на рисунках 2.36 и 2.37.

Рисунок 2.36 — Проводимости при параллельном соединении R, L, С: a – BC <BL, φ > 0, b — BC > BL, φ < 0

 

Рисунок 2.37 — Векторные диаграммы при последовательном соединении R, L, С: a – BC < BL, φ > 0, b — BC > BL, φ < 0

 

Такая схема называется параллельным колебатель-ным контуром. Резонанс в такой цепи называется резонансом токов (рисунок 2.38).

Рисунок 2.38 — Векторная диаграмма при параллельном резонансе

 

 

Условие резонанса: B_L= B_C => 1/ω L=ω C

Формула для частоты резонанса аналогична:

 

 

Свойства схемы параллельного колебательного контура на частоте резонанса:

 

— φ = 0, напряжение и ток совпадают по фазе;

 

— Полное сопротивление Z = R,

проводимость: Y = G;

 

— Ток в цепи минимальный I = I_min= UG;

 

— реактивные сопротивления и проводимости равны:

 

 

 

— Токи через L и C равны: I_L= I_C;

 

— Добротность контура: Q = ρ/ R = Y/ G;

 

— Полная мощность равна активной мощности:

S = P, Q = 0

 

Как видите, наблюдается полная аналогия с последовательным резонансом.

Частотные характеристики параллельного колеба-тельного контура показаны на рисунках 2.39 и 2.40. Они полностью аналогичны характеристикам последователь-ного колебательного контура, если заменить сопротивле-ния на проводимости, а ток на напряжение.

Фазо-частотная характеристика параллельного коле-бательного контура показана на рисунке 2.41.

 

Рисунок 2.39 — Частотные характеристики параллельного колебательного контура

 

 

Рисунок 2.41 – Фазочастотная характеристика параллельного колебательного контура

 

 

cyberpedia.su

треугольник мощностей — это… Что такое треугольник мощностей?



треугольник мощностей

 

треугольник мощностей
—

 

P — активная мощность
Q — реактивная мощность
S — полная мощность

Параллельные тексты EN-RU

In an electrical circuit consisting of several receivers through which sinusoidal currents pass:

• The total active power P (W) consumed is equal to the arithmetical sum of the active power consumed by each device
• The total reactive power Q (VAR) consumed is equal to the algebraic sum of the reactive power consumed by each device
• The apparent power must never be added together algebraically. The total apparent power S is calculated based on the quadratic sum of P and Q

[Legrand]

В электрической цепи переменного синусоидального тока, к которой подключены несколько электроприемников:

• Общая потребляемая активная мощность Р (Вт) равна арифметической сумме активных мощностей, потребляемых каждым электроприемником.
• Общая реактивная мощность Q (вар) равна алгебраической сумме реактивных мощностей, потребляемых каждым электроприемником.
• Полные мощности алгебраически не складывают. Полная мощность S вычисляется как квадратный корень из суммы квадратов P и Q

[Перевод Интент]

Тематики

• электротехника, основные понятия

Справочник технического переводчика. – Интент. 2009-2013.

• треугольник маршрута
• треугольник напряжений

Смотреть что такое «треугольник мощностей» в других словарях:

• треугольник мощностей — galių trikampis statusas T sritis fizika atitikmenys: angl. power triangle vok. Leistungsdreieck, n rus. треугольник мощностей, m pranc. triangle de puissance, m …   Fizikos terminų žodynas

• Коэффициент мощности — Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны между ними нет фазового сдвига ( …   Википедия

• Мощности коэффициент — колебания переменного тока Коэффициент мощности физическая величина, характеризующая энергетические параметры электрического тока. Коэффициент мощности характеризует приёмник электроэнергии переменного тока. Численно равен отношению потребляемой… …   Википедия

• Leistungsdreieck — galių trikampis statusas T sritis fizika atitikmenys: angl. power triangle vok. Leistungsdreieck, n rus. треугольник мощностей, m pranc. triangle de puissance, m …   Fizikos terminų žodynas

• galių trikampis — statusas T sritis fizika atitikmenys: angl. power triangle vok. Leistungsdreieck, n rus. треугольник мощностей, m pranc. triangle de puissance, m …   Fizikos terminų žodynas

• power triangle — galių trikampis statusas T sritis fizika atitikmenys: angl. power triangle vok. Leistungsdreieck, n rus. треугольник мощностей, m pranc. triangle de puissance, m …   Fizikos terminų žodynas

• triangle de puissance — galių trikampis statusas T sritis fizika atitikmenys: angl. power triangle vok. Leistungsdreieck, n rus. треугольник мощностей, m pranc. triangle de puissance, m …   Fizikos terminų žodynas

• Соединённые Штаты Америки — (США)         (United States of America, USA).          I. Общие сведения          США государство в Северной Америке. Площадь 9,4 млн. км2. Население 216 млн. чел. (1976, оценка). Столица г. Вашингтон. В административном отношении территория США …   Большая советская энциклопедия

• Теория волн Эллиотта — (Elliott Wave Theory) Теория волн Эллиотта это математическая теория об изменении поведения общества или финансовых рынков Все о волновой теории Эллиотта: видео, книги, статьи о теории волн, информация о советниках и индикаторах волн Эллиотта… …   Энциклопедия инвестора

• Окись этилена — Окись этилена …   Википедия

technical_translator_dictionary.academic.ru