1.4. Соединение трехфазной цепи треугольником
Чтобы соединить генератор в треугольник, нужно связать конец каждой фазы с началом следующей; в результате фазы генератора образуют замкнутый контур. При таком соединении симметричного генератора с отключенной нагрузкой ток внутри него не возникает, так как сумма ЭДС контура равна нулю. Соединив приемник также в треугольник (рис. 1.16), можно видеть, что фазные напряжения генератора и приемника одновременно являются и линейными, линейные же токи İA, İB, İC – отличны от фазных токов İAB, İBC, İCA.
Для получения симметричных соотношений между линейными и фазными токами следует выбирать их положительные направления единообразно. Тогда по первому закону Кирхгофа
И з полученных соотношений видно, что геометрическая сумма линейных токов равна нулю:
Линейные токи на
векторной диаграмме образуют замкнутый
треугольник.
При соединении трехфазной цепи треугольником можно выделить три частных случая.
Симметричная нагрузка (ZAB=ZBC=ZCA).
Л инейные токи на диаграмме образуют равносторонний треугольник (рис.1.17).
Достаточно определить ток одной фазы, в других фазах токи равны по величине, но имеют фазовый сдвиг +120º или -120º:
2) Несимметричная нагрузка, Zпр=0, (Z ABZBCZCA).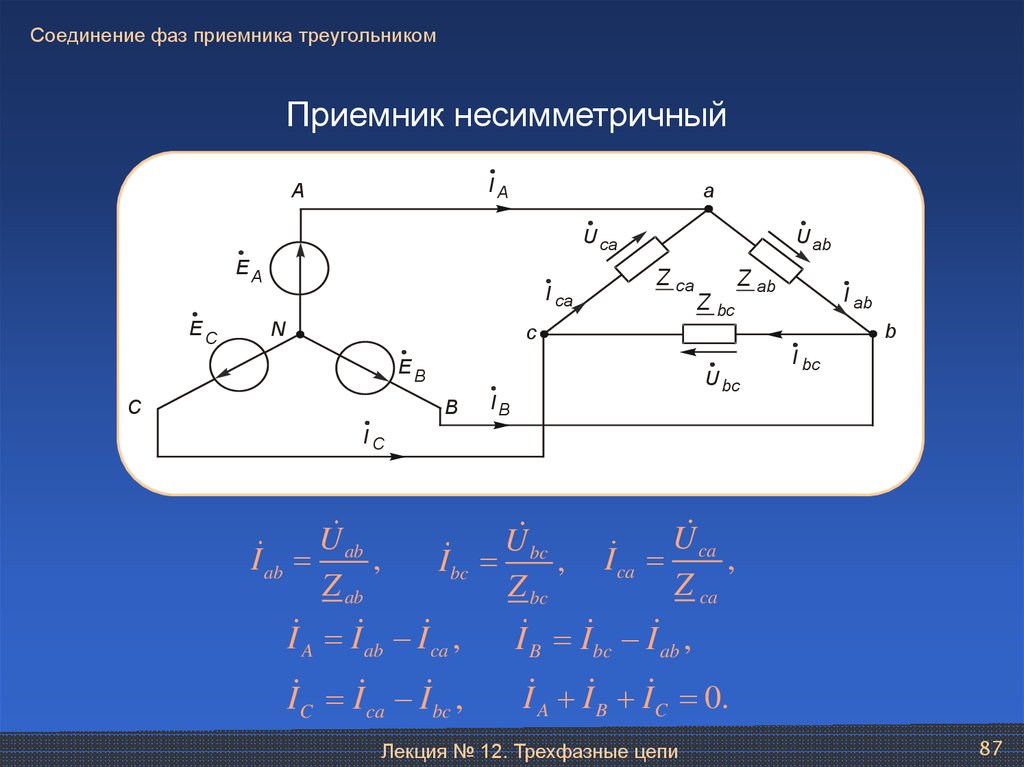
Если пренебречь сопротивлением проводов, напряжения генератора будут равны напряжениям приемника, фазы будут независимы друг от друга: всякое изменение сопротивления какой-либо фазы приемника вызовет изменение тока этой фазы и токов двух примыкающих к этой фазе линейных проводов, но никак не отразится на токах других фаз. Фазные токи определяются следующим образом:
3) Несимметричная нагрузка, Zпр0, (
Преобразуя
треугольник сопротивлений приемника
в эквивалентную звезду сопротивлений,
задачу сводят к случаю соединения
звездой (рис. 1.18).
1.18).
После определения токов звезды необходимо обратиться к исходному треугольнику, чтобы найти его фазные токи.
В любом случае построение диаграммы начинают с равностороннего треугольника линейных напряжений, который является одновременно треугольником фазных напряжений нагрузки, если пренебречь сопротивлением проводов линии. Затем откладывают фазные токи с соответствующим фазовым сдвигом по отношению к напряжению данной фазы. Переносят фазные токи на отдельный чертеж в одну точку и с учетом первого закона Кирхгофа получают линейные токи, замкнув концы фазных токов треугольником. Стрелку линейного тока направляют в сторону уменьшаемого фазного тока.
Пример 1-6.
Соединение
треугольником при симметричной нагрузке ZAB=ZBC=ZCA=Z=(10+j5,7) Ом и Zпр=0, UЛ=220
В (рис. 1.16). Расчитать токи и построить
векторную диаграмму напряжений и токов.
1.16). Расчитать токи и построить
векторную диаграмму напряжений и токов.
Решение
П остроим равносторонний треугольник линейных напряжений. Определим ток каждой фазы (рис. 1.19):
Т ок каждой фазы на диаграмме откладываем под углом
п о отношению к соответствующему фазному напряжению. Затем перенесем все фазные токи на отдельный чертеж в одну точку. С учетом первого закона Кирхгофа получаем линейные токи:
Л инейные токи образуют замкнутый равносторонний треугольник, причем направлен соответствующий линейный ток к соответствующему уменьшаемому фазному току.
Пример 1-7.
В цепи (рис. 1.20) R=XL=XC.
Построить векторную диаграмму напряжений и токов
Решение
П
остроение
диаграммы начинаем с равностороннего
треугольника линейных напряжений UAB, UBC, UCA (рис. 1.21).
1.21).
П одсчитаем токи каждой фазы нагрузки и отложим векторы этих токов с учетом фазового сдвига по отношению к соответствующему напряжению фазы.
П еренесем на отдельный чертеж фазные токи İAB, İBC, İCA в одну точку и, соединив их вершины, получим линейные токи
Стрелка линейного тока направлена в сторону уменьшаемого фазного тока.
Пример 1-8.
В схеме (рис. 1.22) RAB=RBC=RCA=R . Как изменятся токи в цепи: 1) если замкнется рубильник; 2) если сгорит предохранитель Пр1 ?
Решение
П ри замыкании рубильника сопротивление фазы АВ уменьшается в 2 раза:
Токи остальных
фаз не меняются. На векторной диаграмме
(рис. 1.23) покажем токи до замыкания и
после замыкания рубильника. Токи в линии А и В увеличиваются с увеличением
тока фазы АВ, İC – не изменится.
На векторной диаграмме
(рис. 1.23) покажем токи до замыкания и
после замыкания рубильника. Токи в линии А и В увеличиваются с увеличением
тока фазы АВ, İC – не изменится.
Если сгорит предохранитель Пр1, то ток фазы İCA=0, тогда линейные токи (рис. 1.24):
İA=İAB — уменьшится;
İB=İBC -İ AB — не изменится;
İС= -İBC — уменьшится.
Пример 1-9.
Найти линейные и
фазные токи в цепи (рис. 1.25), если UЛ=220
В, XL=5 Ом, XC=3 Ом.
Решение
П реобразуем треугольник abc в эквивалентную звезду:
Определим эквивалентное сопротивление фазы преобразованной схемы
( рис. 1.26):
Расcчитаем линейные токи (рис. 1.26) и перенесем на диаграмму
Определим напряжения Ua0’, Ub0’, Uc0’ (рис. 1.26) и перенесем эти напряжения на векторную диаграмму (рис. 1.27).
Рассчитаем напряжения треугольника abc (рис. 1.25) и перенесем на диаграмму (рис. 1.27).
Р
ассчитаем
фазные токи исходной схемы (рис. 1.25) и
перенесем их на диаграмму (рис. 1.28).
1.28).
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Соединение треугольником в 3-фазной системе — Соотношение между фазным и линейным напряжением и током
В соединении треугольником (Δ) или сеткой конечная клемма одной обмотки соединяется с пусковой клеммой другой фазы и так далее, что дает замкнутую цепь. Трехлинейные проводники проходят от трех соединений сетки, называемой Линейные проводники .
Трехлинейные проводники проходят от трех соединений сетки, называемой Линейные проводники .
Соединение треугольником показано на рисунке ниже:
Состав:
- Соотношение между фазным и линейным напряжением при соединении треугольником
- Соотношение между током фазы и током линии при соединении треугольником
Для получения соединения треугольником , a 2 соединяется с b 1 , b 2 соединяется с c 1 , а c 2 соединяется с 1, как показано выше. фигура. Три проводника R, Y и B проходят от трех соединений, известных как 9.0003 Линейные проводники .
Ток, протекающий через каждую фазу, называется Phase Current (Iph) , а ток, протекающий через каждый линейный провод, называется Line Current (I L ).
Напряжение на каждой фазе называется Phase Voltage (E ph ) , а напряжение между двумя линейными проводниками называется Line Voltage (E L ).
Соотношение между фазным и линейным напряжением при соединении треугольником
Чтобы понять взаимосвязь между фазным напряжением и линейным напряжением при соединении треугольником, рассмотрите рисунок А, показанный ниже:
Из рисунка видно, что напряжение на клеммах 1 и 2 такое же, как и на клеммах R и Y. Следовательно,
Аналогично
: фазные напряжения равны
Линейные напряжения:
Соотношение между фазным и линейным током при соединении треугольником
Как и в уравновешенной системе, трехфазный ток I 12 , I 23 и I 31 равны по величине, но смещены друг относительно друга на 120° эл.
Векторная диаграмма показана ниже:
Следовательно,
Если мы посмотрим на рисунок А, то увидим, что ток делится на каждом соединении 1, 2 и 3.
Применение закона Кирхгофа на разветвлении 1,
Входящие токи равны исходящим токам.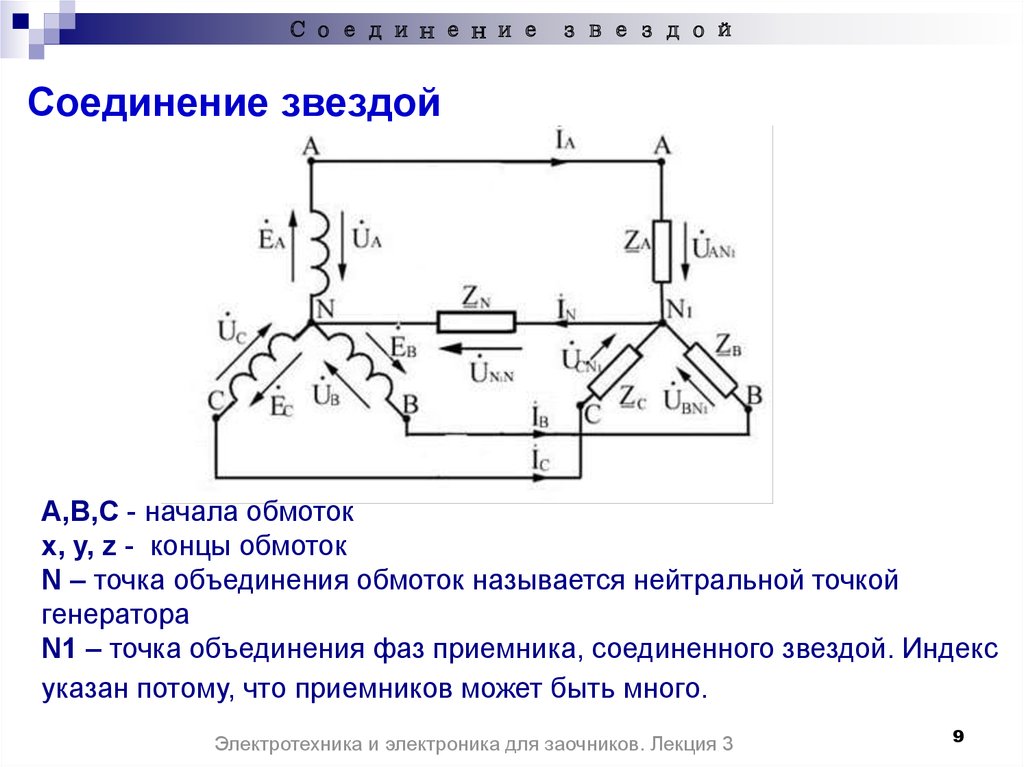
И их разность векторов будет равна:
Вектор I 12 инвертируется и добавляется к вектору I 31 , чтобы получить векторную сумму I 31 и –I , как показано выше на векторной диаграмме. Следовательно,
Как мы знаем, I R = I L , следовательно,
Аналогично,
Следовательно, ток линии при соединении треугольником в три раза больше фазного тока.
Это все о соединении треугольником в трехфазной системе.
Трехфазное соединение треугольником: трехфазное питание, напряжение, ток
Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.
Соединение треугольником При соединении треугольником стороны фаз соединяются циклически, образуя замкнутый контур, как показано на рис. 1. Что касается линейного и фазного токов, то они связаны друг с другом следующим образом: : 9{1}/{}_{\sqrt{3}}$ умножить только на ток линии.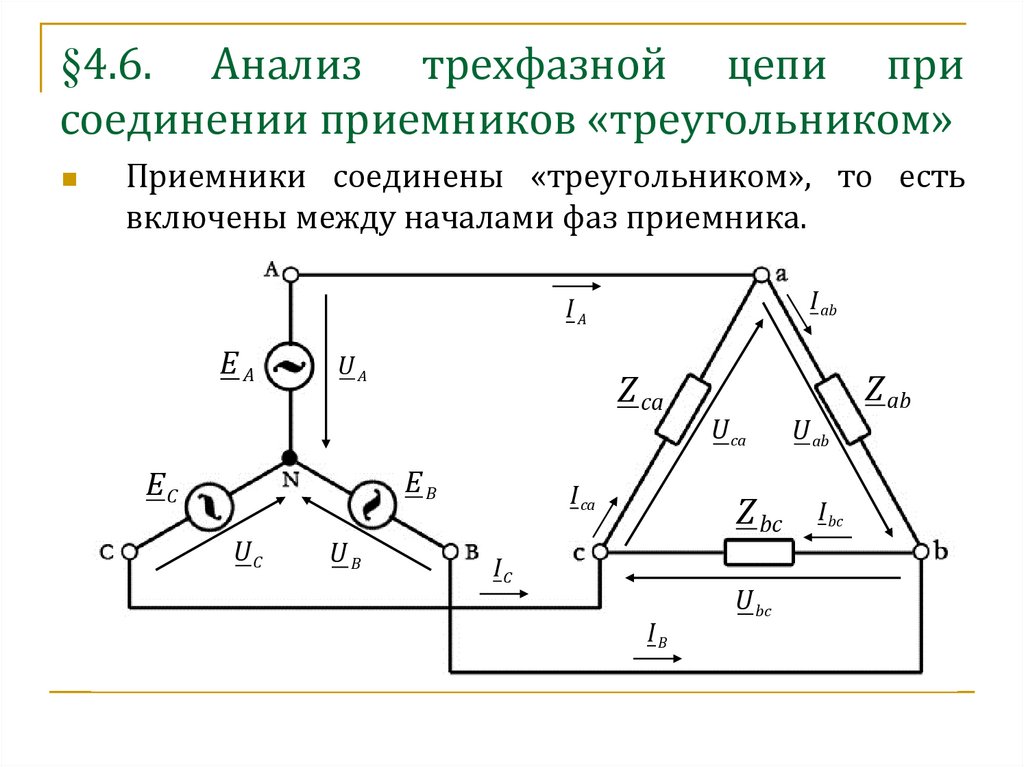 В то время как при соединении треугольником линейное и фазное напряжение одинаковы:
В то время как при соединении треугольником линейное и фазное напряжение одинаковы:
${{\text{V}}_{\text{фаза}}}\text{=}{{\text{V}}_{\text {line}}}$
Сбалансированная нагрузка, соединенная по схеме треугольника (с равными импедансами фаз), показана на рис. 1.
Рис.1: Нагрузка, соединенная по схеме треугольника
Преимущество нагрузки, соединенной по схеме треугольника, по сравнению с нагрузкой, соединенной по схеме треугольник Нагрузка заключается в том, что нагрузки могут быть легко добавлены или удалены на одной фазе треугольника, поскольку нагрузки подключаются непосредственно через линии. Кроме того, для данной мощности, подаваемой на нагрузку, фазные токи в треугольнике меньше, чем в Y. С другой стороны, фазные напряжения в треугольнике выше, чем в соединении Y. Источники редко соединяются треугольником, потому что, если напряжения не идеально сбалансированы, будет чистое напряжение и, следовательно, циркулирующий ток вокруг треугольника.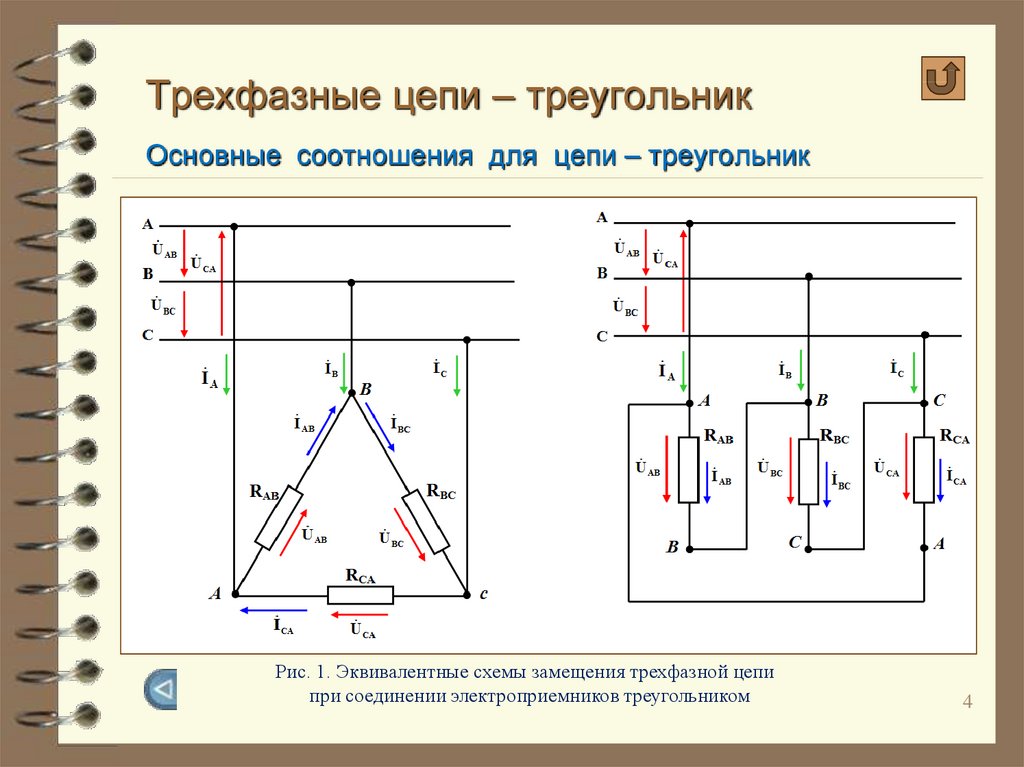

 1). Значения линейного напряжения, активных, индуктивных и емкостных сопротивлений приемников приведены ниже.
1). Значения линейного напряжения, активных, индуктивных и емкостных сопротивлений приемников приведены ниже.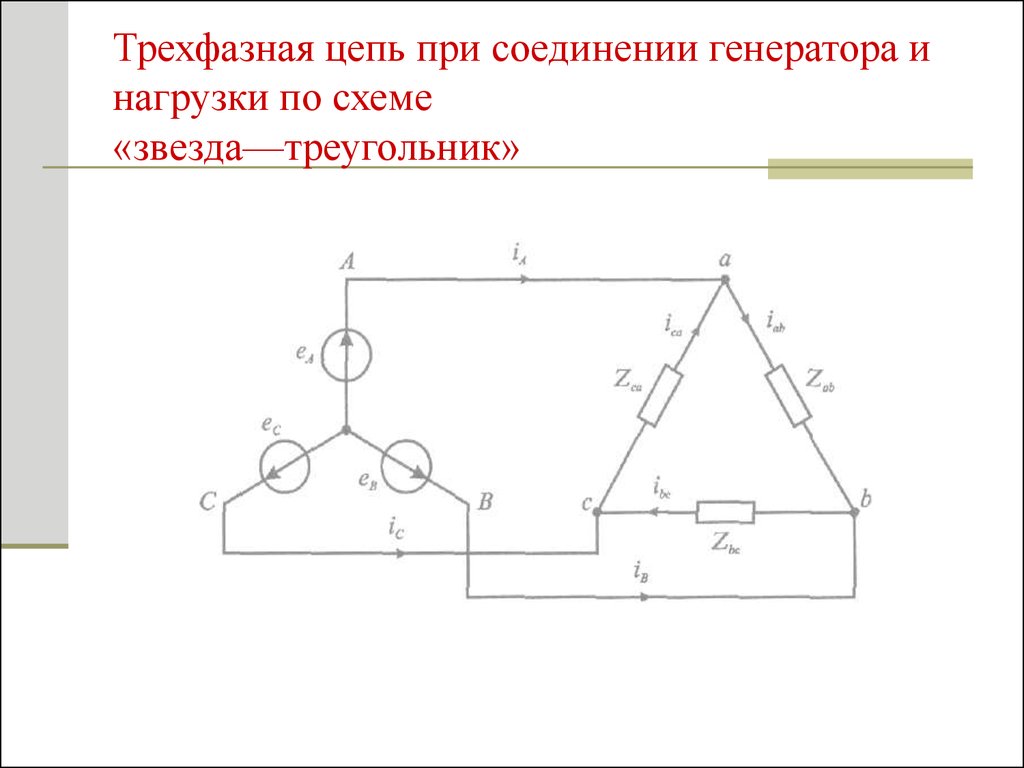 Определим реактивную мощность цепи:
Определим реактивную мощность цепи: