Соединение звезда и треугольник формулы: Свойства звезды и треугольника

Соединение треугольником и звездой

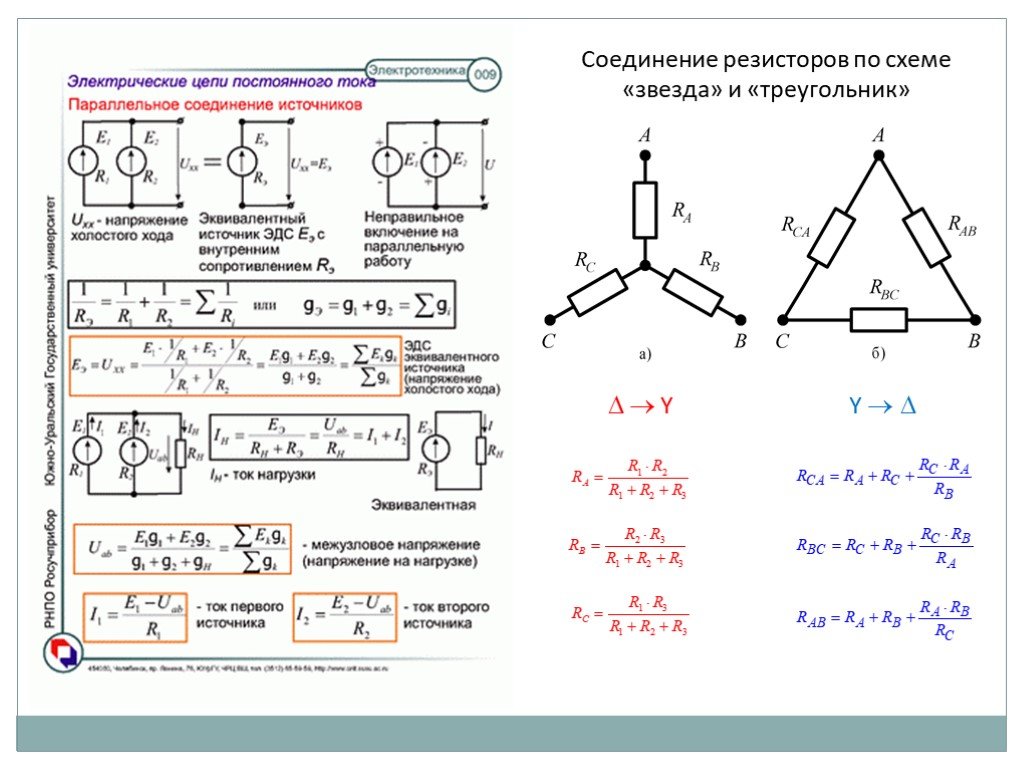
Соединение треугольником и звездой представлены на рисунке 5.

Рисунок 5. Соединение треугольником и звездой

Цифрами в треугольнике помечены узлы, поэтому никакого последовательного соединения в треугольнике нет. Справа изображена эквивалентная этому треугольнику звезда. Точки на ветвях звезды т.1, т.2, т.3, это бывшие узлы треугольника, их потенциалы не изменились. Треугольник образует контур. Преобразуя треугольник в звезду, контур пропадает, следовательно, схема становится проще.

Обычно в схемах треугольники изображены в виде «четырёхугольников», поэтому как треугольники они в глаза не бросаются (рисунок 6).

Исходная схема преобразованная схема

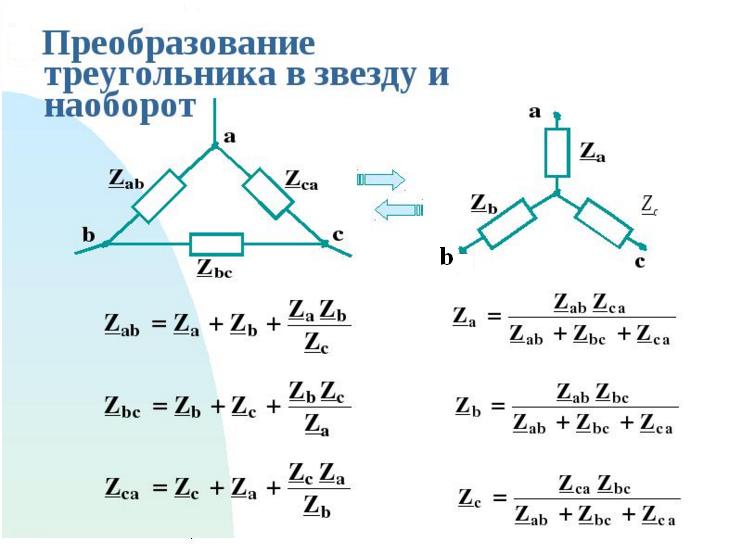
Рисунок 6. Преобразование треугольника в звезду

Исходная схема (левая) содержит три независимых контура (по ячейкам), а правая уже на один контур меньше.

В исходной схеме узлы «2», «3», «4» являются вершинами треугольника со сторонами R₄ R₆ R₅ . Чтобы не ошибиться в преобразовании необходимо внутри треугольника, изобразить звезду, которая должна получиться после преобразования, а резисторы звезды пометить звёздочкой. Формулы преобразования даются без доказательства.

Формулу легко запомнить, она напоминает формулу эквивалентного сопротивления для двух параллельно соединённых резисторов, в числителе – произведение, в знаменателе – сумма, но сумма всех сторон треугольника. В числителе произведение резисторов, которые соединяются в рассматриваемом узле. Определяется сопротивление , то есть узел 2, там соединяются R₅ и R_{6 .}Аналогично для запоминания самостоятельно напишите формулы для определения и .

Такое преобразование целесообразно использовать в случаях, когда не требуется знать величину тока в сопротивлениях треугольника исходной цепи, так как они исчезают в преобразованной схеме, а чтобы найти токи в них, нужно вернуться к исходной схеме и несколько раз применить закон Ома для участка цепи. Например, нужна сила тока в R₄, то есть нужно знать напряжение на участке 3-4. Это напряжение можно найти как разность потенциалов точек 3 и 4, используя преобразованную схему, в которой найдены все токи. Потенциалы этих точек в процессе преобразования не меняются (условие преобразования). Как это делается, рассматривалось в разделе «Закон Ома для активного участка цепи».

Мы рассмотрели все виды соединений и их преобразование.

Токораспределение подчиняется закону Ома, сила тока будет больше в ветви с меньшим сопротивлением.

Резисторы R₁ и R₂ соединены параллельно. Их начала находятся в узле «1», а концы – в узле «2». По свойству параллельного соединения они находятся под одинаковым напряжением . Напомним, что левый индекс у напряжения — индекс большего потенциала. Очевидно, что

После подстановки значения и простых преобразований, получим формулу, позволяющую определить токи в параллельных ветвях, зная только значение тока I до распределения.

Эта формула называется «Формула чужого сопротивления», так как по отношению к определяемому току, в числители дроби стоит «чужое» сопротивление (сопротивление другой параллельно соединённой ветви).

Линейное и фазное напряжение — соотношение и формулы, схема соединения звездой и треугольником

Одним из видов систем с множеством фаз, представлены цепи, состоящие из трех фаз. В них действуют электродвижущие силы синусоидального типа, возникающие с синхронной частотой, от единого генератора энергии, и имеют разницу в фазе.

Электрическое напряжение трехфазных сетей

• Виды напряжения ↓
• Отличия ↓
• Соотношение ↓
• Схема ↓
• Расчет линейного и фазного напряжения ↓

Под фазой, понимаются самостоятельные блоки системы с множеством фаз, имеющие идентичные друг другу параметры тока. Поэтому, в электротехнической области, определение фазы имеет двойное толкование.

Во-первых, как значение, имеющее синусоидальное колебание, а во-вторых, как самостоятельный элемент в электросети с множеством фаз. В соответствии с их количеством и маркируется конкретная цепь: двухфазная, трехфазная, шестифазная и т.д.

Сегодня в электроэнергетике, наиболее популярными являются цепи с трехфазным током. Они обладают целым перечнем достоинств, выделяющих их среди своих однофазных и многофазных аналогов, так как, во-первых, более дешевы по технологии монтажа и транспортировки электроэнергии с наименьшими потерями и затратами.

Во-вторых, они имеют свойство легко образовывать движущееся по кругу магнитное поле, которое является движущей силой для асинхронных двигателей, которые используются не только на предприятиях, но и в быту, например, в подъемном механизме высотных лифтов и т.д.

Электрические цепи, имеющие три фазы, позволяют одновременно пользоваться двумя видами напряжения от одного источника электроэнергии – линейным и фазным.

Виды напряжения

Знание их особенностей и характеристик эксплуатации, крайне необходимо для манипуляций в электрощитах и при работе с устройствами, питаемыми от 380 вольт:

1. Линейное.  Его обозначают как межфазный ток, то есть проходящий между парой контактов или идентичными клеймами разных фаз. Оно определяется разностью потенциалов пары фазных контактов.
2. Фазное. Оно появляется при замыкании начального и конечного выводов фазы. Также, его обозначают как ток, возникающий при замыкании одного из контактов фазы с нулевым выводом. Его величина определяется абсолютным значением разности выводов от фазы и Земли.

Отличия

В обычной квартире, или частном доме, как правило, существует только однофазный тип сети 220 вольт, поэтому, к их щиту электропитания, подведены в основном два провода – фаза и ноль, реже к ним добавляется третий – заземление.

К высотным многоквартирным зданиям с офисами, гостиницами или торговыми центрами, подводится сразу 4 или 5 кабелей электропитания, обеспечивающих три фазы сети 380 вольт.

Почему такое жесткое разделение? Дело в том, что трехфазное напряжение, во-первых, само отличается повышенной мощностью, а во-вторых, оно специфически подходит для питания особых сверхмощных электродвигателей трехфазного типа, которые используются на заводах, в электролебедках лифтов, эскалаторных подъемниках и т. д.

Такие двигатели при включении в трехфазную сеть вырабатывают в разы большее усилие, чем их однофазные аналоги тех же габаритов и веса.

Проводить разводку проводки такого типа можно без использования профессионального оборудования и приборов, достаточно обычных отверток с индикаторами.

Соединяя проводники не нужно монтировать нулевой контакт, ведь вероятность пробоя очень мала, благодаря не занятой нейтрали.

Но такая схема сети имеет и свое слабое место, так как в линейной схеме монтажа крайне сложно найти место повреждения проводника в случае аварии или поломки, что может повысить риск возникновения пожара.

Таким образом, главным отличием между фазным и линейным типами являются разные схемы подключения проводов обмоток источника и потребителя электроэнергии.

Соотношение

Значение напряжения фазы равняется около 58% от мощности линейного аналога. То есть, при обычных эксплуатационных параметрах, линейное значение стабильно и превосходит фазное в 1,73 раза.

Оценка напряжения в сети трехфазного электрического тока, в основном производится по показателям его линейной составляющей. Для линий тока этого типа, подающегося с подстанций, оно, как правило, равняется 380 вольтам, и идентично фазному аналогу в 220 В.

В электросетях с четырьмя проводами, напряжение трехфазного тока маркируется обоими значениями – 380/220 В. Это обеспечивает возможность питания от такой сети устройств, как с однофазным потреблением электроэнергии 220 вольт, так и более мощных агрегатов, рассчитанных на ток 380 В.

Самой доступной и универсальной стала система трехфазного типа 380/220 В, имеющая нулевой провод, так называемое заземление. Электрические агрегаты, работающие на одной фазе 220 В., могут быть запитаны от линейного напряжения при подключении к любой паре фазных выводов.

Электрические агрегаты трехфазного питания работают только при подключении сразу к трем выводам разных фаз.

В этом случае, применение нулевого вывода в качестве заземления, не является обязательным, хотя в случае повреждения изоляции проводов, его отсутствие серьезно повышает вероятность удара током.

Схема

Агрегаты трехфазного тока имеют две схемы подключения в сеть: первая – «звезда», вторая – «треугольником». В первом варианте, начальные контакты всех трех обмоток генератора замыкаются вместе по параллельной схеме, что, как и в случае с обычными щелочными батарейками не даст прироста мощности.

Вторая, последовательная схема подключения обмоток источника тока, где каждый начальный вывод подключается к конечному контакту предыдущей обмотки, дает трехкратный прирост напряжения за счет эффекта суммирования напряжений при последовательном подключении.

Кроме того, такие же схемы подключения имеют и нагрузку в виде электродвигателя, только устройство, подключенное в трехфазную сеть по схеме «звезда», при токе в 2,2 А будет выдавать мощность 2190Вт, а тот же агрегат, подключенный «треугольником», способен выдать в три раза большую мощность – 5570, за счет того, что благодаря последовательному подключению катушек и внутри двигателя, сила тока суммируется и доходит до 10 А.

Имея источник трехфазного напряжения и двигатели, имеющие аналогичную схему подключения, можно получить в разы больше мощности просто за счет эффективного подключения всех агрегатов.

Расчет линейного и фазного напряжения

Сети с линейным током нашли широкое применение за счет своих характеристик меньшей травмоопасности и легкости разведения такой электропроводки. Все электрические устройства в этом случае соединены только с одним фазным проводом, по которому и идет ток, и только он один и представляет опасность, а второй – это земля.

Рассчитать такую систему несложно, можно руководствоваться обычными формулами из школьного курса физики. Кроме того, для измерения этого параметра сети, достаточно использовать обычный мультиметр, в то время как для снятия показаний подключения фазного типа, придется задействовать целую систему оборудования.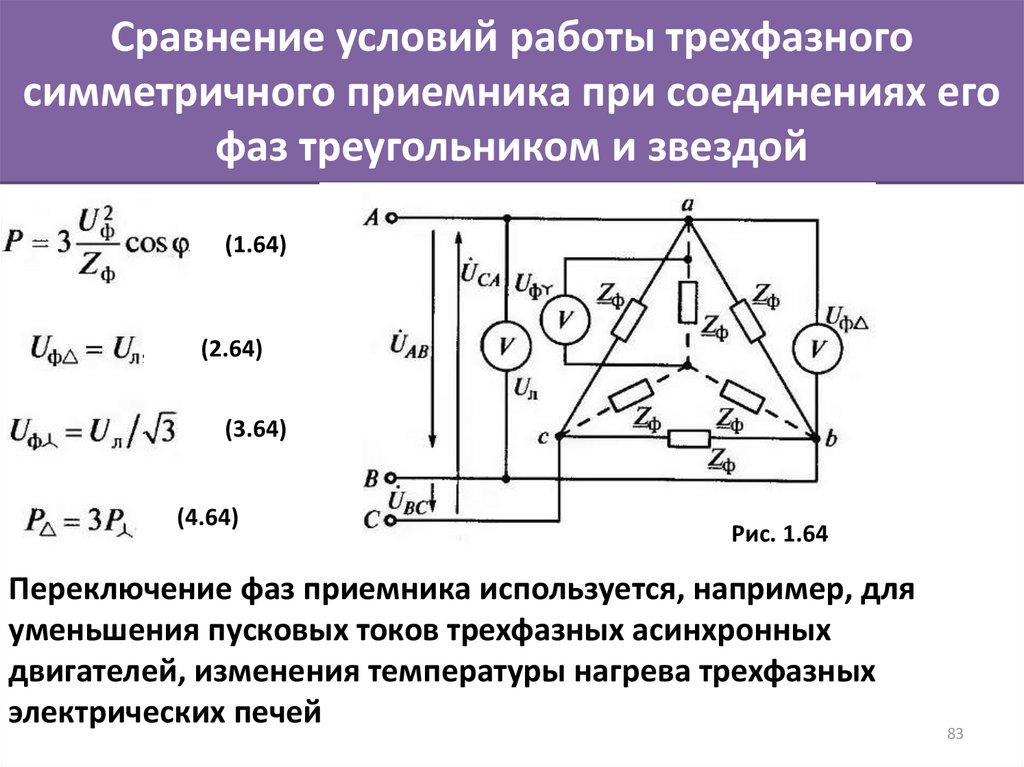

Для подсчета напряжения линейного тока, применяют формулу Кирхгофа:

• ∑ Ik = 0;

Уравнение которой гласит, что каждой из частей электрической цепи, сила тока равна нулю – k=1.

И закон Ома:

• I=U/R;

Используя их, можно без труда произвести расчеты каждой характеристики конкретного клейма или электросети.

В случае разделения системы на несколько линий, может появиться необходимость рассчитать напряжение между фазой и нулем:

• I_L = I_F;

Эти значения являются переменными, и меняются при разных вариантах подключения. Поэтому, линейные характеристики идентичны фазовым.

Однако, в некоторых случаях, требуется вычислить чему равно соотношение фазы и линейного проводника.

Для этого, применяют формулу:

• Uл=Uф∙√3, где:

Uл – линейное, Uф – фазовое. Формула справедлива, только если –  I_L = I_F.

При добавлении в электросистему дополнительных отводящих элементов, необходимо и персонально для них рассчитывать фазовое напряжение. В этом случае, значение Uф заменяется на цифровые данные самостоятельного клейма.

При подключении промышленных систем к электросети, может появиться необходимость в расчете значения реактивной трехфазной мощности, которое вычисляется по следующей формуле:

• Q = Qа + Qb + Qс;

Идентичная структура формулы активной мощности:

• P = Pа + Pb + Pс;

Примеры расчета:

Уравнение звезда-треугольник (Янг-Бакстер) | Высшая статистическая механика

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Термин поиска на микросайте

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Подробнее

CITE

McCoy, Barry M. ,

‘Уравнение Star-Triangle (Yang-Baxster)’

,

Advanced Statistic Mechanics

, Международная серия монографий на физике

(

Oxford,

.

2009 г.,

онлайн-издание,

Oxford Academic

, 1 февраля 2010 г.

), https://doi.org/10.1093/acprof:oso/9780199556632.003.0013,

, по состоянию на 11 декабря 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicAdvanced Statistical MechanicsМатематическая и статистическая физикаКнигиЖурналы Термин поиска на микросайте

Advanced Search

Abstract

В этой главе определяются передаточные матрицы, и существование однопараметрического семейства коммутирующих передаточных матриц определяется как условие интегрируемости. Локальное уравнение звезды-треугольника (Янга-Бакстера) вводится для моделей вершин, спинов и граней и используется для демонстрации коммутации передаточных матриц. Уравнение звезды-треугольника решается для шестивершинной, восьмивершинной, SOS, RSOS, твердого шестиугольника и киральной модели Поттса. Получена коммутация матрицы переноса с соответствующей квантовой спиновой цепочкой.

Ключевые слова: уравнение звезда-треугольник, уравнение Янга–Бакстера, восьмивершинная модель, шестивершинная модель, модель RSOS, киральная модель Поттса, модель жесткого шестиугольника

Предмет

Математическая и статистическая физика

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Щелкните Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
   Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Войти с помощью личного кабинета

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Калькулятор специальных прямоугольных треугольников

| Формула

Создано Ханной Памула, доктором философии

Отзыв от Bogna Szyk и Адены Бенн

Последнее обновление: 26 ноября 2022 г. Другие специальные прямоугольные треугольники

Специальные формулы прямоугольных треугольников

Специальные правила прямоугольного треугольника

Калькулятор специального прямоугольного треугольника — пример

Часто задаваемые вопросы

Этот специальный калькулятор прямоугольных треугольников поможет вам вычислить размеры выбранного треугольника в мгновение ока. Выберите нужный вам треугольник и введите заданные значения — остальные параметры будут рассчитаны автоматически. Специальные прямоугольные треугольники — это прямоугольные треугольники, для которых существуют простые формулы. Это позволяет выполнять быстрые вычисления, поэтому вам не нужно использовать теорему Пифагора или какой-то продвинутый метод. Прокрутите вниз, чтобы узнать больше о специальных формулах и правилах прямоугольного треугольника.

Особые прямоугольные треугольники 30 60 90

Особый прямоугольный треугольник 30°30\градус30° 60°60\градус60° 90°90\градус90° — один из самых популярных прямоугольных треугольников.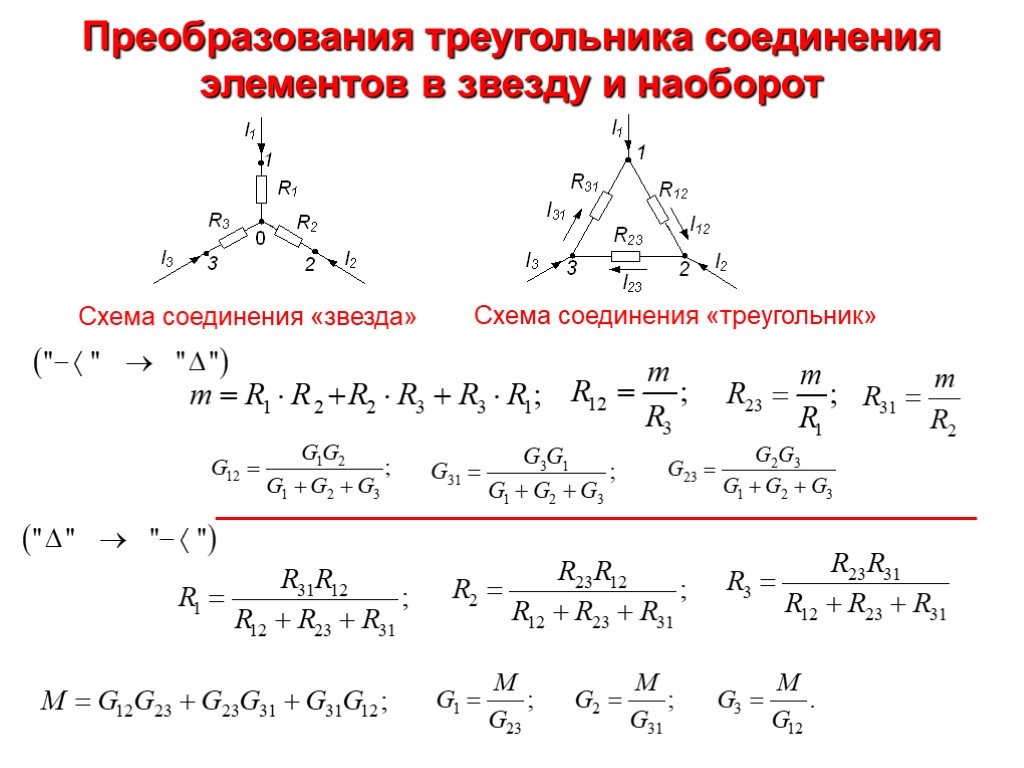 Его свойства уникальны, потому что это половина равностороннего треугольника.

Если вы хотите узнать больше об этой особой форме, проверьте наш специальный калькулятор треугольника 30° 60° 90°.

Особые прямоугольные треугольники 45 45 90

Еще один известный особый прямоугольный треугольник — 45°45\градус45° 45°45\градус45° 9Треугольник 0°90\градус90°. Это единственный возможный прямоугольный треугольник, который также является равнобедренным. Кроме того, это фигура, полученная при разрезании квадрата по диагонали:

Хотите знать свойства этого треугольника? Пожалуйста, посмотрите на наш калькулятор треугольника 45° 45° 90°.

Другие специальные прямоугольные треугольники

Существует много специальных прямоугольных треугольников, ниже вы найдете те, которые реализованы в нашем инструменте:

Специальные формулы прямоугольных треугольников

Если вы ищете формулы для специальных прямоугольных треугольников, вы находитесь в нужное место.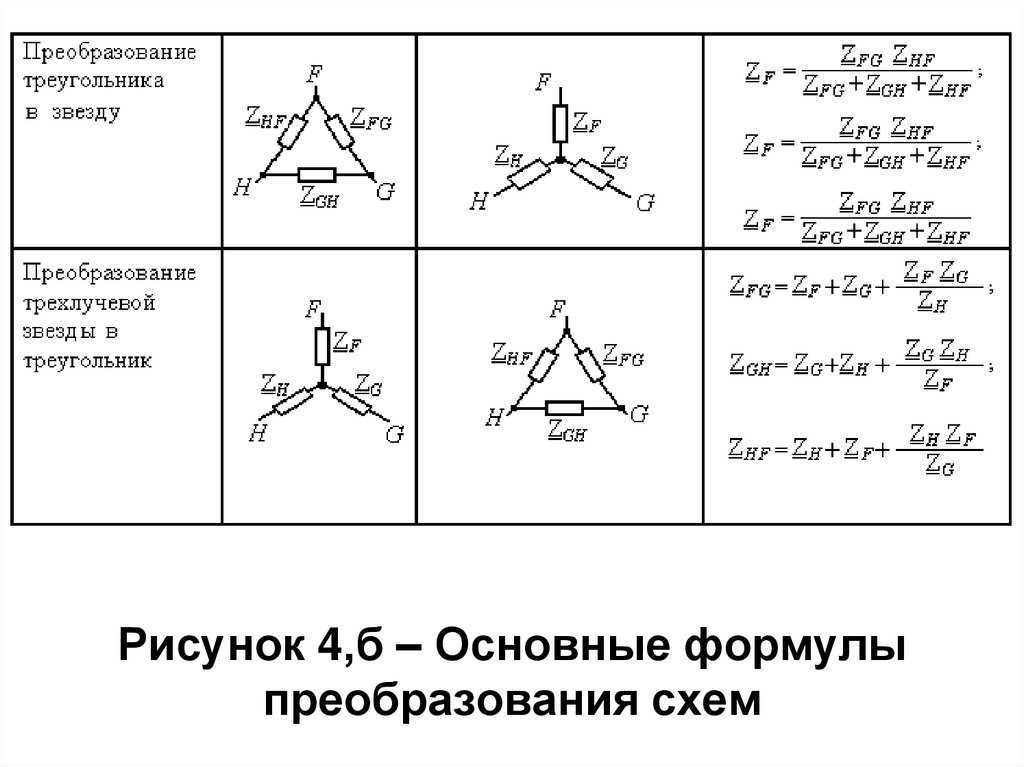 Посмотрите на эту аккуратную таблицу ниже; все должно быть четко! В этой таблице вы найдете формулы для соотношения между углами специального прямоугольного треугольника, катетами, гипотенузой, площадью и периметром:

926×2

Special right triangle	aaa (shorter leg)	bbb (longer leg)	ccc (hypotenuse)	Area	Perimeter	Angle α\alphaα	Angle β\betaβ
30°30\degree30° — 60°60\degree60° — 90°90\degree90°	xxx	12x12x12x	∼37°\sim37\degree∼37°	∼53°\sim53\degree∼53°

Special right triangle rules

Special Прямоугольные треугольники — это треугольники, которые имеют некоторые особенности, облегчающие расчеты.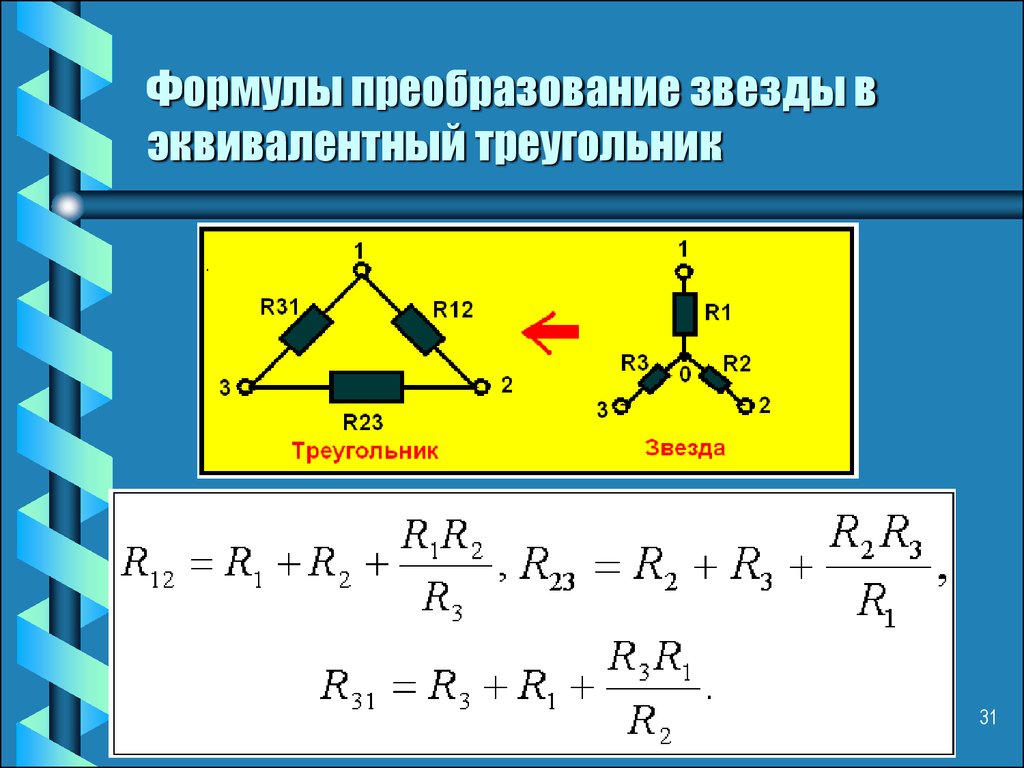 Конечно, самое важное специальное правило прямоугольного треугольника заключается в том, что у них должен быть один прямой угол плюс эта дополнительная функция. Вообще, специальные прямоугольные треугольники можно разделить на две группы:

Существует множество различных правил и вариантов, по которым мы можем выбрать треугольник и назвать его специальным . В нашем специальном калькуляторе прямоугольных треугольников мы реализовали пять выбранных треугольников: два по углам и три по сторонам.

Специальный калькулятор прямоугольного треугольника — пример

Давайте рассмотрим пример: мы хотим найти длину гипотенузы прямоугольного треугольника, если длина одного катета 555 дюймов, а один угол равен 45°45\градус45° .

1. Выберите правильный тип специального прямоугольного треугольника . В нашем случае это треугольник 45°45\градус45°-45°45\градус45°-90°90\градус90°.
2. Введите заданное значение . Мы знаем, что сторона равна 555 дюймов, поэтому мы вводим это значение в поле a или b — неважно, где, потому что это равнобедренный треугольник.
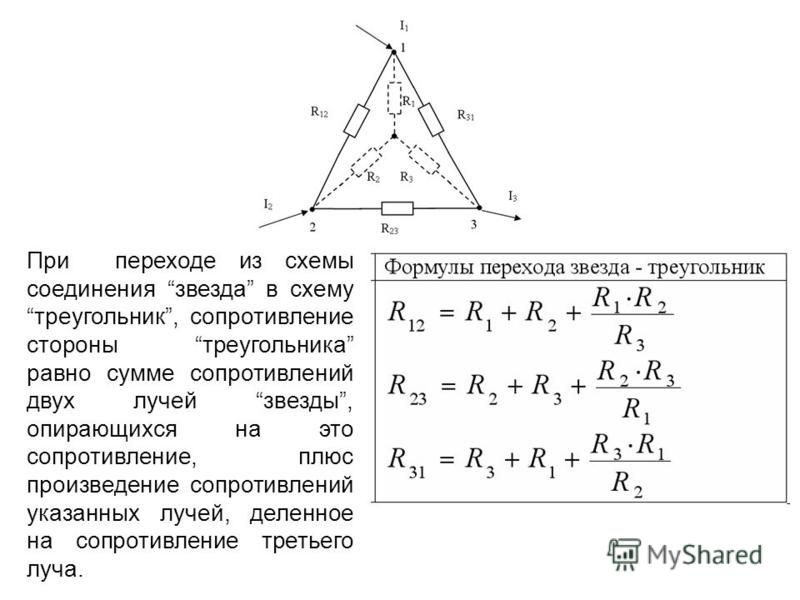
3. Вау! Специальный калькулятор прямоугольного треугольника вычислил размеры вашего треугольника! Теперь мы знаем, что: 92}12,5 дюйма2.

Больше не ждите. Попробуй сам!

Часто задаваемые вопросы

Какие формулы для треугольника 45 45 90?

Треугольник 45° 45° 90° имеет следующие формулы, где x длина любой из равных сторон:

• Гипотенуза = x√2 ;
• Площадь = x²/2 ; и
• Периметр = x(2+√2) ;

Как решить специальный прямоугольный треугольник 30 60 90?

Чтобы решить специальный прямоугольный треугольник 30° 60° 90°, выполните следующие действия:

1. Найдите длину более короткой стороны. Мы назовем это x .
2. Более длинная сторона будет равна x√3 .
3. Его гипотенуза будет равна 2x .
4. Площадь равна A = x²√3/2 .
5. Наконец, периметр равен P = x(3+√3) .

   No related posts.