Соединение треугольником в трехфазной цепи: Трехфазные цепи треугольник. Соединение треугольником.

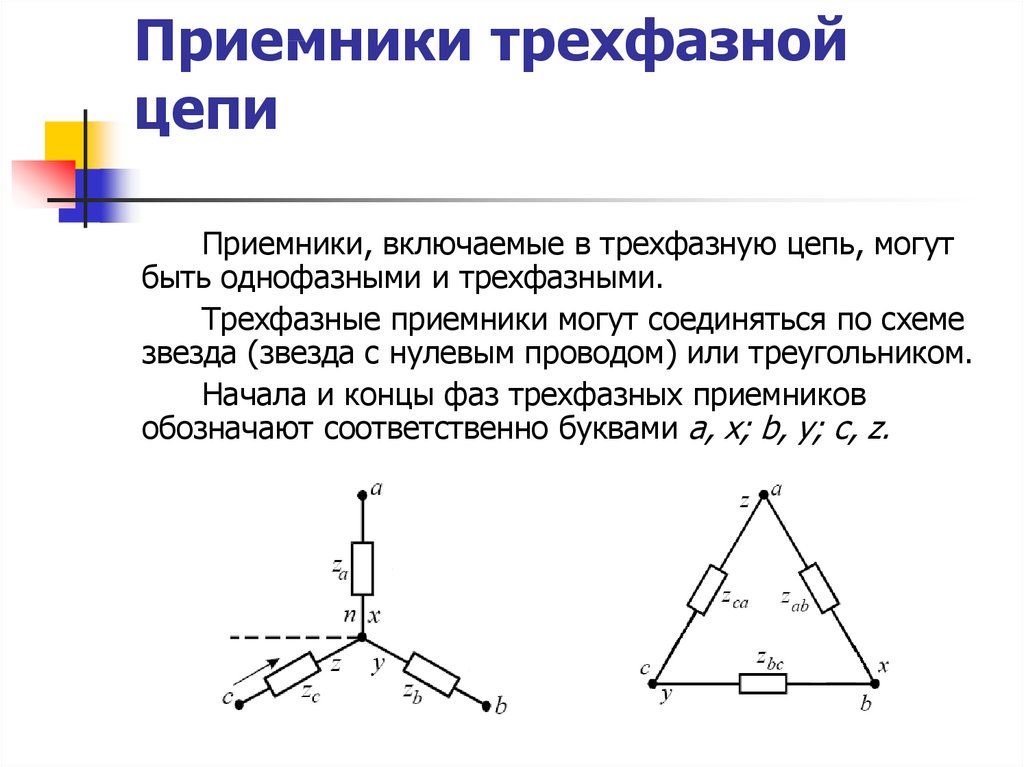
1.4. Соединение трехфазной цепи треугольником

Чтобы соединить генератор в треугольник, нужно связать конец каждой фазы с началом следующей; в результате фазы генератора образуют замкнутый контур. При таком соединении симметричного генератора с отключенной нагрузкой ток внутри него не возникает, так как сумма ЭДС контура равна нулю. Соединив приемник также в треугольник (рис. 1.16), можно видеть, что фазные напряжения генератора и приемника одновременно являются и линейными, линейные же токи İ_A, İ_B, İ_C – отличны от фазных токов İ_AB, İ_BC, İ_CA.

Для получения симметричных соотношений между линейными и фазными токами следует выбирать их положительные направления единообразно. Тогда по первому закону Кирхгофа

И з полученных соотношений видно, что геометрическая сумма линейных токов равна нулю:

Линейные токи на векторной диаграмме образуют замкнутый треугольник.

При соединении трехфазной цепи треугольником можно выделить три частных случая.

1. Симметричная нагрузка (Z_AB=Z_BC=Z_CA).

Л инейные токи на диаграмме образуют равносторонний треугольник (рис.1.17).

Достаточно определить ток одной фазы, в других фазах токи равны по величине, но имеют фазовый сдвиг +120º или -120º:

2) Несимметричная нагрузка, Z_пр=0, (Z

_AB­­_­­­Z_BCZ_CA).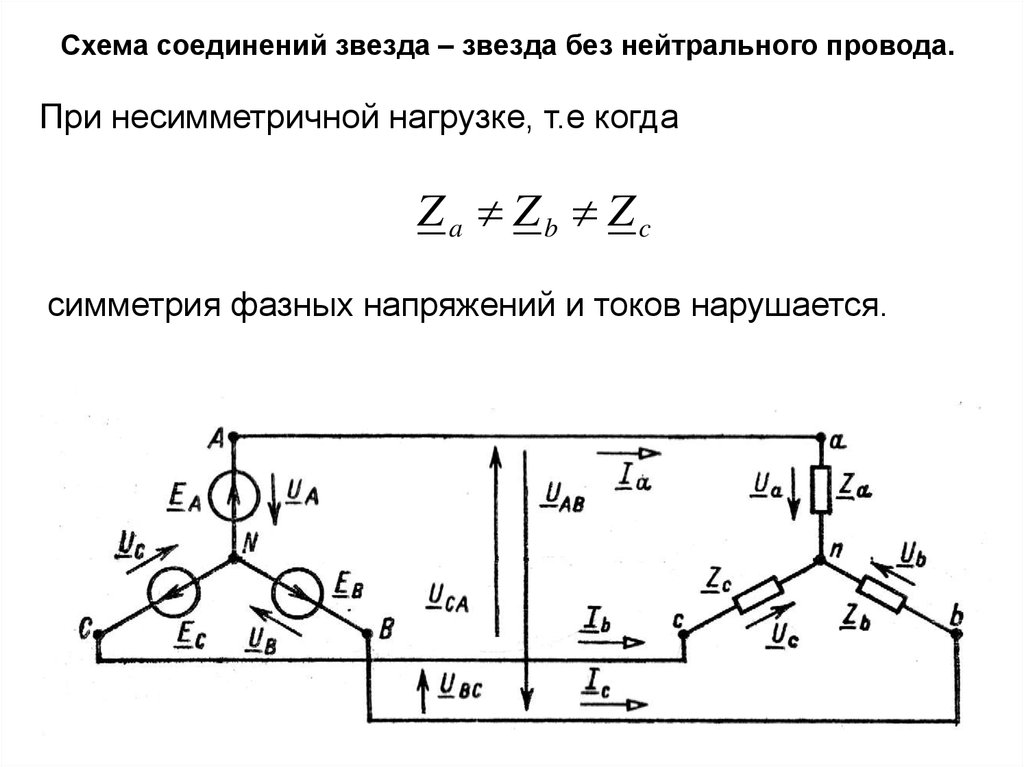

Если пренебречь сопротивлением проводов, напряжения генератора будут равны напряжениям приемника, фазы будут независимы друг от друга: всякое изменение сопротивления какой-либо фазы приемника вызовет изменение тока этой фазы и токов двух примыкающих к этой фазе линейных проводов, но никак не отразится на токах других фаз. Фазные токи определяются следующим образом:

3) Несимметричная нагрузка, Z_пр0, (

Z_AB­­_­­­Z_BCZ_CA) .

Преобразуя треугольник сопротивлений приемника в эквивалентную звезду сопротивлений, задачу сводят к случаю соединения звездой (рис.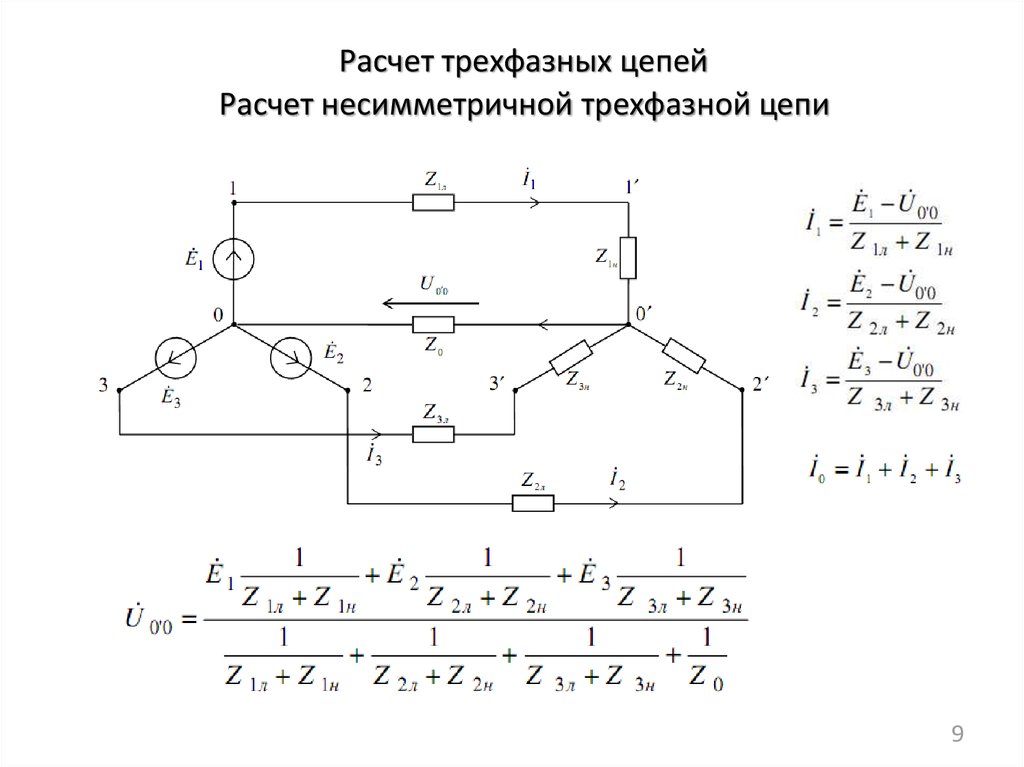 1.18).

После определения токов звезды необходимо обратиться к исходному треугольнику, чтобы найти его фазные токи.

В любом случае построение диаграммы начинают с равностороннего треугольника линейных напряжений, который является одновременно треугольником фазных напряжений нагрузки, если пренебречь сопротивлением проводов линии. Затем откладывают фазные токи с соответствующим фазовым сдвигом по отношению к напряжению данной фазы. Переносят фазные токи на отдельный чертеж в одну точку и с учетом первого закона Кирхгофа получают линейные токи, замкнув концы фазных токов треугольником. Стрелку линейного тока направляют в сторону уменьшаемого фазного тока.

Пример 1-6.

Соединение треугольником при симметричной нагрузке Z_AB=Z_BC=Z_CA=Z=(10+j5,7) Ом и Z_пр=0, U_Л=220 В (рис.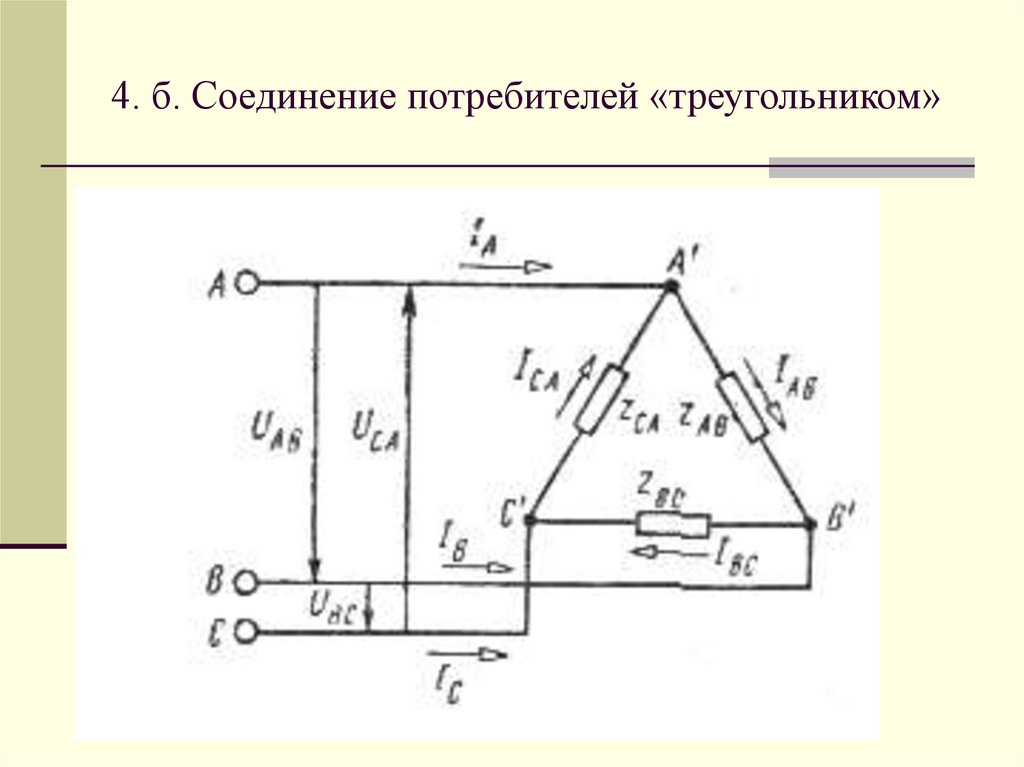 1.16). Расчитать токи и построить векторную диаграмму напряжений и токов.

Решение

П остроим равносторонний треугольник линейных напряжений. Определим ток каждой фазы (рис. 1.19):

Т ок каждой фазы на диаграмме откладываем под углом

п о отношению к соответствующему фазному напряжению. Затем перенесем все фазные токи на отдельный чертеж в одну точку. С учетом первого закона Кирхгофа получаем линейные токи:

Л инейные токи образуют замкнутый равносторонний треугольник, причем направлен соответствующий линейный ток к соответствующему уменьшаемому фазному току.

Пример 1-7.

В цепи (рис. 1.20) R=X_L=X_C.

Построить векторную диаграмму напряжений и токов

Решение

П остроение диаграммы начинаем с равностороннего треугольника линейных напряжений U_AB, U_BC,

U_CA (рис.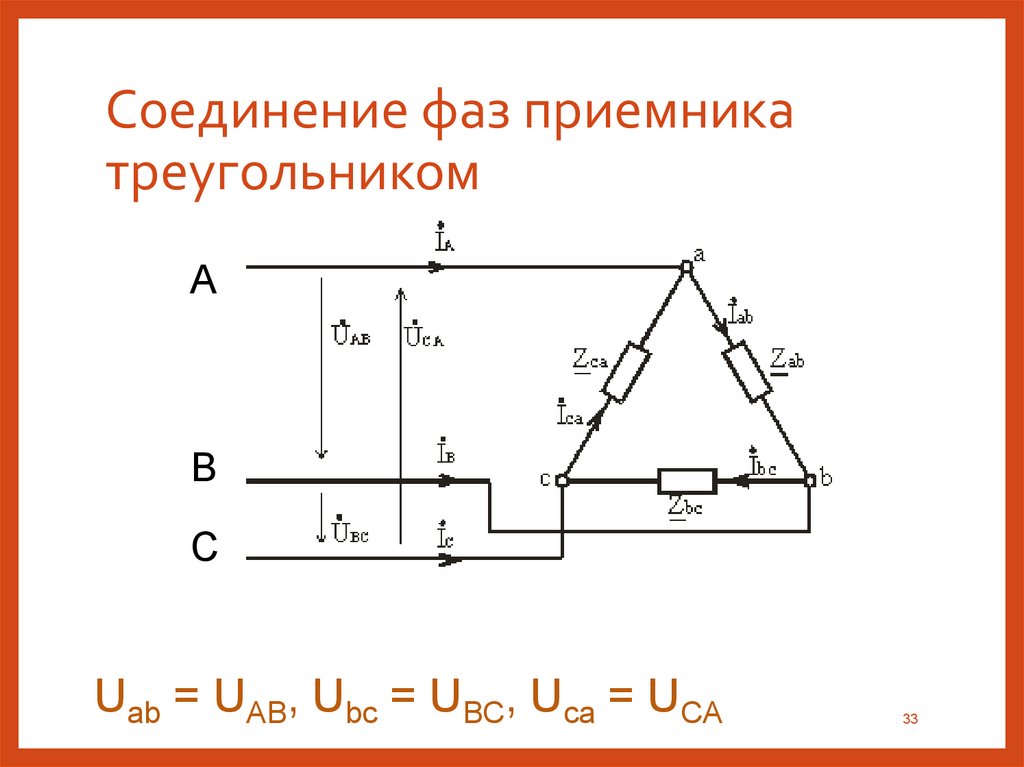 1.21).

П одсчитаем токи каждой фазы нагрузки и отложим векторы этих токов с учетом фазового сдвига по отношению к соответствующему напряжению фазы.

П еренесем на отдельный чертеж фазные токи İ_AB, İ_BC, İ_CA в одну точку и, соединив их вершины, получим линейные токи

Стрелка линейного тока направлена в сторону уменьшаемого фазного тока.

Пример 1-8.

В схеме (рис. 1.22) R_AB=R_BC=R_CA=R . Как изменятся токи в цепи: 1) если замкнется рубильник; 2) если сгорит предохранитель Пр1 ?

Решение

1. П ри замыкании рубильника сопротивление фазы АВ уменьшается в 2 раза:

Токи остальных фаз не меняются.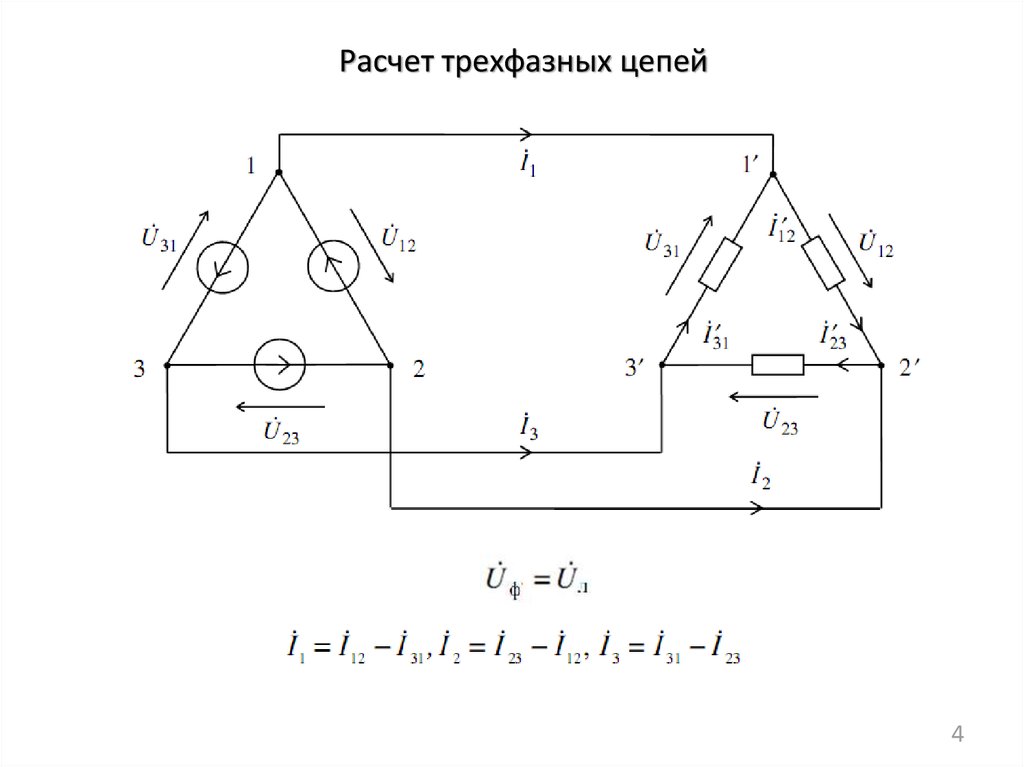 На векторной диаграмме (рис. 1.23) покажем токи до замыкания и после замыкания рубильника. Токи в линии А и В увеличиваются с увеличением тока фазы АВ, İ_C – не изменится.

2. Если сгорит предохранитель Пр1, то ток фазы İ_CA=0, тогда линейные токи (рис. 1.24):

İ_A=İ_AB — уменьшится;

İ_B=İ_BC

-İ_AB — не изменится;

İ_С= -İ_BC — уменьшится.

Пример 1-9.

Найти линейные и фазные токи в цепи (рис. 1.25), если U_Л=220 В, X_L=5 Ом, X_C=3 Ом.

Решение

П реобразуем треугольник abc в эквивалентную звезду:

Определим эквивалентное сопротивление фазы преобразованной схемы

( рис. 1.26):

Расcчитаем линейные токи (рис. 1.26) и перенесем на диаграмму

( рис. 1.28).

Определим напряжения U_a0’, U_b0’, U_c0’ (рис. 1.26) и перенесем эти напряжения на векторную диаграмму (рис. 1.27).

Рассчитаем напряжения треугольника abc (рис. 1.25) и перенесем на диаграмму (рис. 1.27).

Р ассчитаем фазные токи исходной схемы (рис. 1.25) и перенесем их на диаграмму (рис.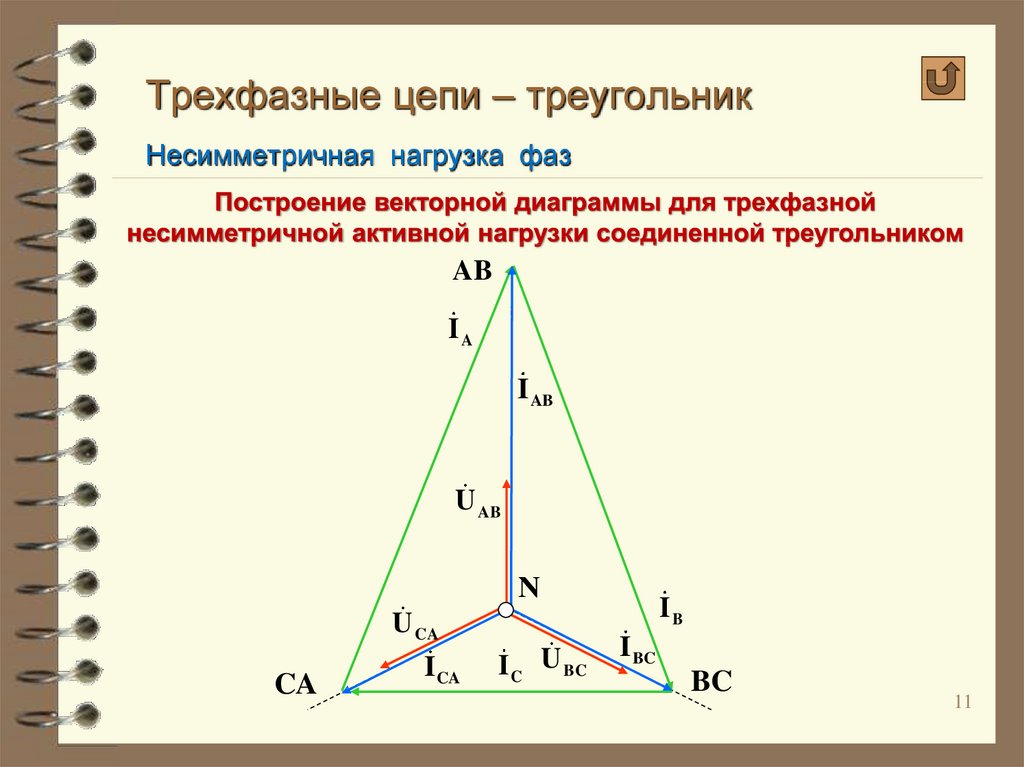 1.28).

СОЕДИНЕНИЕ ТРЕХФАЗНОЙ ЦЕПИ ТРЕУГОЛЬНИКОМ

РАБОТА. II

Соединение трехфазной цепи треугольником

I. Цель работы

Целью работы является исследование трехфазной цепи при соединении приемников энергии треугольником при питании их от симметричной трехфазной системы напряжений.

II. Методические указания

При подготовке к выполнению работы необходимо: к

1. Проработать описание данной работы и по рекомендованной литературе изучить симметричный и несимметричный режимы работы трехфазной цепи при соединении треугольником.

г-‘*

2. Вычертить схему для проведения эксперимента и^; подготовить таблицы для записи данных электроизмерительных приборов и резуль­татов эксперимента.

При соединении трехфазного приемника треугольником (фиг. II .I.) необходимо конец первой фазы соединить с началом второй, конец второй фазы — с началом третьей и конец третьей — с началом первой, а к точкам соединения фаз присоединить линейные провода.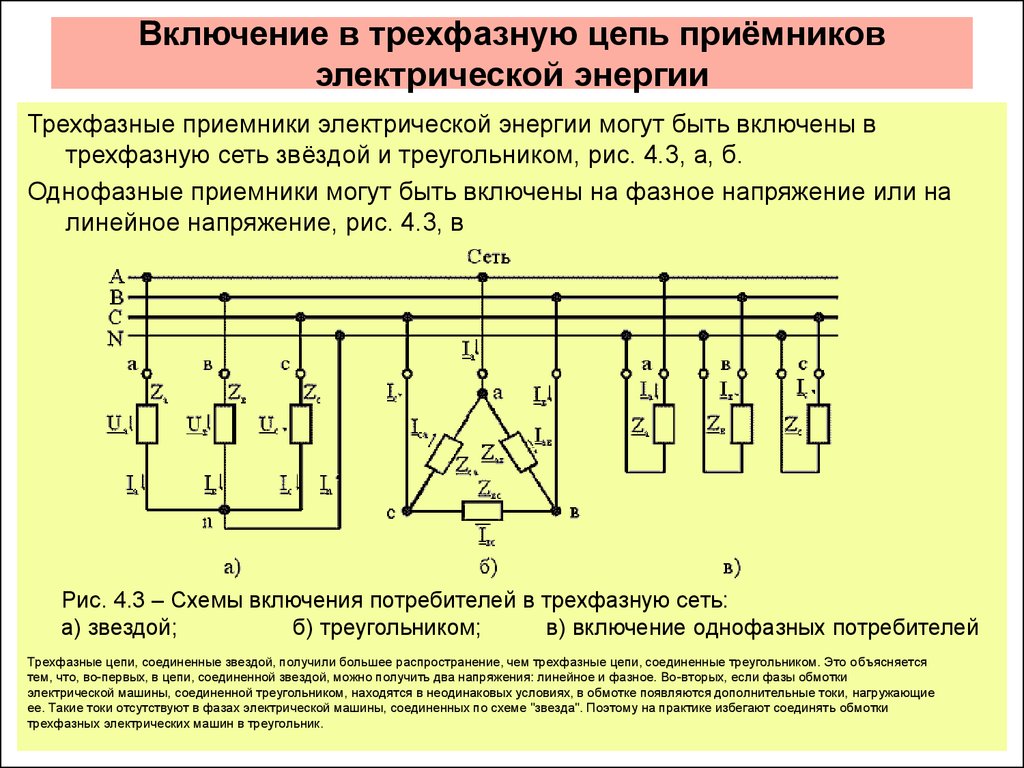

Напряжения U_AB, U_BC

иU_CA называются линейными напряжения­ми. По величине они равны, а по фазе сдвинуты относительно друг друга на угол, 120°, U_AB+U_BC+U_CA=0 .

При соединении треугольником линейные и фазные напряжения равны между собой U_Л = U_Ф

Токи I_AB, I_BC, I_CA называются фазными токами. За положительное их направление принимают направление движения по стрелке часов.

Токи I_A, I_B, I_C называются линейными токами. За положитель­ное их направление принимают направление от источника к потребителям.

Трехфазный приемник называется симметричным, если равны комплексы полных сопротивлений всех его фаз, т. е.

Z_AB= Z_BC= Z_CA

Между линейными и фазными токами существуют зависимости вытекающие из первого закона Кирхгофа :

i_А= i_АБ — i_СА; i_В=i_ВС — i_АВ; i_С= i_СА — i_ВС

При симметричном режиме

I_л=·I_Ф.

Векторная диаграмма напряжений и токов при симметричной ¹

системе приложенных напряжений генератора с прямым порядком чередования фаз А, В, С и симметричной активной нагрузке изобра­жена на фиг II. 2.

Секторные диаграммы для отдельных режимов удобно строить следующим образом:

• выбирается масштаб напряжений и токов;

• откладывается вектор ВС, равный линейному напряжению U_BC ( например, горизонтально) и из точек В и С засечками тем же вектором ВС определяется положение точки А, соединяя ее прямыми с точками В и С — получили треугольник линейных напряжений U_AB, U_BC, U_CA;

• от точек А,В и С откладываются вектора фазных токов, совпадающие по направлению с векторами соответствующих напряжений.

• Строятся вектора линейных токов, как разность соответству­ющих фазных токов. Из конца вектора i_АВ откладывается вектор(- i_СА) параллельно вектору i_СА, затем соединяя прямой точку В с Началом

вектора i_СА получим вектор линейного тока i_А. Векторы i_В и i_С строятся аналогично.

Изменение сопротивления в одной из фаз трехфазного приемника не вызывает изменения режима работы в двух других фазах, но приводит к изменению линейных токов .

Обрыв одной из фаз (первой) симметрической цепи при активной нагрузке (фиг. II. 3.) иллюстрируется век торной диаграммой фиг. II. 4. Линейный ток i_А=- i_СА отстает от линейного напряжения U_AB на угол 60^0,,а линейный ток i_С= ·i_СА отстает по фазе от соответствующего напряжения U_CAна угол 30⁰.

Обрыв одного из линейных проводов, например второго, симметрической цепи при активной нагрузке приводит к образованию схемы параллельного соединения двух ветвей, включенных на линейное напряжение (фиг. II. 5.).

Фазное напряжение Ů_CA по-прежнему берут равно линейному напряжению, а фазные напряжения Ů_AB и Ů_CB в сумму будут равны линейному напряжению U_л (фиг.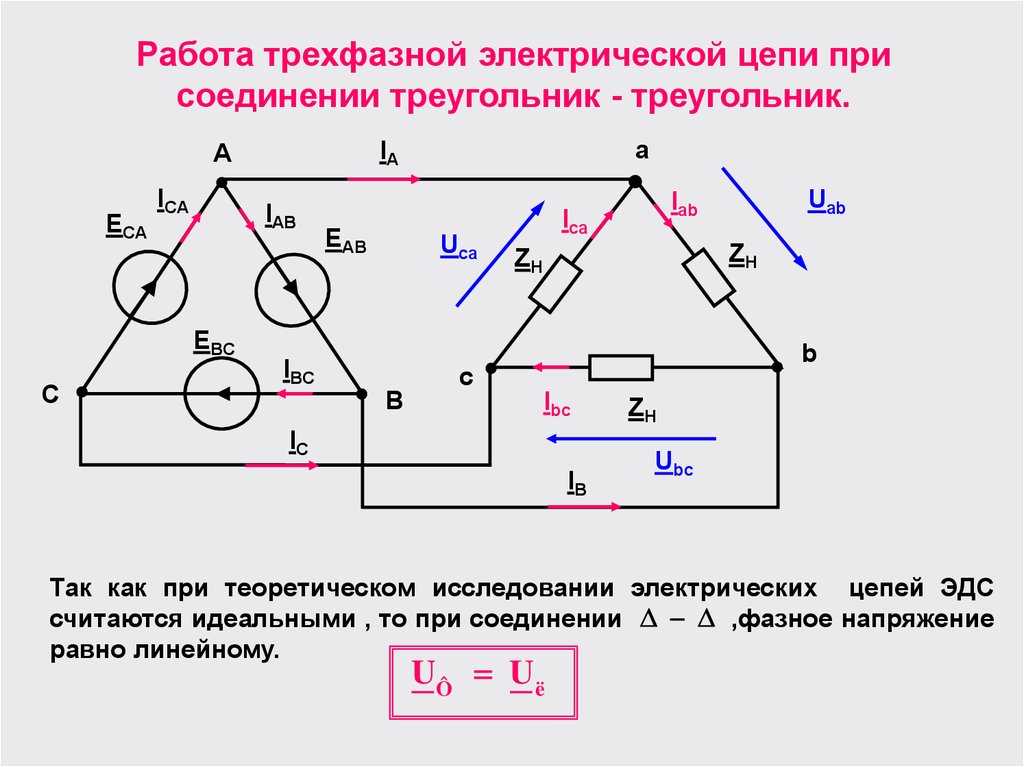 II. 6.)

U_AB=U_BC=

Фазные токи i_АВ и i_ВС уменьшаются и будут равны между собой

i_АВ= i_ВС=

Фазные токи i_АВ и i_ВС уменьшаютсяи будут равны между собой

i_АВ=i_ВС===0,865I_ф

Таким образом, при обрыве второго линейного провода лампы в первой и второй фазах будут гореть темнее, а в третьей фазе – также как до обычного.

Литература

1. Л.Р. Нейман и К.С. Демерчан. Теоретические основы электротехники. Т.І. Энергия. 1966. §7№1 ,7 – 2.

2. Г. В. Зевеке, П.А. Ионкин, А. В. Нетушин, С.В. Страхов. Основы теории цепей. ГЭИ. 1963. §13 – 2, 13 – 4, 13 – 7.

3. Л. А. Бессонов. Теоретические основы электротехники. В. Ш. М. 1964. §131–134, 138.

III. Описание лабораторной установки.

Для исследования трехфазной цепи при соединении треугольником собирается цепь, схема которой изображена на фиг. 11.7.

Приемником в исследуемых цепях служит трехфазный ламповый реостат, состоящий из трех групп ламп, по одной группе на фазу. В каждой группе предусмотрены выключатели для ступенчатой регу­лировки нагрузки. На схеме каждая фаза лампового реостата условно обозначена тремя лампами.

Исследуемая цепь подключается автоматом «Выкл» к сети трех- фазного переменного тока напряжением 127/220 В с частотой 60 Гц.

Обрыв линейного провода осуществляется однополюсным рубиль­ником Р.

Измерение напряжений производится переносным вольтметром, к зажимам которого присоединяются два проводника.

Для измерения линейного напряжения, например, необходимо концами проводов, присоединенных к вольтметру коснуться точек «а» и «в»

Аналогично измеряются два других линейных напряжения. Измерение мощности в цепи осуществляется трехфазным двух- элементным ферродинамическим ваттметром типа Д571

IV. Задание и порядок выполнение работы

1. Собрать электрическую цепь, схема которой изображена на фиг. 11.7.

2. Установить симметрическую нагрузку во всех фазах приемника (например, в каждой фазе включить по пять ламп одинаковой мощности). При этом показания амперметров, измеряющих фазные токи, должны быть одинаковыми, показания приборов, измеряющих линейные токи, также должны быть одинаковыми.

Включить автомат «Выкл.», произвести измерения величин указанных в таблице 1 и записать их.

Таблица 1.

Режим	Измерено
	UАВ	UВС	UСА	IА	IВ	IС	IАВ	IВС	IСА	P
	B	B	B	A	A	A	A	A	A	Вm
Симметрическая нагрузка
Несимметрическая нагрузка
Обрыв фазы
Обрив линейного провода

3. Установить не симметрическую нагрузку фаз, например, в первой фазе оставить включенной пять ламп, во второй – три и в третьей – одну. Включить автомат «Выкл.» произвести измерение величин, указанных в таблице 1 и записать их.

Убедится в том, что изменение нагрузки в одной из фаз трехфазного приемника не вызывает изменения режима работы в двух других фазах.

4. Установить первоначальную симметрическую нагрузку в соответствии с пунктом 2, выключить питание. Отключить провод в одной из фаз, включить автомат «Выкл.» , произвести измерения и результаты записать в таблицу 1.

5. Подсоединить оборванный фазный провод, а один из линейных проводов отключить / величины сопротивлений фаз не изменять /.Включить автомат «Выкл.», произвести измерения и результаты записать в таблицу 1. \

Обратить внимание на яркость горения ламп.

6. По данным таблицы 1 построить векторные диаграммы напряжений и токов для симметрического и несимметрического режимов, обрыва фазы и линейного провода.

7. Вычислить мощность, потребляемую трехфазной цепью, и сравнить ее с данными измерений.

Контрольные вопросы к работе II

1. Какова цель работы ?

2. Какое соединение трехфазной цепи называется треугольником ? Изобразите схему этого соединения.

3. Какая нагрузка трехфазного приемника называется симметрической ?

4. Какое напряжение называется фазным и линейным ? Каково соотношение между этими напряжениями в трехфазной цепи, соединенном треугольником ?

5. Какой ток называется фазным и линейным ? Каково соотношение между этими токами в трехфазной цепи, соединенном треугольником ?

6. Как изменятся фазные и линейные токи при изменении сопротивления в одной из фаз трехфазного приемника, соединенного треугольником ?

7. Три лампочки реостата одинаковой мощности соединены треугольником и подключены к симметрической системе линейных напряжения. Чему будут равны напряжения на зажимах первой и второй фазы, если перегорит предохранитель во втором линейном проводе ?

8. Расскажите порядок построения векторных диаграмм.

9. Постройте векторную диаграмму напряжения и токов несимметрического режима при активной нагрузке фаз.

10. Постройте векторную диаграмму напряжения и токов для случая обрыва одной из фаз.

11. Постройте векторную диаграмму напряжения и токов для случая обрыва одного из линейных проводов.

12. Три ламповых реостата одинаковой мощности соединены треугольником и подключены симметрично системе линейных напряжений. Чему будут равны фазные токи первой и второй фаз, если перегорит предохранитель во втором линейном проводе ?

13. В каком случае можно пользоваться соотношением ? Вывести эту формулу.

14. Что понимают под независимостью работы фаз приемника ? В каком случае возможна независимая работа фаз ?

15. Объясните построение векторных диаграмм, проведенных в отчете по работе.

Соединение треугольником в 3-фазной системе — Соотношение между фазным и линейным напряжением и током

В соединении треугольником (Δ) или сеткой конечная клемма одной обмотки соединяется с пусковой клеммой другой фазы и так далее, что дает замкнутую цепь. Трехлинейные проводники проходят от трех соединений сетки, называемой Линейные проводники .

Соединение треугольником показано на рисунке ниже:

Состав:

• Соотношение между фазным и линейным напряжением при соединении треугольником
• Соотношение между током фазы и током линии при соединении треугольником

Для получения соединения треугольником , a ₂ соединяется с b ₁ , b ₂ соединяется с c ₁ , а c ₂ соединяется с 1_{, как показано выше. фигура. Три проводника R, Y и B проходят от трех соединений, известных как 9.0003 Линейные проводники .}

Ток, протекающий через каждую фазу, называется Phase Current (Iph) , а ток, протекающий через каждый линейный провод, называется Line Current (I _L ).

Напряжение на каждой фазе называется Phase Voltage (E _ph ) , а напряжение между двумя линейными проводниками называется Line Voltage (E _L ).

Соотношение между фазным и линейным напряжением при соединении треугольником

Чтобы понять взаимосвязь между фазным напряжением и линейным напряжением при соединении треугольником, рассмотрите рисунок А, показанный ниже:

Из рисунка видно, что напряжение на клеммах 1 и 2 такое же, как и на клеммах R и Y. Следовательно,

Аналогично

: фазные напряжения равны

Линейные напряжения:

Соотношение между фазным и линейным током при соединении треугольником

Как и в уравновешенной системе, трехфазный ток I ₁₂ , I ₂₃ и I ₃₁ равны по величине, но смещены друг относительно друга на 120° эл.

Векторная диаграмма показана ниже:

Следовательно,

Если мы посмотрим на рисунок А, то увидим, что ток делится на каждом соединении 1, 2 и 3.

Применение закона Кирхгофа на разветвлении 1,

Входящие токи равны исходящим токам.

И их разность векторов будет равна:

Вектор I ₁₂ инвертируется и добавляется к вектору I ₃₁ , чтобы получить векторную сумму I ₃₁ и –I , как показано выше на векторной диаграмме. Следовательно,

Как мы знаем, I _R = I _L , следовательно,

Аналогично,

Следовательно, ток линии при соединении треугольником в три раза больше фазного тока.

Это все о соединении треугольником в трехфазной системе.

Трехфазное соединение треугольником: трехфазное питание, напряжение, ток

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

Соединение треугольником

При соединении треугольником стороны фаз соединяются циклически, образуя замкнутый контур, как показано на рис. 1. Что касается линейного и фазного токов, то они связаны друг с другом следующим образом: : 9{1}/{}_{\sqrt{3}}$ умножить только на ток линии. В то время как при соединении треугольником линейное и фазное напряжение одинаковы:

${{\text{V}}_{\text{фаза}}}\text{=}{{\text{V}}_{\text {line}}}$    

Сбалансированная нагрузка, соединенная по схеме треугольника (с равными импедансами фаз), показана на рис. 1. 

Рис.1: Нагрузка, соединенная по схеме треугольника

Преимущество нагрузки, соединенной по схеме треугольника, по сравнению с нагрузкой, соединенной по схеме треугольник Нагрузка заключается в том, что нагрузки могут быть легко добавлены или удалены на одной фазе треугольника, поскольку нагрузки подключаются непосредственно через линии. Кроме того, для данной мощности, подаваемой на нагрузку, фазные токи в треугольнике меньше, чем в Y. С другой стороны, фазные напряжения в треугольнике выше, чем в соединении Y. Источники редко соединяются треугольником, потому что, если напряжения не идеально сбалансированы, будет чистое напряжение и, следовательно, циркулирующий ток вокруг треугольника.