При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:
Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть UФ = UЛ. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.
На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.
В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:
Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.
Симметричная нагрузка при соединении приемников треугольником
В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:
Очевидно, что при симметричной нагрузке:
Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:
В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения Uab принято направлять вертикально вверх.
Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):
На основании данной векторной диаграммы можно записать: 
. Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке 
Пример
Трехфазная сеть имеет линейное напряжение UЛ = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное rф = 8,65 Ом и индуктивное xф = 5 Ом сопротивления.
Решение
Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.
Линейные и фазные токи, а также полные сопротивления фаз будут равны:
Активная, реактивная и полная мощности электроприемника любой фазы будут равны:
Векторные диаграммы приведены выше.
Несимметричная нагрузка при соединении приемников треугольником
В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:
В пределах каждой группы подключение приемников производится параллельно.
После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:
Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:
Для определения суммарной мощности всех фаз нужно применять выражение:
Пример
Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: UЛ = 220 В, rab = 40 Ом, xLbc = 10 Ом, rbс = 17,3 Ом, xcа = 5 Ом, rCcа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.
Решение
Воспользовавшись выражением для определения комплексных значений получим:
Комплексные значения полных сопротивлений фаз: Zab = 40 Ом, Zbс = 17,3 + j10 Ом, Zbс = 8,65 – j5 Ом.
Комплексные и действующие значения линейных и фазных токов:
Дольше можно проводить расчеты, не прибегая к комплексному методу:
Общие активные и реактивные мощности:
Углы сдвига между токами и напряжениями:
Векторная диаграмма для несимметричного треугольника приводилась выше.
Потребители соединяются треугольником, если их рабочее напряжение равно линейному напряжению. Существуют два вида изображений на схемах: потребители расположены под углом 120˚ или параллельно друг другу.
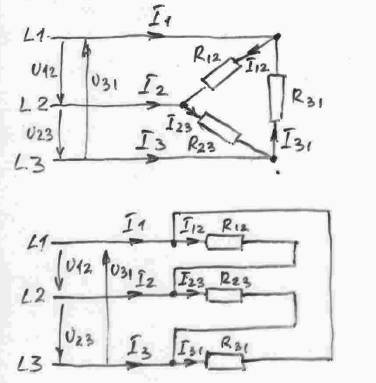
При соединении в треугольник линейные напряжения равны фазному напряжению Uл = Uф. Токи в фазах: I12 = U12/R12, I23 = U23/R23, I31 = U31/R31.
Векторные диаграммы при соединении треугольником можно тоже рисовать по-разному. Можно рисовать векторы, исходящими из одной начальной точки, а можно векторы напряжений изобразить треугольником (рис.130). При симметричной нагрузке векторы фазовых токов равны, и векторная диаграмма симметрична. Если нагрузка не симметрична, то этого не будет.
Пример.
В трёхфазной сети с напряжением 400В объединены в треугольник потребители с разным сопротивлением нагрузки.
Найдём фазовые и линейные токи в этой цепи.
Фазовые токи:
I12 = U12/R12 = 4A;
I23 = U23/R23 = 8A;
I31 = U31/R31 = 2A.
Линейные токи можно найти из векторной диаграммы, учитывая следующие соотношения: I1 + I31 = I12, I2 + I12 = I
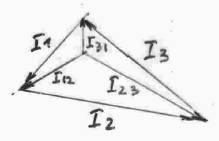
Особый случай несимметричной нагрузки получается при обрыве одного из проводов. Посмотрим, что получится при обрыве L1.
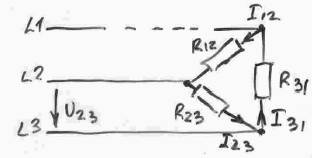
Схема в этом случае приобретёт следующий вид:
R23 будет работать в нормальном режиме: I23 = U23/R23. Потребители R12 и R31 будут подсоединены неправильно и их ток: I12 = I31 = U23/(R12 + R31). Линейный ток I2 будет равен геометрической сумме токов I23 и I12.
49) Понятие о нелинейных цепях переменного тока. Цепи с нелинейными активными элементами
Цепь называют нелинейной, если хотя бы один из её элементов обладает нелинейной характеристикой.
Активные нелинейные сопротивления характеризуются вольтамперной характеристикой
(рис. 4.1).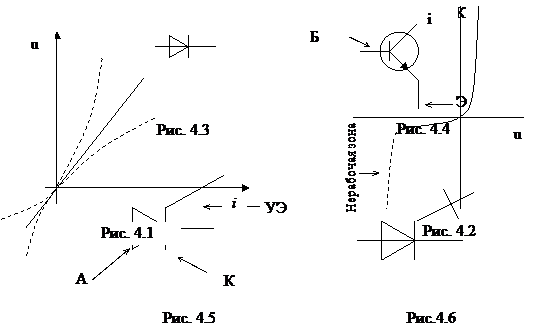
Характеристики элементов могут быть симметричными и несимметричными. Они располагаются в первом и в третьем квадрантах. У нелинейных элементов их сопротивление зависит от напряжения r(u) или от тока, r(i).
Примером активного нелинейного сопротивления является полупроводниковый диод.
Его вольтамперная характеристика (ВАХ) несимметрична (рис. 4.2) и содержит рабочие (сплошная линия) и нерабочие зоны (штриховая линия). На электрических схемах диод изображается, как показано на рис. 4.3. Он относится к неуправляемым элементам.
Примером управляемого активного нелинейного сопротивления является транзистор (рис. 4.4). Током базы (Б) изменяют сопротивление между эмиттером (Э) и коллектором (К).
Другим примером управляемого активного нелинейного сопротивления является тиристор (рис. 4.5).
В нем с помощью управляющего электрода (УЭ) можно только уменьшить сопротивление между анодом и катодом Rak, а увеличить его нельзя. Это не полностью управляемое активное сопротивление.
Существуют и запираемые тиристоры (рис. 4.6). Запираемый тиристор (может увеличивать и уменьшать Rak).
Нелинейные индуктивные элементы характеризуются вебер-амперной характеристикой (рис. 4.7).
Потокосцепление связано с током следующей зависимостью: y = Li. Эта формула и определяет вебер-амперную характеристику (ВбАХ). Если индуктивность L = сonst, то характеристика – прямая (рис. 4.7, а, сплошная линия), но если в ее основе есть ферромагнетик, то это неуправляемая нелинейная индуктивность (рис. 4.7, б).
Нелинейная индуктивность, зависящая от тока, может быть изображена на схемах в виде (рис. 4.8). Нелинейная индуктивность может быть управляемой (рис. 4.9). Постоянным током управления Iу можно изменять рабочий ток iр. Характеристика такой индуктивности при изменении Iу смещается (рис. 4.10).
С помощью нелинейных элементов в электрических цепях осуществляется ряд преобразований электромагнитной энергии. Основные из них: выпрямление переменного напряжения или тока; инвертирование постоянного напряжения или тока; усиление напряжений и токов; регулирование постоянных и переменных напряжений и токов; стабилизация напряжений и токов; преобразование частоты; модуляции и так далее.
50) Соотношение между фазными и линейными напряжениями и токами
При соединении приемников энергии треугольником (рис. 6-11) каждая фаза приемника присоединяется к линейным проводам, т. е. включается на линейное напряжение, которое одновременно будет и фазным напряжением приемника:
Uab = Ua, Ubc = Ub, Uca = Uc.
Таким образом, изменение сопротивления фаз не влияет на фазные напряжения.
Направления линейных токов от генератора к приемнику примем за положительные (рис. 6-11). Направления фазных токов от А’ к В’, от В’ к С‘ и от С’ к А’ также примем за положительные.
Согласно первому правилу Кирхгофа для мгновенных значений токов для узла А’ можно написать:
iA + iCA = iAB
откуда
iA = iAB — iCA
Аналогично для узла В’:
iB = iBC — iAB
и для узла С’:
iC = iCA — iBC
Рис. 6-11. Соединение приемников треугольником
Следовательно, мгновенное значение любого линейного тока равно алгебраической разности мгновенных значений токов тех фаз, которые соединены с данным проводом.
Рис. 6-12. Векторная диаграмма при соединении приемников треугольником.
Вектор любого линейного тока находится как разность векторов соответствующих фазных токов:
IA = IAB — ICA; IB = IBC — IAB; IC = ICA — IBC
На рис. 6-12 дана векторная диаграмма для трехфазной цепи при соединении приемников энергии треугольником. На этой диаграмме все векторы проведены из одного начала. На рис. 6-13 дана вторая диаграмма для той же цепи, на которой векторы напряжений образуют треугольник, а вектор каждого фазного тока проведен из одного начала с вектором соответствующего фазного напряжения.
Рис. 6-13. Векторная диаграмма при соединении приемников треугольником.
Если при симметричной системе линейных напряжений нагрузка фаз равномерная, т. е.
zAB = zBC = zCA = zФ
и
φАВ = φВС = φСА = φФ.
то действующие значения фазных токов равны между собой и они сдвинуты по фазам на одинаковые углы от соответствующих напряжений (рис. 6-14) и, следовательно, на углы 120° один относительно другого. Следовательно, фазные токи представляют симметричную систему. Симметричную систему будут представлять и линейные токи (рис. 6-14).
Восстановив перпендикуляр из середины вектора линейного тока, например IА, получим прямоугольный треугольник OHM, из которого следует, что
1/2IЛ = IФ cos 30° = IФ(√3/2)
или
IЛ = √3IФ
Таким образом, при соединении приемников треугольником при равномерной нагрузке фаз линейные токи больше фазных в √3 раз.
Кроме того, из той же векторной диаграммы следует, что линейные токи отстают от соответствующих фазных токов на углы 30°.
Рис. 6-14. Векторная диаграмма для цепи, соединенной треугольником при равномерной нагрузке фаз.
При соединении приемников треугольником при равномерной нагрузке фаз расчет трехфазной цепи сводится к расчету одной фазы.
В этом случае фазное напряжение UФ = UЛ Фазный ток IФ = UФ/zФ
Линейный ток
IЛ = √3IФ
во фазного напряжения определяются из выражений
cosφ = rФ/zФ; tgφФ = xФ/rФ
Активная мощность одной фазы
PФ = UФIФcosφФ Активная мощность трех фаз
P = 3PФ = 3UФIФ cosφФ = √3 UI cosφ
Реактивная мощность трех фаз
Q = 3UФIФ sinφФ = √3 UI sinφ
Полная мощность трехфазной цепи
S = 3UФIФ = √3UI
При неравномерной нагрузке фаз мощность трехфазной цепи определяется как сумма мощностей отдельных фаз.
Если приемники энергии соединены звездой и за положительное направление линейных токов вобрано направление от генератора к потребителю, то согласно первому правилу Кирхгофа для нейтральной точки можно написать:
iA + iB + iC = 0.
Если приемники энергии соединены треугольником, то сумма линейных токов
iA + iB + iC = iAB — iCA+ iBC — iAB+ iCA — iBC = 0
Следовательно, при любом способе соединения приемников алгебраическая сумма мгновенных значений линейных токов трехфазной трехпроводной цепи равна нулю.
Поэтому, например, намагничивающая сила трех жил трехфазного кабеля равна нулю и, следовательно, не происходит намагничивания стальной брони кабеля, применяемой для защиты от механических повреждений.
ВКЛЮЧЕНИЕ ПРИЕМНИКОВ ЭНЕРГИИ В СЕТЬ ТРЕХФАЗНОГО ТОКА
Электрические лампы изготовляются на номинальные напряжения 127 и 220 в, а трехфазные электродвигатели на номинальные фазные напряжения 127, 220 и 380 в и выше.
Способ включения приемника в сеть трехфазного тока зависит от линейного напряжения сети и от номинального напряжения приемника.
Лампы с номинальным напряжением 127 в включаются треугольником при линейном напряжении сети 127 в и звездой с нейтральным проводом при линейном напряжений сета 220 в. Лампы с номинальным напряжением 220 в включаются треугольником в сеть с линейным напряжением 220 в и звездой с нейтральным проводом в сеть с линейным напряжением 380 в.
Трехфазный электродвигатель включается треугольником в сеть, линейное напряжение которой равно номинальному фазному напряжению электродвигателя. Если линейное напряжение сети превышает в √3 раз номинальное фазное напряжение электродвигателя, то он включается звездой.
Статья на тему Соединение приемников энергии треугольником
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз
P = Pab + Pbc + Pca,
где
Pab = Uab Iab cos φab; Pbc = Ubc Ibc cos φbc; Pca = Uca Ica cos φca;
Uab, Ubc, Uca; Iab, Ibc, Ica – фазные напряжения и токи;
φab, φbc, φca – углы сдвига фаз между напряжением и током.
Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз
Q = Qab + Qbc + Qca,
где
Qab = Uab Iab sin φab; Qbc = Ubc Ibc sin φbc; Qca = Uca Ica sin φca.
Полная мощность отдельных фаз
Sab = Uab Iab; Sbc = Ubc Ibc; Sca = Uca Ica.
Полная мощность трехфазного приемника
.
При симметричной системе напряжений (Uab = Ubc = Uca = UФ) и симметричной нагрузке (Iab = Ibc = Ica = IФ; φab = φbc = φca = φ) фазные мощности равны Pab = Pbc = Pca = PФ = UФ IФ cos φ; Qab = Qbc = Qca = QФ = UФ IФ sin φ.
Активная мощность симметричного трехфазного приемника
P = 3 PФ = 3 UФ IФ cos φ.
Аналогично выражается и реактивная мощность
Q = 3 QФ = 3 UФ IФ cos φ.
Полная мощность
S = 3 SФ = 3 UФ IФ.
Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через линейные величины UЛ и IЛ.
При соединении фаз симметричного приемника звездой UФ = UЛ / 
, IФ = IЛ, при соединении треугольником UФ = UЛ, IФ = IЛ / . Поэтому независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой
P = UЛ IЛ cos φ.
где UЛ и IЛ – линейное напряжение и ток; cos φ – фазный.
Обычно индексы «л» и «ф» не указывают и формула принимает вид
P = U I cos φ.
Соответственно реактивная мощность
Q = U I sin φ.
и полная мощность
S = U I.
При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током, и, что при неизмененном линейном напряжении, переключая приемник со звезды в треугольник его мощность увеличивается в три раза:
Δ P = Υ 3P.
Если фазные обмотки генератора или потребителя соединить так, чтобы были соединены в одну общую точку, а начала обмоток присоединены к линейным проводам, то такое соединение называется соединением звездой и обозначается условным знаком Y. На рис. 1 обмотки генератора и потребителя соединены звездой. Точки, в которых соединены концы фазных обмоток генератора или потребителя, называются соответственно нулевыми точками генератора (0) и потребителя (0’). Обе точки 0 и 0’ соединены проводом, который называется нулевым, или нейтральным проводом. Остальные три провода трехфазной системы, идущие от генератора к потребителю, называются линейными проводами. Таким образом, генератор соединен с потребителем четырьмя проводами. Поэтому эта система называется четырехпроводной системой трехфазного тока.
Рис. 1. Соединение звездой
Сравнивая несвязанную и четырехпроводную системы трехфазного тока, видим, что в первом случае роль обратного провода выполняют три провода системы, а во втором – один нулевой провод. По нулевому проводу протекает ток, равный геометрической сумме токов:
IA, IB и IC, т. е. Ī0= ĪA + ĪB + ĪC .
Напряжения, измеренные между началами фаз генератора (или потребителя) и нулевой точкой (или нулевым проводом), называются фазными напряжениями и обозначаются UA, UB и UC, или в общем виде Uф. Часто задаются величины э.д.с. фазных обмоток генератора. Они обозначаются ЕA, ЕB и ЕC, или Еф. Если пренебречь сопротивлениями обмоток генератора, то можно записать:
ЕA= UA, ЕВ= UВ, ЕC= UС.
Напряжения, измеренные между началами двух фаз: А и В, В и С, С и А – генератора или потребителя, называются линейными напряжениями и обозначаются UАВ, UВС, UСА, или в общем виде Uл. На рис. 1 стрелки показывают выбранное положительное направление тока, которое в линейных проводах принято от генератора к потребителю, а в нулевом проводе – от потребителя к генератору.
Если присоединить зажимы вольтметра к точкам А и В, то он покажет линейное напряжение UАВ. Так как положительные направления фазных напряжений UA, UB и UC выбраны от начал фазных обмоток к их концам, то вектор линейного напряжения UАВ будет равен геометрической разности векторов фазных напряжений UA и UB:
ŪAВ=ŪA- ŪВ.
Аналогично можно записать:
ŪВС=ŪВ- ŪС;
ŪСА=ŪС- ŪА.
Иначе можно сказать, что мгновенное значение линейного напряжения равно разности мгновенных значений соответствующих фазных напряжений. На рис. 2 вычитание векторов заменено сложением векторов:
UA и — UB; UВ и — UС; UС и — UА.
Из векторной диаграммы видно, что векторы линейных напряжений составляют замкнутый треугольник.
Рис. 2. Фазные и линейные напряжения при соединении звездой
Зависимость между линейным и фазным напряжениями:
UBС=2UBcos30o, так как
cos30o=√3/2, то UBС=√3UB,
или в общем виде Uл=√3Uф.
Следовательно, при соединении звездой линейное напряжение в √3
раз больше фазного напряжения.
Ток, протекающий по фазной обмотке генератора или потребителя, называется фазным током и обозначается в общем виде Iф. Ток, протекающий по линейному проводу, называется линейным током и обозначается в общем виде Iл. На рис. 1 видно, что при соединении звездой линейный ток равен фазному току, т. е.
Iл=Iф .
Рассмотрим случай, когда нагрузка в фазах потребителя одинакова как по величине, так и по характеру. Такая нагрузка называется равномерной, или симметричной. Это условие выражается равенством.
z1= z2= z3.
Нагрузка не будет равномерной, если, например, z1= r1=0,5ом; z2=ωL2=0,5ом и z3=1/ωC3=0,5ом , так как здесь выполнено лишь одно условие – равенство сопротивлений фаз потребителя по величине, в то время как характер сопротивлений различен (r1 — активное сопротивление, ωL2 — индуктивное сопротивление, 1/ωC3 — емкостное сопротивление) .
При симметричной нагрузке:
IА=UА/zА; IВ=UВ/zВ; IС=UС/zС; IА=IВ=IС.
Фазные коэффициенты мощности вследствие равенства сопротивлений и одинаковости их характера будут одинаковы:
cosφ1=rА/zА; cosφ2=rB/zB; cosφ3=rC/zC; cosφ1=cosφ2=cosφ3.
В нулевом проводе должна протекать геометрическая сумма токов всех трех фаз. Если посмотреть на кривые изменения токов при симметричной нагрузке трехфазной системы, то увидим, что максимальные значения для всех трех синусоид тока одинаковы. Поскольку при симметричной нагрузке сумма мгновенных значений токов трехфазной системы равна нулю, следовательно, ток в нулевом проводе будет равен нулю.
Отбрасывая нулевой провод в четырехпроводной системе, переходим к трехпроводной системе трехфазного тока. Если имеется симметричная нагрузка, как, например, трехфазного тока, трехфазные печи, трехфазные трансформаторы и т. п., то к такой нагрузке подводятся только три провода. Потребители, включенные звездой с несимметричной нагрузкой фаз, нуждаются в нулевом проводе.
При симметричной нагрузке фазные напряжения отдельных фаз равны между собой. При несимметричной нагрузке трехфазной системы симметрия токов и напряжений нарушается. Однако в четырехпроводных цепях часто пренебрегают незначительной несимметрией фазных напряжений. В этих случаях между линейными и фазными напряжениями существует зависимость:
Uл=√3Uф.
Кроме соединения звездой, генераторы, трансформаторы, двигатели и другие потребители трехфазного тока могут включаться треугольником.
Соединение потребителей энергии в звезду.
1. Передача энергии трёхфазного тока от источника к потребителю.
2. Трёхпроводная трёхфазная цепь.
3. Четырёхпроводная трёхфазная цепь.
1. Передача энергии трёхфазного тока от источника к потребителю.
От трёхфазных источников к потребителям электрическая энергия может быть передана по трёхпроводной или четырёхпроводной цепи. В эти цепи могут быть включены как однофазные, так и трёхфазные потребители.
Симметричный трёхфазный потребитель – потребитель, у которого электрические параметры (R, L, C) всех трёх фаз имеют одно и то же значение. К ним относятся трёхфазные электродвигатели.
Несимметричный потребитель образуется, как правило, при включении в трёхфазную цепь однофазных источников, например электрических светильников.
Условные обозначения на схемах (рис.4.5).
IA, IB, IC, IЛ –действующие значения линейных токов (токов, протекающих в линейных проводах).
IN – ток в нейтральном проводе.
ZA, ZB, ZC – полные сопротивления фаз потребителя.
Из обеих схем видно, что линейные и фазные токи по существу являются одними и теми же токами, поэтому считают, что при соединении фаз звездой
4.4.
2. Трёхпроводная трёхфазная цепь.
При симметричной системе фазных ЭДС генератора системы фазных ЭДС и фазных токов симметричного потребителя так же будут симметричны (рис.4.6, а).
В соответствие с первым законом Кирхгофа: . (рис. 4.5,б). Как видно из векторных диаграмм рис. 4.6,а), при симметричной системе токов IN = 0, следовательно, надобности в нейтральном проводе нет. В этом случае применяют трёхпроводную цепь (рис.4.5,а).
3. Четырёхпроводная трёхфазная цепь.
При несимметричном потребителе IN≠ 0 ( см. рис.4.6,б). В этом случае нейтральный провод нужен и по нему будет проходить ток. Фазные напряжения приёмника при наличии нейтрального провода будет приблизительно равными. Если при несимметричном трёхфазном приёмнике нейтральный провод будет отсутствовать или произойдёт его обрыв, то фазные напряжения приёмника будут иметь разные значения.
В связи с тем, что ток в нейтральном проводе меньше токов в линейных проводах, нейтральный провод имеет площадь поперечного сечении приблизительно в 3 раза меньше площади поперечного сечения линейных проводов.
Лекция 18.
Тема 4.2. Включение нагрузки в цепь трёхфазного тока.
1. Соединение потребителей энергии в треугольник.
2. Включение онофазных источников в трёхфазную цепь
3. Мощность трёхфазной цепи.
4. Вращающееся магнитное поле.
1. Соединение потребителей энергии в треугольник.
ZAB, ZBC, ZCA полные сопротивления фаз потребителя.IAB, IBC, ICA – действующие значения фазных токов.
IA, IB, IC – действующие значения линейных токов.
В соответствие с первым законом Кирхгофа:
; ; 4.5.
При симметричном потребителе векторная диаграмма фазных токов представляет собой звезду векторов (рис. 4.8).
Векторную диаграмму линейных токов строят, используя векторную диаграмму фазных токов и уравнения 4.5.
Из треугольника, образованного векторами следует: IA = 2 IAB cos 300 = IAB.
У симметричного потребителя линейные ток IA = IB = IC = IЛ;
фазные токи IAB = IBC = ICA = IФ, поэтому
(4.6).
2. Включение однофазных источников в трёхфазную цепь.
В трёхфазные цепи могут быть включены как трёхфазные так и однофазные приёмники. Однофазные приёмники присоединяют к разным линейным проводам. В результате такого соединения несколько однофазных приёмников образуют трёхфазный приёмник, фазы которого могут быть соединены звездой или треугольником (рис.4.9).
3. Мощность трёхфазной цепи.
В общем случае активная, реактивная и полная мощность трёхфазной цепи равна сумме соответствующих мощностей каждой фазы, т.е.
P=PA+PB+PC; Q=QA+QB+QC; S=SA+SB+SC.
Если система линейных напряжений и потребитель симметричные, то мощности, потребляемые каждой фазой одинаковы, поэтому:
(4.7).
4. Вращающееся магнитное поле.
На рис. 4.8,а-ж изображены поперечные сечения стального цилиндра. В пазах цилиндра находятся три катушки (АХ, ВY и CZ), оси которых расположены под углами 1200 относительно друг друга. График токов в катушках
показан справа на рис 4.8. условимся считать, что если ток на графике имеет положительное значение, то он течёт от начала катушки к её концу и наоборот, если ток имеет отрицательное значении, то он течёт от конца катушки к её началу.
Направление токов в проводниках для моментов времени а, б, в, г, д, е, ж показан на рис. 4.8: крестиком (если ток течёт за плоскость рисунка) или точкой (если ток течёт из-за плоскости рисунка).
Направление магнитных линий вокруг проводников определено по правилу буравчика и показано на рис. 4.8 пунктирными линиями.
Линия результирующего магнитного поля показана сплошной стрелкой внутри цилиндра.
Как видно из рисунка, магнитное поле внутри цилиндра совершает один оборот по часовой стрелке, т.е. угловая частота вращения поля равна угловой частоте тока.
Если изменить порядок подключения катушек к трёхфазной цепи, то направление вращения поля изменится на противоположное.
В приведённом примере поле имеет одну пару полюсов. Если число катушек будет кратное трём, то при определённом их соединении можно получить вращающееся поле, имеющее большее число пар полюсов. При числе пар полюсов, равном р угловая скорость поля будет в р раз меньше угловой частоты тока.
На использовании вращающегося магнитного поля трёхфазной системы токов основан проинцип работы трёхфазных асинхронных двигателей.
Вращающееся магнитное поле можно получить и для двух катушек, присоединённых к двухфазной системе токов. Для этого нужно, что бы оси катушек были расположены под углом 900 относительно друг друга, а токи, протекающие по катушкам были сдвинуты по фазе на угол, равный π/2.
На использовании вращающегося магнитного поля двухфазной системы токов основан принцип работы конденсаторных электродвигателей переменного тока.
Лекция 19.
Тема 5.1 : Измерение тока и напряжения.
Обмотки трехфазного генератора могут быть соединены и другим способом: если конец первой обмотки соединить с началом второй, конец второй обмотки — с началом третьей и конец третьей — с началом первой, получим соединение треугольником (рис6).
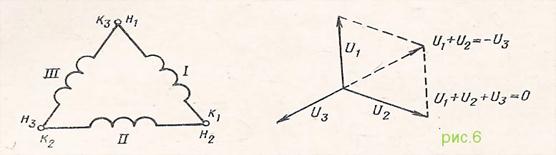
Рассматривая рис.6, мы видим, что обмотки генератора образуют замкнутую последовательную цепь. На первый взгляд создается впечатление, что они замкнуты накоротко, однако фактически короткого замыкания нет, так как сумма э. д. с, действующих в этом замкнутом контуре, в любой момент времени равна нулю, что показано на векторной диаграмме (рис.6). Другое дело, если при соединении спутать концы одной из обмоток (рис.7), тогда фаза соответствующего фазного напряжения опрокинется на 180°и результирующее напряжение, действующее внутри треугольника обмоток, будет равно удвоенной величине фазного напряжения:
векторная сумма Uф1 + Uф3 = Uф2
и общее напряжение U= Uф1+ Uф2+ Uф3=2Uф2
Линейные провода при соединении треугольником отводятся от точек соединения обмоток. Очевидно, что напряжение между линейными проводами в этом случае равно напряжению фазы, включенной между этими проводами. Таким образом, если обмотки генератора соединены треугольником, линейное напряжение равно фазному, т. е.
Uл=Uф
Рассмотрим теперь зависимость между линейными и фазными токами. Если нагрузка равномерна (т. е. если комплексы сопротивлений, включенных на стороне потребителя в каждую из фаз, равны), то фазные токи в каждой из фаз генератора будут равны по величине и сдвинуты относительно друг друга на 120°. На рис.8 показаны обмотки трехфазного генератора, соединенные треугольником, и векторная диаграмма напряжений и токов для данного случая. Примем за положительное направление тока в обмотке направление против часовой стрелки, а за положительное направление тока в линии— направление от генератора к потребителю
Напишем в комплексной форме уравнения первого закона Кирхгофа для узлов I, II и III:
Iл1=Iф1-Iф3; (7)
Iл2=Iф2-Iф1; (8)
Iл3=Iф3-Iф1, (9)
т. е. линейный ток равен геометрической разности токов двух фаз, сходящихся в точке включения данного линейного провода. Произведем вычитание комплексов токов на векторной диаграмме. Фазные токи, как мы уже условились, взяты равной величины и сдвинуты от своих фазных напряжений на одинаковые, углы (φ). Техника вычитания не отличается от рассмотренной нами при определении величины линейного напряжения для системы с соединением обмоток генератора звездой. Для того чтобы не усложнять рисунок, мы показали на нем только определение линейного тока Iл1
Из построения очевидно, что величина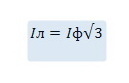 
, т. е. при соединении обмоток генератора треугольником величина линейного, тока больше величины фазного тока в 
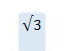раз.
Необходимо подчеркнуть, что эта зависимость имеет место только при равномерной нагрузке фаз. При неравномерной нагрузке необходимо находить линейные токи в каждом отдельном случае по уравнениям (7), (8) и (9) графически или аналитически (пользуясь символическим методом).
Из сравнения двух способов соединения обмоток генераторов следует, что при соединении звездой увеличивается напряжение между проводами линии передачи, но (при одинаковой нагрузке) уменьшаются линейные токи. При соединении обмоток треугольником не может быть проложен нулевой провод между генератором и потребителем, что создает значительные неудобства при неравномерной нагрузке фаз. Поэтому в распределительных сетях низкого напряжения вторичные обмотки силовых трансформаторов, как правило, соединяются звездой.
Треугольник имеет три стороны и три угла | ||
Три угла всегда добавляют к 180 ° |
равносторонний, равнобедренный и скаленовский
Треугольникам присваиваются три специальных имени, которые указывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или без равных сторон / углов:
равносторонний треугольник Три равных сторон | |
равнобедренный треугольник Два равных сторон | |
Треугольник Скалины Нет равных сторон |
Как запомнить? По алфавиту они идут 3, 2, нет:
- Равносторонние : «равные» -сторонние (боковая сторона означает), поэтому они имеют все равных сторон
- равнобедренный : означает «равные ноги», и у нас две ноги , верно? Кроме того, у i SOS есть два равных «S ides», соединенных стороной « O dd».
- Scalene : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой тип угла?
Треугольникитакже могут иметь имена, которые говорят вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямоугольный ТреугольникИмеет прямой угол (90 °) | |
Тупой ТреугольникИмеет угол более 90 ° |
Объединение имен
Иногда треугольник будет иметь два имени, например:Правый равнобедренный треугольникИмеет прямой угол (90 °), а также два равных угла. Можете ли вы угадать, что такое равные углы? |
Играть с ним…
Попробуйте перетащить точки вокруг и сделать разные треугольники:
Вы также можете поиграть с интерактивным треугольником.
Углы
Три внутренних угла всегда добавляют 180 °
Периметр
Периметр — это расстояние вокруг края треугольника: просто сложите три стороны:
Площадь
Площадь составляет от половины базового времени высота .
- «б» — это расстояние вдоль базы
- «h» — высота (измеренная под прямым углом к основанию)
Площадь = ½ × б × ч
Формула работает для всех треугольников.
Примечание: более простой способ написания формулы — чч / 2
Пример: какова площадь этого треугольника?
(примечание: 12 — высота , , а не длина левой стороны)
Высота = h = 12
Base = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть с любой стороны. Просто убедитесь, что «высота» измеряется под прямым углом к «основанию» :
(Примечание. Вы также можете рассчитать площадь по длине всех трех сторон, используя формулу Герона.)
Почему Район «Половина ЧЧ»?
Представьте, что вы «удвоили» треугольник (переверните его вокруг одного из верхних краев), чтобы сделать квадратную форму (параллелограмм), которую можно изменить на простой прямоугольник:
ТОГДА вся площадь составляет bh , что для обоих треугольников, так что только один — ½ × bh .
,Площадь Треугольников
Есть несколько способов найти площадь треугольника.
Знание базы и высоты
Когда мы знаем основание и высоту, это легко.
Это просто половина b раз ч
Площадь = 1 2 чч
(страница «Треугольники» объясняет больше)
Самое главное, чтобы основание и высота были под прямым углом.Поиграйте здесь:
Пример: какова площадь этого треугольника?
(примечание: 12 — высота , , а не длина левой стороны)
Высота = h = 12
Base = b = 20
Площадь = ½ чч = ½ × 20 × 12 = 120
Знание трех сторон
Существует также формула для определения площади любого треугольника, когда мы знаем длины всех трех его сторон.
Это можно найти на странице формулы Герона.
Знание двух сторон и включенного угла
Когда мы знаем две стороны и включенный угол (SAS), есть другая формула (фактически три эквивалентные формулы), которую мы можем использовать.
В зависимости от того, какие стороны и углы нам известны, формулу можно записать тремя способами:
Площадь = 1 2 ab sin C
Площадь = 1 2 до н.э. sin
Площадь = 1 2 ca sin B
Это действительно одна и та же формула, только с измененными сторонами и углом.
Пример: Найти площадь этого треугольника:
Прежде всего мы должны решить, что мы знаем.
Мы знаем угол C = 25º, а стороны a = 7 и b = 10.
Итак, начнем:
Площадь = (½) ab sin C
Введите значения, которые мы знаем: ½ × 7 × 10 × sin (25º)
Выполнить работу калькулятора: 35 × 0,4226 …
Площадь = 14,8 с точностью до одного знака после запятой
Как запомнить
Просто подумайте «abc»: Площадь = ½ a b sin C
Также хорошо помнить, что угол всегда составляет между двумя известными сторонами , называемыми «включенным углом».
Как это работает?
Мы знаем, как найти область, когда мы знаем основание и высоту:
Площадь = ½ × основание × высота
В этом треугольнике:
|
Итак, мы получаем:
Площадь = ½ × (с) × (b × грех A)
Что (проще):
Площадь = 1 2 до н.э. sin
Изменяя метки на треугольнике, мы также можем получить:
- Площадь = ½ ab sin C
- Площадь = ½ ca sin B
Еще один пример:
Пример: Найти, сколько земли
Фермер Джонс владеет треугольным участком земли.
Длина забора АВ составляет 150 м. Длина забора до н.э. составляет 231 м.
Угол между ограждением AB и ограждением BC составляет 123º.
Сколько земли принадлежит фермеру Джонсу?
Прежде всего мы должны решить, какие длины и углы мы знаем:
- AB = c = 150 м,
- г. до н.э. = а = 231 м,
- и угол B = 123º
Итак, мы используем:
Площадь = 1 2 ca sin B
Введите значения, которые мы знаем: ½ × 150 × 231 × грех (123º) м 2
Выполнить работу калькулятора: 17,325 × 0.838 … м 2
Площадь = 14 530 м 2
Фермер Джонс имеет 14 530 м 2 земли
,Соотношение длин сторон и углов треугольника
Соотношение длин сторон и углов треугольника — Math Open Reference В любом треугольнике:- Самая короткая сторона всегда противоположна самой маленькой внутренний угол
- Самая длинная сторона всегда противоположна наибольшему внутреннему углу
Попробуй это Перетащите оранжевые точки на треугольник ниже.
Напомним, что в неравносторонний треугольник, все стороны имеют разную длину и все внутренние углы есть разные меры.В таком треугольнике самая короткая сторона всегда противоположна наименьшему углу. (Они показаны жирным цветом выше) Точно так же самая длинная сторона противоположна наибольшему углу.
На рисунке выше перетащите любой вершина треугольника и увидеть, какая сторона самая короткая, противоположный угол также самый маленький. Затем нажмите «Показать наибольший» и увидите, что как бы вы ни изменили форму треугольника, самая длинная сторона всегда противоположна наибольшему внутреннему углу.
Средние детали
Если наименьшая сторона противоположна наименьшему углу, а самая длинная противоположна наибольшему углу, то из этого следует, что поскольку треугольник имеет только три стороны, сторона среднего размера противоположна углу среднего размера.равносторонние треугольники
Равносторонний треугольник все стороны равны по длине и все внутренние углы равны. Следовательно, в этом случае нет ни «самого большого», ни «самого маленького».равнобедренных треугольников
Равнобедренные треугольники имеют две стороны одинаковой длины и два одинаковых внутренних угла. Следовательно, могут быть две стороны и углы, которые могут быть «самыми большими» или «самыми маленькими». Если вы осторожны с мышью, вы можете создать эту ситуацию на рисунке выше.Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Треугольные центры
Конгруэнтность и Сходство
Решение треугольников
Тесты и упражнения на треугольник
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
Нахождение угла в прямоугольном треугольнике
угол с любых двух сторон
Мы можем найти неизвестный угол в прямоугольном треугольнике, если мы знаем длины двух его сторон .
Пример
Лестница прислоняется к стене, как показано на рисунке.
Что такое угол между лестницей и стеной?
Ответ заключается в использовании синуса, косинуса или тангенса!
Но какой использовать? У нас есть специальная фраза «SOHCAHTOA», чтобы помочь нам, и мы используем ее так:
Шаг 1 : найдите имен двух сторон, которые мы знаем
- Смежный прилегает к углу,
- напротив противоположно углу,
- и самая длинная сторона — Гипотенуза .
Пример: в нашем примере с лестницей мы знаем длину:
- сторона напротив угол «х», который составляет 2,5
- самая длинная сторона, называемая Гипотенуза , что составляет 5
Шаг 2 : теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», чтобы найти, какой из синусов, косинусов или Tangent использовать:
SOH… | S ine: sin (θ) = O pposite / H ypotenuse |
… CAH … | C osine: cos (θ) = A соседний / H ypotenuse |
… TOA | T angent: tan (θ) = O pposite / A jjacent |
В нашем примере это O pposite и H ypotenuse, что дает нам « SOH cahtoa», что говорит нам о необходимости использовать Sine .
Шаг 3 : Поместите наши значения в уравнение синуса:
S in (x) = O pposite / H ypotenuse = 2,5 / 5 = 0,5
Шаг 4 : Теперь решите это уравнение!
грех (х) = 0,5
Далее (поверьте мне на данный момент) мы можем перестроить это в это:
х = грех -1 (0,5)
А затем возьмите наш калькулятор, введите 0,5 и используйте кнопку sin -1 , чтобы получить ответ:
x = 30 °
И у нас есть наш ответ!Но что означает грех -1 …?
Итак, функция синуса «грех» берет угол и дает нам отношение «противоположность / гипотенуза»,
Но грех -1 (называется «обратный синус») идет другим путем…
… это
принимает отношение «противоположное / гипотенуза» и дает нам угол.
Пример:
- Функция синуса: sin ( 30 ° ) = 0,5
- Функция обратного синуса: sin -1 ( 0,5 ) = 30 °
| На калькуляторе нажмите один из следующих вариантов (в зависимости от от вашей марки калькулятора): либо «2ndF грех» или «сдвинуть грех». |
На своем калькуляторе попробуйте использовать sin и sin -1 , чтобы увидеть, какие результаты вы получите!
Также попробуйте cos и cos -1 . А загар и загар -1 .
Продолжай, попробуй сейчас.
Шаг за Шагом
Вот четыре шага, которым мы должны следовать:
- Шаг 1 Найдите, какие две стороны мы знаем — из противоположной, смежной и гипотенузы.
- Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из синусов, косинусов или касательных использовать в этом вопросе.
- Шаг 3 Для синуса вычислите Противоположность / Гипотенуза, для косинуса вычислите Смежный / Гипотенуза или для Касания вычислите Противоположность / Соседний.
- Шаг 4 Найдите угол из своего калькулятора, используя один из грехов -1 , cos -1 или tan -1
Примеры
Давайте рассмотрим еще пару примеров:
Пример
Найти угол места самолета из точки А на земле.
- Шаг 1 Мы знаем две стороны: O pposite (300) и A djacent (400).
- Шаг 2 SOHCAH TOA говорит нам, что мы должны использовать анант T .
- Шаг 3 Рассчитать Противоположно / Смежно = 300/400 = 0,75
- Шаг 4 Найдите угол с помощью калькулятора, используя tan -1
Tan x ° = противоположный / соседний = 300/400 = 0.75
загар -1 от 0,75 = 36,9 ° (с точностью до 1 знака после запятой)
Если не указано иное, углы обычно округляются до одного знака после запятой.
Пример
Найти размер угла а °
- Шаг 1 Мы знаем две стороны: А, соседей (6750) и Н ипотенуз (8100).
- Шаг 2 SOH CAH TOA говорит нам, что мы должны использовать C osine.
- Шаг 3 Рассчитать Соседних / Гипотенуза = 6750 / 8,100 = 0,8333
- Шаг 4 Найдите угол из своего калькулятора, используя cos -1 от 0,8333:
cos a ° = 6750 / 8,100 = 0,8333
cos -1 от 0,8333 = 33,6 ° (до 1 десятичного знака)
,