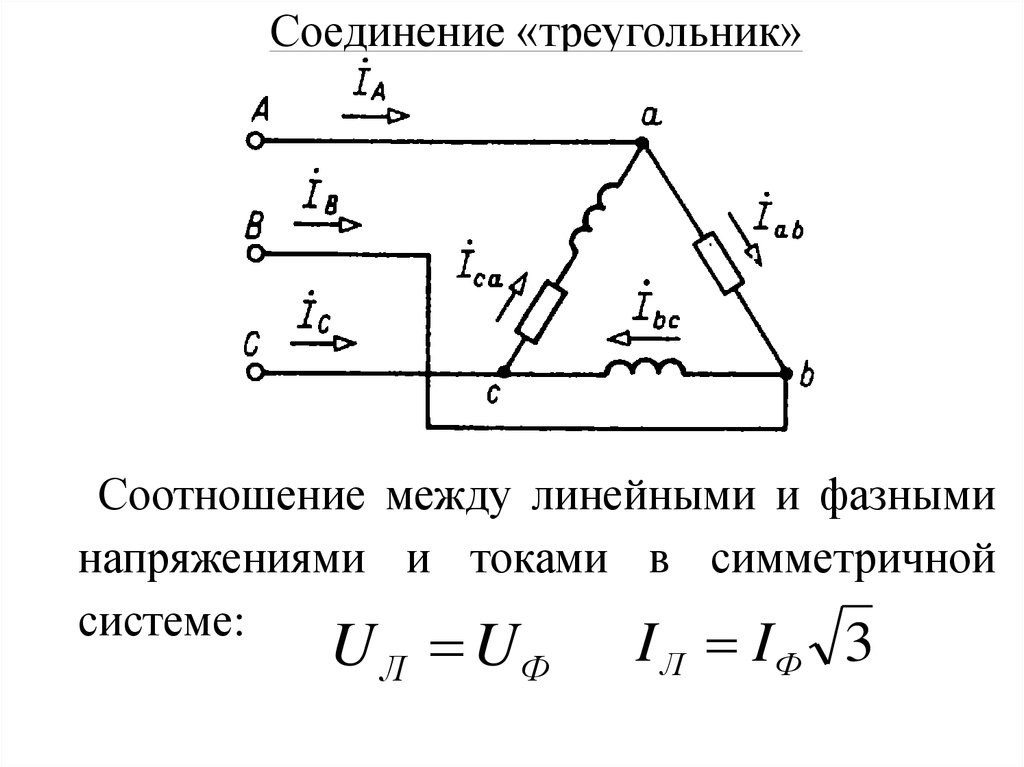
Соединение фаз треугольником: Соединение обмоток «треугольником» | Полезные статьи

Соединение фаз приемника по схеме «треугольник»

Схема «треугольник» образуется при соединении начала одной фазы с концом другой, при этом получается замкнутый контур. Начало фазы а приемника соединяют с концом фазы b — ­ y, (точка а). Далее соединяют точки b и z (точка b) и точки с и х (точка с). Начала фаз выводят в линии.

Схема трехфазного приемника, соединенного по схеме треугольник

По фазам приемника протекают фазные токи İ_ав, İ_вс, İ_са. Условное положительное направление фазных токов приемника от начала к концу фаз. Условные положительные направления фазных напряжений совпадают с положительным направлением фазных токов. Условное положительное направление линейных токов İ_А, İ_В,

İ_С принято от генератора к приемнику.

Напряжение между началом и концом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению:

U_л= U_ф.

При подключении приемника, соединенного треугольником, к источнику питания по фазам приемника протекает фазный ток, который определяется по закону Ома:

İ_ф = U_ф/Z_ф.

Линейные токи можно определить из уравнений, составленных по II ЗК для точек а, в, с соответственно:

İ_са – İ_ав + İ_А = 0;

İ_ав

– İ_вс + İ_В = 0;

İ_вс – İ_са + İ_с = 0.

Таким образом, получаем

İ_А = İ_ав – İ_са;

İ_В = İ_вс – İ_ав;

İс = İ_са – İ_вс.

Итак, линейные токи при соединении треугольником равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.

Как следует из вышеприведенных уравнений, векторная сумма линейных токов всегда равна нулю:

İ_А+ İ_В + İ_С = 0.

Система линейных (фазных) токов при соединении треугольником образует такой же замкнутый треугольник, как система линейных (фазных) напряжений и при соединении звездой. Фазные токи при симметричной нагрузке равны по значению и сдвинуты по отношению к векторам напряжений на одинаковый угол φ.

Для определения линейных токов строем векторную диаграмму фазных токов. Так как линейные токи определяются через фазные так же, как и линейные напряжения через фазные при соединении звездой, то можно сразу построить векторы линейных токов, соединив концы векторов фазных токов.

. Векторная диаграмма фазных и линейных токов при соединении фаз треугольником

Векторы линейных токов образуют замкнутый треугольник. Поскольку при симметричной нагрузке системы фазных и линейных токов симметричны, сравнивая векторные диаграммы токов схемы треугольник и напряжений схемы звезда, можно заключить, что линейные токи при симметричной нагрузке, соединенной треугольником, в = 1,73 раза больше фазных:

I_л = I_Ф

Несимметричная нагрузка при соединении треугольником. Трехпроводная система. При соединении треугольником U_л = U_ф, а линейные напряжения источника всегда симметричны. Поэтому соединение треугольником применяется в трехпроводных системах при любой нагрузке, как симметричной, так и несимметричной, если номинальное напряжение приемника равняется линейному напряжению источника питания.

Примем . Тогда ;

;.

Комплексные сопротивления приемника ; ;

.

.Схема несимметричного приемника, соединенного по схеме треугольник

Фазные токи

; ;

.

Линейные токи определяются по II ЗК для узлов a, b, c:

; ; .

Для построение векторной диаграммы на комплексной плоскости сначала строятся векторы линейных напряжений, затем векторы фазных токов и по ним определяются графически линейные токи, которые должны совпасть с расчетными по модулю и аргументу.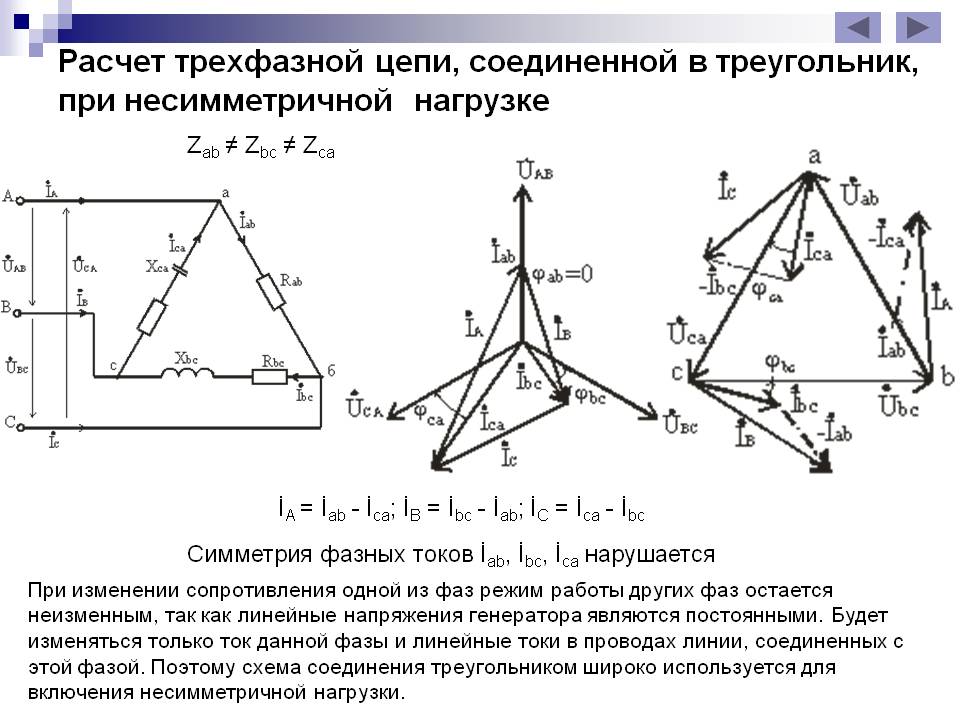

Векторная диаграмма напряжений, фазных и линейных токов при

соединении фаз приемника треугольником при несимметричной нагрузке

Схема соединения «Треугольник»

Соединение в треугольник трехфазного генератора или вторичной обмотки трансформатора.

Соединим конец x обмотки ax с началом b обмотки by, конец y обмотки by с началом c обмотки cz, конец z обмотки cz с началом a обмотки ax так, как показано на рисунке 1. Такое соединение по виду напоминает треугольник, откуда и происходит его название. Линейные провода присоединены в вершинах треугольника.

Рисунок 1. Соединение в треугольник генератора.

Основные соотношения:
1. При соединении в треугольник линейные и фазные напряжения равны потому, что каждые два линейных провода (как видно из рисунка 1) присоединены к началу и концу одной из фазных обмоток, а все фазные обмотки одинаковы.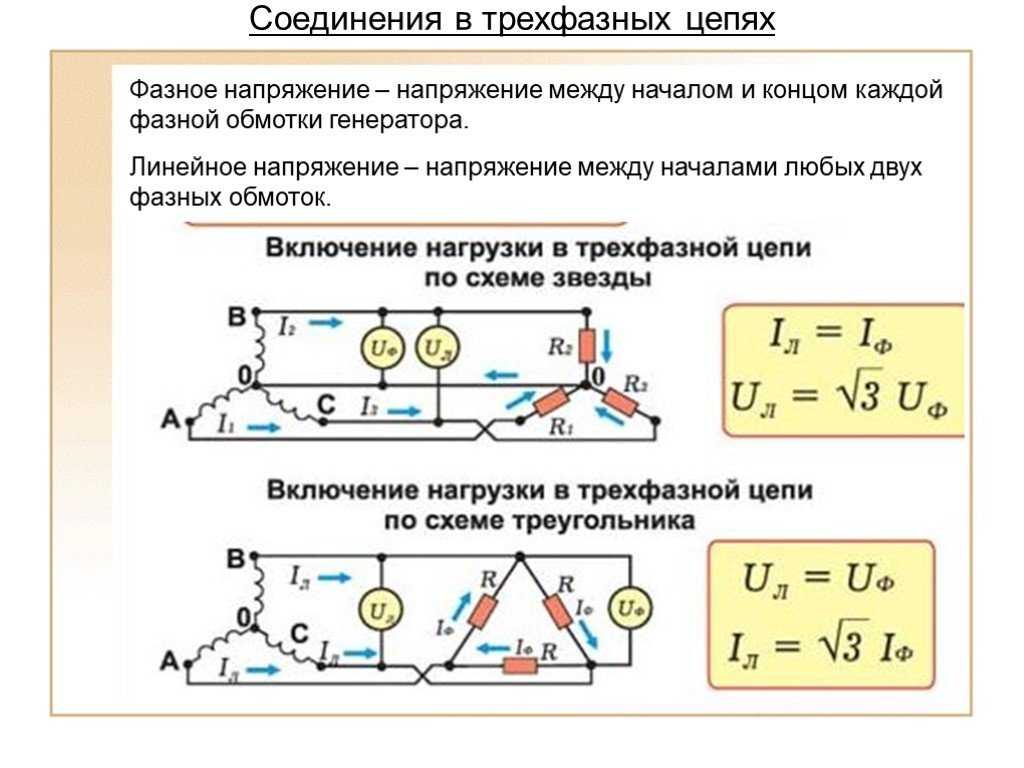
2. Линейные токи I_л больше фазных I_ф в √3 = 1,73 раза.

Как доказать, что I_л = 1,73 × I_ф? Воспользуемся для этого векторной диаграммой рисунка 2.

Рисунок 2. Определение линейных токов при соединении в треугольник.

Фазные токи I_ab, I_bc, I_ca в трех электроприемниках ЭП (рисунок 2, а) изображаются векторной диаграммой (рисунок 2, б), которая получена путем перенесения параллельно самим себе векторов с рисунка 2, а. Вершины треугольника нагрузок a, b и c являются узловыми точками. Поэтому согласно первому закону Кирхгофа справедливы равенства

I_a + I_ca = I_ab, откуда I_a = I_ab – I_ca;
I_b + I_ab = I_bc, откуда I_b = I_bc – I_ab;
I_c + I_bc = I_ca, откуда I_c = I_ca – I_bc.

Понятно, что эти равенства геометрические, поэтому вычитание нужно выполнять по правилам вычитания векторов, что и сделано на рисунке 2, б. Непосредственное измерение длин векторов или вычисления по правилам геометрии показывают, что линейные токи I_a, I_b и I_c больше фазных токов I_ab, I_bc и I_ca в √3 = 1,73 раза.

На рисунке 2, б также видно, что векторная диаграмма симметричных линейных токов I_a, I_b и I_c сдвинута на 30° в сторону, обратную вращению векторов, относительно диаграммы фазных токов I_ab, I_bc и I_ca. Иными словами, ток I_a отстает на 30° от тока I_ab. Ток I_b отстает на 30° от тока I_bc, ток I_c отстает на 30° от тока I_ca.
Порядок индексов в обозначении фазных токов указывает на порядок вращения фаз. В нашем примере порядок следования (вращения) фаз: a, b, c.

На рисунке 2, в показано соединение в треугольник обмоток генератора или вторичных обмоток трансформатора. Векторы токов I_ba, I_ac, I_cb, проходящих в обмотках генератора (вторичных обмотках трансформатора), и векторы токов в нагрузке (I_ab, I_ca, I_bc) соответственно параллельны, но повернуты на 180°. Причина такого расположения векторов станет ясна, если совместить рисунок 2, в с правой частью рисунка 2, а, что и выполнено на рисунке 2, г.

Обращается внимание на то, что все три обмотки внутри генератора (трансформатора) соединены последовательно и образуют замкнутую цепь. Подобное соединение в установках постоянного тока привело бы к короткому замыканию. В установках трехфазного тока в силу того, что электродвижущие силы (э. д. с.) сдвинуты по фазе на 120°, ток в этом замкнутом контуре отсутствует, так как в каждый момент сумма э. д. с. трех обмоток равна нулю ¹.

Необходимо здесь же заметить, что для отсутствия тока в контуре обмоток генератора (трансформатора) необходимо, чтобы обмотки имели одинаковые числа витков, были сдвинуты на 120 электрических градусов и имели э. д. с. строго синусоидальные или во всяком случае не содержащие гармоник, кратных трем (смотрите статью «Понятие о магнитном равновесии трансформатора»).

Генераторы практически никогда не соединяют в треугольник. В трансформаторах такие соединения не только распространены, но иногда выполняются с целью получения внутри трансформатора токов третьих гармоник. Зачем? Понятно не затем, чтобы создавать в трансформаторе дополнительные потери. Причины здесь гораздо сложнее, смотрите статью «Понятие о магнитном равновесии трансформатора».

Соединение в треугольник обмоток трансформаторов в двух вариантах показано на рисунке 3.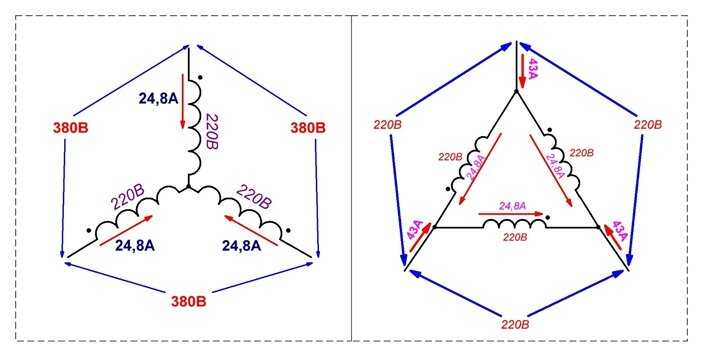 Подробно вопрос о соединениях обмоток трансформаторов рассмотрен в статье «Группы соединения трансформаторов».

Рисунок 3. Соединение в треугольник трансформаторов.

Соединение в треугольник электроприемников и конденсаторных батарей.

Соединение в треугольник обмоток электродвигателей показано на рисунках 4, а – в. При этом на рисунке 4, а обмотки и соединены и расположены треугольником; на рисунке 4, б обмотки соединены треугольником, но расположены произвольно; на рисунке 4, в обмотки расположены звездой, но соединены в треугольник. На рисунке 4, г обмотки расположены треугольником, но соединены в звезду.

Рисунок 4. Соединение в треугольник электроприемников.

Все эти рисунки подчеркивают, что дело отнюдь не в том, как расположены изображения электроприемников на чертежах (хотя их часто удобно располагать в соответствии с видом соединения), а в том, что с чем соединено: концы (начала) всех обмоток между собой или конец одной обмотки с началом другой. В первом случае получается соединение в звезду, во втором – в треугольник.

Соединение в треугольник конденсаторных батарей показано на рисунке 4, д.

На рисунке 4, е показано соединение в треугольник ламп. Хотя лампы территориально разбросаны по разным квартирам, но они объединены сначала в группы в пределах каждой квартиры, затем в группы по стоякам 2 и, наконец, эти группы соединены в треугольник на вводном щите 1. Заметьте: до вводного щита нагрузка трехфазная, после вводного щита (в стояках и квартирах) однофазная, хотя она и включена между двумя фазами.

На каком основании нагрузка, питающаяся от двух фаз названа однофазной? На том основании, что изменения тока в обоих проводах, к которым присоединена нагрузка, происходят одинаково, то есть в каждый момент ток проходит через одни и те же фазы.

Видео 1. Соединение треугольником

---

¹ Отсутствие тока в замкнутом контуре еще не означает, что в фазных обмотках нет тока. Токи в фазных обмотках соответствуют их нагрузкам.

Источник: Каминский Е. А., «Звезда, треугольник, зигзаг» – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.

Понимание основ расчета трансформаторов Delta

Благодарим вас за посещение одной из наших самых популярных классических статей. Если вы хотите ознакомиться с обновленной информацией по этой теме, ознакомьтесь с недавно опубликованной статьей «Расчеты трансформаторов ».

Примечание. Эта статья основана на NEC 2002 года.

Названия конфигураций трансформатора, такие как «треугольник» и «звезда», происходят от способа соединения обмоток внутри трансформатора. Эти соединения определяют поведение трансформатора, а также методы расчета, необходимые для правильного применения данного трансформатора.

Трансформаторы, соединенные треугольником, имеют обмотки трех однофазных трансформаторов, соединенных последовательно друг с другом в замкнутую цепь. Линейные проводники подключаются к блоку в месте соединения двух однофазных трансформаторов. Эта конфигурация получила свое название потому, что на электрическом чертеже она выглядит как треугольник (греческий символ Δ для буквы «дельта»). Многие называют это системой с высокой ветвью, потому что напряжение от линии 2 до земли выше, чем на других ветвях. Например, треугольный трансформатор на 120 В будет иметь ветвь на 208 В.

Рис. 1. Важно отметить, что линейный ток от трансформатора треугольника не равен фазному току. В этом примере линейный ток равен 87 А, а фазный ток равен 50 А.

Дельта-трансформатор тока. В трансформаторе треугольника линейный ток не равен фазному току (как в трансформаторе звезда). Поскольку каждая линия от трансформатора, сконфигурированного треугольником, подключена к двум фазам трансформатора, линейный ток от трехфазной нагрузки будет больше, чем фазный ток, на квадратный корень из 3.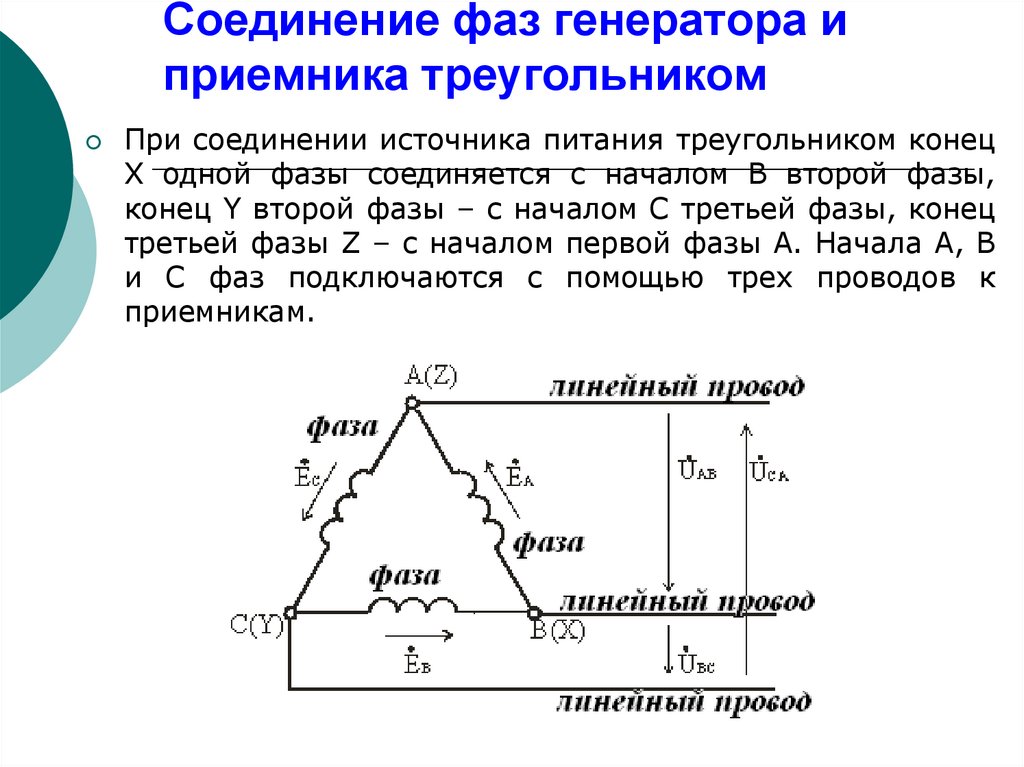 Обратите внимание на следующие формулы:

I

Строка = I _Фаза ×√3

I _Строка = VA _Строка ÷(E _Строка × √3)

9001 4 I _Фаза = I _Строка ÷√3

I _Фаза = ВА _Фаза ÷E _Фаза

Рис. 2. Вы можете использовать одну и ту же формулу, чтобы найти первичный и вторичный линейный ток.

Если вы подставите несколько цифр, вы сможете более четко увидеть влияние дельта-конфигурации на токи. Давайте попробуем это с 3-фазной нагрузкой 240 В, 36 кВА ( рис. 1 выше).

Сначала найдем ток в линии (общая мощность линии = 36 кВА).

I _Строка =VA _Строка ÷(E ^Строка ×√3)

I _Строка =36 000 ВА÷(240 В×√3)

I _Строка =87A

Теперь давайте определите фазный ток (фазная мощность = 12 кВА на обмотку).

I _Фаза =ВА _Фаза ÷E _Фаза

I _Фаза =12000ВА÷240В=50А

Вы также можете найти линейный и фазный токи используя две другие формулы, показанные выше.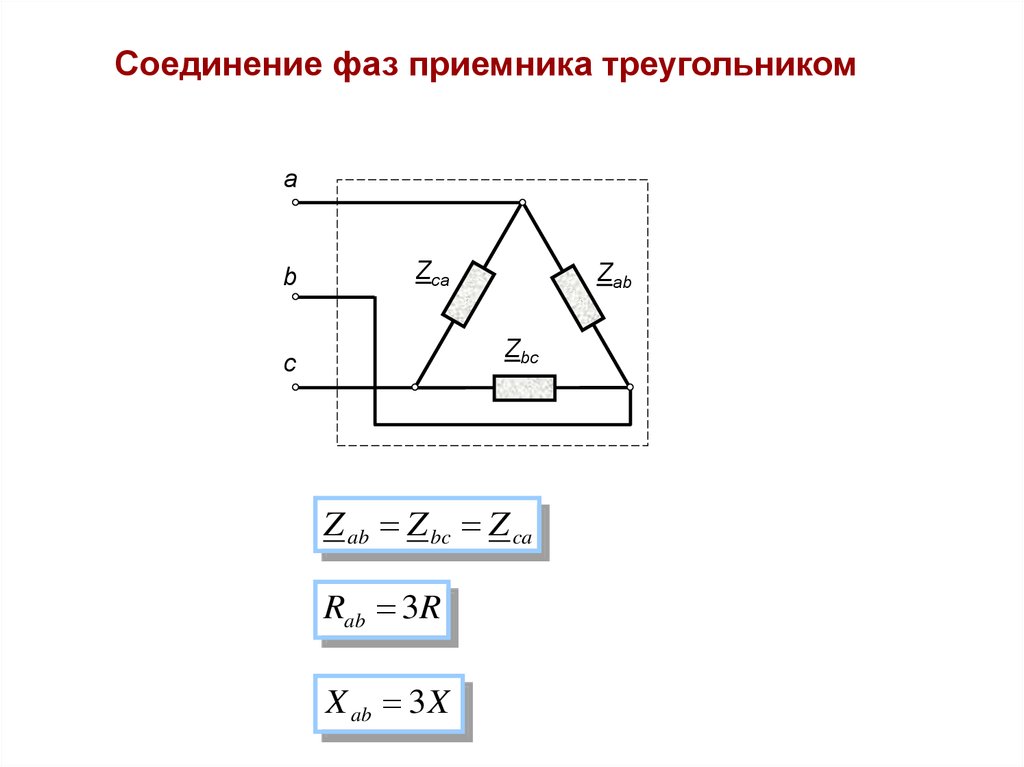

I _Линия =I _Фаза ×√3

I _Линия =50A × 1,732=87A

I _Фаза =I _Линия ÷√3

I _Фаза =87A÷1,732 =50A

Мы также можем использовать формулу: I _Строка = VA _Строка ÷(E _Строка ×√3). Например, каков вторичный ток линии для 480–240/120 В, 150 кВА, 3-фазного трансформатора треугольника (, рис. 2 )? Ответ находится следующим образом:

I _{Строка 9Рис. общую мощность трансформатора кВА на 3.}

Вы можете рассчитать фазный ток обмотки трансформатора треугольника, разделив фазные ВА на фазные напряжения: I _Фаза = ВА _Фаза ÷E _Фаза . Фазная нагрузка в ВА трехфазной нагрузки 240 В равна линейной нагрузке, деленной на три (одна треть нагрузки на каждую обмотку). Фазная нагрузка в ВА однофазной нагрузки 240 В является линейной нагрузкой (все на одну обмотку). Фазная нагрузка в ВА однофазной нагрузки 120 В является линейной нагрузкой (все на одной обмотке).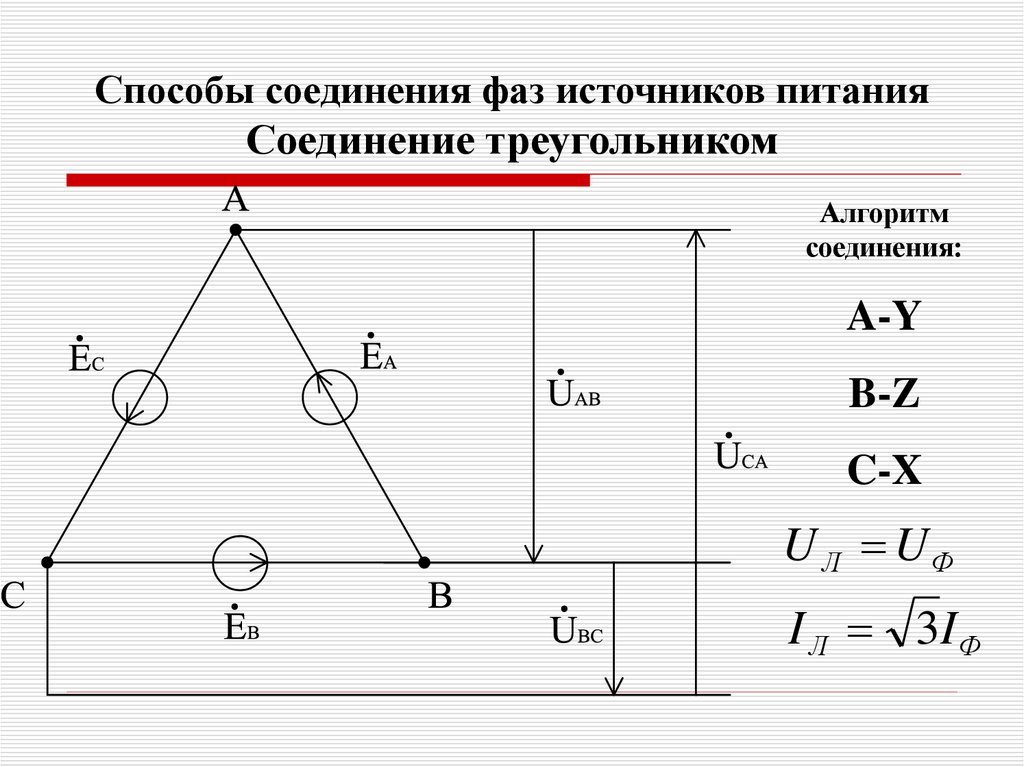

Давайте рассмотрим еще один пример задачи. Каков вторичный фазный ток для 480–240/120 В, 150 кВА, трехфазного трансформатора треугольника (, рис. 3, выше)?

Фазная мощность = 150 000 ВА÷3 на фазу

Фазная мощность = 50 000 ВА на фазу

I _Фаза =50 000 ВА÷240 В

I _Фаза =208 A

Чтобы лучше понять, что происходит в дельта-системе , попробуйте запустить эти числа с нагрузкой 10А, а затем с нагрузкой 75А.

Рис. 4. На этой диаграмме показана балансировка трансформатора. Для простоты защита от перегрузки по току для этих цепей не показана.

Балансировка трансформатора треугольником. Для правильного выбора трансформатора типа «треугольник/треугольник» фазы (обмотки) трансформатора должны быть сбалансированы. Вы можете сделать это с помощью двухэтапного процесса:

Шаг 1 . Определите рейтинг ВА всех нагрузок.

Шаг 2 . Сбалансируйте нагрузки на обмотки трансформатора следующим образом:

• 3-фазные нагрузки: одна треть нагрузки на каждую из фаз.

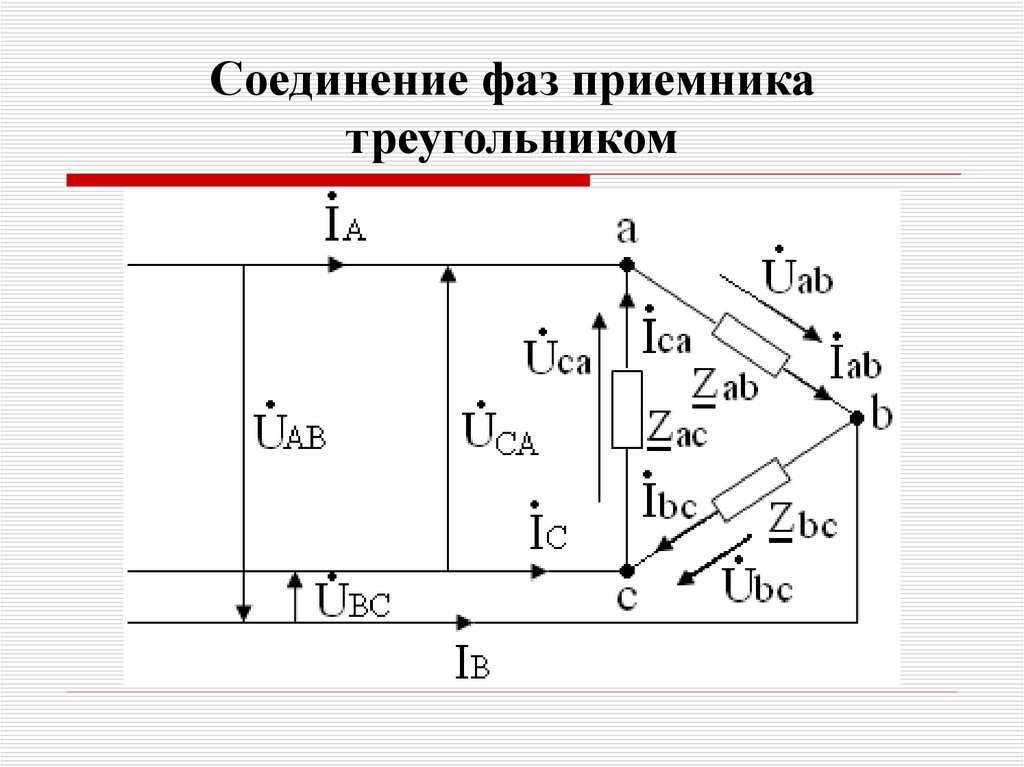
• 240 В, однофазные нагрузки: 100 % нагрузки на фазу A или B. При необходимости для баланса часть однофазной нагрузки 240 В можно поместить на фазу C.

• Нагрузки 120 В: 100 % нагрузки на C1 или C2.

Чтобы определить размеры щита и его проводников, необходимо сбалансировать нагрузки в амперах. Зачем балансировать панель в амперах? Почему бы не взять ВА на фазу и не разделить на фазное напряжение? Поскольку линейный ток трехфазной нагрузки рассчитывается по следующей формуле:

I _Линия =VA÷(E _Линия ×√3)

I _Линия =150 000 ВА÷(240 В×1,732)= 208А на линию.

Если вы возьмете мощность на линию 50 000 ВА и разделите ее на одно линейное напряжение 120 В, вы получите неправильный линейный ток 50 000 ВА ÷ 120 В = 417 А.

Размер трансформатора треугольника. Рассмотрите этот метод в следующий раз, когда будете определять параметры трансформаторов, соединенных треугольником, где большая часть нагрузки является линейной.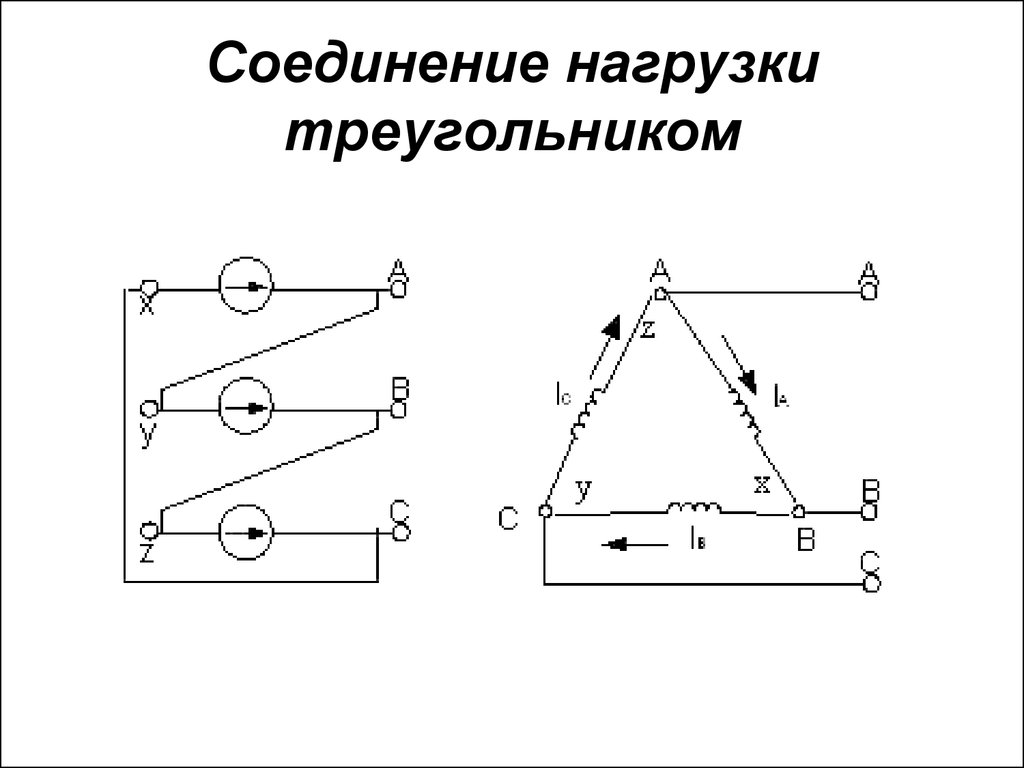 Как только вы сбалансируете трансформатор, определите его размер в соответствии с нагрузкой каждой фазы. Размер трансформатора «C» должен быть в два раза больше, чем «C1» или «C2». Трансформатор «C» на самом деле является единым блоком. Если одна сторона имеет большую нагрузку, эта сторона определяет размер трансформатора.

См. приведенную ниже разбивку нагрузки по фазам для практической задачи.

Давайте попробуем еще одну практическую задачу, чтобы закрепить эти понятия. Какой размер трансформатора с 480 В на 240/120 В требуется для следующих нагрузок: один 3-фазный нагревательный элемент 240 В, 36 кВА; две 240В, 10кВА, 3-х фазные нагрузки; три нагрузки 120 В, 3 кВА, однофазные ( рис. 4 )?

(a) три однофазных трансформатора на 25 кВА

(b) один трехфазный трансформатор на 75 кВА

(c) a или b

(d) ничего из вышеперечисленного

Фазная обмотка A=22 кВА

900 14 Фазная обмотка В=22кВА

Обмотка фазы C=(12 кВА C1×2) = 24 кВА

Ответ: (c), a или b. Для этой нагрузки можно использовать один однофазный трансформатор на 75 кВА или три трансформатора на 25 кВА.

Теперь, когда вы понимаете некоторые основы расчета трансформатора и особенности расчетов дельта-трансформатора, вы сможете правильно определить размер дельта-трансформатора, когда большинство нагрузок являются линейными. Трансформаторы треугольник-треугольник чаще всего встречаются в специальных приложениях. Самая распространенная конфигурация — треугольник-звезда. В случае трансформатора «треугольник-звезда» теперь вы знаете, как определить размер первичной обмотки. После публикации в следующем месяце статьи, в которой будут рассмотрены расчеты трансформаторов типа «звезда», вы сможете рассчитать любую комбинацию трансформаторов «треугольник» и «звезда».

Боковая панель: знай свои термины

Чтобы избежать путаницы с расчетами трансформатора, важно четко понимать некоторые основные понятия ( Рис. 5 ниже). Как только вы освоитесь с этими терминами, вы должны быть готовы заняться всеми типами расчетов трансформаторов.

Рис. 5. Знание параметров трансформатора является ключом к правильным расчетам.

Линия — Незаземленная (горячая) жила(ы).

Линейный ток — Ток по незаземленным проводникам (В1 и В2 в Рис. 6 ). В системе треугольника линейный ток больше фазного тока на квадратный корень из 3, что составляет примерно 1,732). В системе звезда, линейный ток равен фазному току.

Линейное напряжение — Напряжение между любыми двумя линейными (незаземленными) проводниками (А1 и А2 в рис. 6 ). В системе треугольника линейное напряжение равно фазному напряжению. Но дельта-система также имеет высокую ногу.

Рис. 6. Основные показания напряжения и тока в системе треугольник/треугольник.

Фазный ток — Ток, протекающий через обмотку трансформатора (D1 и D2 в рис. 6 ). В системе «треугольник» фазный ток меньше линейного тока на квадратный корень из 3. В системе «звезда» фазный ток равен линейному току.

Фазная нагрузка — Нагрузка на обмотку трансформатора.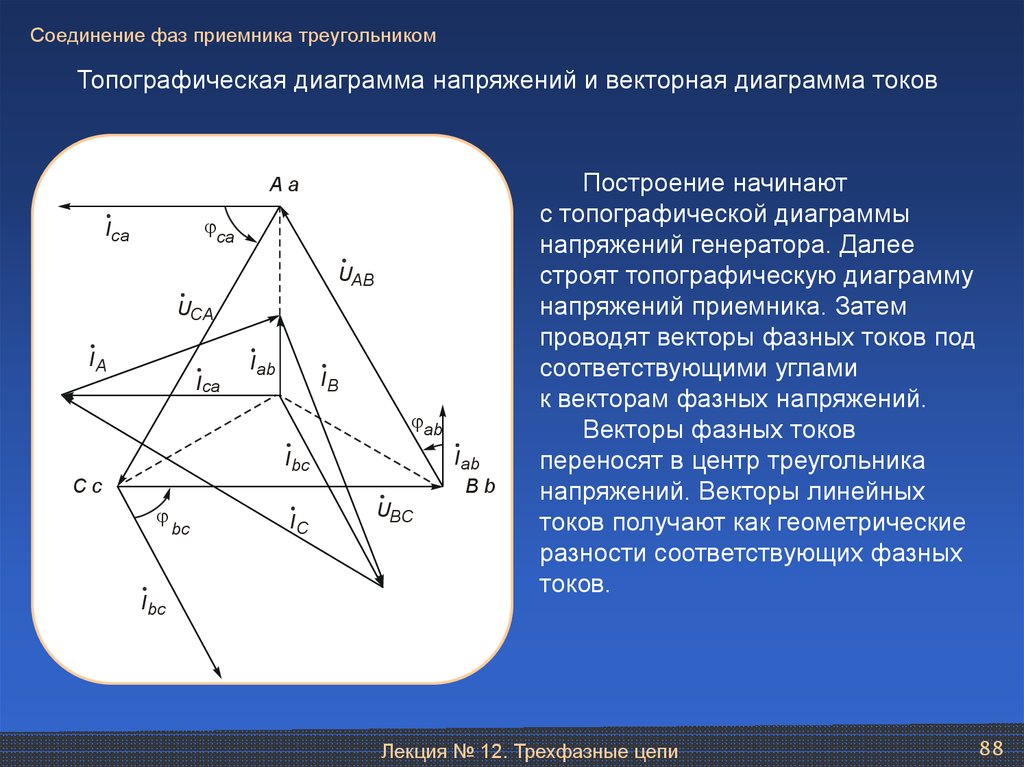

Фазное напряжение — Внутреннее напряжение трансформатора, генерируемое на одной обмотке трансформатора. Для вторичной обмотки треугольника фазное напряжение равно линейному напряжению. В системе звезда, фазное напряжение меньше, чем линейное напряжение на квадратный корень из 3 (A2 и C2 в Рис. 6 ).

Отношение — Количество витков первичной обмотки, деленное на количество витков вторичной обмотки.

Несимметричная нагрузка (нейтральный ток) — Нагрузка на вторичные заземленные (нейтральные) жилы.

3-фазное соединение треугольником | Соотношение напряжения и тока

Система, соединенная треугольником – На рис. 9.26 показана симметричная трехфазная, трехпроводная система, соединенная треугольником. Такое расположение называется сетчатым соединением, поскольку оно образует замкнутый контур. Он также известен как 3-фазное соединение треугольником, потому что три ветви в цепи также могут быть расположены в форме треугольника (Δ).

По способу соединения трех фаз в цепи может показаться, что три фазы закорочены между собой. Однако, это не так. Поскольку система сбалансирована, сумма трех напряжений вокруг замкнутой сетки равна нулю; следовательно, ток не может течь по сетке, когда клеммы разомкнуты.

Стрелки, расположенные рядом с напряжениями, V _RY , V _YB и V _BR , трех фаз, указывают на то, что клеммы R, Y и B положительны по отношению к Y, B и R соответственно. в течение соответствующих им положительных полупериодов.

Соотношение напряжений:

На рис. 9.27 видно, что между любыми двумя линиями
подключается только одна фаза. Следовательно, напряжение между любыми двумя линиями (V _L ) равно фазному напряжению (V _Ph ).

Поскольку система сбалансирована, все фазные напряжения равны, но смещены друг от друга на 120°, как показано на векторной диаграмме на рис. 9.27. Предполагается последовательность фаз RYB.

Текущее отношение:

На рис. 9.28 видно, что, поскольку система уравновешена, токи трех фаз (I _Ph ), т.е. 120° друг от друга, как показано на рис. 9.28(b). I ₁ , I ₂ и I ₃ — линейные токи (I _L ), т. е. I ₁ — линейный ток в линии 1, подключенной к общей точке R. Аналогично, I ₂   и я ₃ — линейные токи в линиях 2 и 3, подключенных к общим точкам Y и B соответственно. Хотя здесь все линейные токи направлены наружу, ни в какой момент все три линейных тока не будут течь в одном и том же направлении, ни наружу, ни внутрь. Поскольку три линейных тока смещены друг от друга на 120 °, когда один положительный, два других могут быть оба отрицательными или один положительный и один отрицательный. Также следует отметить, что стрелки, расположенные рядом с фазными токами на рис. 9.28(а), указывают направление токов, когда они предполагаются положительными, а не их фактическое направление в конкретный момент времени. Мы можем легко определить линейные токи на рис. 9.28 (а), I ₁ , I ₂ и I ₃ , подав KCL на три клеммы R, Y и B соответственно. Таким образом, ток в линии 1 I ₁ = I _R  – I _B ; то есть ток в любой линии равен разности векторов токов в двух фазах, присоединенных к этой линии. Аналогично, ток в линии 2, I ₂ = I _Y  – I _R , а ток в линии 3 I ₃ = I _B  – I _Y .

Сложение векторов этих токов показано на рис. 9.28(b). Из рисунка

Точно так же оставшиеся два линейных тока, I ₂ и I ₃ , также в √3 раза превышают фазные токи; то есть I _L = √3 I _Ph .

Как видно из рис. 9.28(b), все линейные токи равны по величине, но смещены друг от друга на 120°; а линейные токи на 30° отстают от соответствующих фазных токов.

Мощность в системе, соединенной треугольником:

Очевидно, что общая мощность трехфазного соединения треугольником представляет собой сумму мощностей трех фаз.