Сколько градусов в: Washington, DC Weather Forecast and Conditions — The Weather Channel

Погода в Самаре сегодня, прогноз погоды Самара на сегодня, Самара (городской округ), Самарская область, Россия

GISMETEO: Погода в Самаре сегодня, прогноз погоды Самара на сегодня, Самара (городской округ), Самарская область, Россия

Перейти на мобильную версию

Сейчас

18:51

−12 10

По ощущению −12 10

Вт, 7 фев

Сегодня

−147

−916

Ср, 8 фев

Завтра

−171

−916

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

−1210

−147

−147

−147

−1112

−916

−1210

−139

Скорость ветра, м/cкм/ч

1-4 4-14

0-3 0-11

Осадки, мм

Распечатать…

Снег

 

Вт, 7 фев, сегодня

Ср, 8

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

Выпадающий снег, см

Высота снежного покрова, см

31,3

31,3

32

32

32

31,9

31,9

31,9

/

Ветер, м/скм/ч

 

Вт, 7 фев, сегодня

Ср, 8

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

Порывы

—

—

—

—

—

—

Авто

Давление, мм рт.  ст.гПа

 

Вт, 7 фев, сегодня

Ср, 8

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

7611014

7611014

7621016

7631017

7631017

7641018

7651020

7671022

Влажность, %

 

Вт, 7 фев, сегодня

Ср, 8

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

88

89

88

86

73

70

76

78

Солнце и Луна

 

Вт, 7 фев, сегодня

Ср, 8

Долгота дня: 9 ч 20 мин

Восход — 8:13

Заход — 17:33

Сегодня день на 4 минуты длиннее, чем вчера

Луна стареющая, 98%

Восход — 17:57 (6 февраля)

Заход — 9:19

Полнолуние — 7 марта, через 29 дней

Ультрафиолетовый индекс, баллы

 

Вт, 7 фев, сегодня

Ср, 8

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

Геомагнитная активность, Кп-индекс

 

Вт, 7 фев, сегодня

Ср, 8

1⁰⁰

4⁰⁰

7⁰⁰

10⁰⁰

13⁰⁰

16⁰⁰

19⁰⁰

22⁰⁰

Осадки

Температура

Ветер

Облачность

Рождествено

Выползово

Подгоры

Зубчаниновка

Преображенка

Придорожный

Лопатино

Самара (Смышляевка)

Черноречье

Новолопатинский

Николаевка

Торновое

Смышляевка

Дубовый Гай

Новинки

Воскресенка

Петра Дубрава

Новоберезовский

Рамушки

Энергетик

Гаврилова Поляна

Козелки

Заярье

Спутник

Погода в Самаре на 10 дней, прогноз погоды Самара на 10 дней, Самара (городской округ), Самарская область, Россия.

GISMETEO: Погода в Самаре на 10 дней, прогноз погоды Самара на 10 дней, Самара (городской округ), Самарская область, Россия.

Перейти на мобильную версию

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

−916

−147

−916

−171

−523

−155

−621

−155

−621

−1210

−425

−139

−425

−1112

−621

−1112

−621

−1014

−1112

−163

Максимальная скорость ветра, м/cкм/ч

Осадки, мм

Распечатать…

Снег

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

Выпадающий снег, см

Высота снежного покрова, см

32

31,9

32,4

31,8

31,6

31,5

34,2

35,1

37,6

38,7

/

Среднесуточная температура

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

−1210

−147

−916

−1112

−1014

−1014

−818

−818

−818

−139

Ветер, м/скм/ч

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

Максимальная скорость ветра, м/cкм/ч

Давление, мм рт.  ст.гПа

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

7671022

7611014

7681024

7651020

7661021

7621016

7661021

7621016

7611014

7561008

7571009

7551006

7561008

747996

747996

742989

746994

741988

7521002

747996

Влажность, %

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

81

74

80

85

78

79

78

77

77

80

Ультрафиолетовый индекс, баллы

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

3

3

4

3

2

2

2

2

2

3

Геомагнитная активность, Кп-индекс

Вт

7 фев

Ср

8

Чт

9

Пт

10

Сб

11

Вс

12

Пн

13

Вт

14

Ср

15

Чт

16

Осадки

Температура

Ветер

Облачность

Рождествено

Выползово

Подгоры

Зубчаниновка

Преображенка

Придорожный

Лопатино

Самара (Смышляевка)

Черноречье

Новолопатинский

Николаевка

Торновое

Смышляевка

Дубовый Гай

Новинки

Воскресенка

Петра Дубрава

Новоберезовский

Рамушки

Энергетик

Гаврилова Поляна

Козелки

Заярье

Спутник

Сколько градусов в окружности?

МАТЕМАТИКА — Геометрия

Задумывались ли вы когда-нибудь.

..

• Сколько градусов в окружности?
• Какая связь между радиусом и диаметром круга?
• Как называется расстояние вокруг края круга?

Теги:

См. все теги

• 2πr,
• Вавилоняне,
• форма,
• πr2,
• Математика,
• Геометрия,
• Круг,
• Степень,
• Площадь,
• Треугольник,
• Пирог,
• Хулахуп,
• Самолет,
• Точка,
• Расстояние,
• Радиус,
• Диаметр,
• Окружность,
• Район,
• Периметр,
• Пи,
• Экспонента,
• Земля,
• Вс,
• Орбита,
• Календарь

Сегодняшнее чудо дня было вдохновлено Анной Грейс из Зимнего Интервилля. Анна Грейс Уондерс , “ Почему круг имеет бесконечные линии симметрии? «Спасибо, что ДУМАЕТЕ вместе с нами, Анна Грейс!

Любишь геометрию? Мы делаем! Мы хотели сделать Чудо дня об особой форме, но не могли решить, какую фигуру использовать. Однако чем больше мы думали об этом, тем больше мы возвращались к той же форме. Что это было? Круг, конечно!

Что вам больше всего нравится в кругах? Нам нравятся их идеально круглые формы. У них нет тех заостренных концов, которые вы найдете на квадратах и ​​треугольниках.

Некоторые из наших любимых вещей имеют форму кругов. Например, наш любимый десерт — пирог — имеет форму круга. Как и наша любимая игрушка: хула-хуп. Какие еще предметы в форме круга вы видите или используете каждый день?

Учителя геометрии определяют окружность как набор точек на плоскости, находящихся на одинаковом расстоянии от центральной точки. Это означает, что круги плоские. Когда вы изучаете круги, вы узнаете, что у каждого круга есть радиус, диаметр, длина окружности и площадь.

Радиус круга — это расстояние от его центра до края. Диаметр круга — это расстояние поперек круга в его самом широком месте. Диаметр круга всегда ровно в два раза больше его радиуса.

Периметр круга — расстояние вокруг его края — называется его окружностью. Чтобы вычислить длину окружности, нужно знать ее радиус.

Формула длины окружности: 2πr, где r — радиус окружности, а π — число пи (приблизительно 3,141592). Поскольку диаметр круга в два раза больше радиуса, вы также можете представить формулу длины окружности как πd, где d — диаметр круга.

Площадь круга измеряется количеством квадратных единиц внутри круга. Еще раз, вам нужно знать радиус. Формула площади круга: πr ² . ² в формуле — это показатель степени, что означает, что вы умножаете радиус сам на себя. Таким образом, вместо формулы площади круга можно было бы написать πrr.

Одна замечательная вещь о кругах, которую знают все учителя геометрии, заключается в том, что если вы знаете один из этих фактов — радиус, диаметр, длину окружности или площадь — вы можете вычислить все остальные значения! Например, если вы знаете радиус круга, вы можете вычислить его диаметр, длину окружности и площадь.

Еще один интересный аспект кругов заключается в том, что каждый круг можно разделить на 360 единиц, называемых градусами. Итак, если вы совершите полный круг, вы повернетесь на 360 градусов. Если вы просто повернетесь наполовину — полукругом — вы повернетесь на 180 градусов.

Так почему же 360 градусов вместо чего-то попроще, например, 100 градусов? Математики считают, что виноваты древние вавилоняне. Около 2400 г. до н.э. они заметили круговое движение Земли вокруг Солнца. Они также подсчитали, что для завершения этой круговой орбиты потребовалось около 360 дней.

Поэтому круговой путь решили разделить на 360 градусов. Таким образом, они могли легко отслеживать прохождение каждого дня по круговому календарю. Так что если вы запутались в геометрии с количеством градусов в окружности, виноваты вавилоняне!

Интересно, что дальше?

Завтрашнее чудо дня — это глоток свежего воздуха!

Попробуйте

Готовы повеселиться с геометрией? Обязательно проверьте следующие задания с другом или членом семьи:

• Если вы хотите узнать больше о градусах и углах, посмотрите это увлекательное онлайн-занятие «Углы». Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?
• После того, как вы попрактикуетесь с углами, попробуйте онлайн-задание «Угадай случайный угол». Нажмите кнопку, чтобы сгенерировать случайный угол, введите свое предположение, а затем посмотрите, насколько близко вы были к метке!
• Вам трудно представить себе, как определяется число Пи? Зайдите в Интернет, чтобы посмотреть визуальное представление о том, как катящийся круг иллюстрирует число Пи. Попробуйте повторить то, что видите, с помощью круга и линейки дома.

Wonder Sources

• http://www.coolmath.com/reference/circles-geometry.html
• http://mathforum.org/library/drmath/view/59075.html

Получили?

Проверьте свои знания

Wonder Contributors

Благодарим:

Braeden
за ответы на вопросы по сегодняшней теме Wonder!

Продолжайте удивляться вместе с нами!

Что вас интересует?

Wonder Words

• радиус
• диаметр
• окружность
• район
• геометрия
• самолет
• периметр
• формула
• заостренный
• аспект
• расстояние
• показатель степени
• решил
• запутался
• интересно
• рассчитано
• измерение
• математиков

Примите участие в конкурсе Wonder Word

Оцените это чудо

Поделись этим чудом

×

ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО

Подпишитесь на Wonderopolis и получайте Чудо дня® по электронной почте или SMS

Присоединяйтесь к Buzz

Не пропустите наши специальные предложения, подарки и рекламные акции. Узнай первым!

Поделитесь со всем миром

Расскажите всем о Вандополисе и его чудесах.

Поделиться Wonderopolis

Wonderopolis Widget

Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.

Добавить виджет

Ты понял!

Продолжить

Не совсем!

Попробуйте еще раз

Измерение углов

Измерение углов

Концепция угла

Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.

Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы. Градусы могут быть далее разделены на минуты и секунды, но это разделение не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых 9.02:24 мин. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записать 7° 30′. Каждая минута далее делится на 60 равных частей, называемых секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часы в минуты и секунды времени.

Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5&deg.

Когда один угол рисуется на плоскости xy для анализа, мы рисуем его в стандартном положении с вершиной в начале координат (0,0), одна сторона угла вдоль x -ось, а другая сторона выше оси x -оси.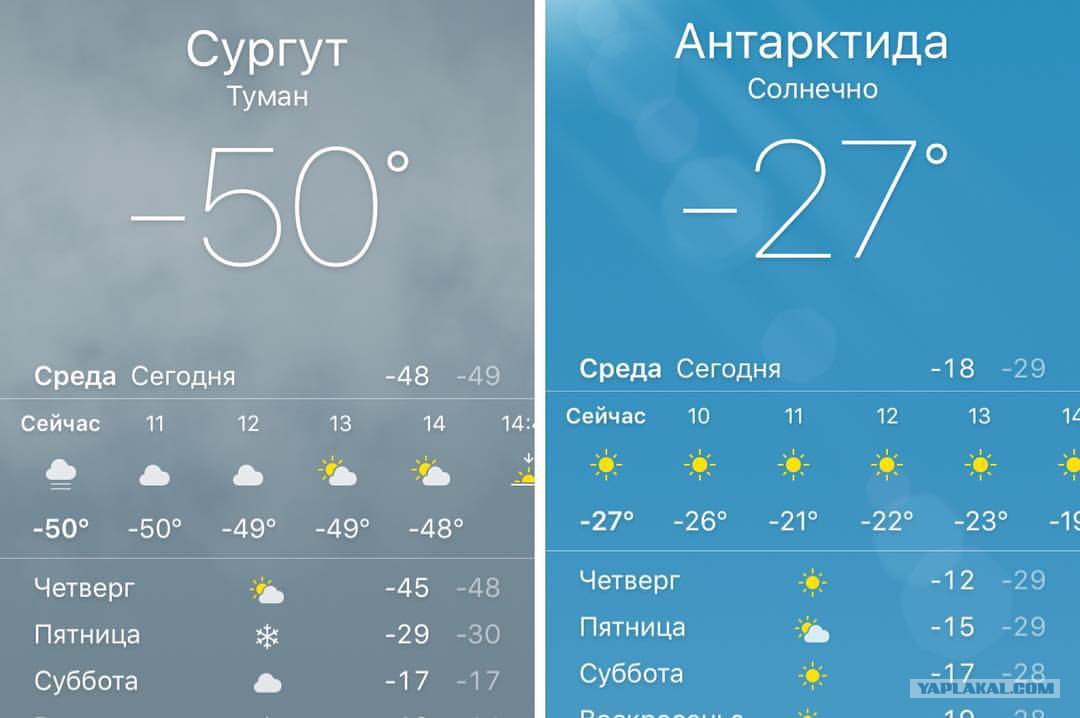

Радиан

Другой распространенной единицей измерения углов являются радианы. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно, 1° равно π /180 радиан и 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор.

Краткая заметка об истории радианов

Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге « Элементы алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной на единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией. e ^iθ = cos θ + i sin θ

где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.

Радианы и длина дуги

Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.

Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.

Например, дуга θ  = 0,3 радиана в окружности радиусом r  = 4 имеет длину 0,3 умножить на 4, то есть 1,2.

Радианы и площадь сектора

Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах. Поскольку площадь всего круга равна πr ² , а сектор относится ко всему кругу как угол θ к 2 π , поэтому

Углы общие

Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дается как π . Его, конечно, можно было бы представить десятичным числом, но радианное измерение часто появляется с коэффициентом 9.0224 номер .

Уголок	градусов	радиан
	90°	№ /2
	60°	№ /3
	45°	№ /4
	30°	№ /6

Упражнения

Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.

Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.

Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.

1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.

2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.

3. Зная угол a и радиус r, найти длину стягивающей дуги.
(а). a  = 0° 17′ 48″, r  = 6,2935.
(б). a  = 121° 6′ 18″, r  = 0,2163.

4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l  = 0,16296, r  = 12,587.
(б). l = 1,3672, r = 1,2978.

5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a  = 0° 44′ 30″, l  = 0,032592.
(б). a  = 60° 21′ 6″, l  = 0,4572.

6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.

7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минуты, радиус от центральной линии пути составляет 2100 футов.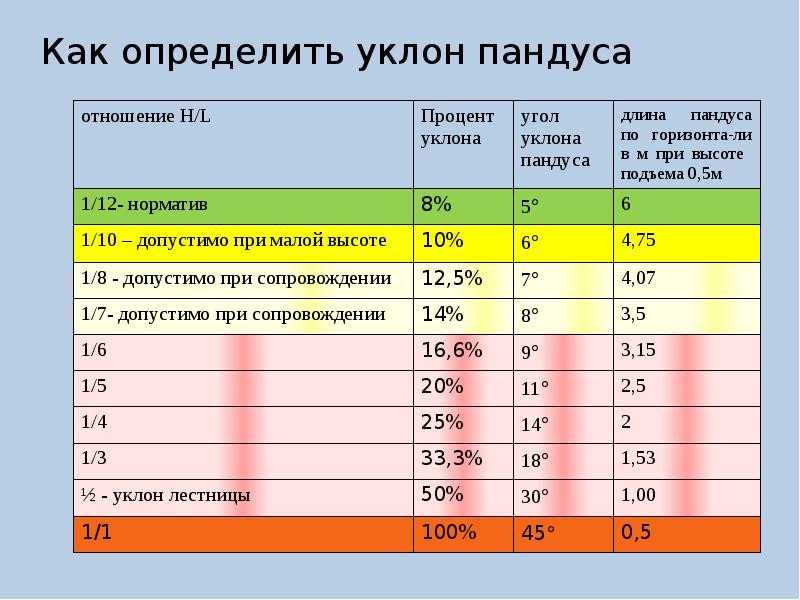 Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.

9. На сколько человек изменит широту, пройдя на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?

10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?

14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?

23. Известно, что воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?

Советы

1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.

2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.

3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.

4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.

5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar  =  l, , но a необходимо сначала преобразовать из градусов в радианы. Итак, чтобы найти радиус 90 224 r, 90 225 сначала преобразуйте угол 90 224 a 90 225 в радианы, а затем разделите его на длину дуги 90 224 l 90 225.

6. Длина дуги равна произведению радиуса на угол в радианах.

7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.

9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)

10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?

14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.

23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?

Ответы

1. (а). 0,2176. (б). 0,6318.

2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».

3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.

4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535 радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.

5. (а). л/год  = 0,032592/0,01294 = 2,518.
(б). л/год  = 0,4572/1,0533 = 0,4340.

6. ra  = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.

7. Угол a  = 0,16776 радиан. Разница в длинах есть 2102,5 а  – 1997,5 а , что равно 5 а. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.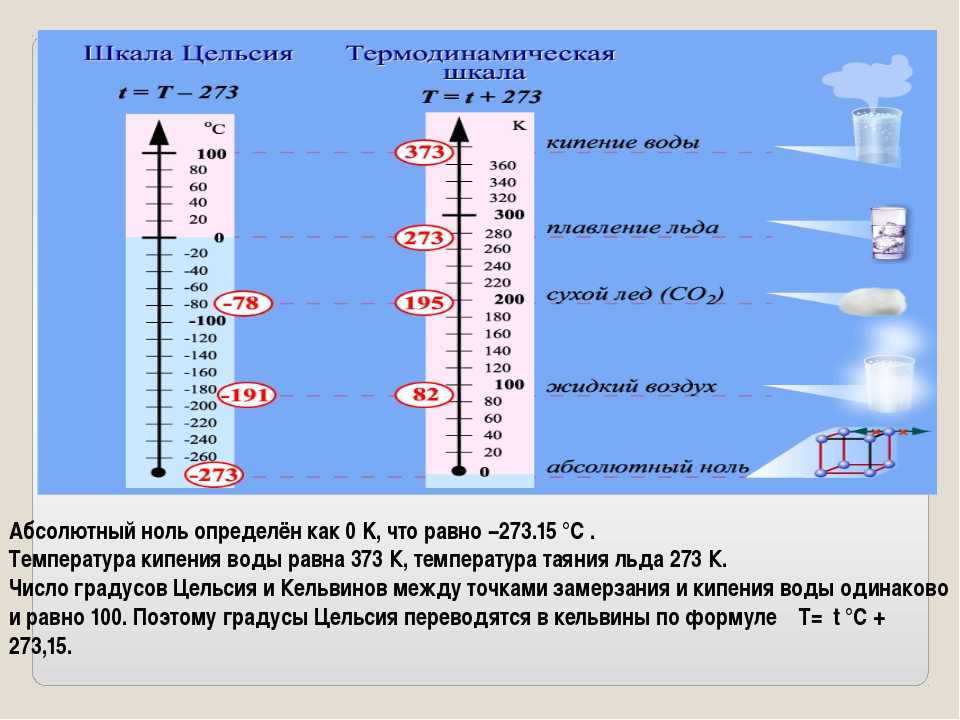

9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.

10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.

14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.

23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.

О разрядах точности.

Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.