Расчет уклона: Калькулятор уклонов

Расчет угла наклона пандуса

Расчет угла наклона пандуса

Безбарьерная среда для
людей с ограничениями
Поддержать нас

+7 (915) 746-45-05
Оставить заявку на
паспортизацию объекта

• Главная
>
• Калькуляторы
>
• Калькулятор для расчета угла наклона пандуса

Одна из самых распространённых ошибок при создании доступной среды это неверный уклон пандуса. К сожалению, исполнители, то есть подрядные строительные организации, которые разрабатывают проект и выполняют установку пандуса, не всегда компетентны в вопросе создания доступной среды и не знают норм и правил организации пандуса.

С помощью нашего калькулятора вы сможете проверить, соответствует ли угол наклона пандуса нормам доступности.

Инструкция:

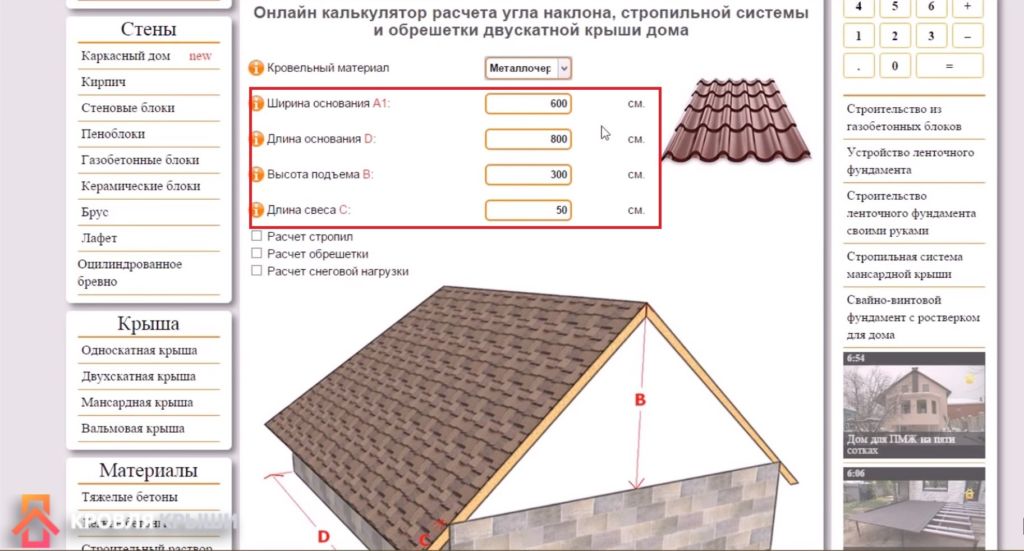
Введите параметры пандуса: высоту — максимальную цифру, длину непрерывного марша пандуса. Параметры необходимо вводить в сантиметрах. Нажмите кнопку «рассчитать». Калькулятор выдаст результат рассчитанного угла уклона проверяемого пандуса в процентах (%). Так будут указаны рекомендации соответствует ли угол наклона проверяемого пандуса нормам доступности.

Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2016 «Доступность зданий и сооружений для маломобильных групп населения».

Допустимые значения угла наклона пандуса. Адаптация входной группы для людей с инвалидностью

Максимальная высота одного подъема (марша) пандуса не должна превышать 0,45 м при уклоне не более 1:20 (5%).

При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 = 10%

Внутри зданий и на временных сооружениях или объектах временной инфраструктуры допускается максимальный уклон пандуса 1:12 (8%) при условии, что подъем по вертикали между площадками не превышает 0,5 м.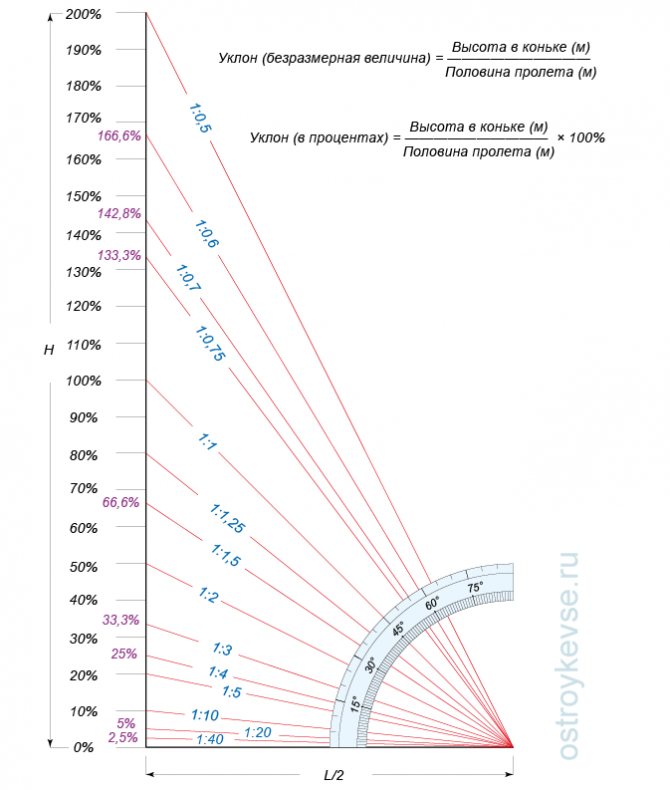

При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий, и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%).

Пандусы при перепаде высот более 3,0 м следует заменять лифтами, подъемными платформами и т.п.

В соответствии с приказом Минстроя России №750/ приказ от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2016 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий, и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».

Что обозначают цифры:

1:20 = 5% т.е. при перепаде высот 1 м, длина пандуса должна быть 20 м, при высоте 0,5 м — 10 м.

1:12 = 8% — т.е. при перепаде высоты в 1 м, длина пандуса должна быть 12 м, при высоте 0,5 м — длина пандуса должна быть не менее 6 метров и т.д.

1:10 = 10% — т.е. при перепаде высот в 1 м, длина пандуса должна быть 10 м, при высоте 0,5 м — длина пандуса должна быть 5 м и т.д.

Я хочу принять участие в Исследовании

Принять участие как:

?ВолонтерИсследователь

Город:

Выберите городБлаговещенскАрхангельскАстраханьБелгородБрянскВладимирВолгоградВологдаВоронежИвановоИркутскКалининградКалугаКемеровоКировКостромаКурганКурскСанкт-ПетербургЛипецкМагаданМоскваМурманскНижний НовгородВеликий НовгородНовосибирскОмскОренбургОрёлПензаПсковРостов-на-ДонуРязаньСамараСаратовЮжно-СахалинскЕкатеринбургСмоленскТамбовТверьТомскТулаТюменьУльяновскЧелябинскЯрославль

Мероприятие:

Выберите мероприятиеПосещение общепитаОбщественный транспортПолучение гос. услугСоциальные услуги

Группа инвалидности:

Выберите группу инвалидностиНет123

Телефон или e-mail:

Прикрепить файлы

Согласие на обработку персональных данных:

Условия участия в мероприятии

Контент временно отсутствует!

Я хочу принять участие в мероприятии

Группа инвалидности

Выберите группу инвалидностиНет123

Согласие на обработку персональных данных

Прикрепить файлы

Условия участия в мероприятии

Контент временно отсутствует!

Заявка на паспортизацию

Организация:

Город:

Выберите городБлаговещенскАрхангельскАстраханьБелгородБрянскВладимирВолгоградВологдаВоронежИвановоИркутскКалининградКалугаКемеровоКировКостромаКурганКурскСанкт-ПетербургЛипецкМагаданМоскваМурманскНижний НовгородВеликий НовгородНовосибирскОмскОренбургОрёлПензаПсковРостов-на-ДонуРязаньСамараСаратовЮжно-СахалинскЕкатеринбургСмоленскТамбовТверьТомскТулаТюменьУльяновскЧелябинскЯрославль

Объект паспортизации:

Контактное лицо:

Телефон

Прикрепить файлы

Согласие на обработку персональных данных:

Выделите опечатку и нажмите Ctrl + Enter, чтобы отправить сообщение об ошибке.

Как работает инструмент Уклон—Справка | ArcGIS Desktop

Доступно с лицензией 3D Analyst.

• Методы вычисления и эффект ребер
• Плоскостной метод
• Геодезический метод
• Использование графического процессора (GPU)
• Справочная информация

Инструмент Уклон определяет крутизну в каждой ячейке растровой поверхности. Чем меньше значение уклона, тем более плоской является земная поверхность; чем больше значение уклона, тем более крутые склоны расположены на поверхности.

Выходной растр уклонов может быть вычислен в двух различных единицах измерения, в градусах или в процентах (‘процент подъема’). Процент подъема можно лучше понять, если вы рассматриваете его как подъем, деленный на пробег (спуск), умноженный на 100. Рассмотрим треугольник B на рисунке внизу. Когда угол равен 45 градусам, подъем равен пробегу (спуску), а процент подъема равен 100 процентам. По мере того, как угол наклона приближается к вертикальному (90 градусов), как в треугольнике

C, процент подъема стремится к бесконечности.

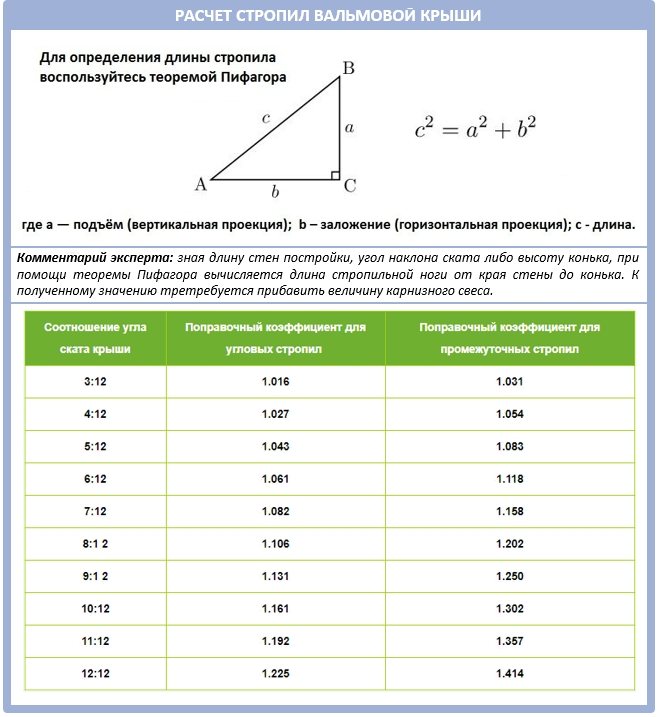Сравнение значений уклонов в градусах и процентах.

Инструмент Уклон чаще всего работает с набором данных высот, как показано на следующих рисунках. Более крутые уклоны заштрихованы красным на выходном растре уклона.

Инструмент также может использоваться с другими типами непрерывных данных, например, численность населения, для выявления резких изменений значения.

Методы вычисления и эффект ребер

Для вычисления уклона доступно два метода. Вы можете выбрать метод вычисления Плоскостной или Геодезический, используя параметр Метод.

Для плоскостного метода, уклон измеряется как максимальное соотношение изменения значений ячейки и ее непосредственного окружения. Расчет выполняется на проецированной плоскости при использовании декартовой системы координат 2D. Значение уклона вычисляется с использованием методики усредненного максимума (Burrough, 1998).

По геодезическому методу вычисления будут выполняться в декартовой системе координат 3D учетом формы земной поверхности в виде эллипсоида.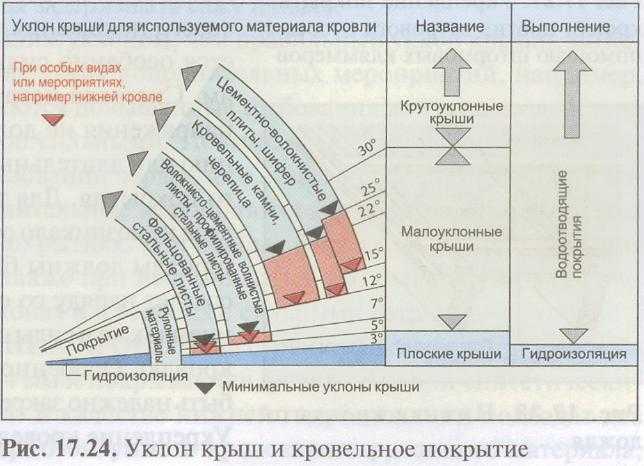 Значение уклона вычисляется измерением угла между топографической поверхностью и базовым датумом.

Плоскостные и геодезические вычисления выполняются с помощью окрестности размером 3 на 3 ячейки (плавающее окно). Для каждой окрестности, если обрабатываемая (центральная) ячейка имеет значение NoData, выходное значение будет NoData. Для вычислений также необходимо, чтобы не менее семи окрестных ячеек имели допустимые значения. Если менее семи ячеек имеют корректные значения, вычисление не производится, а выходным значением обрабатываемой ячейки будет NoData.

Ячейки в наиболее удаленных строках и столбцах выходного растра получат значение NoData. Это происходит потому, что вдоль границы входного набора данных у ячеек нет достаточного количества соседей.

Плоскостной метод

Для каждой ячейки инструмент вычисляет максимальную степень изменения в значении z между конкретной ячейкой и соседними с ней ячейками. По сути, максимальная степень изменения в значениях высоты на единицу расстояния между ячейкой и восемью соседними с ней ячейками определяет самый крутой спуск вниз по склону из ячейки.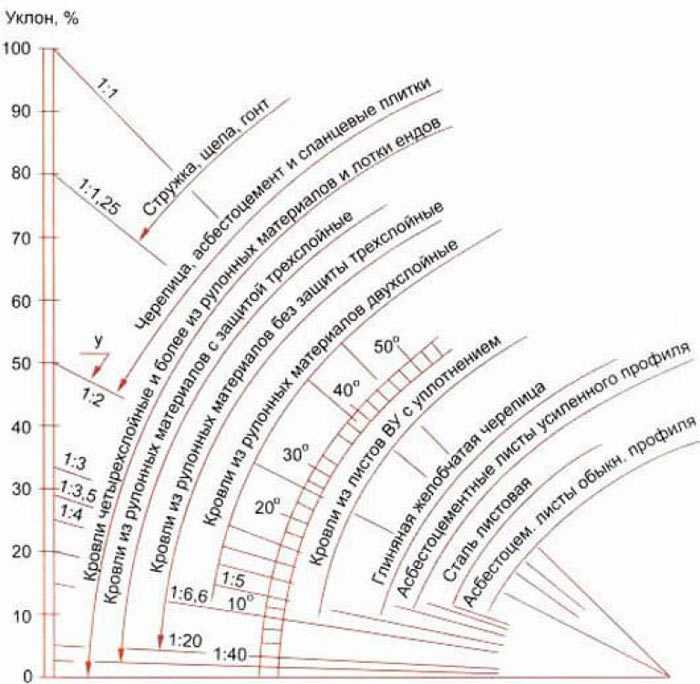

Алгоритм вычисления плоскостного уклона

Уклон определяет степень изменения (дельту) поверхности в горизонтальном (dz/dx) и вертикальном (dz/dy) направлениях из центральной ячейки. Базовый алгоритм, используемый для вычисления уклона, выглядит так:

 slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )

Уклон обычно измеряется в градусах с использованием следующего алгоритма:

 slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57.29578

Примечание:

Показанное здесь значение 57,29578 – это сокращенная версия результата операции 180/pi.

Алгоритм уклона может быть проинтерпретирован также следующим образом:

 slope_degrees
  = ATAN (rise_run) * 57.29578

Горизонтальную и вертикальную дельты определяют значения центральной ячейки и восьми соседних с ней ячеек. Соседние ячейки обозначаются буквами от a до i, при этом буква e обозначает ячейку, для которой вычисляется уклон.

Окно сканирования поверхности

Степень изменения по направлению x для ячейки ‘e‘ вычисляется с помощью следующего алгоритма:

  [dz/dx] = ((с + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)

• , где:

  wght1 и wght2 являются горизонтально взвешенным числом корректных ячеек.

  Например, если:

  • c, f и i имеют корректные значения, wght1 = (1+2*1+1) = 4.
  • i является NoData, wght1 = (1+2*1+0) = 3.
  • f является NoData, wght1 = (1+2*0+1) = 2.

  Аналогичная логика применяется к wght2, за исключением того, что соседними местоположениями являются a, d и g.

Степень изменения по направлению y для ячейки ‘e‘ вычисляется с помощью следующего алгоритма:

  [dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + с)*4/wght4) / (8 * y_cellsize)

Пример вычисления плоскостного уклона

В качестве примера будет вычислено значение уклона центральной ячейки скользящего окна.

Пример входных данных инструмента Уклон

Степень изменения для центральной ячейки ‘e‘ по направлению x:

  [dz/dx] = ((с + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * 
 x_cellsize)          = ((50 + 60 + 10)*4/(1+2+1) - (50 + 60 + 8)*4/(1+2+1)) / (8 * 5)          = (120 - 118) / 40          = 0.05

Степень изменения для центральной ячейки ‘e‘ по направлению y:

  [dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + с)*4/wght4) / (8 * y_cellsize)          = ((8 + 20 + 10)*4/(1+2+1) - (50 + 90 + 50)*4/(1+2+1)) / (8 * 5)          = (38 - 190 ) / 40          = -3.8

Учитывая степень изменения в направлении x и y, уклон для центральной ячейки e вычисляется с использованием следующего алгоритма:

  rise_run = √ ([dz/dx]2 + [dz/dy]2)           = √ ((0.05)2 + (-3.8)2)           = √ (0. 0025 + 14.44)           = 3.80032

  slope_degrees = ATAN (rise_run) * 57.29578                = ATAN (3.80032) * 57.29578                = 1.31349 * 57.29578                = 75.25762

Целочисленное значение уклона для ячейки ‘e‘ составляет 75 градусов.

Пример выходных данных инструмента Уклон

Геодезический метод

При геодезическом методе уклон поверхности измеряется в геоцентрической 3D системе координат – также называющейся системой координат Earth Centered, Earth Fixed (ECEF) – с учетом эллипсоидной формы земли. Проекция набора данных на результаты вычислений не влияет. При этом используются единицы измерения z входного растра, если они заданы в пространственной привязке. Если в пространственной привязке входных данных не заданы единицы измерения z, необходимо сделать это с помощью параметра задания z-единиц. Геодезический метод дает более точный результат, чем плоскостной.

Преобразование геодезических координат

Система координат ECEF является 3D правосторонней Декартовой системой координат с центром земли в качестве начальной точки, в которой любое местоположение представлено координатами X, Y и Z.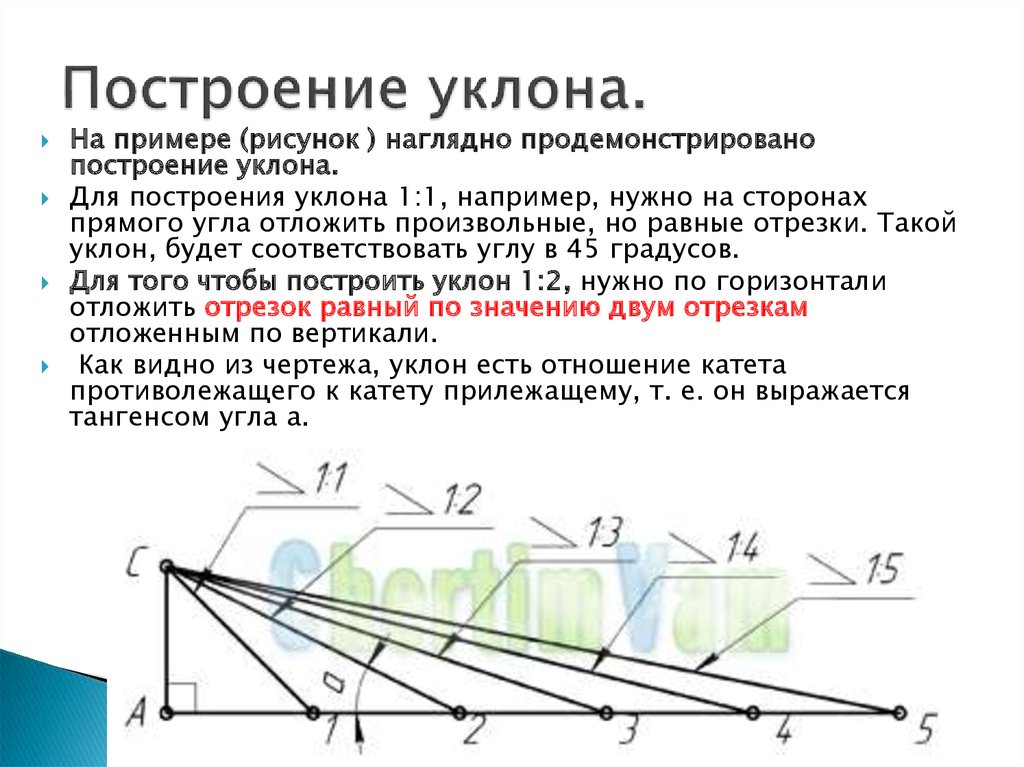 На следующем рисунке приводится пример целевого местоположения T, выраженного в геоцентрических координатах.

Растр поверхности трансформируются из входной системы координат в 3D геоцентрическую систему координат.

В геодезических вычислениях используются координаты X, Y, Z, которые вычисляются на основе геодезических координат(широта φ, долгота λ, высота h). Если система координат входного растра поверхности является системой координат проекции, растр сначала перепроецируется в географическую систему координат, в которой каждое местоположение имеет геодезические координаты, затем он преобразуется в систему координат ECEF. Высота h (z-значение) является эллипсоидной высотой, основанной на поверхности эллипсоида. См. иллюстрацию ниже.

Эллипсоидальная высота

Для преобразования геодезических координат (широта φ, долгота λ, высота h) в координаты ECEF используются следующие формулы:

X = (N(φ)+h)cosφcosλ

Y = (N(φ)+h)cosφsinλ

Z = (b2/a2*N(φ)+h)sinφ

• , где:
  • N( φ ) = a²/ √(a²cosφ²+b²sinφ²)
  • φ = широта
  • λ = долгота
  • h = эллипсоидальная высота
  • a = большая полуось эллипсоида
  • b = малая полуось эллипсоида

Эллипсоидная высота h в следующих формулах дается в метрах.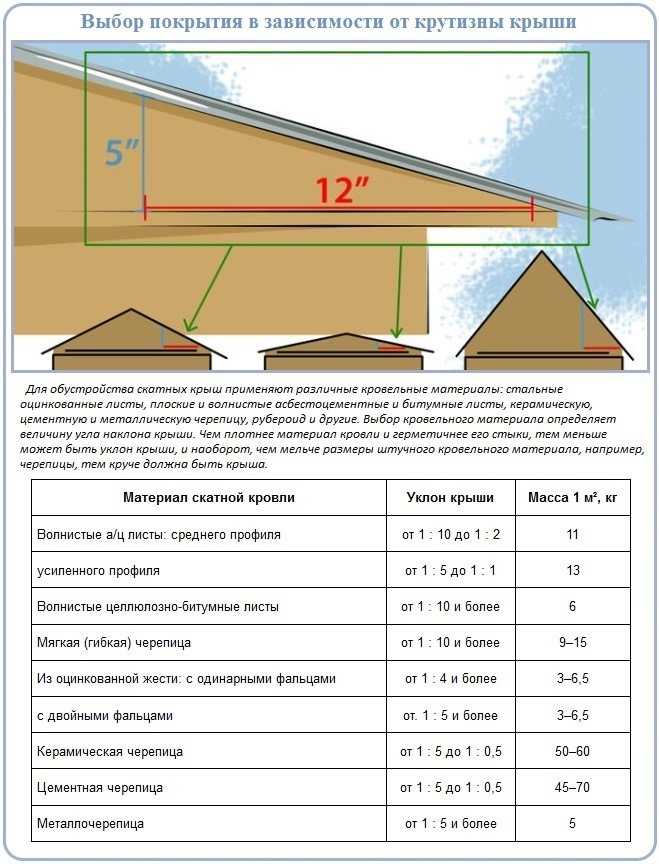 Если z-значения входного растра даны в других единицах измерения, они будут преобразованы в метры.

Вычисление уклона

Геодезический уклон является углом между топографической поверхностью и поверхностью эллипсоида. Любая поверхность, параллельная поверхности эллипсоида, имеет уклон 0. Чтобы вычислить уклон в каждом местоположении, вокруг обрабатываемой ячейки создается плоскость окрестности размером 3 x 3 ячейки, по методу наименьших квадратов. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов разницы (dz_i) между реальным и подобранным z-значением. Пример приведен на рисунке ниже.

Пример использования метода наименьших квадратов

Здесь плоскость представлена в виде z = Ax + By + C. Для каждого центра ячейки, dz_i является разницей между реальным z-значением и подобранным.

Наилучшее соответствие плоскости достигается, когда ∑⁹_i=1dz_i² минимальна.

После подгонки плоскости, в местоположении ячейки вычисляется нормаль к поверхности.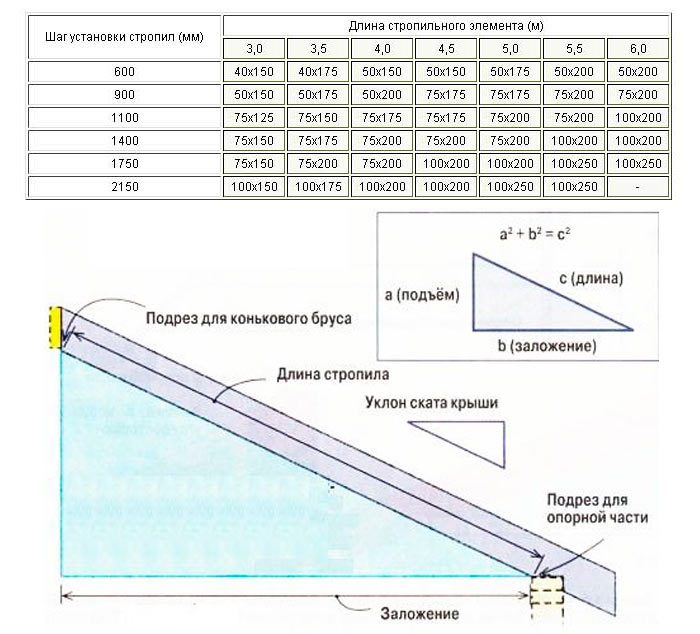 В том же местоположении вычисляется нормаль эллипсоида, перпендикулярная плоскости, проходящей по касательной к поверхности эллипсоида.

Вычисление геодезического уклона

Уклон, в градусах, вычисляется по углу между нормалью к эллипсоиду и нормалью к топографической поверхности, который здесь обозначается как β. Согласно рисунку выше, угол α является геодезическим уклоном, что соответствует углу β, согласно закону подобной геометрии.

Для вычисления уклона в процентах используется следующая формула:

Slope_PercentRise = ATAN(β) * 100%

Использование графического процессора (GPU)

При использовании геодезического метода, производительность инструмента значительно повышается если используются GPU определенных моделей. Дополнительные сведения о поддержке этого механизма, его настройке и включении см. в разделе Работа GPU с Spatial Analyst.

Справочная информация

Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.

Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159

B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS — theory and practice. Section 10.2.1. p. 282.

David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.

Связанные разделы

склона калькулятора

, созданный Матеуш Муда и Джулия Жулавиньска

, рассмотренные Bogna Szyk и Jack Bowater

Последний темы

Часто задаваемые вопросы

Калькулятор уклона определяет уклон или градиент между двумя точками в декартовой системе координат. Наклон — это в основном величина наклона линии, которая может иметь положительное, отрицательное, нулевое или неопределенное значение. Прежде чем пользоваться калькулятором, наверное, стоит научиться находить уклон по формуле уклона.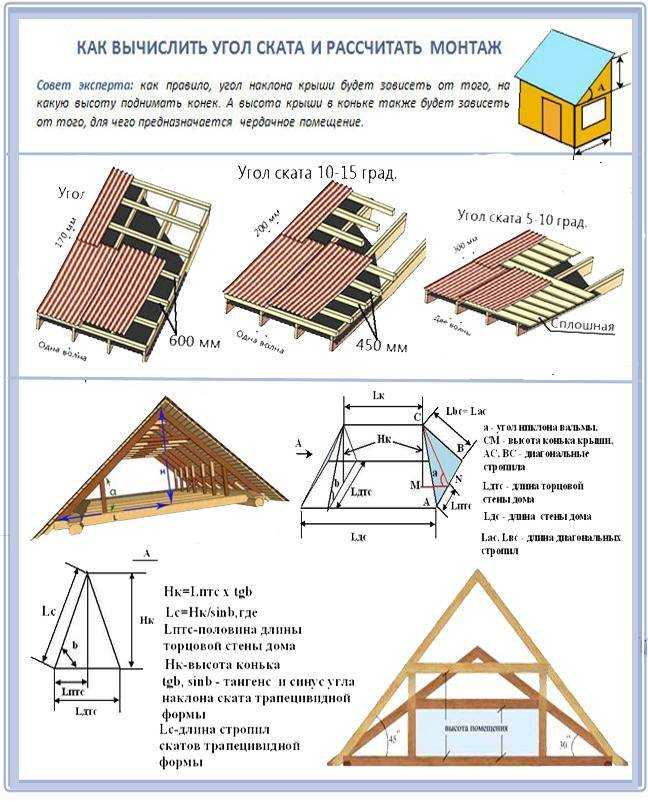 Чтобы найти уравнение прямой для любых двух точек, через которые проходит эта линия, используйте наш калькулятор формы пересечения наклона.

Как найти уклон

1. Определите координаты (x1,y1)(x_1, y_1)(x1​,y1​) и (x2,y2)(x_2, y_2)(x2​,y2​). Мы будем использовать формулу для расчета наклона линии, проходящей через точки (3,8)(3, 8)(3,8) и (−2,10)(-2, 10)(−2,10) .
2. Введите значения в формулу. Это дает нам (10-8)/(-2-3)(10-8)/(-2-3)(10-8)/(-2-3).
3. Вычтите значения в скобках, чтобы получить 2/(-5)2/(-5)2/(-5).
4. Упростите дробь, чтобы получить наклон −2/5–2/5–2/5.
5. Проверьте результат с помощью калькулятора уклона.

Чтобы найти наклон линии, нам нужны две координаты на линии. Достаточно любых двух координат. В основном мы измеряем величину изменения координаты y, часто известную как рост , деленную на изменение координаты x, известную как run . Вычисления по нахождению наклона просты и включают в себя не что иное, как базовое вычитание и деление.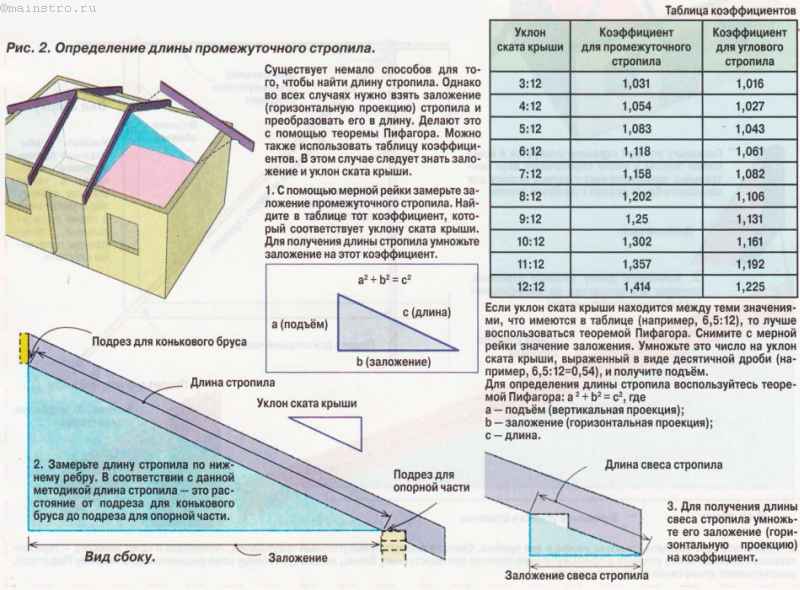

🙋 Чтобы найти градиент нелинейных функций, вы можете использовать калькулятор средней скорости изменения.

Формула наклона

наклон=y2−y1x2−x1\mathrm{наклон} = \frac{y_2 — y_1}{x_2 — x_1}slope=x2​−x1​y2​−y1​​

Обратите внимание, что наклон линии легко вычисляется вручную с использованием небольших целых чисел координат. Формула становится все более полезной по мере того, как координаты принимают большие значения или десятичные значения.

Стоит отметить, что любая горизонтальная линия имеет нулевой градиент, потому что горизонтальная линия имеет те же координаты y. Это приведет к нулю в числителе формулы наклона. С другой стороны, вертикальная линия будет иметь неопределенный наклон, поскольку координаты x всегда будут одинаковыми. Это приведет к ошибке деления на ноль при использовании формулы.

Точно так же, как наклон можно вычислить, используя конечные точки сегмента, можно вычислить и среднюю точку. Середина — важное понятие в геометрии, особенно при вписании многоугольника внутрь другого многоугольника, когда его вершины касаются середины сторон большего многоугольника. Это можно получить с помощью калькулятора средней точки или просто взяв среднее значение каждой координаты x и среднее значение координаты y, чтобы сформировать новую координату.

Наклон линий важен для определения того, является ли треугольник прямоугольным. Если любые две стороны треугольника имеют наклоны, которые умножаются на -1, то треугольник является прямоугольным. Вычисления для этого можно выполнить вручную или с помощью калькулятора прямоугольного треугольника. Вы также можете использовать калькулятор расстояний, чтобы вычислить, какая сторона треугольника является самой длинной, что поможет определить, какие стороны должны образовывать прямой угол, если треугольник прямоугольный.

Знак перед градиентом, предоставленным калькулятором наклона, указывает, является ли линия возрастающей, убывающей, постоянной или неопределенной. Если график линии перемещается из нижнего левого угла в верхний правый, он увеличивается и, следовательно, является положительным. Если он уменьшается при движении из левого верхнего угла в правый нижний, то градиент отрицательный.

Часто задаваемые вопросы

Как найти наклон по уравнению?

Метод для определения наклона по уравнению зависит от формы уравнения перед вами. Если форма уравнения y = mx + c, то наклон (или градиент) просто m . Если уравнение не в этой форме, попробуйте изменить уравнение. Чтобы найти градиент других полиномов, вам нужно будет продифференцировать функцию по x .

Как рассчитать уклон холма?

1. Используйте карту, чтобы определить расстояние между вершиной и основанием холма по прямой.
2. Используя ту же карту или GPS, найдите высоту между вершиной и основанием холма . Убедитесь, что точки, от которых вы измеряете, такие же, как и в шаге 1.
3. Преобразуйте оба измерения в одни и те же единицы.
4. Разделите разницу высот на расстояние между двумя точками.
5. Это число представляет собой уклон холма, если он увеличивается линейно. Если это не так, повторите шаги, но там, где есть заметное изменение наклона.

Как рассчитать длину склона?

1. Измерьте разницу между верхней и нижней частью уклона относительно осей x и y.
2. Если вы можете измерить только изменение по оси x, умножьте это значение на градиент, чтобы найти изменение по оси y.
3. Убедитесь, что единицы измерения для обоих значений одинаковы.
4. Используйте теорему Пифагора, чтобы найти длину склона . Возведите в квадрат как изменение x, так и изменение y.
5. Сложите два значения вместе.
6. Найдите квадратный корень из суммы.
7. Это новое значение представляет собой длину склона.

Что такое наклон 1 из 20?

Уклон 1/20 — это уклон, который увеличивается на 1 единицу за каждые 20 единиц, пройденных по горизонтали . Так, например, пандус длиной 200 футов и высотой 10 футов будет иметь уклон 1/20.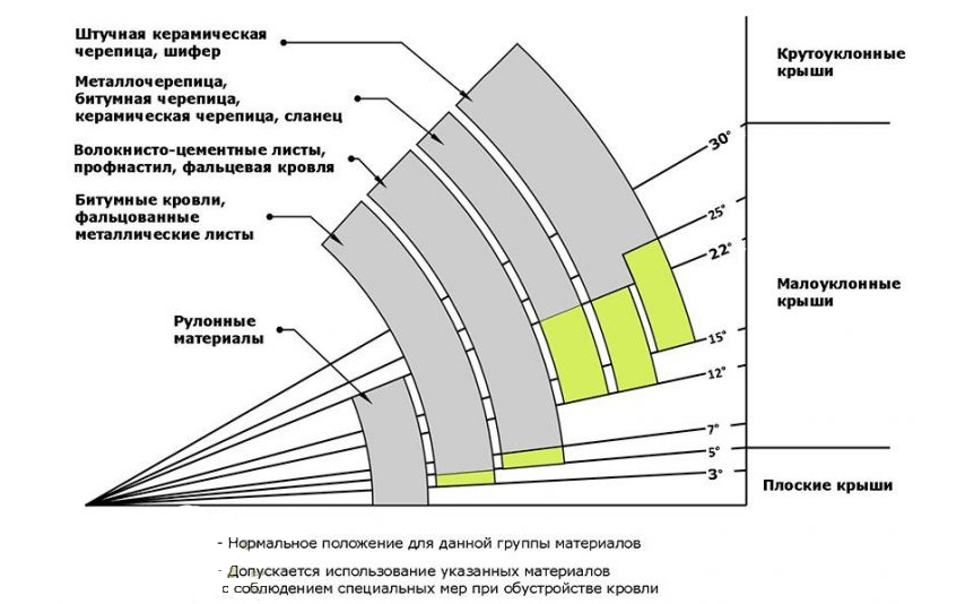 Наклон 1/20 эквивалентен градиенту 1/20 (как ни странно) и образует угол 2,86° между собой и осью x.

Как найти наклон кривой?

Поскольку наклон кривой изменяется в каждой точке, вы можете найти наклон кривой, продифференцировав уравнение по x и в полученном уравнении подставив x вместо точки, в которой вы хотите найти градиент.

Скорость изменения равна наклону?

Скорость изменения графика также является его наклоном , который также совпадает с градиентом. Скорость изменения можно найти, разделив изменение в направлении y (по вертикали) на изменение в направлении по оси x (горизонтально), если, конечно, оба числа выражены в одних и тех же единицах. Скорость изменения особенно полезна, если вы хотите предсказать будущее предыдущего значения чего-либо , так как при изменении переменной x будет присутствовать соответствующее значение y (и наоборот).

Где вы используете уклон в повседневной жизни?

Склоны (или уклоны) имеют множество применений в повседневной жизни . Есть несколько очевидных физических примеров — у каждого холма есть склон, и чем круче холм, тем больше его уклон . Это может быть полезно, если вы смотрите на карту и хотите найти лучший холм для спуска на велосипеде. Вы тоже, наверное, спите под скатом, под крышей . Наклон крыши будет меняться в зависимости от стиля и места вашего проживания. Но, что более важно, если вы когда-нибудь захотите узнать, как что-то меняется со временем, вы в конечном итоге построите график с наклоном .

Что такое уклон 10%?

Уклон 10 % — это наклон, который увеличивается на 1 единицу за каждые 10 единиц, пройденных по горизонтали (10 %). Например, крыша с уклоном 10% и шириной 20 м будет иметь высоту 2 м. Это то же самое, что и градиент 1/10 , и между линией и осью x формируется угол 5,71°.

Как найти площадь под уклоном?

Чтобы найти площадь под уклоном, необходимо проинтегрировать уравнение и вычесть нижнюю границу площади из верхней границы. Для линейных уравнений:

1. Запишите уравнение в виде y = mx + c .
2. Напишите новую строку, в которой вы добавляете 1 к порядку x (например, x становится x ² , х ^2,5 становится х ^3,5 ).
3. Разделите m на новый номер заказа и поставьте его перед новым x.
4. Умножьте c на x и добавьте это в новую строку.
5. Решите эту новую строку дважды, где x — верхняя граница области, которую вы хотите найти, и где x — нижняя граница.
6. Вычесть нижнюю границу из верхней.
7. Поздравьте себя с достижением.

Какой градус наклона 5 к 1?

Наклон 5 к 1 — это уклон, который при каждом увеличении на 5 единиц по горизонтали увеличивается на 1 единицу . Число градусов между наклоном 5 к 1 и осью x составляет 11,3°. Это можно найти, сначала вычислив наклон, разделив изменение в направлении y на изменение в направлении x, а затем найдя арктангенс наклона.

Матеуш Муха и Юлия Жулавиньская

Координаты первой точки

Координаты второй точки

Результат

Наклон (M)

Связанные номера

Y — перехват

Угол (θ)

процент класса

Расстояние (D)

Расстояние между x (Δx)

Расстояние Y (ΔY)

чек. из 38 похожих калькуляторов координатной геометрии 📈

Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… Еще 35

Уравнение точки-наклона прямой

Форма «точка-наклон» уравнения прямой:

у — у ₁ = м(х — х ₁ )

Уравнение полезно, когда мы знаем:

• одна точка на линии: (x ₁ , y ₁ )
• и уклон линии: м ,

и хотите найти другие точки на линии.

Поиграйте с ним (переместите точку, попробуйте разные наклоны):

. ./geometry/images/geom-line-equn.js?mode=pt

Теперь давайте узнаем больше.

Что это означает?

(x ₁ , y ₁ ) — известная точка

м — откос линии

(x, y) — любая другая точка на прямой

.

Понимание этого

Основан на уклоне:

Уклон м = изменение у изменение в х знак равно г − г ₁ х — х ₁

 

Старт с уклоном: переставляем так:   , чтобы получить это:

Так это просто формула наклона по-другому!

Теперь давайте посмотрим, как его использовать.

Пример 1:

Slope «M» = 3 1 = 3

Y — Y ₁ = M (x — x ₁ )

Мы знаем m, а также знаем, что (x ₁ ) x ₁ , y ₁ ) = (3, 2), поэтому мы имеем:

y − 2 = 3(x − 3)

Это отличный ответ, но мы можем его немного упростить. :

у — 2 = 3х — 9

у = 3х — 9 + 2

у = 3х — 7

Пример 2:

м = −3 1 = −3

y − y ₁ = m(x − x ₁ )

Мы можем выбрать любую точку для (x ₁ , y ₁ ), поэтому давайте выберем (0,0), и мы :

y — 0 = -3(x — 0)

Что можно упростить до:

y = -3x

Пример 3: Вертикальная линия

Каково уравнение вертикальной линии?
Наклон не определен!

На самом деле это частный случай , и мы используем другое уравнение, например: х = 1,5

А как насчет y = mx + b ?

Возможно, вы уже знакомы с формой y=mx+b (называемой формой уравнения прямой с наклоном).

Это то же уравнение, только в другой форме!

Значение «b» (называемое точкой пересечения с осью y) находится там, где линия пересекает ось y.