Расчёт снеговой нагрузки | Высотные работы в Киеве
Расчет снеговой нагрузки на кровлю
Самой большой по величине из всех нагрузок, которые должна выдерживать кровля, является снеговая. Она действует в течение всего зимнего сезона, распределена неравномерно и зависит от угла наклона скатов. Расчет снеговой нагрузки выполняют на стадии проектирования, причем это необходимо не только для определения параметров стропильной системы, но и для вычисления суммарного веса здания при выборе типа фундамента.
Влияние снеговой нагрузки на конструкцию крыши
Одна из ключевых особенностей снежного покрова на крыше — переменная масса. Каждый снегопад увеличивает его высоту и, как следствие, общий вес. Когда осадки заканчиваются, часть свежевыпавшего снега падает на землю или сдувается ветром, соответственно, давление на кровлю снижается. Но самое больше влияние на величину снеговой нагрузки оказывают температурные колебания:
- во время оттепели снег набирает много воды и становится тяжелым;
- при похолодании он спрессовывается, а вода превращается в лед.

Таким образом, циклы потепления-оттаивания уплотняют снежную массу, делают ее гораздо более тяжелой. Если свежевыпавший пушистый снежок весит около 100 кг/м³, то к весне слежавшийся обледеневший ком может потянуть уже на 350-400 кг/м³. Съезжая под действием собственного веса, он может повредить не только кровельное покрытие, но и карнизы вместе с водосточной системой.
Чтобы предотвратить разрушение кровли зимой и избавить себя от необходимости чистки крыши от снега, на этапе строительства следует заложить в ее устройство некоторые конструктивные элементы, позволяющие уменьшить давление снежной массы и сделать его более равномерным:
- предусмотреть максимально возможный угол наклона скатов. Чем круче крыша, тем легче с нее сходит снег. Но необходимо иметь в виду, что увеличение уклона повышает ветровую нагрузку и требует больше стройматериалов, т. е. удорожает кровлю. В каждом случае выбор угла наклона — это разумный компромисс между указанными факторами, подтверждаемый расчетами;
- установить снегозадержатели.
 Они разбивают снежный покров на несколько частей и распределяют его по крыше более равномерно. Кроме того, снегозадержатели защищают людей и технику от падения на них больших пластов снега;
Они разбивают снежный покров на несколько частей и распределяют его по крыше более равномерно. Кроме того, снегозадержатели защищают людей и технику от падения на них больших пластов снега; - смонтировать систему подогрева. Она растопит снег и решит проблему в корне. Правда, наличие такой системы не освобождает от учета снеговой нагрузки на крышу при ее проектировании, потому что подогрев может отказать в самый неподходящий момент;
- использовать металлическое кровельное покрытие. Профнастил, металлочерепица, фальцевая кровля имеют скользкую поверхность, по которой снег скатывается намного лучше.
Расчет нагрузки снега на кровлю
Расчет снеговой нагрузки производится по формуле:
S = Sg · μ,
где S — искомая величина, Sg — нормативная нагрузка в регионе строительства, μ — коэффициент, учитывающий влияние угла наклона крыши.
Нормативная снеговая нагрузка определяется по специальной карте снеговых районов, которую выпускает Гидрометцентр.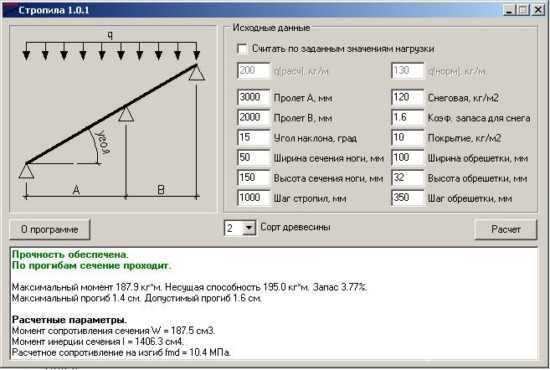 На ней вся территория Украины разделена на 6 регионов, каждому из которых присвоено свое нормативное значение.
На ней вся территория Украины разделена на 6 регионов, каждому из которых присвоено свое нормативное значение.
Посмотреть их можно в следующей таблице.
| № региона | 1 | 2 | 3 | 4 | 5 | 6 |
| Sg, кг/м² | 80 | 100 | 120 | 140 | 160 | 180 |
Коэффициент μ вычисляется следующим образом: μ = 0,033 · (60 — α), где α — угол наклона скатов кровли. Нетрудно заметить, что при α > 60° μ становится отрицательным, т. е. считается, что расчет снеговой нагрузки на кровлю такой крутизны производить не нужно, поскольку снег в любом случае будет сходить сам. На таких крышах главной проблемой является защита от ветра.
Для определения полной нагрузки на кровлю полученное значение необходимо умножить на ее площадь.
Пример расчета
Покажем, как рассчитать снеговую нагрузку на конкретном примере:
- регион строительства — Киев, размеры дома 12 х 8 м;
- двускатная крыша;
- высота чердачного помещения до конька — 4 м.
Последовательность действий будет следующей:
- Определяем угол наклона кровли. Для этого применяем формулу вычисления длины противолежащего катета в треугольнике, образованном высотой крыши в коньке и половиной длины фронтона: tg α = H/l = 4/4 = 1. Следовательно, α = 45°.
- Вычисляем коэффициент μ: μ = 0,033 · (60 — 45) = 0,495.
- Получаем величину снеговой нагрузки S = Sg · μ = 320 · 0,495 = 158,4 кг/м².
- Находим длину ската — применяем теорему Пифагора к рассмотренному выше треугольнику: D = √l² + H² = √32 ≈ 5,66.
- Рассчитываем полную нагрузку на крышу, для чего величину удельной нагрузки умножаем на площадь ската и удваиваем результат (поскольку крыша состоит из двух скатов): P = 158,4 · 5,66 · 12 · 2 = 21 517 кг.
Получается, что крыша такого, в общем-то, небольшого дома будет нести на себе снежную массу почти в 22 тонны. И это еще с учетом довольно большого угла наклона скатов, из-за которого нормативная нагрузка уменьшилась в 2 раза. Приведенный пример наглядно иллюстрирует важность правильного расчета нагрузки на кровлю.
Приведенный пример наглядно иллюстрирует важность правильного расчета нагрузки на кровлю.
Нагрузка на плоскую кровлю
Плоские кровли идеально защищены от ветровых нагрузок, но удерживают на себе практически весь выпавший снег. Поэтому в районах с интенсивными снегопадами их применять не рекомендуется.
Расчет снеговой нагрузки на плоскую кровлю производится в том же порядке, что и на скатную. Поправочный коэффициент μ при этом берется равным 1. Нетрудно подсчитать, что если в приведенном выше примере изменить конструкцию крыши на плоскую, снеговая нагрузка на нее увеличится в два раза и составит почти 43,5 тонны. Вывод однозначен: в Уфе (и не только) дома таких размеров лучше строить со скатными крышами.
Для расчета допустимого сечения стропил необходимо определить полный вес всей крыши. Для этого величину снеговой нагрузки на плоскую кровлю нужно сложить с массой кровельного пирога. Вес каждого его элемента можно взять из справочных таблиц или с сайтов производителей. Обычно для инженерных расчетов берется суммарное значение в 55 кг/м².
Обычно для инженерных расчетов берется суммарное значение в 55 кг/м².
Способы очистки крыши от снега
Учитывая столь значительные величины снеговых нагрузок, особенно в регионах с высокими нормативными показателями, необходимо предпринимать меры по снижению массы снега, находящегося на крыше, прежде всего в период оттепелей и перед его массовым таянием. Основные пути решения проблемы мы уже перечислили в начале статьи. Расскажем теперь подробнее о самых действенных их них.
Наиболее простой способ — почистить крышу. Это можно сделать:
- вручную. Снег передвигается по крыше лопатами, с использованием физической силы людей. Для того чтобы не нанести ущерб кровельному покрытию, следует применять пластиковые или деревянные лопаты и оставлять на поверхности слой снега в 5–10 см. Критической нагрузки он не создаст, но будет хорошей преградой между обувью, лопатами и защитным покрытием кровли;
- с помощью подогрева. Для использования этого метода необходима предварительная укладка специальных кабелей.
 Это сложная инженерная система, для ее установки нужны специальные знания и навыки, но она очень эффективно растапливает снег, поэтому в последнее время применяется все чаще;
Это сложная инженерная система, для ее установки нужны специальные знания и навыки, но она очень эффективно растапливает снег, поэтому в последнее время применяется все чаще; - вибрацией. Преимущество этого способа в том, что работа выполняется с чердака, выходить на крышу необязательно. Но применение вибраторов допустимо только на кровлях с прочной стропильной системой и наиболее эффективно в период оттепелей;
- механическим способом. Большие и плотные пласты обледеневшего снега разрезаются бензопилой и удаляются с крыши. Это довольно трудоемкий способ, поэтому он применяется редко, когда почистить крышу по-другому не получается.
Установка снегозадержателей
Как мы уже говорили, большой объем снега на крыше может не только создать критические нагрузки на конструктивные элементы здания, но и нанести ущерб людям и имуществу, находящимся внизу. Эта опасность значительно возрастает в весенний период и особенно на кровлях с металлическим покрытием. Для того чтобы избежать неприятных последствий, на крышу устанавливают снегозадержатели — специальные металлические конструкции, окрашенные в цвет основного покрытия кровли, задерживающие пласты снега и льда и разбивающие их на части. В результате снег быстрее тает и удаляется с крыши через водосточную систему.
В результате снег быстрее тает и удаляется с крыши через водосточную систему.
Снегозадержатели бывают нескольких видов:
- трубчатые;
- решетчатые;
- уголковые;
- точечные.
Каждый из них рассчитан на конкретную снеговую нагрузку и применяется на определенных типах кровель. Подробнее об отличиях, критериях выбора и особенностях монтажа снегозадержателей можно почитать в отдельной статье.
Расчет снеговой нагрузки на крышу нужно производить независимо от того, в каком регионе вы строите дом, в каком режиме будете его использовать и какой тип крыши предусмотрен проектом. Параллельно рассчитывается ветровая нагрузка и вычисляется вес самой кровельной конструкции. Затем все эти величины складываются и к ним добавляется вес людей, которые могут находиться на крыше при выполнении профилактических работ. Так вычисляется полная нагрузка, на основании которой подбираются основные несущие элементы стропильной системы. Только правильно выполнив все этапы этого расчета, вы можете быть уверены, что ваша крыша сможет противостоять любым природным катаклизмам в течение всего периода своей эксплуатации.
Только правильно выполнив все этапы этого расчета, вы можете быть уверены, что ваша крыша сможет противостоять любым природным катаклизмам в течение всего периода своей эксплуатации.
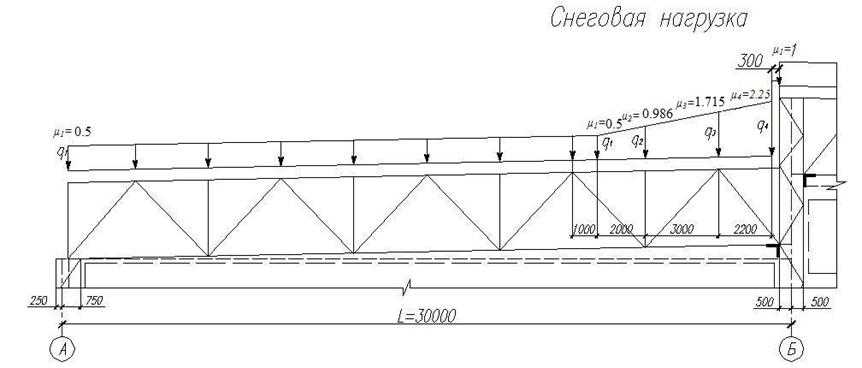
Расчет покрытий, применение снеговой нагрузки на поверхность
Задание снеговой нагрузки на покрытие здания может быть не таким очевидным, как кажется на первый взгляд. Инженеру-расчетчику приходится учитывать снеговой район, снос и таяние снега, а также наличие снеговых мешков, которые образуются из-за криволинейной поверхности покрытия, наличия перепадов высот и парапетов.
В версии ЛИРА 10.10 появился новый тип нагрузок, позволяющий уменьшить затраты по времени для сбора нагрузок на покрытие.
Рисунок 1
Разбираемся в деталях
Ранее мы уже писали в заметке об особенностях произвольной нагрузки.
Снеговая нагрузка на поверхность обладает теми же свойствами, только теперь для построения площади загружения пользователь может вносить исходные данные непосредственно в программу.
Рисунок 2
Для начала в окне необходимо выбрать вид нормативного документа, по которому будет производится расчет.
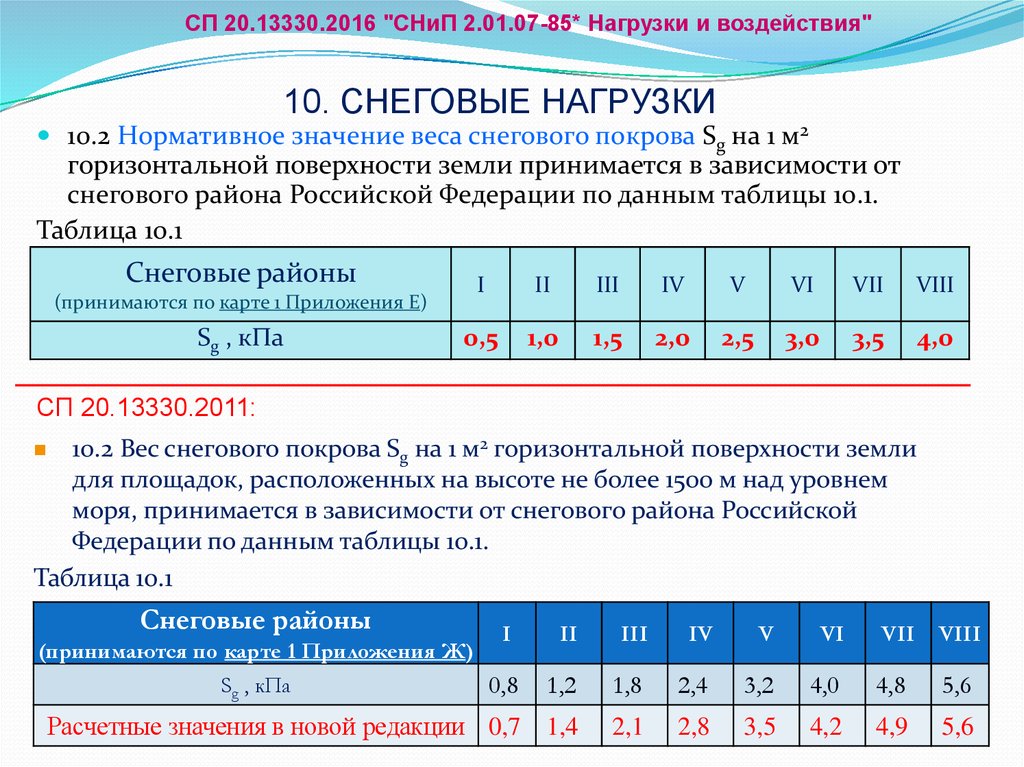
По СП 20.13330.2016 нам доступны коэффициенты:
- Се — учитывающий снос снега с покрытий зданий под действием ветра или иных факторов
- Сt — термический коэффициент
- ɣ — коэффициент надежности по нагрузке (если коэффициент учитывается в загружениях, то ɣ=1)
- μ — коэффициент формы, учитывающий переход от веса снегового покрова земли к снеговой нагрузке на покрытие
Вдоль Х/ Вдоль Y — ось в направлении которой будет изменяться значение μ
Использование в расчетах
Для примера использования новой функции возьмем плоскую кровлю здания, ограждённую парапетом высотой 1.2 м. В одной из части покрытия разместим лестнично-лифтовой узел высотой 2.8 м. Здание расположим в третьем снеговом районе с нормативным значением веса снегового покрова равным 1.5 Мпа
Снеговая нагрузка возле парапета
Рисунок 3.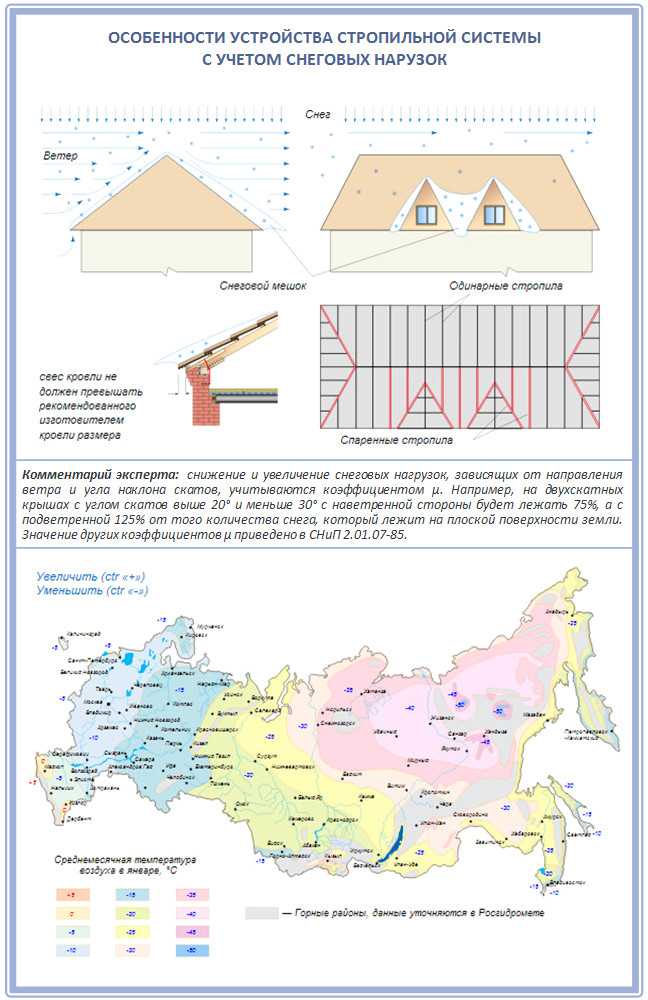 Схема распределения снеговой нагрузки в районе парапета
Схема распределения снеговой нагрузки в районе парапета
Исходные данные:
h=1,2м;
b=2х1,2=2,4м;
µ=2h/S0=2х1,2/1,5=1,6.
Принимаем µ=1,6., b=2.4 м
Снеговая нагрузка возле лестнично-лифтового узла
Рисунок 4. Схема распределения снеговой нагрузки в районе лестнично-лифтового узла
h=4 м, d=8,5 м
µ=2h/S0=2х4/1,5=5,34
µ=2 при 5<d≤10 м
b1=2h=8 м
Принимаем µ=2., b=8 м
Для приложения нагрузки необходимо иметь четыре точки, две из них будут находится в углах архитектурных элементов, две другие можно настроить с помощью сети построения.
Рисунок 5
Точки выделения также появляются на концах нагрузок на поверхность
Рисунок 6
Получаем картину сплошного покрытия снеговой нагрузки с учетом снеговых мешков
Рисунок 7.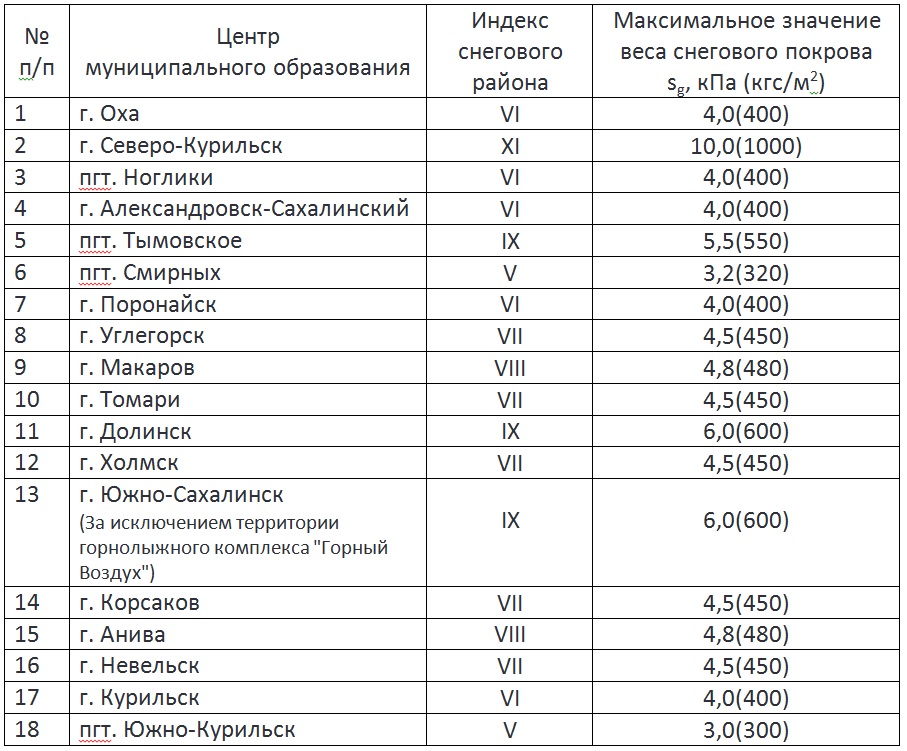 Схема загружения покрытия снеговой нагрузкой
Схема загружения покрытия снеговой нагрузкой
Во вкладке анализ и документирование можно посмотреть полученные значения нагрузок, распределенные на конечные элементы
Рисунок 8. Распределение нагрузки на пластинчатые КЭ
Примечание:
- Данный тип загружения можно прикладывать не только на архитектурные, но и на конечные элементы с последующим расчетом
- Все нагрузки, попадающие в область отверстий, автоматически исключатся из расчета.
Сегодня мы узнали о новом типе нагрузки на расчетную схему в ЛИРА 10.10, которая позволит задать равномерные и переменные снеговые нагрузки в модель, а также избежать дополнительных расчетов.
Склоненные наклоны на крыше Расчеты снежных нагрузок и региональная конструкция
Связанные ресурсы: Анализ
Наклонный наклонной крыша Расчеты снежных нагрузок и региональный дизайн
Инженерный анализ
Поверхность крыши :
Снеж. считается действующим на горизонтальную проекцию этой поверхности. Снеговая нагрузка на скатную крышу, p s , должна быть получена путем умножения снеговой нагрузки на плоскую крышу, p f , по коэффициенту уклона крыши, C s :
считается действующим на горизонтальную проекцию этой поверхности. Снеговая нагрузка на скатную крышу, p s , должна быть получена путем умножения снеговой нагрузки на плоскую крышу, p f , по коэффициенту уклона крыши, C s :
p s = C s p f
Тепловой коэффициент, C s определить по таблице E-9013 бывает «холодным» или «теплым». Значения «скользкой поверхности» следует использовать только в том случае, если поверхность крыши свободна и под карнизом имеется достаточно места для приема всего сползающего снега. Крыша считается свободной, если на ней нет предметов, препятствующих скольжению по ней снега. К скользким поверхностям относятся металлические, сланцевые, стеклянные, а также битумные, резиновые и пластиковые покрытия с гладкой поверхностью. Мембраны со встроенным заполнителем или поверхностью минеральных гранул не должны считаться гладкими. Асфальтовая черепица, деревянная черепица и щебень не считаются скользкими.
Коэффициент уклона теплой крыши , C s .
Для теплых крыш (C t ≤ 1,0, как определено по таблице E-3) с беспрепятственной скользкой поверхностью, позволяющей снегу соскальзывать с карниза, коэффициент уклона крыши C s определяется с помощью пунктирной линии на рис. Д-2а, при условии, что для невентилируемых теплых крыш их термическое сопротивление (значение R) равно или превышает 30 ft 2 ч ◦F/Btu (5,3 ◦C м 2 /Вт), а для теплых вентилируемых крыш, их R-значение равно или превышает 20 футов 2 ч ◦F/Btu (3,5 ◦Cm 2 /Вт). Наружный воздух должен иметь возможность свободно циркулировать под вентилируемой крышей от ее карниза до конька. Для теплых крыш, не отвечающих вышеуказанным условиям, сплошная линия на рис. Д-2а должна использоваться для определения коэффициента уклона крыши C s .
Коэффициент уклона холодной крыши , C s .
Холодные крыши – это крыши с C t > 1,0, как определено по Таблице E-3. Для холодных крыш с C t = 1,1 и беспрепятственной скользкой поверхности, которая позволит снегу соскальзывать с карниза, коэффициент уклона крыши Cs должен определяться с помощью пунктирной линии на рис. E-2b. Для всех других холодных крыш с C t = 1,1 сплошная линия на рис. E-2b должна использоваться для определения коэффициента уклона крыши C
Коэффициент уклона для изогнутых крыш.
Участки изогнутых крыш с уклоном более 70° считаются свободными от снеговой нагрузки (т.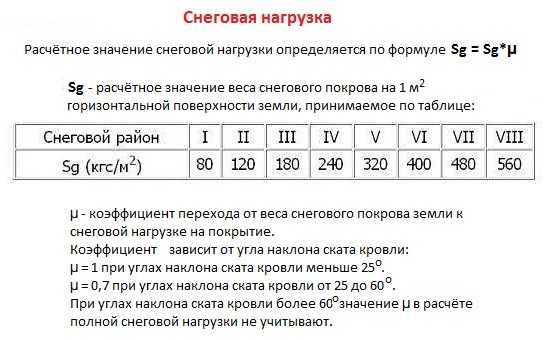 е. C s = 0). Сбалансированные нагрузки должны быть определены по диаграммам сбалансированных нагрузок на рис. E-3 с C s , определенным по соответствующей кривой на рис. E-2.
е. C s = 0). Сбалансированные нагрузки должны быть определены по диаграммам сбалансированных нагрузок на рис. E-3 с C s , определенным по соответствующей кривой на рис. E-2.
Коэффициент уклона крыши для многослойных фальцевых, пилообразных и сводчатых крыш
.Крыши из нескольких фальцевых, пилообразных или бочкообразных сводов должны иметь C s = 1,0 без уменьшения снеговой нагрузки из-за уклона (т. е. p s = p f ).
Ледяные запруды и сосульки вдоль карнизов.
Два типа теплых крыш, которые отводят воду через карниз, должны выдерживать равномерно распределенную нагрузку 2p f на все выступающие части: те, которые не вентилируются и имеют значение R менее 30 футов 2 ч ◦F/БТЕ (5,3 ◦C м 2 /Вт) и те, которые вентилируются и имеют значение R менее 20 футов 2 ч ◦F/БТЕ (3,5 ◦См 2 / Вт). При приложении этой равномерно распределенной нагрузки на крышу не должны воздействовать никакие другие нагрузки, кроме статических.
См. Символы и обозначения, используемые в расчетных данных по снеговым нагрузкам, для получения информации о символах
Рисунок E-2
Рисунок E-30005
Родственные
- Программа анализа снеговой нагрузки согласно ASCE702S
- Калькулятор анализа снеговой нагрузки в соответствии со стандартом ASCE798S
- Расчеты снеговых нагрузок на наклонную крышу и региональное проектирование
- Снеговая нагрузка на плоскую крышу Снеговая нагрузка на плоскую крышу
- Символы и обозначения, используемые в расчетных данных по снеговым нагрузкам
- Формулы гражданского строительства
- Калькуляторы строительных и проектных данных
Как рассчитать снеговую нагрузку скатной крыши
В этом сообщении блога мы покажем, как рассчитывается характеристическая снеговая нагрузка скатной крыши в соответствии с Еврокодом.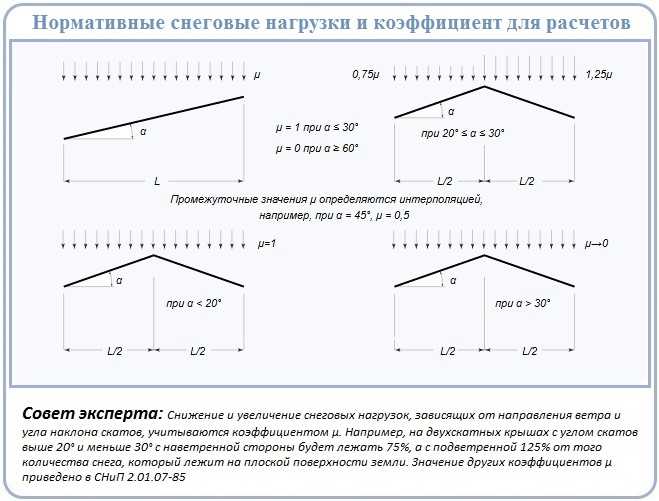 Скатные крыши представляют собой, например, прогонные, стропильные или балочные крыши.
Скатные крыши представляют собой, например, прогонные, стропильные или балочные крыши.
Расчет снеговой нагрузки для скатной крыши немного сложнее, чем для плоской крыши, но нам нужно всего лишь выполнить 6 шагов .
- Сначала нужно найти коэффициент формы снеговой нагрузки $\mu_{1}$
- Затем коэффициент экспозиции $C_{e}$
- Тепловой коэффициент $C_{t}$
- Характеристическое значение снеговой нагрузки на землю $s_{k}$
- Значение снеговой нагрузки на крышу
- На последнем шаге мы должны создать 3 варианта с различной нагрузкой соображения о левом и правом шаге.
Снеговая нагрузка на крыши
Постоянная/кратковременная расчетная ситуация EN 1991-1-3 (5.1) используется для расчета характеристической снеговой нагрузки:
$s = \mu_{i } * C_{e} * C_{t} * s_{k} $
Где
$\mu_{i}$ представляет собой коэффициент формы снеговой нагрузки,
$C_{e}$ представляет собой коэффициент воздействия,
$C_{t}$ представляет собой тепловой коэффициент, а
$s_{k}$ представляет собой характеристическое значение снеговой нагрузки на грунт
Рассмотрим подробнее, как мы получаем эти параметры.
Коэффициент формы снеговой нагрузки $\mu_{1}$
Прогонная крыша, которую мы рассматриваем в этом примере, считается скатной крышей.
При увеличении угла наклона кровли более 30° коэффициент формы снеговой нагрузки $\mu_{1}$ может быть снижен ниже 0,8 за счет сползания снега с кровли.
Значение для $\mu_{1}$ указано в таблице 5.2 стандарта EN 1991-1-3. Для $\alpha$ = 40, что означает, что уклон крыши равен 40°, получаем:
$\mu_{1} = 0,8 * (60 – \alpha)/30 $
$\mu_{1} = 0,8 * (60 – 40)/30 = 0,53 $
Угол наклона 40° уменьшает $\mu_{1}$, следовательно, на $ \frac{0,533-0,8}{0,8}*100 = -33,4%$
Экспозиция коэффициент $C_{e}$
EN 1991-1-3 5.2 (7) рекомендует принимать $C_{e}$ равным 1,0. Однако это значение зависит от топографии местности. EN 1991-1-3 В таблице 5.1 топография классифицируется как продуваемая ветрами, нормальная и защищенная с различными значениями $C_{e}$. В этом сообщении блога мы предполагаем нормальную топографию для нашего проекта.
Эта нагрузка теперь приложена вертикально к скатной крыше.
По сравнению с постоянной нагрузкой снеговая нагрузка не следует наклону стропила.
Но поскольку крыша скатная, нам необходимо рассмотреть 3 различных случая из-за расположения смещенной нагрузки (EN 1991-1-3 5.3.3 (3) + (4)).
Вариант 1: s = 0,53 кН/м2 применяется ко всей площади
Снеговая нагрузка 3D вариант 1Преобразовав в 2d статическую систему, мы рассчитываем линейную нагрузку (кН/м) из нагрузки на площадь (кН/м2 ) путем умножения площади нагрузки на шаг стропил = 0,8м. 92} * 0,8м = 0,42 \frac{кН}{м}$
Снеговая нагрузка 2D Вариант 1Преобразование в 2d статическую систему, мы вычисляем s/2 как {m}$
Снеговая нагрузка 2D, вариант 2Вариант 3: s/2 = 0,27 кН/м2 применяется на левом склоне и s = 0,53 кН/м2 на правом склоне
Снеговая нагрузка 3D, случай 3Снеговая нагрузка, 2D вариант 3 Эти 3 загружения необходимо учитывать отдельно при расчете сочетаний нагрузок.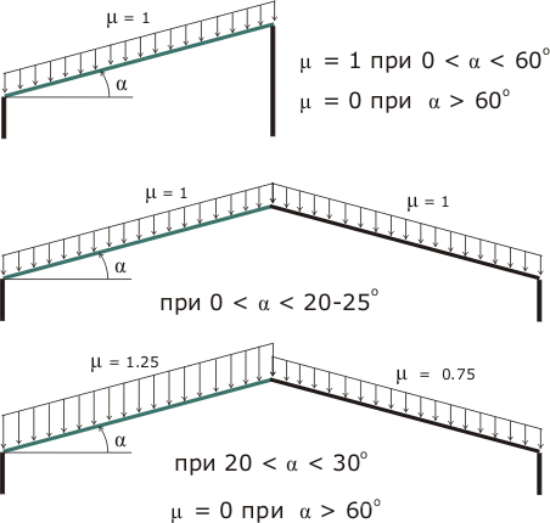
Это означает, что каждое сочетание нагрузки, включающее снеговую нагрузку, должно выполняться 3 раза для 3 разных случаев.
Я знаю, это трудно понять словами, давайте рассмотрим пример.
Мы выбираем LC8 из нашей статьи о сочетаниях нагрузок из сочетаний ULS.
| LC8 | $\gamma_{g} * g_{k} + \gamma_{q} * s_{k} $ |
LC8 необходимо выполнить 3 раза, теперь это приводит к
| LC8-1 | $\gamma_{g} * g_{k} + \gamma_{q} * s_{k.case1} $ |
| LC8-2 | $\gamma_{g} * g_{k} + \gamma_{q} * s_{k.case2} $ |
| LC8-3 | $\gamma_{g} * g_{k} + \gamma_{q} * s_{k.case3} $ |
Мы предполагаем следующие значения параметров. Прочтите статью, если хотите узнать, почему.
| $\gamma_{g}$ | 1.35 |
| $\gamma_{q}$ | 1.5 |
| $g_{k}$ | 0.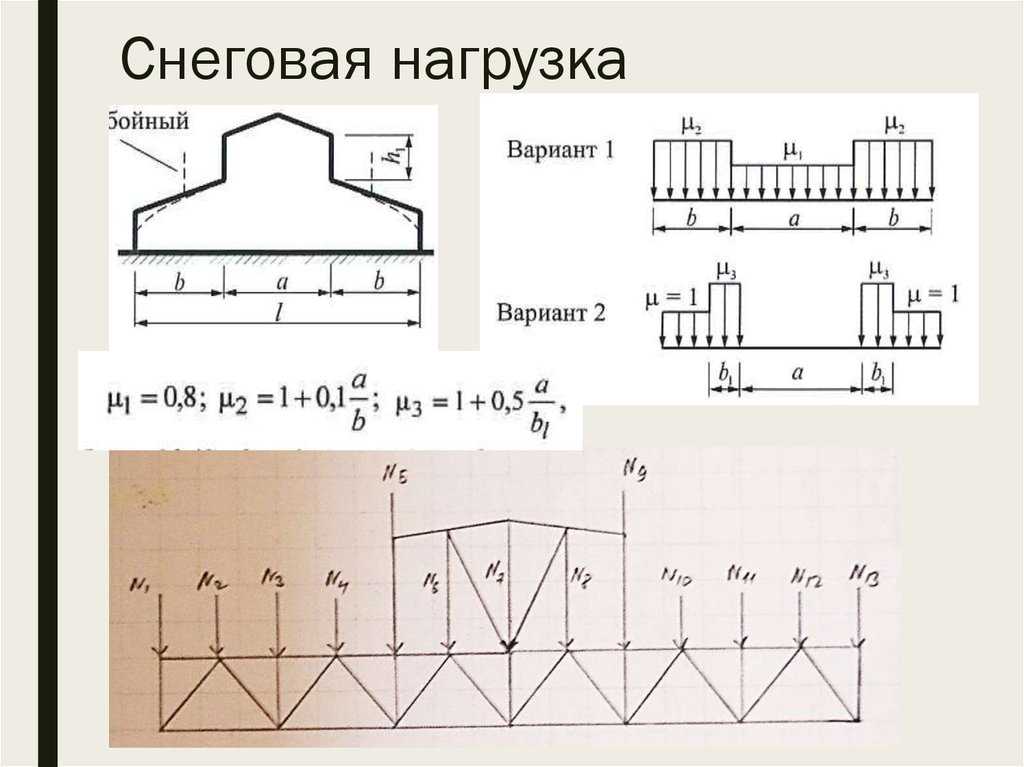 Навигация по записям |

