Расчет секций: Как рассчитать радиаторы отопления

Содержание

Точный расчет количества радиаторов (секций) отопления

Можно провести расчет радиаторов отопления по площади, с помощью калькулятора, размещенного на каком-либо сайте. Но данные не будут точными. Калькуляторов (программ) расчета секций радиаторов отопления много, но точную информацию можно получить только в том случае, если провести расчет вручную индивидуально для каждого помещения.

Упрощенные варианты расчета радиаторов отопления в доме

Первый способ: Расчет по объему комнат

Он прописан в положениях СНиП и применим для панельных домов, Правила предлагают в качестве нормы взять 41 Вт мощности отопления на один кубический метр отапливаемого помещения. Чтобы рассчитать количество необходимых секций достаточно объем комнаты разделить на мощность одной секции устанавливаемых радиаторов (этот параметр указывается производителем в сопроводительной технической документации).

Второй способ: Расчет по площади помещений

Данный способ расчета ориентирован на помещения с потолками до 2500 мм, и за норму берется 100 Вт мощности на один квадрат площади.

Для расчёта количества секций необходимо разделить площадь помещения на мощность одной секции (указывается в технической документации радиаторов).

Примерный расчет количества секций радиатора для типового помещения

N=S/P*100, где:

N — Количество секций (дробная часть округляется по правилам математического округления))
S — Площадь комнаты в м²
P — Теплоотдача 1 секции, Ватт

Для этих вариантов расчета применим ряд поправок. Например, если в помещении имеется балкон, или более двух окон, или оно находится на углу здания, то к полученному количеству секций рекомендуется приплюсовать еще 20%. Если при расчете получается конечный результат (количество секций) дробное число, то его следует округлять до целого в большую сторону.

Обратите внимание:

полученное значение рассчитано для идеальных условий.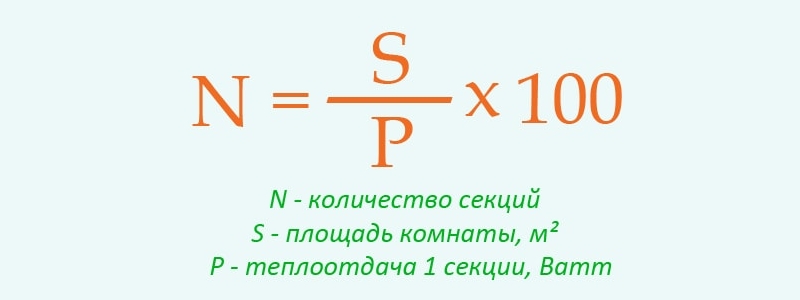 То есть, в доме нет дополнительных теплопотерь, сама система отопления работает эффективно, окна и двери герметично закрываются, а соседние помещения также отапливаются. В реальных условиях секций может потребоваться больше.

Точный расчет необходимого количества секций радиаторов

Выше приведены упрощенные способы расчета радиаторов, которые актуальны для типовых квартир со стандартными параметрами. С их помощью получить адекватный результат для частных жилых домов и квартир в современных новостройках нереально. Для этого следует использовать специальную формулу:
КТ = 100Вт/м2 * S * К1 * К2 * К3 * К4 * К5 * К6 * К7,

Где за основу также берется норма в 100 Вт на квадратный метр, общая площадь помещения и дополняется коэффициентами, значения которых приведены ниже:

K1 — коэффициент, учитывающий остекление оконных проемов:

для окон с обычным двойным остеклением: 1. 27;
для окон с двойным стеклопакетом: 1.0;
для окон с тройным стеклопакетом: 0.85;

K2 — коэффициент теплоизоляции стен:

низкая степень теплоизоляции: 1.27;
хорошая теплоизоляция (кладка в два крипича или слой утеплителя): 1.0;
высокая степень теплоизоляции: 0.85;

K3 — соотношение площади окон и пола в помещении:

50%: 1.2;
40%: 1.1;
30%: 1.0;
20%: 0.9;
10%: 0.8;

K4 — коэффициент, позволяющий учесть среднюю температуру воздуха в самую холодную неделю года:

для -35°C: 1.5;
для -25°C: 1.3;
для -20°C: 1.1;
для -15°C: 0.9;
для -10°C: 0.7;

K5 — корректирует потребность в тепле с учетом количества наружных стен:

одна стена: 1. 1;
две стены: 1.2;
три стены: 1.3;
четыре стены: 1.4;

K6 — учет типа помещения, которое расположено выше:

холодный чердак: 1.0;
отапливаемый чердак: 1.0;
отапливаемое жилое помещение: 1.0;

K7 — коэффициент, учитывающий высоту потолков:

при 2.5 м: 1.0;
при 3.0 м: 1.05;
при 3.5 м: 1.1;
при 4.0 м: 1.15;
при 4.5 м: 1.2;

По этой формуле вы сможете рассчитать общее количества тепла, необходимого для того или иного помещения. Для определения количества секций радиаторов, вам необходимо полученный результат разделить на мощность одной секции.

Расчет количества секций биметаллического радиатора

Выбирая радиатор отопления очень важно сразу правильно рассчитать необходимое количество секций. Это создаст в помещении полный комфорт и не нужно будет вносить изменения в систему обогрева.

Выбор приборов отопления достаточно большой, и каждый найдет среди устройств те, которые соответствуют параметрам помещения.

Почему именно биметаллические батареи

Многие потребители ищут формулу, как рассчитать количество секций биметаллического радиатора. Спрос на модели из биметалла достаточно высокий, на это есть немало причин:

Универсальность. Модели из биметалла подходят для частных домов, квартир в многоэтажных домах, коммерческих объектов. Они выдерживают любую нагрузку и отличаются надежностью.
Устойчивость к коррозии.
Превосходная работа на любом теплоносителе.
Стильный минималистичный дизайн. Такие батареи гармонируют с любыми интерьерами.
Большой выбор конструкций. Есть возможность купить цельную батарею или приобрести определенное количество секций.
Хорошая теплоотдача.

Все преимущества таких радиаторов перечислить сразу сложно – это займет немало времени. Основные достоинства биметаллических батарей: надежность, высокое качество, универсальность.

Базовый расчет

Покупая секции поштучно, можно собрать конструкцию нужной мощности. Такая батарея будет полностью отвечать потребностям объекта. Существует базовая формула для расчета нужного количества секций, она применяется в 90% случаев. Именно по ней часто подбирают радиаторы для квартир, частных домов, офисов.

Формула выглядит так:

W = 100 * S / P

В этом расчете S является площадью помещения, а P – мощностью отдельно взятой секции. Число 100 остается неизменным, это количество Вт на 1 м² площади территории. W – это число секций. Мощность отдельной секции зависит от особенностей конфигурации и составляет 100-200 Вт. Эту информацию надо уточнять в документации к радиатору.

При расчете вычисления производятся последовательно: сначала умножение площади помещения на 100, потом – деление на мощность одной секции. Полученный результат округляется, обычно округление производится в большую сторону, чтобы в помещении было комфортно даже при резком падении температуры.

Эта формула имеет несколько нюансов, поэтому ее нельзя применять везде. Например, подразумевается, что в средней квартире высота потолка не превышает 3 м. Формула работает, если высота потолков в жилище – от 2,2 до 3,0 м. На объектах, которые отличаются по параметрам, требуется другой расчет. Также указанная формула грешит неточностями – она довольно приблизительная. Чтобы вычислить точно необходимое количество тепла, нужно принять во внимание еще множество параметров.

Устанавливая секции в квартире, частном доме, офисе, рекомендуется использовать несколько батарей. Например, если для отопления требуется 18 секций, то лучше поставить 2 радиатора по 9 секций или три по 6.

Формула для расчета по объему

Как рассчитать количество секций биметаллического радиатора, если высота потолков довольно большая? Для таких случаев придумана специальная формула. Если на объекте потолки выше 2,6 м, можно использовать следующий вид расчетов:

S * H * 41 / P

Батарея подбирается с учетом произведения площади помещения на высоту (S*H). Далее полученное число делится на число 41, если речь идет о панельном доме. Для дома из кирпича можно использовать число 38 – именно сколько Вт нужно на обогрев 1 м3 в доме из более теплого материала. Число P – это мощность секции радиатора.

Если в помещении установлены герметичные пластиковые стеклопакеты, то можно вместо 41 и 38 Вт использовать 34 Вт. Однако этот параметр весьма условный, лучше проконсультироваться со специалистом.

Когда нужна повышенная точность

Для экономии тепла и максимального комфорта требуется повышенная точность при расчетах. Здесь можно применять формулу:

100 * S * ((K1 + K2 + K3 + K4 + K5 + K6 + K7)/7) / P

Число 100 отражает необходимое количество Вт на 1 м² помещения. Здесь не идет речь о промышленных площадках, которые требуют расчета тепла на 1 м³, но высота потолков отражена в коэффициенте. S – это площадь объекта, для которого производится расчет. Далее учитывается множество различных коэффициентов:

поправка на остекление;
поправка на теплоизоляцию стен на объекте;
соотношение точность площади стеклопакетов к площади пола в квартире, офисе;
учет самой холодной температуры;

количество наружных стен;
учет типа помещения;
высота потолка.

Число 7, вынесенное за скобки, обозначает количество коэффициентов, которые были перечислены выше. Вместо P надо вставить значение мощности одной секции. С учетом коэффициентов обычно получается больше секций, чем без дополнительных данных. Зная значение поправок, можно выбрать оптимальный радиатор отопления.

Остекление и теплоизоляция

При проведении точных расчетов по формуле учитываю поправку на остекление теплоизоляцию стен. Если на объекте установлено обычно двойное стекло, то значение поправки будет 1,27. При герметичном двойном стеклопакете параметр К1 равен 1,0. Если установлен тройной герметичный стеклопакет, то К1 равен 0,85. При увеличении количества стекол в стеклопакете параметр снижают на 0,25 пунктов.

Теплоизоляция стен тоже имеет значение, она отражена в коэффициенте К2. При стандартной теплоизоляции помещение плохо защищено от холода, в этом случае параметр составляет 1,27. Улучшенная теплоизоляция в квартире или доме позволяет использовать коэффициент 1,0. Если использована отличная изоляция, то К2 составит 0,85.

Еще один важный пункт – К3. В нем отражено соотношение площади окон к площади пола. Известно, что стекло лучше пропускает холод, чем стена. В квартирах и офисах с большими окнами требуется более мощный обогрев. Когда площадь окон составляет около 40% от площади пола, можно использовать коэффициент 1,1. Далее при снижении площади на каждые 10% параметр уменьшается на 0,1%.

Температура, тип помещения, высота потолков

При выборе радиатора для дома или офиса было бы ошибкой не учитывать климатическую зону, а точнее – наиболее низкую температуру в самый холодный месяц. Если температура опускается до -35, надо использовать коэффициент 1,5. При повышении температуры на 5 градусов параметр К4 можно уменьшать на 0,2. Если температура падает, то коэффициент, наоборот, увеличивается на 0,2.

Также принимается в расчет тип помещения, в котором используется батарея. Если это отапливаемое жилое помещение, то используется параметр 0,8. Коэффициент К6 для неотапливаемых чердаков – 1,0.

К5 обозначает количество наружных стен. Чем больше стен, тем больше «мостиков холода». Если это только одна наружная стенка, то применяется коэффициент 1,1, если четыре – то уже 1,4. Важно обязательно учитывать этот нюанс, чтобы в помещении не было холодно.

Имеет значение и высота потолков в квартире, офисе. Для объектов с высотой потолков 2,5 м используется параметр 1,0. При увеличении высоты на 5 метров коэффициент растет на 0,05. Этого достаточно, чтобы можно было обогреть территорию. Высота потолков прописывается в параметре К7. При расчетах надо обязательно учесть мощность секции радиатора – она может быть разной.

Также можно просто доверить расчет специалистам – они точно не ошибутся и подберут оптимальный по мощности радиатор.

Расчет количества секций радиаторов отопления на 1 кв.м

При планировании капитального ремонта в вашем доме или же квартире, а так же при планировке постройки нового дома необходимо произвести расчет мощности радиаторов отопления. Это позволит вам определить количество радиаторов, способных обеспечить теплом ваш дом в самые лютые морозы. Для проведения расчетов необходимо узнать необходимые параметры, такие как размер помещений и мощность радиатора, заявленной производителем в прилагаемой технической документации. Форма радиатора, материал из которого он выполнен, и уровень теплоотдачи в данных расчетах не учитываются. Зачастую количество радиаторов равно количеству оконных проемов в помещении, поэтому, рассчитываемая мощность разделяется на общее количество оконных проемов, так можно определить величину одного радиатора.

Следует помнить, что не нужно производить расчет для всей квартиры, ведь каждая комната имеет свою отопительную систему и требует к себе индивидуальный подход. Так если у вас угловая комната, то к полученной величине мощности необходимо прибавить еще около двадцати процентов. Такое же количество нужно прибавить, если ваша система отопления работает с перебоями или имеет другие недостатки эффективности.

Расчет мощности радиаторов отопления может осуществляться тремя способами:

Стандартный расчет радиаторов отопления

Согласно строительным нормами и другими правилами необходимо затрачивать 100Вт мощности вашего радиатора на 1метр квадратный жилплощади. В таком случае необходимые расчеты производятся при использовании формулы:

С*100/Р=К, где

К— мощность одной секции вашей радиаторной батареи, согласно заявленной в ее характеристике;

С— площадь помещения. Она равна произведению длины комнаты на ее ширину.

К примеру, комната имеет 4 метра в длину и 3.5 в ширину. В таком случае ее площадь равна:4*3.5=14 метров квадратных.

Мощность, выбранной вами одной секции батареи заявлена производителем в 160 Вт. Получаем:

14*100/160=8.75. полученную цифру необходимо округлить и получается что для такого помещения потребуется 9 секций радиатора отопления. Если же это угловая комната, то 9*1. 2=10.8, округляется до 11. А если ваша система теплоснабжения недостаточно эффективна, то еще раз добавляем 20 процентов от первоначального числа: 9*20/100=1.8 округляется до 2.

Итого: 11+2=13. Для угловой комнаты площадью 14 метров квадратных, если система отопления работает с кратковременными перебоями понадобиться приобрести 13 секций батарей.

Примерный расчет — сколько секций батареи на квадратный метр

Он базируется на том, что радиаторы отопления при серийном производстве имеют определенные размеры. Если помещение имеет высоту потолка равную 2.5 метра, то на площадь в 1.8 метров квадратных потребуется лишь одна секция радиатора.

Подсчет количества секций радиатора для комнаты с площадью в 14 метров квадратных равен:

14/1.8=7.8, округляется до 8. Так для помещения с высотой до потолка в 2.5м понадобится восемь секций радиатора. Следует учитывать, что этот способ не подходит, если у отопительного прибора малая мощность (менее 60Вт) ввиду большой погрешности.

Объемный или для нестандартных помещений

Такой расчет применяется для помещений с высокими или очень низкими потолками. Здесь расчет ведется из данных о том, что для обогрева одного метра кубического помещения необходима мощность в 41ВТ. Для этого применяется формула:

К=О*41, где:

К- необходимое количество секций радиатора,

О-объем помещения, он равен произведению высоты на ширину и на длину комнаты.

Если комната имеет высоту-3.0м; длину – 4.0м и ширину – 3.5м, то объем помещения равен:

3.0*4.0*3.5=42 метра кубических.

Расчитывается общая потребность в тепловой энергии данной комнаты:

42*41=1722Вт, учитывая, сто мощность одной секции составляет 160Вт,можно расчитать необходимое их количество путем деления общей потребности в мощности на мощность одной секции: 1722/160=10. 8, округляется до 11 секций.

Если выбраны радиаторы, которые не делятся на секции, от общее число нужно поделить на мощность одного радиатора.

Округлять полученные данные лучше в большую сторону, так как производители иногда завышают заявленную мощность.

Расчет количества секций биметаллического радиатора – сколько нужно ребер

Секрет популярности биметаллических радиаторов заключается в том, что по своей эффективности они не уступают традиционным чугунным батареям, однако при этом они имеют лучшие технико-эксплуатационные характеристики. К числу неоспоримых преимуществ относят:

Высокий коэффициент теплоотдачи.
Продолжительный срок службы, составляющий более 20 лет.
Стильный и аккуратный внешний вид.
Сравнительно небольшой вес, что существенно упрощает установочные работы.
Наличие ниппелей, обеспечивающих возможность соединять секции, благодаря чему радиатор можно «нарастить».

Отметим, что зачастую необходимость в наращивании возникает, например, если при покупке был выбран прибор с неподходящим числом секций или по другим причинам. Чтобы изначально не ошибиться в подборе оптимальной модели, нужно знать, как выполнить расчет радиаторов отопления биметаллических, то есть оптимального числа секций. Кстати, сделать это можно самостоятельно, не прибегая к помощи профессионалов, при этом для расчета используются различные методики.

Почему нужно делать расчет, а не выбирать радиатор «на глаз»?

Обратите внимание: зачастую при покупке биметаллического прибора некоторые ориентируются на то, сколько секций было в прежде эксплуатируемых чугунных батареях. Такой подход в корне неверный.

Теплоотдача секции биметаллического прибора значительно выше, чем чугунного, поэтому количество ребер будет разным. А в частности, тепловая мощность одной секции чугунного радиатора составляет в среднем от 80 до 160 Ватт, а для биметаллического этот параметр соответствует примерно 200 Ватт.

Некоторые решают выполнить расчет количества секций «на глаз», например, если в чугунной батарее их было 9, то выбрать биметаллический радиатор с 6 секциями. Но в конечном итоге вероятность «угадать» крайне мала, и получается, что после установки нового прибора в помещении либо очень холодно, либо наоборот — слишком жарко. Именно поэтому правильнее изначально сделать точный расчет биметаллических радиаторов. К счастью, современные производители выпускают устройства с различным числом секций и не составляет сложности подобрать модель для помещения фактически с любыми планировочными особенностями.

Выполнить корректный расчет количества биметаллических радиаторов и секций не так уж сложно, но для этого нужно знать технические характеристики помещения, в котором планируется установка. А в частности, потребуются следующие значения: фактическая площадь помещения и объем отапливаемой комнаты. Далее выбираем, как именно (т.е. по какой методике) будет удобнее всего рассчитать количество секций биметаллического радиатора.

Определение по площади комнаты

Проще всего выполнить расчет биметаллических радиаторов отопления по площади, но в этом случае нужно, чтобы высота потолка была около 2,5 метров. В соответствии со СНиП, нагрузка на один метр составляет 100 Ватт — такой норматив установлен для средней полосы РФ. Отметим, что в регионах Крайнего Севера это значение гораздо больше.

В «стандартном» случае необходимо умножить площадь комнаты на 100, в результате чего мы получим мощность нормативного потребления тепла. После делим полученное значение на паспортную теплоотдачу одной секции биметаллического радиатора (она указывается в техническом описании или паспорте на прибор) — итоговая цифра показывает, сколько секций биметаллического радиатора нужно.

Расчет по объему

Расчет оптимальных параметров биметаллических радиаторов для помещений с высотой потолков более 2,6 метра осуществляется по объему. В соответствии с установленными нормами, для отопления одного кубического метра необходимо:

41 Ватт, если помещение находится в многоквартирном панельном доме.
34 Ватта, если помещение находится в кирпичном доме.

Определение нужного количества секций биметаллического радиатора выполняется по следующей схеме:

Определяем расчетный объем в кубических метрах. Для этого умножаем высоту комнаты на ее площадь.
Умножаем полученное значение на норматив теплопотребления (то есть на 34 или 41 Ватт), так мы получим мощность нормативного потребления тепла.
Итоговое значение делим на паспортную теплоотдачу одного ребра биметаллического радиатора (берем значение из технического описания или паспорта на изделие) — так удалось узнать, сколько секций нужно.

Альтернативные методы расчета

Существует и еще одна методика расчета секций биметаллических радиаторов, которая очень проста, но дает лишь приблизительный результат. Чаще всего ее используют сантехники, когда им предстоит выполнить расчет множества приборов, имеющих высокую суммарную мощность.

Считается, что в квартире со стандартной высотой потолков, расположенной в средней полосе России, одна секция биметаллического радиатора, имеющая среднюю мощность, способна обеспечивать теплом 1,8 кв. метров площади. Таким образом, для определения нужного количества секций биметаллического радиатора остается лишь поделить площадь комнаты на 1,8.

Наиболее точная методика расчета числа секций с учетом поправочных коэффициентов

Конечно, такая методика расчета привлекает своей простотой, но рассчитывать на ее точность не приходится. Если вы хотите получить более достоверные значения, то придется учесть множество сторонних факторов, в том числе касающихся:

Состояния остекления.
Количества наружных стен.
Качества теплоизоляции наружных стен.
Климатических характеристик региона и проч.

Рекомендуем, если вы покупаете радиаторы биметаллические, расчет секций выполнить именно по формуле с поправочными коэффициентами, так как полученное значение будет максимально точным. Итоговая формула в данном случае выглядит следующим образом: нормативное значение тепла (то есть 100 Ватт/кв.м) необходимо умножить на все поправочные коэффициенты, определяющие особенности теплопотребления комнаты.

Описание и расшифровка поправочных коэффициентов

Поправочные коэффициенты:

К1 — он учитывает конструкцию остекления в помещении. Для двойных деревянных рам этот коэффициент соответствует 1,27, для двойных пластиковых стеклопакетов — 1,0, а для тройных — 0,85.
К2 — определяет качество утепления стен. Если стены дома созданы из кирпича, то этот коэффициент принимают за 1, во всех остальных случаях — 1,27. Кстати, наличие дополнительной теплоизоляции стен дает возможность использовать понижающий коэффициент 0,85.
К3 — отражает отношение площади окон к полу. В числителе ставится процент остекления, присутствующий в помещении, а в знаменателе — коэффициент теплопотребления (то есть 50/0,8; 40/0,9; 30/1,0; 20/1,1; 10/1,2).
K4 — коэффициент, учитывающий среднюю температуру в самую холодную неделю года. Если это значение соответствует -35 градусам по Цельсию, то К4=1,5, при -25 — 1,3, при -20 — 1,1, при -15 — 0,9, а при -10 — 0,7.
К5 — учитывает число наружных стен. При наличии одной наружной стены в помещении он соответствует 1,1, а каждая последующая увеличивает это значение на 0,1.
К6 — необходим для учета влияния теплового режима помещения, находящегося на этаж выше. Если там расположен холодный чердак, то К6 принимают на 1, если отапливаемый, то за 0,6, если жилое помещение — 0,8.
К7 — коэффициент, с помощью которого выражается зависимость от высоты потолков. При стандартном значении 2,5 метра он принимается равным 1. Повышение этого значения на 0,5 метра делает К7 больше на 0,05, при 3 метрах — 1,05, при 3,5 метрах — 1,1, при 4,0 метрах — 1,15, а при 4,5 метрах — 1,2.

Как показывает практика, очень большое значение оказывает, какое именно помещение расположено над комнатой, где планируется установка биметаллических радиаторов, а также существенную «лепту» вносит количество наружных стен квартиры. Если сделать расчет без учета этих факторов, то с большой долей вероятности в помещении будет слишком жарко, или наоборот — со временем придется наращивать радиатор. Намного правильнее и удобнее сразу сделать точный расчет и выполнить установку биметаллического радиатора отопления с идеально подходящими техническими характеристиками.

Пример

Рассмотрим пример расчета и определим, сколько секций биметаллического радиатора нужно для полноценного обогрева помещения, находящегося в доме из кирпича, на последнем этаже здания с неотапливаемым чердаком. При этом в комнате установлены двойные стеклопакеты, а отношение остекления к площади пола соответствует 30%. Отметим, что квартира, где находится комната — угловая, площадь помещения — 18 квадратных метров. Сам многоквартирный дом расположен в средней полосе РФ, где в самую холодную неделю в году средняя температура составляет -10 градусов по Цельсию.

При таких вводных данных формула расчета секций биметаллического радиатора будет выглядеть следующим образом:

100 Ватт/метр*1,0*1,0*1,0*0,7*1,2*1,0*=84 Вт/кв.м
Полученное значение необходимо умножить на площадь комнаты: 18*84=1512 Ватт.
Остается лишь разделить 1512 Ватт на тепловую мощность одной секции, мы примем это значение за 170 Вт (на практике нужно уточнить в паспорте или описании на изделие). В итоге получаем 8,89, то есть идеальное количество секций биметаллического радиатора в представленном примере — 9.

Использование онлайн-калькулятора для расчета: в чем преимущества?

Если времени или желания выполнять самостоятельные расчеты нет, то можно воспользоваться бесплатными онлайн-программами. Для этого необходимо найти специальный калькулятор для расчета секций биметаллических радиаторов. В таких программах, помимо обозначенных выше коэффициентов, также требуется указать информацию, которая касается:

Особенностей установки радиатора. Например, возможен монтаж устройства открыто на стене, под подоконником, в стеновой нише.
Наличия или отсутствия декоративного кожуха.
Схемы подключения радиатора.
Расположения дома (а точнее — на какую сторону света выходят внешние стены дома).

Использование дополнительных данных позволяет выполнить наиболее точный расчет. Если у вас появились вопросы по способам определения необходимого количества секций биметаллического радиатора или вы хотите доверить проведение работ по расчету профессионалам, достаточно связаться с менеджером «САНТЕХПРОМ» по телефону +7 (495) 730-70-80. Представитель компании предоставит необходимые консультации и поможет точно узнать, сколько секций биметаллического радиатора нужно для вашей комнаты.

Расчет секций радиаторов: по площади, объему

При модернизации системы отопления кроме замены труб меняют и радиаторы. Причем сегодня они есть из разных материалов, разных форм и размеров. Что не менее важно, имеют они разную теплоотдачу: количество тепла, которые могут передать воздуху. И это обязательно учитывают, когда делают расчет секций радиаторов.

В помещении будет тепло, если количество тепла, которое уходит, будет компенсироваться. Поэтому в расчетах за основу берут теплопотери помещений (они зависят от климатической зоны, от материала стен, утепления, площади окон и т.д.). Второй параметр — тепловая мощность одной секции. Это то количество тепла, которое она может выдать при максимальных параметрах системы (90°C на входе и 70°C на выходе). Эта характеристика обязательно указывается в паспорте, зачастую присутствует на упаковке.

Делаем расчет количества секций радиаторов отопления своими руками, учитываем особенности помещений и системы отопления

Один важный момент: проводя расчеты самостоятельно, учтите, что большинство производителей указывают максимальную цифру, которую они получили при идеальных условиях. Потому любое округление производите в большую сторону. В случае с низкотемпературным отоплением (температура теплоносителя на входе ниже 85°C) ищут тепловую мощность для соответствующих параметров или делают перерасчет (описан ниже).

Содержание статьи

Расчет по площади

Это — самая простая методика, позволяющая примерно оценить число секций, необходимое для отопления помещения. На основании многих расчетов выведены нормы по средней мощности отопления одного квадрата площади. Чтобы учесть климатические особенности региона, в СНиПе прописали две нормы:

для регионов средней полосы России необходимо от 60 Вт до 100 Вт;
для районов, находящихся выше 60°, норма отопления на один квадратный метр 150-200 Вт.

Почему в нормах дан такой большой диапазон? Для того, чтобы можно было учесть материалы стен и степень утепления. Для домов из бетона берут максимальные значения, для кирпичных можно использовать средние. Для утепленных домов — минимальные. Еще одна важная деталь: эти нормы просчитаны для средней высоты потолка — не выше 2,7 метра.

Как рассчитать количество секций радиатора: формула

Зная площадь помещения, умножаете ее норму затрат тепла, наиболее подходящую для ваших условий. Получаете общие теплопотери помещения. В технических данных к выбранной модели радиатора, находите тепловую мощность одной секции. Общие теплопотери делите на мощность, получаете их количество. Несложно, но чтобы было понятнее, приведем пример.

Пример расчета количества секций радиаторов по площади помещения

Угловое помещение 16 м², в средней полосе, в кирпичном доме. Устанавливать будут батареи с тепловой мощностью 140 Вт.

Для кирпичного дома берем теплопотери в середине диапазона. Так как помещение угловое, лучше взять большее значение. Пусть это будет 95 Вт. Тогда получается, что для обогрева помещения требуется 16 м²* 95 Вт = 1520 Вт.

Теперь считаем количество радиаторов для отопления этой комнаты: 1520 Вт / 140 Вт = 10,86 шт. Округляем, получается 11 шт. Столько секций радиаторов необходимо будет установить.

Расчет батарей отопления на площадь прост, но далеко не идеален: высота потолков не учитывается совершенно. При нестандартной высоте используют другую методику: по объему.

Считаем батареи по объему

Есть в СНиПе нормы и для обогрева одного кубометра помещений. Они даны для разных типов зданий:

для кирпичных на 1 м³ требуется 34 Вт тепла;
для панельных — 41 Вт

Этот расчет секций радиаторов похож на предыдущий, только теперь нужна не площадь, а объем и нормы берем другие. Объем умножаем на норму, полученную цифру делим на мощность одной секции радиатора (алюминиевого, биметаллического или чугунного).

Формула расчета количества секций по объему

Пример расчета по объему

Для примера рассчитаем, сколько нужно секций в комнату площадью 16 м²и высотой потолка 3 метра. Здание построено из кирпича. Радиаторы возьмем той же мощности: 140 Вт:

Находим объем. 16 м² * 3 м = 48 м³
Считаем необходимое количество тепла (норма для кирпичных зданий 34 Вт). 48 м³ * 34 Вт = 1632 Вт.
Определяем, сколько нужно секций. 1632 Вт / 140 Вт = 11,66 шт. Округляем, получаем 12 шт.

Теперь вы знаете два способа того, как рассчитать количество радиаторов на комнату.

Подробнее о расчетах площади комнаты и объема читаем тут.

Теплоотдача одной секции

Сегодня ассортимент радиаторов большой. При внешней схожести большинства, тепловые показатели могут значительно отличаться. Они зависят от материала, из которого изготовлены, от размеров, толщины стенок, внутреннего сечения и от того, насколько хорошо продумана конструкция.

Потому точно сказать, сколько кВт в 1 секции алюминиевого (чугунного биметаллического) радиатора, можно сказать только применительно к каждой модели. Эти данные указывает производитель. Ведь есть значительная разница в размерах: одни из них высокие и узкие, другие — низкие и глубокие. Мощность секции одной высоты того же производителя, но разных моделей, могут отличаться на 15-25 Вт (смотрите в таблице ниже STYLE 500 и STYLE PLUS 500) . Еще более ощутимые отличия могут быть у разных производителей.

Технические характеристики некоторых биметаллических радиаторов. Обратите внимание, что тепловая мощность одинаковых по высоте секций может иметь ощутимую разницу

Тем не менее, для предварительной оценки того, сколько секций батарей нужно для отопления помещений, вывели средние значения тепловой мощности по каждому типу радиаторов. Их можно использовать при приблизительных расчетах (приведены данные для батарей с межосевым расстоянием 50 см):

Биметаллический — одна секция выделяет 185 Вт (0,185 кВт).
Алюминиевый — 190 Вт (0,19 кВт).
Чугунные — 120 Вт (0,120 кВт).

Точнее сколько кВт в одной секции радиатора биметаллического, алюминиевого или чугунного вы сможете, когда выберете модель и определитесь с габаритами. Очень большой может быть разница в чугунных батареях. Они есть с тонкими или толстыми стенками, из-за чего существенно изменяется их тепловая мощность. Выше приведены средние значения для батарей привычной формы (гармошка) и близких к ней. У радиаторов в стиле «ретро» тепловая мощность ниже в разы.

Это технические характеристики чугунных радиаторов турецкой фирмы Demir Dokum. Разница более чем солидная. Она может быть еще больше

Исходя из этих значений и средних норм в СНиПе вывели среднее количество секций радиатора на 1 м²:

биметаллическая секция обогреет 1,8 м²;
алюминиевая — 1,9-2,0 м²;
чугунная — 1,4-1,5 м²;

Как рассчитать количество секций радиатора по этим данным? Все еще проще. Если вы знаете площадь комнаты, делите ее на коэффициент. Например, комната 16 м², для ее отопления примерно понадобится:

биметаллических 16 м² / 1,8 м² = 8,88 шт, округляем — 9 шт.
алюминиевых 16 м² / 2 м² = 8 шт.
чугунных 16 м² / 1,4 м² = 11,4 шт, округляем — 12 шт.

Эти расчеты только примерные. По ним вы сможете примерно оценить затраты на приобретение отопительных приборов. Точно рассчитать количество радиаторов на комнату вы сможете выбрав модель, а потом еще пересчитав количество в зависимости от того, какая температура теплоносителя в вашей системе.

Расчет секций радиаторов в зависимости от реальных условий

Еще раз обращаем ваше внимание на то, что тепловая мощность одной секции батареи указывается для идеальных условий. Столько тепла выдаст батарея, если на входе ее теплоноситель имеет температуру +90°C, на выходе +70°C, в помещении при этом поддерживается +20°C. То есть, температурный напор системы (называют еще «дельта системы») будет 70°C. Что делать, если в вашей системе выше +70°C на входе на бывает? или необходима температура в помещении +23°C? Пересчитывать заявленную мощность.

Для этого необходимо рассчитать температурный напор вашей системы отопления. Например, на подаче у вас +70°C, на выходе +60°C, а в помещении вам необходима температура +23°C. Находим дельту вашей системы: это среднее арифметическое температур на входе и выходе, за минусом температуры в помещении.

Формула расчета температурного напора системы отопления

Для нашего случая получается: (70°C+ 60°C)/2 — 23°C = 42°C. Дельта для таких условий 42°C. Далее находим это значение в таблице пересчета (расположена ниже) и заявленную мощность умножаем на этот коэффициент. Поучаем мощность, которую сможет выдать эта секция для ваших условий.

Таблица коэффициентов для систем отопления с разной дельтой температур

При пересчете действуем в следующем порядке. Находим в столбцах, подкрашенных синим цветом, строчку с дельтой 42°C. Ей соответствует коэффициент 0,51. Теперь рассчитываем, тепловую мощность 1 секции радиатора для нашего случая. Например, заявленная мощность 185 Вт, применив найденный коэффициент, получаем: 185 Вт * 0,51 = 94,35 Вт. Почти в два раза меньше. Вот эту мощность и нужно подставлять когда делаете расчет секций радиаторов. Только с учетом индивидуальных параметров в помещении будет тепло.

Расчёт количества секций радиатора отопления

Очень важно купить современные качественные и эффективные батареи. Но куда важнее правильно произвести расчёт количества секций радиатора, чтобы в холодную пору он должным образом прогревал помещение и не пришлось думать об установке дополнительных переносных отопительных приборов, которые увеличат расход средств на отопление.

Содержание статьи:

СНиП и основные предписания

Сегодня можно назвать огромное количество СНиПов, которые описывают правила проектирования и эксплуатации отопительных систем в различных помещениях. Но наиболее понятным и простым является документ «Отопление, вентиляция и кондиционирование» под номером 2. 04.05.

В нем подробно описаны следующие разделы:

Общие положения, касающиеся проектирования систем отопления
Правила проектирования систем отопления зданий
Особенности прокладки труб отопительной системы

Монтировать радиаторы отопления необходимо также согласно СНиП под номером 3.05.01. Он предписывает следующие правила монтажа, без которых произведенные расчеты количества секций окажутся малоэффективны:

Максимальная ширина радиатора не должна превысить 70% от аналогичной характеристики оконного проема, под которым он устанавливается
Радиатор должен крепиться по центру оконного проема (допускается незначительная погрешность – не более 2 см)
Рекомендуемое пространство между радиаторами и стеной – 2-5 см
Над полом высота не должны быть более 12 см
Расстояние до подоконника от верхней точки батареи – не менее 5 см
В иных случаях для улучшения теплоотдачи поверхность стен покрывают отражающим материалом

Следовать таким правилам необходимо для того, чтобы воздушные массы могли свободно циркулировать и сменять друг друга.

Читайте так же, наш сравнительный обзор различных видов радиаторов отопления

Расчет по объему

Чтобы точно произвести расчёт количества секций отопительного радиатора, необходимых для эффективного и комфортного отопления жилого помещения, следует принимать во внимания его объем. Принцип весьма прост:

Определяем потребность тепла
Узнаем количество секций, способных его отдавать

СНиП предписывает учитывать потребность в тепле для любого помещения – 41 Вт на 1 м. куб. Однако этот показатель весьма относителен. Если стены и пол плохо утеплены, это значение рекомендуют увеличить до 47-50 Вт, ведь часть тепла будет утрачиваться. В ситуациях, когда по поверхностям уже уложен качественный теплоизолятор, смонтированы качественные окна ПВХ и устранены сквозняки – данный показатель можно принять равным 30-34 Вт.

Если в комнате расположены экранированные радиаторы отопления, потребность в тепле необходимо увеличить до 20%. Часть тепловой нагретых воздушных масс не будет пропускаться экраном, циркулируя внутри и быстро остывая.

Формулы расчета количества секций по объему помещения, с примером

Определившись с потребностью на один куб, можно приступит к вычислениям (пример на конкретных цифрах):

На первом шаге рассчитываем объем помещения по простой формуле: [высота]*[длина]*[ширина] (3х4х5=60 куб м.)
Следующий этап – определение потребности теплоты для конкретно рассматриваемого помещения по формуле: [объем]*[потребность на м. куб.] (60х41=2460 Вт)
В паспорте, прилагаемом к радиатору отопления, необходимо узнать мощность одной секции – средний показатель современных моделей 170 Вт
Определить желаемое количество ребер можно по формуле: [общая потребность в тепле]/[мощность одной секции] (2460/170=14.5)
Округление рекомендуется делать в большую сторону – получаем 15 секций

Многие производители не учитывают, что теплоноситель, циркулирующий по трубам, имеет далеко не максимальную температуру. Следовательно, мощность ребер будет ниже, чем указанное предельное значение (именно ее прописывают в паспорте). Если нет минимального показателя мощности, значит имеющийся для упрощения расчетов занижают на 15-25%.

Расчет по площади

Предыдущий метод расчета – прекрасное решение для помещений, у которых высота более 2.7 м. В комнатах с более низкими потолками (до 2.6 м) можно воспользоваться другим способом, приняв за основу площадь.

В этом случае, рассчитывая общее количество тепловой энергии, потребность на один кв. м. берут равной 100 Вт. Каких-либо корректировок в него покуда вносить не требуется.

Формулы расчета количества секций по площади помещения, с примером

На первом этапе определяется общая площадь помещения: [длина]* [ширина] (5х4=20 кв. м.)
Следующий шаг – определение тепла, необходимого для обогрева всего помещения: [площадь]* [потребность на м. кв.] (100х20=2000 Вт)
В паспорте, прилагаемом к радиатору отопления, необходимо узнать мощность одной секции – средний показатель современных моделей 170 Вт
Для определения необходимого количества секций следует воспользоваться формулой: [общая потребность в тепле]/[мощность одной секции] (2000/170=11. 7)
Вносим поправочные коэффициенты (рассмотрены далее)
Округление рекомендуется делать в большую сторону – получаем 12 секций

Поправки, вносимые в расчет и советы

Рассмотренные выше методы расчёта количества секций радиатора прекрасно подходят для помещений, высота которых достигает 3-х метров. Если этот показатель больше, необходимо увеличивать тепловую мощность прямо пропорционально росту высоты.

Если весь дом оснащен современными пластиковыми окнами, у которых коэффициент тепловых потерь максимально снижен – появляется возможность сэкономить и уменьшить полученный результат до 20%.

Считается, что стандартная температура теплоносителя, циркулирующего по отопительной системе – 70 градусов. Если она ниже этого значения, необходимо на каждые 10 градусов увеличивать полученный результат на 15%. Если выше – наоборот уменьшать.

Помещения, площадь которых более 25 кв. м. отопить одним радиатором, даже состоящим из двух десятков секций, будет крайне проблематично. Чтобы решить подобную проблему, необходимо вычисленное число секций поделить на две равные части и установить две батареи. Тепло в этом случае будет распространяться по комнате более равномерно.

Если в помещении два оконных проема, радиаторы отопления нужно размещать под каждым из них. Они должны быть по мощности в 1.7 раза больше номинальной, определенной при расчетах.

Купив штампованные радиаторы, у которых поделить секции нельзя, необходимо учитывать общую мощность изделия. Если ее недостаточно, следует подумать о покупке второй такой же батареи или чуть менее теплоемкой.

Поправочные коэффициенты

Очень многие факторы могут оказывать влияние на итоговый результат. Рассмотрим, в каких ситуациях необходимо вносить поправочные коэффициенты:

Окна с обычным остеклением – увеличивающий коэффициент 1.27
Недостаточная теплоизоляция стен – увеличивающий коэффициент 1.27
Более двух оконным проемов на помещение – увеличивающий коэффициент 1. 75
Коллекторы с нижней разводкой – увеличивающий коэффициент 1.2
Запас в случае возникновения непредвиденных ситуаций – увеличивающий коэффициент 1.2
Применение улучшенных теплоизоляционных материалов – уменьшающий коэффициент 0.85
Установка качественных теплоизоляционных стеклопакетов – уменьшающий коэффициент 0.85

Количество вносимых поправок в расчет может быть огромным и зависит от каждой конкретной ситуации. Однако следует помнить, что уменьшать теплоотдачу радиатора отопления значительно легче, чем увеличить. Потому все округления делаются в большую сторону.

Подводим итоги

Если необходимо произвести максимально точный расчёт количества секций радиатора в сложном помещении – не стоит бояться обратиться к специалистам. Самые точные методы, которые описываются в специальной литературе, учитывают не только объем или площадь комнаты, но и температуру снаружи и изнутри, теплопроводность различных материалов, из которых построена коробка дома, и множество других факторов.

Безусловно, можно не бояться и набрасывать несколько ребер к полученному результату. Но и чрезмерное увеличение всех показателей может привести к неоправданным расходам, которые не сразу, порой и не всегда удается окупить.

Расчет радиаторов отопления, как рассчитать количество секций радиаторы калукулятор

Главный критерий при расчете мощности радиаторов отопления — площадь помещения. Чем просторнее помещение, тем мощнее необходима теплоотдача. Расчет нужен для безошибочного измерения оптимальной теплоотдачи данного помещения. Отопление может использоваться как основное или дополняющее. Чтобы правильно рассчитать мощность нужны следующие вводные данные: площадь помещения, этаж, зональность, параметры ниши, высоту потолка, другие отопительные приборы. Радиаторы отопления обычно монтируются под всеми окнами, для предотвращения тепловых потерь и образования конденсата. Для угловых комнат стоит рассматривать более мощные модели, добавив 1-2 секции «про запас». Для высоких потолков (более 3 м), требуется добавочная тепловая энергия, учитывающаяся при расчетах.

Немаловажно при расчете мощности батареи отопления учитывать наличие/отсутствие стеклопакетов и качество общей теплоизоляции помещения. Все эти характеристики необходимо учитывать при выборе оборудования.

Формула, помогающая рассчитать должную тепловую мощность радиаторов в помещении с высотой потолков не более 3 м:
S пом. * 100 Вт / ∆T
где:/
S пом. — площадь помещения,
∆T — тепловой поток от одной секции.

Для основной отопительной системы (без дополнительных источников тепла) следует умножить всю площадь помещения на 100 Вт и разделить на тепло отдачу одной секции. Формула, по которой можно рассчитать мощность батарей в помещении с высотой потолков не менее 3 м :
S пом.* h * 40 / ∆T
где:
Sпом. — площадь помещ.,
∆T — отдача тепла одной секцией прибора,

H — высота потолка.

Есть и более простая формула: в помещении с единственной наружной стеной и одним стандартным окном 1 кВт мощности отопительного оборудования хватит для поддержания нормальной температуры на 10 кв. м.
Если же в помещ. 2 внешние стены — вам потребуется уже 1,3 кВт мощности на каждые 10 м2.
Стоит также заранее решить, где устанавливать радиатор, измерить высоту и длину подоконника, размеры ниши. После чего, подбирать тип, подходящий не только по мощности, но и по размерам.

Что такое межосевое расстояние радиаторов? Межосевое расстояние радиатора — это промежуток между серединой отверстий вход. и выход. коллекторов и прилагающимися соответствующими по размеру батарее трубами. Чаще всего встречается 2 размера — 500 мм либо 300 мм.

Оптимальные параметры монтажа:
а) промежуток от стояка до соединения с радиатором — от 30 сантиметров;
б) промежуток от пола до низа радиатора — от 15 сантиметров;

Расчет статического или первого момента площади сечения балки

font-size: 15 пикселей;
}
]]>

Как рассчитать статический или первый момент площади секций балки

Статический или первый момент площади (Q) просто измеряет распределение площади сечения балки относительно оси.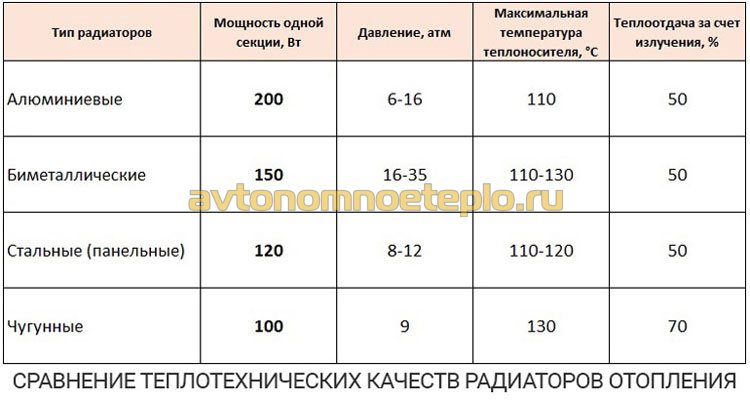 Он рассчитывается путем суммирования всех площадей, умноженных на их расстояние от конкретной оси (Площадь на расстояние).

На самом деле, возможно, вы этого не осознавали, но если вы вычислили центроид сечения балки, вы бы уже вычислили первый момент площади.Кроме того, это свойство, часто обозначаемое Q, чаще всего используется при определении напряжения сдвига сечения балки.

Так как секции балки обычно состоят из множества геометрических фигур, сначала необходимо разделить секцию на сегменты. После этого вычисляется площадь и центроид каждого сегмента, чтобы найти общий статический момент площади.

Рассмотрим сечение двутавровой балки, показанное ниже. В нашем предыдущем уроке мы уже обнаружили, что центр тяжести находится на расстоянии 216,29 мм от нижней части секции.Чтобы вычислить статический момент площади относительно горизонтальной оси x, сечение можно разделить на 4 сегмента, как показано на рисунке:

Помните, что первый момент площади — это сумма площадей, умноженная на расстояние от оси.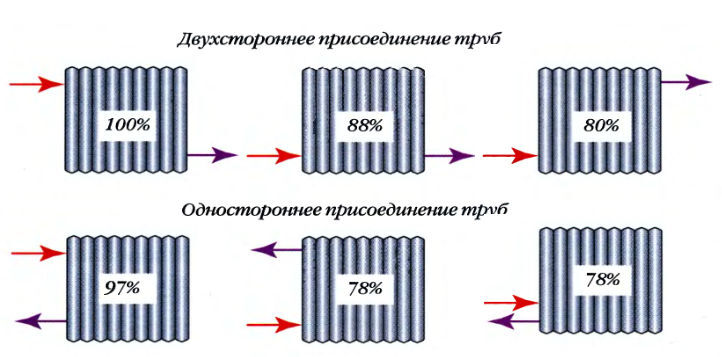 Таким образом, формула для статического момента площади относительно горизонтальной оси x:

Теперь для такого результата, как напряжение сдвига, нам часто нужен статический момент ВЕРХНЕЙ или НИЖНЕЙ части сечения относительно нейтральной оси (NA) XX.Начнем с ВЕРХНЕЙ части раздела (то есть с сегментов 1 и 2). Мы найдем A _i и y _i для каждого сегмента двутаврового сечения над нейтральной осью, а затем вычислим статический момент площади (Q _x). Помните, что мы измеряем расстояния от нейтральной оси!

Аналогичным образом мы можем рассчитать статический момент площади НИЖНЕЙ части сечения. Это включает сегменты 3 и 4, которые находятся ниже нейтральной оси.

Вы заметите, что статический момент области над нейтральной осью равен моменту под нейтральной осью!

[математика]
{Q} _ {x, вверху} = {Q} _ {x, bottom}
[математика]

Конечно, вам не нужно делать все эти вычисления вручную, потому что вы можете использовать наш фантастический калькулятор свободного момента инерции, чтобы определить статический момент площади секций балки.

Калькулятор свободного момента инерции

Посетите следующий шаг: «Как рассчитать момент инерции секции балки».

Свойства поперечного сечения | MechaniCalc

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

Поведение элемента конструкции определяется его материалом и геометрией. Поперечное сечение и длина элемента конструкции влияют на то, насколько этот элемент прогибается под нагрузкой, а поперечное сечение определяет напряжения, которые существуют в элементе при данной нагрузке.

Недвижимость участков

Центроид

Центроид формы представляет собой точку, вокруг которой равномерно распределена площадь сечения. Если область дважды симметрична относительно двух ортогональных осей, центр тяжести лежит на пересечении этих осей. Если область симметрична только относительно одной оси, то центр тяжести лежит где-то вдоль этой оси (необходимо вычислить другую координату).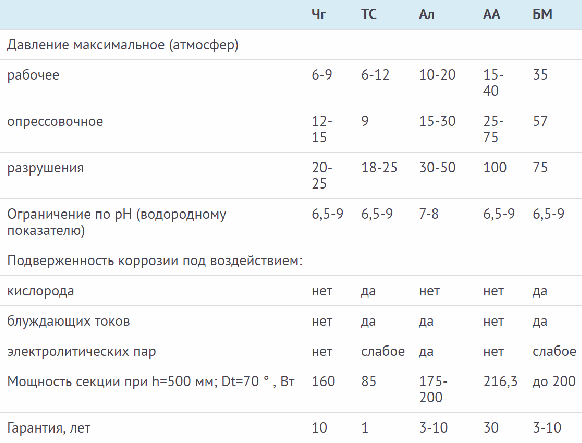 Если точное местоположение центроида не может быть определено путем осмотра, его можно рассчитать следующим образом:

где dA представляет собой площадь бесконечно малого элемента, A — общая площадь поперечного сечения, а x и y — координаты элемента dA относительно интересующей оси.

Центроидальные положения общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать местоположение с помощью приведенных выше уравнений.

Если поперечное сечение состоит из набора основных форм, центроидальное положение которых известно относительно некоторой контрольной точки, то центральное положение составного поперечного сечения можно рассчитать как:

где х _{с, я} и у _{с, я} являются прямоугольные координаты центра тяжести расположения я ^-й сечения относительно опорной точки, и А _я является площадь я ^-й раздел.

Центроидное расстояние

Центроидное расстояние , c — это расстояние от центра тяжести поперечного сечения до крайнего волокна. Центроидное расстояние в направлении y для прямоугольного поперечного сечения показано на рисунке ниже:

Обычно центроидное расстояние используется:

Первый момент области

Первый момент области относительно интересующей оси рассчитывается как:

Q _x = ∫ y dA

Q _y = ∫ x dA

где Q _x — это первый момент относительно оси x, а Q _y — это первый момент относительно оси y.Если область состоит из набора основных форм, чьи центроидные положения известны по отношению к интересующей оси, то первый момент составной области можно рассчитать как:

Обратите внимание, что первый момент площади используется при вычислении центра тяжести поперечного сечения относительно некоторого начала координат (как обсуждалось ранее). Первый момент также используется при вычислении значения напряжения сдвига в определенной точке поперечного сечения.В этом случае первый момент рассчитывается для области, которая составляет меньшую часть поперечного сечения, где область ограничена интересующей точкой и крайним волокном (верхним или нижним) поперечного сечения. Первый момент рассчитывается относительно оси, проходящей через центр тяжести поперечного сечения.

На рисунке выше заштрихованная синяя область представляет собой интересующую область в общем поперечном сечении. Первый момент этой области относительно оси x (которая проходит через центр тяжести поперечного сечения, точку O на рисунке выше) рассчитывается как:

Если центральное положение интересующей области известно, то первый момент области относительно оси можно рассчитать как (см. Рисунок выше):

Q _cx = y _c1 A ₁

Следует отметить, что первый момент области будет положительным или отрицательным в зависимости от положения положения области относительно оси интереса. Следовательно, первый момент всей площади поперечного сечения относительно его собственного центроида будет равен нулю.

Площадь Момент инерции

Второй момент площади, более известный как момент инерции , , I, поперечного сечения, является показателем способности конструктивного элемента сопротивляться изгибу. ^{(Примечание 1)} I _x и I _y — моменты инерции относительно осей x и y, соответственно, и рассчитываются по формуле:

I _x = ∫ y ² dA

I _y = ∫ x ² dA

где x и y — координаты элемента dA относительно интересующей оси.

Чаще всего моменты инерции рассчитываются относительно центра тяжести сечения. В этом случае они обозначаются как центроидных моментов инерции и обозначаются как I _cx для инерции относительно оси x и I _cy для инерции относительно оси y.

Моменты инерции общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать их с помощью приведенных выше уравнений. Свойства нескольких распространенных поперечных сечений приведены в конце этой страницы.

Если поперечное сечение состоит из набора основных форм, все центроиды которых совпадают, то момент инерции составного сечения является просто суммой отдельных моментов инерции. Примером этого является балка коробчатого сечения, состоящая из двух прямоугольных секций, как показано ниже. В этом случае внешняя часть имеет «положительную площадь», а внутренняя часть имеет «отрицательную площадь», поэтому составной момент инерции представляет собой вычитание момента инерции внутренней части из внешней части.

В случае более сложного составного поперечного сечения, в котором центральные положения не совпадают, момент инерции может быть вычислен с использованием теоремы о параллельных осях .

Важно не путать момент инерции площади с массой момента инерции твердого тела . Момент инерции площади указывает на сопротивление поперечного сечения изгибу, тогда как момент инерции массы указывает на сопротивление тела вращению.

Теорема о параллельной оси

Если известен момент инерции поперечного сечения относительно центральной оси, то для вычисления момента инерции относительно любой параллельной оси можно использовать теорему о параллельной оси :

I _{параллельная ось} = I _c & plus; А д ²

где I _c — момент инерции относительно центральной оси, d — расстояние между центральной осью и параллельной осью, а A — площадь поперечного сечения.

Если поперечное сечение состоит из набора основных форм, центроидные моменты инерции которых известны вместе с расстояниями центроидов до некоторой контрольной точки, то теорема о параллельных осях может использоваться для вычисления момента инерции составного поперечного сечения.

Например, двутавровая балка может быть аппроксимирована 3 прямоугольниками, как показано ниже. Поскольку это составное сечение симметрично относительно осей x и y, центр тяжести сечения можно определить путем осмотра на пересечении этих осей. Центроид расположен в начале координат O на рисунке.

Момент инерции составной секции можно рассчитать с помощью теоремы о параллельности осей. Центроидный момент инерции секции относительно оси x, I _cx, рассчитывается как:

I _cx.IBeam = I _cx.W & plus; (I _cx.F1 & plus; A _F1 d ₁ ²) & plus; (I _cx.F2 & plus; A _F2 d ₂ ²)

где члены I _cx представляют собой моменты инерции отдельных секций относительно их собственных центроидов в ориентации оси x, члены d представляют собой расстояния от центроидов отдельных секций до центроидов составной секции, а Термины — это площади отдельных разделов.Поскольку центроид сечения W и центроид составного сечения совпадают, d для этого сечения равно нулю, поэтому член Ad ² отсутствует.

Важно отметить, что из теоремы о параллельных осях следует, что по мере того, как отдельная секция перемещается дальше от центра тяжести составной секции, вклад этой секции в момент инерции составной секции увеличивается в d ² раз. Следовательно, если намерение состоит в том, чтобы увеличить момент инерции секции относительно определенной оси, наиболее эффективно расположить область как можно дальше от этой оси.Это объясняет форму двутавровой балки. Фланцы вносят основной вклад в момент инерции, а перегородка служит для отделения фланцев от оси изгиба. Однако полотно должно сохранять некоторую толщину, чтобы избежать коробления, а также потому, что полотно принимает на себя значительную часть напряжения сдвига в сечении.

Полярный момент инерции

Полярный момент инерции , , I, поперечного сечения является показателем способности конструктивного элемента противостоять скручиванию вокруг оси, перпендикулярной сечению.Полярный момент инерции для сечения относительно оси можно рассчитать следующим образом:

J = ∫ r ² dA = ∫ (x ² & plus; y ²) dA

где x и y — координаты элемента dA относительно интересующей оси, а r — расстояние между элементом dA и интересующей осью.

Хотя полярный момент инерции может быть вычислен с использованием приведенного выше уравнения, обычно удобнее рассчитывать его с помощью теоремы о перпендикулярной оси , которая утверждает, что полярный момент инерции области является суммой моментов инерции относительно любые две ортогональные оси, проходящие через интересующую ось:

J = I _x и плюс; Я _y

Чаще всего интересующая ось проходит через центр тяжести поперечного сечения.

Модуль упругости сечения

Максимальное изгибающее напряжение в балке рассчитывается как σ _b = Mc / I _c, где c — расстояние от нейтральной оси до крайнего волокна, I _c — центроидный момент инерции, а M — изгибающий момент. Модуль сечения объединяет члены c и I _c в уравнении напряжения изгиба:

S = I _c / c

Используя модуль упругости сечения, напряжение изгиба рассчитывается как σ _b = M / S. Полезность модуля сечения заключается в том, что он характеризует сопротивление сечения изгибу одним термином. Это позволяет оптимизировать поперечное сечение балки, чтобы противостоять изгибу, за счет максимального увеличения одного параметра.

Радиус вращения

Радиус вращения представляет собой расстояние от центроида секции, на котором вся площадь может быть сосредоточена без какого-либо влияния на момент инерции. Радиус вращения формы относительно каждой оси определяется как:

Полярный радиус вращения также может быть вычислен для задач, связанных с кручением вокруг центральной оси:

Прямоугольные радиусы вращения также можно использовать для вычисления полярного радиуса вращения:

r _p ² = r _x ² & plus; г _г ²

Свойства общих сечений

В таблице ниже приведены свойства общих сечений.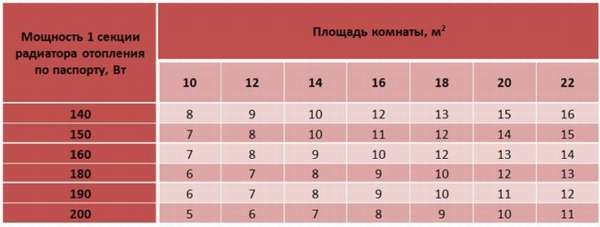 Более подробные таблицы можно найти в перечисленных ссылках.

Свойства, вычисленные в таблице, включают площадь, центроидный момент инерции, модуль упругости сечения и радиус вращения.

Банкноты

Примечание 1: Прогиб балки

Прогиб балки при изгибе определяется моментом инерции поперечного сечения, длиной балки и модулем упругости материала.Более подробная информация представлена в этом обсуждении отклонения балки.

Список литературы

Гир, Джеймс М., «Механика материалов», 6-е изд.
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е изд.

Свойства секции канала (U) | calcresource

Определения

Геометрия

U-образная секция (также называемая каналом) — довольно распространенная форма сечения, обычно используемая в стальных конструкциях.Однако U-образные поперечные сечения могут быть выполнены и из других материалов (например, из бетона, алюминия, пластика и т. 2 \ right)

Мы достигли последнего уравнения, разбив U-образный профиль на более простые компоненты (фланцы и стенку), а затем определив статический момент каждый, от оси, выровненной по внешнему краю полотна.Если вам понадобятся дополнительные сведения об этой технике, вы можете прочитать нашу статью о поиске центроида составных областей здесь.

Момент инерции

Момент инерции секции канала можно найти, если общую площадь разделить на три меньших, A, B, C, как показано на рисунке ниже. Последняя область может рассматриваться как аддитивная комбинация A + B + C. Однако, поскольку фланцы равны, более простая комбинация может быть (A + B + C + V) -V (то есть разница между двумя прямоугольными областями).3} {12}

, где h высота канала, b ширина полок, t_f толщина полок и t_w толщина стенки. Обратите внимание, что нет необходимости применять теорему о параллельных осях для любой из двух прямоугольных областей (V и A + B + C + V), потому что их центроиды лежат над исследуемой осью x.

Момент инерции I_y секции канала вокруг центральной оси y лучше всего находить с применением теоремы о параллельных осях. Момент инерции I_ {y0} сечения канала вокруг нецентроидной оси y0 легко найти, если мы рассмотрим все сечение как сборку двух фланцев (области B и C на рисунке) и одной стенки. (область А).2

Почему полезен момент инерции

Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:

M = E \ times I \ times \ kappa

, где E — модуль Юнга, свойство материала, и \ kappa кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения можно увидеть, что когда к поперечному сечению балки прилагается определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I.

Полярный момент инерции

Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту; аналогично описанные выше плоские моменты инерции связаны с изгибом при изгибе. Расчет полярного момента инерции I_z вокруг оси z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях:

I_z = I_x + I_y

, где I_ {x} и I_ {y} равны моменты инерции вокруг осей x и y, которые взаимно перпендикулярны оси z и пересекаются в общем начале.4.

Модуль упругого сечения

Модуль упругого сечения S_x любого сечения вокруг оси x (центроидный) описывает реакцию сечения при упругом изгибе при изгибе вокруг той же оси. Он определяется как:

S_x = \ frac {I_x} {Y}

, где I_ {x} — момент инерции сечения вокруг оси x, а Y — расстояние от центра тяжести данного сечения волокна ( параллельно оси). Обычно для этого расчета используется более удаленное волокно, что приводит к минимальному модулю упругости сечения.Если поперечное сечение симметрично относительно оси (например, U-образное сечение вокруг оси x) и его размер, перпендикулярный этой оси, равен h, то самое удаленное волокно находится на расстоянии Y = h / 2 от оси. Следовательно, последняя формула принимает следующий вид:

S_x = \ frac {2 I_x} {h}

Для модуля упругости S_y сечения вокруг оси y можно определить два значения: одно для левого волокна сечения (расстояние x_c от центроида) и один для правых волокон, которые являются кончиками фланцев (на расстоянии b-x_c от центроида):

\ begin {split} & S_ {y, max} & = \ frac {I_y} {x_c} \\ & S_ {y, min} & = \ frac {I_y} {b-x_c} \ end {split}

, где обозначение max / min основано на предположении, что x_c \ lt b-x_c, что актуально для любого раздела канала.Обычно требуется только минимальный модуль упругости сечения (почему см. В следующем абзаце).

Если изгибающий момент M_x приложен к оси x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Вдоль нейтральной оси напряжения равны нулю. Абсолютный максимум \ sigma будет иметь место в самом удаленном волокне с величиной, определяемой формулой:

\ sigma = \ frac {M_x} {S_x}

Из последнего уравнения модуль упругости сечения можно рассматривать при изгибе при изгибе, a свойство, аналогичное поперечному сечению A, для осевой нагрузки. 3.

Модуль упругости сечения при пластике

Модуль упругости сечения аналогичен модулю упругости, но определяется исходя из предположения о полной пластической деформации поперечного сечения из-за изгиба при изгибе. В этом случае вся секция делится на две части, одну на растяжение и одну на сжатие, каждая из которых находится под однородным полем напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t при растяжении и A_c при сжатии, разделенных нейтральной осью.Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. Действительно, сжимающая сила, реализуемая по всей сжимаемой области, будет A_cf_y, если предположить, что условия пластичности (т.е. материал податился бы везде), и что предел текучести при сжатии равен f_y. Точно так же растягивающая сила будет A_t f_y, используя те же предположения. Обеспечение равновесия:

A_cf_y = A_t f_y \ Rightarrow

A_c = A_t

Ось называется , пластичная нейтральная ось , и для несимметричных секций не совпадает с упругой нейтральной осью (которая снова является центроидной).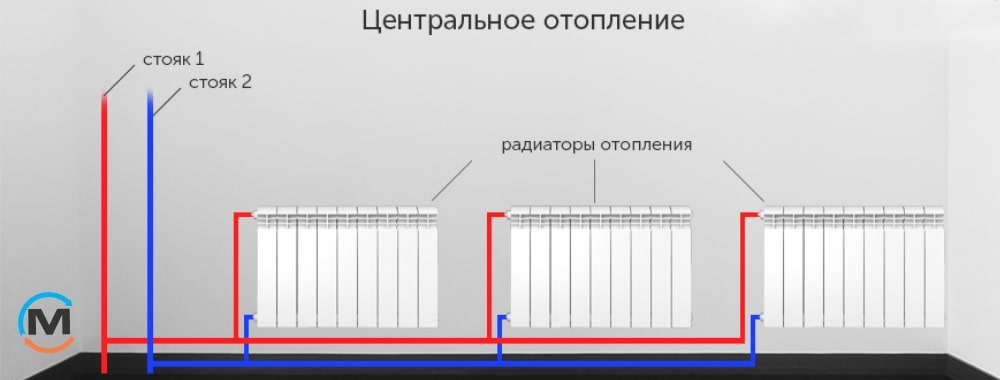 один).Модуль упругости пластического сечения задается общей формулой:

Z = A_c Y_c + A_t Y_t

, где Y_c — расстояние от центра тяжести области сжатия A_c от нейтральной оси пластика, а Y_t — соответствующее расстояние от центра тяжести растяжения. площадь А_т.

Пластиковая нейтральная ось делит поперечное сечение на две равные части при условии, что материал имеет одинаковый предел текучести на растяжение и сжатие.

Вокруг оси x

В случае U-образного сечения существует симметрия относительно оси, параллельной фланцам.Другими словами, центральная ось x также является осью симметрии. В этом случае пластичная нейтральная ось, разделяющая всю площадь на две равные части, также должна быть центроидальной. Из-за симметрии это Y_c = Y_t, и применение последнего уравнения приводит к следующей формуле для модуля пластического сечения поперечного сечения канала при изгибе xx:

Z_x = 2 A_c Y_c

Нахождение центра тяжести сжатая область проста. Как показано на следующем рисунке, площадь сжатия считается эквивалентной разнице между большим прямоугольником с размерами b и h / 2 и меньшим (синим цветом).2} {4}

Вокруг оси Y

U-образная секция не имеет симметрии, вокруг оси, параллельной стенке. В этом случае пластиковая нейтральная ось не видна только при осмотре, и ее необходимо определить в первую очередь. Можно использовать свойство пластиковой нейтральной оси делить все сечение на две равные части. В частности, для U-образного сечения получены следующие два уравнения для изгиба вокруг оси y:

\ left \ {\ begin {array} {ll} 2 (b-x_ {pna}) t_f = \ frac {A } {2} & \ text {, if} x_ {pna} \ ge t_w \\ x_ {pna} h = \ frac {A} {2} & \ text {, if} x_ {pna} \ lt t_w \\ \ end {array} \ right.

, что становится:

x_ {pna} = \ left \ {\ begin {array} {ll} b- \ frac {A} {4t_f} & \ text {, если:} t_w \ le {A \ over2 h } \\ \ frac {A} {2h} & \ text {, если:} t_w \ gt {A \ over2 h} \\ \ end {array} \ right.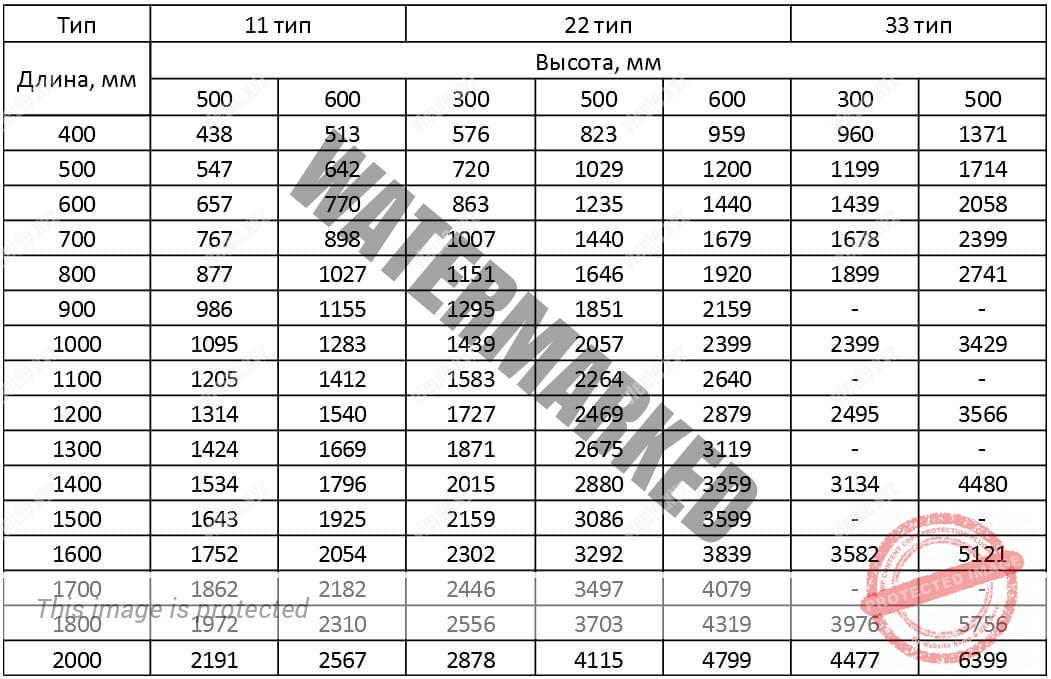

где x_ \ textit {pna} — расстояние от нейтральной оси пластика до внешнего края полотна (левый край на рисунке). Первое уравнение справедливо, когда пластиковая нейтральная ось проходит через два фланца, а второе — когда проходит через стенку. Как правило, заранее невозможно узнать, какое уравнение имеет значение.2) — 4bt_f h_wt_w \ right) \ quad, t_w \ gt {A \ over2 h}

где: h_w = h-2t_w.

Радиус вращения

Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:

R_g = \ sqrt {\ frac {I} {A}}

где I момент инерции поперечного сечения вокруг той же оси и А его площади. Размеры радиуса вращения [Длина]. Он описывает, как далеко от центроида распределена область. Маленький радиус указывает на более компактное сечение.Круг — это форма с минимальным радиусом вращения по сравнению с любой другой секцией с той же площадью A. Однако U-секция должна иметь значительно больший радиус вращения, особенно вокруг оси x, поскольку большая часть материала в секции расположена далеко от центроида. 2) — 4bt_f h_wt_w \ right) & \ quad, t_w \ gt {A \ over2 h} \ end {array} \ right.3} {3}

Расчетные модули> Прочие расчетные модули> Калькулятор свойств общего раздела

Нужно больше? Задайте нам вопрос

Обзор

Этот модуль определяет свойства сечения для составных сечений с прямоугольниками, полыми кругами, сплошными кругами, стандартных стальных профилей AISC и общих многосторонних сплошных форм.Нажмите здесь, чтобы посмотреть видео:

Разделы

AISC могут быть вызваны из файлов базы данных и могут быть включены в построенный раздел. Все разделы 13-го издания Руководства по стальным конструкциям AISC доступны и при необходимости могут быть переориентированы.

Расчетные значения свойств сечения включают: площадь, моменты инерции, положение центра тяжести, экстремальные расстояния между волокнами, модули сечения и радиус вращения.

Базовое использование

• Перед началом ввода данных убедитесь, что вы настроили систему координат X-Y для согласованной привязки всех местоположений компонентов.

• Для каждой прямоугольной формы, введите высоту, ширину и центр области, измеренной от опорной точки.

• Полые круглые сечения вводятся с указанием внешнего радиуса и толщины. Сплошные круглые сечения вводятся путем указания внешнего радиуса и установки нулевой толщины.

• Для секций AISC вы можете использовать поля ввода Xcg и Ycg, чтобы определить положение центроида секции относительно нулевой точки. Модулю известно расположение центроидов элементов AISC по отношению к их собственным крайним расположениям волокон.Однако вам необходимо ввести расположение центроида элемента по отношению к другим элементам в построенной секции. Будьте осторожны, так как это может быть сложно при вводе каналов, углов и тройников, которые поворачиваются.

• Уникальная функция позволяет пользователю указать, что секции AISC можно поворачивать с шагом 90 градусов, а стальные угловые секции также можно зеркально отображать относительно их оси Y.

Допущения и ограничения

Модуль работает по простой процедуре расчета:

• Вычислить момент инерции каждой формы,

• Вычислить нейтральную ось группы форм, и

• Вычислить момент инерции группы, используя уравнения I + A * D2.

Более сложный анализ, такой как полярный момент инерции, пластические модули и константы продольного изгиба, в настоящее время выходит за рамки модуля, но продолжающиеся разработки добавят эти элементы в будущих обновлениях.

Прокатный профиль / вкладка стола

Эта вкладка позволяет вам указать до 10 разделов из базы данных AISC 13th Edition для использования во встроенном элементе.

Квадратные кнопки в верхней части вкладки используются для представления частей компонентов, составляющих вашу построенную форму. Если для конкретной кнопки указан раздел, под соответствующей кнопкой будет показан маленький зеленый треугольник, направленный вверх. Нажмите любую кнопку, чтобы добавить раздел или вид и изменить раздел, который уже назначен этой кнопке.

Примечание. Важно понимать, что пронумерованные кнопки на различных вкладках НЕ представляют разные застроенные формы. Вместо этого каждый экземпляр этого модуля создает только ОДНУ построенную форму, а общая построенная форма состоит из композиции ВСЕХ секций, которые в настоящее время существуют на ЛЮБЫХ кнопках на вкладке Свернутое сечение / Таблица, на вкладке Прямоугольные и круглые, и вкладка Общие фигуры.

Чтобы вставить раздел AISC, вы можете:

• Введите имя раздела и нажмите [Tab]. Модуль будет искать в базе данных и извлекать информацию.

• Используйте кнопку [Обзор стальных профилей], чтобы отобразить базу данных стали, в которой вы можете перемещаться и выбирать желаемое сечение.

Угол поворота: против часовой стрелки

Если вам нужно повернуть секцию, нажмите одну из четырех кнопок углового поворота.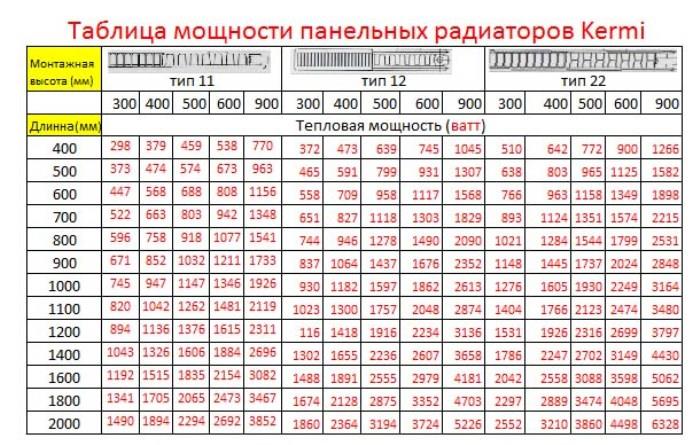

Повернуть секцию на 180 градусов вокруг оси Y

Этот флажок отображается только для одноугловых секций.При необходимости он предлагает возможность зеркального отражения одноугловой секции.

Xcg и Ycg

Введите положение центральной оси сечения, отсчитываемой от точки отсчета (начало вашей предполагаемой декартовой системы координат X-Y).

Раздел Недвижимость

Эти значения будут заполнены после того, как вы сделаете выбор из базы данных AISC. ОДНАКО вы можете изменить эти значения самостоятельно. Особое значение для несимметричных секций имеет ввод правильного положения «Xbar» и «Ybar».Это расстояние от нижнего левого края секции, измеренное вверх и вправо, до положения центральной оси секции.

База данных стальных профилей

Нажмите кнопку [Обзор стальных профилей], чтобы открыть окно базы данных AISC:

Прямоугольный и круглый язычок

На этой вкладке можно указать простые прямоугольные и круглые формы.

Квадратные кнопки в верхней части вкладки используются для представления частей компонентов, составляющих вашу построенную форму.Если для конкретной кнопки указан раздел, под соответствующей кнопкой будет показан маленький зеленый треугольник, направленный вверх. Нажмите любую кнопку, чтобы добавить раздел или вид и изменить раздел, который уже назначен этой кнопке.

Не используется / Прямоугольный / Круглый

Выберите форму, которую вы хотите использовать для этого предмета.

Прямоугольный ввод данных

Если выбрана прямоугольная форма, ввод данных состоит из высоты и ширины.

Круговой ввод данных

Когда выбрана круглая форма, ввод данных состоит из внешнего радиуса и толщины стенки (не внутреннего радиуса). Чтобы смоделировать твердое круглое сечение, введите соответствующий внешний радиус и установите для толщины стенки ноль.

Xcg и Ycg

Вкладка General Shapes

Эта вкладка позволяет вам выбирать из ряда распространенных многоугольных форм. При каждом выборе будут меняться справочные чертежи и подсказки для ввода данных.

Квадратные кнопки в верхней части вкладки используются для представления частей компонентов, составляющих вашу построенную форму. Если для конкретной кнопки указан раздел, под соответствующей кнопкой будет показан маленький зеленый треугольник, направленный вверх.Нажмите любую кнопку, чтобы добавить раздел или вид и изменить раздел, который уже назначен этой кнопке.

Xcg и Ycg

Угол поворота: против часовой стрелки

Для этих форм вы можете повернуть секцию с шагом в один градус. Положительные углы соответствуют вращению против часовой стрелки.

Вкладка результатов

Подробная таблица свойств

В этой таблице перечислены все компоненты, которые вы добавили в раздел. Он сообщает об их индивидуальном расположении, свойствах и максимальном расстоянии от центра тяжести для каждого из четырех ребер.

Примечание. Эта таблица прокручивается вправо. Просто используйте полосу прокрутки внизу таблицы.

Общая площадь

Общая площадь всех определенных форм, включая площадь любых секций AISC, которые были включены в построенную форму.

Инерция: Ixx и Iyy

Общий момент инерции составной секции определяется путем применения следующего уравнения ко всем заданным формам:

Ixx = Iox + (A * dy2) и Iyy = Ioy + (A * dx2)

, где d = расстояние от центра тяжести фигуры. в целом C.G. составного сечения, измеренного в направлении, указанном нижним индексом.

Модуль упругости сечения: Sxx и Syy

Эти значения являются расчетными модулями сечения композитного сечения. Значения определяются путем деления Ixx или Iyy на крайние расстояния между волокнами выше, ниже, справа и слева от центра тяжести секции.

Радиус вращения

Радиус вращения составного сечения определяется с помощью типичного уравнения: rxx = (Ixx / A) ½ и ryy = (Iyy / A) ½.

Максимальное расстояние от CG

Для каждой из секций построенной формы в этих столбцах указано расстояние от крайних волокон этой секции до C.Г. составного раздела.

Эскиз

Калькулятор свободного момента инерции (второй момент площади)

Как пользоваться калькулятором свободного сечения

Калькулятор сечения ClearCalcs позволяет пользователю вводить геометрию произвольного поперечного сечения, используя любые простые размеры. формы или полностью настраиваемые определения контуров. Затем он определяет упругие, деформирующие и / или пластические свойства этого сечения, включая площади, координаты центра тяжести, вторые моменты площади / моменты инерции, модули сечения, главные оси, постоянную кручения и многое другое!

Вы можете использовать свойства поперечного сечения из этого инструмента в нашем калькуляторе свободных балок.

Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов, а также позволит использовать эти индивидуальные поперечные сечения в этих проектах. ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.

Лист разделен на два основных раздела:

«Ключевые свойства», в которых определяется геометрия поперечного сечения.
«Сводка», где выбирается тип анализа и отображаются рассчитанные свойства.

Раздел «Комментарии» также включен для того, чтобы пользователь мог оставить какие-либо конкретные примечания по дизайну. Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.

1. Свойства входного ключа

Сначала выберите Тип поперечного сечения из раскрывающегося меню чуть ниже диаграммы. Когда вы это сделаете, поля ввода под ним изменится на те, которые требуются для данного типа поперечного сечения.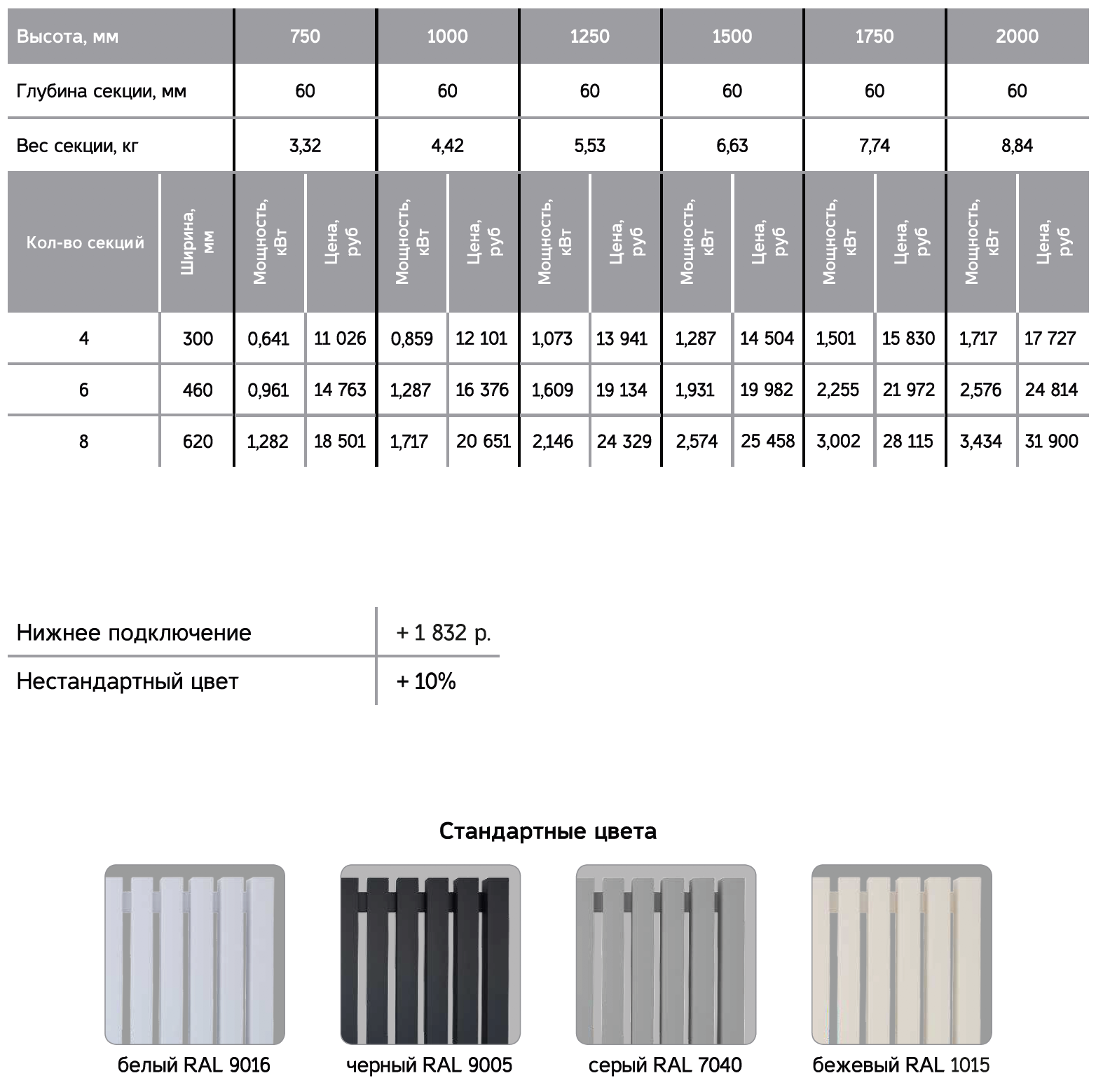

Например, прямоугольник имеет два измерения для его определения: глубина и ширина .Оба размера должны быть больше нуля, но других ограничений нет.

Некоторые другие типы поперечного сечения имеют особые ограничения. Например, двутавровое сечение . Глубина должна быть больше, чем в два раза больше толщины фланца плюс два раза внутреннего радиуса . Подобные ограничения являются просто логическими ограничениями геометрии; перекрытия или неполные радиусы скругления физически невозможны.

На схеме в этом разделе будет показано поперечное сечение в том виде, в каком оно было введено, а также некоторые ключевые свойства этого поперечного сечения, включая центроид, ориентацию главной оси и, если были выполнены соответствующие типы анализа , центр тяжести пластика и центр сдвига.

Итоговые результаты вычислений и типы анализа

Доступны четыре различных варианта анализа Тип : «Только эластичность», «Упругость + деформация», «Эластичность + пластик» и «Все». По умолчанию и самый быстрый вариант — «Только эластичность», в то время как другие варианты также добавляют анализ деформации и / или пластичности. Обратите внимание, что эластичный анализ всегда выполняется в каждом варианте. Различные выходные данные, рассчитанные в каждом из этих типов анализа, описаны ниже:

Анализ упругости

Угол главной главной оси : Большая главная ось (ось «1») может быть наклонена для несимметричных участков, или она может быть под углом 90 градусов, если поперечная жесткость секции больше, чем вертикальная.Это определяет его угол относительно оси X. Обратите внимание, что малая главная ось (ось «2») точно перпендикулярна ей. Ориентация главной оси также указана на диаграмме поперечного сечения.
Площадь : Площадь поперечного сечения сечения. Это значение обычно используется при определении осевой прочности колонны.
Первые моменты площади : Первые моменты площади важны для определенных расчетов сдвига, например, сдвигового потока. 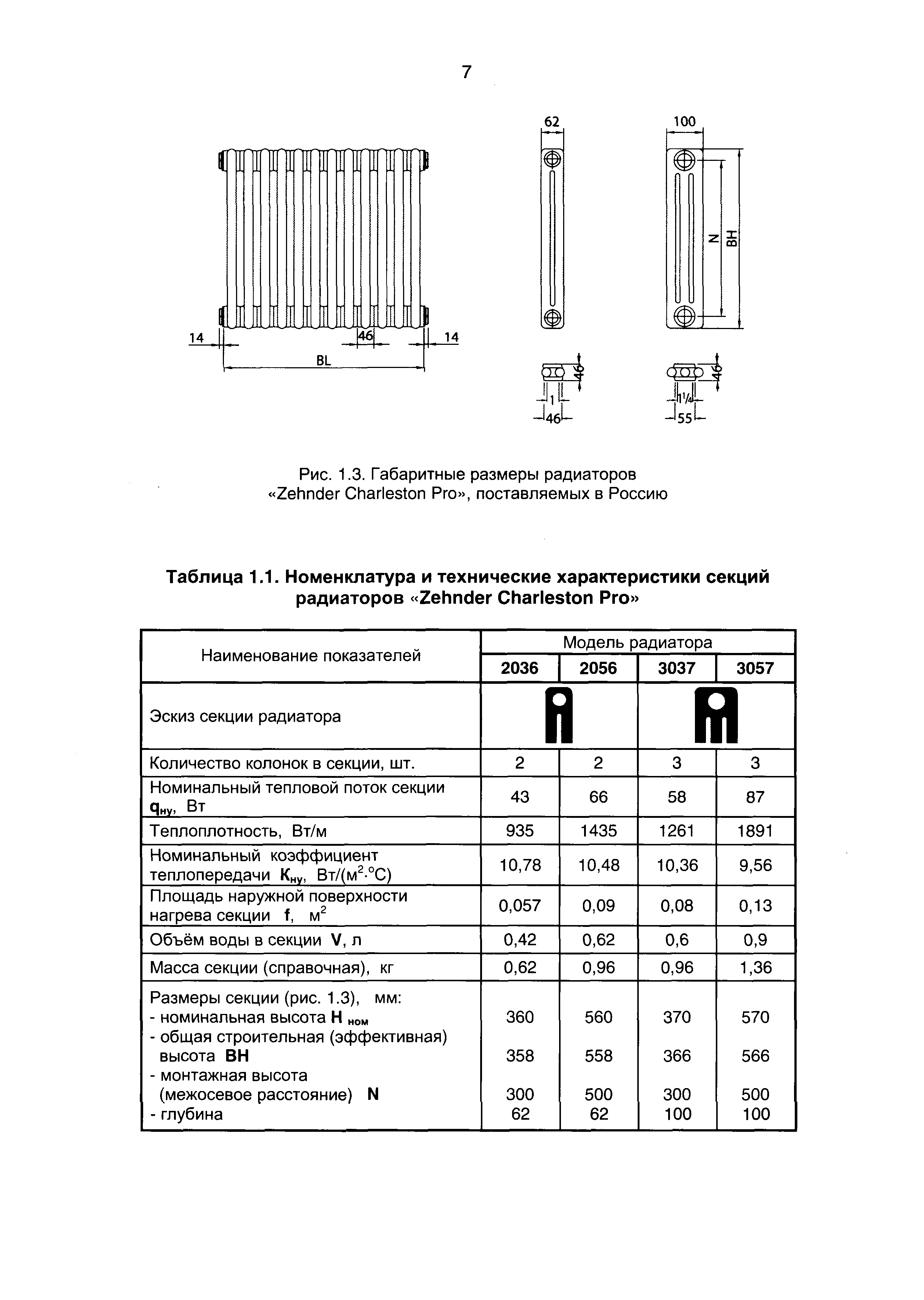Обратите внимание, что первые моменты измеряются относительно центроида и геометрических осей.
Вторые моменты площади / моменты инерции : Вторые моменты площади, также известные в технике как моменты инерции, связаны с прочностью на изгиб и прогибом балки. Обратите внимание, что все значения берутся относительно центра тяжести поперечного сечения, хотя значения доступны как для геометрической, так и для главной осей. Полярный момент инерции идентичен для обоих типов осей, поскольку ось «Z» всегда считается такой же, как ось «3».Момент инерции продукта по определению равен нулю для главных осей.
Модули упругого сечения : Модули упругого сечения равны вторым моментам площади / моментам инерции, деленным на расстояние до самого дальнего волокна в поперечном сечении, перпендикулярном оси изгиба. Предусмотрены значения как для положительного, так и для отрицательного изгиба, где положительный изгиб определяется как самая верхняя или самая левая часть поперечного сечения, находящаяся в состоянии сжатия. Значения также предоставляются как для геометрической, так и для главной осей и всегда находятся около центра тяжести.N.B. Модуль упругого сечения также известен как модуль статического сечения.
Расстояние от центра тяжести до крайних волокон : расстояние между центром тяжести поперечного сечения и крайним волокном поперечного сечения, перпендикулярно оси изгиба. Вторые моменты площади / моменты инерции, разделенные на эти расстояния, будут равны модулям упругого сечения.
Радиусы вращения : Радиусы вращения представляют собой среднеквадратичные расстояния каждого волокна в поперечном сечении относительно данной оси.Значения всегда относятся к центроиду и доступны как по геометрической, так и по главной осям. Полярный радиус вращения одинаков для обоих типов осей, поскольку ось «Z» всегда считается такой же, как ось «3».
Центроид : Расположение центроида показано на диаграмме поперечного сечения. Наведите указатель мыши на значок зеленого круга, и всплывающая подсказка отобразит точные координаты центроида. Обратите внимание, что исходная точка (0,0) обозначена синим перекрестием.

Анализ коробления

Константа кручения Сен-Венана : Постоянная кручения связана с тем, насколько хорошо поперечное сечение может противостоять чистым скручивающим силам, и обычно используется в формулах продольного изгиба при кручении.
Константа деформации : При приложении силы скручивания или эксцентрика поперечное сечение может не только скручиваться, но и деформироваться. Эта константа является мерой того, насколько легко может произойти коробление, и часто используется в формулах продольного изгиба при кручении.
Зоны сдвига : Только часть поперечного сечения будет эффективно противостоять силе сдвига, приложенной вокруг данной оси (то есть силе сдвига, перпендикулярной данной оси). Показанные значения основаны на интегрировании сдвигового потока и поэтому могут не точно соответствовать классическим расчетам, основанным на областях полотна.
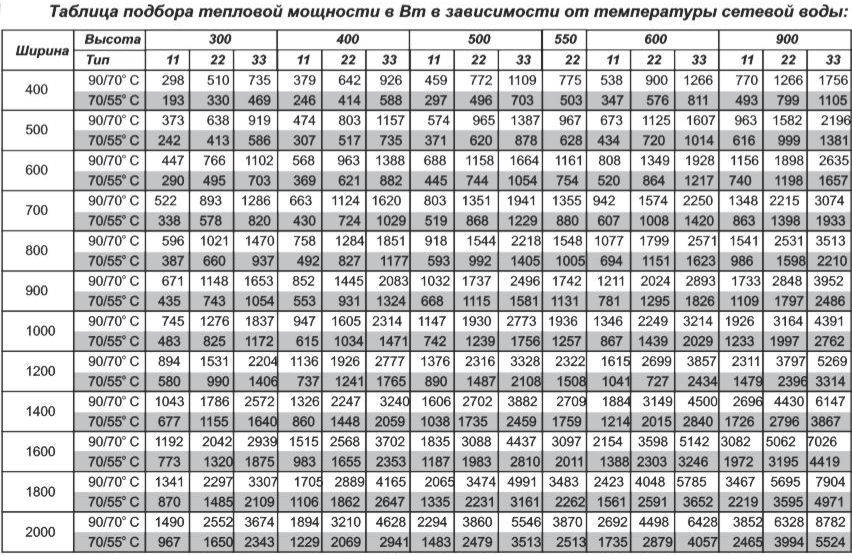
Константы моносимметрии : Константы моносимметрии определяют, насколько близко сечение должно быть симметричным. Константа приближается к нулю, когда поперечное сечение симметрично относительно данной оси.
Центр сдвига : Расположение центра сдвига показано на диаграмме поперечного сечения. Наведите указатель мыши на значок звездочки, и всплывающая подсказка отобразит точные координаты центра сдвига. Обратите внимание, что исходная точка (0,0) обозначена синим перекрестием.

Анализ пластичности

Модули пластического сечения : Модули пластического сечения показаны как для геометрической, так и для главной осей. Обратите внимание, что хотя модуль пластического сечения не зависит от направления изгиба, коэффициент формы, который представляет собой отношение модулей пластического сечения к упругому сечению, зависит от этого.
Пластиковый центроид : Расположение пластикового центроида показано на диаграмме поперечного сечения. Наведите указатель мыши на оранжевый квадратный значок, и всплывающая подсказка отобразит точные координаты пластикового центроида. Обратите внимание, что исходная точка (0,0) обозначена синим перекрестием.

Расчет и оптимизация модуля сечения: Skill-Lync

Для расчета катионов модуля упругости сечения для сечения кожуха и оптимизации сечения кожуха для улучшения модуля сечения.

Модуль упругости сечения — это геометрическое свойство данного поперечного сечения, используемое при проектировании изгибаемых элементов. Модуль сечения зависит только от формы поперечного сечения балки или конструкции. Для симметричных сечений значение модуля сечения одинаково как выше, так и ниже центра тяжести сечения. Асимметричное сечение имеет два значения для верхней и нижней части центроида: максимальный модуль упругости (S _max) и минимальный модуль упругости (S _min)

Важное значение модуля упругости сечения

Модуль упругости сечения является важным фактором при проектировании балок и изгибаемых элементов
Чем выше модуль сечения, тем выше сопротивление изгибу.
Проще рассчитать прочность и напряжения в балках.
Если две балки изготовлены из одного материала и сравнивается модуль сечения двух балок, и наоборот, балка с большим модулем сечения будет более жесткой и более способной выдерживать большие нагрузки.

Модуль упругости сечения определяется как

`S = I / Y` …………………………………… (1)

Где I — второй момент площади (или момент инерции), а y — расстояние от нейтральной оси до крайнего конца.Это часто указывается с использованием Y = c, где c — расстояние от нейтральной оси до самого крайнего конца.

Символ S обычно используется для обозначения модуля сечения. Как правило, по мере увеличения модуля сечения увеличивается и прочность на изгиб. Что касается изгиба, максимальное изгибающее напряжение σ, действующее на внешнюю поверхность детали, можно рассчитать с помощью следующего уравнения.

`σ = M / S` …………………………………… (2)

Где σ — максимальное напряжение изгиба (кгс / см ²), а M — максимальный изгибающий момент (кгс * м)

Таким образом, из уравнений (1) и (2) можно сказать, что чем выше модуль упругости сечения, тем выше модуль упругости сечения, тем выше будет сопротивление изгибу.

Данное сечение будет из нержавеющей стали AISI 302 — холодный валок — y = 520 МПа, здесь сечение будет рассматриваться как сечение кожуха.

Случай 1: — Модуль упругости сечения первоначальной конструкции вытяжки

Момент инерции поперечного сечения кожуха определяется с помощью команды под названием «Анализ инерции сечения» в NX 12. Следующие результаты получены, как показано ниже.

Рисунок 1 Поперечный разрез кожуха 1

Рисунок 2 Секция Инерция вытяжки 1

Из приведенного выше анализа получаем следующие минимальный и максимальный момент инерции

I _макс = 5.145 e ⁺⁰⁶ мм ⁴

I _мин = 1,537 e ⁺⁰⁴ мм ⁴

^“ Y ^” для секции вытяжки 1 = 447,3 мм

S _макс = I _макс / Y = 5,145 e ⁺⁰⁶ / 447,3 = 11502,34 мм ³

S _мин = I _мин / Y = 1,537 e ⁺⁰⁴ / 447,3 = 34,37 мм ³

Случай 2: — Модуль сечения конструкции капота после модификации

Модуль упругости сечения также может быть представлен как

S = Σ м _i A _i ² / Y где A — площадь сечения, а M — масса тела

Из приведенного выше уравнения можно заметить, что модуль упругости сечения тела прямо пропорционален площади сечения тела.

Здесь площадь сечения увеличивается за счет уменьшения глубины тиснения на 2-3 мм, смещения внешней панели на 1-2 мм и увеличения количества тиснений для лучшей инерции. Это, в свою очередь, увеличивает значение модуля сечения

Рисунок 3 Поперечный разрез кожуха 2 после модификации

Рисунок 4 Сечение Инерция кожуха 2 после модификации

Из приведенного выше анализа получаем следующие минимальный и максимальный момент инерции

I _макс = 5.190 e ⁺⁰⁶ мм ⁴

I _мин = 1,696 e ⁺⁰⁴ мм ⁴

^“ Y ^” для секции вытяжки 2 = 447,3 мм

S _макс = I _макс / Y = 5,190 e ⁺⁰⁶ / 447,3 = 11603,01 мм ³

S _мин = I _мин / Y = 1,696 e ⁺⁰⁴ / 447,3 = 37,93 мм ³

При сравнении значений сечения в случае 1 и случае 2, мы видим, что улучшенная модель увеличилась на 1%.
Первоначальная конструкция вытяжки оптимизирована для расчета второй модели вытяжки.
За счет увеличения сопротивления изгибающему напряжению оптимизируем конструкцию.

Как рассчитать модуль упругости сечения трубы

Обновлено 22 декабря 2020 г.

Автор: Кевин Бек

Модуль упругости сечения — это геометрическое (то есть связанное с формой) свойство балки, используемой в строительстве. Обозначается Z , это прямая мера прочности балки.Этот вид модуля упругости сечения является одним из двух в инженерии и конкретно называется модулем упругости сечения. Другой вид модуля упругости — это модуль упругости пластмассы .

Трубы и другие формы трубок столь же важны, как и автономные балки в мире строительства, а их уникальная геометрия подразумевает, что расчет модуля сечения для этого типа материала отличается от расчета модуля сечения для других типов. Для определения модуля упругости сечения необходимо знать различные внутренние или встроенные и неизменяемые свойства рассматриваемого материала.

Основа модуля упругости сечения

Различные балки, изготовленные из различных комбинаций материалов, могут иметь большие различия в распределении более мелких отдельных волокон в этом участке балки, трубы или другого рассматриваемого структурного элемента. «Крайние волокна» или волокна на концах секций вынуждены нести большую часть нагрузки, которой подвергается секция.

Определение модуля сечения Z требует определения расстояния y от центра тяжести сечения, также называемого нейтральной осью , до крайних волокон.

Уравнение модуля сечения

Уравнение модуля сечения для упругого объекта задается следующим образом: Z = I / y , где y — расстояние, описанное выше, и I — второй момент области сечения. (Этот параметр иногда называют моментом инерции , но, поскольку есть и другие применения этого термина в физике, лучше всего использовать «второй момент площади».)

Поскольку разные лучи имеют разные формы, конкретные уравнения для разных разделов принимают разные формы.4).

Что такое «Второй момент области»?

Второй момент области I является внутренним свойством секции и отражает тот факт, что масса секции может распределяться асимметрично и влиять на то, как обрабатываются нагрузки.

Представьте себе прочную стальную дверь заданного размера и массы и дверь такого же размера и массы, у которой почти вся масса находится на внешнем крае, но при этом очень тонкая в середине. Интуиция и опыт, вероятно, подсказывают вам, что последняя дверь менее охотно отреагирует на попытку открыть ее ближе к петле, чем дверь с однородной конструкцией и, следовательно, с большей массой, расположенная ближе к петле.2} {6}

, где b — ширина поперечного сечения, а h — высота.

Онлайн-калькулятор модуля сечения

Хотя онлайн-калькуляторы модуля сечения легко найти для всех видов форм, хорошо иметь четкое представление об уравнениях и о том, почему переменные такие, какие они есть, и почему они появляются там, где они формулы.

Точный расчет количества радиаторов (секций) отопления

Упрощенные варианты расчета радиаторов отопления в доме

Первый способ: Расчет по объему комнат

Второй способ: Расчет по площади помещений

Примерный расчет количества секций радиатора для типового помещения

Точный расчет необходимого количества секций радиаторов

Расчет количества секций биметаллического радиатора

Почему именно биметаллические батареи

Базовый расчет

Формула для расчета по объему

Когда нужна повышенная точность

Остекление и теплоизоляция

Температура, тип помещения, высота потолков

Расчет количества секций радиаторов отопления на 1 кв.м

Стандартный расчет радиаторов отопления

Примерный расчет — сколько секций батареи на квадратный метр

Расчет количества секций биметаллического радиатора – сколько нужно ребер

Определение по площади комнаты

Наиболее точная методика расчета числа секций с учетом поправочных коэффициентов

Описание и расшифровка поправочных коэффициентов

Расчет секций радиаторов: по площади, объему

Расчет по площади

Пример расчета количества секций радиаторов по площади помещения

Считаем батареи по объему

Пример расчета по объему

Теплоотдача одной секции

Расчет секций радиаторов в зависимости от реальных условий

Расчёт количества секций радиатора отопления

СНиП и основные предписания

Расчет по объему

Расчет по площади

Поправки, вносимые в расчет и советы

Расчет радиаторов отопления, как рассчитать количество секций радиаторы калукулятор

Расчет статического или первого момента площади сечения балки

Свойства поперечного сечения | MechaniCalc

Недвижимость участков

Центроид

Центроидное расстояние

Первый момент области

Площадь Момент инерции

Теорема о параллельной оси

Полярный момент инерции

Модуль упругости сечения

Радиус вращения

Свойства общих сечений

Банкноты

Примечание 1: Прогиб балки

Список литературы

Свойства секции канала (U) | calcresource

Определения

Оглавление

Геометрия

Момент инерции

Почему полезен момент инерции

Полярный момент инерции

Модуль упругого сечения

Модуль упругости сечения при пластике

Вокруг оси x

Вокруг оси Y

Радиус вращения

Похожие страницы

Расчетные модули> Прочие расчетные модули> Калькулятор свойств общего раздела

Калькулятор свободного момента инерции (второй момент площади)

Как пользоваться калькулятором свободного сечения

1. Свойства входного ключа

Итоговые результаты вычислений и типы анализа

Анализ упругости

Анализ коробления

Анализ пластичности

Расчет и оптимизация модуля сечения: Skill-Lync

Как рассчитать модуль упругости сечения трубы

Основа модуля упругости сечения

Уравнение модуля сечения

Что такое «Второй момент области»?

Онлайн-калькулятор модуля сечения

Добавить комментарий Отменить ответ