Основы расчёта ферм: ручной и машинный счёт
 Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.
Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.
Рисунок 1
Фермы классифицируются:
- по очертанию внешнего контура;
- по виду решётки;
- по способу опирания;
- по назначению;
- по уровню проезда транспорта.
Также выделяют простейшие и сложные фермы. Простейшими называют фермы, образованные последовательным присоединением шарнирного треугольника. Такие конструкции отличаются геометрической неизменяемостью, статической определимостью. Фермы со сложной структурой, как правило, статически неопределимы.
Для успешного расчёта необходимо знать виды связей и уметь определять реакции опор. Эти задачи подробно рассматриваются в курсе теоретической механики. Разницу между нагрузкой и внутренним усилием, а также первичные навыки определения последних дают в курсе сопротивления материалов.
Рассмотрим основные методы расчёта статически определимых плоских ферм.
Способ проекций
На рис. 2 симметричная шарнирно-опёртая раскосная ферма пролётом L = 30 м, состоящая из шести панелей 5 на 5 метров. К верхнему поясу приложены единичные нагрузки P = 10 кН. Определим продольные усилия в стержнях фермы. Собственным весом элементов пренебрегаем.
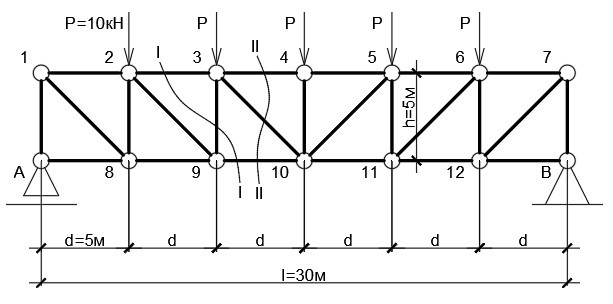
Рисунок 2
Опорные реакции определяются путём приведения фермы к балке на двух шарнирных опорах. Величина реакций составит R (A) = R (B) = ∑P/2 = 25 кН. Строим балочную эпюру моментов, а на её основе — балочную эпюру поперечных усилий (она понадобится для проверки). За положительное направление принимаем то, что будет закручивать среднюю линию балки по часовой стрелке.
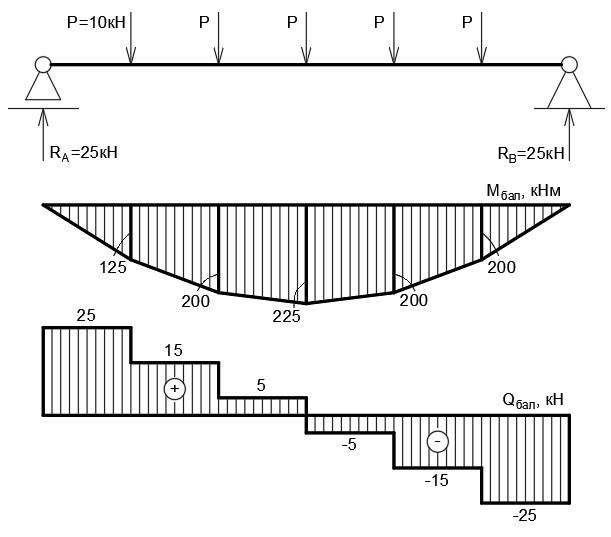
Рисунок 3
Метод вырезания узла
Метод вырезания узла заключается в отсечении отдельно взятого узла конструкции с обязательной заменой разрезаемых стержней внутренними усилиями с последующим составлением уравнений равновесия. Суммы проекций сил на оси координат должны равняться нулю
Рационально начинать с узла, в котором сходится не более двух стержней. Составим уравнения равновесия для опоры, А (рис. 4).
∑ F (y) = 0: R (A) + N (A-1) = 0
∑ F (x) = 0: N (A-8) = 0
Очевидно, что N (A-1) = -25кН. Знак «минус» означает сжатие, усилие направлено в узел (мы отразим это на финальной эпюре).
Условие равновесия для узла 1:
∑ F (y) = 0: -N (A-1) — N (1−8)∙cos45° = 0
∑ F (x) = 0: N (1−2) + N (1−8)∙sin45° = 0
Из первого выражения получаем N (1−8) = —N (A-1)/cos45° = 25кН/0,707 = 35,4 кН. Значение положительное, раскос испытывает растяжение. N (1−2) = -25 кН, верхний пояс сжимается. По этому принципу можно рассчитать всю конструкцию (рис. 4).
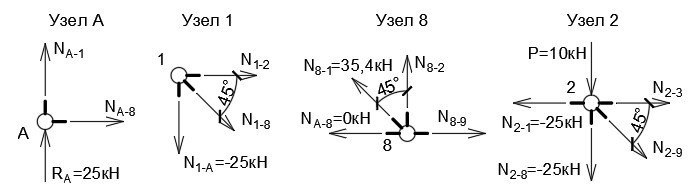
Рисунок 4
Метод сечений
Ферму мысленно разделяют сечением, проходящим как минимум по трём стержням, два из которых параллельны друг другу. Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.
Проведём сечение I-I (рис. 5) и отбросим правую часть. Заменим стержни растягивающими усилиями. Просуммируем силы по осям:
∑ F(y) = 0: R(A) — P + N(9−3)
N(9−3) = P — R(A) = 10 кН — 25 кН = -15 кН
Стойка 9−3 сжимается.
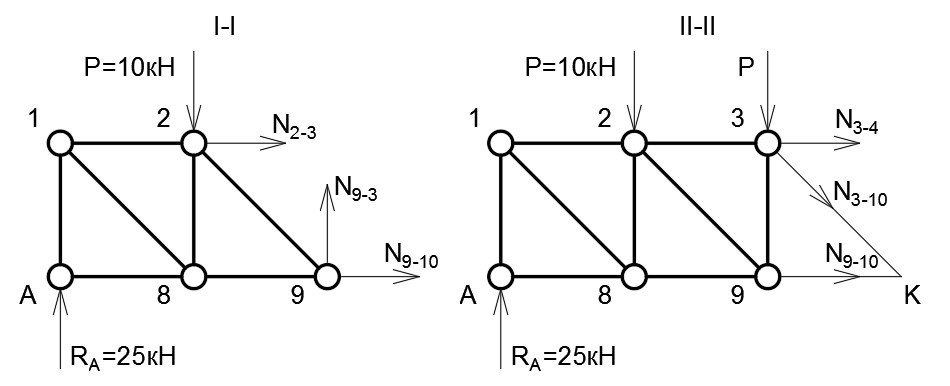
Рисунок 5
Способ проекций удобно применять в расчётах ферм с параллельными поясами, загруженными вертикальной нагрузкой. В этом случае не придётся вычислять углы наклона усилий к ортогональным осям координат. Последовательно вырезая узлы и проводя сечения, мы получим значения усилий во всех частях конструкции. Недостатком способа проекций является то, что ошибочный результат на ранних этапах расчёта повлечёт за собой ошибки во всех дальнейших вычислениях.
Способ моментной точки
Способ моментной точки требует составлять уравнение моментов относительно точки пересечения двух неизвестных сил. Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.
Рассмотрим сечение II-II (рис. 5). Стержни 3−4 и 3−10 пересекаются в узле 3, стержни 3−10 и 9−10 пересекаются в узле 10 (точка K). Составим уравнения моментов. Суммы моментов относительно точек пересечения будут равняться нулю. Положительным принимаем момент, вращающий конструкцию по часовой стрелке.
∑ m(3) = 0: 2d∙R(A) — d∙P — h∙N(9−10) = 0
∑ m(K) = 0: 3d∙R(A) — 2d∙P — d∙P + h∙N(3−4) = 0
Из уравнений выражаем неизвестные:
N(9−10) = (2d∙R(A) — d∙P)/h = (2∙5м∙25кН — 5м∙10кН)/5м = 40 кН (растяжение)
N(3−4) = (-3d∙R(A) + 2d∙P + d∙P)/h = (-3∙5м∙25кН + 2∙5м∙10кН + 5м∙10кН)/5м = -45 кН (сжатие)
Способ моментной точки позволяет определить внутренние усилия независимо друг от друга, поэтому влияние одного ошибочного результата на качество последующих вычислений исключено. Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).
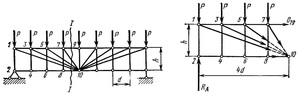
Рисунок 6
Требуется определить усилие в верхнем поясе 7−9. Известны размеры d и h, нагрузка P. Реакции опор R(A) = R(B) = 4,5P. Проведём сечение I-I и просуммируем моменты относительно точки 10. Усилия от раскосов и нижнего пояса не попадут в уравнение равновесия, так как сходятся в точке 10. Так мы избавляемся от пяти из шести неизвестных:
∑ m(10) = 0: 4d∙R(A) — d∙P∙(4+3+2+1) + h∙O(7−9) = 0
O(7−9) = -8d∙P/h
Аналогично можно рассчитать остальные стержни верхнего пояса.
Признаки нулевого стержня
Нулевым называют стержень, в котором усилие равно нулю. Выделяют ряд частных случаев, в которых гарантированно встречается нулевой стержень.
- Равновесие ненагруженного узла, состоящего из двух стержней, возможно только в том случае, если оба стержня нулевые.
- В ненагруженном узле из трёх стержней одиночный (не лежащий на одной прямой с остальными двумя) стержень будет нулевым.
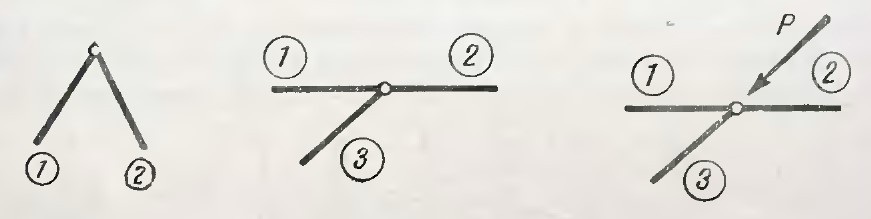
Рисунок 7
- В трехстержневом узле без нагрузки усилие в одиночном стержне будет равно по модулю и обратно по направлению приложенной нагрузке. При этом усилия в стержнях, лежащих на одной прямой, будут равны друг другу, и определятся расчётом N(3) = -P, N(1) = N(2).
- Трехстержневой узел с одиночным стержнем и нагрузкой, приложенной в произвольном направлении. Нагрузка P раскладывается на составляющие P’ и P» по правилу треугольника параллельно осям элементов. Тогда N(1) =
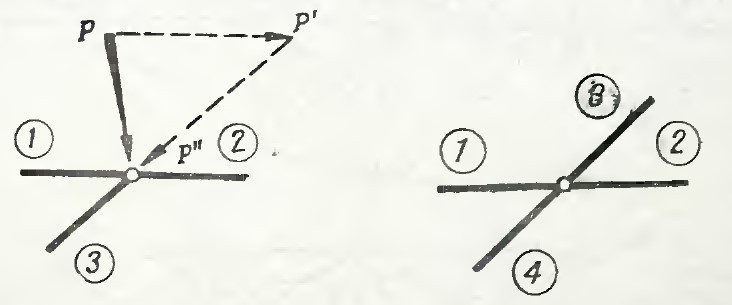
Рисунок 8
- В ненагруженном узле из четырёх стержней, оси которых направлены по двум прямым, усилия будут попарно равны N(1) = N(2), N(3) = N(4).
Пользуясь методом вырезания узлов и зная правила нулевого стержня, можно проводить проверку расчётов, проведённых другими методами.
Расчёт ферм на персональном компьютере
Современные вычислительные комплексы основаны на методе конечного элемента. С их помощью осуществляют расчёты ферм любого очертания и геометрической сложности. Профессиональные программные пакеты Stark ES, SCAD Office, ПК Лира обладают широким функционалом и, к сожалению, высокой стоимостью, а также требуют глубокого понимания теории упругости и строительной механики. Для учебных целей и подойдут бесплатные аналоги, например Полюс 2.1.1.
В Полюсе можно рассчитывать плоские статически определимые и неопределимые стержневые конструкции (балки, фермы, рамы) на силовое воздействие, определять перемещения и температурное воздействие. Перед нами эпюра продольных усилий для фермы, изображённой на рис. 2. Ординаты графика совпадают с полученными вручную результатами.

Рисунок 9
Порядок работы в программе Полюс
- На панели инструментов (слева) выбираем элемент «опора». Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
- Двойной клик по опоре. Во всплывающем окне «свойства узла» задаём точные координаты в метрах. Положительное направление осей координат — вправо и вверх соответственно. Если узел не будет использоваться в качестве опоры,
- Далее размещаем узлы фермы. Выбираем элемент «свободный узел», кликаем по свободному полю, точные координаты прописываем для каждого узла в отдельности.
- На панели инструментов выбираем «стержень». Кликаем на начальном узле, отпускаем кнопку мышки. Затем кликаем на конечном узле. По умолчанию стержень имеет шарниры на двух концах и единичную жёсткость. Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
- Для загружения ферм используем инструмент «сила», нагрузка прикладывается в узлах. Для сил, прикладываемых не строго вертикально или горизонтально, устанавливаем параметр «под углом», после чего вводим угол наклона к горизонтали. Альтернативно можно сразу ввести значение проекций силы на ортогональные оси.
- Программа считает результат автоматически. На панели задач (вверху) можно переключать режимы отображения внутренних усилий (M, Q, N), а также опорных реакций (R). Результатом будет эпюра внутренних усилий в заданной конструкции.
В качестве примера рассчитаем сложную раскосную ферму, рассмотренную в методе моментной точки (рис. 6). Примем размеры и нагрузки: d = 3м, h = 6м, P = 100Н. По выведенной ранее формуле значение усилия в верхнем поясе фермы будет равно:
O(7−9) = -8d∙P/h = -8∙3м∙100Н/6м = -400 Н (сжатие)
Эпюра продольных усилий, полученная в Полюсе:
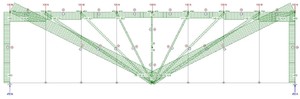
Рисунок 10
Значения совпадают, конструкция смоделирована верно.
Список литературы
- Дарков А. В., Шапошников Н. Н. — Строительная механика: учебник для строительных специализированных вузов — М.: Высшая школа, 1986.
- Рабинович И. М. — Основы строительной механики стержневых систем — М.: 1960.
Сегодня фермы из профильной трубы по праву считаются идеальным решением для строительства гаража, жилого дома и приусадебных построек. Прочные и долговечные, такие конструкции обходятся недорого, быстры в исполнении, и с ними способен справиться любой, кто хоть немного разбирается в математике и имеет навыки резки и сварки.
А как правильно подобрать профиль, рассчитать ферму, сделать в ней перемычки и установить, мы сейчас подробно расскажем. Для этого мы подготовили для вас подробные мастер-классы изготовления таких ферм, видео-уроки и ценные советы от наших экспертов!
И так, что такое ферма? Это конструкция, которая связывает опоры вместе в одно единое целое. Другими словами, ферма относится к простым архитектурным конструкциям, среди ценных преимуществ которой выделим такие: высокая прочность, отличные показатели эксплуатации, невысокая стоимость и хорошая устойчивость к деформациям и внешним нагрузкам.
Благодаря тому, что такие фермы обладают высокой несущей способностью, их ставят под любые кровельные материалы, независимо от их веса.
Использование в строительстве металлических ферм из новых или прямоугольных замкнутых профилей считается одним из самых рациональных и конструктивных решений. И неспроста:
- Главный секрет – в экономии благодаря рациональной форме профиля и соединения всех элементов решетки.
- Еще одно ценное преимущество профильных труб для использования их изготовлении фермы – это равная устойчивость в двух плоскостях, замечательная обтекаемость и удобство эксплуатации.
- При всем своем малом весе такие фермы выдерживают серьезные нагрузки!
Отличаются стропильные фермы по очертанию поясов, типу сечения стержней и видам решетки. И при правильном подходе вы самостоятельно сможете сварить и установить ферму из профильной трубы любой сложности! Даже такую:
Итак, прежде, чем составить проект будущих ферм, сначала нужно определиться с такими важными пунктами:
- контуры, размер и форма будущей крыши;
- материал изготовления верхнего и нижнего пояса фермы, а также ее решетки;
- угол наклона и планируемая нагрузка.
Запомните одну простую вещь вещь: у каркаса из профильной трубы есть так называемые точки равновесия, которые важно определить для устойчивости всей фермы. И очень важно подобрать под эту нагрузку качественный материал:
Строят фермы из профильной трубы таких видов сечений: прямоугольного или квадратного. Таковые выпускаются разного размера сечения и диаметра, с разной толщиной стенок:
- Мы рекомендуем те, которые специально продаются для малогабаритных построек: такие идут до 4,5 метров длиной и имеют сечение 40х20х2 мм.
- Если вы будете изготавливать фермы длиннее 5 метров, тогда выбирайте профиль с параметрами 40х40х2 мм.
- Для полномасштабного строительства крыши жилого дома вам понадобятся профильные трубы с такими параметрами: 40х6
Как рассчитать ферму онлайн?

Продолжаем серию статей о расчетах сопромата онлайн. В этой статье я хочу поделиться онлайн-сервисами, которые позволяют рассчитывать фермы. С помощью сайтов, указанных в этой статье, Вы узнаете, как произвести расчет фермы онлайн: определить реакции в опорах и узнать усилия, возникающие в стержнях.
В такой отрасли, как строительство, ферма — элемент, который ничем нельзя заменить. Ее используют для построения мостов, ангаров, стадионов. Без нее не обойдется строительство павильонов, сцен, подиумов. Кузов автомобиля, корпус корабля, самолета также считают фермой. Что немаловажно, при создании проекта корабля или самолета расчеты прочности производят так же, как и при подсчете силы действия на структуру.
Данная система уникальна тем, что она неизменна под действием факторов внешней среды. Нагрузки на нее приходятся очень больше, но благодаря своему строению она заслужила особого внимания. Ферма — это огромное количество стержней, соединенных в одну систему. Давление приходится на места, в которых соединяются детали. На сегодняшний день в строительной отрасли отдают предпочтение жесткому скреплению, а не шарнирному.
Free Truss and Roof Calculator
Данный сервис расположен по адресу — skyciv.com/free-truss-calculator
Авторы данного проекта позиционируют свой онлайн-калькулятор как инструмент для проектирования ферм, который позволяет рассчитывать продольные усилия в стержнях, определить реакции, возникающие в опорах фермы и д.р.
Создатели также отмечают, что данный софт особенно полезен для проектирования мостовых ферм и стропильных систем деревянных крыш.
Сразу оговорюсь, бесплатный функционал программы имеет определенные ограничения: можно добавить не более 12-ти стержней, 2-ух опор и 5-ти сосредоточенных внешних сил. В платной версии ограничений нет. Для расчета простых ферменных конструкций, бесплатного функционала вполне хватает.
Пример расчета фермы онлайн
В этом разделе я покажу как создать расчетную схему простейшей фермы и получить результаты расчета.
Задаем узлы фермы
Первым делом необходимо задать узлы будущей фермы, которые дальше будут учитываться в расчете как простые шарниры. Для создания нового узла нужно выбрать кнопку – «Nodes».
Каждый задаваемый узел имеет свой уникальный идентификатор, к которому по ходу формирования расчетной схемы будем обращаться: при создании стержней фермы и приложении нагрузок. Для того чтобы создать новый узел, нужно задать его координаты по X и Y:

Примечание: рекомендуется первый узел задавать с координатами (0;0), так легче будет высчитывать координаты всех последующих узлов.
Создаем стержни фермы
Стержни задаются достаточно просто. Для создания нового стержня нужно выбрать кнопку — «Members». Далее нужно будет указать идентификатор узла, с которым будет соединятся стержень в начале и в конце. Вот что получилось у меня:

Назначаем опоры
 Для того, чтобы задать связи (опоры) фермы нужно выбрать кнопку – «Support». Эта программа имеет в своем функционале 6 видов связей. Я выберу классическую шарнирно-подвижную и неподвижную опору. Для того чтобы установить опору, нужно выбрать вид опоры и указать узел где ее нужно установить.
Для того, чтобы задать связи (опоры) фермы нужно выбрать кнопку – «Support». Эта программа имеет в своем функционале 6 видов связей. Я выберу классическую шарнирно-подвижную и неподвижную опору. Для того чтобы установить опору, нужно выбрать вид опоры и указать узел где ее нужно установить.
Прикладываем нагрузку
В данной программе на ферму можно накладывать все виды нагрузок: сосредоточенные силы (Point Loads) и моменты (Moments), распределенную нагрузку (Distributed Loads). Например, для приложения сосредоточенной силы, нужно выбрать узел и задать ее численное значение.
Получаем результаты расчета
После выполнения всех вышеописанных шагов, можно получить результаты расчета. Для этого нужно нажать кнопку – «Solve». Бесплатно можно вывести реакции в опорах фермы, значения продольных усилий. Также для каждого стержня указывается растянут он или сжат:

Вот такая есть полезная программа для расчета фермы онлайн!
Также для расчета фермы можно воспользоваться программой, описываемой на этой страничке.

3D Расчёт треугольной фермы — онлайн калькулятор
Инструкция для калькулятора расчета треугольной фермы
Введите значения размеров в миллиметрах:

X – Длина треугольной стропильной фермы зависит от размера пролета, который необходимо накрыть и способа ее крепления к стенам. Деревянные треугольные фермы применяют для пролетов длиной 6000-12000 мм. При выборе значения X нужно учитывать рекомендации СП 64.13330.2011 «Деревянные конструкции» (актуализированная редакция СНиП II-25-80).
Y – Высота треугольной фермы задается соотношением 1/5-1/6 длины X.

Z – Толщина, W – Ширина бруса для изготовления фермы. Искомое сечение бруса зависит от: нагрузок (постоянные – собственный вес конструкции и кровельного пирога, а также временно действующие – снеговые, ветровые), качества применяемого материала, длины перекрываемого пролета. Подробные рекомендации о выборе сечения бруса для изготовления фермы, наведены в СП 64.13330.2011 «Деревянные конструкции», также следует учитывать СП 20.13330.2011 «Нагрузки и воздействия». Древесина для несущих элементов деревянных конструкций должна удовлетворять требованиям 1, 2 и 3-го сорта по ГОСТ 8486-86 «Пиломатериалы хвойных пород. Технические условия».
S – Количество стоек (внутренних вертикальных балок). Чем больше стоек, тем выше расход материала, вес и несущая способность фермы.
Если необходимы подкосы для фермы (актуально для ферм большой протяженности) и нумерация деталей отметьте соответствующие пункты.
Отметив пункт «Черно-белый чертеж» Вы получите чертеж, приближенный к требованиям ГОСТ и сможете его распечатать, не расходуя зря цветную краску или тонер.
Нажмите «Рассчитать».
Треугольные деревянные фермы применяют в основном для кровель из материалов требующих значительного уклона. Онлайн калькулятор для расчета деревянной треугольной фермы поможет определить необходимое количество материала, выполнит чертежи фермы с указанием размеров и нумерацией деталей для упрощения процесса сборки. Также с помощью данного калькулятора Вы сможете узнать общую длину и объем пиломатериалов для стропильной фермы.
Расчет ферм
К вопросу о расчете плоских ферм (приложение к дискуссии)
Расчет фермы на прочность по способу вырезаний узлов довольно громоздкий. Расчет состоит из таких этапов (по Леоненко Д. В.):
1. Определение реакций опор фермы путем составления уравнений равновесия относительно точек опор:
2. Поочередно вырезаются узлы, в которых сходятся пояса (верхний и нижний), стойки и раскосы решетки фермы. Проектируя усилия на координатные оси хоу определяют характер (сжатие или растяжение) и величину усилий в стойках, раскосах и поясах панелей фермы. Таких узлов для фермы с тремя стойками и двумя раскосами –восемь:
3. По полученным результатам расчетов строится опора продольных сил во всех элементах фермы. Исходя из эпюры сил переходят к расчету прочности элементов фермы и подбору сечений этих элементов. Следуя технологичности изготовления фермы, при выборе сечения элементов принимают за расчетное максимальное усилие (например, в нижнем растянутом поясефермы действуют усилия 425 кГс, 425 кГс, 550 кГс, 375 кГс, следовательно, в расчет берут 550 кГс). Используя классическую формулу,
определяют напряжение в элементах фермы или момент сопротивления профиля (W), если определены положения, с последующим выбором определенного профиля из сортамента профилей.
Этот расчет классический и может применяться для расчета ответственных ферм в строительстве.
Если возникает необходимость запроектировать молонагруженную ферму для укрытия или козырька входа, когда на ферму действует снеговая нагрузка, ветровая нагрузки и собственный вес, можно рассматривать ферму, как балку с разнесенным сечением и следовательно расчет существенно упрощается что ведет к значительной экономии средств в малых предприятиях занимающихся металлоконструкциями.
В качестве примера можно привести способ увеличения несущей способности балки путем рассечения ее по стойке с последующей сваркой частей балки со смещением в местах примыкания (см. схему).
Такой способ применяли для производства панелей покрытия и стеновых панелей при строительстве быстромонтируемых зданий производственного назначения.
Определяем величину увеличения несущей способности балки после ее рассечения и сварки.
Стандартный профиль балки №30.
Балка рассеченная, сварная
Видно, что момент сопротивления балки в 4,3 раза, а значит возросла ее несущая способность.
Рассмотрим упрощенный расчет фермы из профильных труб (нижний и верхний пояса), стойки и раскосы из листового проката или труб меньшего поперечного сечения:
Сечение фермы в точке приложения сечения силы: используем формулу для определения момента сопротивления относительно оси Х (сопромат, табл. 1, стр. 37).
Определив изгибающий момент от действия Р вычисляется напряжение в нижнем (растянутом) поясе формы.
Где – допускаемое напряжение для материала (Сталь 3)
– момент сопротивления сечения составил 510,6 см3.
Для сравнения момент сопротивления двутавровой балки №30е (ГОСТ 8239-56) составляет 518 см3 (сопромат, табл. 6, стр. 90).
Рассмотрим расчет фермы из круглих труб (нижний и верхний пояса), стойки и раскосы из листового материала (или профильного) проката:
Сечения фермы в точке приложения силы Р будет. Используем известную методику определения момента сопротивления сложного сечения.
Где I – момент инерции трубчатого сечения. (сопромат, стр. 55, таб.1)
ymax – максимальное удаление поперечного сечения трубы от главной оси Х – Х.
(сопромат, стр. 21)
Определив изгибающий момент от действия силы Р, определим напряжение в нижнем (растянутом) поясе фермы.
Где – допускаемое напряжение для материала (Сталь 3)
Wx – момент сопротивления сечения составил 110,4 см3.
Для сравнения момент сопротивления двутавровой балки №22 (ГОСТ 8239-56) составляет 230 см3 (сопромат, табл. 6).
Рассмотрим расчет фермы из профильных труб прямоугольного сечения. Используем известную методику определения момента сопротивления сложного сечения.
Общий момент сопротивления будет относительно оси Х – Х.
(сопромат, стр. 31)
где
Общий момент сопротивления будет относительно оси х-х:
Рассчитав момент сопротивления сечения, можно определить напряжение в нижнем поясе фермы и выбрать необходимый профиль.
Выводы
1. Классический расчет фермы позволяет определить усилия во всех элементах фермы, однако он сложный и м. б. использован при расчете ответственных конструкций.
2. Упрощенный расчет фермы дает возможность определить прочностные характеристики опоеного сечения фермы и выбрать необходимые профили нижнего и верхнего поясов фермы.
Ткаченко Н.А. зам главного конструктора » ТОВ Стальмира «
Использованные источники
1. Г.С. Писаренко и др. Справочник по сопротивлению материалов. К. 1975г.
2. С.П. Фесик. Справочник по сопротивлению материалов. К. 1982г.
3. Д.В. Леоненко. Расчет плоских ферм. Б: 2006г.
Рисунок 293.1. Общая предварительная схема арочной галереи.
В целом, если изготовление ферм планируется из одного-двух типоразмеров профиля, то расчет такой прямоугольной фермы много времени не займет.
Сосредоточенными нагрузками для данных прямоугольных ферм будут опорные реакции для рассчитывавшихся ранее арочных ферм. Эти нагрузки Q будут приложены в узлах фермы, как показано на рисунке 554.1.б). Общая геометрия фермы показана на рисунке 554.1.а):
Рисунок 554.1. Общая геометрия и расчетные схемы для прямоугольной фермы.
Для упрощения расчетов длины всех пролетов между узлами в верхнем поясе приняты одинаковыми.
Определение усилий в стержнях фермы
Расчет ферм будет производиться методом сечений, основные положения которого изложены отдельно.
Когда мы рассчитывали арочные фермы, то выяснили, что опорные реакции у этих ферм могут быть разными в зависимости от рассматриваемого варианта снеговой нагрузки. Для дальнейших расчетов примем максимально возможное значение опорных реакций, тогда нагрузки на ферму от арочных ферм будут Q = 796.1 кг.
Кроме того на ферму будет действовать равномерно распределенная нагрузка от собственного веса фермы, к тому же изначально нам не известная, а это означает, что ферму следует дополнительно рассчитать на эту нагрузку. Однако с учетом того, что собственный вес фермы будет относительно небольшой, то для упрощения расчетов эту распределенную нагрузку от собственного веса можно условно привести к сосредоточенным в узлах фермы. Например, если ферма будет весить около 28 кг, то дополнительные сосредоточенные нагрузки составят 28/7 = 4 кг, тогда расчетные нагрузки составят:
Q = 796.1 + 4 ≈ 800 кг
Так как у нас симметричная ферма, к которой одинаковые нагрузки также приложены симметрично, то опорные реакции будут равны между собой и составят:
VA = VB = 7Q/2 = 7·800/2 = 2800 кгс
Значение горизонтальной составляющей опорной реакции на опоре А будет равно нулю, так как горизонтальных нагрузок в нашей расчетной схеме нет, поэтому горизонтальная составляющая реакции на опоре А показана на рисунке 554.1.в) бледно фиолетовым цветом.
Также на рисунке 554.1.в) показаны сечения, по которым можно рассчитать усилия во всех стержнях фермы с учетом симметричности фермы и нагрузок. Далее будет рассматриваться расчет только по 4 сечениям.
Маркировка, показанная на рисунке 554.1.г) означает, что у фермы есть:
Стержни нижнего пояса: 1-а, 1-в, 1-д, 1-ж;
Стержни верхнего пояса: 3-б, 3-г, 3-е;
Стойка: 2-а;
Раскосы: а-б, б-в, в-г, г-д, д-е, е-ж.
При необходимости для маркировки стержней, симметричных указанным, можно использовать апостроф ‘.
Если стоит задача рассчитать все стержни фермы, то лучше составить таблицу, в которую вносятся все стержни фермы. Затем в эту таблицу будут внесены результаты расчетов, в частности значения сжимающих или растягивающих напряжений.
Во всех сечениях, показанных на рисунке 554.1, силы N направлены так, что вызывают растяжения в рассматриваемых стержнях. Если по результатам расчетов усилие в рассматриваемом стержне будет отрицательным, то это означает, что в этом стержне будут действовать сжимающие нормальные напряжения.
Приступим к рассмотрению сечений.
сечение II-II (рис. 554.1.е)
Составим уравнение моментов относительно узла 3, это позволит определить усилие в стержне 3-б:
М3 = VAl — Ql + N3-бh = 0;
N3-бh =Ql — VAl;
где l — плечо действия силы Q и опорной реакции VA, равное расстоянию от узла 1 до узла 3 по горизонтали, согласно принятой нами расчетной схемы l = 0.525 м; h — плечо действия силы N3-a, равное высоте фермы, в данном случае h = 0.4м. Это означает, что в действительности общая высота фермы с учетом сечений верхнего и нижнего пояса будет немного больше, так как в данном случае высота — это расстояние между нейтральными осями верхнего и нижнего поясов.
Тогда:
N3-б =(Ql — VAl)/h = ((800 — 2800)0.525)/0.4 = — 2625 кг
Чтобы определить напряжения в стержне а-б составим уравнение моментов относительно узла 1:
М1 = Nа-бh’ + N3-бh = 0;
Na-б = 2625·0.4/0.318 = 3300.4 кг
В данном случае h’ — плечо приложения силы Nа-б — это высота прямоугольного треугольника. Плечо было определено следующим образом, сначала вычисляется значение угла а между стержнями 1-а и а-б.
tga = 0.4/0.525 = 0.762
где 0.4 и 0.525 — длины стержней — катетов прямоугольного треугольника.
a = 37.3°
тогда
h’ = 0.525sina = 0.525·0.606 = 0.318 м
Усилия в стержне 1-а будут равны нулю, в чем легко убедиться,составив уравнение моментов относительно узла 2:
М2 =- N1-а·0.4 = 0;
Проверим правильность вычислений, составив уравнения проекций сил на основные оси:
ΣQy = — Q1 +VA — Na-бsin37.3о = -800 +2800 — 3300.4·0.606 = 0.004 кг
ΣQx = N3-б + Na-бсos37.3o = -2625 + 3300.4·0.795 = 0.38 кг
Небольшая погрешность в вычислениях набежала из-за того, что вычисления ведутся с точностью до одного знака после запятой, а в значениях тригонометрических функций указываются только 3-4 знака после запятой. Но в данном случае большая точность и не нужна. В целом при таких нагрузках, на погрешность до 1 кг можно не обращать внимания.
сечение VII-VII (рис. 554.1.д)
Для определения усилий в стержне 1-ж составим уравнение моментов относительно узла 8:
М8 = -Q(1.05 + 2.1 + 3.15) + 3.15VA — 0.4N1-ж = 0;
N1-ж = (-6.3·800 + 3.15·2800)/0.4 = 9450 кг
Для определения усилий в стержне 3-е составим уравнение моментов относительно узла 7:
М7 = -Q(0.525 + 1.575 + 2.625) + 2.625VA + 0.4N3-е = 0;
N3-е = (800·4.725 — 2800·2.625)/0.4 = — 8925 кг (работает на сжатие)
Для определения усилий в стержне е-ж составим уравнение моментов относительно узла 9:
М9 = -Q(1.575 + 2.625 + 3.675) + 3.675VA + 0.4N3-е + 0.636Nе-ж = 0;
Nе-ж = (800·7.875 — 2800·3.675 + 0.4·8925)/0.6363 = — 660 кг
Проверим правильность расчетов
ΣQх = N3-е + N1-ж + Nе-жcos37.3° =- 8925 + 9450 — 660·0.7955 = 0.012 кг
Для лучшего представления общей картины проверим еще пару сечений
сечение VI-VI (рис. 554.1.ж)
Для определения усилий в стержне 1-д составим уравнение моментов относительно узла 6:
М6 = -Q(1.05 + 2.1)+ 2.1VA — 0.4N1-д = 0;
N1-д = (- 3.15·800 + 2.1·2800)/0.4 = 8400 кг
Для определения усилий в стержне д-е составим уравнение моментов относительно узла 5:
М5 = 1.575(-Q + VA)+ 0.4N3-е + 0.6363Nд-е = 0;
Nд-е = (1.575(800 — 2800) + 0.4·8925)/0.6363 = 660 кг
Проверим правильность расчетов, определив проекции сил на ось х:
ΣQx = N3-е + N1-ж + Nд-еcos37.3° = -8925 + 8400 + 660·0.7955 = 0.06 кг;
сечение III-III
Усилия в стержне 3-б нам уже известны, поэтому для определения усилий в стержне б-в составим уравнение моментов относительно узла 5:
М5 = -1.575Q + 1.575VA — 0.4N3-б + 0.6363Nб-в = 0;
Nб-в = (1.575(800 — 2800) + 0.4·2625)/0.6363 = -3300.4 кг
Усилие в стержне 1-в будет явно значительно меньше, чем в стержне 1-ж и потому в данном случае оно нас не интересует, так как мы планируем делать нижний пояс из трубы одного сечения. А чтобы определить правильность расчетов в данном случае определим проекции сил на ось у:
ΣQy = — Q1 +VA + Nб-вsin37.3о = -800 +2800 — 3300.4·0.606 = 0.04 кг
Теперь у нас есть все основные данные для дальнейшего расчета
Подбор сечения
На первый взгляд самым загруженным является стержень нижнего пояса 1-ж, на который действует продольная растягивающая сила N1-ж = 9450 кг. Однако напряжения в сжатом стержне 3-е в результате продольного изгиба могут быть даже больше, поэтому в первую очередь проверим прочность именно этого стержня по следующей формуле:
σ = N/φF ≤ R
где φ — коэффициент продольного изгиба, F — площадь сечения профиля, см, R — расчетное сопротивление материала профиля. Если расчетное сопротивление стали зараннее не известно, то для надежности рекомендуется принимать одно из минимальных R = 2300 кг/см2.
Расчет сжатых стержней ничем не отличается от расчета колонн, поэтому далее приводятся только основные этапы расчета без подробных пояснений.
по таблице 1 (см. ссылку выше) определяем значение μ = 1, это значение будет наиболее оптимальным с учетом рекомендаций нормативных документов, в частности СНиП II-23-81*(1990) «Стальные конструкции», а также того, что основные нагрузки к ферме приложены именно в узлах.
Предварительно определим площадь сечения профиля. Для растянутого стержня 1-ж эта площадь составит:
F = N/R = 9450/2300 = 4.11 см2
По сортаменту для прямоугольных профильных труб этому требованию удовлетворяет труба сечением 50х30х3 мм, площадь сечения такой трубы составит F = 4.21 см2, минимальный радиус инерции i = 1.16 см. Проверим, подходит ли эта труба для сжатого верхнего пояса фермы, так как делать пояса из труб разного сечения — дополнительное усложнение технологии, мало оправданное при таких малых объемах работ, всего-то нужно сделать 2 фермы.
При радиусе инерции i = 1.14 см, значение коэффициента гибкости составит
λ = μl/i = 1·105/1.16 = 90.5 ≈ 90
тогда по таблице 2 коэффициент изгиба φ = 0.629 (определяется интерполяцией значений 2050 и 2450)
8925/(0.629·4.21) = 3368 кгс/см2 >> R = 2300 кгс/см2;
Как видим, такое значение напряжений значительно больше допустимого. Если для изготовления поясов использовать трубу 50х40х3 мм, имеющую площадь сечения 4.81 см и минимальный радиус инерции i = 1.54 см, то результат расчетов будет следующим:
λ = 1·105/1.54 = 68.2 ≈ 68
φ = 0.77
8925/(0.77·4.81) = 2409 кгс/см2 > R = 2300 кгс/см2;
Как видим и такой трубы для обеспечения прочности не достаточно. Ну а дальше возможны разные варианты, можно для изготовления поясов использовать трубу 50х40х3.5 мм с площадью сечения 5.49 см2, которая явно обеспечит требуемый запас прочности, можно рассматривать и другие варианты, но мы остановимся на этом.
Теперь нужно проверить максимально допустимую гибкость для растянутого пояса из плоскости фермы. Согласно СНиП II-23-81* «Стальные конструкции» эта гибкость для растянутых элементов ферм не должна превышать 400. Соответственно трубы при изготовлении нужно располагать так, чтобы 50 — это была ширина трубы, а не высота, тогда при радиусе i = 1.81 см гибкость нижнего пояса составит:
λ = 1·630/1.81 = 348
Это требование нами соблюдено, можно переходить к расчету раскосов и стоек. Наиболее нагруженным раскосом будет сжатый стержень б-в. Его расчетная длина составит:
l = 0.525/cos37.3° = 0,525/0.7954 = 0.66 м или 66 см
Для соседнего растянутого раскоса, при заданном расчетном сопротивлении для обеспечения прочности потребуется труба сечением не менее
F = N/R = 3300.4/2300 = 1.43 см2
Для сжатого раскоса с учетом возможного продольного изгиба сечение должно быть больше, насколько именно — неизвестно, но мы теперь ученые и потому сразу примем трубу с хорошим запасом по площади сечения.
Для начала проверим квадратную трубу 25х25х2.5 мм, имеющую сечение 2.14 см2, радиус инерции i = (1.77/2.14)1/2 = 0.91 см. Тогда:
λ = 1·66/0.91 = 72.6
φ = 0.74
3300.4/(0.74·2.14) = 2084 кгс/см2 < R = 2300 кгс/см2;
Данная труба удовлетворяет требованиям и даже с некоторым запасом. Осталось выяснить какова будет примерно общая масса фермы:
m = 1.41(0.66·12 + 0.4·2) + 4.31·6.3·2 = 66.6 кг
Это в 2 раза больше, чем мы предположили вначале, но в целом общее увеличение нагрузки с учетом собственного веса фермы будет очень незначительным, около 0.6%.
Тем не менее поиск оптимального варианта можно продолжать, в данной статье остановимся на том, что есть.
Все необходимые условия по прочности и устойчивости нами соблюдены, но при этом никто не запрещает использовать для изготовления ферм профили большего сечения.
Осталось рассчитать длины и катеты сварных швов, но это уже отдельная тема.
Расчет усилий в стержнях фермы
Сервис ЭПЮРЫ ОНЛАЙН / РАСЧЕТ ФЕРМЫ может помочь Вам расчитать любую ферму, а если она является статически определимой (а фермы в большинстве случаев делают статически определимыми) — то и расписать уравнения равновесия во всех узлах фермы, как показано на рисунке.
Кроме этого, сервис выдает усилия в стержнях фермы в табличном виде
Поскольку количество стержней бывает большое, расстояния неудобные, то напрямую вводить данные в расчетчике долго. Для упрощения мы создали ГЕНЕРАТОР ОДНОСКАТНОЙ ФЕРМЫ, в котором достаточно указать основные размеры фермы — и расчетная схема будет создана автоматически.
Если уж Вы решили самостоятельно расчитать ферму (даже с помощью этого сайта), неплохо бы ознакомиться с основными понятиями в теории расчета ферм 🙂
Фермой называется конструкция, состоящая из стержней, соединённых между собой шарнирами, которые называются узлами фермы. Внешняя нагрузка на ферму передаётся через эти узлы. Каждый стержень в ферме находится в условиях простого осевого растяжения – сжатия, но общая деформация фермы – изгибная, то есть ферма работает на изгиб.
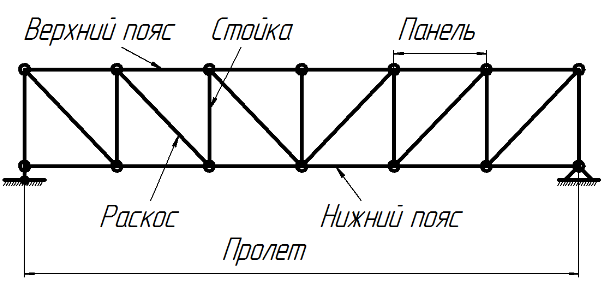
Пролет фермы — это расстояние между опорами. Расстояние между узлами фермы по горизонтали называется панелью фермы и обозначается d.
Выполнить расчет фермы, это значит, что в первую очередь нужно определить усилия в стержнях фермы. Общепринятые обозначения усилий в стержнях фермы:
O – усилие в стержнях верхнего пояса,
U – усилие в стержнях нижнего пояса,
V – усилие в стойках,
D – усилие в раскосах.
Расчет фермы начинают с определения опорных реакций. Опорные реакции в ферме определяются как в простой балке, работающей на изгиб.
Для определения усилий в стержнях ферм существуют несколько способов. Рассмотрим некоторые из них (аналитические):
а) Способ моментной точки. Применяется, когда можно разрезать ферму на две части так, чтобы в разрез попало три стержня. Для нахождения усилия в одном из них необходимо найти точку пересечения двух других разрезанных стержней (моментная точка) и записать уравнение равновесия (сумма моментов всех сил вокруг этой точки) любой отсечённой части фермы.
б) Способ проекций. Применяется, когда можно разрезать ферму на две части так, чтобы в разрез попало три стержня. При нахождении усилия в одном из них два других стержня оказываются параллельны (т.е. моментная точка оказывается в бесконечности). Записывается сумма проекций сил на вертикальную ось У любой отсечённой части фермы. Способ проекций чаще всего применяется для нахождения усилий в раскосах или стойках фермы с параллельными поясами.
в) Способ вырезания узлов. Применяется, когда два предыдущих способа не неприменимы, т.е. нельзя провести сечение через три стержня. Данный способ заключается в вырезании узла, к которому принадлежит искомый стержень и рассмотрении равновесия этого узла.
ПЕРЕЙТИ К РАСЧЕТУ ОДНОСКАТНОЙ ФЕРМЫ >>
90000 Loan Calculator 90001 90002 A loan is a contract between a borrower and a lender in which the borrower receives an amount of money (principal) that they are obligated to pay back in the future. Most loans can be categorized into one of three categories: 90003 90004 90005 90006 Amortized Loan: 90007 Fixed payments paid periodically until loan maturity 90008 90005 90006 Deferred Payment Loan: 90007 Single lump sum paid at loan maturity 90008 90005 90006 Bond: 90007 Predetermined lump sum paid at loan maturity (the face, or par value of a bond) 90008 90017 90018 90019 Amortized Loan: Paying Back a Fixed Amount Periodically 90020 90002 Use this calculator for basic calculations of common loan types such as mortgages, auto loans, student loans, or personal loans, or click the links for more detail on each.90003 90023 90024 90025 90026 90027 90026 90025 90019 Results: 90020 90023 90024 90027 Payment Every Month 90026 90036 90006 $ 1,110.21 90007 90026 90040 90024 90027 Total of 120 Payments 90026 90036 90006 $ 133,224.60 90007 90026 90040 90024 90027 Total Interest 90026 90036 90006 $ 33,224.60 90007 90026 90040 90057 90026 90040 90057 90019 90062 Deferred Payment Loan: Paying Back a Lump Sum Due at Maturity 90020 90023 90024 90025 90026 90027 90026 90025 90019 Results: 90020 90023 90024 90027 Amount Due at Loan Maturity 90026 90036 90006 $ 179,084.77 90007 90026 90040 90024 90027 Total Interest 90026 90036 90006 $ 79,084.77 90007 90026 90040 90057 90026 90040 90057 90019 90062 Bond: Paying Back a Predetermined Amount Due at Loan Maturity 90020 90002 Use this calculator to compute the initial value of a bond / loan based on a predetermined face value to be paid back at bond / loan maturity. 90003 90023 90024 90025 90026 90027 90026 90025 90019 Results: 90020 90023 90024 90027 Amount Received When the Loan Starts: 90026 90112 90006 $ 55,839.48 90007 90026 90040 90024 90027 Total Interest 90026 90036 90006 $ 44,160.52 90007 90026 90040 90057 90026 90040 90057 90062 RelatedMortgage Calculator | Auto Loan Calculator | Lease Calculator 90062 90019 Amortized Loan: Fixed Amount Paid Periodically 90020 90002 Many consumer loans fall into this category of loans that have regular payments that are amortized uniformly over their lifetime. Routine payments are made on principal and interest until the loan reaches maturity (is entirely paid off).Some of the most familiar amortized loans include mortgages, car loans, student loans, and personal loans. In everyday conversation, the word «loan» will probably refer to this type, not the type in the second or third calculation. Below are links to calculators related to loans that fall under this category, which can provide more information or allow specific calculations involving each type of loan. Instead of using this Loan Calculator, it may be more useful to use any of the following for each specific need: 90003 90019 Deferred Payment Loan: Single Lump Sum Due at Loan Maturity 90020 90002 Many commercial loans or short-term loans are in this category.Unlike the first calculation which is amortized with payments spread uniformly over their lifetimes, these loans have a single, large lump sum due at maturity. Some loans, such as balloon loans, can also have smaller routine payments during their lifetimes, but this calculation only works for loans with a single payment of all principal and interest due at maturity. 90003 90019 Bond: Predetermined Lump Sum Paid at Loan Maturity 90020 90002 This kind of loan is rarely made except in the form of bonds.Technically, bonds are considered a form of loan, but operate differently from more conventional loans in that the payment at loan maturity is predetermined. The face, or par value of a bond is the amount that is paid when the bond matures, assuming the borrower does not default. The term «face value» is used because when bonds were first issued in paper form, the amount was printed on the «face,» meaning the front of the bond certificate. Although face value is usually important just to denote the amount received at maturity, it can also help when calculating coupon interest payments.Note that this calculator is mainly for zero-coupon bonds. After a bond is issued, its value will fluctuate based on interest rates, market forces, and many other factors. Due to this, because the face value due at maturity does not change, the market price of a bond during its lifetime can fluctuate. 90003 90019 Loan Basics for Borrowers 90020 90145 Interest Rate 90146 90002 Nearly all loan structures include interest, which is the profit that banks or lenders make on loans. Interest rate is the percentage of a loan paid by borrowers to lenders.For most loans, interest is paid in addition to principal repayment. Loan interest is usually expressed in APR, or annual percentage rate, which include both interest and fees. The rate usually published by banks for saving accounts, money market accounts, and CDs is the annual percentage yield, or APY. It is important to understand the difference between APR and APY. Borrowers seeking loans can calculate the actual interest paid to lenders based on their advertised rates by using the Interest Calculator.For more information about or to do calculations involving APR, please visit the APR Calculator. 90003 90145 Compounding Frequency 90146 90002 Compound interest is interest that is earned not only on initial principal, but also on accumulated interest from previous periods. Generally, the more frequently compounding occurs, the higher the total amount due on the loan. In most loans, compounding occurs monthly. Use the Compound Interest Calculator to learn more about or do calculations involving compound interest.90003 90145 Loan Term 90146 90002 A loan term is the duration of the loan, given that required minimum payments are made each month. The term of the loan can affect the structure of the loan in many ways. Generally, the longer the term, the more interest will be accrued over time, raising the total cost of the loan for borrowers, but reducing the periodic payments. 90003 90019 Consumer Loans 90020 90002 There are two basic kinds of consumer loans: secured or unsecured. 90003 90145 Secured Loans 90146 90002 A secured loan means that the borrower has put up some form of asset as a form of collateral before being granted a loan.The lender is issued a lien, which is a right to possession of property belonging to another person until a debt is paid. In other words, defaulting on a secured loan will give the loan issuer legal ability to seize the asset that was put up as collateral. The most common secured loans are mortgages and auto loans. In these examples, the lender holds the title or deed, which is a representation of ownership, until the secured loan is fully paid. Defaulting on a mortgage typically results in the bank foreclosing on a home, while not paying a car loan means that the lender can repossess the car.90003 90002 Lenders are generally hesitant to lend large amounts of money with no guarantee. Secured loans reduce the risk of the borrower defaulting, since they risk losing whatever asset they put up as collateral. If the collateral is worth less than the outstanding debt, the borrower can still be liable for the remainder of the debt. 90003 90002 Secured loans generally have a higher chance of approval compared to unsecured loans and can be a better option for those who would not qualify for an unsecured loan, 90003 90145 Unsecured Loans 90146 90002 An unsecured loan is an agreement to pay a loan back without collateral.Because there is no collateral involved, lenders need a way to verify the financial integrity of their borrowers. This can be achieved through the five C’s of credit, which is a common methodology used by lenders to gauge the creditworthiness of potential borrowers. 90003 90173 90005 90006 Character 90007 -may include credit history and reports to showcase the track record of a borrower’s ability to fulfill debt obligations in the past, their work experience and income level, and any outstanding legal considerations 90008 90005 90006 Capacity 90007 -measures a borrower’s ability to repay a loan using a ratio to compare their debt to income 90008 90005 90006 Capital 90007 -refers to any other assets borrowers may have, aside from income, that can be used to fulfill a debt obligation, such as a down payment, savings, or investments 90008 90005 90006 Collateral 90007 -only applies to secured loans.Collateral refers to something pledged as security for repayment of a loan in the event that the borrower defaults 90008 90005 90006 Conditions 90007 -the current state of the lending climate, trends in the industry, and what the loan will be used for 90008 90194 90002 Unsecured loans generally have higher interest rates, lower borrowing limits, and shorter repayment terms than secured loans, mainly since they do not require any collateral. Lenders may sometimes require a co-signer (a person who agrees to pay a borrower’s debt if they default) for unsecured loans if the borrower is deemed too risky.Examples of unsecured loans include credit cards, personal loans, and student loans. Please visit our Credit Card Calculator, Personal Loan Calculator, or Student Loan Calculator for more information or to do calculations involving each of them. 90003 .90000 Present Value Calculator — easy PV calculation 90001 90002 Use this online PV calculator to easily calculate the Present Value, a.k.a. Present Worth of a future sum of money or stream of cash flow based on the rate of return and the investment term. Calculates present value of annuity or any other periodicity. 90003 90004 Using the PV calculator 90005 90002 Our 90007 Present Value calculator 90008 is a simple and easy to use tool to calculate the present worth of a future asset.All you need to provide is the expected future value (FV), the interest rate / return rate per period and the number of periods over which the value will accumulate (N). Once these are filled, press «Calculate» to see the present value and the total interest accumulated over the period. 90003 90004 What is Present Value? 90005 90002 The present value, a.k.a. present worth is defined as the value of a future sum of money or cash flow stream at present, given a rate of return over a specified number of periods.The concept reflects the time value of money, which is the fact that receiving a given sum today is worth more than receiving the same amount in some future date. It is practically compound interest calculation done backwards to find the amount you have to invest now to get to a desired amount in the specified point in the future. It is widely used in finance and stock valuation, although Net Present Value (NPV) is often preferred by experienced experts. 90003 90002 NPV is used in financial analysis, investment assessment and accounting, e.g. in calculating capital expenditure and depreciation. The difference between PV and NPV is that present value does not take outflows into account while net present value does ( «net» means combining positive and negative flows). To compare it to simpler concepts: PV is like revenue while NPV is like net income of a business or individual after deductions for expenses. Still, a PV calculator has utility in certain situations. 90003 90004 PV formula 90005 90002 If you wonder how to calculate the Present Value (PV) / Present Worth (PW) by yourself or using an Excel spreadsheet, all you need is the formula: 90003 90002 90021 90003 90002 where 90007 r 90008 is the return rate and 90007 n 90008 is the number of periods over which the return is expected to happen.For example, with a period of 5 years and expected future value of $ 1,000,000, given a return rate of 8%, n is 5, C 90028 1 90029 is $ 1,000,000 and r is 0.08, leading to the calculation: 1000000 / (1.08) 90030 5 90031 = $ 680583.20. 90003 90002 When the interest rate is annual, and the period is a year, this is equivalent to the 90007 present value of annuity formula 90008. This equation is used in our present value calculator as well, so you can use it for checking your PV calculations.It can be used in Excel to build your own calculation table. 90003 90004 Prsent Value calculation example 90005 90002 Let us assume an investment with known annual interest rate, hence annual periodicity, and known (or estimated) future value of $ 100,000. What is the present value of this investment if we expect to receive this payment 1, 2, 3, 5, or 10 years from now? The answers are shown in the table below. 90003 90041 90042 Present value of annuity example table 90043 90044 90045 90046 Future Value 90047 90046 Rate of Return 90047 90046 Number of Years 90047 90046 Present Value 90047 90054 90055 90056 90045 90058 $ 100,000 90059 90058 14% 90059 90058 1 90059 90058 $ 87,719 90059 90054 90045 90058 $ 100,000 90059 90058 14% 90059 90058 2 90059 90058 $ 76,946 90059 90054 90045 90058 $ 100,000 90059 90058 14% 90059 90058 3 90059 90058 $ 67,497 90059 90054 90045 90058 $ 100,000 90059 90058 14% 90059 90058 5 90059 90058 $ 51,937 90059 90054 90045 90058 $ 100,000 90059 90058 14% 90059 90058 10 90059 90058 $ 26,974 90059 90054 90107 90108 90002 This is a great example of the time value of money concept in action.The present value of the annuity decreases the more time it takes to pay off if the future value and rate of return staying the same. In other words, to maintain the same present value the interest rate would need to increase parallel to the increasing number of years one is locked into an investment. 90003 90004 Financial caution 90005 90002 This is a simple online software which is a good starting point in estimating the Present Value for any investment, but is by no means the end of such a process.You should always consult a qualified professional when making important financial decisions and long-term agreements, such as long-term bank deposits. Use the information provided by the tool critically and at your own risk. 90003 .rt. 90005 90006 Compound Interest Equation 90003 90004 90009 A = P (1 + r / n) 90010 nt 90011 90012 90005 90004 Where: 90005 90016 90017 A = Accrued Amount (principal + interest) 90018 90017 P = Principal Amount 90018 90017 I = Interest Amount 90018 90017 R = Annual Nominal Interest Rate in percent 90018 90017 r = Annual Nominal Interest Rate as a decimal 90018 90017 r = R / 100 90018 90017 t = Time Involved in years, 0.5 years is calculated as 6 months, etc. 90018 90017 n = number of compounding periods per unit t; at the END of each period 90018 90033 90006 Compound Interest Formulas and Calculations: 90003 90016 90017 Calculate Accrued Amount (Principal + Interest) 90018 90017 Calculate Principal Amount, solve for P 90018 90017 Calculate rate of interest in decimal, solve for r 90018 90017 Calculate rate of interest in percent 90018 90017 Calculate time, solve for t 90016 90017 t = ln (A / P) / n [ln (1 + r / n)] = [ln (A) — ln (P)] / n [ln (1 + r / n)] 90018 90033 90018 90033 90052 Formulas where n = 1 (compounded once per period or unit t) 90053 90016 90017 Calculate Accrued Amount (Principal + Interest) 90018 90017 Calculate Principal Amount, solve for P 90018 90017 Calculate rate of interest in decimal, solve for r 90018 90017 Calculate rate of interest in percent 90018 90017 Calculate time, solve for t 90016 90017 t = t = ln (A / P) / ln (1 + r) = [ln (A) — ln (P)] / ln (1 + r) 90018 90033 90018 90033 90052 Continuous Compounding Formulas (n → ∞) 90053 90016 90017 Calculate Accrued Amount (Principal + Interest) 90018 90017 Calculate Principal Amount, solve for P 90018 90017 Calculate rate of interest in decimal, solve for r 90018 90017 Calculate rate of interest in percent 90018 90017 Calculate time, solve for t 90018 90033 90052 Example Calculation 90053 90004 I have an investment account that increased from $ 30,000 to $ 33,000 over 30 months.If my local bank offers savings account with daily compounding (365), what annual interest rate do I need to get from them to match the return I got from my investment account? 90005 90004 In the calculator select «Calculate Rate (R)». The equation the calculator will use is: r = n [(A / P) 1 / nt — 1] and R = r * 100. 90005 90004 Enter: 90091 Total P + I (A): $ 33,000 90091 Principal (P): $ 30,000 90091 Compound (n): Daily (365) 90091 Time (t in years): 2.5 years (2.5 years is 30 months) 90091 Your Answer: R = 3.8126% per year 90005 90004 Interpretation: You will need to put $ 30,000 into a savings account that pays a rate of 3.8126% per year and compounds interest daily in order to get the same return as your investment account. 90005 .90000 Variance Calculator 90001 90002 Calculator Use 90003 90004 Variance is a measure of dispersion of data points from the mean. Low variance indicates that data points are generally similar and do not vary widely from the mean. High variance indicates that data values have greater variability and are more widely dispersed from the mean. 90005 90004 The variance calculator finds variance, standard deviation, sample size 90007 n 90008, mean and sum of squares.You can also see the work peformed for the calculation. 90005 90004 Enter a data set with values separated by spaces, commas or line breaks. You can copy and paste your data from a document or a spreadsheet. 90005 90004 This standard deviation calculator uses your data set and shows the work required for the calculations. 90005 90014 How to Calculate Variance 90003 90016 90017 Find the mean of the data set.2} \) 90005 .