Расчет фермы на прогиб калькулятор: Расчет фермы — онлайн-калькулятор

Содержание

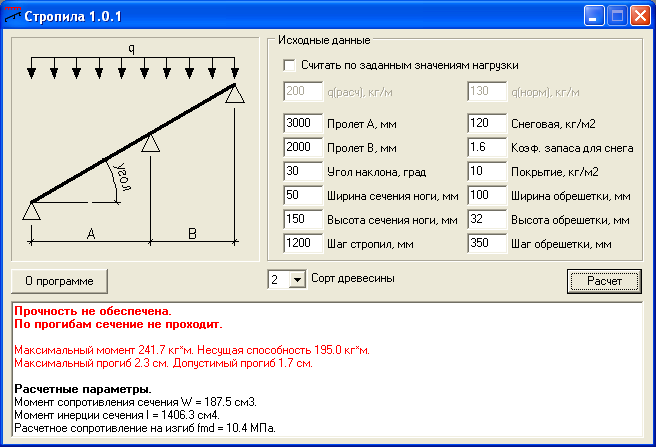
Расчет несущей способности и прогиба деревянных балок

Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.

Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.

Что нужно для того чтобы сделать правильный расчёт

Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.

Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками. Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.

Длина

Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски. Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.

Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.

При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.

Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.

Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.

Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.

К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.

Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус. Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.

Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.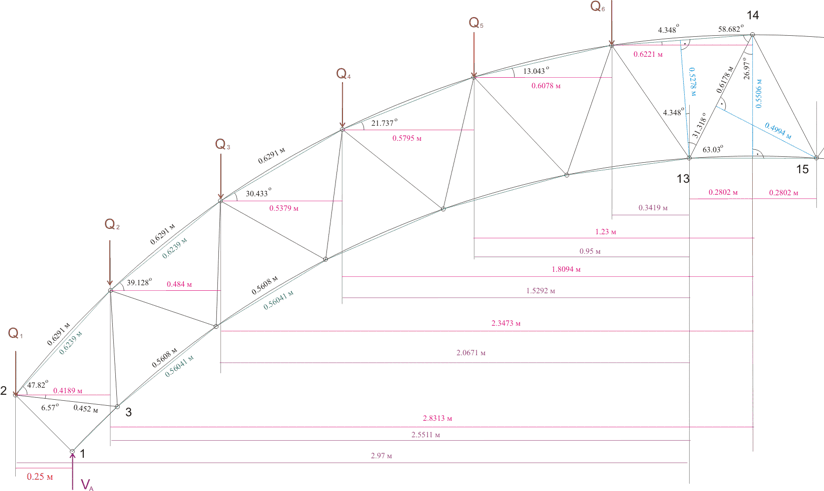

Общая информация по методологии расчёта

В большинстве случаев в малоэтажном строительстве применяются однопролётные балки. Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.

Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.

Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.

Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.

Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.

Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.

Как рассчитать несущую способность и прогиб

Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:

M/W<=Rд

Расшифруем значение каждой переменной в формуле:

Буква М вначале формулы указывает на изгибающий момент. Он исчисляется в кгс*м.
W обозначает момент сопротивления. Единицы измерения см³.

Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква М указывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:

M=(ql²)/8

В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:

Символ q показывает нагрузку, которую способна выдержать доска.
В свою очередь буква l — это длина одной деревянной балки.

Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.

Насколько важно правильно рассчитать прогиб

Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.

Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.

Так зачем нужен калькулятор

Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.

Прогиб ферм | Рабочий пример

Фермы прогибаются под нагрузкой. При гравитационных нагрузках это обычно характеризуется провисанием верхнего и нижнего поясов и последующим перемещением стенок и диагональных элементов. При проектировании ферменных конструкций, таких как крыши и мосты, всегда важно свести прогиб ферм к минимуму, чтобы сохранить внешний вид и функциональность конструкции. Прогиб ферм можно оценить вручную, используя метод виртуальной работы (метод единичной нагрузки), метод прямой жесткости или анализ методом конечных элементов.

Прогиб ферм крыши часто ограничен пролетами/240 . С другой стороны, отношение пролета к глубине, равное 15, часто считается достаточным для всех практических целей. Для мостов в нормах проектирования AASHTO указано, что максимальное отклонение ферменного моста из-за динамической нагрузки не должно превышать пролетов/800 . Принцип виртуальной работы можно использовать для вычисления максимального прогиба фермы, который затем сравнивается с допустимым прогибом.

В этой статье мы рассмотрим, как определить прогиб ферм, используя метод виртуальной работы (метод единичной нагрузки). В методе виртуальной работы ферма анализируется на осевые силы из-за внешней приложенной нагрузки. Затем внешние силы удаляются и заменяются единичной виртуальной нагрузкой в узле, где должен быть получен прогиб. Направление единичной нагрузки должно совпадать с искомым направлением прогиба. Ферма повторно анализируется на наличие осевых сил в элементах из-за виртуальной единичной нагрузки.

Суммирование прогиба отдельных элементов по приведенной ниже формуле дает прогиб фермы крыши в интересующей точке. где;
n = осевая сила в элементе i из-за виртуальной единичной нагрузки
N = осевая нагрузка в элементе i из-за внешней нагрузки
L = длина элемента
E = модуль упругости элемента
A = площадь элемента

Ферма нагружена, как показано ниже. Получите вертикальное отклонение в точке C из-за внешней нагрузки (AE = постоянная).

Опорная реакция из-за внешней нагрузки
Пусть ∑ M _G = 0;
9A _y – (6 × 6) – (4 × 3) + (10 × 3) = 0
A _y = 2 кН↑

Пусть ∑ M _A = 0;
9G _у – (10 × 3) – (4 × 6) – (6 × 3) = 0
G _y = 8 kN ↑

Let ∑ F _x = 0
A _x = 10 kN ←

Internal forces due to the externally applied loads

Joint A

∑ F _y = 0
2 + F _AB SIN45 = 0
F _AB = -2,8 КН (компресс)

∑ F _{x 9599599595959 40005 ∑ F _{x 95 9004 ∑ F _{x 95 9004 ∑ F _{x 9002 9004}}}}

∑ F _{x 9002 9004 9004 c _{F _{x 9003 9002 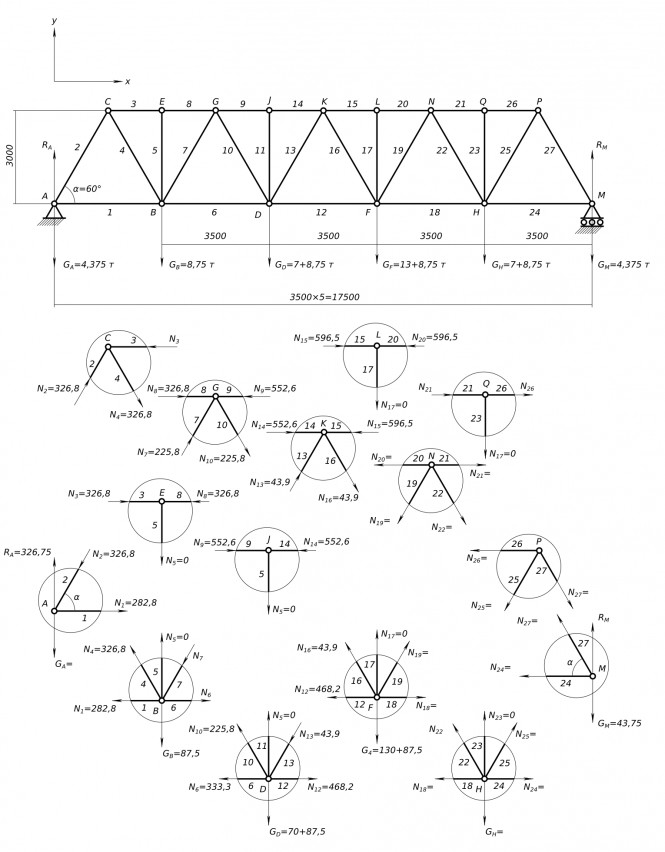. + F _AC + F _AB cos45 = 0
-10 + F _AC -2,8COS45 = 0
F _AC = 12 кН (натяжение)}}}

∑ F _x = 0 9955 ∑ F _x = 099955 ∑ _{F _x = 0}999595 ∑ _x = 0 999595. F _x = 0 _{5. F _BA cos45 = 0
F _BD – 2.8cos45 = 0
F _BD = -2 kN (compression)}

∑ F _y = 0
-6 – F _BC – F _BA sin45 = 0
-6 – F _BC + 2.8sin45 = 0
F _{до н.э.} = -4 кН (натяжение)

СОВЕТ C

∑ F _Y = 0
F _BC + F _CD SIN45 = 0_{+ F _{+ F _CD SIN45 = 0_{+ F _CD = 0 _{+ F _{+ F _CD = 0 _{+ F _{+ F _CD.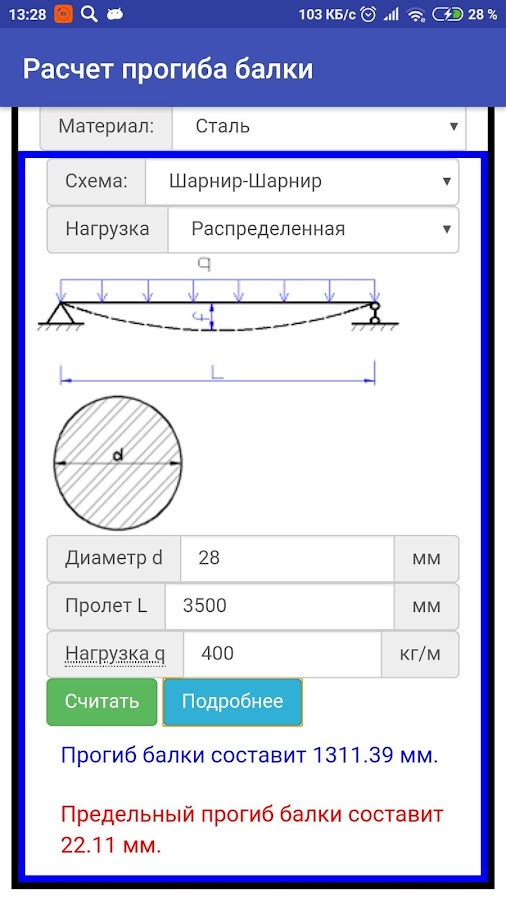} COS45 = 0
F _CD = 5,656 кН (натяжение)}}}}}}

∑ F _x = 0
-F _CA + F _CD COS45 + F = CE -0 _CD COS45 + F = CE -0 _CEN COS45 + F = 00017 -0 _CE = 0 -0 _CD COS45 + F = CE -0 _CD COS45 + F = CE + F _CD COS45 + F = CE . + 5.656cos45 + F _CE = 0
F _CE = 8 кН (растяжение)

СОВЕТ G

∑ F _Y = 0
8 + F _GF = 0
F _GF = -8 KN (Compression)

49 0005656. = -8 кН (Compression)

9,65656. F 

= _{. 0}
F _GE = 0
JOINT F

∑ F _y = 0
-F _FG – F _FE sin45 = 0
-(-8) – F _FE sin45 = 0
F _FE = 11,31 кН (растяжение)
∑ F _x = 0
-F _FD -F _FE COS45 + 10 = 0
-F _FD -11,31COS45 + 10 = 0
6 FD -11,31COS45 + 10 = 0
F _FD FD FD FD -11,31COS45 + 10 = 0
F _FD FD -11,31COS45 + 10 = 0
F _FD -11. 31COS45 + 10 = 0
F FD -11.31COS45 + 10 = 0
F FD . (tension)
JOINT E
∑ F _y = 0
F _ED + F _EF sin45 = 0
F _ED + 11.31sin45 = 0
F _ED = -8 кН (сжатие)
Получив внутренние силы во всех элементах из-за внешних приложенных нагрузок, удалим все нагрузки и заменим их единичной вертикальной нагрузкой в точке C, как показано ниже;
Реакция поддержки из-за виртуальной нагрузки
Пусть ∑ M _G = 0;
9A _y – (1 × 6) = 0
A _y = 6/9 = 0,667 ↑
Пусть ∑ M _A = 0;
9G _Y — (1 × 3) = 0
G _Y = 3/9 = 0,333 ↑
Let ∑ F _x = 0
A _x = 0
, когда анализируется с использованием использования, используя с помощью использования, используя с помощью использования, используя с помощью использования, используя с помощью использования. та же процедура, что и выше;
F _AC = 0,665 (натяжение)
F _AB = -0,941 (сжатие)
F _{до н.э.} = 0,665 (натяжение)
F _CE = 0,334 (натяжение)
F _CD = 0,47 (Тенсирование)
F _{BD _{= 0,47 (Тенсирование)
F _{BD _{= 0,47 (TENSION)
F _{BD _{= 0,47 (TENSION)
F _{BD _{= 0,47 (Тенсирование)
F _BD = 0,47 (TENSION)
F _{. )
F _DE = 0.331 (compression)
F _DF = 0.333 (compression)
F _EF = 0.47 (tension)
F _EG = 0
F _GF = 0.333 (compression)}}}}}}}}}
Теперь мы можем сформировать таблицу следующим образом;
Member n N (kN) L (m) nNL/AE
AC +0. 665 +12.00 3.000 23.940
AB -0.940 -2.80 4.243 11.167
BC +0.665 -4.00 3.000 -7.980
CE +0.334 +8.00 3.000 8.016
CD +0.470 +5.65 4.243 11.267
BD -0. 665 -2.00 3.000 3.990
DE -0.331 -8.00 3.000 7.944
DF -0.331 +2.00 3.000 -1.986
EF +0.470 +11.31 4.243 22.554
EG 0 0 3.000 0.000
GF -0.333 -8. 00 3.000 7.992
∑n _i N _i L = 86.904/AE
Therefore the vertical deflection at point C is 86.904/AE счетчики .
Фермы | Инженерная библиотека
На этой странице представлена глава по анализу ферм из «Руководства по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
4.1 Общие сведения о фермах
Ферма — это конструкция, полностью состоящая из двухсиловых элементов; то есть элементы, к которым в двух точках приложены две равные и противоположные силы. Таким образом, поскольку элементы не оказывают никакого крутящего момента друг на друга в соединениях, они считаются соединенными штифтами. Однако сварные и заклепочные соединения могут считаться штифтовыми соединениями, если элемент настолько длинный по сравнению с его поперечными размерами, что соединение может оказывать незначительное сопротивление вращению.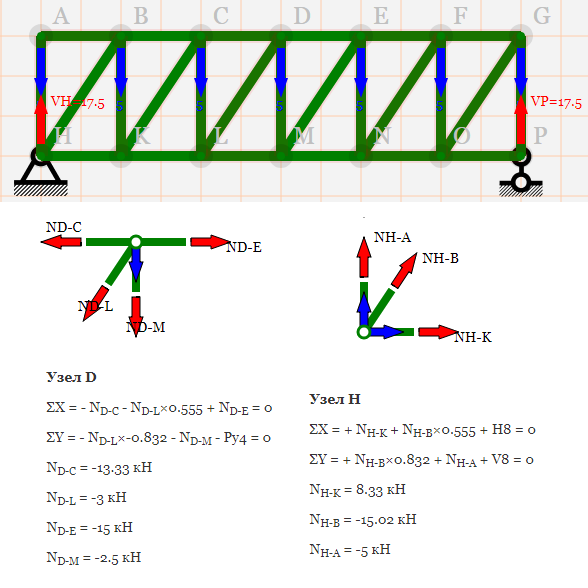

В разделе 4.3 рассматриваются статически определимые фермы, а в разделе 4.4 рассматриваются статически неопределимые фермы.
4.2 Номенклатура ферм
А = площадь поперечного сечения фермы
Е = модуль упругости
Л = длина фермы
Р = усилие в стержне фермы
Р = сила реакции
и = сила в стержне фермы от единичной нагрузки
Х = усилие в лишнем элементе фермы
δ = отклонение
4.3 Статически определяемые фермы
4.3.1 Введение в статически определяемые фермы
Силы, воспринимаемые элементами статически определимой фермы, можно определить, пропуская сечения через определенные элементы и применяя уравнения статики.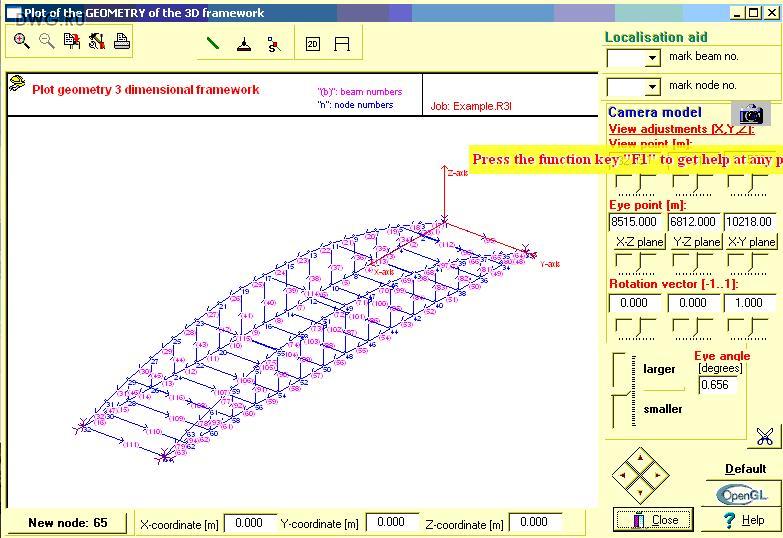
Метод стыков (раздел 4.3.2) заключается в выборе этих сечений таким образом, чтобы они полностью окружали один стык. Если выбранные сечения не окружают ни одного соединения, используемая процедура называется методом сечений (раздел 4.3.4). Этот метод особенно удобен, если требуется определить нагрузку только в определенных элементах. Во многих случаях комбинация метода соединений и метода сечений может оказаться выгодной при расчете данной фермы.
Перед применением любого из этих методов силы реакции на ферму должны быть определены уравнениями статики.
Прогибы в статически определимых фермах рассматриваются в разделе 4.3.6.
4.3.2 Применение метода соединений к статически определимым фермам
Если ферма в целом находится в равновесии, то каждое соединение в ферме также должно быть в равновесии. Метод суставов состоит в выделении сустава как свободного тела и применении уравнений равновесия к результирующей системе сил. Поскольку силы в элементах в узле фермы пересекаются в одной точке, для каждого узла плоской фермы можно написать только два уравнения равновесия.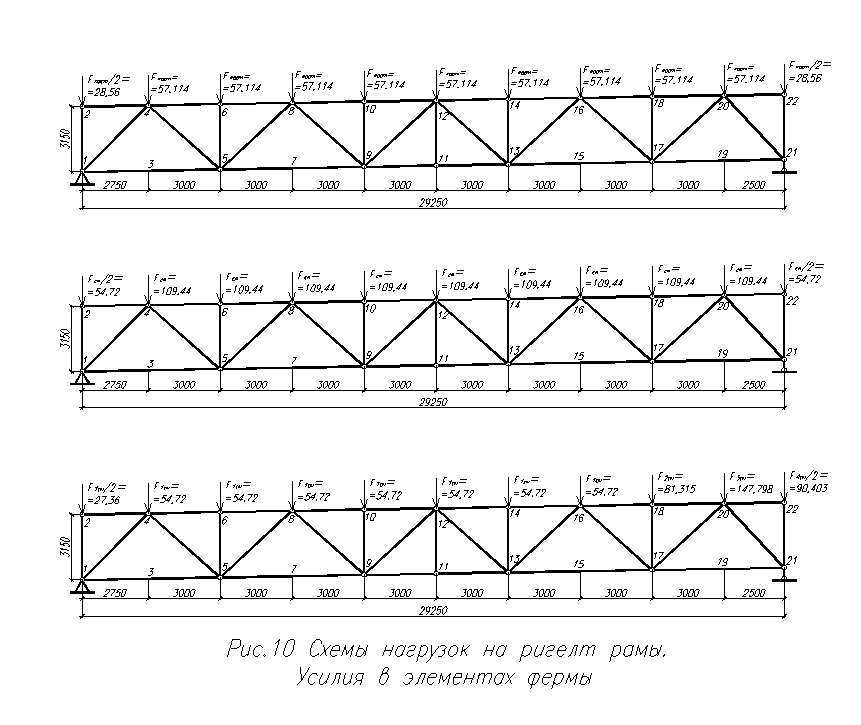
Таким образом, в стыке могут существовать только два неизвестных, и процедура должна начинаться с стыка, где существуют только два неизвестных, и продолжаться постепенно по стыку фермы за стыком. Эта процедура проиллюстрирована в Разделе 4.3.3.

У нас есть несколько структурных калькуляторов на выбор. Здесь только несколько:
Калькулятор луча
Калькулятор болтовых соединений
Распределение усилия по схеме расположения болтов
Калькулятор наконечников
Калькулятор потери устойчивости колонны
Калькулятор роста усталостной трещины

4.3.3 Пример задачи. Применение метода соединений к статически определимым фермам
Дано : Ферма, показанная на рис. 4-1.
Находка : Силы во всех членах.
Решение : Применение уравнений статики ко всей ферме дает R ₁ = 1667 фунтов и R ₂ = 1333 фунтов. Можно нарисовать диаграммы свободного тела для соединений в порядке, показанном на рис.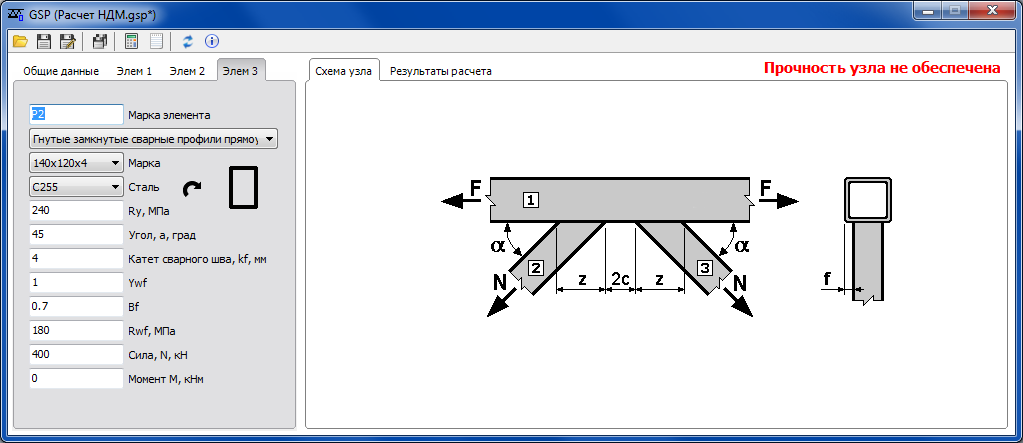 4-2, и решить их. для сил в членах. Подводя итог, если растягивающие силы считаются положительными, силы в стержнях равны
P _AB = -1925 фунтов P _CF = -382 фунта
P _AG = 962 фунта P _CG = 382 фунта
P _BC = -1925 фунтов P _{Немецкий} = -1541 фунт
P _BG = 1925 фунтов P _DF = 1541 фунт

P _CD = -1541 фунт P _EF = 770 фунтов
P _FG = 1734 фунта

4.3.4 Применение метода сечений к статически определяемым фермам
Метод секций состоит в разбиении фермы на секции и применении уравнений равновесия к полученным частям фермы. Этот метод предпочтительнее метода соединений, если желательна нагрузка на какой-либо внутренний элемент, поскольку может быть устранена необходимость расчета сил на другие элементы. Это преимущество метода сечений показано в разделе 4.3.5.
4.3.5 Пример задачи. Статически определимые фермы методом сечений
Дано : Ферма, показанная на рис. 4-1.
Находка : Сила в элементе FG.
Решение : из статики, R ₁ = 1667 фунтов и R ₂ = 1333 фунтов. Если провести разрез по элементам BC, CG и FG, получится свободное тело, показанное на рис. 4-3. Суммирование моментов относительно точки C дает P _FG

(30 sin60°) — 1667(45) + 2000(15). Решение дает P _FG = 1734 фунта.
4.3.6 Прогибы в статически определимых фермах
Основное уравнение прогиба статически определимых ферм:
$$ \delta = \sum { P ~u ~L \over A~E } $$
(4-1)
В этом уравнении L, A и E — это длина, площадь поперечного сечения и модуль упругости каждого из элементов фермы. P — сила, приложенная к элементу фермы, а u — сила в элементе фермы, вызванная единичной нагрузкой, приложенной в направлении требуемого отклонения в точке, отклонение которой требуется.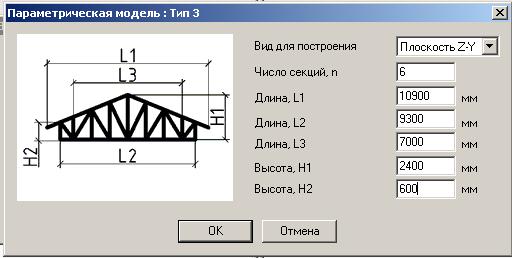 Применение этого уравнения проиллюстрировано в разделе 4.3.7.
4.3.7 Пример задачи. Прогибы статически определимых ферм
Дано : Ферма, показанная на рис. 4-4.
Находка : вертикальное отклонение сустава D.
Решение : Силы в элементах могут быть найдены как: P _AB = 3500 фунтов, P _BC = 1000 фунтов, P
BD = 1414 фунтов, P _BE = -2121 фунтов 1, P7 CD = -1414 фунтов, а P _DE = -2000 фунтов. Ферму можно перечертить с единичной нагрузкой в направлении желаемого прогиба в стыке D, как показано на рис. 4-5. Силы в элементах снова рассчитываются с результатами, показанными на рисунке 4-5. Теперь можно решить уравнение (4-1), как показано в таблице 4-1.

У нас есть несколько структурных калькуляторов на выбор. Здесь только несколько:
Калькулятор луча
Калькулятор болтовых соединений
Распределение усилия по схеме расположения болтов
Калькулятор наконечников
Калькулятор потери устойчивости колонны
Калькулятор роста усталостной трещины

4.
4 Статически неопределимые фермы
4.4.1 Введение в статически неопределимые фермы
Если ферма статически неопределима, уравнения прогиба должны применяться в дополнение к уравнениям равновесия для определения сил во всех элементах. В разделе 4.4.2 рассматриваются фермы с одним резервированием, а фермы с несколькими резервами рассматриваются в разделе 4.4.4.

4.4.2 Статически неопределимые фермы с одним резервированием
Фермы с одним резервом можно обрабатывать, удаляя один элемент, чтобы получить статически определимую ферму. Этот элемент заменяется неизвестной силой, приложенной этим элементом, X _и. Одно уравнение может быть написано для отклонения статически определенной фермы из-за приложенных нагрузок, включая X, а другое уравнение может быть написано для отклонения удаленного элемента из-за неизвестной силы X. Затем эти два уравнения могут быть решены одновременно чтобы найти X. Как только X найдено, силы в других элементах фермы могут быть получены из уравнений статики. Эта процедура проиллюстрирована в Разделе 4.4.3.
4.4.3 Стандартная задача — статически неопределимые фермы с одной избыточностью
Дано: ферма, показанная на рис. 4-6.
Находка : Сила на члене AC.

Решение . Ферму можно перечертить, заменив элемент AC на силу сопротивления этого элемента, X, как показано на рис. 4-7. Усилие в любом элементе фермы, P, может быть получено путем наложения усилия, вызванного только вертикальными нагрузками, P _o, и усилием, вызванным только горизонтальными нагрузками. Эта последняя сила может быть представлена как X _u, где u — сила в элементе фермы из-за единичной горизонтальной нагрузки, приложенной в точках A и C. Таким образом, 92 л \over AE}\) дюйм/фунт АБ -32000 1,785 1.600 x 10 ^-6 -0,0915 5,11 x 10 ^-6 н.э. 26900 -3,0 1,795 x 10 ^-6 -0,1450 16,15 x 10 ^-6 до н. э.
-32000 1,785 1.600 x 10 ^-6 -0,0915 5,11 x 10 ^-6 БД 20000 -2,23 0,67 х 10 ^-6 -0,0292 3,32 x 10 ^-6 CD 26900 -3,0 1,795 x 10 ^-6 -0,1450 16,15 x 10 ^-6 $ \sum {P_o u L \over AE} $ = -0,5150 92 L \over AE } \) = 47,63 x 10 ^-6 дюйм/фунт
4.4.4 Статически неопределимые фермы с множественными резервами
Анализ ферм с более чем одним резервом аналогичен анализу фермы с одним резервом. Первым шагом является удаление избыточных элементов или реакций, чтобы получить статически определимую базовую структуру. Прогибы статически определяемой базовой конструкции в направлениях избыточных элементов затем могут быть рассчитаны с точки зрения избыточных сил и приравнены к известным прогибам. Например, рассмотрим ферму на рис. 4-8. Элементы а и b могут быть удалены для получения статически определимой базовой конструкции. Окончательная сила P в любом элементе может быть получена путем суммирования усилий, вызванных приложенными нагрузками и избыточными силами. Таким образом,
$$ P = P_o + X_a u_a + X_b u_b $$
(4-3)
где P _o – усилие в элементе статически определимой базовой конструкции от внешней нагрузки, а u _a и u _b – усилия в элементе статически определимой базовой конструкции от единичных нагрузок, приложенных в члены а и б соответственно. Применение этого уравнения к элементам a и b соответственно дает
$$ \delta_a = \sum { P ~u_a ~L \over A~E } $$ 92 ~L \над А~Е } $$
(4-7)
Кроме того,
$$ \delta_a = { -X_a L_a \over A_a E } $$
(4-8)
и
$$ \delta_b = { -X_b L_b \over A_b E } $$
(4-9)
Уравнения с (4-6) по (4-9) можно решить одновременно, чтобы получить силы в избыточных элементах.
No related posts.