Расчет диаметра: Диаметр окружности круга • как найти ⬅️ формула

Выбор воздуховода и расчет диаметра

Промышленная вентиляция проектируется с учетом нескольких фактов, на все существенное влияние оказывает сечение воздухопроводов.

1. Кратность обмена воздуха. Во время расчетов принимаются во внимание особенности технологии, химический состав выделяемых вредных соединений, и габариты помещения.
2. Шумность. Системы вентиляции не должны ухудшать условия труда по параметру шумности. Сечение и толщина подбирается таким образом, чтобы минимизировать шум воздушных потоков.
3. Эффективность общей системы вентиляции. К одному магистральному воздухопроводу могут присоединяться несколько помещений. В каждом из них должны выдерживаться свои параметры вентиляции, а это во многом зависит от правильности выбора диаметров. Они выбираются с таким расчетом, чтобы размеры и возможности одного общего вентилятора могли обеспечивать регламентируемые режимы системы.
4. Экономичность. Чем меньше размеры потерь энергии в воздуховодах, тем ниже потребление электрической энергии. Одновременно нужно принимать во внимание стоимость оборудования, выбирать экономически обоснованные габариты элементов.

Эффективная и экономичная система вентиляции требует сложных предварительных расчетов, заниматься этим могут только специалисты с высшим образованием. В настоящее время для промышленной вентиляции чаще всего используются пластиковые воздуховоды, они отвечают всем современным требованиям, дают возможность уменьшить не только габариты и себестоимость вентиляционной системы, но и затраты на ее обслуживание.

Пластиковая промышленная вентиляция

Расчет диаметра воздухопровода

Для расчетов габаритов нужно иметь исходные данные: максимально допустимую скорость движения воздушного потока и объем пропускаемого воздуха в единицу времени. Эти данные берутся из технических характеристик вентиляционной системы. Скорость движения воздуха оказывает влияние на шумность системы, а она строго контролируется санитарными государственными организациями. Объем пропускаемого воздуха должен отвечать параметрам вентиляторов и требуемой кратности обмена.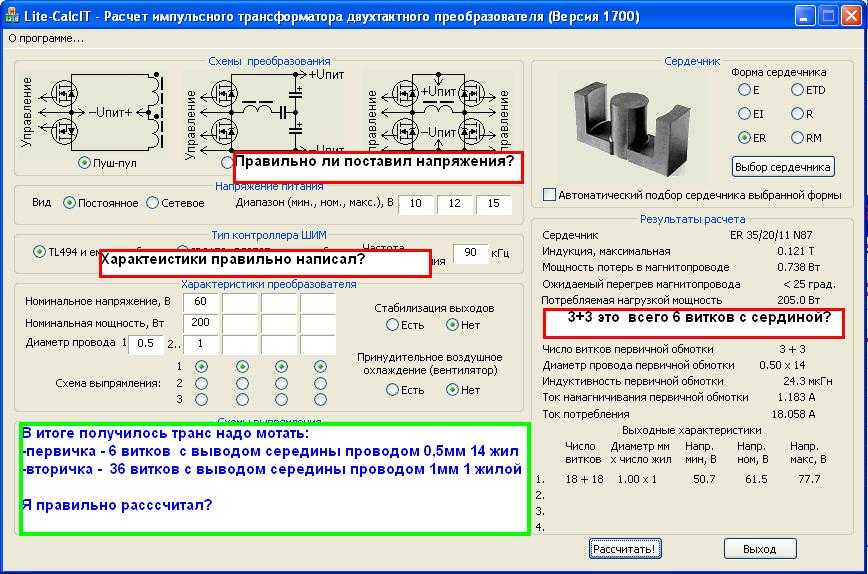 Расчетная площадь воздухопровода определяется по формуле Sс = L × 2,778 / V, где:

Sс – площадь сечения воздуховода в квадратных сантиметрах; L – максимальная подача (расход) воздуха в м³/час;
V – расчетная рабочая скорость воздушного потока в метрах за секунду без пиковых значений;
2,778 – коэффициент для перевода различных метрических чисел к значениям диаметра в квадратных сантиметрах.

Проектировщики вентиляционных систем учитывают следующие важные зависимости:

1. При необходимости подачи одинакового объема воздуха уменьшение диаметра воздухопроводов приводит к возрастанию скорости воздушного потока. Такое явление имеет три негативных последствия. Первое – увеличение скорости движения воздуха увеличивает шумность, а этот параметр контролируются санитарными нормами и не может превышать допустимых значений. Второе – чем выше скорость движения воздуха, тем выше потери энергии, тем мощнее нужны вентиляторы для обеспечения заданных режимов функционирования системы, тем больше их размеры.
   Третье – небольшие габариты воздухопроводов не в состоянии правильно распределять потоки между различными помещениями.

Зависимость скорости воздуха от диаметра воздухопровода

2. Неоправданное увеличение диаметров воздуховодов повышает цену вентиляционной системы, создает сложности во время монтажных работ. Большие размеры оказывают негативное влияние на стоимость обслуживания системы и себестоимость изготавливаемой продукции.

Чем меньше диаметр воздухопровода, тем быстрее скорость движения воздуха. А это не только повышает шумность и вибрацию, но и увеличивает показатели сопротивления воздушного потока. Соответственно, для обеспечения необходимой расчетной кратности обмена требуется устанавливать мощные вентиляторы, что увеличивает их размеры и экономически невыгодно при современных ценах на электрическую энергию.

При увеличении диаметров вышеописанные проблемы исчезают, но появляются новые – сложность монтажа и высокая стоимость габаритного оборудования, включая различную запорную и регулирующую арматуру. Кроме того, воздуховоды большого диаметра требуют много свободного места для установки, под них приходится проделывать отверстия в капитальных стенах и перегородках. Еще одна проблема – если они используются для обогрева помещений, то большие размеры воздуховода требуют увеличенных затрат на мероприятия по теплозащите, из-за чего дополнительно возрастает сметная стоимость системы.

В упрощенных вариантах расчетов принимается во внимание, что оптимальная скорость воздушных потоков должна быть в пределах 12–15 м/с, за счет этого удается несколько уменьшить их диаметр и толщину. В связи с тем, что магистральные воздуховоды в большинстве случаев прокладываются в специальных технических каналах, уровнем шумности можно пренебрегать. В ответвлениях, заходящих непосредственно в помещения, скорость воздуха уменьшается до 5–6 м/с, за счет чего уменьшается шумность. Объем воздуха берется из таблиц СаНиПина для каждого помещения в зависимости от его назначения габаритов.

Проблемы возникают с магистральными воздуховодами значительной протяженности на больших предприятиях или в системах с множеством ответвлений. К примеру, при нормируемом расходе воздуха 35000 м³/ч и скорости воздушного потока 8 м/с диаметр воздухопровода должен быть не менее 1,5 м толщиной более двух миллиметров, при увеличении скорости воздушного потока до 13 м/с габариты воздуховодов уменьшаются до 1 м.

Таблица потери давления

Потери давления

Диаметр ответвлений воздухопроводов рассчитывается с учетом требований к каждому помещению. Допускается использовать для них одинаковые размеры, а для изменения параметров воздуха устанавливать различные регулируемые дроссельные заслонки. Такие варианты вентиляционных систем позволяют в автоматическом режиме изменять показатели работы с учетом фактической ситуации. В помещениях не должно быть сквозняков, вызванных работой вентиляции. Создание благоприятного микроклимата достигается за счет правильного выбора места монтажа вентиляционных решеток и их линейных размеров.

Сами системы рассчитываются методом постоянных скоростей и методом потери давления. Исходя из этих данных, подбираются размеры, тип и мощность вентиляторов, рассчитывается их количество, планируются места установки, определяются размеры воздуховода.

Если вас интересует стоимость изготовления продукции, отправьте нам техническое задание на почту info@plast‑product.ru или позвоните по телефону 8 800 555‑17‑56

Расчет и выбор диаметра водосточной системы

Водосточная система – неотъемлемый элемент любого жилого дома. Ее задача – сбор, а также выведение талых и осадочных вод для защиты кровли, фасадов и фундамента от преждевременного износа. Однако чтобы она функционировала, как следует, в первую очередь необходимо грамотно рассчитать требуемый диаметр труб и желобов.

 

Устройство наружного водостока

Среди большого количества элементов водосточной системы большую роль играют, конечно же, трубы. Они организуют отвод воды, собранной в желоба, выводя ее за пределы кровли. Таким образом, представляя собой важнейший элемент защиты крыши и фундамента от преждевременного разрушения. Основной материал, используемый в производстве – оцинкованная сталь. Относительно небольшой вес оцинковки позволяет проводить монтаж водостока даже на кровле старого дома. А за счет современного полимерного покрытия материал устойчив к коррозии. Преимущество стали – она не подвержена деформации при резкой смене температуры, поэтому заказчик может не опасаться, что при похолодании или потеплении конструкция даст трещину, как это бывает с пластиковыми водостоками. Диаметр сечения и размеры оцинкованных водосточных систем различаются в зависимости от площади и конструктивных особенностей кровли. Этот вопрос рассмотрим подробнее чуть дальше.

Устройство наружного водостока включает в себя несколько составляющих. Это желоба, задача которых – направление водных потоков к воронке; сами трубы и воронки; соединители с системой кронштейнов, а также обводы, использующиеся на кровле сложной архитектуры – с нишами, колоннами или выступами.

В зависимости от формы сечения трубы подразделяются на: круглые или прямоугольные. Наиболее практичными и простыми в обслуживании считаются именно круглые. Прямоугольное сечение ввиду своей оригинальности встречается не так часто.

Разумеется, что одной водосточной трубой организовать водоотвод не удастся, поэтому вместе с ней монтируются:

• Водоприемная воронка.
• Крепежные хомуты.
• Колена (позволяют соединить звенья на выступах).
• Отводы (организуют отвод воды за пределы сооружения).

 

На что влияет и от чего зависит диаметр водосточной системы

Грамотный расчет диаметра – ключевой фактор, который влияет на эффективность конструкции и ее возможность выполнять возлагаемые функции. Чем больше d, тем лучшей пропускной способностью обладает водосточный желоб и труба, но и цена увеличивается.

Такой широкий «диапазон» диаметра и его выбор зависят от следующих моментов:

• Площади сбора воды
• Схемы размещения точек слива и от их количества (нагруженная и ненагруженная схема слива)

Площадь сбора

Для расчета данного параметра на один желоб, следует воспользоваться формулой:

S= L (а+в/2), где

L – длина крыши вдоль конька;

а – проекция на горизонтальную плоскость ската крыши, с которого стекают осадки;

в – высота крыши.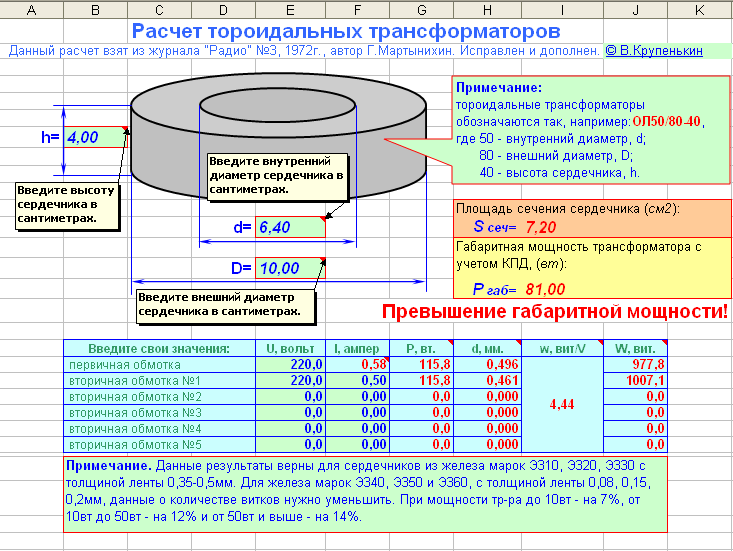

Приведем пример. Данные кровли:

• Высота – 2 м.
• Длина – 10 м.
• Ширина проекции – 5 м.

Следовательно, используя формулу, выполним расчет: S= 10(5+2/2)=60 м2.

Размещение точек слива

При достаточном количестве точек слива, т.е. при ненагруженной системе, можно выбрать параметры водостока – 125/100 мм с площадью кровли от 100 кв. м.

Точное количество точек слива зависит от диаметра желоба. Данные представлены в таблице.

S, кв. м	d желоба, мм	d трубы, мм
До 79	90	75
Более 100	125	100

 

При нагруженной схеме (система водоотвода к одной воронке) – 150/120 мм с площадью кровли от 100 кв. м.

Нагруженная система предполагает использование размеров с запасом. Данные представлены в таблице.

Площадь, кв.м	d желоба, мм	d трубы, мм
До 42	75	63
До 52	100	80
До 75	125	100
До 100	150	120

 

При выборе лучше останавливаться на элементах большего d, что позволяет снизить риски загрязнения или образования ледяной корки. Важно, чтобы все элементы были от одного производителя, это поможет избежать ошибок в расчетах и монтаже.

На что обращать внимание при выборе

При выборе мы рекомендуем обращать внимание на:

• Норму осадков конкретного региона.
• Площадь крыши.
• Специфику архитектуры постройки.
• Уклон кровли.

Согласно требованиям DIN 18460-1989 диаметр трубы водосточной системы выбирается исходя из площади кровли и водопропускной способности. Данные представлены в таблице.

Площадь крыши, м2	Водопропускная способность, л/с	Водосточная труба
		d, мм	Поперечный срез, см2
40	1,2	60	28
60	1,8	70	38
86	2,6	80	50
156	4,7	100	79
253	7,6	120	113
283	8,5	125	122
459	13,8	150	177

 

Для расчета количества труб водостока используют следующий вариант: 1 труба на 50 м2 площади ската кровли, расстояние между ними не должно превышать 10 м. В случае с диаметром на каждый квадратный метр площади кровли приходиться по 1,5 мм² площади сечения трубы.

Существующие на сегодня диаметры водостока

Размеры, предлагаемые российскими производителями – от 50 до 200 мм. Ранее применялось всего лишь три основных параметра – 100, 150 и 200 мм. Но за счет большого ассортимента от производителей и поставляемой на наш рынок импортной продукции диаметр водосточных труб значительно видоизменился. Сегодня какого-то одного установленного стандарта по ГОСТу в России не существует.

Ниже мы представим распространенные размеры водосточных труб и желобов:

• 80/100;
• 90/125;
• 100/125;
• 120/150;
• 150/200.

Наша компания предлагает оптимальные для множества крыш диаметры труб и желобов. Если система необходима для отвода осадков с кровли значительной площади, например, со складского или торгового здания, обратите внимание на большую водосточную систему из оцинкованной стали 120/150 или 150/200 мм. Такая конструкция справится с высокой нагрузкой без деформации. Водостоки больших размеров подойдут также для крыш производственных и промышленных помещений.

Толщина стали составляет 0,5 мм, защитное полимерное покрытие – полиэстер. Собственник жилья может выбрать любой оттенок из каталога RAL, чтобы водосточная система стала не только защитой, но и украшением кровли.

«Водостокстрой» предлагает также системы для частного строительства – «Стандарт» и Евро «Aquarius» с размерами 100/125 мм. Системы обладают хорошей пропускной способностью и доступной стоимостью.

Для негабаритных построек хозяйственно-бытового назначения (хозблоков, бань, беседок) мы рекомендуем малую водосточную систему 80/100 мм.

Расчет диаметра водостока

Для труб

Первостепенный параметр, который необходимо учитывать при расчете диаметра труб наружного водостока – площадь кровли. При наличии нескольких скатов на крыше для получения совокупной величины показатели отдельных участков складываются. Угол наклона и площадь кровли помогут определить объем всей стекающей с крыши воды.

Кроме того, необходимо учитывать максимальный уровень осадков, характерный для определенного региона. В интернете можно воспользоваться справочниками, где предоставлены данные средних и максимальных осадков конкретной местности.

Для расчета рабочего сечения следует использовать соотношение 1 кв. см сечения / 0,75-1 кв.м кровли. Далее уточняются результаты с учетом информации об осадках.

Например, если труба имеет d=100мм, ее можно устанавливать для кровли площадью 75-100 кв.м. А при d=200 мм можно использовать на площадь крыши 150-200 кв.м.

Кроме того, необходимо учитывать следующие особенности:

• Чтобы рассчитать сечение желоба, учитывается угол наклона, от которого зависит высота бортиков канала. Минимально допустимое значение параметра – 120 мм.
• Количество желобов зависит от периметра карниза.
• Ранее размеры труб фиксировались ГОСТом. Однако после внедрения на российский рынок продукции зарубежного производства, появились иные типоразмеры, поэтому подобрать оптимальный труда не составит.

Для воронок

Здесь также следует ориентироваться на площадь крыши:

• На 0,75 кв. м кровли будет достаточно одной воронки.
• Диаметр воронки равен сечению водостока на нижнем участке.
• Параметры водосточных труб и желобов всегда находятся в соотношении. К примеру, при сечении желоба 200 мм идет труба 150 мм. Диаметр воронки водостока должен совпадать с рабочим сечением желоба. Иначе при повышенной нагрузке на систему осадки будут скапливаться.
• При длине желоба 12 метров с преградами для расширения, дополнительно потребуется монтаж компенсационной воронки.

Самый точный расчет окажется бесполезным, если конструкции выпускаются недобросовестным производителем, а поэтому сперва разберитесь с этим моментом. «Водостокстрой» гарантирует соответствие размеров производимых труб и желобов, которые при монтаже идеально подойдут друг к другу.

Опытные специалисты проведут для вас расчет, помогут подобрать необходимый диаметр водостока, чтобы система работала без перебоев, надежно защищала кровлю и фундамент от негативного воздействия осадочных и талых вод.

«Водостокстрой» предлагает водосточные системы большого и стандартного диаметра, которые помогут организовать защиту вашей кровли вне зависимости от ее площади.

В нашем каталоге вы найдете водосточные желоба различного диаметра (все данные в мм):

• 100;
• 125;
• 150
• 200

Длина может быть 1, 2 или 3 метра.

В каталог

Возможно изготовление конструкций на заказ по индивидуальному проекту. Уточнить моменты и задать вопросы можно по тел. +7 (495) 514-56-30.

Калькулятор эквивалентного диаметра | ВЕНТА

Длина стороны A (мм):

Длина стороны B (мм):

Результат:

0.00 (мм)

Эквивалентный диаметр — диаметр круглого воздуховода, в котором потеря давления на трение при одинаковой длине равна его потере в прямоугольном воздуховоде.

Эквивалентный диаметр прямоугольного воздуховода

Эквивалентный диаметр прямоугольного воздуховода можно вычислить по формуле

d_e = 1.30 x ((a x b)^0.625) / (a + b)^0.25) (1)

где

d_e = эквивалентный диаметр (мм)

a = длина стороны A (мм)

b = длина стороны B (мм)

Эквивалентный диаметр — de (мм)
Сторона воздуховода A мм.	Сторона воздуховода — B (мм.)
	100	150	200	250	300	400	500	600	800	1000	1200	1400	1600	1800	2000
100	109	133	152	168	183	207	227
150	133	164	189	210	229	261	287	310
200	152	189	219	244	266	305	337	365
250	168	210	246	273	299	343	381	414	470
300	183	229	266	299	328	378	420	457	520	574
400	207	260	305	343	378	437	488	531	609	674	731
500	227	287	337	381	420	488	547	598	687	762	827	886
600		310	365	414	457	531	598	656	755	840	914	980	1041
800			414	470	520	609	687	755	875	976	1066	1146	1219	1286
1000				517	574	674	762	840	976	1093	1196	1289	1373	1451	1523
1200					620	731	827	914	1066	1196	1312	1416	1511	1598	1680
1400						781	886	980	1146	1289	1416	1530	1635	1732	1822
1600							939	1041	1219	1373	1511	1635	1749	1854	1952
1800								1096	1286	1451	1598	1732	1854	1968	2073
2000										1523	1680	1822	1952	2073	2186

 

Эквивалентный диаметр овального воздуховода

Эквивалентный диаметр овального воздуховода можно вычислить по формуле

d_e = 1. 55 A^0.625/P^0.2 (2)

где

A = площадь поперечного сечения овального воздуховода (м²)

P = периметр овального воздуховода (м)

Площадь поперечного сечения овального воздуховода можно вычислить по формуле

A = (π b²/4) + b(a — b) (2a)

где

a = большая сторона овального воздуховода (м)

b = меньшая сторона овального воздуховода (м)

Периметр овального воздуховода можно вычислить по формуле

P = π b + 2(a — b)  (2b)

Диаметр круга – определение, формула, примеры

В круге диаметр – это линия, проходящая через центр и пересекающаяся с окружностью на противоположных концах. Он в два раза больше радиуса окружности. Другими словами, диаметр круга — это линия, проходящая через центр и делящая круг на две равные части. Давайте узнаем больше об определении диаметра и свойствах в этой статье.

1.	Каков диаметр круга?
2.	Диаметр окружности Формула
3.	Как найти диаметр круга?
4.	Диаметр против радиуса
5.	Часто задаваемые вопросы о Diameter

Каков диаметр круга?

Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности окружности. Диаметр также известен как самая длинная хорда окружности.

Определение диаметра

Диаметр определяется как удвоенная длина радиуса окружности. Радиус измеряется от центра круга до одной конечной точки на границе круга, тогда как расстояние диаметра измеряется от одного конца круга до точки на другом конце круга, проходящей через центр. Обозначается буквой D. На окружности окружности бесконечное количество точек, это означает, что окружность имеет бесконечное число диаметров, и каждый диаметр окружности имеет одинаковую длину.

Символ диаметра

Ø — это символ, который используется в технике для обозначения диаметра. Этот символ обычно используется в технических спецификациях и чертежах. Ø25 мм означает, что диаметр круга составляет 25 мм.

Диаметр окружности Формула

Все мы знаем, что диаметр является частью круга. Давайте разберемся с некоторыми терминами, прежде чем мы узнаем формулу диаметра круга.

• Радиус (r) — это длина отрезка от центра окружности до конечной точки окружности.
• Окружность (C) относится к замкнутой границе круга. Он также известен как периметр круга.
• Площадь круга — это общее пространство внутри границы круга. Он рассчитывается по формуле πr ² , где r — радиус.

Мы можем вывести формулу диаметра из длины окружности, площади и радиуса круга.

Диаметр круга с использованием длины окружности

Мы можем легко вывести формулу диаметра из длины окружности. Формула длины окружности: C = πd; здесь, C = длина окружности, d = диаметр окружности, π = 22/7 или 3,142 прибл. Формула диаметра с использованием окружности:

Диаметр = Окружность ÷ π.

Диаметр круга с использованием радиуса

Радиус — это длина отрезка от центра круга до конечной точки на круге, а диаметр в два раза превышает длину радиуса круга. Используя это определение, формула для диаметра равна D = Радиус × 2 .

Формула диаметра, использующая площадь круга

Мы можем вывести формулу диаметра круга, используя формулу площади круга, то есть площадь (A) = π(радиус) ² . Подставляя значение радиуса в качестве D/2, мы получаем A/π = (D/2) ² .

⇒ D/2 = √(A/π)

⇒ D = 2 × √(A/π)

Следовательно, формула диаметра круга с использованием площади: D = 2√Площадь/π .

Как найти диаметр круга?

Диаметр круга можно рассчитать, если известны радиус, длина окружности или площадь. Выполните шаги, указанные ниже, чтобы найти диаметр круга:

• Шаг 1: Первый шаг — определить, что дано в вопросе: радиус, площадь или окружность.
• Шаг 2: Примените соответствующую формулу из трех приведенных выше формул.
• Шаг 3: Упрости и получи ответ.

Попробуем найти диаметр с помощью приведенных выше формул на практическом примере. Обратите внимание на приведенный ниже пример.

Пример: Джек нарисовал круг радиусом 3 единицы. Каков диаметр круга?

Решение:

Дано: Радиус окружности = 3 единицы.
Диаметр круга = 2 × радиус
= 2 × 3 = 6 шт.
Следовательно, диаметр круга равен 6 единицам.

Диаметр против радиуса

Как мы уже говорили, длина диаметра в два раза больше радиуса. Есть некоторые сходства и различия между диаметром и радиусом, которые мы собираемся изучить в этом разделе. Прежде чем перейти к разнице между диаметром и радиусом, сначала поговорим об их сходстве. И диаметр, и радиус являются частями круга, которые определяют различные свойства, такие как размер круга, длина окружности и площадь круга. Они разделяют отношения в форме уравнения. и.в. Диаметр = 2 × Радиус.

Посмотрите на приведенную ниже таблицу, чтобы понять диаметр и радиус.

Диаметр	Радиус
Диаметр круга в два раза больше его радиуса.	Это половина длины от диаметра.
Для любой окружности длина диаметра больше длины радиуса.	Длина радиуса меньше диаметра.
Начинается с границы круга и заканчивается на самой границе.	Начинается из центра и в точке касается окружности круга.

☛ Похожие темы

Проверьте эти интересные статьи, связанные с диаметром круга.

• Хорды ​​и диаметры
• Формула диаметра сферы с использованием объема
• Окружность к диаметру

 

Примеры диаметров

1. Пример 1: Радиус круга составляет 15 единиц. Вычислите его диаметр.

   Решение:
   Дано, радиус = 15 единиц
   Мы это знаем,
   Диаметр = 2 × радиус 90 141 = 2 × 15
   Следовательно, диаметр = 30 единиц.

2. Пример 2: Можете ли вы определить значение радиуса, если диаметр окружности равен 36 единицам?

   Решение:
   Дано: Диаметр = 36 единиц
   Мы знаем, что диаметр в два раза больше радиуса. Это означает, что радиус равен половине значения диаметра.
   Диаметр = 2 × радиус 90 141 Р = Д ÷ 2
   Радиус = 36 ÷ 2 = 18 единиц
   Следовательно, радиус = 18 единиц.

3. Пример 3: Диаметр круглого бассейна составляет 7 футов. Какова окружность бассейна? Выразите ответ через число π.

   Решение:
   Дано: Диаметр = 7 футов
   Мы знаем, что длина окружности = π × d
   . Таким образом, длина окружности бассейна = π × 7 
   . Следовательно, окружность бассейна = 7π футов.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по Diameter

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по диаметру

Какой диаметр?

Диаметр – это прямая линия, проходящая через центр окружности и делящая окружность на две части/полуокружности. Это самая длинная хорда окружности, которая пересекает окружность на противоположных концах.

Какой символ используется для обозначения диаметра?

В технике для обозначения диаметра используется символ ⌀. Его часто называют «фи». Этот символ фи используется для описания диаметра круглого сечения. Например, «⌀20» означает, что диаметр круга составляет 20 единиц измерения.

Что такое радиус и диаметр?

Радиус и диаметр круга являются двумя важными частями круга, которые взаимозависимы друг от друга. Радиус круга — это отрезок, который начинается от центра круга и заканчивается на окружности круга. Это половина длины диаметра круга, т. Е. Радиус = диаметр / 2. Диаметр окружности — это отрезок, проходящий через центр окружности и имеющий две точки на окружности. Это в два раза больше длины радиуса окружности, т. е. диаметр = 2 × радиус.

Как рассчитать диаметр?

Диаметр круга можно рассчитать по заданным параметрам. Если заданы такие параметры, как радиус, окружность или площадь, мы можем напрямую использовать следующие формулы.

• Диаметр = длина окружности ÷ π (если дана длина окружности)
• Диаметр = 2 × радиус (если указан радиус)
• Диаметр = 2√[Площадь/π] (если дана площадь)

Пример диаметра?

Если вы посмотрите на колесо цикла, шипы, идущие от одного конца к другому через центр, являются примером диаметра. Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.

Как найти диаметр по окружности?

Если длина окружности известна, то мы можем легко найти значение диаметра, подставив значения в формулу: Диаметр = C ÷ π; где «C» — длина окружности, а значение π равно примерно 22/7 или 3,14.

Как найти площадь круга по диаметру?

Площадь круга рассчитывается по формуле: πr ² . Если диаметр задан, мы можем найти радиус, разделив значение диаметра на 2. Получив радиус, мы можем подставить его значение в формулу: πr ² , чтобы получить площадь круга, или напрямую применить формулу площади. с диаметром, A = π(d/2) ² = πd ² /4 кв.

Для чего нужен калькулятор отношения диаметра к окружности?

Калькулятор отношения диаметра к окружности — это онлайн-инструмент, используемый для определения значения длины окружности. В калькуляторе диаметра окружности введите размер диаметра и получите значение окружности в течение нескольких секунд. Вы также можете попробовать калькулятор диаметра для прямых расчетов.

Какова формула диаметра круга, если известен радиус круга?

Если радиус окружности указан в единицах ‘r’, то легко определить диаметр окружности по формуле. С определением радиуса мы знаем, что это половина диаметра, следовательно, формула диаметра = 2r.

Как называется половина диаметра круга?

Диаметр круга — это отрезок линии от одного конца круга до другого конца круга, проходящий через центр круга. Принимая во внимание, что радиус круга — это длина отрезка линии от центра круга до точки на окружности круга. Следовательно, радиус равен половине диаметра окружности.

Как диаметр связан с радиусом окружности?

Радиус круга равен половине диаметра. Отношение между радиусом и диаметром можно математически выразить формулой: Диаметр = 2 × радиус.

Является ли диаметр половиной радиуса?

Нет, диаметр не равен половине радиуса. Это в два раза больше радиуса окружности. Он представлен формулой: Диаметр = 2 × Радиус.

калькулятор окружности

, созданный Bogna Szyk и Mateusz Muga

, рассмотрено Jack Bowater

Последнее обновление: 11 марта 2022 г.

Содержание:

• Определение окружности
• Формула для окружности
• Как найти окружность круга
• Окружность к диаметру
• Часто задаваемые вопросы

Если вам нужно решить некоторые геометрические задачи, этот калькулятор длины окружности — страница для вас. Это инструмент, специально созданный для определения диаметра, длины окружности и площади любого круга. Читайте дальше, чтобы узнать:

• Что такое определение окружности
• Как найти длину окружности
• Как преобразовать длину окружности в диаметр

Как и в случае со всеми нашими инструментами, калькулятор длины окружности работает во всех направлениях — он также является калькулятором длины окружности в диаметр и может использоваться для преобразования длины окружности в радиус, окружности в площадь, радиуса в окружность, радиуса в диаметр (да!), радиус в площадь, диаметр в окружность, диаметр в радиус (да, опять же с ракетостроением), диаметр в площадь, площадь в окружность, площадь в диаметр или площадь в радиус.

Если вы хотите нарисовать круг на декартовой плоскости, вам может пригодиться это уравнение калькулятора окружности.

Определение длины окружности

Длина окружности — это линейное расстояние от края окружности. Это то же самое, что и периметр геометрической фигуры, но термин «периметр» используется исключительно для многоугольников.

Окружность часто неправильно пишется как окружность .

Формула для длины окружности

Следующее уравнение описывает соотношение между длиной окружности и радиусом R круга:

C = 2πR

Где π — константа, приблизительно равная 3,14159265…

💡 Точное значение числа π найти невозможно. Это иррациональное число, поэтому мы обычно используем приблизительные значения, такие как 3,14 или 22/7. Если вам интересна эта тема, взгляните на первый миллион цифр числа π!

Такая же простая формула определяет отношение между площадью круга и его радиусом:

A = π * R²

Как найти длину окружности

1. Определить радиус окружности. Предположим, что она равна 14 см.
2. Подставьте это значение в формулу длины окружности: C = 2 * π * R = 2 * π * 14 = 87,9646 см .
3. Вы также можете использовать его, чтобы найти площадь круга: A = π * R² = π * 14² = 615,752 см² .
4. Наконец, вы можете найти диаметр — он просто удваивает радиус: Д = 2 * Р = 2 * 14 = 28 см .
5. Используйте наш калькулятор окружности, чтобы найти радиус, когда у вас есть только длина окружности или площадь круга.

Если вы хотите рассчитать свойства трехмерного твердого тела, такого как сфера, цилиндр или конус, лучше всего использовать наш калькулятор объема.

Окружность к диаметру

Вы, наверное, заметили, что, поскольку диаметр в два раза больше радиуса, отношение длины окружности к диаметру равно π:

C/D = 2πR / 2R = π

Эта пропорция (длина окружности к диаметру) является определением константы числа пи. Он используется во многих областях, таких как физика и математика. Например, вы можете найти его в калькуляторе центробежной силы.

🔎 Если вас интересует взаимосвязь между окружностью и другими переменными, вы можете взглянуть на наши калькуляторы окружности к диаметру и окружности и площади круга .

FAQ

Как найти длину окружности?

Чтобы вычислить длину окружности, вам нужен радиус окружности :

1. Умножьте радиус на 2, чтобы получить диаметр.
2. Умножьте результат на π или 3,14 для оценки.
3. Вот и все; вы нашли длины окружности .

Или вы можете использовать диаметр круга :

1. Умножьте диаметра на π, или 3,14.
2. Результатом является длина окружности .

Какова длина окружности?

Длина окружности равна линейному расстоянию от края окружности . Он эквивалентен периметру геометрической формы, хотя этот термин периметр используется только для многоугольников.

Кто первым вычислил окружность Земли?

Первым человеком, вычислившим длину окружности Земли, был Эратосфен, греческий математик г., в 240 г. до н.э. Он обнаружил, что объекты в городе в северном тропике не отбрасывают тень в полдень в день летнего солнцестояния, а находятся в более северном месте. Зная это и расстояние между точками, ему удалось вычислить окружность Земли.

Как найти диаметр по окружности?

Если вы хотите найти диаметр окружности , выполните следующие действия:

1. Разделите длину окружности на π или 3,14 для оценки.
2. Вот и все; у вас есть диаметр круга .

Как найти площадь круга по длине окружности?

Чтобы найти площадь круга из окружности , выполните следующие действия:

1. Разделите длину окружности на π.
2. Разделите результат на 2, чтобы получить радиус круга .
3. Умножьте радиуса на самого себя, чтобы получить его квадрат.
4. Умножьте квадрата на π или 3,14 для оценки.
5. Вы нашли площадь круга из длины окружности .

Как найти радиус окружности?

Чтобы найти радиус окружности , вы должны сделать следующее:

1. Разделите длину окружности на π или 3,14 для оценки. В результате получится диаметр круга.
2. Разделить диаметр на 2.
3. Ну вот, вы нашли радиус окружности .

Как измерить окружность?

• Длина окружности вычисляется как 2 ⨉ радиус ⨉ π .
• Вычислите длину окружности как диаметр ⨉ π .
• Оберните нить вокруг предмета и измерьте его длину.
• Используйте калькулятор окружности Omni .

Какова формула длины окружности?

Формула для длины окружности , если задан радиус окружности, выглядит так:

• 2 ⨉ радиус ⨉ π

Или, если дана длина окружности:

• Окружность ⨉ π

Вы можете оценить π как 3,14.

Какова длина окружности с радиусом 1 метр?

Чтобы рассчитать длину окружности с радиусом 1 метр , просто выполните следующие действия:

1. Умножьте радиус на 2, чтобы получить диаметр 2 метра.
2. Умножьте результат на π или 3,14 для оценки.
3. Вот и все; длина окружности радиуса 1 метр равна 6,28 метра .

Как найти длину окружности цилиндра?

Чтобы найти длину окружности цилиндра , вы должны знать, что поперечное сечение цилиндра представляет собой круг. Если вы знаете радиус цилиндра:

1. Умножьте радиус на 2, чтобы получить диаметр.
2. Умножьте результат на π или 3,14 для оценки.
3. Вот и все; вы нашли окружность цилиндра .

Или вы можете использовать диаметр цилиндра :

1. Умножьте диаметр на π, или 3,14.
2. Результатом является длина окружности цилиндра .

Как найти площадь круга с длиной окружности 1 метр?

Если вы хотите найти площадь круга с длиной окружности 1 метр , сделайте следующее:

1. Разделите длину окружности на π. Это диаметр круга , в данном случае 31,8 сантиметра.
2. Разделите на 2. Этот результат равен радиусу окружности 15,9 см.
3. Умножьте радиуса на себя, получив квадрат, в нашем случае 256 см².
4. Умножить на π или 3,14 для оценки.
5. Вот и все; круг с окружностью 1 метр имеет площадь 795,78 см² .

Как найти радиус окружности с длиной окружности 10 сантиметров?

Чтобы найти радиус окружности с длиной окружности 10 сантиметров , вы должны сделать следующее:

1. Разделите длину окружности на π или 3,14 для оценки. В результате получается диаметр круга 3,18 сантиметра.
2. Разделить диаметр на 2.
3. И вот, радиус круга с окружностью 10 сантиметров равен 1,59 сантиметра .

Какова единица длины окружности?

Поскольку длина окружности представляет собой линейное расстояние от края окружности, она описывает длину. Таким образом, наиболее распространенных единиц измерения длины окружности — это миллиметры, сантиметры, метры для метрической системы и дюймы, футы и ярды для имперской системы9. 0004 .

Богна Шик и Матеуш Муха

Радиус (r)

Диаметр

Окружность (c)

Проверить 8 подобных калькуляторов окружности … 5 more

Калькулятор площади круга

Создано Луцией Заборовской, доктором медицинских наук, кандидатом наук

Отредактировано Домиником Черня, доктором философии и Джеком Боутером

Последнее обновление: 26 августа 2022 г.

Содержание:

• Как вычислить площадь круга? Формула площади круга
• Как использовать калькулятор площади круга? Диаметр к площади и радиус к площади.
• Зачем нужны калькуляторы площади поверхности круга?

Калькулятор площади круга поможет вам вычислить поверхность круга по заданному диаметру или радиусу . Наш инструмент работает в обоих направлениях — независимо от того, ищете ли вы калькулятор площади в радиус или радиус в площадь один, вы нашли нужное место ◔

Мы познакомим вас с наиболее важной информацией о площади круга, его диаметре и радиусе. Мы узнаем , как найти площадь круга , поговорим о формуле площади круга и обсудим другие разделы математики, в которых используется то же самое уравнение.

Как вычислить площадь круга? Формула площади круга

Итак, давайте посмотрим, как найти площадь круга. Есть несколько способов добиться этого. Здесь мы можем вычислить площадь круга с использованием диаметра или с использованием радиуса .

💡 Диаметр — это линия, которая пересекает центр фигуры и касается обоих ее краев. Радиус начинается в центре фигуры и заканчивается на краю фигуры.

Диаметр окружности можно найти, умножив радиус окружности на два:

Диаметр = 2 * Радиус

Площадь радиуса окружности. Калькулятор радиуса круга использует следующую формулу площади круга:

Площадь круга = π * r 2

Площадь диаметра круга. Калькулятор диаметра круга использует следующую формулу:

Площадь круга = π * (d/2) 2

Где:

• π приблизительно равно

  9 0,04 0,03 3. Неважно, хотите ли вы найти площадь круга с помощью диаметра или радиуса — вам нужно будет использовать эту константу почти в каждом случае.

🔎 Другим важным аспектом кругов является их длина окружности. Вы можете узнать больше об этом и его связи с площадью в нашем калькуляторе формулы круга . Универсальный круговой инструмент ;

Окружность и периметр круга;

Сектор круга;

Круговая диаграмма;

Площадь наибольшего круга в квадрате.

Сектор круга – это часть круга между двумя радиусами. Вы можете думать об этом как о гигантском куске пиццы.

• Сегмент круга;

Это «отсеченная» часть окружности, ограниченная хордой или секущей.

• Круглый уголок;

Угол с вершиной в центре, стороны которого выходят на окружность.

• Площадь полукруга; и

• Если вы хотите знать , как нарисовать круг? может пригодиться уравнение для координат и центра окружности в системе координат.

Как использовать калькулятор площади круга? Диаметр к площади и радиус к площади.

Вы можете легко рассчитать все, площадь круга, его диаметр и радиус, используя наш калькулятор площади круга в мгновение ока:

1. Определите , является ли заданное вами значение диаметром или радиусом , используя изображение справа и определения, доступные в разделе выше (вы можете рассчитать площадь круга, используя его диаметр, а также радиус).

2. Введите значение в соответствующее поле калькулятора .

3. Это не заняло много времени — ваши результаты уже здесь ! Мы решили разместить пошаговое решение и все самые важные данные прямо под калькулятором.

Вот как быстро вычислить площадь круга 😉.

🔎 Площадь — это не единственное свойство, связанное с диаметром, как и длина окружности. Узнайте больше об этом в нашем калькуляторе длины окружности в диаметр.

Зачем нужны калькуляторы площади поверхности круга?

Площадь круга, найденная с помощью калькуляторов радиуса и диаметра , служит основой для многих других уравнений — не только в математике, но и в повседневной жизни! Вот несколько примеров, когда знание того, как найти площадь круга, может быть полезным:

• Нам нужно знать площадь поверхности круга, чтобы вычислить объем конуса и площадь его поверхности 🎉

• Ваша вечеринка с пиццей была бы неполной без нашего инструмента для пиццы, основанного на калькуляторе отношения диаметра к площади 🍕

• Мы используем вычисления, подобные этому, при получении информации о сфере, такой как объем сферы.

  No related posts.