Преобразование звезда треугольник: Эквивалентное преобразование треугольника в звезду

Причина преобразования треугольника в звезду

При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.

Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.

 Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.

Формулы для расчета  преобразования треугольника в звезду

              

Пример преобразования

Для электрической цепи необходимо выполнить преобразование треуголькника R12 — R23 — R31 в звезду. 

Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.

Удаляем соединение сопротивлений треугольником.

В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.

4. Звезда в треугольник

Любые сложные электрические цепи можно упростить. Один из методов — эквивалентное преобразование звезды в треугольник. При этом в электрической схеме уменьшается количество узлов или количество ветвей. Преобразование треугольника в звезду возможно только для пассивных элементов, т.е. для потребителей электрической энергии.

Определение соединения сопротивлений звездой

 Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой. 

В курсе теоретических основ электротехники обычно принято электрические элементы цепи изображать горизонтально и вертикально. Так что схема ниже так же является соединением звездой.

Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.

Причина использования преобразования звезды в треугольник

При выполении расчета сложной электрической цепи иногда необходимо выполнить упрощение (свертку, преобразование) схемы. Обычно для этого ищут сначала последовательное или параллельное соединений сопротивлений. Если таких соединений не находят то выполняют экивалентное преобразование звезды в треугольник, если в электрической цепи есть соединение сопротивлений звездой.

Если в электрической цепи нашли соединение сопротивлений звездой, то между концами лучей подставляем сопротивления в виде треугольника.

Удаляем соединение звездой. Получается эквивалентное преобразование звезды в треугольник.

Формулы для расчета эквивалентного преобразования звезды в треугольник

         

Пример преобразования

Для приведенной электрической цепи необходимо выполнить экивалентное преобразование звезды R1 -R2 -R3 в треугольник R12 — R23 — R31.

Дорисовываем три сопротивления R12, R23, R31 к концам лучей сопротивлений R1, R2 и R3.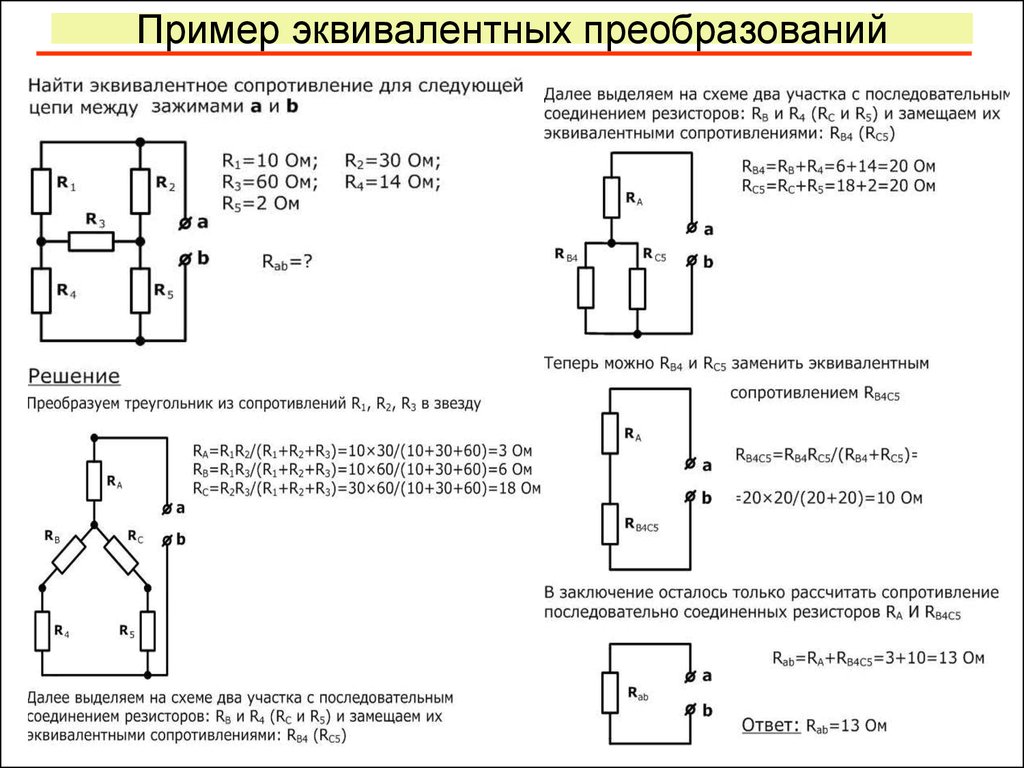

Удаляем сопротивления R1, R2 и R3. Параметры эквивалентных сопротивлений R12, R23, R31 рассчитываем по формулам.

4.1.3. Взаимные преобразования “треугольник — звезда”,

“звезда — треугольник”

В ряде случаев сложную электрическую цепь можно упростить путем преобразования треугольника сопротивлений в эквивалентную звезду и наоборот (рис. 4.4).

Рис. 4.4

При этом токи и напряжения остальной части цепи должны остаться неизменными.

Формулы преобразования имеют вид:

а) треугольник – звезда

, (4.9)

, (4.10)

; (4.11)

б) звезда – треугольник

, (4.12)

, (4.13)

. (4.14)

Рассмотрим пример расчета цепи рис. 4.5 методом преобразования.

Рис. 4.5

Проведем преобразование треугольника сопротивлений , , в эквивалентную звезду (рис. 4.6):

,

,

.

Рис. 4.6

Ветви схемы рис. 4.6 содержат последовательно включенные сопротивления ( и , и , и ), эквивалентные преобразования которых приводят к цепи рис. 4.7.

Рис. 4.7

Сопротивления , и (рис. 4.7) определяют по формулам:

,

,

.

На следующем этапе преобразуют параллельно включенные сопротивления и в одно эквивалентное (рис. 4.8):

.

На завершающем этапе эквивалентных преобразований последовательно включенные сопротивления и (рис. 4.8) заменяют одним эквивалентным (рис.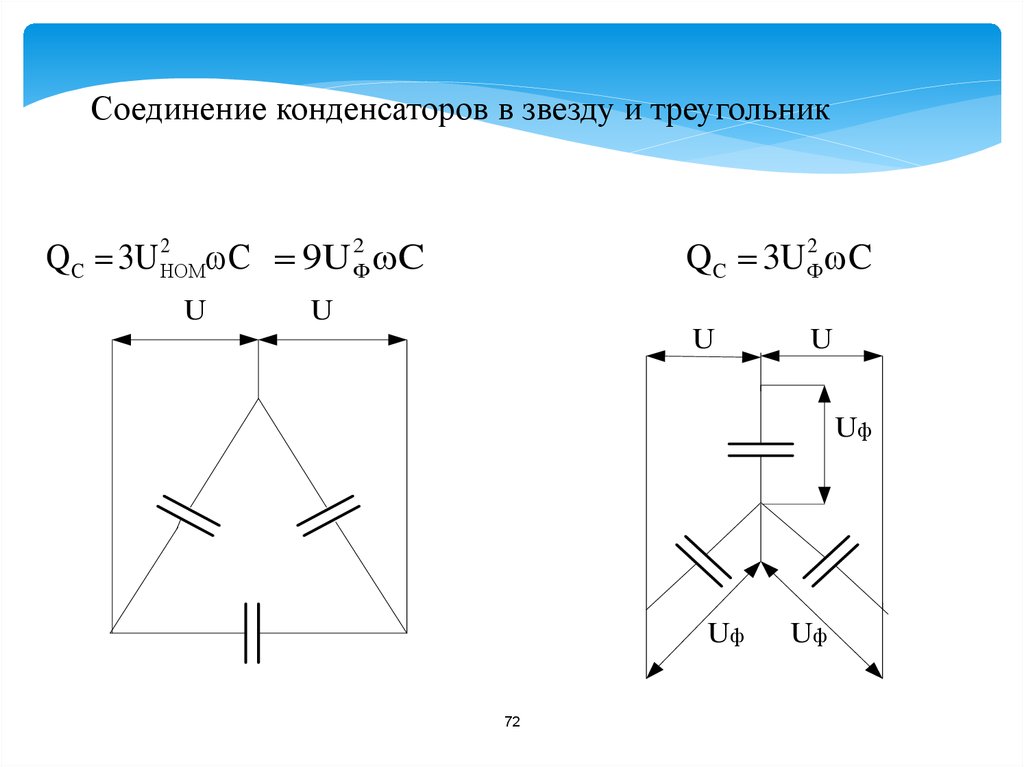 4.9):

.

Рис. 4.8

Рис. 4.9

Таким образом, сложная разветвленная цепь рис. 4.5 путем ряда преобразований приведена к простейшей одноконтурной (рис. 4.9), содержащей одно эквивалентное сопротивление . Достоинство полученной схемы – простота определения тока:

.

Расчет токов , будем осуществлять с учетом того обстоятельства, что напряжения между точками o и d () в схемах рис. 4.7 и рис. 4.8 одинаковы. Для цепи рис. 4.8 справедливо

.

Тогда (схема рис. 4.7)

,

.

Для расчета токов , , в ветвях треугольника (рис. 4.5) найдем напряжения , , в цепи рис. 4.6:

,

,

.

Тогда (схема рис. 4.5)

,

,

.

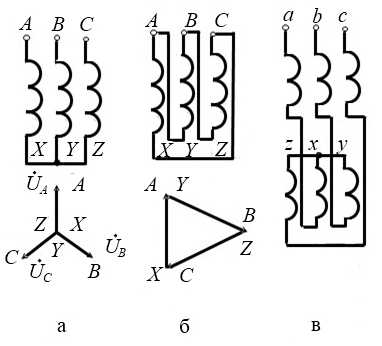
Расчёт линейных электрических цепей методом законов Кирхгофа сводится к составлению и решению систем алгебраических уравнений относительно неизвестных токов.

Пусть цепь содержит в качестве источников электрической энергии источники ЭДС. Так как число неизвестных токов равно числу ветвей n этой цепи, то система алгебраических уравнений должна иметь n-й порядок.

Обозначим k – число узлов цепи. Из принципа непрерывности токов следует, что число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (k — 1). Недостающие уравнения, количество которых равно [n – (k – 1)], составляются по второму закону Кирхгофа для независимых контуров.

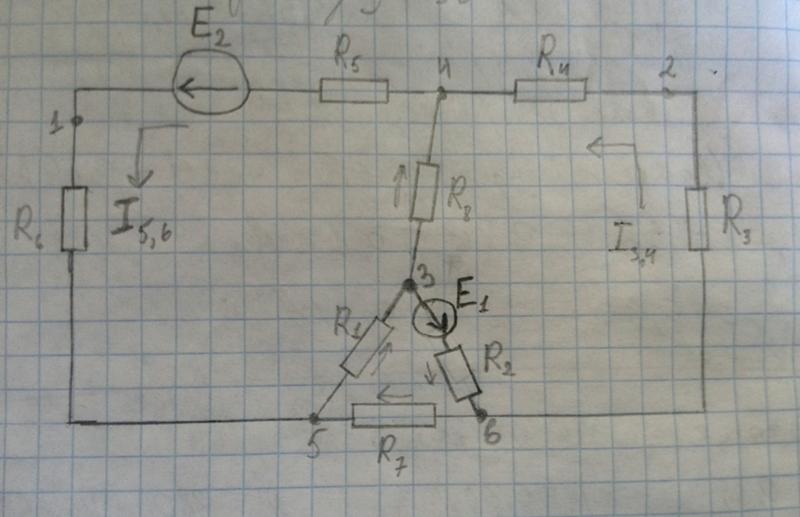
Рассмотрим в качестве примера расчёт токов в схеме рис. 4.10, которая содержит n=6 ветвей, k=4 узла и 3 независимых контура.

Рис. 4.10

Выберем произвольно направление токов в ветвях и направление обхода независимых контуров.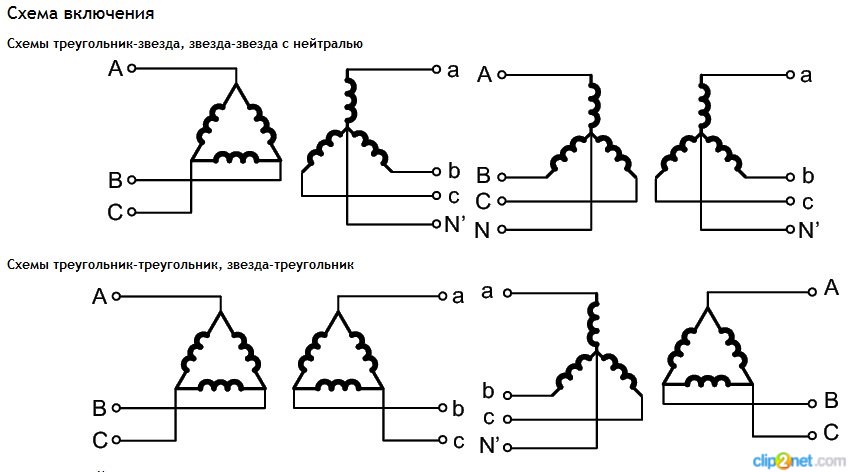 Первые три уравнения (4 – 1 = 3) запишем по первому закону Кирхгофа, а оставшиеся три (6 – 3 = 3) – по второму закону Кирхгофа.

Пусть цепь наряду с источниками ЭДС содержит m источников тока. Так как токи в ветвях с источниками тока равны токам этих источников, то число неизвестных токов уменьшается до величины (n – m). Однако в цепи появляются новые неизвестные величины – напряжения на зажимах источников тока, количество которых равно m. Поэтому общее количество неизвестных величин в цепи остается прежним, равным n.

Изложенные обстоятельства обусловливают возможность составления двух вариантов систем уравнений по законам Кирхгофа.

1. Если по условию задачи необходимо найти токи в ветвях и не требуется определять напряжения на зажимах источников тока, достаточно составить систему из (n – m) уравнений относительно неизвестных токов. В этой системе по-прежнему (k-1) уравнений составляется по первому закону Кирхгофа, а по второму – [n – m – (k – 1)].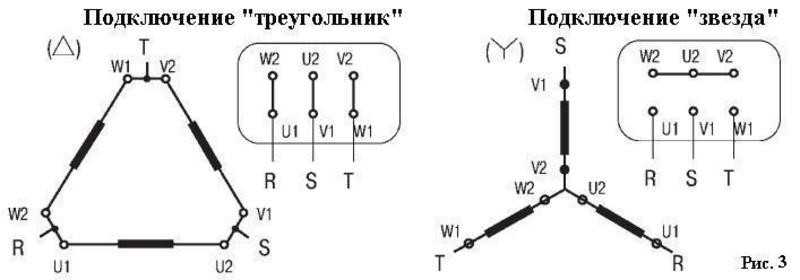

Естественно, что при записи уравнений по второму закону Кирхгофа выбираются независимые контуры, не содержащие источников тока.

2. Если по условию задачи необходимо найти токи в ветвях и напряжения на зажимах источников тока, необходимо составить систему из n уравнений. В ней (k-1) уравнение составляется по первому закону Кирхгофа и [n – (k – 1)] уравнений – по второму закону для всех независимых контуров.

Рассмотрим в качестве примера расчёт цепи рис. 4.11. Если требуется определить только токи в ее ветвях, то система уравнений имеет вид:

Данная система не содержит уравнение для независимого контура III, содержащего источник тока .

Рис. 4.11

Если в цепи рис. 4.11 необходимо рассчитать токи в ветвях и напряжение на зажимах источника тока , то система уравнений имеет вид

Трансформация Звезды Дельты – Learnchannel-TV.

com

Трансформация Звезда Дельта — как это работает

Трансформация Дельты в Звезду

Превращение звезды в дельту

Преобразование звезда-треугольник — это инструмент для упрощения сложных цепей резисторов. Здесь три резистора пересоединены с треугольника на звезду — и наоборот, с соответственно измененными значениями сопротивлений, так что соотношения между выводами остаются одинаковыми в обоих вариантах схемы.

Преобразование треугольника в звезду

Объяснение преобразования треугольника в звезду

Докажем это: оба типа цепи!

Считаем пины 1 и 2:

U _D12   =  U _S12     =>   => 909 R _{D1920028 S12}
I _D12 I _S12

Мы рассмотрим штифты 2 UND 3:

U _D23 = U _{8. D23} = U_{8.9. D23} = U_{8. D23} = U 8 23. _D23 . R _S23
I _D23 I _S23

Мы рассмотрим штифты 1 UND 3:

U _D13 = U U _D13 = U S1399.>> _{S1388. S138.0028 D13 = R S13
I D13 I S13}

Расчет сопротивлений между штифтами:

R _D12 = R _{D2 9 R D12 = R D2 D D12 = R D2 D D12 = R D2 D D12 = R DAI )  = R D2 (R D1 + R D3 )     must be equal to   R S12 = R S1 + R S2
. р D1 + R D2 + R D3}

Resulting in:

R _D12 =  R _D1 R _D2 + R _D2 R _D3   = R _S12 = R _S1 + R _S2                                       …Уравнение (1)
. R _D1 + R _D2 + R _D3

также:

R _D31 = R _D1 R _D2 + R _D1 R _D3 = R _S31 = R _{S3 + + + + + S3 . R D1 + R D2 + R D3}

R _D23 = R _D3 R _D1 + R _D3 R _D2    =  Р _С23 = R _S2 + R _S3            … Уравнение (3)
. R _D1 + R _D2 + R _D3

---

Сложим уравнение (1) + уравнение (2) — уравнение (3):

R _D1 + R _D2 R _D3 + R _D1 R _{D 2} + R _D1 R _D3 — (R _D3 R _D1 + R _D3 R _D2 )   = R _S1 + R _S2 + R _S1 + R _S3 — R _S2 — R _S3   = 2R _S1                                          . R _D1 + R _D2 + R _D3

Получаем в итоге:

R _S1 =      R _{R 9002 D2     .
. R D1 + R D2 + R D3}

То же, как мы получаем:

R _S2 = R _D2 R _{D3 .}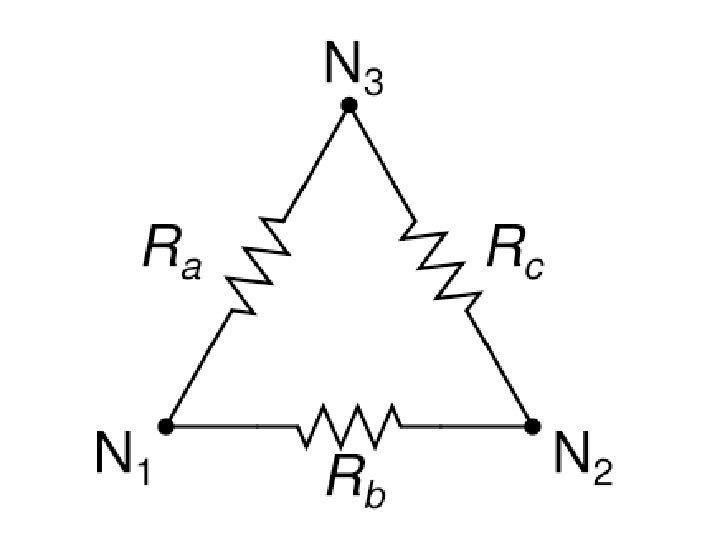
. R _D1 + R _D2 + R _D3

R _S3 = R _D1 R _{D3 .}
. Р _Д1 + R _D2 + R _D3

Если система, соединенная треугольником, имеет одинаковое сопротивление R _D с трех сторон, то эквивалентное сопротивление звезды R _S будет:

R S =      R _D R _D         . = R _D   .
. R _D + R _D + R _D       3

---

Преобразование звезды в треугольник

Таким же образом поступаем для преобразования звезды в треугольник. Резисторы RS1, RS2 и RS3 схемы «звезда» преобразуются в резисторы RD1, RD2 и RD3 схемы «треугольник» с соответствующими значениями сопротивлений таким образом, чтобы значения тока и напряжения между выводами 1 и 3 были одинаковыми.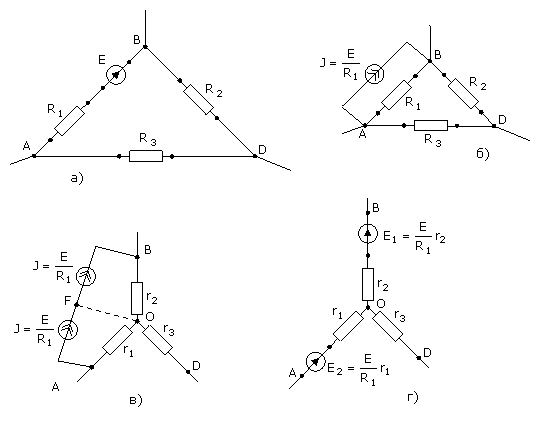

Преобразование звезды в треугольник

---

Докажем это:
При соединении звездой эквивалентное сопротивление между точками соединения 1 и 2 (соответственно 3) получается за счет короткого замыкания соединений 2 и 3. Таким образом, эквивалентное сопротивление между точками соединения 1 и 2 (соответственно 3) получается проводимость формируется из R _S1 и параллельное соединение R _S2 с R _S3 .
Если одни и те же точки замкнуты накоротко в схеме эквивалентного треугольника, общая проводимость получается в результате параллельного соединения резисторов R _D1 и R _D2 .

Преобразование звезды в треугольник – как это работает

Левая сторона приводит к общему знаменателю:

То же относится к клемме 3 и короткозамкнутым клеммам 1 и 2:

То же самое относится к клемме 2 и короткозамкнутым клеммам 1 и 3:

Добавим:   Ур. (1) + уравнение (2) — уравнение (3):

Решите это уравнение для R _D1 :

Та же процедура применима к остальным ветвям или резисторам.

Объяснение преобразования звезда-треугольник с советами по запоминанию формул

Почему и как мы выполняем преобразование звезды в дельту или дельты в звезду

Преобразование звезды и треугольника включает в себя преобразование из звезды в треугольник или из треугольника в звезду, и мы это когда наши резисторы не соединены параллельно или последовательно.

Этот метод весьма полезен, но в большинстве случаев учащиеся забывают формулу для быстрого использования, но, в В этом разделе я дам вам наглядный совет, чтобы никогда не забывать об этом, так что давайте начнем.

Способ соединения треугольника и звезды проиллюстрирован ниже в сравнении с последовательностью и последовательностью. параллельное соединение резисторов.

Дельта может быть структурирована двумя способами как треугольник форму или форму пирога, в то время как звезда имеет звезда или Т-образная форма, поэтому обязательно обратите внимание на это.

Маленький самородок

Звезду иногда называют звездой, а дельту — буквой Пи.

Преобразование или преобразование из треугольника в звезду не легче работать, за исключением того, что мы преобразуем его в другую форму, а затем решаем, поэтому мы выполнить это преобразование.

Итак, чтобы преобразовать дельту в звезду, это делается следующим образом, хотя формула указана как —

Формула преобразования дельты в звезду

Как запомнить формулу преобразования дельты в звезду

Итак, давайте вспомним эту формулу начиная с R ₁ .

Глядя на R ₁ , мы видим, что узел в верхней части R ₁ имеет два резистора. из дельта сети, связаны или привязаны к нему. Итак, в этом случае мы говорим, что есть 2 ноги, воздействующие на R 9.0028 1 который R _и и Р _б .

Затем, поскольку дельта является нашим источником преобразования и также соединены последовательно (помните в резисторы, соединенные последовательно, значения складываются и через них протекает одинаковый ток) поэтому, мы суммируем (R _a + R _b + R _c ), а затем делим его на наш первый результат это R _a и R _b (помните, что нам нужно умножить R _на и R _{b на} , поскольку они влияют на R ₁ ).

Таким образом, преобразование дает R ₁ = (R _a R _b ) / (R _a + R _b + R _c ).

Проделав то же самое для R ₂ , получим R ₂ = (R _a R _c ) / (R _a + R _b + R _c ) а за Р ₃ что будет если сделать самому не глядя в ответ.

Если вы получили ответ правильно, это хорошо и по существу видно, это только ножка, привязанная к нашему резистору в фокусе имеет значение, так как нижняя часть (R _a + R _b + R _c ) то же самое для R ₁ , R ₂ и R ₃ .

Преобразование или преобразование из звезды в треугольник

Во-первых, в этом преобразовании мы должны найти R _a , R _b и R _c как напротив последнего раздела, где мы должны найти R ₁ , R ₂ и R ₃ .

Формула представлена ​​как

R _a = (R ₁ R ₂ + Р ₂ Р ₃ + Р ₃ Р ₁ ) / Р ₃ , Р _б = (Р ₁ Р ₂ + Р ₂ Р ₃ + Р ₃ Р ₁ ) / Р ₂ и Р _с = (Р ₁ Р ₂ + Р ₂ Р ₃ + R ₃ R ₁ ) / R ₁

Формула преобразования звезда в треугольник

Как запомнить формулу преобразования звезда в треугольник

Теперь вспомним формулу с помощью нашей подсказки.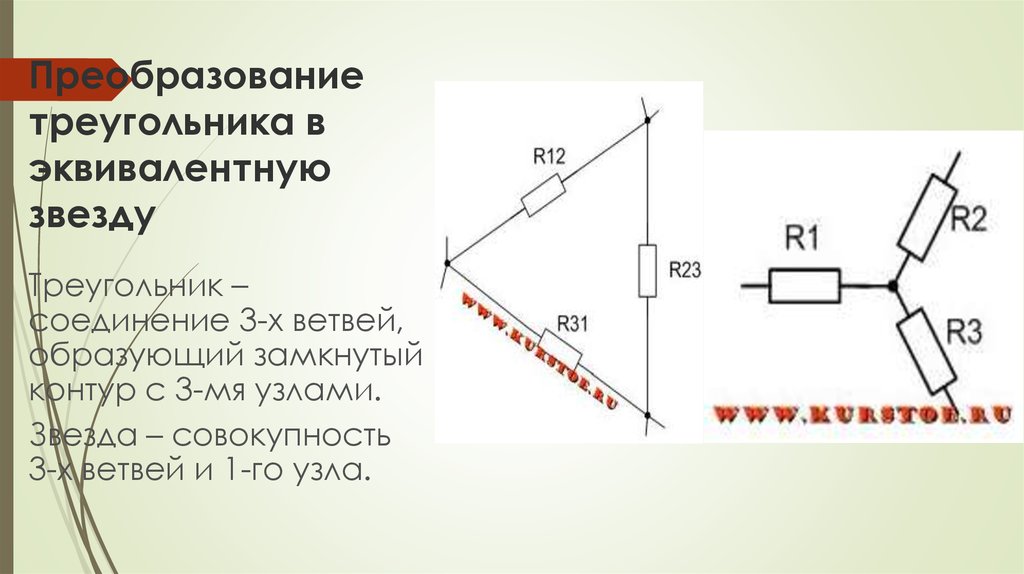 Прежде всего, вы можете видеть, что R _и затронуты по R ₁ и R ₂ . И эти R ₁ и R ₂ также соединены в средней точки друг к другу с R ₃ , поэтому в этом случае мы не можем просто применить то же правило, что и предыдущий мы сделали для преобразования из дельты в звезду.

Но что нам нужно сделать, так это то, что _{руб. 1} и ₂ руб. привязаны к _{руб. и} , а также р ₁ и R ₂ соединены в узле с R ₃ , тогда мы просто умножаем R ₁ R ₂ и затем добавить R ₂ R ₃ и в последнюю очередь добавить R ₃ R ₁ что дает это.

Этот шаг может показаться немного запутанным, но просто повторите его еще раз, пока не поймете, что к чему. этого.

Подсказка

Если вы посмотрите на два предыдущих изображения, вы обнаружите, где показан шаблон — это также может помочь вспомнить формулу.

Затем после этого мы делим наш первый результат (R ₁ R ₂ + R ₂ R ₃ + R ₃ R _{1 2 R} ) на ногу, противоположную нашей 8 это R ₃ , или мы можем сказать, что ветвь не связана напрямую с R _a .

Аналогично, R _b = (R ₁ R ₂ + R ₂ R ₃ + R ₃ R _{90 2} 2 ) /

Примечание

Поскольку верхняя сторона одинакова для всех случаев, а меняется только нижняя, вспомните нижнюю часть как ногу напротив искомого резистора. И в этом случае R _b и противоположная сторона R ₂ .

Теперь ваша очередь сделать R _c и позже проверить свой ответ.

Наконец, давайте попробуем резюмировать все, что мы только что обсудили, решив несколько примеров.

Пример преобразования треугольника в звезду

Пример 1 преобразовать приведенную ниже схему треугольника в эквивалент звезды.

No related posts.