Правила аксонометрии: 6. Аксонометрические проекции

Аксонометрические проекции — презентация онлайн

Похожие презентации:

Основы архитектуры и строительных конструкций. Основы проектирования

Конструктивные схемы многоэтажных зданий

Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)

Правила выполнения архитектурно-строительных чертежей

ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)

задачи на построение (геометрия 7 класс)

Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)

Параллельность в пространстве. (Графическая работа 2)

Строительное черчение. Графическое оформление и чтение строительных чертежей

Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты

1. Аксонометрические проекции

Дисциплина: ИНЖЕНЕРНАЯ ГРАФИКА

2. Наглядные изображения

Перспектива
метод центрального проецирования

3. Наглядные изображения

Параллельная и центральная
аксонометрия

4.

Метод аксонометрииОбъект относят к прямоугольной
системе координат и проецируют на
картинную плоскость вместе с осями
координат параллельным
проецированием.

5. Классификация аксонометрических проекций

Прямоугольная — направление
проецирования перпендикулярно
плоскости проекций
Косоугольная — направление
проецирования не перпендикулярно
плоскости проекций

6. Классификация аксонометрических проекций

Коэффициенты искажения:
соотношение величины координаты
на аксонометрической проекции к
истинной величине
k=x’/x m=y’/y n=z’/z

7. Классификация аксонометрических проекций

Изометрия k=m=n
Диметрия k≠m=n
Триметрия k≠m ≠ n

8. Классификация аксонометрических проекций

По положению картинной плоскости:
Горизонтальная
Фронтальная

9. Аксонометрические проекции

Применяются для наглядного изображения
различных предметов
1.
2.
3.
Гост 2.317-69 предусматривает:
Прямоугольные аксонометрические проекции
Изометрическая проекция
Прямоугольная диметрическая проекция
Косоугольные аксонометрические проекции
Фронтальная изометрическая
Горизонтальная изометрическая
Фронтальная диметрическая

10.

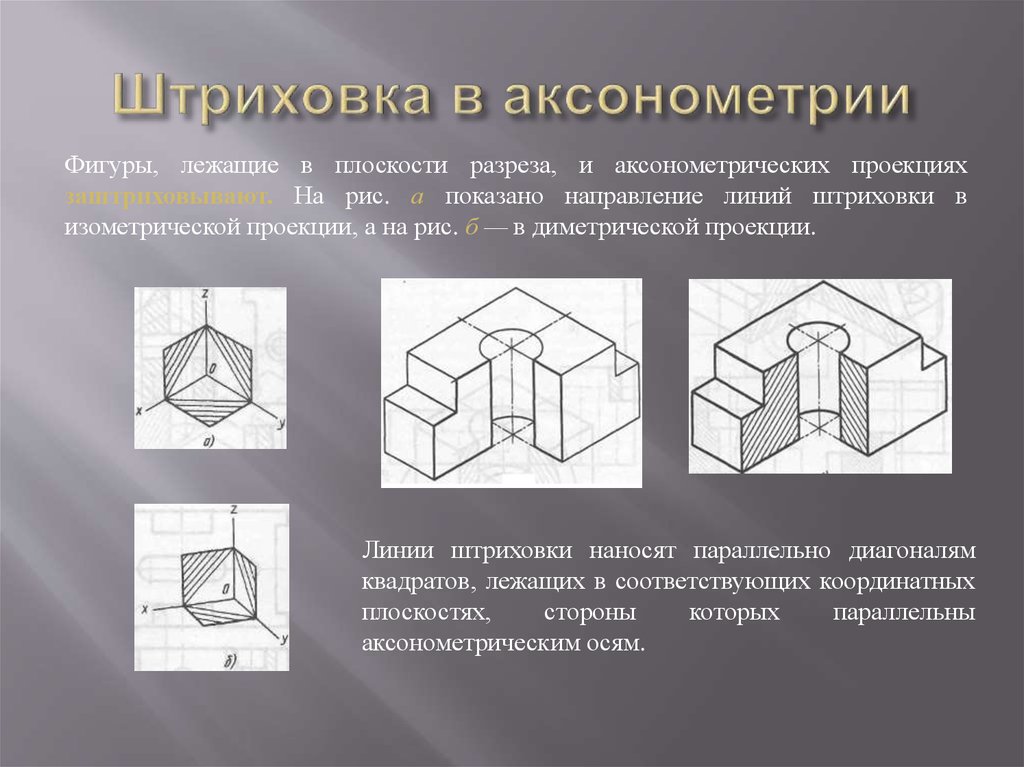Изометрическая проекцияКоэффициент искажения 0,82

11. Прямоугольная диметрическая проекция

Коэффициент искажения по оси Z и X = 0,94,
по оси Y – 0,47

12. Фронтальная изометрическая проекция

Угол наклона
оси 0Y к горизонтали обычно равен 45°, но
может иметь значение 30 или 60°
K=n=m=1.

13. Горизонтальная изометрическая проекция.

Угол наклона оси 0Y к
горизонтали обычно равен 30°,
но может иметь значение 45
или 60°. При этом угол 90°
между осями 0X и 0Y дол
должен сохраняться. K=n=m=1

14. Фронтальная диметрическая проекция

Допускается ось 0Y проводить под углом 30 или 60° к горизонтали.
Коэффициент искажения по оси 0X и 0Z принят равным 1, а по оси 0Y —
0,5.

15. Фронтальная диметрическая проекция

16. Аксонометрические проекции плоских фигур

Фигура, все точки которой принадлежат одной и той
же плоскости, называется плоской фигурой.
Краткое обозначение проекций:
Фронтальная диметрическая проекция — ФДП
Прямоугольная диметрическая проекция – ПДП
Прямоугольная изометрическая проекция – ИП

17.

Фронтальная диметрическая проекция (ФДП) прямоугольникаРазмеры прямоугольника
30х20 мм
Угол наклона оси 0Y
относительно горизонтали 450
Длина прямоугольника
направлена по оси 01Х1 и
отложена без сокращения, а
ширина по ости 01 Y1 — с
сокращением в два раза.

18. Фронтальная диметрическая проекция (ФДП) шестиугольника

Размеры шестиугольника:
сторона 30 мм
Угол наклона оси 0Y
относительно горизонтали
450
Большая диагональ
направлена по оси 01Х1 и
отложена без сокращения, а
меньшая диагональ
отложенная по оси 01Y1 — с
сокращением в два раза.

19. Прямоугольная диметрическая проекция (ПДП) шестиугольника

Размеры шестиугольника: сторона
30 мм
Угол наклона оси 0Y относительно
горизонтали 410, оси 0X
относительно горизонтали 70.
Большая диагональ направлена
по оси 01Х1 и отложена без
сокращения, а меньшая
диагональ отложенная по ости
01Y1 — с сокращением в два
раза.

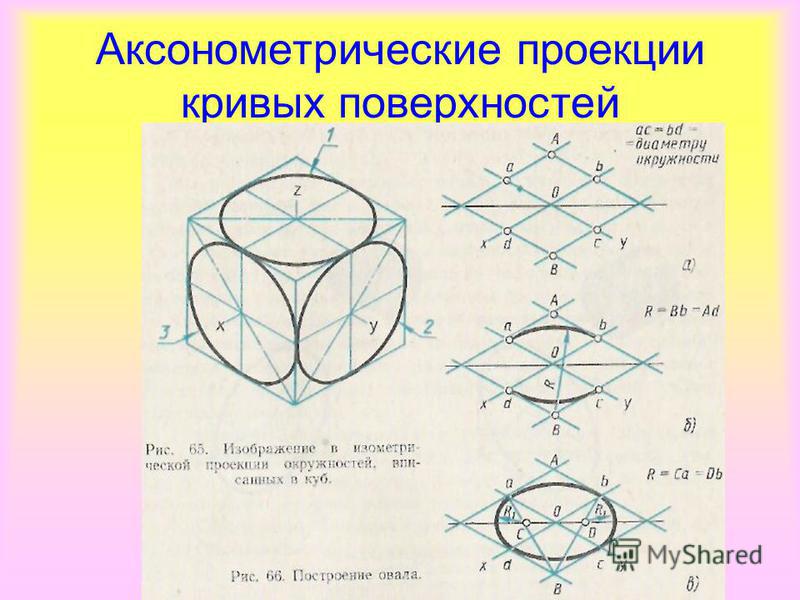
20. Прямоугольная изометрическая проекция (ИП) шестиугольника

Размеры шестиугольника:
сторона 30 мм
Углы между осями равны 1200
Диагонали и стороны
шестиугольника откладываются
без искажения

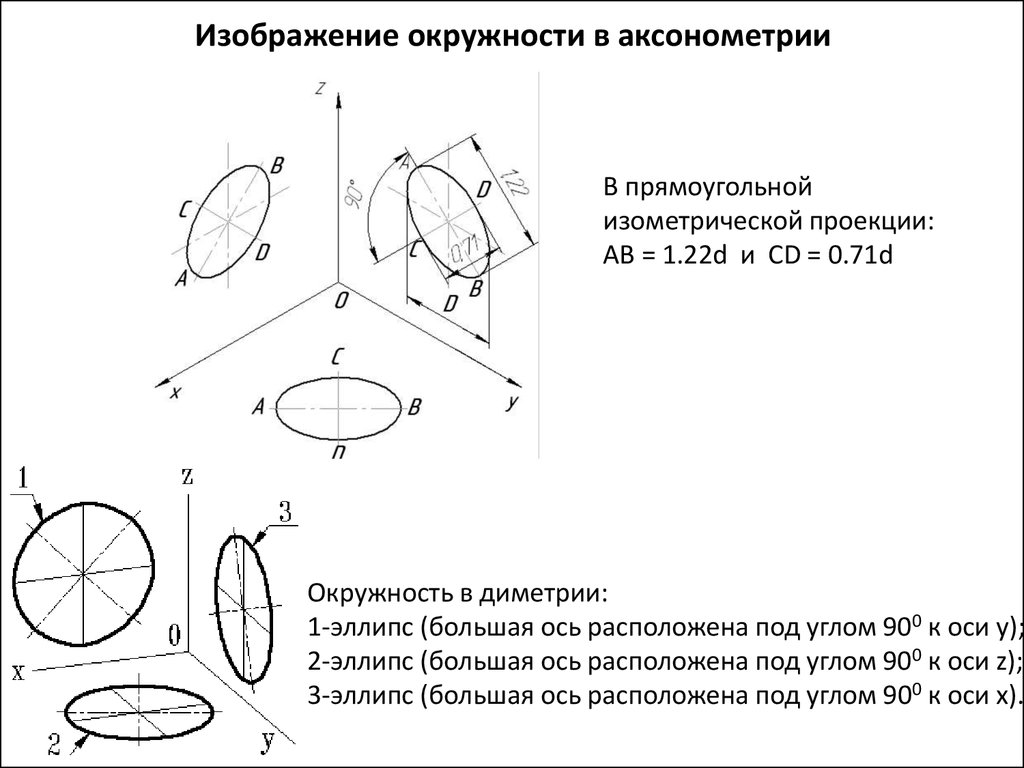
21. Изометрическая проекция окружности

22. Изображение окружности в прямоугольной изометрической проекции (ИП)

23. Проекции окружностей во ФДП и ПДП

Приемы вычерчивания
овалов, соответствующих
по длине и ширине узким
эллипсам — проекциям
окружностей, лежащих в
горизонтальной (рис. с,б)
и профильной (рис. в)
плоскостях во фронтальной и прямоугольной
диметрической проекции.
Спасибо за внимание

English     Русский Правила

Аксонометрические проекции — презентация онлайн

Похожие презентации:

Основы архитектуры и строительных конструкций. Основы проектирования

Конструктивные схемы многоэтажных зданий

Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)

Правила выполнения архитектурно-строительных чертежей

ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)

задачи на построение (геометрия 7 класс)

Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)

Параллельность в пространстве. (Графическая работа 2)

Строительное черчение. Графическое оформление и чтение строительных чертежей

Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты

ТЕМА: Аксонометрические проекции
ЦЕЛЬ: изучить правила построения аксонометрических

проекций
ЗАДАЧА:
проекций
Научить
построению
аксонометрических
Аксонометрические проекции
“Аксонометрия” образовано из слов древнегреческого
языка: “аксон”- ось и “метрео”- измеряю — измерение
по осям.
Аксонометрической проекцией называется
изображение, полученное на аксонометрической
плоскости в результате параллельного
проецирования предмета вместе с системой
координат, которое наглядно отображает его
форму.
Аксонометрия – это чертеж, на котором изображение
в трех измерениях.
Аксонометрические проекции.
Классификация.
По направлению проецирования:
(от направления проецирования делятся на две
группы):
— Прямоугольные — направление
проецирования перпендикулярно плоскости
проекций.
— Косоугольные — направление проецирования
не перпендикулярно аксонометрической
плоскости проекций.
Аксонометрические проекции.
Классификация.
По коэффициентам искажения:
— Изометрия – коэффициенты искажения по всем
трем осям равны между собой (Kx = Ky = Kz)
— Диметрия – коэффициенты искажения по двум осям
равны между собой, а третий им не равен
(Kx = Kz Ky)
— Триметрия – коэффициенты искажения по всем
трем осям не равны между собой (Kx Ky Kz)
Аксонометрические
проекции
ГОСТ 2.317-69, рекомендует применять пять
стандартных аксонометрических проекций:
Прямоугольные
изометрия
диметрия
Косоугольные
фронтальная изометрия
горизонтальная изометрия
фронтальная диметрия.
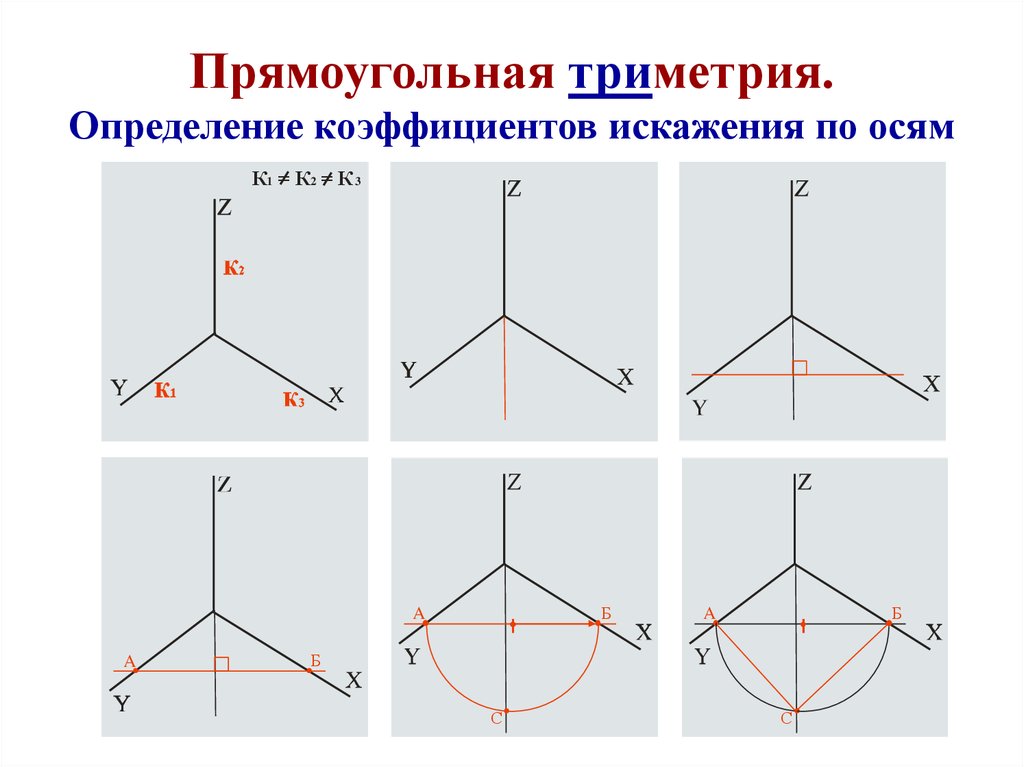
Прямоугольная
изометрическая проекция
коэффициент искажения по всем осям ГОСТ
рекомендует строить без сокращения равной единице,
что соответствует увеличению изображения в 1,22
раза
Прямоугольная диметрическая
проекция
коэффициент искажения: Kx = Kz = 1; Ky = 0,5,
При этом изображение получается увеличенным
в = 1,06 раза
Косоугольная фронтальная
изометрическая проекция
Коэффициенты искажения по всем осям будут равны
единице. Допускается применять фронтальные
изометрические проекции с углом наклона оси y ,
равным 30 и 60 .
Косоугольная
горизонтальная изометрическая
проекция
Коэффициенты искажения по всем осям принимаются
равными единице. Допускается применять
горизонтальные изометрические проекции с углом
наклона оси y = 45 и 60 ,сохраняя угол между осями x ,
y = 90 .
Косоугольная
фронтальная диметрическая
проекция
Коэффициенты искажения по осям x и z равны
единице, а по оси y
принимается равным 0,5.
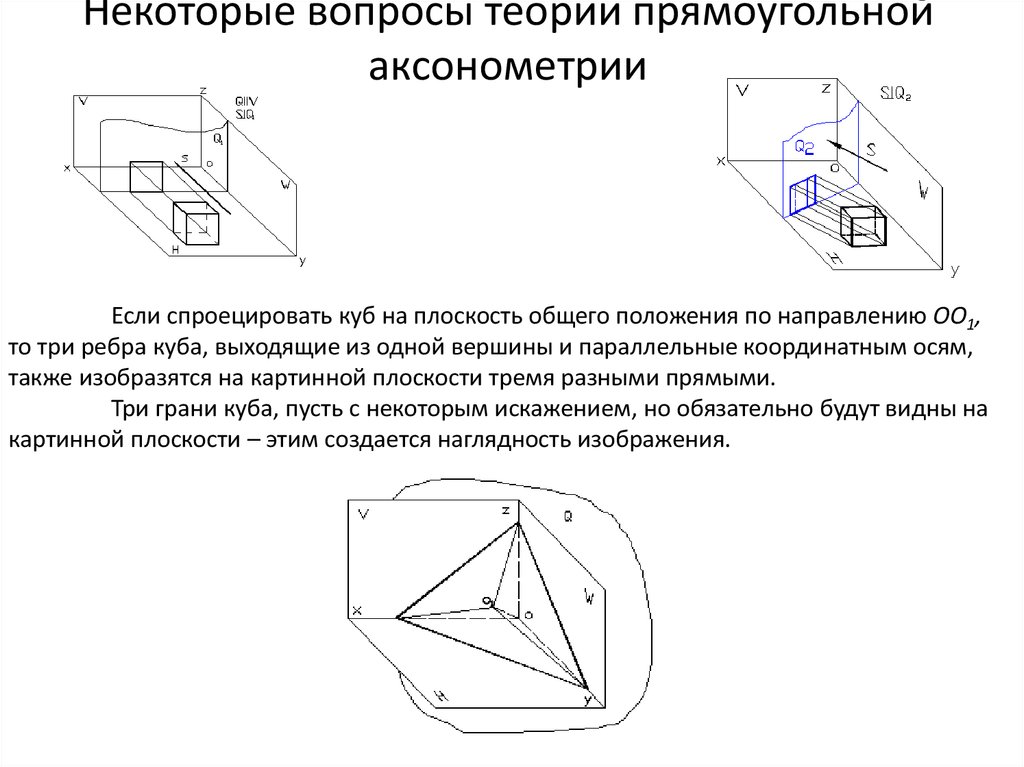
Допускается применять фронтальные диметрические
проекции с углом наклона оси y , равным 30 и 60 .
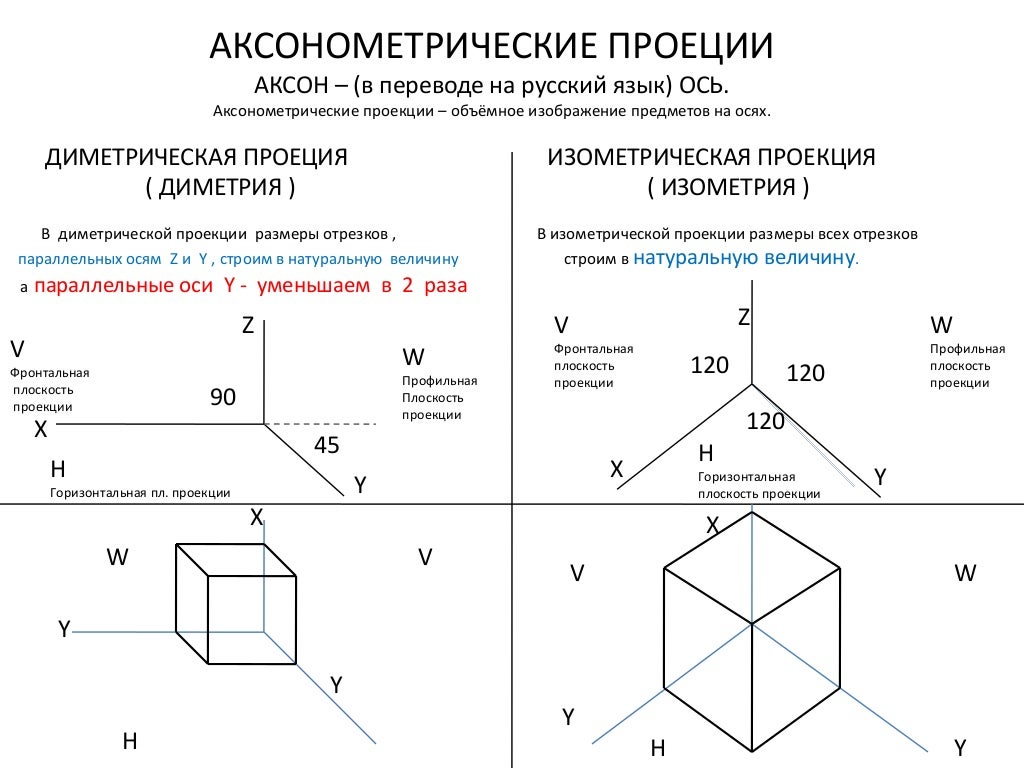
Аксонометрическая проекция
окружности в прямоугольной
изометрии
Прямоугольная диметрическая
проекция окружности
При построении диметрической проекции окружности
коэффициент искажения по оси y равен 0,5.
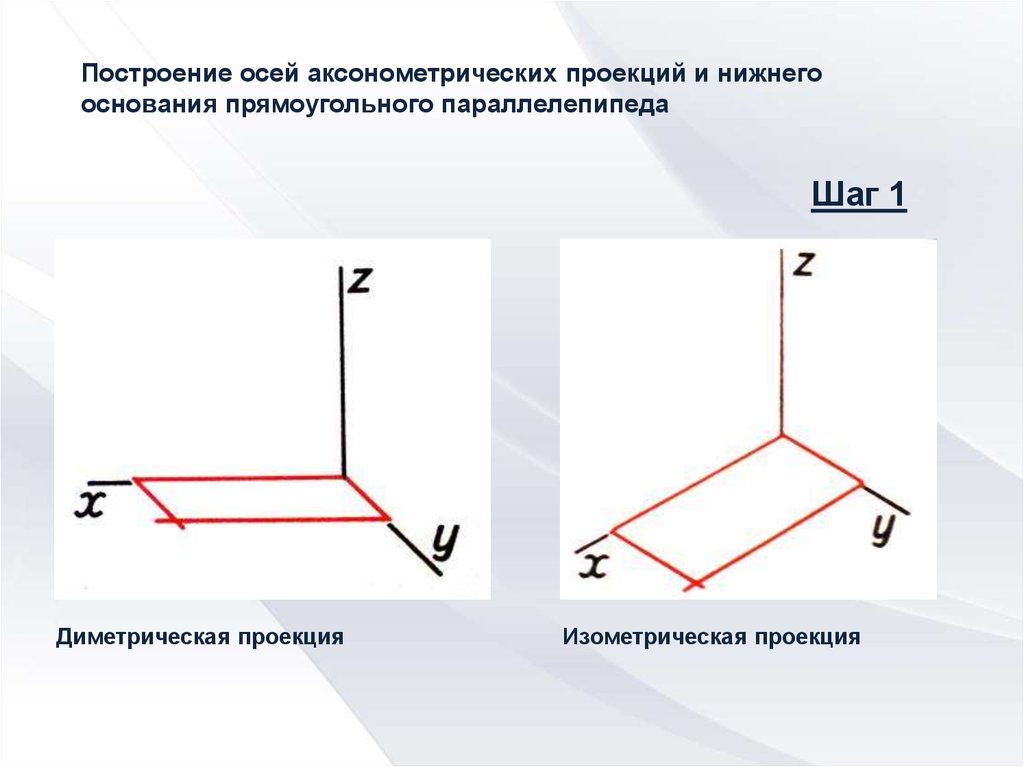
ПОСЛЕДОВАТЕЛЬНОСТЬ ПОСТРОЕНИЯ
АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
На ортогональном чертеже обозначают оси
прямоугольной системы координат, к которой и относят
данный предмет. Оси ориентируют так, чтобы они
допускали удобное измерение координат точек предмета.
У поверхностей вращения эти оси целесообразно
совмещать с осями симметрии, а у гранных – с ребрами.
Строят аксонометрические оси с расчетом, чтобы
была обеспечена наилучшая наглядность изображения и
видимость отдельных элементов предмета.
По одной из ортогональных проекций предмета чертят
вторичную проекцию. Вычерчивать рекомендуется ту
вторичную проекцию предмета, которая проще других.
Таким образом, используют два измерения предмета.
Создают аксонометрическое изображение, откладывая
третье измерение предмета.
Построение точки А в прямоугольной
изометрии по заданным ортогональным
проекциям
1. Относим точку А к координатным осям x, y, z.
2. Проводим аксонометрические оси x , y , z под углом 120 .
3. Строим проекцию точки А на горизонтальной проекции.
4. Строим аксонометрическую проекцию точки А. Проводим прямую,
параллельную аксонометрической оси z и откладываем отрезок, равный
координате z. Получим точку А – аксонометрическая проекция точки А .
ИЗОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
ГЕОМЕТРИЧЕСКИХ ТЕЛ
Контрольные вопросы
1.
2.
3.
4.
Какие виды аксонометрических проекций вы знаете?
5.
Какие приняты коэффициенты искажения по осям X, Y, Z для построения

диметрической проекции?
6.
7.
8.
Под какими углами расположены оси в диметрии?
9.
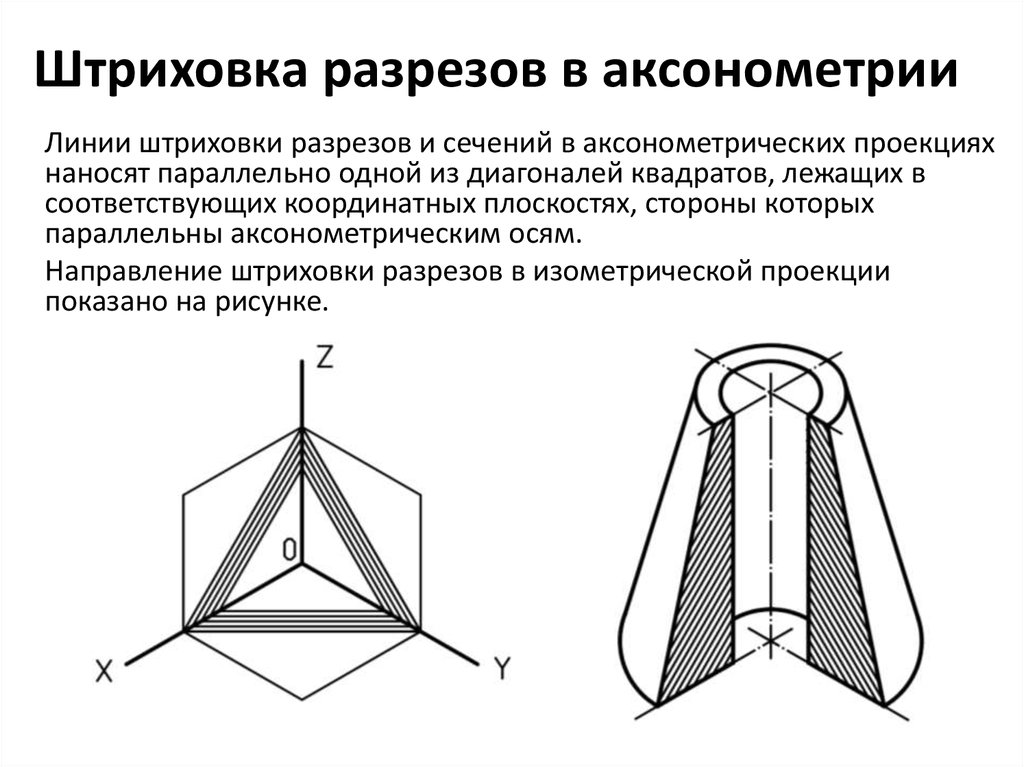
Основные правила нанесения штриховки в аксонометрических проекциях.
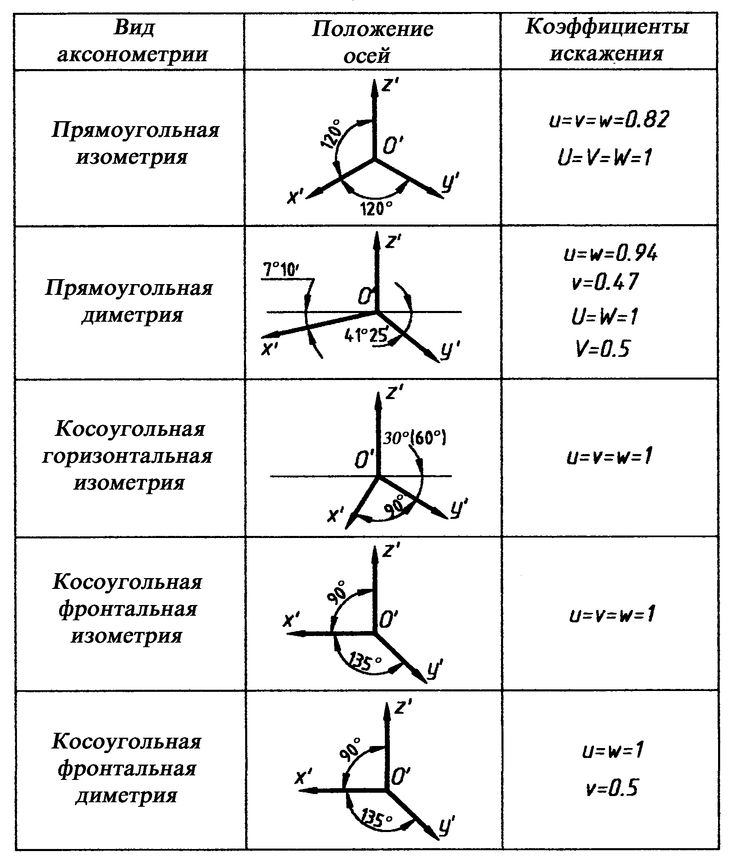
Под каким углом расположены оси в изометрии?
Какую фигуру представляет изометрическая проекция окружности?
Как расположена большая ось эллипса для окружности, принадлежащей
профильной плоскости проекций?
Какой фигурой будет являться диметрическая проекция квадрата?
Как построить диметрическую проекцию окружности, расположенной во
фронтальной проскости проекций?
Список рекомендуемой литературы
1.
ГОСТ 2.317-2011 ЕСКД. Аксонометрические проекции. [Элек-тронный
ресурс] URL: http://docs.cntd.ru/document/gost-2-317-2011-eskd
2.
Фролов С.А. Начертательная геометрия: Учебник для вузов/С.А. Фролов. 3-е изд., перераб. и доп. — М.: ИНФРА, 2007. — 286 с.
3.
Чекмарев А. А. Инженерная графика: Учеб. для немаш. спец. вузов/А.А.
Чекмарев. — 10-е изд. стер. — М.: Высшая школа., 2008.-382 с.:ил.
4.
Боголюбов С.К. Инженерная графика: Учебник для средних специальных
учебных заведений. – 3-е изд., испр. и дополн. – М.: Машиностроение, 2000.
– 352 с.:ил.

English     Русский Правила

Арт-умный блог | Художественные классы Манила

04.01.2017

6 комментариев

 

Всего несколько дней назад мы поделились с вами 7 навыками, которые, по нашему мнению, должен знать и иметь каждый начинающий художник. Сегодня мы сосредоточимся на одном из упомянутых нами навыков, а именно на правилах перспективы.

Что такое правило перспективы?

Правила перспективы — это техника, применяемая в рисовании и живописи, чтобы придать плоской поверхности или изображению ощущение глубины. Это фантастический навык, который нужно изучать и совершенствовать, поскольку вы можете сделать свои рисунки и картины очень реалистичными и точными!

Начните учиться создавать иллюзию расстояния и глубины, ознакомившись с этими тремя правилами.

Одноточечная перспектива

Это правило перспективы, самое простое из всех трех правил.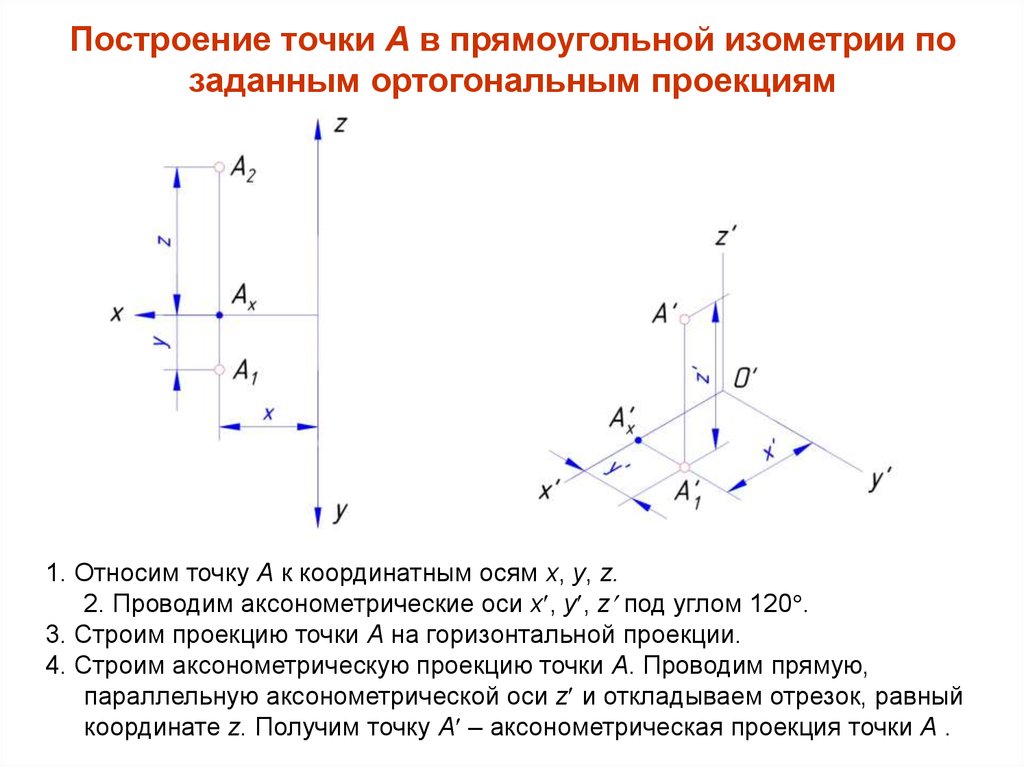 Рабочее определение этого принципа можно обобщить на Dictionary.com. Читать дальше:

…математическая система для представления трехмерных объектов и пространства на двухмерной поверхности с помощью пересекающихся линий, проведенных вертикально и горизонтально и исходящих из одной точки на линии горизонта…

Источник фото: www.olejarz.com

Звучит сложно? Не беспокоиться!

Одноточечная перспектива говорит о том, что объекты кажутся меньше по мере их удаления, встречаясь в точке схода на линии горизонта. Проще говоря, это самый простой способ сделать плоский лист бумаги трехмерным или реалистичным.

Правило одноточечной перспективы применяется, когда ваш объект рассматривается спереди (например, сторона куба или лицо, смотрящее прямо на вас) или если вы хотите, чтобы ваша аудитория смотрела прямо вниз на что-то длинное. Это довольно распространенное правило также при рисовании комнат, дорог и пейзажей, поскольку оно обеспечивает по-настоящему реалистичное ощущение.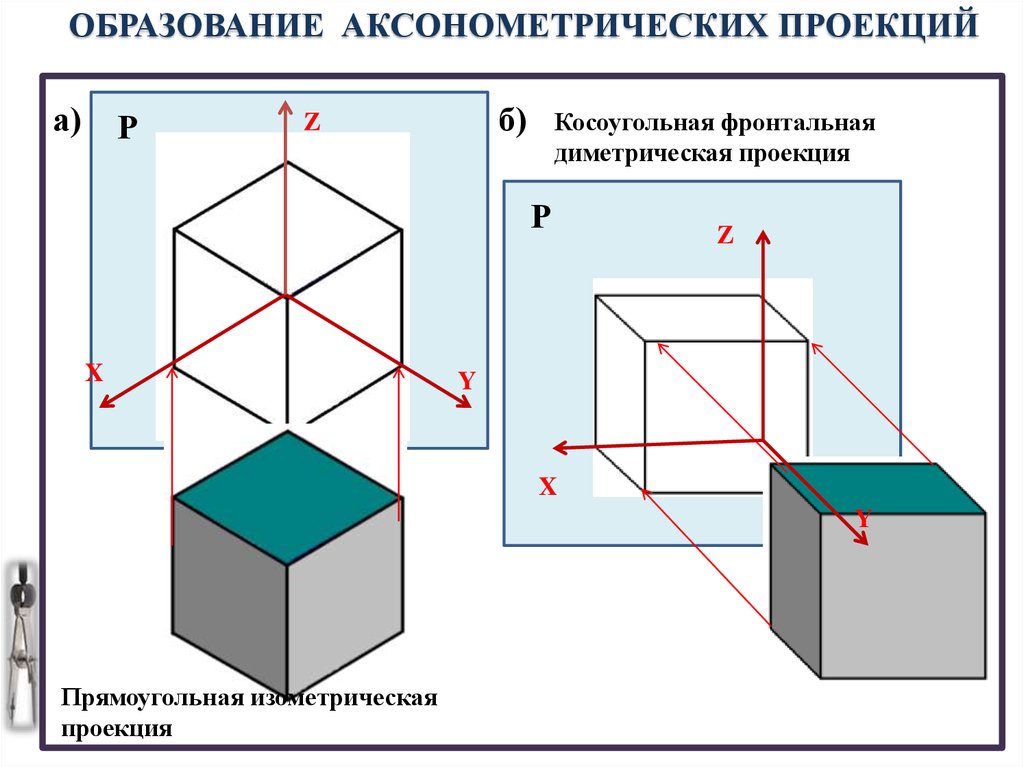 Посмотрите приведенные ниже примеры, которые мы нашли в сети, для вдохновения.

Источник фото: http://www.studentartguide.com/articles/one-point-perspective-drawing

Источник фото: http://www.pinterest.com

​Посмотрите также это 3-минутное руководство, которое мы найдено на YouTube:

Двухточечная перспектива

Это правило применяется, когда ваш рисунок или картина содержит две точки схода в очень произвольных местах вдоль линии горизонта. В словаре Merriam-Webster Dictionary есть такое определение:

(Это) линейная перспектива, в которой параллельные линии по ширине и глубине объекта представлены как встречающиеся в двух отдельных точках на горизонте, отстоящих друг от друга на 90 градусов, если измерять от общего пересечения линий проекции.

Создание двухточечной перспективы начинается с определения линии горизонта, которая представляет собой линию, отделяющую небо от земли.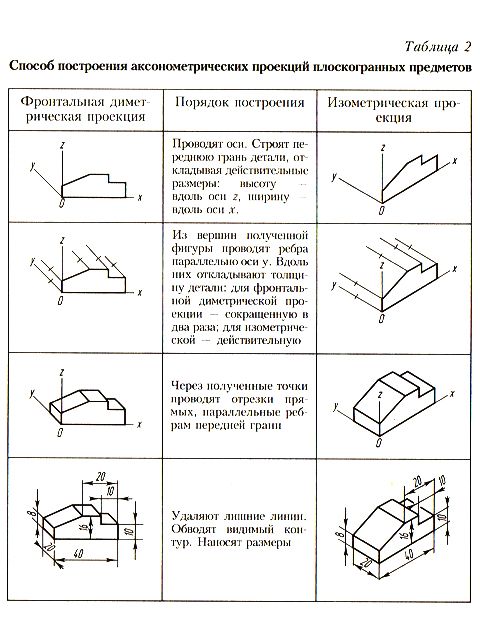 Эта линия также представляет собой «линию видимости» для вашей аудитории.

После определения линии горизонта вам нужно указать следующие точки схода. При создании точек схода просто подумайте о точке на линии, в которой вы хотите, чтобы объекты начали исчезать на расстоянии, которое вы пытаетесь включить в свой рисунок.

​Вдохновитесь следующими рисунками в двухточечной перспективе:

Источник фото: wwww.pinterest.com

Источник фото: www.gogi665.deviantart.com

Посмотрите также это руководство по рисованию, которое мы нашли на YouTube. Это 12 минут, но мы думаем, что оно того стоит.

Нажмите, чтобы установить пользовательский HTML

Трехточечная перспектива

Это немного сложнее, чем два других, которые мы только что обсуждали. Это правило перспективы включает в себя две точки схода на линии горизонта и третью над или под горизонтом, куда ведут все вертикальные линии.

Звучит сложно? Вот иллюстрация того, что мы пытаемся сказать.

Источник фото: www.craftsy.com

Трехточечная перспектива применяется при визуализации объектов — зданий, горизонтов, городских пейзажей, видимых с высоты птичьего полета или с земли. Когда третья точка схода находится на земле, это происходит с точки зрения муравья. И наоборот, если третья точка схода находится высоко вверху, это происходит с высоты птичьего полета.

Источник фото: www.archilibs.com

​Вот расслабляющее видео о том, как рисовать город, используя трехточечную перспективу.

Вы также можете проверить это. Как использовать точки схода в фотографии

Теперь ваша очередь!

Правила перспективы — один из основных навыков, которые вам необходимо выучить и освоить. Особенно, если вы готовитесь к экзаменам по изобразительному искусству в будущем, лучшее время, чтобы начать учиться или осваивать его сейчас.

Здесь, в Art Smart, мы следуем правилу соотношения 2 к 1, то есть 2 ученика к 1 учителю, чтобы ученики получали надлежащее внимание, инструкции и руководство.

Пожалуйста, ознакомьтесь с нашим расписанием уроков рисования на 2017 год, чтобы узнать дату и время, удобные для вас.

Позвоните нам по телефонам 0915-5948191, 0917-8784766 или (02)7886766, чтобы задать вопросы или забронировать занятия.

6 комментариев

Правила рисования в перспективе

Рисование в перспективе — это так же просто, как с одной, двумя, тремя точками!

Перспектива — это техника рисования или живописи. Это придает изображению на плоской поверхности ощущение глубины. Художники используют этот инструмент, чтобы сделать свои изображения более реалистичными и точными, как мы видим их в реальной жизни. Перспектива создает иллюзию глубины и расстояния на плоской поверхности.

Существует три основных типа перспективы: одноточечная, двухточечная и трехточечная. Одно-, двух- и трехточечный относится к количеству точек схода присутствующих при создании иллюзии глубины и пространства. В дополнение к ним существует также перспектива с нулевой точкой.

Правила перспективы

Одноточечная перспектива

Одноточечная перспектива — простейший метод рисования перспективы. Он использует только одну точку схода на линии горизонта. Точка схода — это место, где две или более параллельных линий сходятся друг в друге в «бесконечности». Длинный коридор, железнодорожные пути или дорога со зрителем, расположенным лицом к центру и смотрящим вниз, являются прекрасным примером этой перспективы. Как видно на иллюстрации, две дорожки параллельны друг другу, и вы знаете, что расстояние между ними будет одинаковым. Однако чем дальше они удаляются, тем ближе они кажутся, пока в конце концов не исчезают за горизонтом.

Правило: Используйте одноточечную перспективу, чтобы создать иллюзию расстояния на рисунке или картине.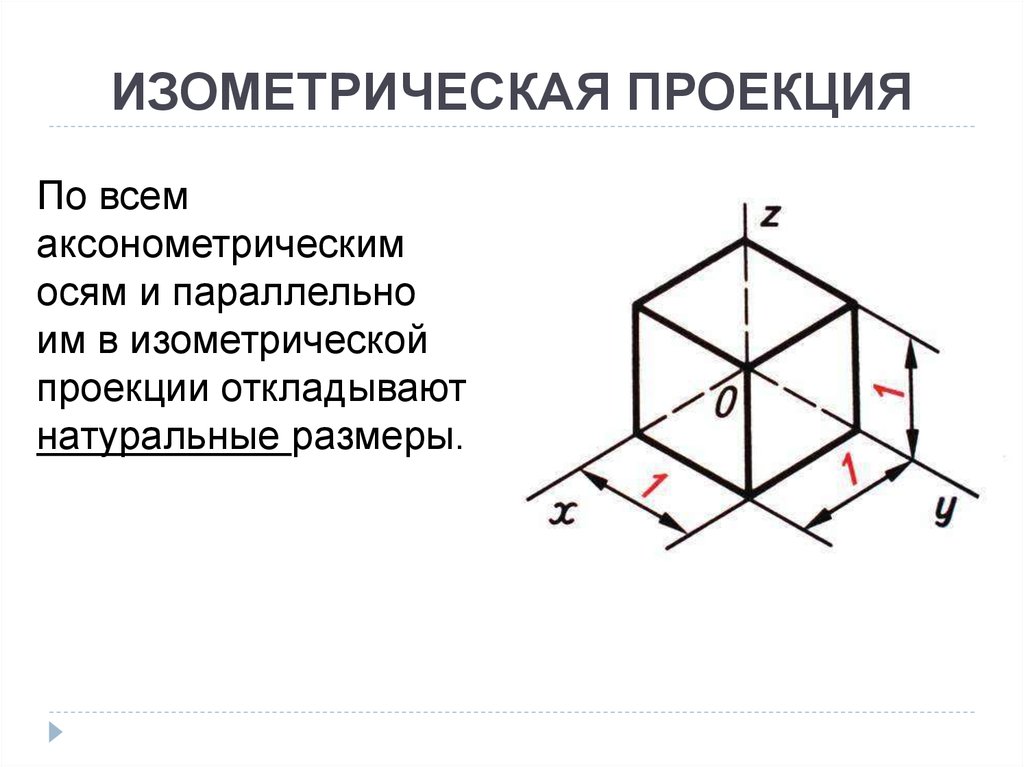

Двухточечная перспектива

Двухточечная перспектива вступает в игру, когда рисунок содержит две точки схода, произвольно расположенные вдоль линии горизонта. Эта перспектива помещает объект так, чтобы зритель мог смотреть на него под углом и видеть две стороны одновременно. То есть, глядя в один угол, два набора параллельных линий удаляются.

Коробка, куб или другие геометрически подобные объекты, такие как дом или здание, могут использоваться для демонстрации двухточечной перспективы. При взгляде на объект из угла одна сторона отступает к одной точке схода, а другая сторона отступает к противоположной точке схода. Как видно на иллюстрации, каждый набор параллельных линий имеет свою точку схода. Двухточечная перспектива — это то, что придает геометрическому объекту иллюзию трехмерности.

Правило: Используйте двухточечную перспективу, чтобы сделать геометрический объект трехмерным.

Трехточечная перспектива

Трехточечная перспектива немного сложнее, чем два других, потому что этот тип имеет дело с тремя точками схода. Он включает в себя две точки схода где-то на линии горизонта. Существует также точка схода над или под горизонтом, к которой ведут все вертикальные линии. Этот тип перспективы отлично подходит для визуализации объектов, таких как здания и городские пейзажи, видимых с высоты птичьего полета или с земли. Когда третья точка схода находится над горизонтом, изображение создается с точки зрения червя, смотрящего вверх на изображение снизу. Когда он находится ниже горизонта, создается точка зрения с высоты птичьего полета, где создается впечатление, что вы смотрите на объект сверху вниз.

Правило: Используйте трехточечную перспективу, когда вы хотите визуализировать сцены зданий, такие как городские пейзажи, сложные объекты крупным планом и высокодетализированные внутренние сцены.

Нулевая перспектива — это техника, используемая для создания иллюзии глубины, когда на изображении нет параллельных линий и, следовательно, точек схода. Точки схода могут существовать только при наличии параллельных линий.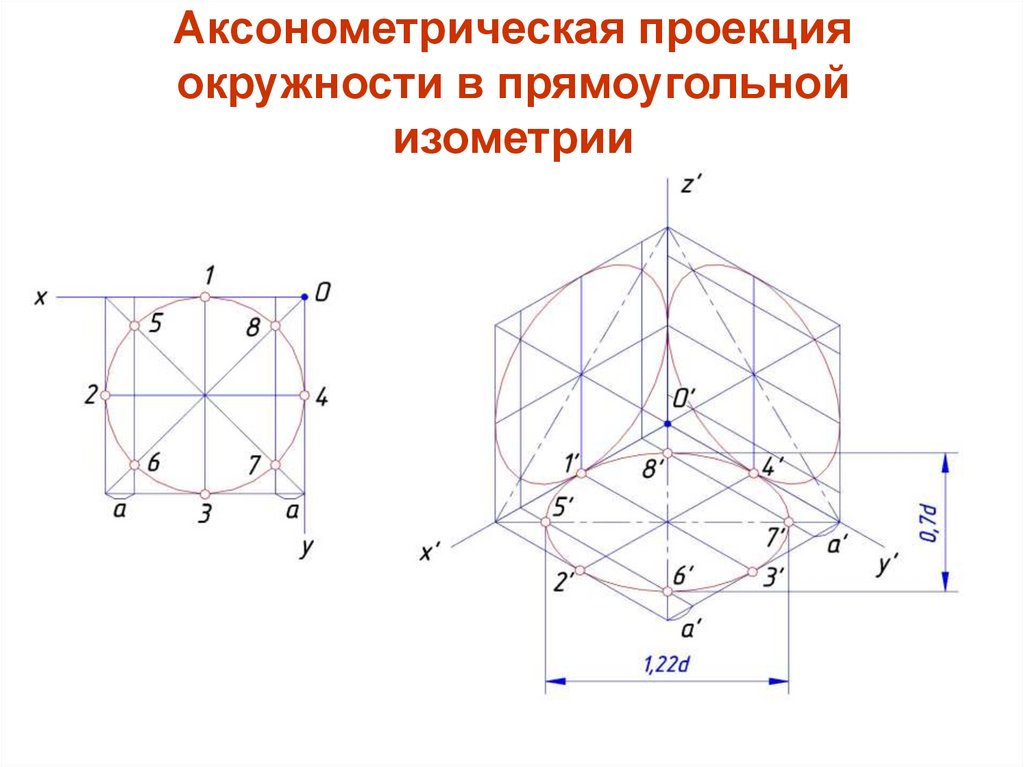 Однако перспектива без точек схода может создать ощущение глубины; именно здесь вступает в силу нулевая точка. Наиболее распространенным примером глубины без параллельных линий или точек схода является естественная обстановка, такая как горный хребет или ландшафт холмов и долин.

В нулевой перспективе ощущение глубины может быть создано следующими  способами:

• Объекты тем больше, чем они ближе, и уменьшаются в размерах пропорционально удалению.
• Чем ближе объекты, тем они более детализированы. Вещи теряют детали, чем дальше они находятся.
• Цвет бледнеет, становится более приглушенным, сливаясь с фоновыми цветами.
• Объекты, расположенные выше на плоскости, создают больше ощущения глубины или расстояния.
• Перекрывающиеся формы создают ощущение глубины.

Правило: Используйте нулевую перспективу, когда на изображении нет параллельных линий, чтобы создать ощущение глубины.

Дополнительное чтение

Использование атмосферной перспективы для придания глубины вашим картинам

Использование линейной перспективы для придания глубины вашим картинам

Есть вопрос?

Если у вас есть вопросы об этой картине, свяжитесь с нами, и мы будем рады ответить на любые ваши вопросы.