Под каким углом чертится аксонометрия: Под каким углом располагаются оси изометрической проекции. Изометрическая проекция

Под каким углом располагаются оси изометрической проекции. Изометрическая проекция

Что такое диметрия

Диметрия представляет собой один из видов аксонометрической проекции. Благодаря аксонометрии при одном объемном изображении можно рассматривать объект сразу в трех измерениях. Поскольку коэффициенты искажений всех размеров по 2-м осям одинаковы, данная проекция и получила название диметрия.

Прямоугольная диметрия

При расположении оси Z» вертикально, при этом оси Х» и Y» образуют с горизонтального отрезка углы 7 градуса 10 минут и 41 градус 25 минут. В прямоугольной диметрии коэффициент искажения по оси Y будет составлять 0,47, а по осям Х и Z в два раза больше, то есть 0,94.

Чтобы осущесвить построение приближенно аксонометрические оси обычной диметрии, необходимо принять, что tg 7 градусов 10 минут равен 1/8, а tg 41 градуса 25 минут равен 7/8.

Как построить диметрию

Для начала необходимо начертить оси, чтобы изобразить предмета в диметрии. В любой прямоугольной диметрии углы, находящиеся между осями Х и Z, равны 97 градусов 10 минут, а между осями Y и Z – 131 градусов 25 минут и между Y и Х – 127 градусов 50 минут.

Теперь требуется нанести оси на ортогональные проекции изображаемого предмета, учитывая выбранное положение предмета для вычерчивания в диметрической проекции. После того, как завершите перенос на объемное ихображение габаритных размеров предмета, можете приступать к чертежу незначительных элементов на поверхности предмета.

Стоит запомнить, что окружности в каждой плоскости диметрии изображаются соответствующими эллипсами. В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет составлять 1,06 диаметра нарисованной окружности. А малая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY – 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях.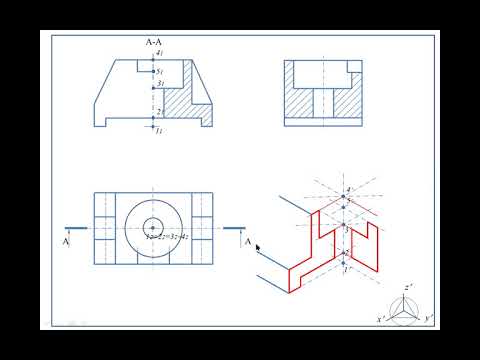 В плоскости ХОZ малая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.

Чтобы получить более детально изображение, необходимо выполнить вырез через детали на диметрии. Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции выбранного квадрата на необходимую плоскость.

Что такое изометрия

Изометрия является одним из видов аксонометрической проекции, где расстояния единичных отрезков на всех 3-х осях одинаковые. Изометрическая проекция активно используется в машиностроительных чертежах, чтобы отобразить внешний вид предметов, а также в разнообразных компьютерных играх.

В математике изометрия известна как преобразование метрического пространства, которое сохраняет расстояние.

Прямоугольная изометрия

В прямоугольной (ортогональной) изометрии аксонометрические оси создают между собой углы, которые равны 120 градусам. Ось Z находится в вертикальном положении.

Как начертить изометрию

Построение изометрии предмета дает возможность получить наиболее выразительное представление о пространственных свойствах изображаемого объекта.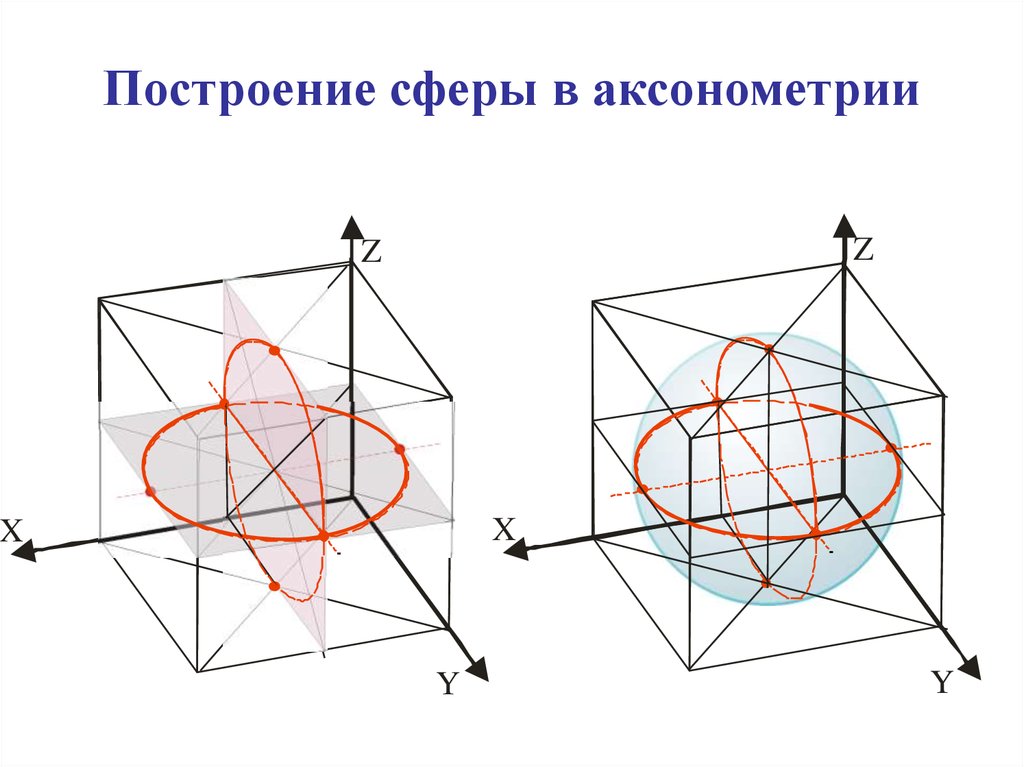

Перед тем, как начать построение чертежа в изометрической проекции, необходимо выбрать такое расположение изображаемого предмета, чтобы были максимально видны его пространственные свойства.

Теперь вам требуется определиться с видом изометрии, которую будете чертить. Существует два ее вида: прямоугольная и горизонтальная косоугольная.

Нарисуйте оси легкими тонкими линиями, чтобы изображение получилось по центру листа. Как уже раньше говорилось, углы в прямоугольном виде изометрической проекции должны составлять 120 градусов.

Начинайте рисовать изометрию с именно верхней поверхности изображения предмета. От углов получившейся горизонтальной поверхности нужно провести две вертикальные прямые и отложить на них соответствующие линейные размеры предмета. В изометрической проекции все линейные размеры по всех трем осям будут оставаться кратны единице. Затем последовательно требуется соединить созданные точки на вертикальных прямых. В результате получиться внешний контур предмета.

Стоит учитывать, что при изображении любого предмета в изометрической проекции видимость криволинейных деталей будет обязательно искажаться. Окружность должна изображаться эллипсом. Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.

Если изображаемый объект имеет скрытые полости ли сложные элементы, постарайтесь выполнить заштриховку. Она может быть простой либо ступенчатой, все зависит сложности элементов.

Запомните, что все построение должно выполнять строго с применением чертежных инструментов. Применяйте несколько карандашей с разными видами твердости.

Для тoгo чтобы получить аксонометрическую проекцию пред­мета (рис. 106), необходимо мысленно: поместить предмет в сис­тему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление парал­лельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей.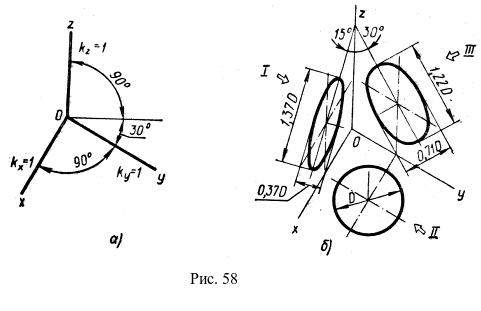

На аксонометрической плоскости проекций получают изобра­жение — аксонометрическую проекцию предмета, а также про­екции осей систем координат, которые называют аксонометриче­скими осями.

Аксонометрической проекцией называется изображение, по­лученное на аксонометрической плоскости в результате парал­лельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму.

Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Сис­тема координат позволяет производить измерения по осям, определяя положение предметов в пространстве.

Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции

Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис.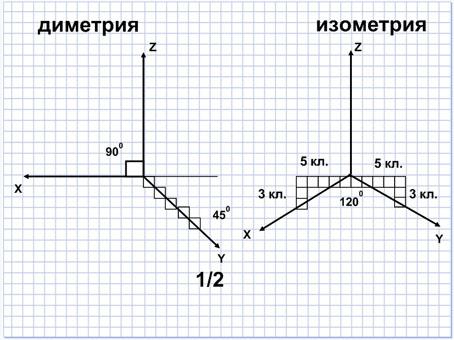 107).

Наиболее употребляемой является так называемая прямо­угольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проек­ция). Изометрической проекцией (см. рис. 107, а) называется та­кая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью па­раллельного проецирования.

Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317-69:
а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция;
в — косоугольная фронтальная изометриче­ская проекция;
г — косоугольная фронтальная диметрическая проекция

Рис. 107. Продолжение: д — косоугольная горизонтальная изометриче­ская проекция

При этом проецирующие лучи пер­пендикулярны аксонометрической плоскости проекций, а коор­динатные оси одинаково наклонены к аксонометрической плоско­сти проекций (cм.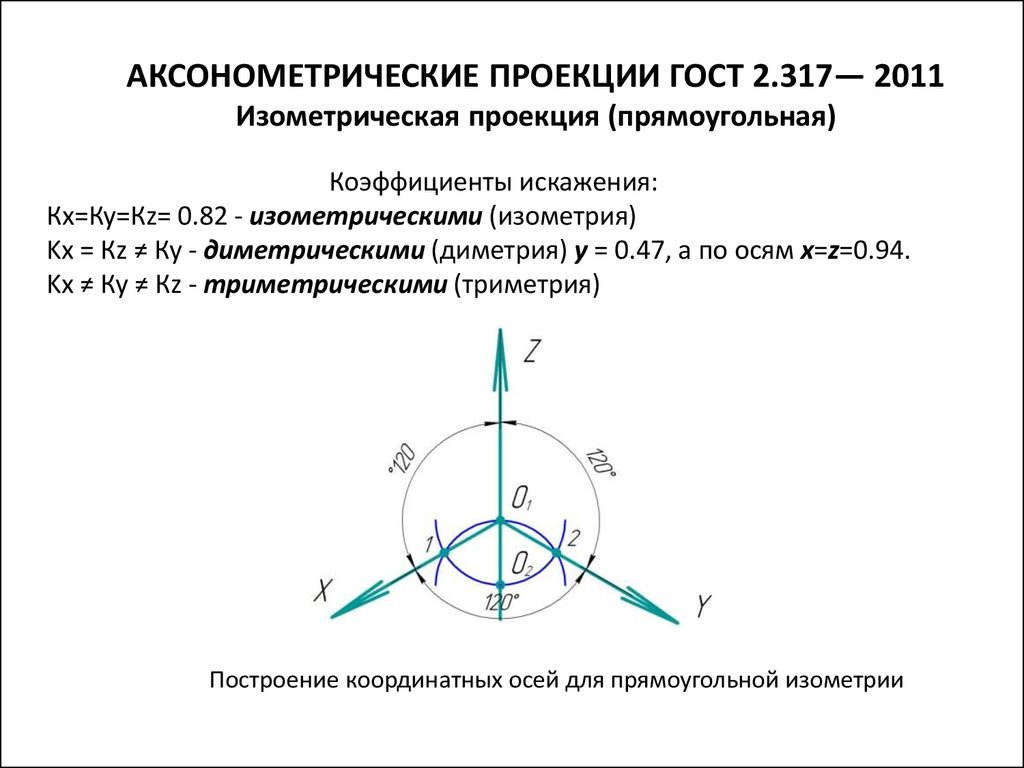

рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отноше­ние размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициен­ты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис. 108).

Рис. 108. Положение осей и коэффициенты искажения изометрической проекции

Существуют изометрические, диметрические и триметрические проекции. К изометрическим проекциям относятся такие проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковые, а величина третьего отличается от них. К триметрическим проекциям относятся проекции, у которых все коэффици­енты искажения различны.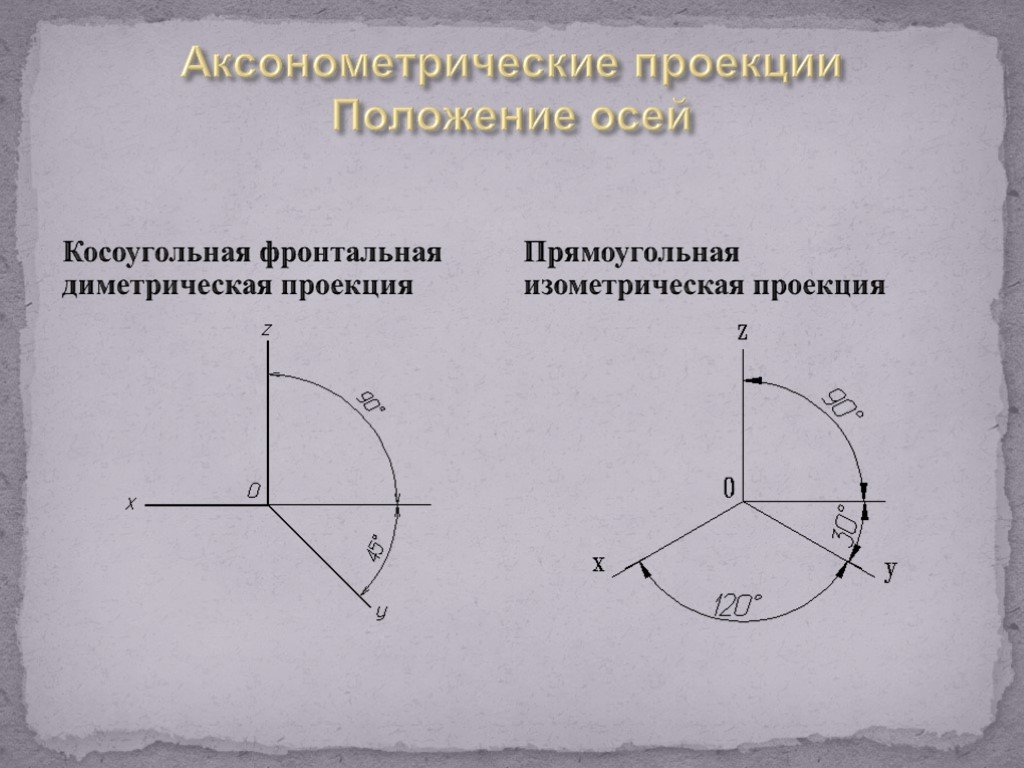

Аксонометрические проекции применяются для наглядного изображения различных предметов. Предмет здесь изобра­жают так, как его видят (под определенным углом зрения). На таком изображении отраже­ны все три пространственных измерения, по­этому чтение аксонометрического чертежа обычно не вызывает затруднений.

Аксонометрический чертеж можно получить как с помощью прямоугольного проецирова­ния, так и с помощью косоугольного проеци­рования. Предмет располагают так, чтобы три основных направления его измерений (высота, ширина, длина) совпадали с осями координат и вместе с ними спроецировались бы на плос­кость. Направление проецирования не должно совпадать с направлением осей координат, т. е. ни одна из осей не будет проецироваться в точ­ку. Только в этом случае получится наглядное изображение всех трех осей.

Для получения прямоугольных аксонометри­ческих проекций оси координат наклоняют от­носительно плоскости проекций Р А так, чтобы их направление не совпадало с направлением проецирующих лучей. При косоугольном прое­цировании можно варьировать как направле­нием проецирования, так и наклоном коорди­натных осей относительно плоскости проекций. При этом координатные оси в зависимости от их угла наклона к аксонометрической плоско­сти проекций и направления проецирования будут проецироваться с разными коэффициен­тами искажения. В зависимости от этого будут получаться разные аксонометрические проек­ции, отличающиеся расположением осей коор­динат. ГОСТ 2.317-69 (СТ СЭВ 1979-79) предусматривает следующие аксонометричес­кие проекции: прямоугольная изометрическая проекция; прямоугольная диметрическая про­екция; косоугольная фронтальная изометриче­ская проекция; косоугольная горизонтальная изометрическая проекция; косоугольная фрон­тальная диметрическая проекция.

§ 26. ПРЯМОУГОЛЬНЫЕ АКСОНОМЕТРИ­ЧЕСКИЕ ПРОЕКЦИИ

Изометрическая проекция отлича­ется большой наглядностью и широко приме­няется в практике. Координатные оси при по­лучении изометрической проекции наклоняют относительно аксонометрической плоскости проекций так, чтобы они имели одинаковый угол наклона (рис.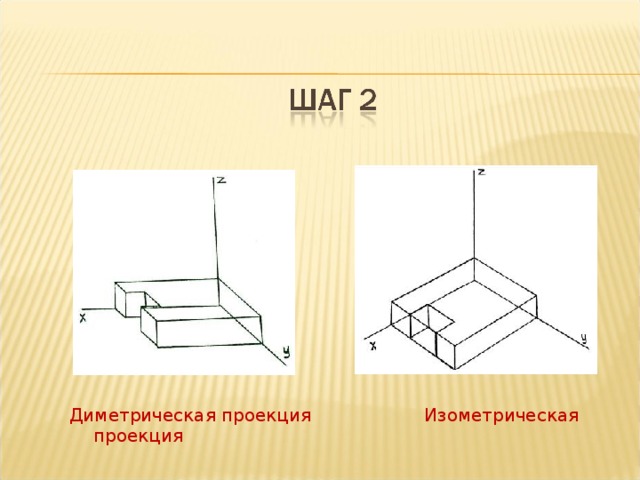 236). В этом случае они проецируются с одинаковым коэффициентом искажения (0,82) и под одинаковым углом друг к другу (120°).

В практике коэффициент искажения по осям обычно принимают равным единице, т. е. от­кладывают действительную величину размера. Изображение получается увеличенным в 1,22 раза, но это не приводит к искажениям формы и не сказывается на наглядности, а упрощает построения.

Аксонометрические оси в изометрии прово­дят, предварительно построив углы между ося­ми

х, у и z (120°) или углы наклона осей х и у к горизонтальной прямой (30°). Построение осей в изометрии с помощью циркуля показано на рис. 237, где радиус R взят произвольно. На рис. 238 показан способ построения осей х и у с использованием тангенса угла 30°. От точки О — точки пересечения аксонометриче­ских осей откладывают влево или вправо по горизонтальной прямой пять одинаковых отрез­ков произвольной длины и, проведя через последнее деление вертикальную прямую, откла­дывают на ней вверх и вниз по три таких же отрезка. 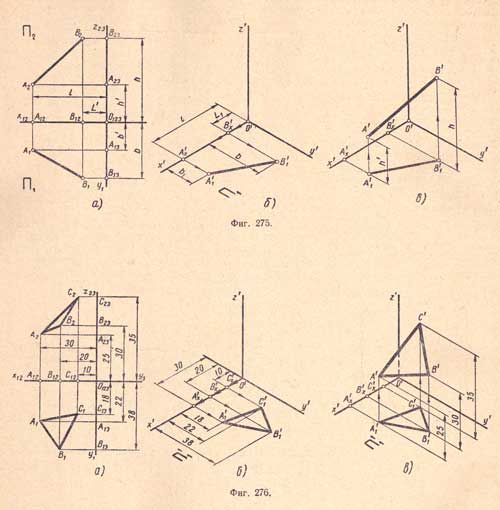Построенные точки соединяют с точ­кой О и получают оси Ох и Оу.

Откладывать (строить) размеры и произво­дить измерения в аксонометрии можно только по осям Ох, Оу и Оz или на прямых, парал­лельных этим осям.

На рис. 239 показано построение точки

А в изометрии по ортогональному чертежу (рис. 239, а). Точка А расположена в плоско­сти V. Для построения достаточно построить вторичную проекцию а » точки А (рис. 239, б) на плоскости xOz по координатам Х А и Z A . Изображение точки А совпадает с ее вторичной проекцией. Вторичными проекциями точки называют изображения ее ортогональ­ных проекций в аксонометрии.

На рис. 240 показано построение точки В в изометрии. Сначала строят вторичную проек­цию точки В на плоскости хОу. Для этого от начала координат по оси Ох откладывают коор­динату Х в (рис. 240, б), получают вторичную проекцию точки b х. Из этой точки параллельно оси Оу проводят прямую и на ней откладывают координату Y B .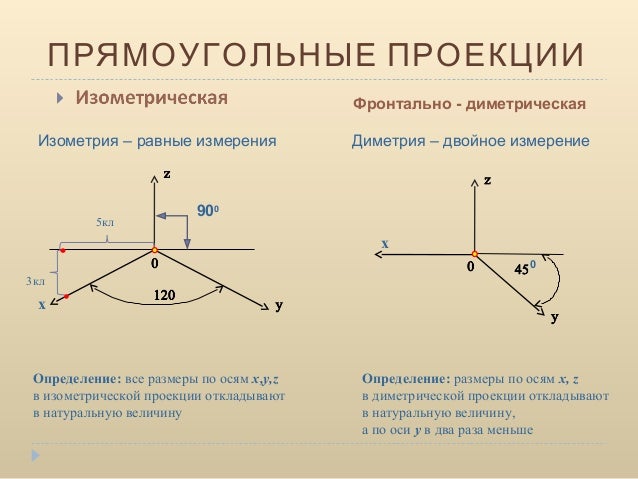

Построенная точка b на аксо­нометрической плоскости будет вторичной про­екцией точки

В. Проведя из точки b прямую, параллельную оси Oz, откладывают координа­ту Z B и получают точку В, т. е. аксонометри­ческое изображение точки В. Аксонометрию точки В можно построить и от вторичных про­екций на плоскости zОх или zОу.

Прямоугольная диметрическая проекция. Координатные оси располагают так, чтобы две оси Ох и Оz имели одинаковый угол наклона и проецировались с одинаковым коэффициентом искажения (0,94), а третья ось Оу была бы наклонена так, чтобы коэффициент искажения при проецировании был в два раза меньше (0,47). Обычно коэффициент искажения по осям Ох и Oz принимают рав­ным единице, а по оси Оу — 0,5. Изображение получается увеличенным в 1,06 раза, но это так же, как и в изометрии, не сказывается на наглядности изображения, а упрощает постро­ение. Расположение осей в прямоугольной диметрии показано на рис.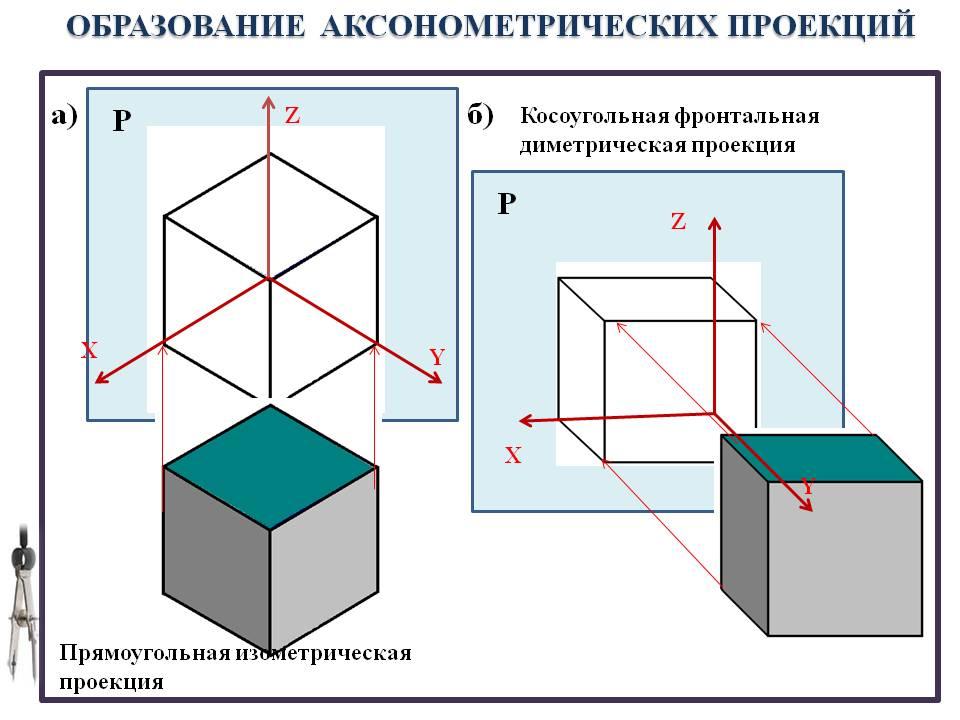 241. Строят их, от­кладывая углы 7° 10″ и 41°25″ от горизонталь­ной линии по транспортиру, или откладывая одинаковые отрезки произвольной длины, как показано на рис. 241. Полученные точки сое­динить с точкой О . При построении прямо­угольной диметрии необходимо помнить, что действительные размеры откладывают только на осях Ох и Oz или на параллельных им линиях. Размеры по оси Оу и параллельно ей откладывают с коэффициентом искажения 0,5.

§ 27. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИ­ЧЕСКИЕ ПРОЕКЦИИ

Фронтальная изометрическая проекция. Расположение аксонометриче­ских осей показано на рис. 242. Угол наклона оси Оу к горизонтали обычно равен 45°, но может иметь значение 30 или 60°.

Горизонтальная изометрическая проекция. Расположение аксонометричес­ких осей показано на рис. 243. Угол наклона оси Оу к горизонтали обычно равен 30°, но может иметь значение 45 или 60°. При этом угол 90° между осями Ох и Оу должен сохра­няться.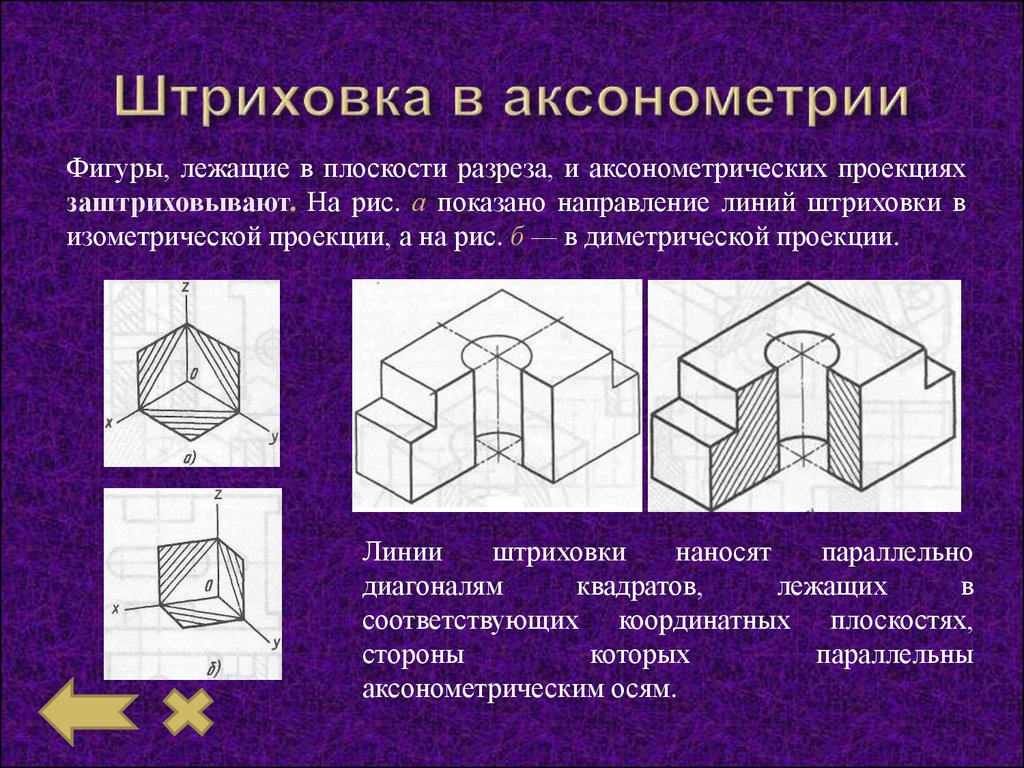

Фронтальную и горизонтальную косоуголь­ные изометрические проекции строят без иска­жения по осям Ох, Оу и Oz.

Фронтальная диметрическая про­екция. Расположение осей показано на рис. 244. Рис. 245 иллюстрирует проецирова­ние осей координат на аксонометрическую плоскость проекций. Плоскость xOz параллель­на плоскости Р. Допускается ось Оу прово­дить под углом 30 или 60° к горизонтали, коэффициент искажения по оси Ох и Oz при­нят равным 1, а по оси Оу — 0,5.

ПОСТРОЕНИЕ ПЛОСКИХ ГЕОМЕТ­РИЧЕСКИХ ФИГУР В АКСОНОМЕТРИИ

Основанием ряда геометрических тел явля­ется плоская геометрическая фигура: много­угольник или окружность. Чтобы построить геометрическое тело в аксонометрии, надо уметь строить прежде всего его основание, т. е. плоскую геометрическую фигуру. Для примера рассмотрим построение плоских фигур в пря­моугольной изометрической и диметрической проекции. Построение многоугольников в аксо­нометрии можно выполнять методом коорди­нат, когда каждую вершину многоугольника строят в аксонометрии как отдельную точку (построение точки методом координат рассмотрено в § 26), затем построенные точки соеди­няют отрезками прямых линий и получают ло­маную замкнутую линию в виде многоугольни­ка.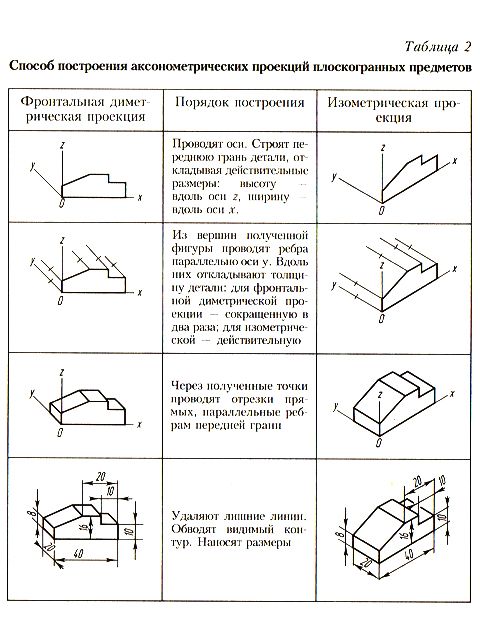 Эту задачу можно решить иначе. В пра­вильном многоугольнике построение начинают с оси симметрии, а в неправильном много­угольнике проводят дополнительную прямую, которая называется базой, параллельно одной из осей координат на ортогональном чертеже.

Для трёхмерных объектов и панорам.

Ограничения аксонометрической проекции

Изометрическая проекция в компьютерных играх и пиксельной графике

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

Примечания

1. По ГОСТ 2 .317-69 — Единая система конструкторской документации. Аксонометрические проекции.
2. Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z»).
3. Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM , декабрь 1978. — Т. 10. — № 4. — С. 465-502. — ISSN 0360-0300 . — DOI :10. 1145/356744.356750
4. Jeff Green. GameSpot Preview: Arcanum (англ.) . GameSpot (29 февраля 2000).(недоступная ссылка — история ) Проверено 29 сентября 2008.
5. Steve Butts. SimCity 4: Rush Hour Preview (англ.) . IGN (9 сентября 2003). Архивировано
6. GDC 2004: The History of Zelda (англ.) . IGN (25 марта 2004). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
7. Dave Greely, Ben Sawyer.

Построение аксонометрического изображения детали, чертеж которой приведен на Рис.а.

Все аксонометрические проекции должны выполняться по ГОСТ 2.317-68.

Аксонометрические проекции получаются проецированием предмета и связанной с ним системы координат на одну плоскость проекций. Аксонометрии делятся на прямоугольные и косоугольные.

Для прямоугольных аксонометрических проекций проецирование осуществляется перпендикулярно плоскости проекций, причем предмет располагается так, чтобы были видны все три плоскости предмета.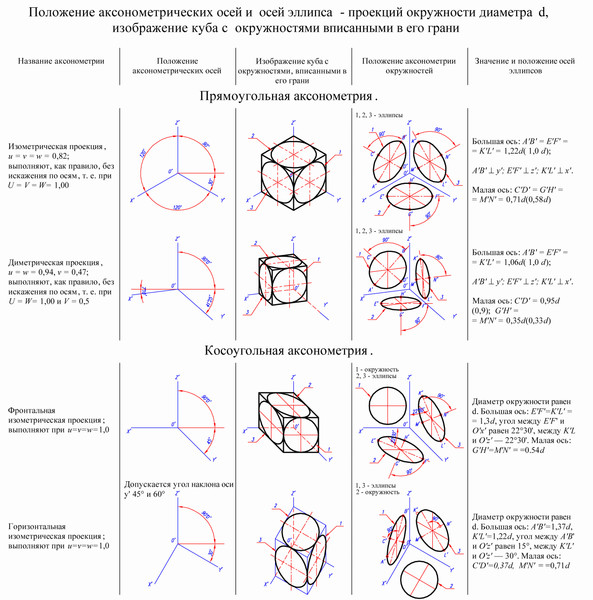 Это возможно, например, при расположении осей, как на прямоугольной изометрической проекции, для которой все оси проекций располагаются под углом 120 градусов (см. рис.1). Слово «изометрическая» проекция означает, что коэффициент искажения по всем трем осям одинаковый. Согласно стандарту коэффициент искажения по осям можно принять равным 1. Коэффициент искажения – это отношение размера отрезка проекции к истинному размеру отрезка на детали, измеренного вдоль оси.

Построим аксонометрию детали. Для начала зададим оси, как для прямоугольной изометрической проекции. Начнем с основания. Отложим по оси х величину длины детали 45, а по оси у величину ширины детали 30. Из каждой точки четырехугольника поднимем верх вертикальные отрезки на величину высоты основания детали 7 (Рис.2). НА аксонометрических изображениях при нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку.

Далее проводим диагонали верхнего основания и находим точку, через которую будет проходить ось вращения цилиндра и отверстия.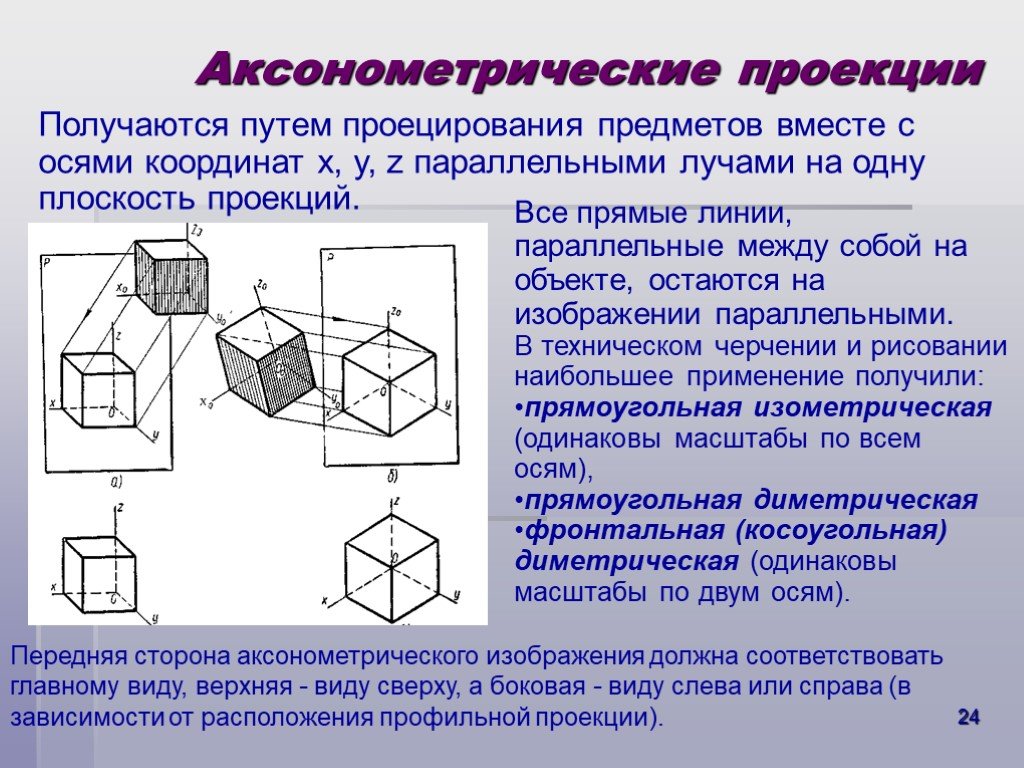 Невидимые линии нижнего основания стираем, чтобы они не мешали нашему дальнейшему построению (Рис.3)

.

Недостаток прямоугольной изометрической проекции заключается в том, что окружности во всех плоскостях будут проецироваться на аксонометрическом изображении в эллипсы. Поэтому сначала научимся строить приближенно эллипсы.

Если вписать окружность в квадрат, то у нее можно отметь 8 характерных точек: 4 точки касания окружности и середины стороны квадрата и 4 точки пересечения диагоналей квадрата с окружностью (Рис.4,а). На рис.4,в и рис.4,б показан точный способ построения точек пересечения диагонали квадрата с окружностью. На рис.4,д показан приближенный способ. При построении аксонометрические проекции половина диагонали четырехугольника, в который спроецируется квадрат, разделится в таком же соотношении.

Переносим эти свойства на нашу аксонометрию (рис.5). Строим проекцию четырехугольника, в которую проецируется квадрат. Далее строим эллипс рис.6.

Далее поднимаемся на высоту 16мм и переносим туда эллипс (Рис.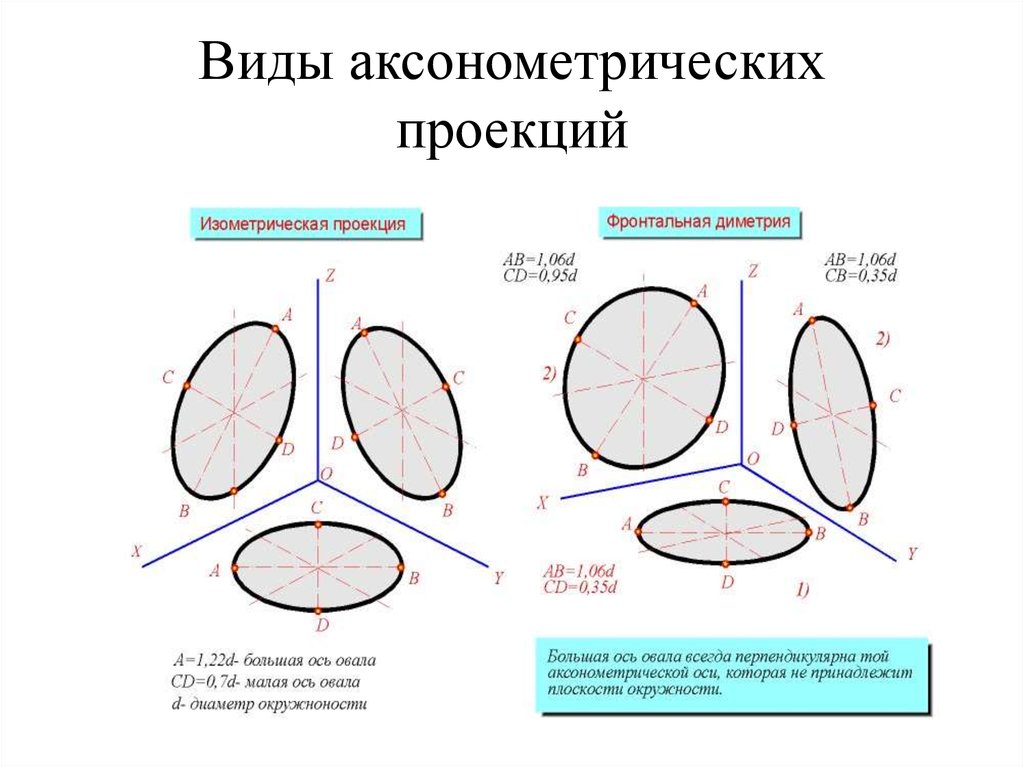 7). Убираем лишние линии. Переходим к построению отверстий. Для этого строим на верху эллипс, в который спроецируется отверстие диаметром 14 (Рис.8). Далее, чтобы показать отверстие диаметром 6мм необходимо мысленно вырезать четверть детали. Для этого построим середину каждой стороны, как на рис.9. Далее строим эллипс, соответствующий окружности диаметра 6 на нижнем основании, а затем на расстоянии 14 мм от верхней части детали рисуем уже два эллипса (один соответствующий окружности диаметром 6, а другой соответствующий окружности диаметром 14) Рис.10. Далее выполняем разрез четверти детали и убираем невидимые линии (Рис.11).

Перейдем к построению ребра жесткости. Для этого на верхней плоскости основания отмеряем 3 мм от края детали и проводим отрезок длиной половине толщины ребра (1.5мм) (Рис.12), также намечаем ребро на дальней стороне детали. Угол 40 градусов нам при построении аксонометрии не подходит, поэтому рассчитываем второй катет (он будет равен 10.35мм) и по нему строим вторую точку угла по плоскости симметрии. Чтобы построить границу ребра, строим прямую на расстоянии 1.5мм от оси на верхней плоскости детали, затем проводим линии параллельно оси х до пересечения с внешним эллипсом и опускаем вертикальную прямую. Через нижнюю точку границы ребра проводим прямую параллельно ребру по плоскости разреза (Рис.13) до пересечения с вертикальной прямой. Дальше соединяем точку пересечения с точкой в плоскости разреза. Для построения дальнего ребра проводим прямую параллельную оси Х на расстоянии 1.5мм до пересечения с внешним эллипсом. Дальше находим, на каком расстоянии находится верхняя точка границы ребра (5.24мм) и такое же расстояние откладываем на вертикальной прямой с дальней стороны детали (см. Рис.14) и соединяем с дальней нижней точкой ребра.

Убираем лишние линии и штрихуем плоскости сечений. Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рис.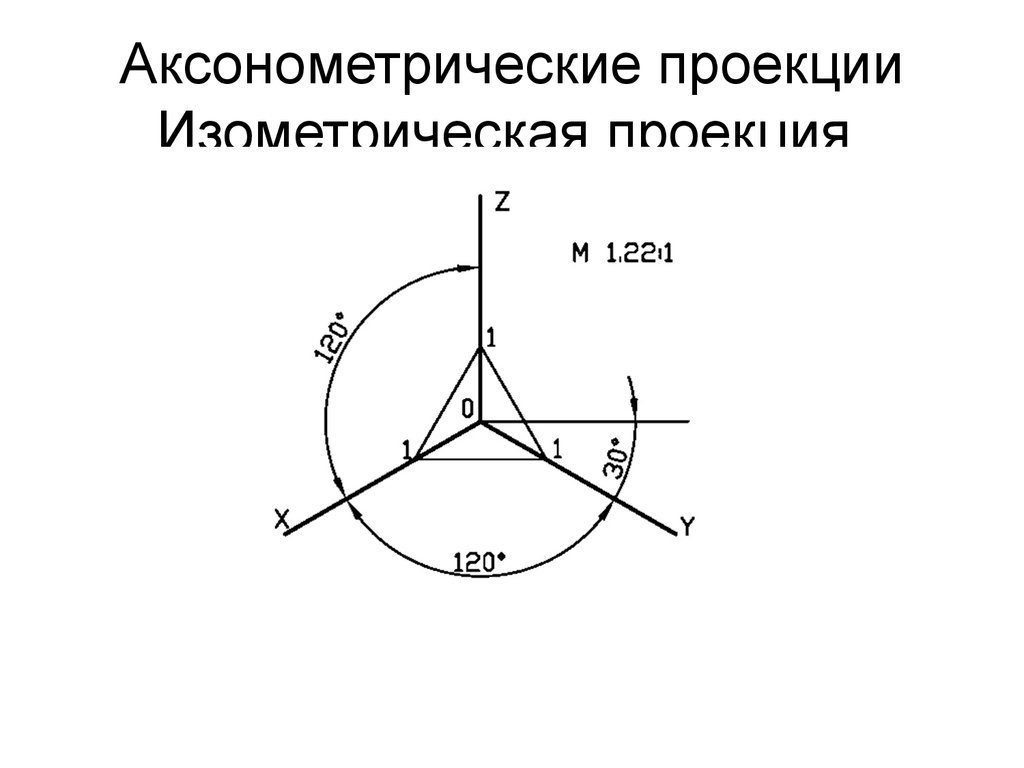 15).

Для прямоугольной изометрической проекции линии штриховки будут параллельны линиям штриховки, показанным на схеме в правом верхнем углу (Рис.16). Осталось изобразить боковые отверстия. Для этого размечаем центры осей вращения отверстий, и строим эллипсы, как было указано выше. Аналогично строим радиусы скруглений (Рис.17). Итоговая аксонометрия показана на рис.18.

Для косоугольных проекций проецирование осуществляется под углом к плоскости проекций, отличным от 90 и 0 градусов. Примером косоугольной проекции может служить косоугольная фронтальная диметрическая проекция. Она хороша тем, что на плоскость заданную осями X и Z окружности, параллельные этой плоскости будут проецироваться в истинную величину (угол между осями X и Z 90 градусов, ось Y наклонена под углом 45 градусов к горизонту). «Диметрическая» проекция означает, что коэффициенты искажения по двум осям X и Z одинаковый, по оси Y коэффициент искажения меньше в два раза.

При выборе аксонометрической проекции необходимо стремиться, чтобы наибольшее количество элементов проецировалось без искажения.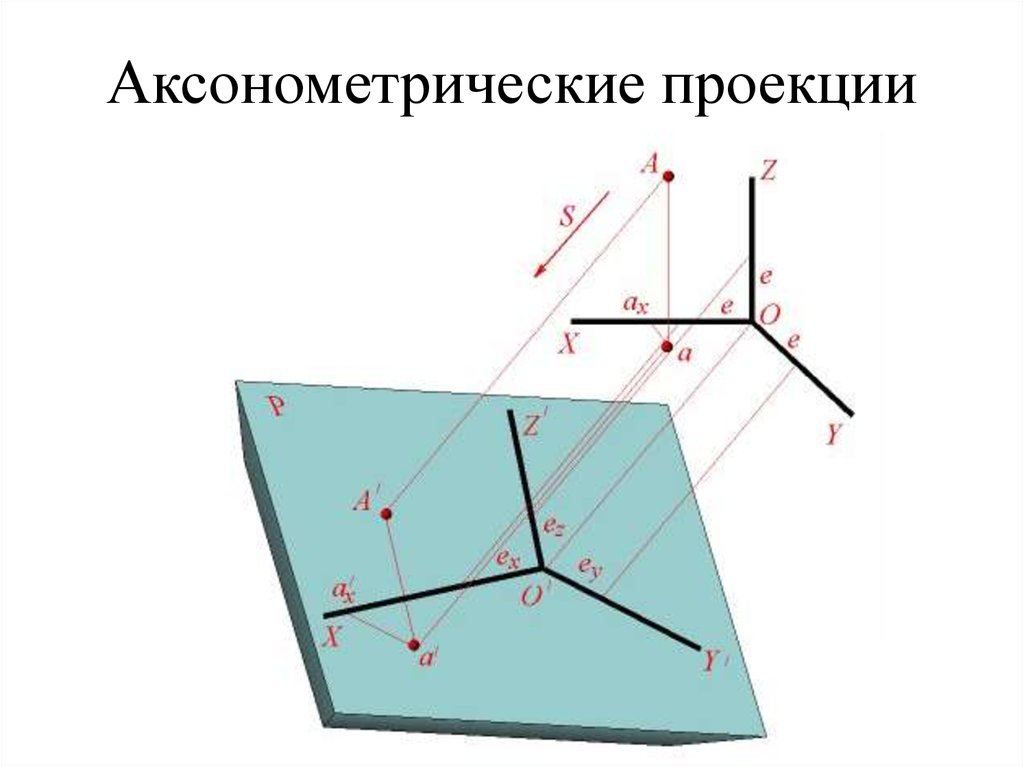 Поэтому при выборе положения детали в косоугольной фронтальной диметрической проекции ее надо расположить так, чтобы оси цилиндра и отверстий были перпендикулярны фронтальной плоскости проекций.

Схема расположения осей и аксонометрическое изображение детали «Стойка» в косоугольной фронтальной диметрической проекции приведена на рис.18.

Аксонометрические проекции

• ЕСКД
• СПДС
• 3D
• Чертежи
• Таблицы

• ЕСКД
• Аксонометрические проекции

Для того чтобы наиболее наглядно передать форму изделий и предметов, ясно и понятно представить схемы взаимодействия различных деталей, по мере надобности применяются аксонометрические проекции.

Прямоугольная изометрическая проекция

Проекция этого вида отличается тем, что в ней оси аксонометрии располагаются друг по отношению к другу под углом 120°. При этом искажения изображения по всем аксонометрическим осям имеют один и тот же коэффициент, равный 0,82.

Чтобы упростить изометрическую проекцию, по осям x, y и z, как правило, выполняют без искажений, то есть его коэффициент выбирают равным единице.

 

Изображение окружностей в прямоугольной изометрии

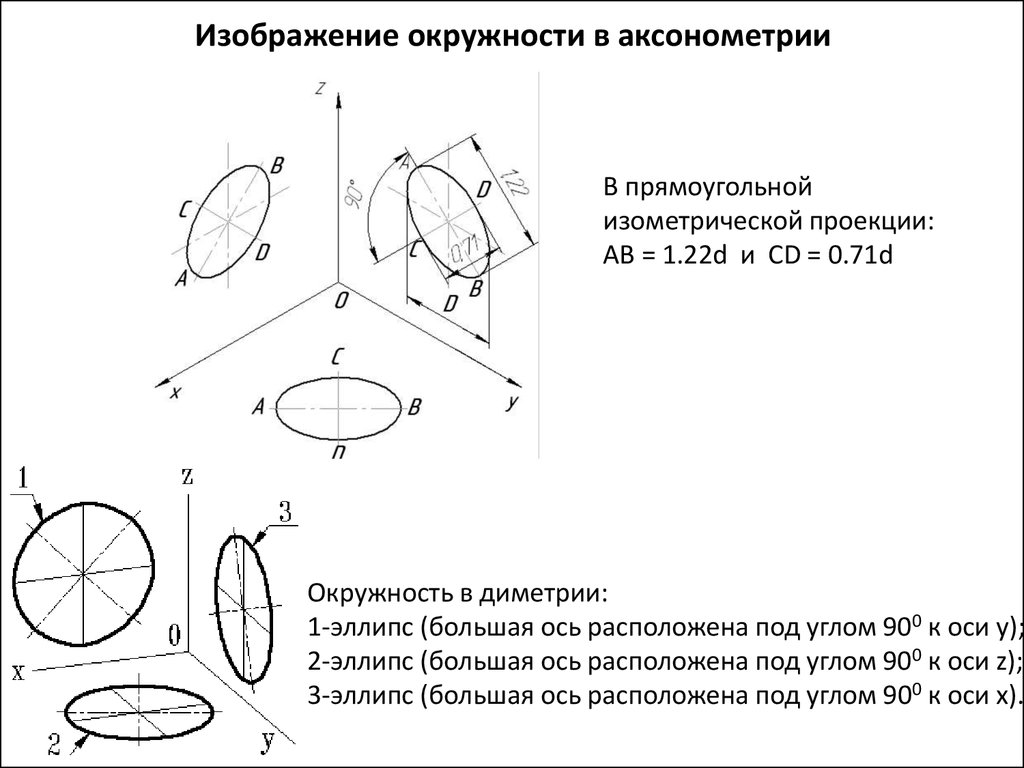
Если окружности располагаются в тех плоскостях, которые параллельны плоскостям проекций, то в аксонометрической плоскости они изображаются в виде эллипсов.

В тех случаях, когда по осям x, y, и z изометрическая проекция выполняется без искажений, длина большой и малой осей эллипсов составляет, соответственно, 1,22 и 0,71 от диаметра отображаемой окружности.

В тех случаях, когда по осям x, y и z изометрическая проекция выполняется с искажениями, длина большой оси эллипсов равняется диаметру отображаемой окружности, а длина малой оси – 0,58 от нее.

 

Изображение детали в прямоугольной изометрии

Чтобы наиболее наглядно передать особенности формы различных изделий и предметов, их изображают в прямоугольной изометрической проекции.

 

Прямоугольная диметрическая проекция

Отличительной особенностью прямоугольной диметрической проекции является то, что она имеет различные коэффициенты искажения по разным аксонометрическим осям: для x и z он имеет значение 0,94, а по y, равна значению 0,47.

В большинстве случаев диметрическая проекция выполняется с коэффициентом искажения по оси аксонометрии y, равным 0,5, и по осям аксонометрии z и x, равным единице.

 

Изображение окружностей в прямоугольной диметрии

Те окружности, которые располагаются в плоскостях, являющихся параллельными по отношению к плоскости проекции, при проецировании на аксонометрическую плоскость изображаются в виде эллипсов.

В тех случаях, когда диметрическая проекция окружности выполняется в неискаженном виде по осям z и x, длина большой оси эллипсов составляет 1,06 от диаметра изображаемой окружности, при этом малая ось эллипса под номером 1 ровна 0,95, а эллипсов под номерами 2 и 3 ровна 0,35 диаметра окружности.

В тех случаях, когда диметрическая проекция окружности выполняется в искаженном виде по осям x и z, длина больших осей всех эллипсов соответствует диаметру окружности, малой оси эллипса под номером 1 равна 0,9, а эллипсов с номерами 2 и 3 равна 0,33 длины диаметров окружности.

 

Изображение детали в прямоугольной диметрии

Для того чтобы в печатных изданиях и на некоторых других видах носителей информации представить деталь или изделие наиболее наглядно, ее изображают в прямоугольной диметрии.

 

Косоугольная фронтальная изометрическая проекция

Для этой проекции характерно то, что проекции с углом наклона оси у допускается располагать с углом наклона от 30° до 60°.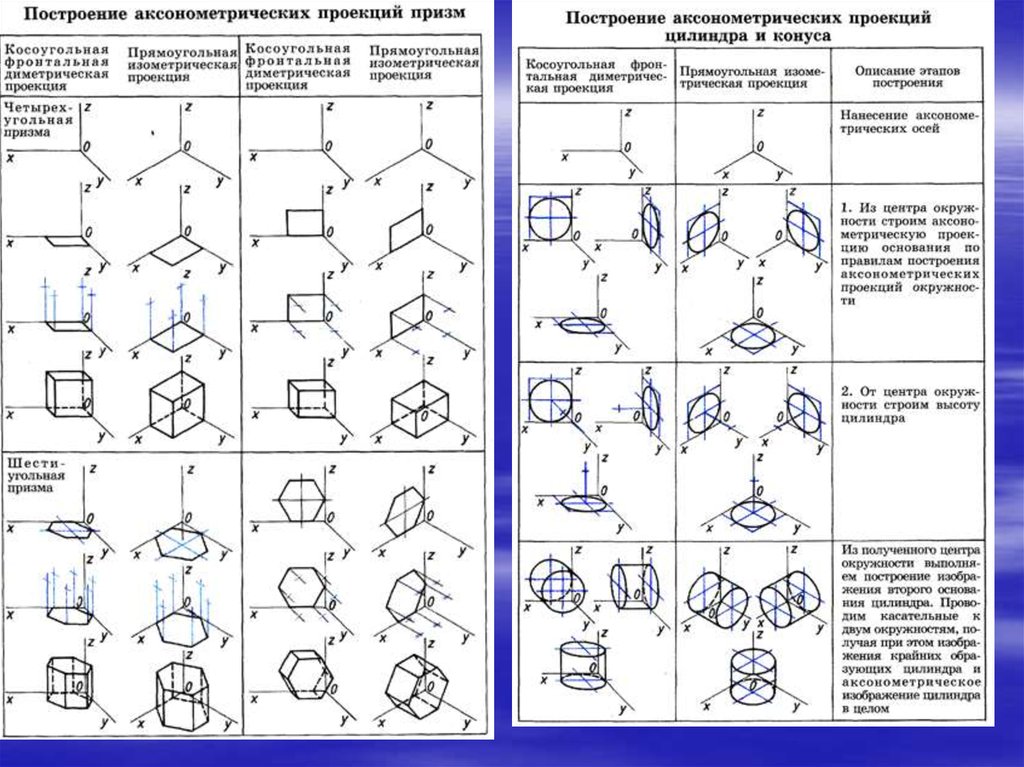 Фронтальная изометрическая проекция по осям x, y и z искажений не имеет.

 

Изображения окружности в косоугольной фронтальной изометрии

Те окружности, которые располагаются в плоскостях, лежащих параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в виде окружностей. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,3 диаметра окружности, а малой оси – 0,54 диаметра окружности.

Изображение детали в косоугольной фронтальной изометрии

Изображение деталей в косоугольной фронтальной изометрии, используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

 

Косоугольная горизонтальная изометрическая проекция

Отличительной особенностью косоугольной горизонтальной изометрической проекции является то, что здесь допускается применять, что проекции с углом наклона оси у допускается располагать под углом наклона от 45° до 60°, при этом угол 90° между осями x и y должен сохраняться неизменным.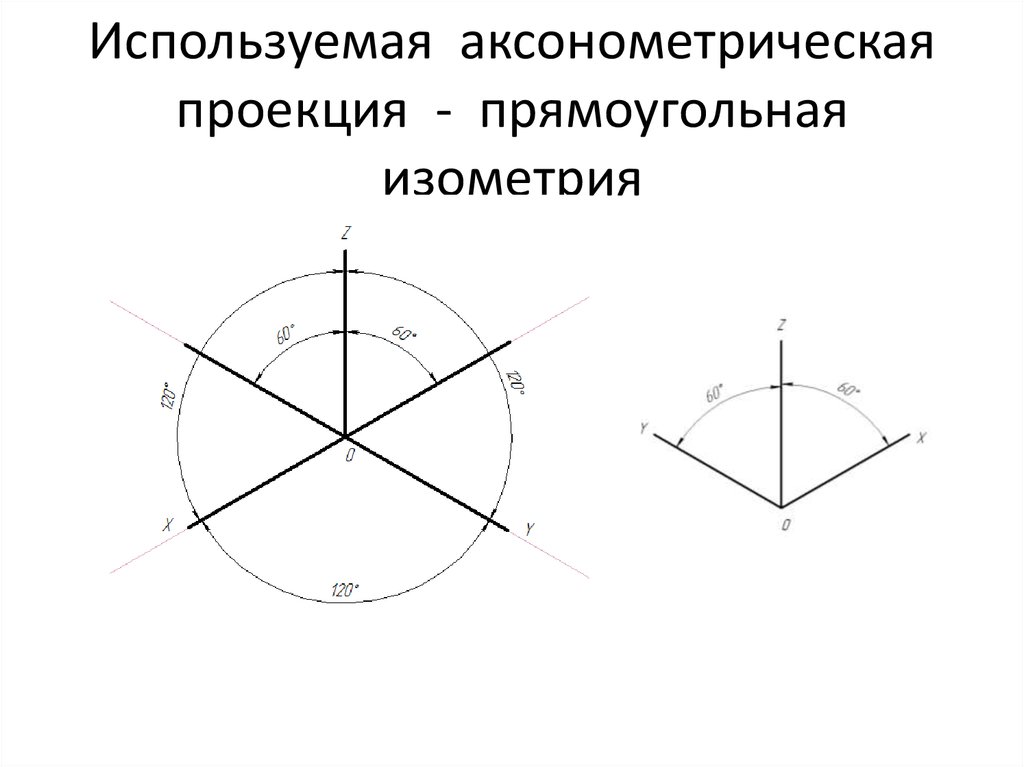 В данной проекции искажения отсутствуют по всем осям.

 

Изображения окружности в косоугольной горизонтальной изометрической проекции

Те окружности, которые располагаются в плоскостях, находящихся параллельно горизонтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и фронтальной плоскостям проекций, проецируются в эллипсы.

Наибольшая ось эллипса под номером 1 равна 1,37, а малая ось равна 0,37 от диаметра окружности. Большая ось эллипса номер 3 равна 1,22, а малая ось равна 0,71 от диаметра окружности.

 

Изображение детали в косоугольной горизонтальной изометрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

 

Косоугольная фронтальная диметрическая проекция

Отличительной чертой этой проекции является то, что аксометрическая ось y может иметь угол наклона от 30° до 60°.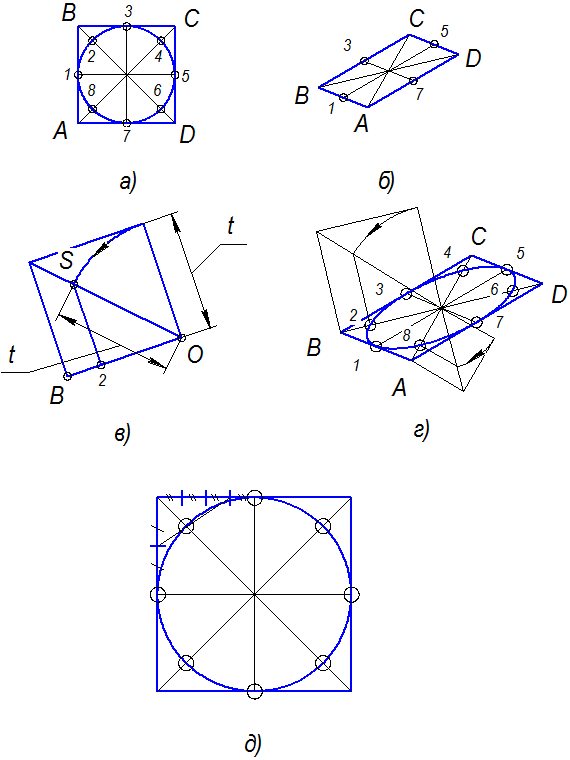 При этом коэффициент искажения по осям x и z равняется единице, а по оси y – 0,5.

 

Изображения окружности в косоугольной фронтальной диметрии

Те окружности, которые располагаются в плоскостях, находящихся параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,07 диаметра окружности, а малой оси – 0,33 диаметра окружности.

 

Изображение детали в косоугольной фронтальной диметрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

 

Нанесение размеров

Размерные линии при изображении аксонометрических проекций должны наноситься параллельно измеряемым отрезкам, а выносные – параллельно аксонометрическим осям.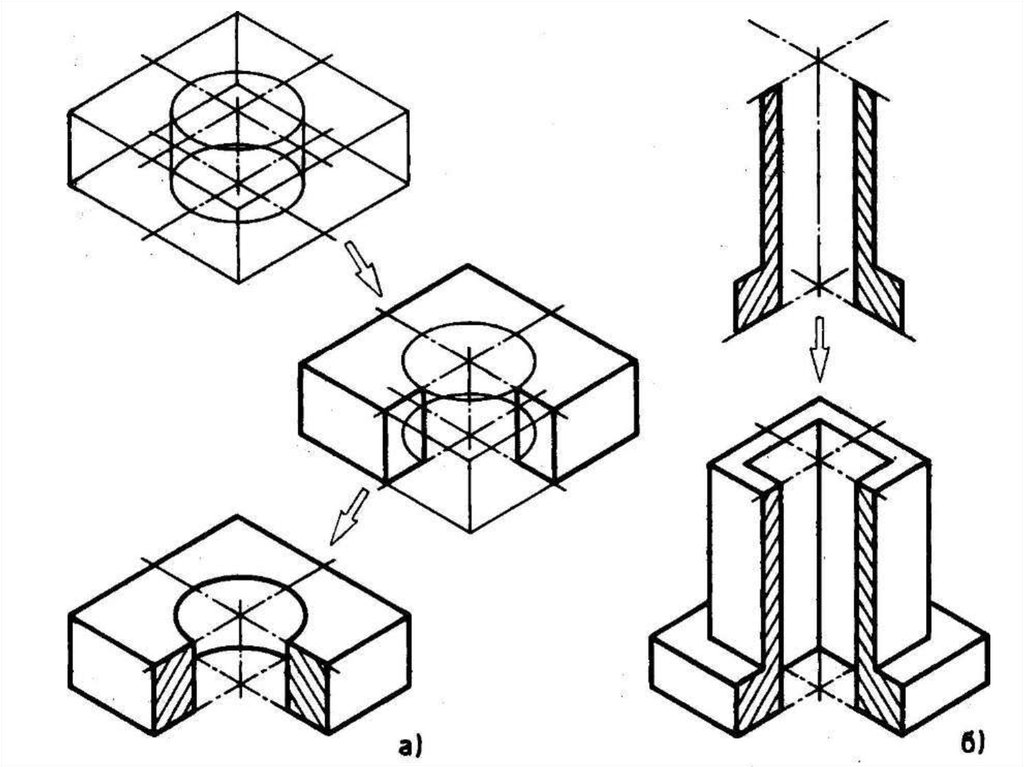

 

Штриховка

Сечения во всех аксонометрических проекциях наносится штриховкой. При этом ее линии должны быть параллельны лежащим в соответствующих координатных плоскостях диагоналям проекций квадратов.

 

 

 

Написать письмо

Аксонометрические проекции – технический обзор

Перейти к основному содержанию (пропустить меню навигации)

Пожалуйста, включите JavaScript для отображения математики на этой странице.

Реферат

В этой статье обсуждается, как аксонометрические проекции могут использоваться в компьютерных технологиях. графика, мультимедийные приложения и компьютерные игры. Он сравнивает аксонометрическая проекция, или параллельная перспектива , на линейную перспектива, перечисляет основные свойства и решает некоторые вопросы реализации Детали. Более ранняя версия этой статьи включена в книгу «Продвинутое программирование игр».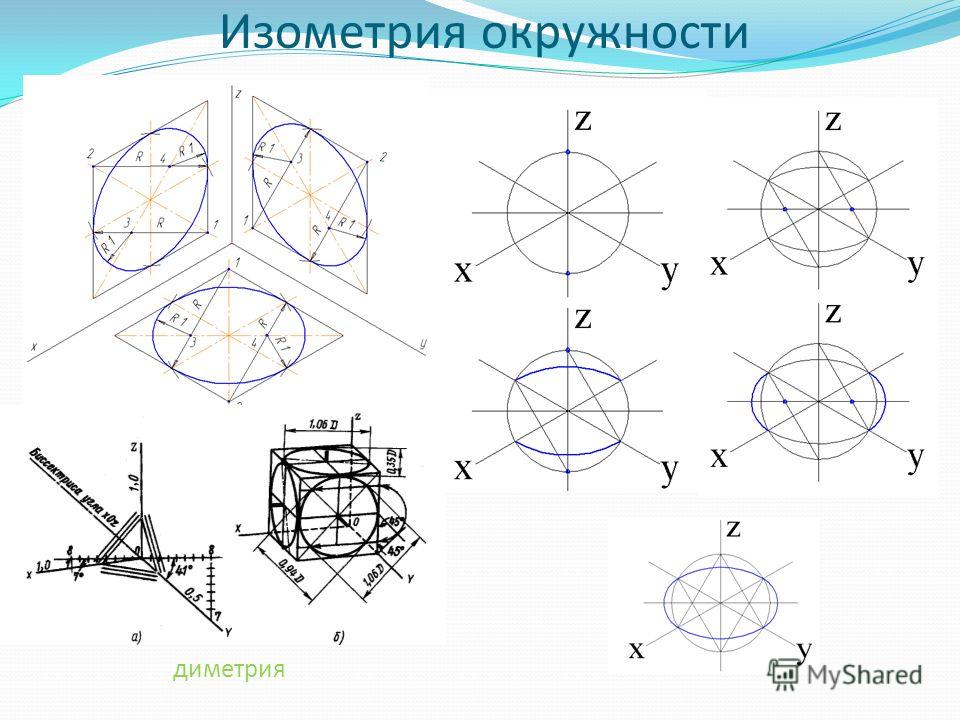

Основное внимание в этой статье уделяется изометрическим и диметрическим проекциям. наиболее широко используемые разновидности аксонометрической проекции. Эта бумага также представляет две диметрические проекции, которые подходят для (плиточного) компьютера графика.

Введение — первая попытка

В западном мире мы привыкли к линейной перспективе, которая пытается добиться визуального реализма в картинах трехмерных сред. Линейная перспектива, которая совершенствовалась на протяжении 17 ^-й век в Европе, основан на евклидовой оптике: глаз как точечный объект, улавливающий прямые световые лучи и воспринимает только цвет, интенсивность и угол лучей, а не их длина.

В восточном искусстве развилась еще одна перспектива: «китайская перспектива». была неотъемлемой частью классической живописи на свитках (на самом деле, «китайской перспектива» немного неправильное название, потому что та же самая перспектива также использовалась в искусстве Японии и других восточных стран).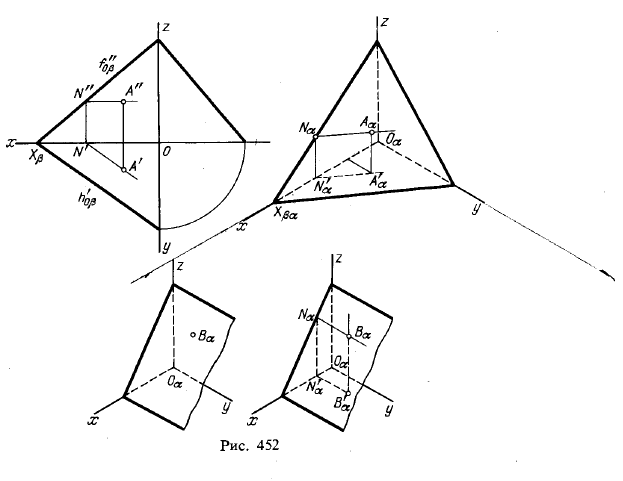 Типичный китайский свиток картина имела размер примерно 40 сантиметров в высоту на несколько метров широкий. Картину рассматривают, развернув ее (справа налево). на столе сегментами шириной около 60 сантиметров. Китайский свиток картины показывают развитие во времени — форма «нарративного искусства», напротив к картинам, которые были сделаны в Европе в то время, которые показывают «ситуацию» а не разработка.

Для этих картин на свитках китайским художникам нужна была перспектива, которая не имел явных точек схода; каждая сцена картины свитка была бы видны по отдельности, а точка схода, находящаяся за пределами области просмотра, создает дезориентированный взгляд на сцену. (По той же причине китайский свиток картины обычно не имеют явного источника света или отбрасывают тени.) Китайские художники решили эту проблему, нарисовав линии вдоль оси Z в виде параллельные линии в живописи свитка. Это приводит к размещению горизонт на воображаемой линии, бесконечно высоко над картиной. аксонометрическая проекция — это технический термин для класса перспектив, которому также принадлежит китайская параллельная перспектива.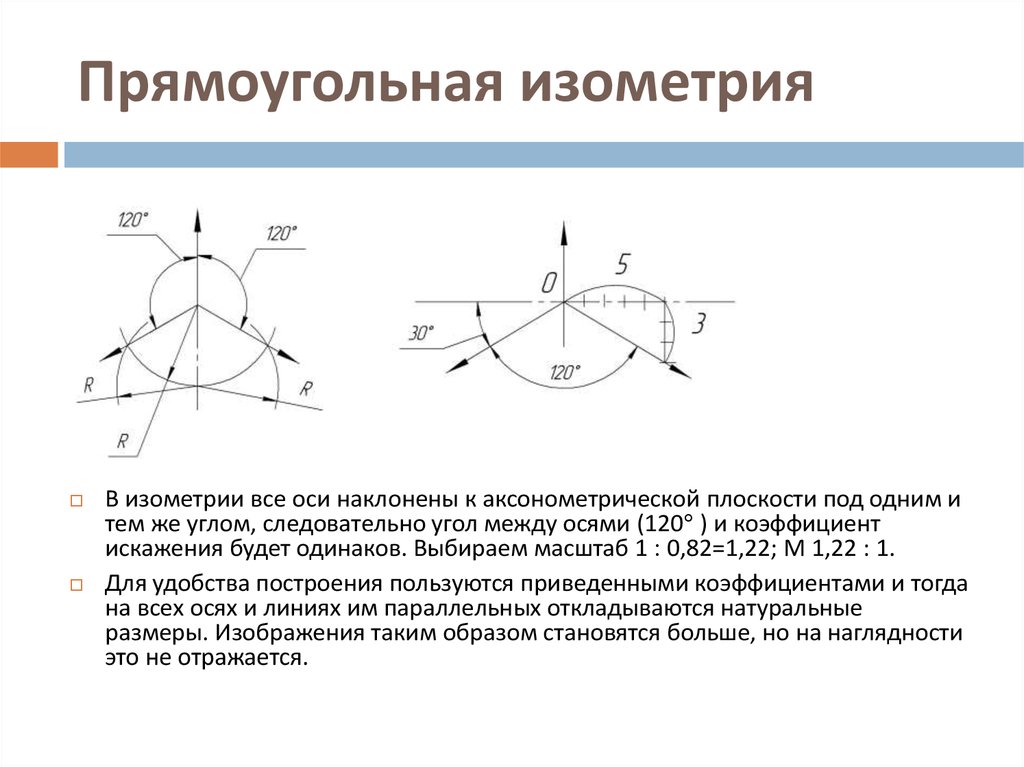 Эти перспективы не только отсутствие точки схода, но и несколько других, в основном полезных, характеристики. Они обсуждаются ниже.

Свиток

Введение — вторая попытка

Технические чертежи должны быть точными, точными и однозначными. Технические чертежи предназначены для инженеров и монтажников. Национальные институты официально стандартизировать технические чертежи, чтобы плотник мог построить конкретный стул, который придумал дизайнер мебели. Технические чертежи – это средство общение, для тех, кто может это понять.

Если бы мир был населен инженерами, все остальное не имело бы значения — но это не так, и инженеры (и монтажники, и плотники) должны общаться с менеджерами и клиентами. Проблема, конечно, в том, что технические рисунки трудно разобрать непосвященному. Хотя они показывают объекта под шестью углами, все эти углы нереалистичны: прямо спереди, прямо сверху и т.д. Что надо передать общая форма объекта представляет собой перспективный рисунок, на котором показаны три сторон куба одновременно.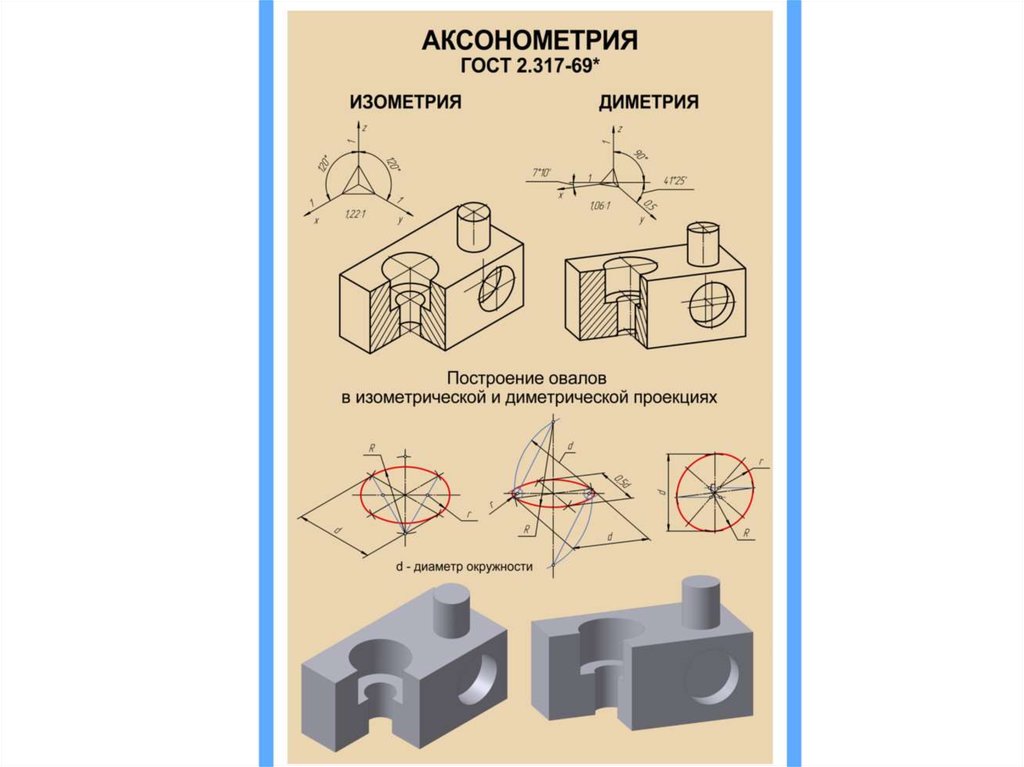

На данный момент следующий вопрос: как? Инженеры такие, какие они есть, они хотят простой метод, который не теряет большую часть точности оригинала рисунков и не требующих художественных навыков. Также обратите внимание, что в большинстве случаях объект, который вы должны нарисовать, еще не существует, поэтому обычно вы не можете взгляните на объект, чтобы понять его пропорции. Это делает это почти невозможно правильно расположить точки схода и оценить ракурс.

Компромисс, который стал известен как аксонометрия, представляет собой технику рисования где ортогональные оси x, y и z (трехмерного) мирового пространства равны проецируется на (неортогональные) оси на бумаге. В проекции ось Y обычно остается вертикальной осью, ось z скошена, а ось x может либо быть горизонтальным, как на рисунке справа, либо также быть наклонным. Более важным свойством аксонометрии является ее фиксированное соотношение между размерами объектов в мировом пространстве и в проекционном пространстве, независимо от положения объектов в проецируемом пространстве.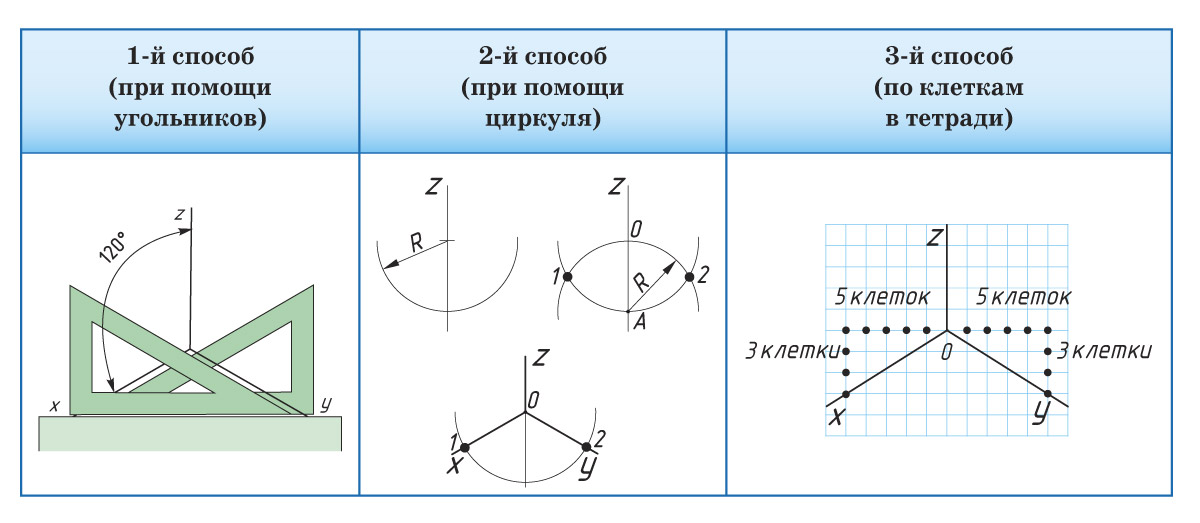 В линейной перспективе объекты становятся меньше, когда они удаляются дальше; не так в аксонометрической перспективе. Это означает, что вы можете измерить размер объекта аксонометрического чертежа. и знать, насколько велик реальный объект (вам нужно знать масштаб чертежа и свойства проекции, но не более того), то, что не может быть выполнено с линейной перспективой. Это приводит к названию проекции: слово «аксонометрия» означает «измеряемый от осей».

Хотя существует бесчисленное множество возможных аксонометрических проекций, только две из них стандартизированы для технических чертежей. Они подробно описаны ниже.

Введение — третья попытка

Компьютерные игры традиционно изобилуют графикой и анимация. На самом деле игры классифицируются по типу графики. они использовали. Два популярных типа игр — это «игры-платформеры», в которых вы смотреть со стороны, а «настольные игры» откуда смотришь в основном выше. Эти игры также объединяет то, что они часто используют плитки для построения «мир» из.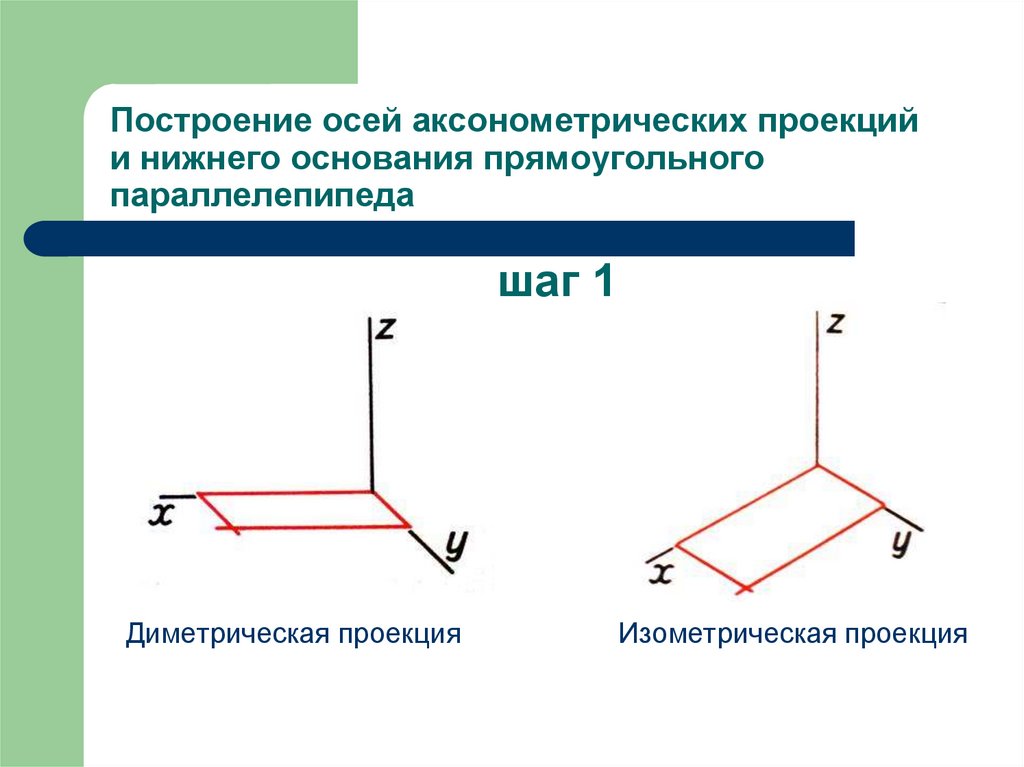 Учитывая это сходство и учитывая тупость нереалистичные точки зрения как платформеров, так и настольных игр, попытка поиск компромисса между этими крайними точками зрения является логичным следующим шаг.

Итак, что нужно сделать, это взять доску настольной игры, масштабировать ее высоту (она станет ось z для «глубины») и наклоните ее так, чтобы эта ось z на дисплее компьютера представляет собой диагональную линию. Для лучшего внешнего вида вы также можете наклонить ось X. (новый) ось Y остается вертикальной. Это все, что нужно, при условии, что вы получаете пропорции масштабирования и наклона вправо.

Из-за грубости цифровых координат и требования, края плиток (шахматной доски) должны точно совпадать, без каких-либо пикселей перекрытия или промежутки, углы наклона и коэффициенты масштабирования, которые разработчики игр использование является приближением к визуально оптимальным пропорциям. Один из упрощение, которое сделали разработчики игр, заключается в использовании аксонометрического проекция, в которой единица вдоль оси имеет одинаковую длину для всех трех оси.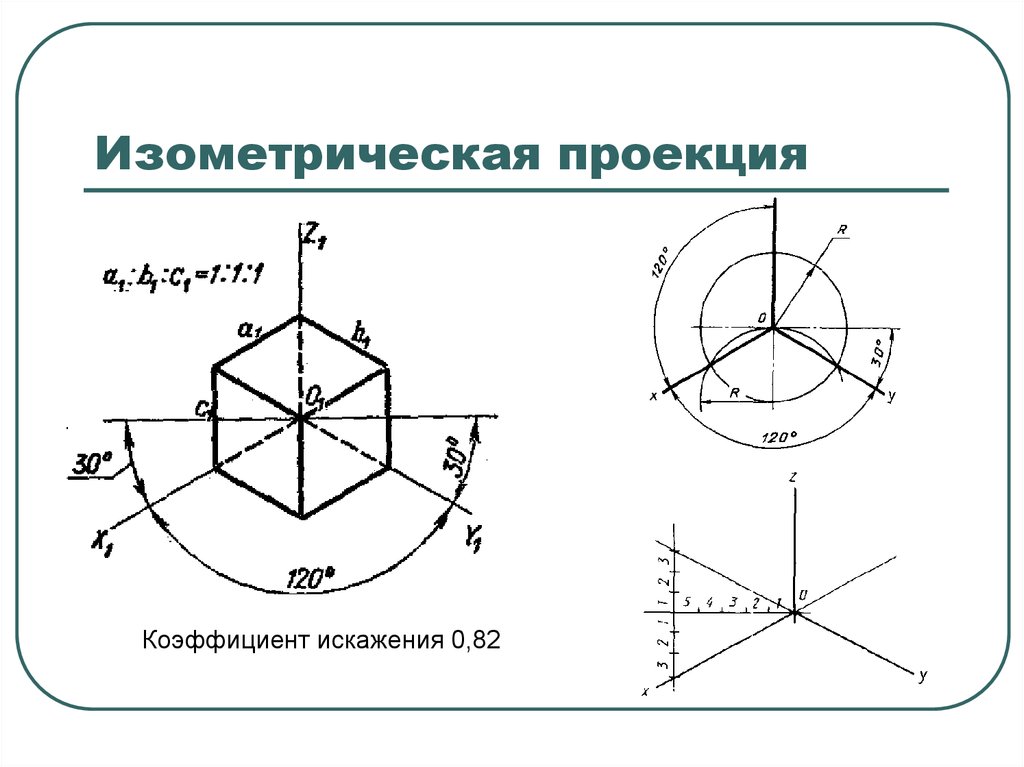 То есть каждая ось имеет одинаковую метрику; следовательно, проекция называется «изометрический». Аксонометрические проекции и тайловые изображения не обязательно связаны. Но большинство компьютерных игр, использующих изометрическую перспективу также используйте изображения на основе плитки.

А теперь, вперед…

Три вопроса, которые занимали меня при планировании этой статьи:

• Каковы общие (или пропорциональные) аксонометрические проекции и как убедительно каждый выглядит?
• Под какими углами смотреть на доску в аксонометрической проекции? это заманчиво использовать визуализированные трехмерные объекты на аксонометрической карте в качестве спрайтов. К указать положение и ориентацию «камеры» по отношению к объекта, вам нужно будет знать внутренние углы аксонометрической карты что вы используете.
• Что вообще пишут во введении?

Целью этой статьи является представление двух общих аксонометрических проекций, изометрическая проекция (кратко представленная выше) и диметрическая проекции и дать ответ на поставленные выше вопросы.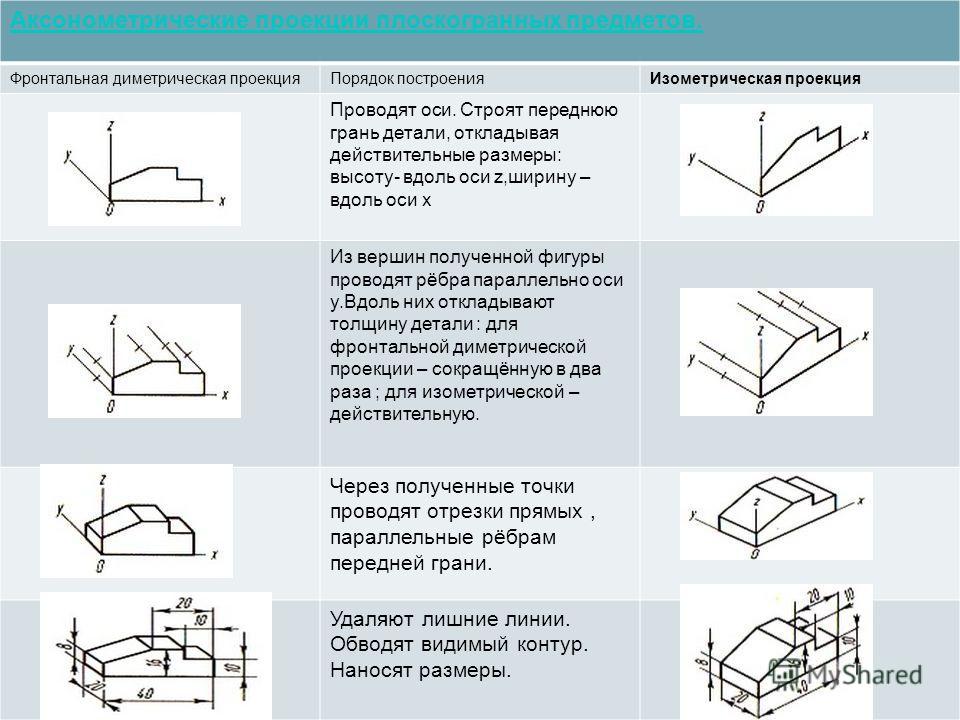

Я намеренно пренебрежение правильными определениями терминов и категорий; аксонометрический проекции и «косые параллельные» проекции настолько похожи, что я просто объединили их под термином «аксонометрия». В любом случае косая параллель проекцию следует рассматривать как частный случай диметрики (иногда изометрическая) проекция. Косые параллельные проекции, кавалерные проекции, кабинетные проекции, военные проекции, аксонометрические проекции,… плюс ça изменение, плюс c’est la même выбрал.

Подводя итог, основные свойства аксонометрических проекций:

• Нет точек схода. Это позволяет прокручивать большое изображение под видового экрана и иметь одинаковую перспективу в любой точке. В случае мозаичные изображения, изображение строится на лету и не требует физические границы или края.
• Прямые, параллельные в трехмерном пространстве, остаются параллельными и в 2-х мерная картинка. Это отличается от linear. перспектива , где параллельные линии вдоль оси z в трехмерном космический коллапс в единую точку схода на горизонте в 2-х мерная картинка.
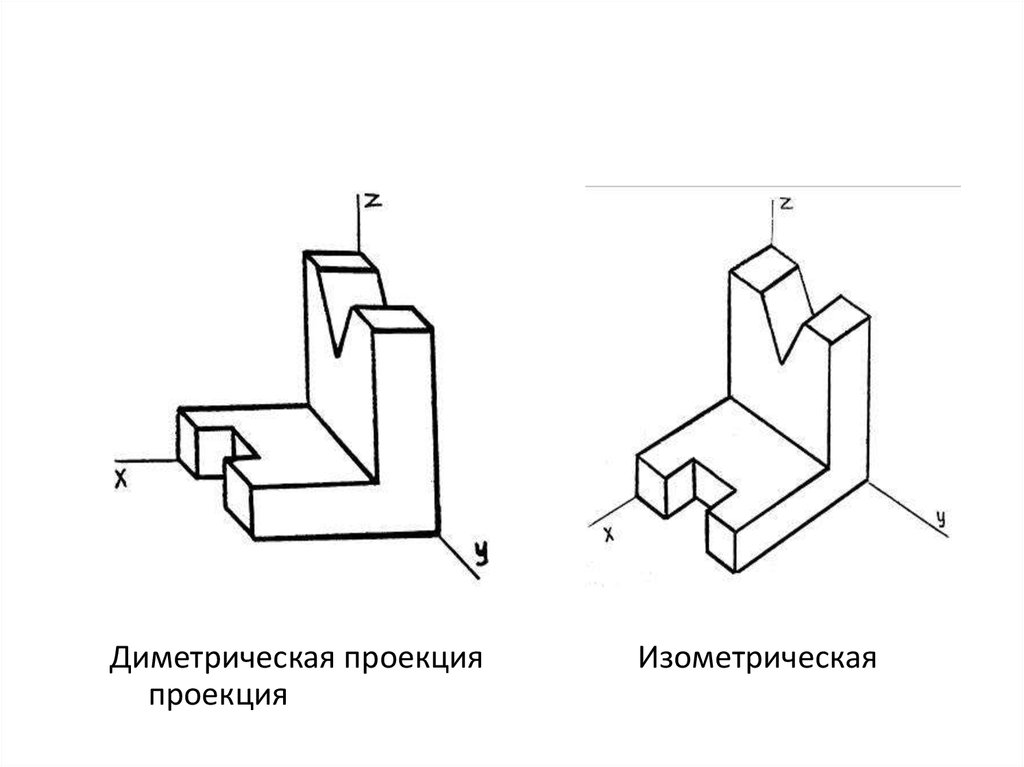
• Удаленные объекты имеют тот же размер, что и близкие; объекты не становятся меньше по мере удаления от зрителя. Если вы знаете масштаб осей, можно измерить размеры (ширину, высоту, длину, глубины) объекта прямо с картинки, вне зависимости от его положения на ось Z; отсюда и название аксонометрия .
• Аксонометрические проекции стандартизированы для технических чертежей. Эти стандарты оптимизированы для простоты использования по сравнению с визуальным реализмом. Даже если ты решите отклониться от стандартов, используйте их как источник вдохновения. Два прогнозы, стандартизированные институтом стандартизации ISO, представлены в этой статье.

Одно слово предостережения относительно любого из приведенных ниже рисунков и проекции углы, которые представляют эти фигуры: углы только приблизительны. Я рассчитал углы, исходя из форм ромбов одного или двух сторон спроецированного куба. Эти расчеты были бы справедливы, если бы перспективные проекции не исказили исходный куб. Теперь пропорции большинство проекций были выбраны так, чтобы свести к минимуму искажения (особенно те, стандартизированы для технических чертежей), но тем не менее не являются точно . Углы, которые я даю, также являются хорошим приближением, но не более того.

Изометрическая проекция

В изометрической проекции оси x, y и z имеют одинаковую метрику: a единица (скажем, сантиметр) по оси абсцисс одинаково длинна по оси у и оси Z. Другими словами, если вы визуализируете каркасный куб, все ребра в 2-мерные изображения имеют одинаковую длину. Еще одно свойство изометрии проекции заключается в том, что спроецированный каркасный куб также симметричен. Все стороны спроецированного куба являются ромбами.

NEN 2536 описывает изометрическую проекцию, которая симметричны относительно вертикальной оси; угол между осями x и y, а между осями z и y — 60 градусов. Проекция показывает три стороны куба, а поверхности каждой стороны равны. Угол 30° между оси x и z и «горизонт» удобны для технических чертежей, потому что синус 30° равен ½.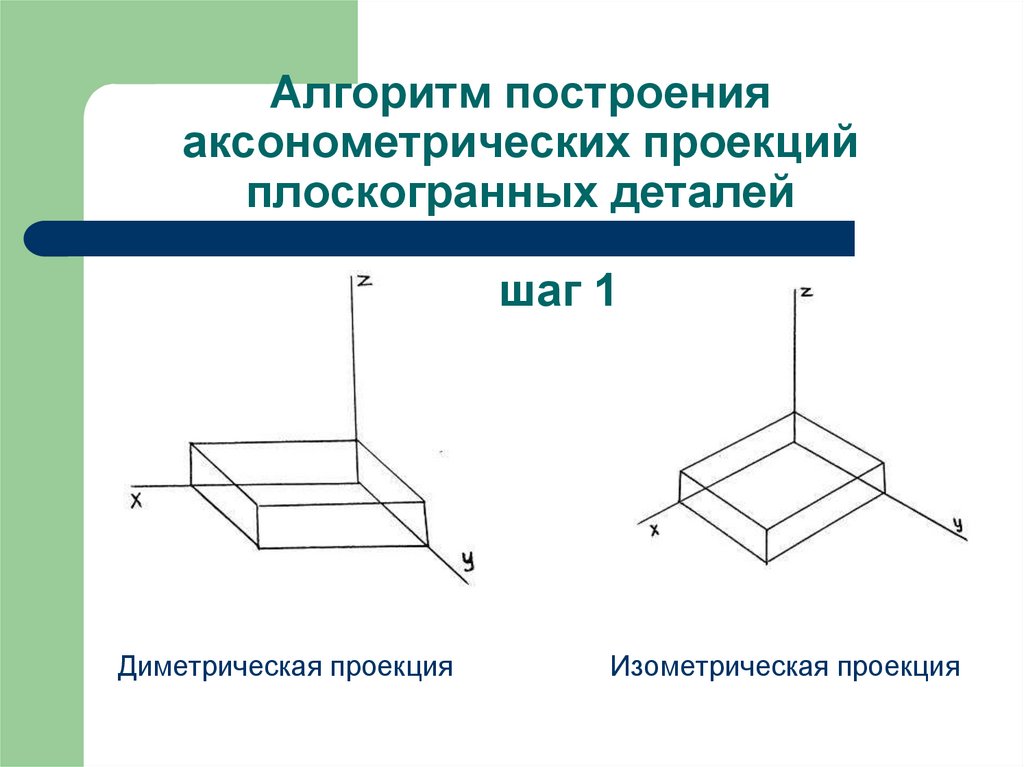 Эта проекция объясняется Уильям Фариш, опубликовавший трактат об этом в 1822 году (ссылка: Ян Крикке). NEN 2536 был пересмотрен и переиздан. в качестве международного стандарта ISO 5456-3.

На рисунке ниже показан куб в изометрической проекции, как определено ISO 5456-3. Первый объект слева на рисунке — куб без украшений; в второй объект — это тот же куб с аннотациями углов и мер вокруг него. Третий и четвертый рисунки представляют собой вид сверху и сбоку в перспективе. сцену, и они дают положение камеры, которое соответствует перспективному виду. положение камеры — это то, что вы вводите в 3D-рендерер (или трассировщик лучей) для создайте спрайты или тайлы для изометрической проекции.

Изометрическая проекция 30° (NEN/ISO)

Компьютерные игры с изометрическими картами часто основаны на тайлах. Для изготовления плитки соответствия, геймдизайнер должен учитывать, как прочерчены диагональные линии дискретными шагами (Bresenham и все такое).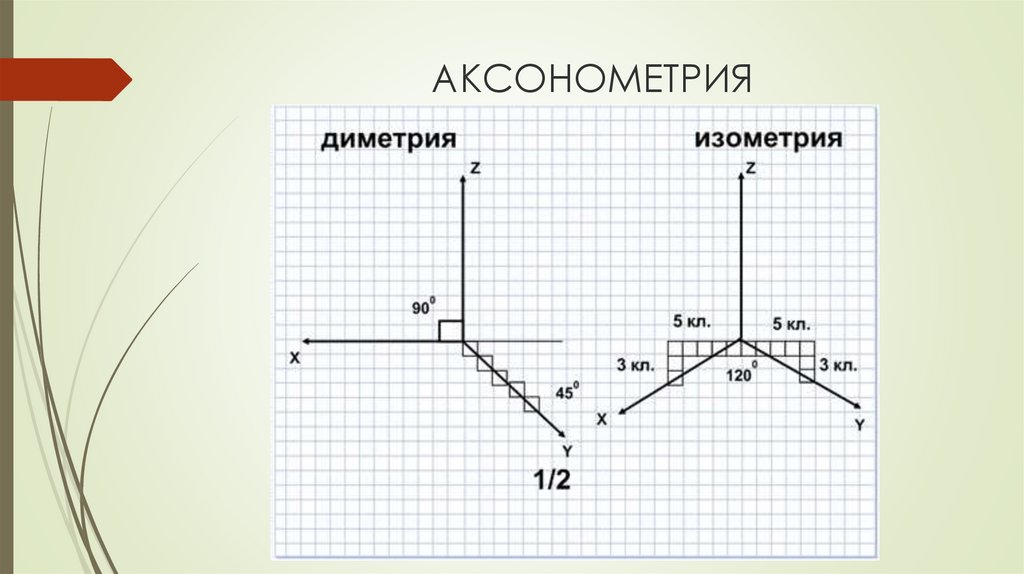 Как оказалось, очередь на 30 градусов (синус равен 0,5) дает слишком неравномерные шаги. Линия в угол, где тангенс равен 0,5 имеет ли хороший правильный узор: два шаг вправо, шаг вверх. Таким образом, изометрическая проекция, используемая большинством игры наклоняют оси x и z примерно на 27 градусов (точный угол «арктангенс (0,5)»). Кстати, поскольку тангенс угла ромб равен 0,5, ширина ромба вдвое больше его высоты. Вот почему во многих источниках упоминается масштаб 1: 2 для изометрической перспективы. (Чтобы сделать ребра ромбов совпадают, ширина ромба должна быть кратна четыре пикселя, а высота должна быть на один пиксель меньше ½ ширины. В других Другими словами, отношение высоты к ширине ромба обычно не равно 9.0011 ровно 1:2, а скорее около 1:2.1. Это никак не влияет на принципы изометрическая перспектива.)

Опять же, на рисунке ниже показано, как выглядит эта изометрическая проекция как.

Изометрическая проекция 1:2

Две упомянутые выше изометрические проекции «искажают» все грани примера куб. В приложениях, где наиболее важными гранями являются горизонтальные, например, в приложениях, где карты или планы этажей имеют первостепенное значение, другой распространена изометрическая проекция. Называется «военная» проекция, наверное из-за его происхождения или использования.

«Военная» проекция

В военной проекции углы осей x и z составляют 45°, это означает, что угол между осью x и осью z составляет 90°. То есть плоскость x-z имеет наклон , а не . это повернутый 45°, однако.

На виде сбоку военного выступа (график справа) у меня есть указано, что угол обзора вниз на объект (куб) примерно 45°. Военная проекция дает довольно неточную перспектива — в числовом выражении, и схема, которую я использовал для расчета углов не работает на этой проекции. Таким образом, этот угол является оценка, основанная на концепции симметрии, а не на визуальной точности.

Диметрическая проекция

В диметрической проекции одна из трех осей имеет другой масштаб чем два других.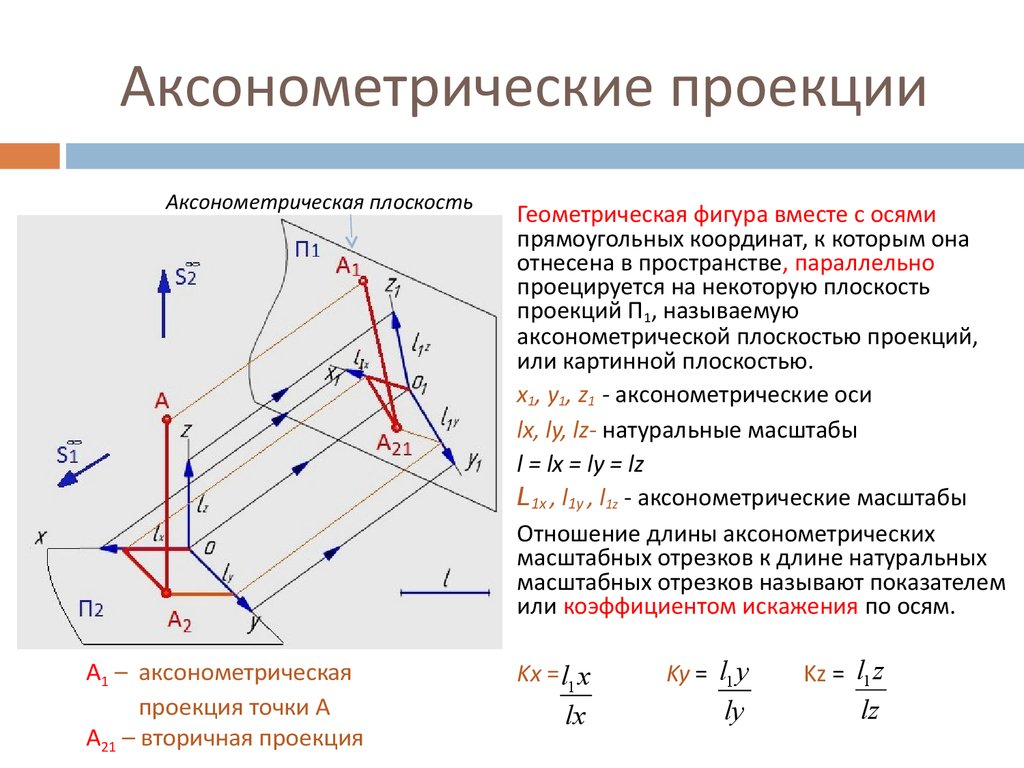 На практике масштабируемой осью является ось z и, следовательно, куб, нарисованный в диметрической проекции, не является симметричным рисунком (как в изометрическая проекция).

Диметрические проекции более гибкие, чем изометрические, т.к. вы меняете масштабный коэффициент (и соответственно настраиваете другие параметры). асимметрия в диметрической проекции также дает вам дополнительную угол для игры. С художественной точки зрения мне также нравятся диметрические проекции лучше, чем изометрические проекции, из-за асимметрии. Или же скорее, симметрия изометрической проекции придает сцене вид «искусственный» или сюрреалистический. Еще одним преимуществом является то, что в компьютере игра, что если вы отразите графику диметрической проекции, вы глядя на сцену в новом, « свежий «, перспектива, в то время как основные вычисления для системы координат остаются прежними.

NEN 2536 также представляет диметрическую проекцию для технические рисунки. Это кратко показано на рисунке ниже.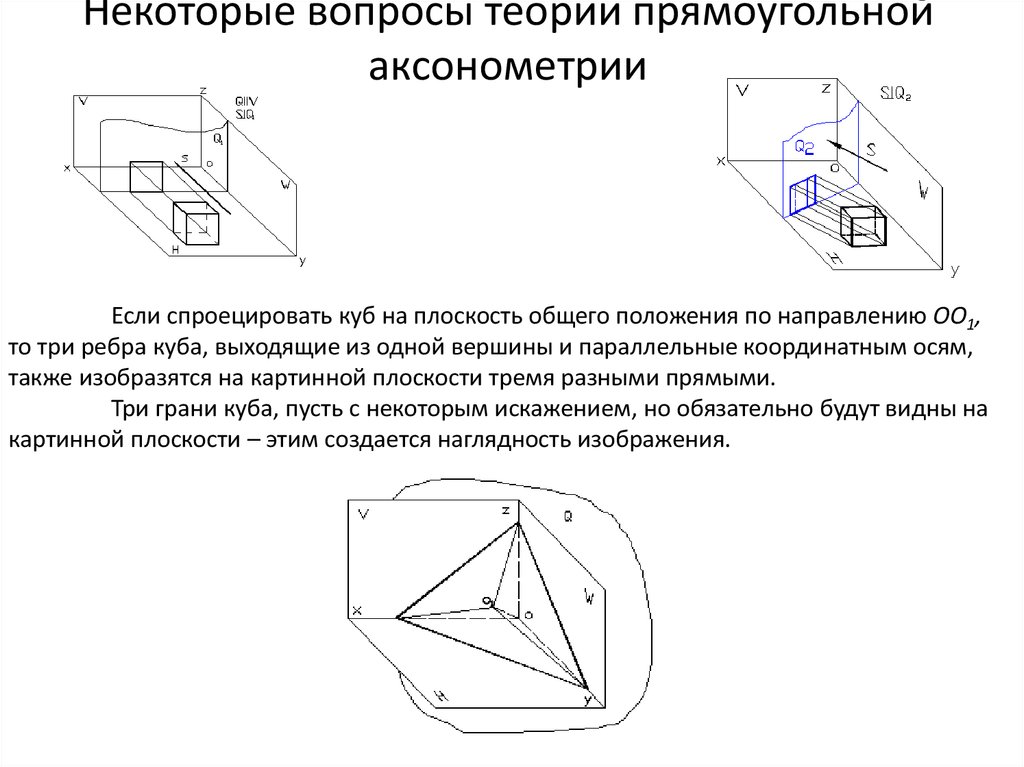 Любое расстояние вдоль ось z (нарисованная под углом 42°) масштабируется с коэффициентом ½.

Проекция 42°/7° (NEN/ISO)

Во введении упоминались китайские свитки, и мне потребовалось некоторое время. взяв метрики (репродукции) двух картин на свитках. Проекция отличается на этих двух картинах, и я предполагаю, что существует больше вариаций. Во всех виденных мною до сих пор картинах на свитках заметно то, что ось x остается горизонтальной.

Первая прокрутка проецирует ось Z под довольно малым углом (примерно 30 градусов). В результате вид в перспективе, расчетно далеко не точно. Причины, по которым мы все еще видим 3-мерный куб, а не какой-то плоский многоугольник, заключается в том, что угол в «виде сбоку» перспективного вида тоже мало и потому что наш визуальный система вполне снисходительна к ошибкам в коррекции перспективы.

Масштаб оси Z не может быть точно определен по прокрутке картина. По моей оценке, ось Z на картине (с углом наклона 30°) спроецированная ось Z) масштабируется вдвое (50%).

«Китайская перспектива»

Также обратите внимание (снова), что перспектива искажена и что углы вид сверху и вид сбоку следует рассматривать как «эмпирическое правило»; Я рассчитал эти углы так же, как и углы в диметрике. прогноз представлен в NEN 2536/ISO 5456-3, но эти расчеты фактически уже не применимы.

Другая картина, воспроизведенная ниже, имеет спроецированную ось z на чуть менее 40 градусов, но с наклоном в другую сторону. С одной стороны, Я мог бы сказать, что ось Z наклонена примерно на 130° (90° + 40°), но с другой стороны направление наклона несущественно для обсуждение аксонометрической проекции.

Репродукция 18 ^го века ремейка 11-метрового свитка, созданного художниками двора Цин, опубликованного в «Город Катай»

Я могу дать только приблизительную оценку масштабирование оси Z в этот свиток («Город Катай»): между 0,6 и 0,7 (но, вероятно, ближе к 0,6).

Диметрические проекции для компьютерной графики и игр

Как и в случае с изометрической проекцией, в компьютерной графике некоторые углы предпочтительнее других. Первая диметрическая проекция, которую я предлагаю для (тайловой) компьютерной графики очень похоже на проекцию китайской прокручивать картины. Разница заключается в масштабе оси Z и угле, который это делает с осью x. Начнем с угла, ось Z наклонена с примерно 27 градусов (точный угол равен «арктангенс (0,5)»). Это тот же угол, что и в изометрической проекции для использования в компьютерной графике. Масштаб таков, что ширина бокового вида куба при измерении по оси абсцисс составляет половину ширины лицевой стороны. Ключевая фраза в предыдущее предложение «при измерении по оси x». в две предыдущие проекции, масштабный коэффициент, примененный к расстояниям, измеренным вдоль ось Z.

Диметрическая проекция 1:2 «вид сбоку»

Вышеупомянутая проекция дает перспективу, которая видна в основном с сторона.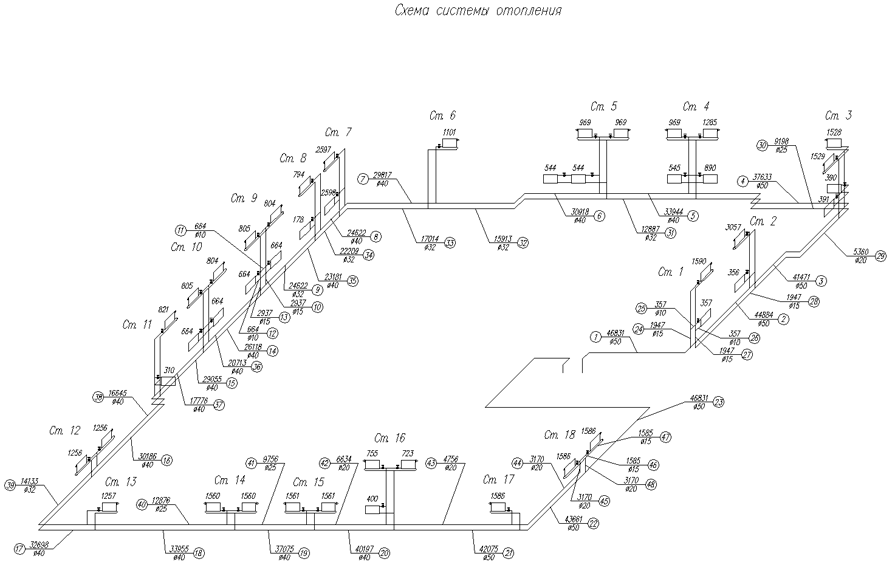 Мне может быть полезно добавить немного глубины боковой прокрутке (или «платформа») игра. Для настольных игр перспектива, которая просматривается с большей высоты более уместно. Второй предлагаемый диметр проекция для игр служит этой цели.

Диметрическая проекция 1:2 «вид сверху»

Опять же, обратите внимание, что перспектива двух предложенных выше проекций искаженный. Углы на видах сверху и сбоку равны , на самом деле приблизительные. Например, во второй проекции угол, под которым смотришь сверху на месте дается как 24 градуса. Однако использование угла в 30 градусов может на самом деле выглядеть лучше. Кроме того, 30-градусный угол позволяет использовать тот же объекты как для диметрической, так и для изометрической проекций для игр.

Другие диметрические проекции приведены в таблице ниже. Эти прогнозы были взяты из программы CARTESIO. За каждой проекции я даю имя, которое программа дает проекции, наклон для осей x и z и масштаб для оси z.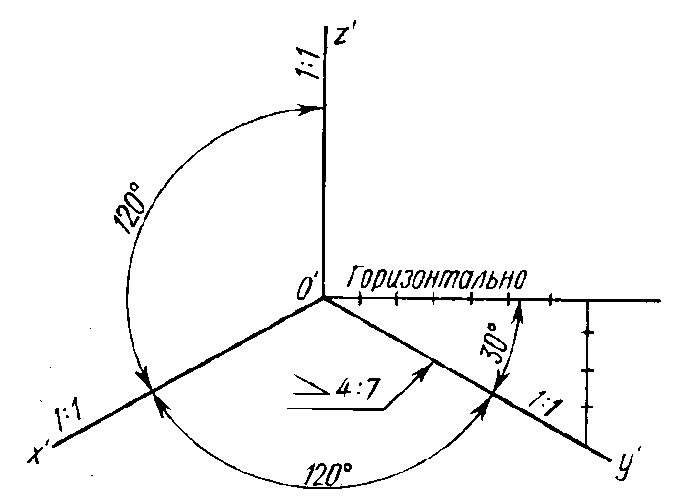 Во всех представленных здесь проекциях, ось y остается вертикальной, а x- и оси Y имеют одинаковый масштаб.

projection name	x-axis angle	z-axis angle	z-axis scale
130, 130, 100	10	40	0.59
1, 1 , 2/3	12.8	38.6	0.667
1, 1, 3/4	16.3	36.8	0.75

Программа CARTESIO перечисляет больше проекций, чем несколько приведенных выше, в том числе те, стандартов NEN 2536/ISO 5456-3 и нескольких таких искажено, что я не вижу в них практического применения.

Перемещение по аксонометрической проекции

Преобразование пространственных координат (x, y, z) в пиксельные координаты (x’, y’) в проекция требует только тривиальной геометрии. В таблице ниже представлены формулы полноты.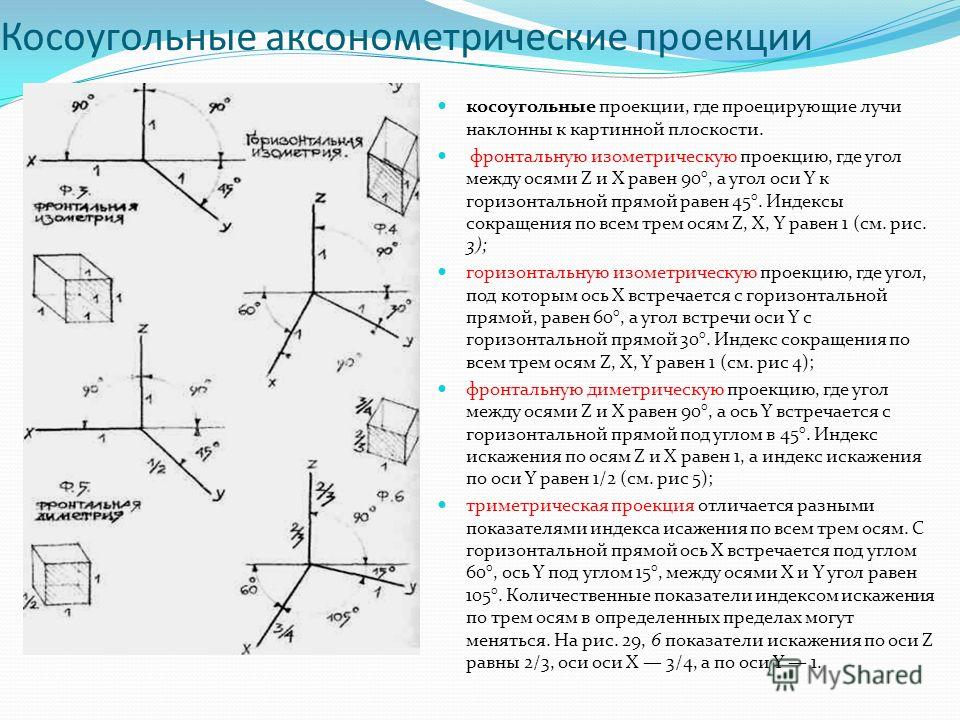 Пожалуйста, обратитесь к системе координат на рисунке справа мое определение осей x, y и z; в трехмерном пространстве ось Y указывает вверх, а плоскость определяется осями x и z.

Преобразование 3D-координат в 2D-координаты проекции 9\circ}) \cr} \]
Китайские свитки	\[ \выравнивание{ х’ &= х + {\bf n} \cdot z \cdot \cos ({\bf T}) \cr y’ &= y + {\bf n} \cdot z \cdot \sin ({\bf T}) \cr} \] где \( {\bf n} \) от 0,5 до 0,7 и \( {\bf T} \) от 30° до 40°
Компьютерные игры: вид сбоку	\[ \выравнивание{ х’ &= х + {z \более 2} \cr y’ &= y + {z \более 4} \cr} \]
Компьютерные игры: вид сверху	\[ \выравнивание{ х’ &= х + {z \более 4} \cr y’ &= y + {z \over 2} \cr} \]

Обратите внимание, что в приведенных выше уравнениях различные синусы и косинусы постоянны. для данной проекции и их нужно вычислить только один раз.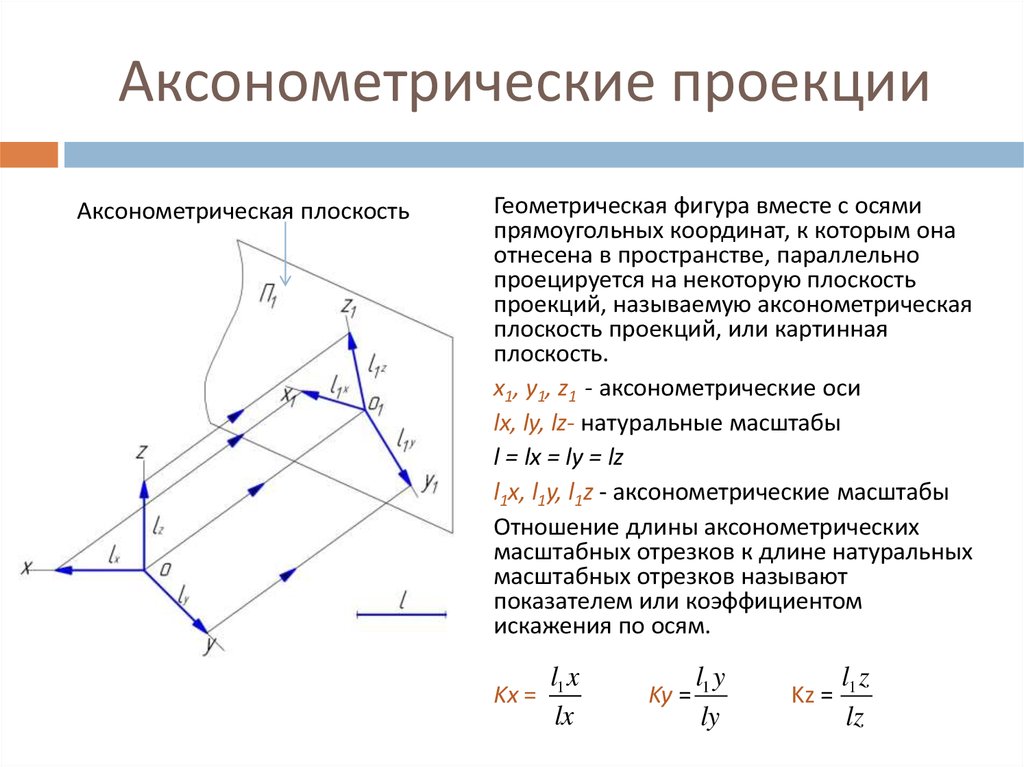

Преобразование координат в проекции в пространственные координаты другое дело. В общем виде это просто невозможно сделать: нельзя вычислить три независимых выходных параметра из двух входных параметров. Если можно «зафиксировать» один из выходных параметров, два других можно рассчитать из входных параметров. Пример: если аксонометрическая проекция представляет собой карту, и вы можете предположить, что область на карте практически не имеет рельеф, то можно зафиксировать положение по оси Y равным нулю (уровень земли), и вам нужно только вычислить x и z из x’ и y’. (Опять же отметим, что в трехмерная система координат, которую я использую, точки оси Y вверх.) 9\circ })}} \cr} \] Китайские свитки \[ \выравнивание{ х &= х’ — {{\ cos ({\bf T}) \cdot (y’ — y)} \over {\sin ({\bf T})}} \cr z &= {{y’ — y} \over {{\bf n} \cdot \sin ({\bf T})}} \cr} \] где \( {\bf n} \) от 0,5 до 0,7 и \( {\bf T} \) от 30° до 40° Компьютерные игры: вид сбоку \[ \выравнивание{ х &= х’ — 2 \cdot (y’ — y) \cr z &= 4 \cdot (y’ — y) \cr} \] Компьютерные игры: вид сверху 9\цирк }) \) в одной дроби для проекции NEN 2536 является константой с (приблизительное) значение 1,397.

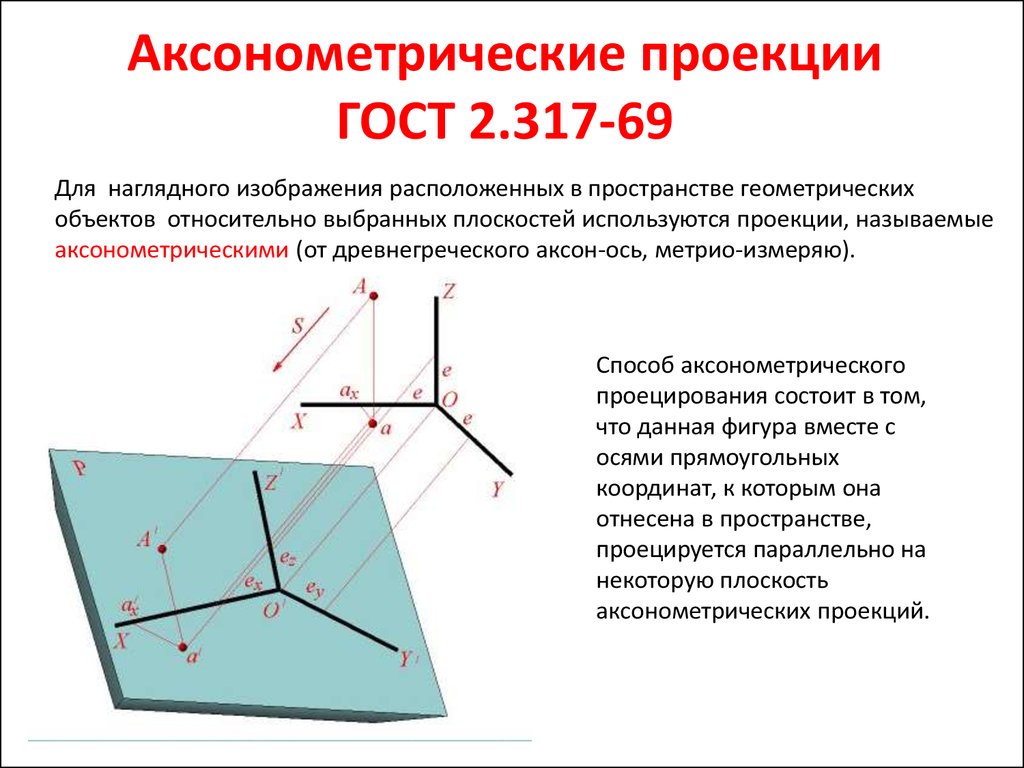
Уточнение вышеизложенного заключается в поддержке некоторого облегчения. расчет выходных координат начинается как и прежде, только теперь y-координата является оценкой, а не «известным» значением. После расчета координаты x и z, вы можете найти соответствующее значение «высоты» в положение (х, z). Как правило, они не будут совпадать с координатой Y, которую вы угадали при вычислении координат x и z. Теперь вы можете настроить вас оценка координаты y и вычисление соответствующих координат x и z опять таки. Эта итерация продолжается до тех пор, пока предполагаемая координата y (до вычисления x и z) достаточно близко подходит к искомому значению (после расчет x и z).

Главный вопрос при следовании этой итеративной процедуре: сходятся?» Следуя интуиции, процедура считается сходящейся, если нет пятно на поверхности проекта закрывает другое место в 3D-пространстве. То есть, если уклоны рельефа поверхности остаются ниже угла обзора (в «направление взгляда»), у каждого местоположения на карте в 3D-пространстве есть уникальный «близнец».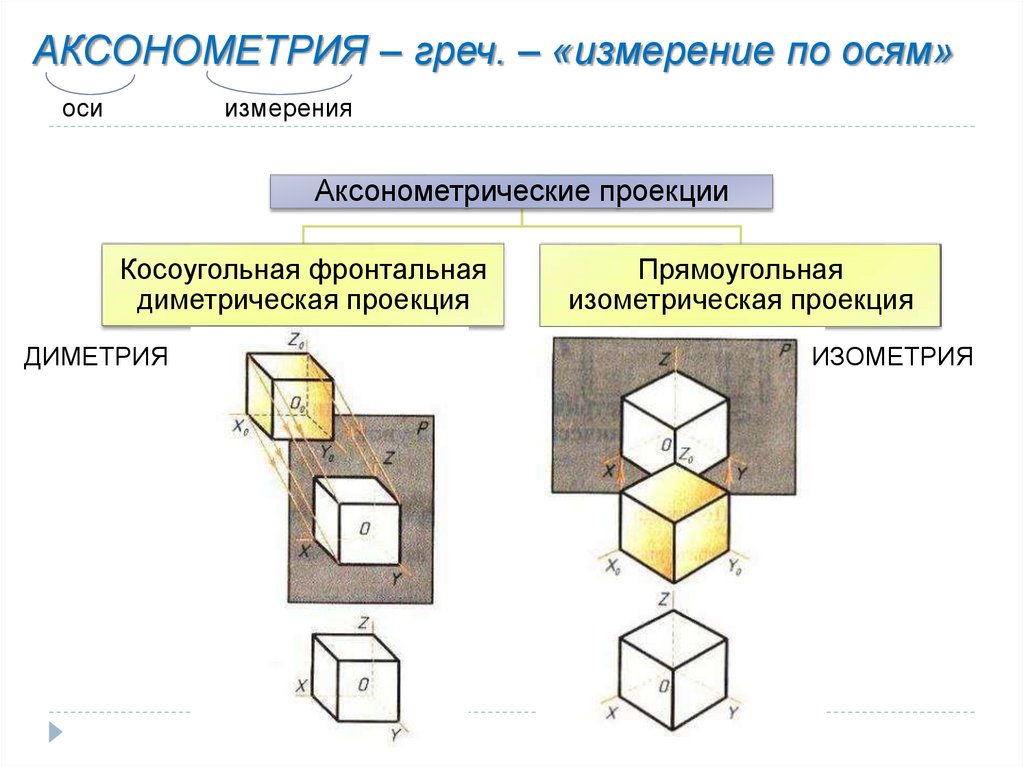 расположение в аксонометрической проекции, которое видно с точки обзора.

На приведенном выше изображении угол обзора от горизонтальной плоскости составляет 30 градусов. и самый крутой уклон в направлении взгляда составляет примерно половину этого. Рисунки с проволочными каркасными кубами в этой статье показывают угол, под которым вы смотрите на плоскость (для изометрической проекции NEN 2536 это 35° а для проекции 1:2, используемой в большинстве изометрических игр, это 30°). Если склоны на вашей доске остаются ниже этого предела, итеративная процедура расчета x и z при заданном y, а затем корректировка y до тех пор, пока y больше не изменится, будет сходятся.

Если у вас есть экстремальный рельеф или перекрывающиеся «уровни земли», такие как мосты или зданий, я предлагаю вам разделить спроецированную карту на части, которые, себя, придерживайтесь ограничения не более крутых углов, чем угол обзора угол. Эти части могут быть отдельными «слоями» или «спрайтами», и вы строите полную карту, объединив их.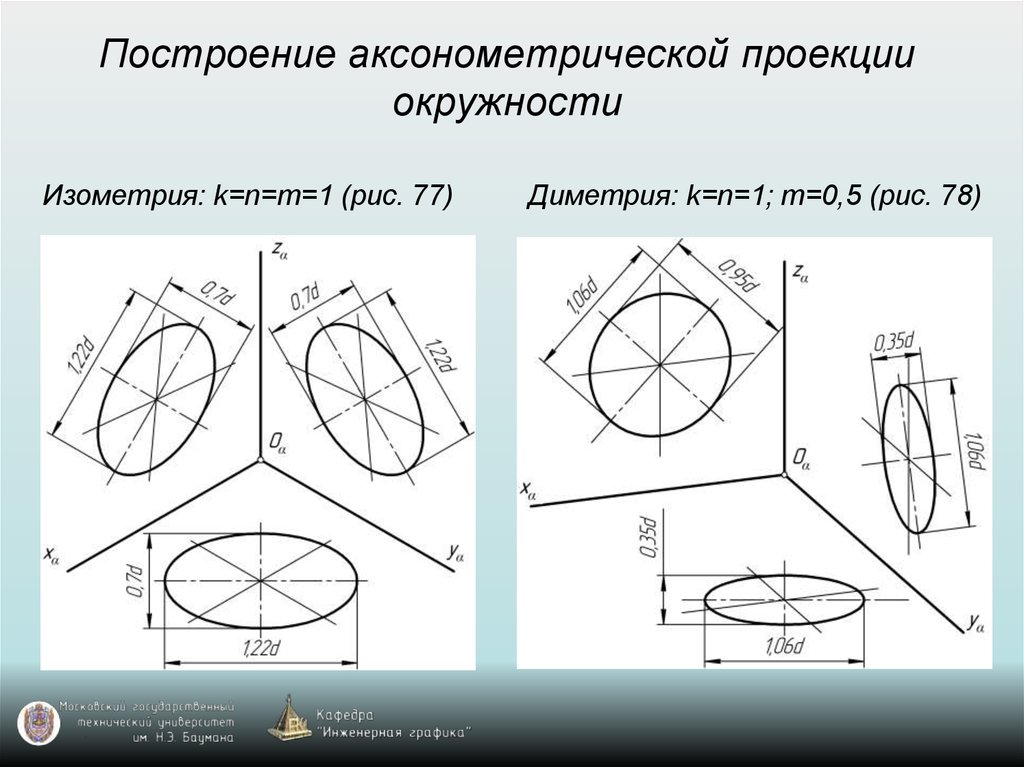 Чтобы вычислить (x, y, z) из (x’, y’), вы сначала решаете на каком слое/спрайте находится местоположение (x’,y’), а затем используйте итеративный Процедура нахождения значений x, y и z.

Дополнительная информация

Культурное кафе; «Город Катай: взгляд на китайскую жизнь через известную картину»; компакт-диск; Том 2; без даты .

Этот компакт-диск содержит подробную презентацию знаменитой картины на свитке.

Фоли, Джеймс Д. [ et al. ]; «Компьютерная графика: принципы и практика»; Аддисон-Уэсли; второе издание, 1990 г.; ISBN 0-201-121107.

Эта энциклопедическая книга посвящена перспективным проекциям в пятой главе.

Крикке, Дж.; «Аксонометрия: вопрос перспективы»; Компьютерная графика и приложения IEEE; Июль/август 2000 г.

(исторический) обзор аксонометрических проекций с точек зрения восточного искусства, технических рисунков и компьютерных игр — в том же духе как три введения к этой статье, но в более подробном и связная статья.
    В статье утверждается, что слово «аксонометрия» должно относятся только к конкретной проекции, используемой восточными художниками (т. так называемая «китайская перспектива»), тогда как общий термин — «орфографическая прогнозы». Со ссылкой на NEN 2536 и Фоли [и др.] в качестве эталона я рассматриваю аксонометрические проекции и параллельные проекции как синонимы, в то время как орфографический проекция — это та, где направление взгляда перпендикулярно плоскости, вообще без перспективы.

НЕН 2536; «Инженерный чертеж. Аксонометрическая проекция»; Нидерланды Институт нормализации; август 1966 года.

Голландский стандарт аксонометрических проекций для технических чертежей.
    Этот стандарт был заменен NEN 5456-3, опубликовано в 1997 г. (голландский язык) и соответствует стандарту ISO 5456-3 под названием «Технические чертежи». — Методы проекции — Часть 3: Аксонометрические представления», опубликовано в 1999 г. (на английском языке).

Тревизан, Камилло; КАРТЕСИО программа; версия 3. 03e.

Образовательное и интерактивное приложение, содержащее множество геометрических проекции. Это бесплатно для личного использования.

Что такое архитектура аксонометрического чертежа | Arch Articulate

Аксонометрическая перспектива , также известная как параллельная проекция или архитектура аксонометрического рисования, представляет собой ортогональную проекцию на косвенную плоскость как метод представления трехмерных объектов.

Аксонометрия» означает «измерение вдоль осей». В немецкой литературе аксонометрия основана на теореме Польке, так что объем аксонометрической проекции может включать в себя каждый своего рода параллельная проекция вместе с не только ортогональной проекцией (и многоракурсной проекцией), но и дополнительной косой проекцией.

Однако за пределами немецкой литературы период времени «аксонометрический» обычно используется исключительно для различия между ортогональными видами, где главные оси объекта не ортогональны плоскости проекции, и ортогональными видами, через которые проходят главные оси объекта ортогональны проекционному самолету.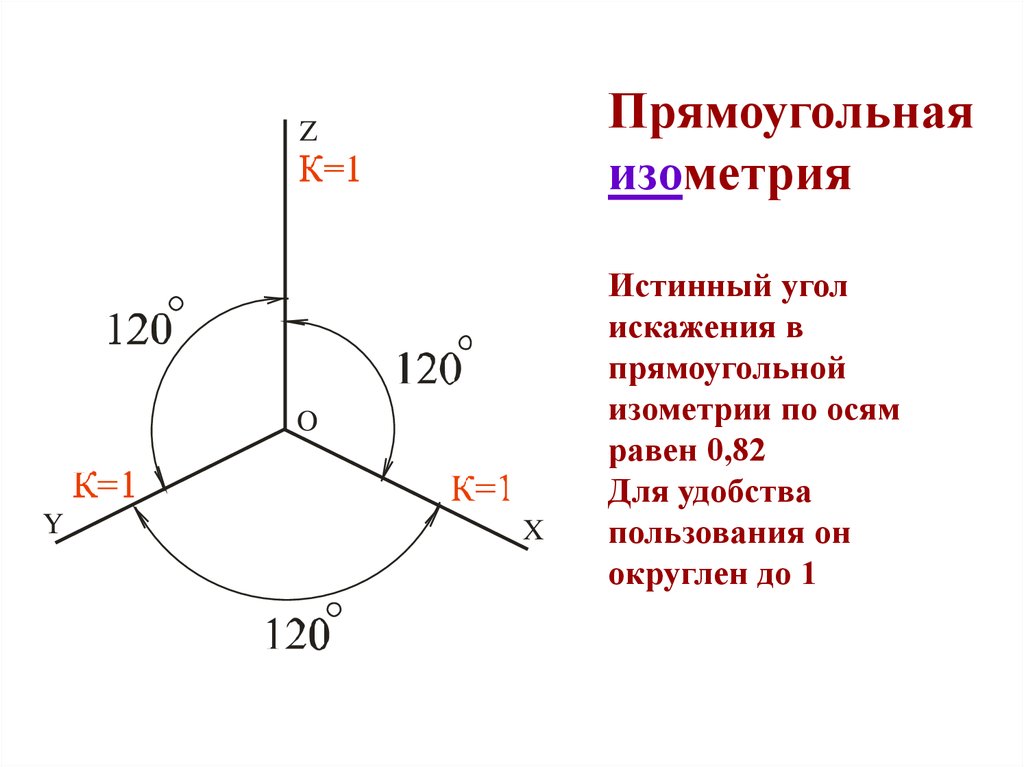 (В проекции Multiview они могут называться вспомогательных видов и основных видов соответственно.) Как ни странно, временной период «ортогональная проекция» также обычно может быть зарезервирован только для первых видов.

Архитектура аксонометрического чертежа

Содержание

• 0.1 В чем разница между изометрической и аксонометрической архитектурой чертежа?
• 0.2 Что такое изометрия в архитектуре?
• 0.3 Является изометрическим и аксонометрическим?
• 0.4 Как сделать аксонометрию в AutoCAD?
• 1 Часто задаваемые вопросы
  • 1.1 Под каким углом выполняется аксонометрический чертеж?
  • 1.2 Какие существуют 2 типа непрямого вытягивания?
  • 1.3 Какие существуют три формы перспективного рисунка?
  • 1.4 Связанные

В чем разница между изометрической и аксонометрической архитектурой чертежа?

Тремя формами аксонометрических  проекций являются изометрическая  проекция, диметрическая проекция и триметрическая проекция.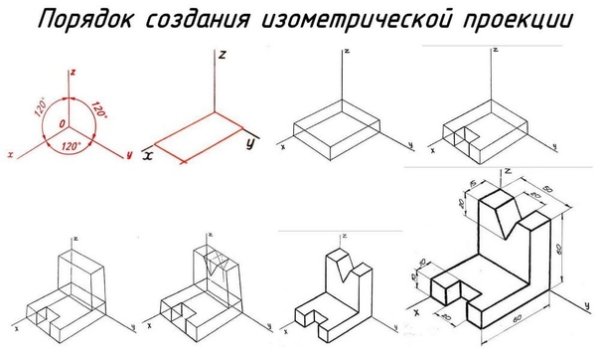 Иногда в аксонометрический чертеж , одна ось дома доказана, потому что вертикальная.

Что такое изометрия в архитектуре?

Архитектура аксонометрического чертежа

Изометрическая проекция — это метод визуального представления трехмерных объектов в двух измерениях на технических и инженерных чертежах. Это аксонометрическая проекция, в которой три оси координат кажутся одинаково укороченными, а угол между любыми двумя из них составляет 120 градусов.

Изометрический и аксонометрический?

Изометрический  рисунок – это форма 3D-чертежа, в которой почти не используются углы в 30 градусов. Это своего рода аксонометрический рисунок, поэтому для каждой оси используется одинаковый масштаб, что приводит к неискаженному изображению.

Как сделать аксонометрию в AutoCAD?