Подготовка к олимпиаде. Методы расчета резисторных схем постоянного тока. 3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
Методы расчета резисторных схем постоянного тока
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.
Подобные преобразования широко известны для случая двух выводов.
Так, например, два резистора сопротивлениями R1 и R2, включенные последовательно, можно заменить одним резистором сопротивлением R1 + R2. Если резисторы включены параллельно, то их можно заменить одним резистором сопротивлением
$\frac{R_1R_2}{R_1 + R_2}$
И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения. Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (рис. а) в «треугольник» (рис. б), и наоборот.
Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r1 соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R13 подключен к точкам 1 и 3. Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек).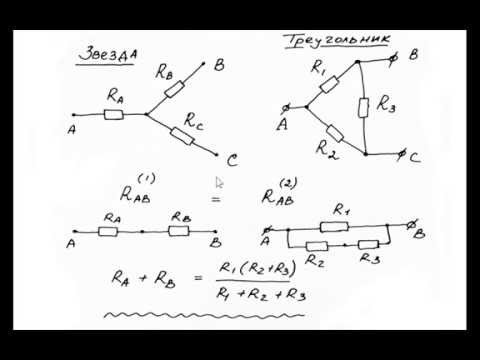
Так, в «звезде» сопротивление между точками 1 и 2 равно r1 + r2, в «треугольнике»
$\frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$,
следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:
$r_1 + r_2 = \frac{R_{12}(R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}$.
Аналогично для точек 2 и 3 и для точек 1 и 3:
$r_2 + r_3 = \frac{R_{23}(R_{12} + R_{13})}{R_{12} + R_{13} + R_{23}}$,
$r_1 + r_3 = \frac{R_{13}(R_{12} + R_{23})}{R_{12} + R_{13} + R_{23}}$.
Сложим все эти уравнения и, поделив обе части на 2, получим:
$r_1 + r_2 + r_3 = \frac{R_{12}R_{13} + R_{12}R_{23} + R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.
Вычитая из этого уравнения поочередно предыдущие, получим:
$r_1 = \frac{R_{12}R_{13}}{R_{12} + R_{13} + R_{23}}$,
$r_2 = \frac{R_{12}R_{23}}{R_{12} + R_{13} + R_{23}}$,
$r_3 = \frac{R_{13}R_{23}}{R_{12} + R_{13} + R_{23}}$.
Эти выражения легко запомнить:
знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:
$r_1 \rightarrow R_{12}R_{13}, r_2 \rightarrow R_{12}R_{23}, r_3 \rightarrow R_{13}R_{23}$.
Аналогично получают и формулы обратного преобразования:
$R_{12} = \frac{r_1r_2 + r_1r_3 + r_2r_3}{r_3}$,
$R_{13} = \frac{r_1r_2 + r_1r_3 + r_2r_3}{r_2}$,
$R_{23} = \frac{r_1r_2 + r_1r_3 + r_2r_3}{r_1}$.
Последние выражения также легко запомнить и проверить:
числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.
Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.
Задача 27. Определите сопротивление цепи АВ (рис.), если R1 = R5 = 1 Ом, R2 = R6 = 2 Ом, R3 = R7 = 3 Ом, R4 = R8 = 4 Ом.
Решение. Преобразуем «треугольники» R1R2R8 и R4R5R6 в эквивалентные «звезды». Схема примет иной вид (рис.).
Сопротивления $r_1, r_2, …, r_6$ найдем по формулам:
$r_1 = \frac{R_1R_8}{R_1 + R_2 + R_8} = \frac{4}{7}$ Ом;
$r_2 = \frac{R_1R_2}{R_1 + R_2 + R_8} = \frac{2}{7}$ Ом;
$r_3 = \frac{R_2R_8}{R_1 + R_2 + R_8} = \frac{8}{7}$ Ом;
$r_4 = \frac{R_4R_6}{R_4 + R_5 + R_6} = \frac{8}{7}$ Ом;
$r_5 = \frac{R_5R_6}{R_4 + R_5 + R_6} = \frac{2}{7}$ Ом;
$r_6 = \frac{R_4R_5}{R_4 + R_5 + R_6} = \frac{4}{7}$ Ом.
Теперь нет никаких препятствий для расчета схемы, которая состоит из последовательно и параллельно соединенных резисторов (рис.). После простых расчетов получим
$R_{AB} = \frac{47}{14}$ Ом
1.1. Шаговый (рекуррентный) метод
1.2. Метод преобразования
1.3. Метод равнопотенциальных узлов
1.3.1.
Метод исключения «пассивных» участков цепи
1.3.2. Метод объединения равнопотенциальных узлов
1.3.3. Метод разделения узлов
1.3.4. Метод расщепления ветвей
1.4.1 Расчет эквивалентных сопротивлений линейных бесконечных цепей
1.4.2. Расчет эквивалентных сопротивлений плоскостных бесконечных цепей
1.4.3. Расчет эквивалентных сопротивлений объемных бесконечных цепей
2. Расчет цепей по правилам Кирхгофа
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
треугольник – English translation
Sign in | English | Terms of Use
Russian ⇄ AbkhazAfrikaansArabicAzerbaijaniBashkirChineseDutchEnglishEsperantoEstonianFinnishFrenchGeorgianGermanGreekHebrewItalianJapaneseKalmykLatinLatvianNorwegian BokmålPolishPortugueseRussianSpanishSwedishTajikUkrainianVietnameseGoogle | Forvo | +
to phrases
| треугольник n | |
gen. |
triangle; triangular ruler |
| chess.term. | triangulation |
| cook. | turnover (со сладкой или солёной начинкой Kate1411) |
| el., Makarov. | delta network |
| Gruzovik, inf. | triumvir (= factory director, secretary of the party, and trade-union representative) |
| IT | twistie (треугольник, показывающий, что под этой строкой ещё что-то есть. Щелчок по треугольнику вызывает свертывание – развертывание следующего уровня иерархии Georgy Moiseenko) |
| math. | two-dimensional simplex |
| med. | trigone |
| mus., inf. | triumvir (= factory director, secretary of ike party, and trade-union representative) |
| oil | trigon |
| phys. | delta circuit; triangular; trigonometric |
| sport. | triangle choke (яп. sankaku-jime. Удушающий захват в борьбе. r313) |
| tech. | delta |
| theatre., mus. | triangle (ударный инструмент) |
| «треугольник» n | |
| prof.jarg., Makarov. | triangle (передняя четвертина говяжьей туши без спинной части) |
| любовный треугольник n | |
| gen. | eternal triangle |
| треугольники n | |
| gen. | triangles |
| Russian thesaurus | |
| треугольник n | |
| gen. | самозвучащий музыкальный инструмент — стальной прут, согнутый в виде треугольника, по которому ударяют палочкой. Применяется в оркестрах и инструментальных ансамблях. Большой Энциклопедический словарь ; созвездие Северного полушария; с территории России лучше всего видно в конце лета, осенью и зимой. |
| треугольник: 1185 phrases in 121 subjects |
| Advertising | 1 |
| Aerohydrodynamics | 3 |
| Agriculture | 3 |
| Agrochemistry | 4 |
| Air defense | 1 |
| Anatomy | 40 |
| Anti-air artillery | 1 |
| Architecture | 11 |
| Armored vehicles | 3 |
| Artillery | 6 |
| Astronautics | 8 |
| Astronomy | 23 |
| Australian | 2 |
| Automated equipment | 22 |
| Automobiles | 4 |
| Aviation | 7 |
| Billiards | 2 |
| Biology | 1 |
| Biotechnology | 1 |
| Cables and cable production | 3 |
| Cardiology | 11 |
| Cartography | 35 |
| Chemistry | 2 |
| Chess | 6 |
| Combustion gas turbines | 1 |
| Computers | 2 |
| Construction | 14 |
| Cooking | 1 |
| 1 | |
| Cycling other than sport | 8 |
| Dentistry | 5 |
| Drilling | 1 |
| Drug-related slang | 1 |
| Electrical engineering | 76 |
| Electricity | 1 |
| Electronics | 85 |
| Energy system | 6 |
| Engineering geology | 1 |
| European Union | 1 |
| Finances | 1 |
| Firefighting and fire-control systems | 1 |
| Food industry | 4 |
| Football | 1 |
| General | 48 |
| Geography | 1 |
| Geology | 1 |
| Geometry | 6 |
| Geomorphology | 1 |
| Geophysics | 2 |
| Gold mining | 1 |
| Gyroscopes | 1 |
| Heat exchangers | 1 |
| Heraldry | 2 |
| Hydrobiology | 2 |
| Ice hockey | 1 |
| Informal | 1 |
| Information technology | 5 |
| Insurance | 2 |
| Jargon | 1 |
| Jewelry | 1 |
| Lasers | 2 |
| Latin | 1 |
| Leather | 1 |
| Librarianship | 2 |
| Linguistics | 7 |
| Makarov | 55 |
| Management | 1 |
| Mathematics | 207 |
| Mechanic engineering | 6 |
| Mechanics | 2 |
| Medical | 72 |
| Metallurgy | 4 |
| Metrology | 2 |
| Microsoft | 1 |
| Military | 11 |
| Mining | 2 |
| Music | 1 |
| Nautical | 14 |
| Navigation | 35 |
| Oil / petroleum | 6 |
| Ophthalmology | 2 |
| Optics branch of physics | 1 |
| Pharmacy and pharmacology | 1 |
| Physics | 10 |
| Polygraphy | 1 |
| Power system protection | 3 |
| Professional jargon | 1 |
| Programming | 7 |
| Project management | 2 |
| Psychology | 3 |
| Psychotherapy | 1 |
| Pulp and paper industry | 1 |
| Rail transport | 16 |
| Refrigeration | 2 |
| Road construction | 3 |
| Road traffic | 3 |
| Road works | 5 |
| Robotics | 1 |
| Sakhalin | 2 |
| School | 1 |
| Shipbuilding | 3 |
| Slang | 1 |
| Sociology | 1 |
| Solar power | 1 |
| Sports | 5 |
| Stock Exchange | 5 |
| Surgery | 1 |
| Surveying | 4 |
| Technology | 149 |
| Telecommunications | 5 |
| Television | 2 |
| Tengiz | 1 |
| Textile industry | 1 |
| Theatre | 1 |
| Thermal engineering | 4 |
| Topology | 4 |
| Transport | 4 |
| United Nations | 2 |
| Weapons and gunsmithing | 1 |
| Wood processing | 2 |
| Yachting | 2 |
Add | Report an error | Get short URL | Language Selection Tips
Ночное небо в переходе: от лета к осени
На этой карте неба показано расположение ярких звезд Веги, Альтаира и Денеба на востоке ночного неба летом 2012 года.
Звезды образуют Летний треугольник, видимый на ночном небе Северного полушария.
(Изображение предоставлено: Starry Night Software)Осенние созвездия ночного неба следуют за летними звездами так близко, что их можно увидеть задолго до того, как воздух станет холодным. По мере того, как мы приближаемся к последним дням перед официальным приходом осени в Северном полушарии 22 сентября, наблюдатели за небом теперь могут увидеть переходное небо.
Многие яркие звездные группы и богатые поля Млечного Пути летним вечером все еще остаются с нами в западной части неба, а яркая звезда Капелла, восходящая над северо-восточным горизонтом, обещает появление новых светил. Действительно, еще через шесть-восемь недель Орион и его соседи будут доминировать на вечернем небе, напоминая нам о приближающемся зимнем сезоне.
По-прежнему очень удачно расположен «Летний треугольник», примерно равнобедренная фигура, состоящая из трех звезд первой величины: Веги, Альтаира и Денеба.
Кто-то может задаться вопросом, почему мы называем его Летним Треугольником, поскольку он находится почти над головой в поздние вечерние часы, когда лето переходит в осень.
В середине и позднем вечере звезды осеннего сезона покрывают большую часть восточного и южного неба. Вся эта область была названа «Небесным морем», потому что многие созвездия ассоциируются с водой.
Например, если посмотреть на юго-юго-восток, можно увидеть одного члена этого водного братства, единственного, чье имя связано с популярной песней: «Водолей». И все же, многие ли из тех, кто слышал эту песню, знают, что такое Водолей на самом деле?
Этот зодиакальный узор со звездами традиционно изображает мужчину, держащего кувшин с водой (отмеченный перевернутой Y-образной группой из четырех звезд), из которого нечетко обозначенный поток воды проливается на юг в устье Piscis Austrinus, Южной Рыбы.
На юге Канады, на севере США и большей части Европы звезды, составляющие это созвездие, обычно не видны.
Хотя они и находятся над горизонтом, они слишком низки, чтобы проникнуть сквозь дымку горизонта. В более южных широтах эти звезды находятся намного выше в небе, хотя и довольно тусклые.
Главная звезда созвездия гораздо заметнее: серебристо-белый Фомальгаут, 18-я по яркости звезда на небе и единственная звезда первой величины во всей коллекции водянистых созвездий. Действительно, Фомальгаут — единственная настоящая осенняя звезда первой величины. (Величина — это мера яркости, при этом меньшие величины обозначают объекты, которые кажутся более яркими на небе.
Для сравнения, полная луна имеет звездную величину около минус 13.)
Фомальгаут находится в пустой области осеннего неба, и его иногда называют «одиноким». Его можно определить, протянув линию вдоль западной (правой) стороны Большой площади Пегаса примерно в три раза больше ее собственной длины.
Фомальгаут часто описывается в книгах по наблюдениям как «красноватая», хотя вполне вероятно, что это впечатление вызвано влиянием нашей атмосферы, поскольку северные наблюдатели всегда видят эту звезду на низкой высоте.
Фомальгаут в переводе с арабского означает «рот рыбы». Эта звезда, которая находится примерно в 25 световых годах от нас, примерно в два раза шире нашего Солнца и в 19 раз ярче.
В своей книге «Дружелюбные звезды» Марта Эванс Мартин писала: «Одиночество этой звезды в сочетании с мрачными приметами приближающейся осени иногда навевает нотку меланхолии. В ноябре и декабре, когда на нас обрушится зимняя тишина, взгляд на юго-запад обнаружит Фомальгаут, все еще безмятежного и одинокого».
0003
И вторя тому, что написал Мартин, могу только добавить, что это время года, когда дни становятся короче, а лица длиннее.
Джо Рао работает инструктором и приглашенным лектором в планетарии Хейдена в Нью-Йорке. Он пишет об астрономии для The New York Times и других изданий, а также работает метеорологом на камеру для News 12 Westchester, Нью-Йорк.
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: [email protected].
Джо Рао — обозреватель Space.com, наблюдающий за небом, а также опытный метеоролог и охотник за затмениями, который также работает инструктором и приглашенным лектором в планетарии Хейдена в Нью-Йорке. Он пишет об астрономии для журнала «Естественная история», «Фермерского альманаха» и других изданий. Джо — восьмикратный номинант на премию «Эмми» метеоролог, работавший в районе Патнэм-Вэлли в Нью-Йорке более 21 года.