Какой емкости конденсатор нужно включить: Какой емкости конденсатор нужно включить в колебательный контур с катушкой индуктивности 0.76 Гн, чтобы получить…

Какой конденсатор нужен для двигателя от стиральной машины?

Прекрасно, когда есть возможность подключить мотор к нужному типу напряжения. Но иногда возникает ситуация, что трехфазный мотор приходится «питать» от однофазной сети. Например, если умельцы берут движок от стиралки и создают на его основе токарный станок или другую «самоделку». В таких случаях придется использовать конденсатор для двигателя от стиральной машины. Но их целое множество, поэтому не лишним будет разобраться, как правильно подобрать устройство.

Если нужно запустить трехфазный мотор

Подобрать конденсатор для двигателя от стиральной машины непросто. Самое главное – правильно определить емкость устройства. Но как ее посчитать? Для более точного вычисления показателя применяется сложная формула, но можно воспользоваться и более упрощенным вариантом.

Как быстро прикинуть, какое устройство подойдет в вашем случае? Для расчета конденсаторной емкости упрощенным методом необходимо узнать мощность движка и на каждые 100 Ватт «набросить» примерно 7-8 мкФ. Однако важно не забыть во время вычислений учесть показатель напряжения, воздействующий на статорную обмотку. Это значение не должно превышать номинальный уровень.

Когда запуск электромотора может осуществляться только на основе максимальной загрузки, нужно включить в цепь пусковой конденсатор. Данное устройство характеризуется кратковременным периодом работы – оно функционирует около 3 секунд, до тех пор, пока обороты ротора не достигнут своего пика.

При выборе пускового конденсатора необходимо учитывать, что:

• по емкости он должен в 2-3 раза превышать показатели рабочего конденсатора;
• его номинальное напряжение должно превышать сетевой минимум в 1,5 раза.

Главная функция пускового конденсатора – довести ротор электромотора до оптимальной частоты вращения.

Разобравшись в нюансах, можно подбирать и сетевой, и пусковой конденсатор для трехфазного электромотора. Чтобы не ошибиться, важно следовать всем рекомендациям.

Подбираем конденсатор для однофазного мотора

В подавляющем большинстве случаев конденсаторы для асинхронных движков применяются для подключения к «стандартному» напряжению (220 В) с учетом включения устройства в однофазную сеть. Однако процесс их применения гораздо сложнее. Разберемся, почему.

Трехфазные моторы функционируют на основе конструктивного подключения, в то время как для однофазных движков приходится достигать смещенного вращательного момента. Обеспечивается это дополнительным слоем роторной обмотки для запуска. Фаза сдвигается конденсатором.

Почему непросто подобрать конденсатор?

Хотя существенных отличий нет, но разные конденсаторы для асинхронных движков требуют отличные друг от друга способы вычисления допустимого показателя напряжения. Обычно необходимо примерно 100 Ватт на 1 мкФ емкости прибора. У таких моторов существуют несколько возможных режимов работы:

• ставится пусковой конденсатор, организуется вспомогательный слой обмотки (именно для этапа пуска). 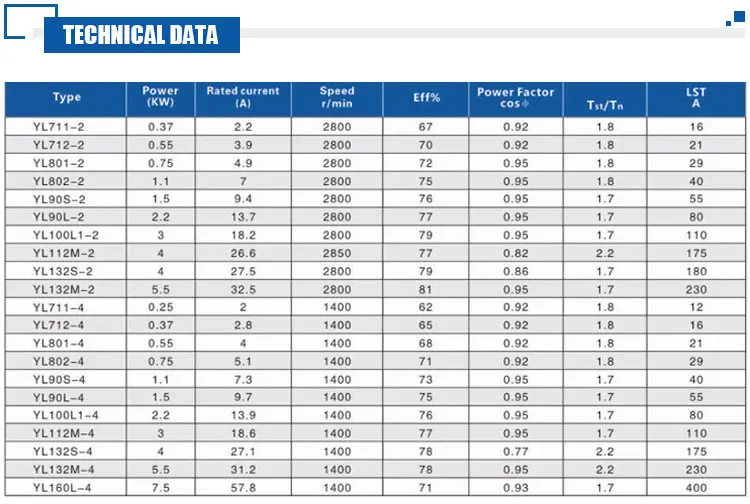В данной ситуации расчет емкости устройства будет таковым – 70 мкФ на киловатт мощности электродвигателя;
• устанавливается рабочее устройство, конденсаторная емкость которого в пределах 25-35 мкФ. В этом случае будет нужна дополнительная обмотка и постоянное подключение конденсатора на протяжении всего срока работы мотора;
• используется сетевой конденсатор при одновременном подключении пускового устройства.

В любом случае важно отслеживать уровень нагрева электромотора в ходе его эксплуатации. Заметив перегревание элементов двигателя, следует принять срочные меры. Если стоит рабочий конденсатор, потребуется уменьшить его емкость. Специалисты рекомендуют применять устройства, функционирующие на основе мощности от 450 Ватт или больше, так как они считаются универсальными.

Еще до установки рекомендуется проверить работоспособность конденсатора специальным прибором – мультиметром.

Пусковой конденсатор – это маленький элемент электрической цепи, необходимый для того, чтобы движок как можно скорее «набрал» нужные обороты.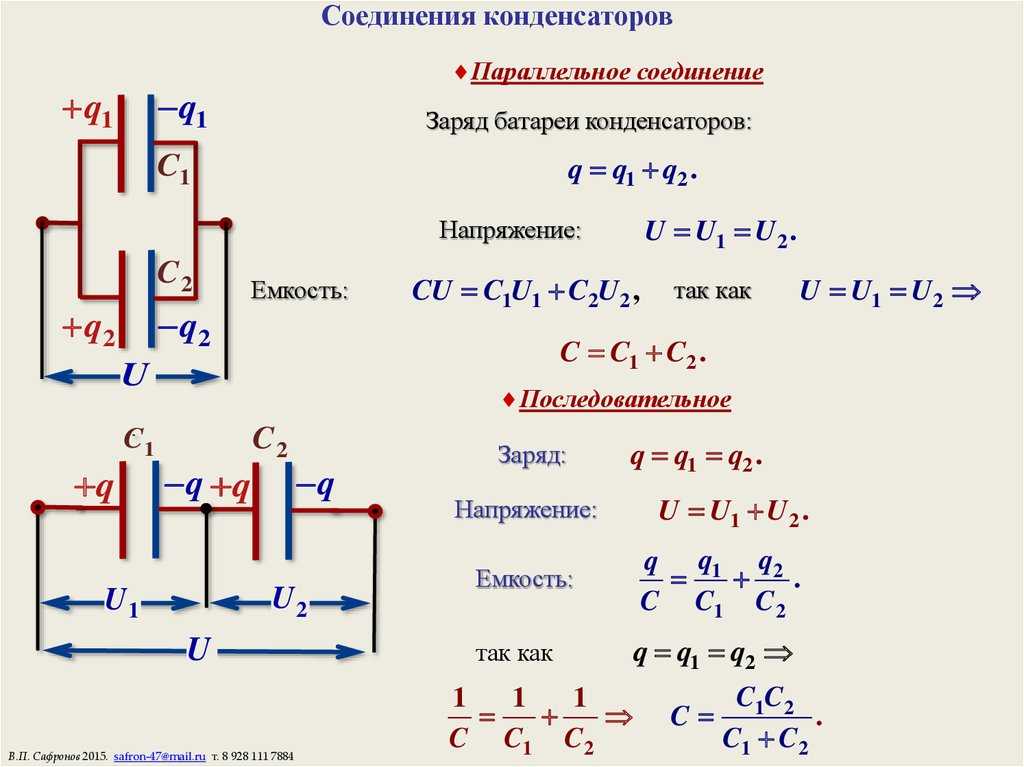 Рабочее устройство служит для поддержания оптимальной нагрузки на мотор.

Сконструировать полностью работоспособную схему можно самостоятельно. Между электромотором и кнопкой ПНВС нужно поставить рабочий, а, при необходимости, еще и пусковой конденсатор. Обычно выводы обмоток расположены в клеммной части движка, поэтому модернизация подключения может быть любой.

Следует помнить, что рабочее напряжение пускового конденсатора должно составлять 330-400 Вольт. Это объясняется «всплеском» мощности при запуске или завершении работы мотора.

Так в чем же отличие однофазного асинхронного мотора? Такой тип двигателя чаще встречается в бытовой технике, для его активации необходима вспомогательная пусковая обмотка и конденсатор для смещения фазы. Подключить его допускается на основе множества доступных схем. В продаже встречаются конденсаторы трех видов:

• полярные;
• неполярные;
• электролитические.

Полярные запрещено применять для подключения электромоторов в сеть переменного тока. Диэлектрик внутри устройства быстро разрушится и произойдет замыкание.

Поэтому в данном случае нужно использовать неполярные конденсаторы. Их обкладки будут одинаково взаимодействовать и с источником тока, и с диэлектриком.

   

• Поделитесь своим мнением — оставьте комментарий

Гасящий конденсатор вместо гасящего резистора

Иногда возникает задача понизить переменное напряжение сети 220 вольт до некоторого заданного значения, причем применение понижающего трансформатора (в таком случае) не всегда бывает целесообразным. Скажем, низкочастотный понижающий трансформатор, выполненный традиционно на трансформаторном железе, способный преобразовать мощность 200 Ватт, весит больше килограмма, не говоря о высокой стоимости. Следовательно в некоторых случаях можно применить гасящий резистор, который ограничит ток, однако при этом на самом гасящем резисторе выделится мощность в виде тепла, а это не всегда является приемлемым. Например, если нужно запитать 200 Ваттную лампу только на половину ее наминала, потребовалось бы рассеять мощность в 100 Ватт на гасящем резисторе, а это крайне сомнительное решение. Весьма удобной альтернативой, для данного примера, может служить применение гасящего конденсатора, емкостью около14мкф, (такой можно собрать из трех металлопленочных типа К73-17 по 4,7мкф, рассчитанных на 250в, а лучше – на 400в) это позволит получить нужный ток без необходимости рассеивать значительную мощность в виде тепла. Рассмотрим физическую сторону этого решения. Как известно, конденсатор, включенный в цепь переменного тока, является реактивным элементом, обладающим емкостным сопротивлением, связанным с частотой переменного тока в цепи, а также с собственной емкостью. Чем больше емкость конденсатора и чем выше частота переменного напряжения в цепи, тем больший ток проходит через конденсатор, значит емкостное сопротивление конденсатора обратно пропорционально его емкости, а также частоте переменного тока, в цепи, куда он включен. Это видно и из формулы для емкостного сопротивления конденсатора: Если в цепь переменного тока включены последовательно резистор (активная нагрузка) и конденсатор, то их общее сопротивление можно найти по формуле: А поскольку и то Итак, зная напряжение на нагрузке, силу тока нагрузки и напряжение на гасящем конденсаторе, можно определить емкость гасящего конденсатора, который нужно включить последовательно нагрузке для получения требуемых параметров питания: Рассмотрим пример: требуется запитать лампу накаливания мощностью 100 Ватт, рассчитанную на напряжение 110 вольт от розетки 220 вольт. В первую очередь найдем значение рабочего тока лампы: Получим значение тока лампы равное 0,91 А. Теперь можно найти требуемое значение емкости гасящего конденсатора, она будет равна 15,2 мкФ. Следует отметить, что этот расчет верен для чисто активной нагрузки, когда имеет место эффективное значение. При использовании же выпрямителя, необходимо учесть, что эффективное значение тока будет немного меньше в силу действия пульсаций. Также следует помнить, что в качестве гасящих конденсаторов, полярные конденсаторы применять ни в коем случае нельзя. Конденсаторы в Hi End аппаратуре | звук и ценообразование Бумажные и плёночные конденсаторы для High End звука Электролитические конденсаторы в усилителях мощности Устройство электролитического конденсатора «НЕТ» электролитическим конденсаторам в Hi-End Audio Резисторы | сопротивление | влияние на звук

Лучшее сочетание вакуумных и          полупроводниковых характеристик — однотактный гибридный усилитель звука.           Мы не создаём иллюзий,           Мы делаем звук живым!

Наверх

мощность — Развязывающие конденсаторы: какой размер и сколько?

Конденсаторы из X7R (и уж тем более Y5V) имеют огромную зависимость ёмкость/напряжение. Вы можете сами убедиться в этом в отличном онлайн-браузере характеристик продуктов Murata (Simsurfing) по адресу ttp://ds.murata.co.jp/software/simsurfing/en-us/

Зависимость напряжения керамического конденсатора поразительна. Для конденсатора X7R нормально иметь не более 30% номинальной емкости при номинальном напряжении. Например, конденсатор Murata 10 мкФ GRM21BR61C106KE15 (упаковка 0805, X5R), рассчитанный на 16 В, даст вам емкость всего 2,3 мкФ при 12 В постоянного тока при температуре 25 ° C. Y5V в этом отношении намного хуже.

Чтобы получить емкость, близкую к 10 мкФ, вы должны использовать GRM32DR71E106K с номиналом 25 В (корпус 1210, X7R), который дает 7,5 мкФ при тех же условиях.

Отличие от постоянного напряжения (и температуры). Настоящие «керамические микросхемы-конденсаторы» сильно зависят от частоты, когда действуют как шунты развязки по мощности. На сайте Murata представлены графики частотных зависимостей |Z|, R и X для их конденсаторов, просмотр которых дает вам представление о фактической производительности части, которую мы называем «конденсатором», на разных частотах.

Реальный керамический конденсатор можно смоделировать идеальным конденсатором (C), соединенным последовательно с внутренним сопротивлением (Resr) и индуктивностью (Lesl). Существует также R-изоляция параллельно C, но если вы не превышаете номинальное напряжение конденсатора, это не имеет значения для приложений с развязкой по мощности.

^{смоделируйте эту схему – Схема создана с помощью CircuitLab}

Таким образом, чиповые керамические конденсаторы будут действовать как конденсаторы только до определенной частоты (собственно резонансной для последовательного LC-контура, которой фактически является реальный конденсатор), выше которой они начинают действовать как индукторы. Эта частота Fres равна sqrt(1/LC) и определяется как составом керамики, так и геометрией конденсатора — как правило, меньшие корпуса имеют более высокое значение Fres. и определяет минимальное полное сопротивление, которое может обеспечить конденсатор. Обычно оно находится в диапазоне миллиом.

На практике для хорошей развязки я использую 3 типа конденсаторов.

Более высокая емкость около 10 мкФ в корпусе 1210 или 1208 на интегральную схему, охватывающая диапазон от 10 кГц до 10 МГц с шунтом менее 10-15 мОм для шума линии электропередачи.

Затем на каждый вывод питания микросхемы я поставил два конденсатора: один 100 нФ в корпусе 0806, покрывающий от 1 МГц до 40 МГц с шунтом 20 мОм, и один 1 нФ в корпусе 0603, покрывающий от 80 МГц до 400 МГц с шунтом 30 мОм. Это более или менее охватывает диапазон от 10 кГц до 400 МГц для фильтрации шума линии электропередач.

Для чувствительных силовых цепей (таких как цифровая PLL и особенно аналоговая мощность) я поставил ферритовые кольца (опять же, у Murata есть браузер характеристик для них) с номиналом от 100 до 300 Ом на частоте 100 МГц.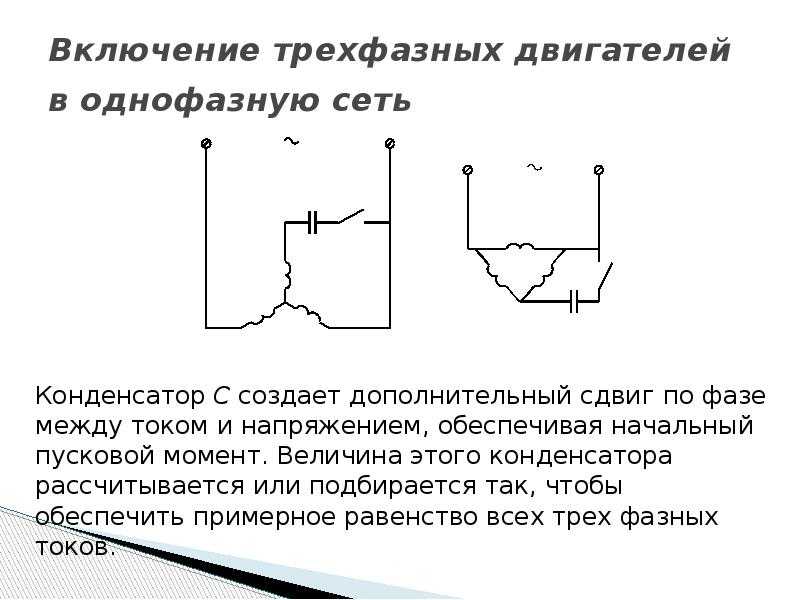 Также рекомендуется разделить заземление между чувствительными и обычными силовыми цепями. Таким образом, общая схема схемы питания ИС выглядит следующим образом, с 10 мкФ C6 на корпус ИС и 1 нФ/100 нФ C4/C5 на каждый вывод питания:

^{имитация этой схемы сначала направляется на конденсаторы, только на конденсаторах мы подключаемся к силовым и заземляющим слоям через переходные отверстия. Конденсаторы емкостью 1 нФ расположены ближе к выводам микросхемы. Конденсаторы должны быть размещены как можно ближе к выводам питания, не более 1 мм длины дорожки от площадки конденсатора до площадки микросхемы.}

Переходные отверстия и даже короткие дорожки на печатной плате создают значительную индуктивность для частот и емкости, с которыми мы имеем дело. Например, переходное отверстие диаметром 0,5 мм на печатной плате толщиной 1,5 мм имеет индуктивность 1,1 нГн от верхнего до нижнего слоя. Для конденсатора 1 нФ это приводит к частоте, равной всего 15 МГц. Таким образом, подключение конденсатора через переходное отверстие делает конденсатор емкостью 1 нФ с низким Resr непригодным для использования на частотах выше 15 МГц. На самом деле реактивное сопротивление 1,1 нГн на частоте 100 МГц равно 0,7 Ом.

След длиной 1 мм шириной 0,2 мм, на 0,35 мм выше силовой плоскости будет иметь индуктивность, сравнимую с 0,4 нГн, что снова делает конденсаторы менее эффективными, поэтому мы пытаемся ограничить длину дорожек конденсаторов долей миллиметра и сделать их максимально широкими имеет большой смысл.

8.1 Конденсаторы и емкости — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните понятия конденсатора и его емкости
• Опишите, как оценить емкость системы проводников

Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии. Конденсаторы обычно имеют два электрических проводника, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но правильнее было бы назвать их «пластинами конденсатора».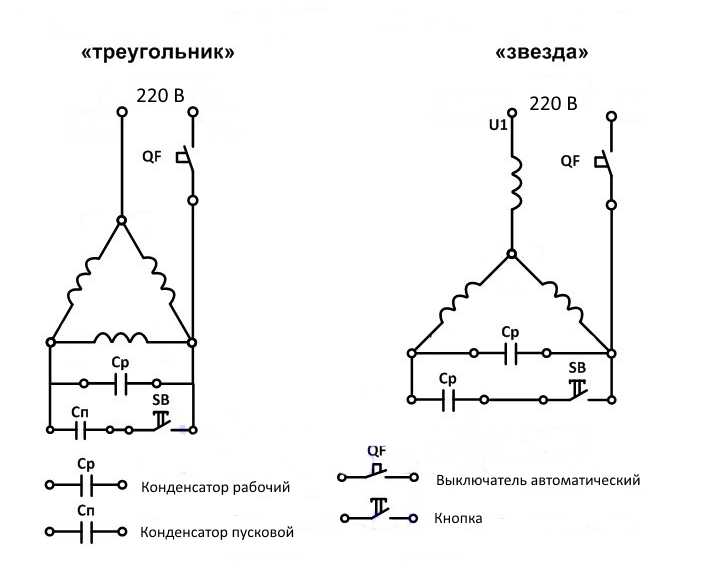

) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор называется «вакуумный конденсатор». Однако это пространство обычно заполнено изоляционным материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем памяти в конденсаторе определяется свойством, называемым емкость , о которой вы узнаете подробнее чуть позже в этом разделе.

Применение конденсаторов варьируется от фильтрации статического электричества от радиоприема до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к изначально незаряженному конденсатору, потенциал батареи перемещает небольшое количество заряда величиной 9.0053 Q

с положительной пластины на отрицательную. Конденсатор в целом остается нейтральным, но с зарядами +Q+Q и -Q-Q, расположенными на противоположных пластинах.

Рисунок 8.2 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды +Q+Q и −Q−Q (соответственно). (a) Конденсатор с плоскими пластинами состоит из двух пластин противоположного заряда площадью A , разделенных расстоянием d . (b) Скрученный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).

Система, состоящая из двух одинаковых пластин с параллельными проводниками, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами равна E=σ/ε0E=σ/ε0, где σσ — поверхностная плотность заряда на одной пластине (напомним, что σσ — заряд Ом , приходящийся на площадь поверхности А). ). Таким образом, величина поля прямо пропорциональна Q .

Рисунок 8.3 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора. Линии электрического поля в конденсаторе с плоскими пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.

Конденсаторы с разными физическими характеристиками (такими как форма и размер их пластин) сохраняют разное количество заряда при одинаковом напряжении В , приложенном к их пластинам. Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В на его обкладках. Другими словами, емкость — это наибольшее количество заряда на вольт, которое может храниться на устройстве:

C=QV. C=QV.

8.1

Единицей измерения емкости в системе СИ является фарад (Ф), названный в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или

1F=1C1V.1F=1C1V.

По определению, конденсатор емкостью 1,0 Ф способен хранить 1,0 Кл заряда (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Таким образом, один фарад — это очень большая емкость. Типичные значения емкости находятся в диапазоне от пикофарад (1 пФ = 10–12 Ф) (1 пФ = 10–12 Ф) до миллифарад (1 мФ = 10–3 Ф) (1 мФ = 10–3 Ф), включая микрофарад (1 мкФ = 10–6 Ф1 мкФ = 10–10–3). 6F). Конденсаторы могут изготавливаться различных форм и размеров (рис. 8.4).

Рисунок 8.4 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно связан со значением его емкости. (кредит: Windell Oskay)

Расчет емкости

Мы можем рассчитать емкость пары проводников с помощью следующего стандартного подхода.

Стратегия решения проблем

Расчет емкости

1. Предположим, что конденсатор имеет заряд Q .
2. Определите электрическое поле E→E→ между проводниками. Если в расположении проводников присутствует симметрия, вы можете использовать закон Гаусса для этого расчета.
3. Найдите разность потенциалов между проводниками из

   VB-VA=-∫ABE→·dl→, VB-VA=-∫ABE→·dl→,

   8,2

   где путь интегрирования ведет от одного проводника к другому. Тогда величина разности потенциалов равна V=|VB-VA|V=|VB-VA|.
4. С В известно, получите емкость непосредственно из уравнения 8.1.

Чтобы показать, как работает эта процедура, мы теперь рассчитаем емкости пластинчатых, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.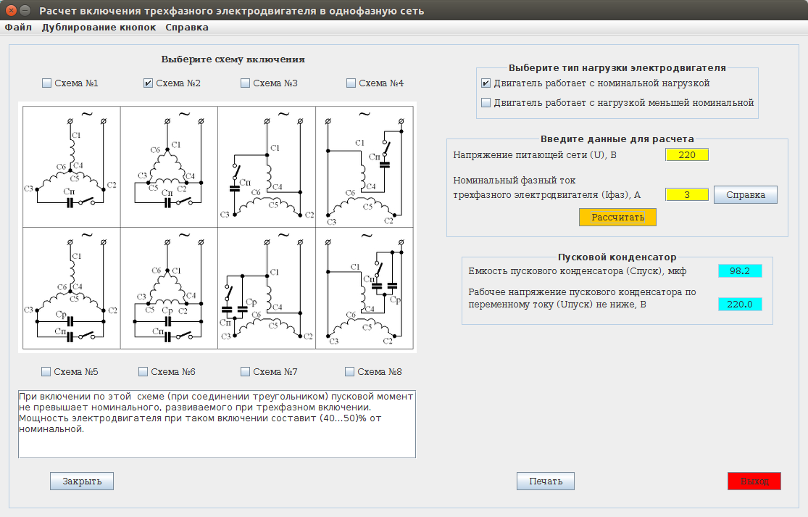

Конденсатор с параллельными пластинами

Конденсатор с плоскими пластинами (рис. 8.5) имеет две одинаковые проводящие пластины, каждая из которых имеет площадь поверхности А , разделенные расстоянием d . Когда к конденсатору прикладывается напряжение В , он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить. Таким образом, C должно быть больше для большего значения А . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Следовательно, C должно быть больше для меньшего d .

Рисунок 8,5 В конденсаторе с пластинами, расположенными на расстоянии d , каждая пластина имеет одинаковую площадь поверхности A .

Определим поверхностную плотность заряда σσ на пластинах как

σ=QA.σ=QA.

Мы знаем из предыдущих глав, что когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов), а его величина определяется выражением

E=σε0,E=σε0,

, где константа ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0=8,85×10−12F/м.ε0=8,85×10−12F/м. Единица СИ Ф/м эквивалентна C2/N·m2.C2/N·m2. Поскольку электрическое поле E→E→ между пластинами однородно, разность потенциалов между пластинами равна

.

V=Ed=σdε0=Qdε0A.V=Ed=σdε0=Qdε0A.

Следовательно, уравнение 8.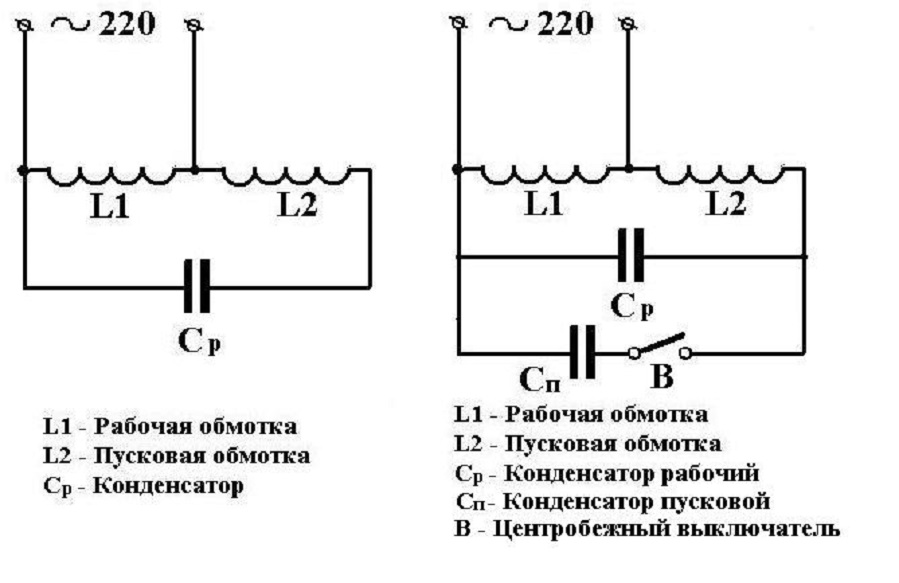 1 дает емкость плоского конденсатора как

C=QV=QQd/ε0A=ε0Ad.C=QV=QQd/ε0A=ε0Ad.

8.3

Обратите внимание, что из этого уравнения емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора. На самом деле это справедливо не только для плоского конденсатора, но и для всех конденсаторов: Емкость не зависит от Q или V . Если заряд меняется, соответственно изменяется и потенциал, так что Q / В остается постоянным.

Пример 8.1

Емкость и заряд, хранящиеся в конденсаторе с параллельными пластинами

а) Какова емкость пустого плоского конденсатора с металлическими пластинами площадью 1,00 м21,00 м2, разделенными расстоянием 1,00 мм? б) Сколько заряда накопится в этом конденсаторе, если к нему приложить напряжение 3,00×103 В3,00×103 В?

Стратегия

Нахождение емкости C является прямым применением уравнения 8. 3. Как только мы найдем C , мы можем найти накопленный заряд, используя уравнение 8.1.

Решение

1. Ввод данных значений в уравнение 8.3 дает

   C=ε0Ad=(8,85×10−12Fm)1,00m21,00×10−3m=8,85×10−9F=8,85nF.C=ε0Ad=(8,85×10−12Fm)1,00m21,00×10−3m= 8,85×10-9Ф=8,85нФ.

   Это маленькое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью.
2. Инвертирование уравнения 8.1 и ввод известных значений в это уравнение дает

   Q=CV=(8,85×10−9F)(3,00×103 В)=26,6 мкКл. Q=CV=(8,85×10-9F)(3,00×103 В)=26,6 мкКл.

Значение

Этот заряд лишь немного больше, чем в типичных приложениях статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3,0 МВ/м, на этом конденсаторе больше не может накапливаться заряд при увеличении напряжения.

Пример 8.

2

A 1-F Конденсатор с параллельными пластинами

Предположим, вы хотите построить конденсатор с плоскими пластинами емкостью 1,0 Ф. Какую площадь вы должны использовать для каждой пластины, если расстояние между пластинами составляет 1,0 мм?

Решение

Преобразуя уравнение 8.3, мы получаем

A=Cdε0=(1,0F)(1,0×10-3м)8,85×10-12F/м=1,1×108м2.A=Cdε0=(1,0F)(1,0×10-3м)8,85×10-12F/ м=1,1×108м2.

Каждая квадратная пластина должна иметь диаметр 10 км. Раньше было обычной шуткой просить студента пойти на склад лаборатории и попросить конденсатор с плоскими пластинами 1-Ф, пока обслуживающему персоналу не надоела эта шутка.

Проверьте свое понимание 8.1

Проверьте свое понимание Емкость плоского конденсатора 2,0 пФ. Если площадь каждой пластины 2,4 см22,4 см2, каково расстояние между пластинами?

Проверьте свое понимание 8.

2

Проверьте свое понимание Убедитесь, что σ/Vσ/V и ε0/dε0/d имеют одинаковые физические единицы.

Сферический конденсатор

Сферический конденсатор представляет собой еще один набор проводников, емкость которых можно легко определить (рис. 8.6). Он состоит из двух концентрических проводящих сферических оболочек радиусами R1R1 (внутренняя оболочка) и R2R2 (внешняя оболочка). Оболочки получают равные и противоположные заряды +Q+Q и −Q−Q соответственно. Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической поверхности Гаусса радиусом 9dr)=Q4πε0∫R1R2drr2=Q4πε0(1R1−1R2).

В этом уравнении разность потенциалов между пластинами равна V=-(V2-V1)=V1-V2V=-(V2-V1)=V1-V2. Подставим этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:

C=QV=4πε0R1R2R2−R1.C=QV=4πε0R1R2R2−R1.

8,4

Рисунок 8,6 Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды проводника находятся на его поверхности.

Пример 8.3

Емкость изолированной сферы

Рассчитайте емкость одиночной изолированной проводящей сферы радиусом R1R1 и сравните ее с уравнением 8.4 в пределе, когда R2→∞R2→∞.

Стратегия

Мы предполагаем, что заряд на сфере равен Q , и поэтому мы следуем четырем шагам, описанным ранее. Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.

Раствор

Снаружи изолированной проводящей сферы электрическое поле определяется уравнением 8.2. Величина разности потенциалов между поверхностью изолированной сферы и бесконечностью равна 9dr)=Q4πε0∫R1+∞drr2=14πε0QR1.

Таким образом, емкость изолированной сферы равна

C=QV=Q4πε0R1Q=4πε0R1.C=QV=Q4πε0R1Q=4πε0R1.

Значение

Тот же результат можно получить, взяв предел уравнения 8.4 при R2→∞R2→∞. Таким образом, отдельная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.

Проверьте свое понимание 8.3

Проверьте свое понимание Радиус внешней сферы сферического конденсатора в пять раз больше радиуса его внутренней оболочки. Каковы размеры этого конденсатора, если его емкость 5,00 пФ?

Цилиндрический конденсатор

Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рис. 8.7). Внутренний цилиндр радиусом R1R1 может быть как оболочкой, так и сплошным телом. Внешний цилиндр представляет собой оболочку с внутренним радиусом R2R2. Предположим, что длина каждого цилиндра равна l и что избыточные заряды +Q+Q и −Q−Q располагаются на внутреннем и внешнем цилиндрах соответственно.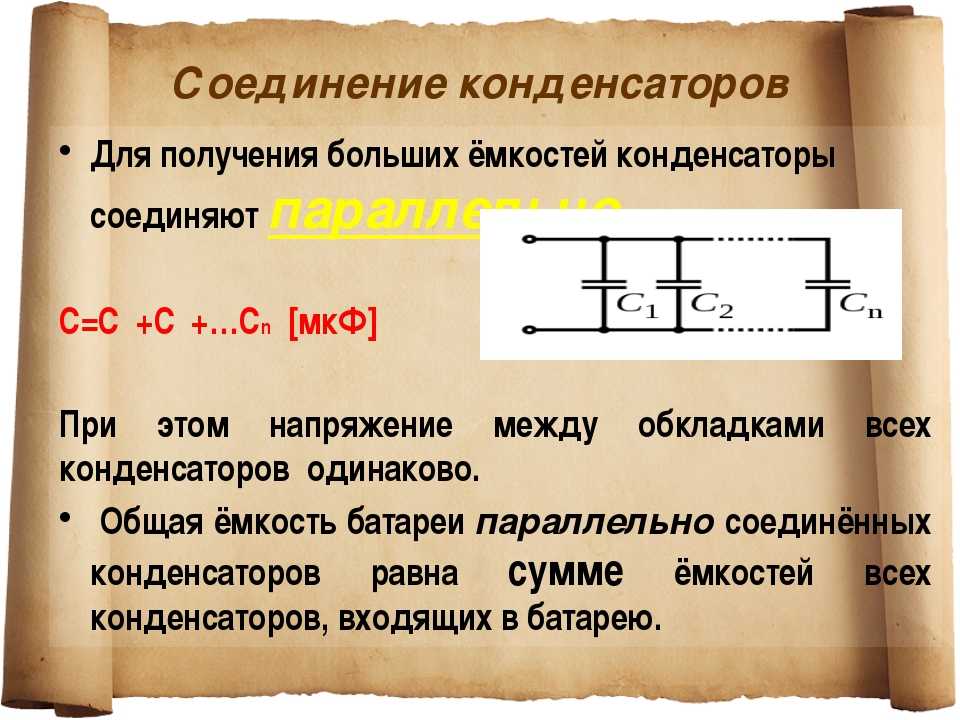

Рисунок 8,7 Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров. Здесь заряд на внешней поверхности внутреннего цилиндра положителен (обозначен ++), а заряд на внутренней поверхности внешнего цилиндра отрицателен (обозначен —). 9dr)=Q2πε0l∫R1R2drr=Q2πε0llnr|R1R2=Q2πε0llnR2R1.

Таким образом, емкость цилиндрического конденсатора равна

C=QV=2πε0lln(R2/R1).C=QV=2πε0lln(R2/R1).

8,6

Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом. (Здесь мы предполагаем вакуум между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком. ) Такая конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен. Теперь из уравнения 8.6 емкость на единицу длины коаксиального кабеля равна

Cl=2πε0ln(R2/R1).Cl=2πε0ln(R2/R1).

В практических приложениях важно выбрать конкретные значения C / l . Этого можно добиться соответствующим выбором радиусов проводников и изоляционного материала между ними.

Проверьте свое понимание 8.4

Проверьте свои знания Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Чему равна емкость этой системы? б) Чему равно отношение их радиусов, если длина цилиндров 1,0 м?

На рис. 8.4 показаны несколько типов практических конденсаторов. Обычные конденсаторы часто изготавливают из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. рис. 8.2(b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторыми распространенными изоляционными материалами являются слюда, керамика, бумага и антипригарное покрытие Teflon™.

Другим популярным типом конденсатора является электролитический конденсатор. Он состоит из окисленного металла в токопроводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость алюминиевого электролитического конденсатора одного типа может достигать 1,0 Ф. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое воздействие разрушает оксидную пленку. Конденсатор этого типа нельзя подключать к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет полярность (см. Цепи переменного тока в цепях переменного тока).

Переменный воздушный конденсатор (рис. 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначен как «ротор»). Поворачивая вал, можно изменить площадь поперечного сечения в области нахлеста пластин; следовательно, емкость этой системы может быть настроена на желаемое значение. Конденсаторная настройка находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильный радиоприемник на любимую станцию, подумайте о емкости.

Рисунок 8,8 В переменном воздушном конденсаторе емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спроула)

Символы, показанные на рис. 8.9, представляют собой схемы различных типов конденсаторов. Обычно мы используем символ, показанный на рис. 8.9(а). Символ на рис. 8.9(c) обозначает конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией плоского конденсатора. Электролитический конденсатор представлен символом в части рисунка 8.9.(б), где изогнутая пластина указывает на отрицательную клемму.

Рисунок 8,9 Это показывает три различных представления схемы конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет собой конденсатор переменной емкости.

Интересный прикладной пример модели конденсатора взят из клеточной биологии и касается электрического потенциала плазматической мембраны живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым избранным ионам проходить внутрь или наружу клетки.