- Расчёт угла наклона крыши
- Математика для блондинок: Простое построение углов
- как рассчитать минимальный угол наклона крыши, малоуклонная и наклонная конструкции
- Некоторые свойства прямоугольных треугольников
- Измерение углов. Транспортир | Математика
- Калькулятор прямоугольного треугольника
- Угол наклона крыши для металлочерепицы: как рассчитать оптимальный?
- Как рассчитать углы: 9 шагов (с изображениями)
- 30 60 90 Правые треугольники
- Специальные значения углов: 30-60-90 и 45-45-90 Треугольники
- Простое руководство к треугольнику 30-60-90
- Калькулятор угла и гипотенузы прямоугольного треугольника
- Треугольник 30 ° -60 ° -90 ° — объяснение и примеры
- Измерение углов
Расчёт угла наклона крыши
Поскольку от его величины зависит и количество кровельного материала, то выбор угла наклона и его предварительные расчеты производят до начала закупки выбранного кровельного материала.
Что на него влияет
В зависимости от величины уклона скатов крыши зависит особенность ее эксплуатации.
Принято выделять 4 типа крыш: высокие — с углом в 45–60 градусов; скатные — с наклоном от 30 до 45 градусов; пологие — с углом уклона 10–30 градусов; плоские — с углом 10 градусов и меньше.
На выбор величины этого параметра оказывают влияние, в первую очередь, природные факторы, которые характерны для данной местности.
Ветровая нагрузка
Сильный ветер самое большое давление оказывает на кровли высокие. Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы.
Нагрузка снеговая
Если в той местности, где строится дом, в холодное время года снегопад обильный, то следует строить кровлю с большим углом уклона. В этом случае высокая крыша вне конкуренции. На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах.
Выбираем уклон в зависимости от используемого кровельного материала
Прошли те времена, когда для покрытия использовали всего два вида кровельных материалов: черепицу и шифер. Каждый материал имеет свои индивидуальные технические характеристики и это при расчете необходимого значения угла наклона обязательно следует учитывать. Ведь может произойти так, что понравившийся вам материал по своим параметрам просто не подойдет.
Минимальный угол наклона
Существует понятие минимального значения этого параметра. Для каждого из материалов этот параметр свой. И если угол наклона, полученный в результате ваших расчетов, окажется меньше, чем минимальная величина для выбранного вами кровельного материала, то использовать его для устройства кровли нельзя.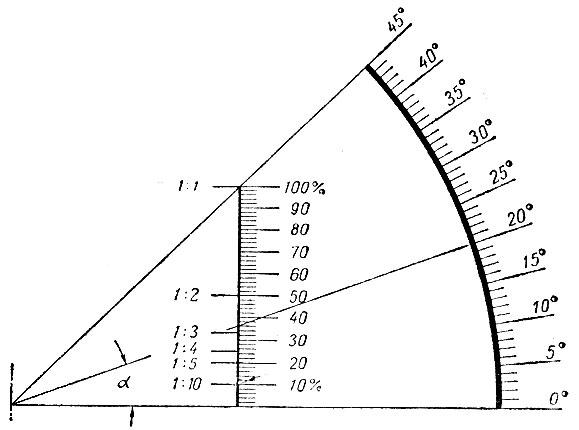
В дальнейшем может возникнуть очень много проблем, если нарушить это правило:
- для любых штучных наборных кровельных материалов, таких как черепица или шифер, минимальная величина уклона составляет 22 градуса. Именно при таком значении на стыках не скапливается влага и внутрь крыши влага не просачивается;
- угол наклона для рулонных материалов (рубероид, бикрост и пр.) зависит от того, какое вы планируете укладывать количество слоев. Если три слоя, то уклон может составлять 2–5 градусов. Если же два слоя, то его требуется увеличить до 15 градусов;
- производители профнастила рекомендуют при устройстве кровли из этого материала устраивать угол уклона 12 градусов. Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком;
- для металлической черепицы значение этого параметра равняется 14;
- для ондулина — это величина в 6 градусов;
- минимальный уклон для мягкой черепицы равняется 11 градусам.
 Но при этом обязательное условие — сплошная обрешетка;
Но при этом обязательное условие — сплошная обрешетка; - для мембранных кровельных покрытий не существует жестких требований по минимальному значению этого параметра.
Это о минимальных величинах. Дадим совет — придерживайтесь этих правил, чтобы посреди зимы не пришлось всю кровлю перестилать.
Если в регионе дожди и снега случаются часто, то оптимальной будет крыша, угол наклона скатов у которой будет составлять 45 — 60 градусов. Ведь с кровли необходимо как можно скорее снимать нагрузку от воды и снега. Потому что прочность стропильной системы не беспредельна. А благодаря большому уклону кровли дождь и снег будут сходить максимально быстро.
Если в регионе, где построен дом, постоянно сильные ветра, то с крышей поступают иначе. При меньшем наклоне снижается ее парусность. И не возникает запредельных нагрузок на кровельный материал и стропила. Также не произойдет срывания крыши при резких порывах ветра. При этом оптимальный угол уклона кровли равняется 9–20 градусов.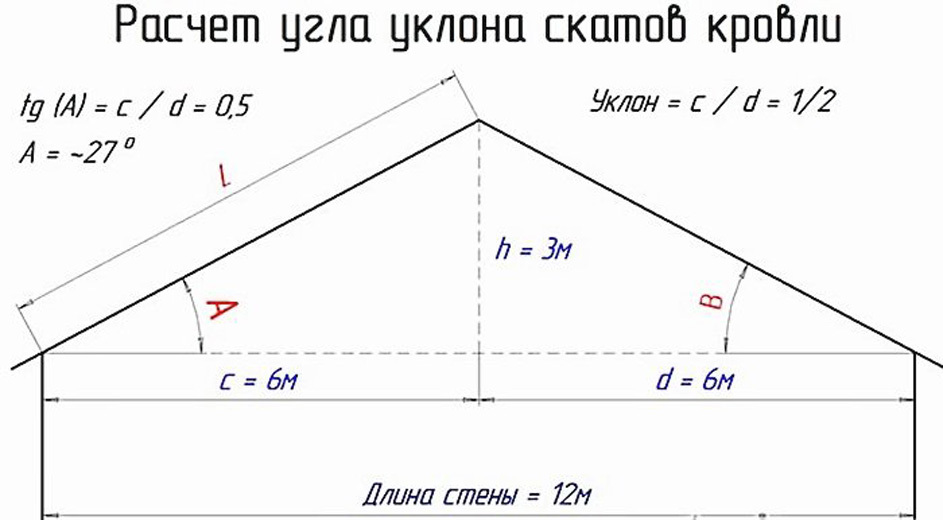
Очень часто в регионе есть и снега, и ветер. Например, Оренбургская область. В таком случае выбирают среднее значение угла наклона. Как правило, его величина находится в диапазоне 20 — 45 градусов. Если вы обратите внимание, большинство скатных крыш имеют именно такое его значение.
Рассчитываем его величину
Для односкатной
Поскольку односкатная крыша опирается на стены, имеющие разную высоту, то формирование заданного угла наклона производят, просто поднимая одну из стен. Проводим вдоль стены перпендикуляр L сд, берущий свое начало в точке, где оканчивается короткая стена и опирающийся на стену, имеющую максимальную дину. В итоге образуется прямоугольный треугольник.
Для того, чтобы рассчитать длину стороны L bc, надо воспользоваться тригонометрической формулой.
Если длина стены L сд равняется 10 метрам, то, чтобы получить угол наклона 45 градусов, длина стены L bc должна ровняться 14.08 метра.
Для двускатной
Принцип расчета для двускатной крыши похож на предыдущий принцип.
Рассмотрим пример. Катет С — это половина ширины здания. Катет, а — это высота от перекрытия до конька. Гипотенуза является длиной ската. Если нам известны любые два параметра, то величину угла наклона можно легко рассчитать с использованием калькулятора.
Если ширина равна 8, а высота — 10 метров, то следует пользоваться формулой:
cos A = c+b
Ширина с = 8/2 = 4 метра.
В итоге формула выглядит так:
cos A = 4/10 = 0.4
По таблицам Брадиса находим значение угла, которому соответствует данная величина косинуса. Он равняется 66 градусов.
Для четырехскатной
И снова не обойтись без рулетки и таблиц Брадиса. Зная несколько параметров, можно без проблем вычислить другие. В том числе и угол наклона четырехскатной крыши. Следует помнить о том, что все размеры необходимо снимать максимально точно. А измерить уклон уже построенной крыши поможет специальный инструмент — уклономер. Ведь если вы ошибетесь, то углы наклона, длины и площади могут быть не верны. А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.
А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.
Математика для блондинок: Простое построение углов
Тут мне в комментариях задали интересный вопрос. Простое построение углов — как это сделать? Вот сам вопрос.| Вопрос о построении углов |
И так, вопрос сводится к следующему — в декартовой системе координат, если брать одинаковый икс и игрек, получим прямую под углом в 45 градусов к осям координат. А как построить углы другой величины? Можно, конечно, заняться гаданием на кофейной гуще и попробовать высчитать, сколько нужно откладывать по иксам, сколько по игрекам, чтобы получился другой удобочитаемый угол. Не 156пи/911, а что-то типа 1, 5, 10, 15 градусов.
Угол в тридцать градусов получается, когда по оси игрек мы возьмем половинку, а расстояние от центра системы координат до точки будет равно единице.
| Построение угла в 30 градусов |
И так, четвертое-пятое тысячелетие до нашей эры, древняя Месопотамия… Тогда зародилось то, чем мы пользуемся и сегодня. Астрономия, письменность, математика, углы… Какими инструментами тогда пользовались для построения углов? Линейка, циркуль…Возможно, были тогда и угольники, хотя это не принципиально — для построения прямого угла достаточно циркуля и линейки.
Теперь попробуем строить углы при помощи циркуля и линейки без всяких координатных систем.
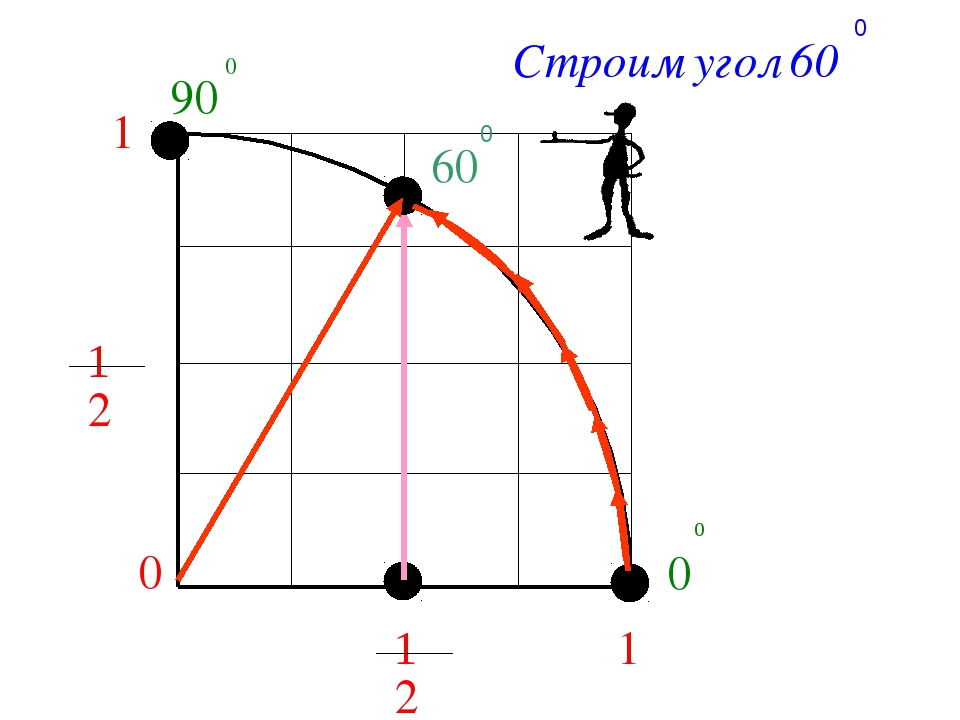
| Построение угла в 60 градусов |
Почему возле углов я поставил циферки 1, 2, 3, 4, 5, 6? Я считаю, что именно такую единицу измерения углов использовали наши предки. Назовем эту единицу измерения углов «вавилонский угол». Дальше один угол делится на 60 градусов. Почему именно на 60? В те времена, в тех местах, использовалась шестидесятеричная система счисления. Вы такой системой счисления никогда не пользовались и понятия о ней не имеете? Ошибаетесь. Когда вы выражаете время в минутах и секундах, вы используете именно шестидесятеричное счисление. «Подожди пять минут» в переводе на десятичные дроби, если за единицу брать один час, будет звучать как «Подожди 0,083333333.

Давайте посмотрим на структуру вавилонских шестидесятеричных чисел. Единицу целого числа вавилоняне делили на шестьдесят частей. Потом каждую эту часть делили ещё на шестьдесят частей и так дальше. У шестидесятых долей были свои названия: минута, секунда, терция…
| Минута, секунда, терция, кварта, квинта |
Я просто хотел обратить ваше внимание на то, что 360 градусов окружности приблизительно равны 365 дням в году (если отбросить градусы и дни, а тупо сравнивать только числа, как это любят делать наши математики). Почему я сравниваю окружность с днями в году? За сутки Солнце смещается по эклиптике приблизительно на один градус. С другой стороны, вавилонский угол в 60 градусов приблизительно равен одному радиану. Ведь 1 радиан ≈ 57,295779513° ≈ 57° 17′ 44,806″ При этом, у вавилонского угла есть точное числовое значение, а вот радиан точного числового значения не имеет — он построен на бесконечности числа «пи». Один — ноль в пользу древних математиков. Что бы там не утверждали наши математики, но принимать в качестве единицы измерения бесконечное число — это не совсем разумно. Думаю, физики меня поймут — создать точный измерительный прибор для измерения неточной величины даже теоретически невозможно.
Почему я сравниваю окружность с днями в году? За сутки Солнце смещается по эклиптике приблизительно на один градус. С другой стороны, вавилонский угол в 60 градусов приблизительно равен одному радиану. Ведь 1 радиан ≈ 57,295779513° ≈ 57° 17′ 44,806″ При этом, у вавилонского угла есть точное числовое значение, а вот радиан точного числового значения не имеет — он построен на бесконечности числа «пи». Один — ноль в пользу древних математиков. Что бы там не утверждали наши математики, но принимать в качестве единицы измерения бесконечное число — это не совсем разумно. Думаю, физики меня поймут — создать точный измерительный прибор для измерения неточной величины даже теоретически невозможно.
Но продолжим наши построения углов. Через центр первой окружности проводим перпендикуляр, затем строим ещё две окружности с центрами в точках пересечения перпендикуляра и первой окружности.
| Построение угла в 30 градусов |
 Как видите, построение очень простое, даже циркуль с переменным радиусом не нужен. Достаточно отрезать кусок разветвления ветки вместо циркуля и всё прекрасно получится. В этой первозданной простоте родились наши современные часы.
Как видите, построение очень простое, даже циркуль с переменным радиусом не нужен. Достаточно отрезать кусок разветвления ветки вместо циркуля и всё прекрасно получится. В этой первозданной простоте родились наши современные часы.| Вавилонские углы и циферблат часов |
Особо стоит отметить, что в древности использовались солнечные часы.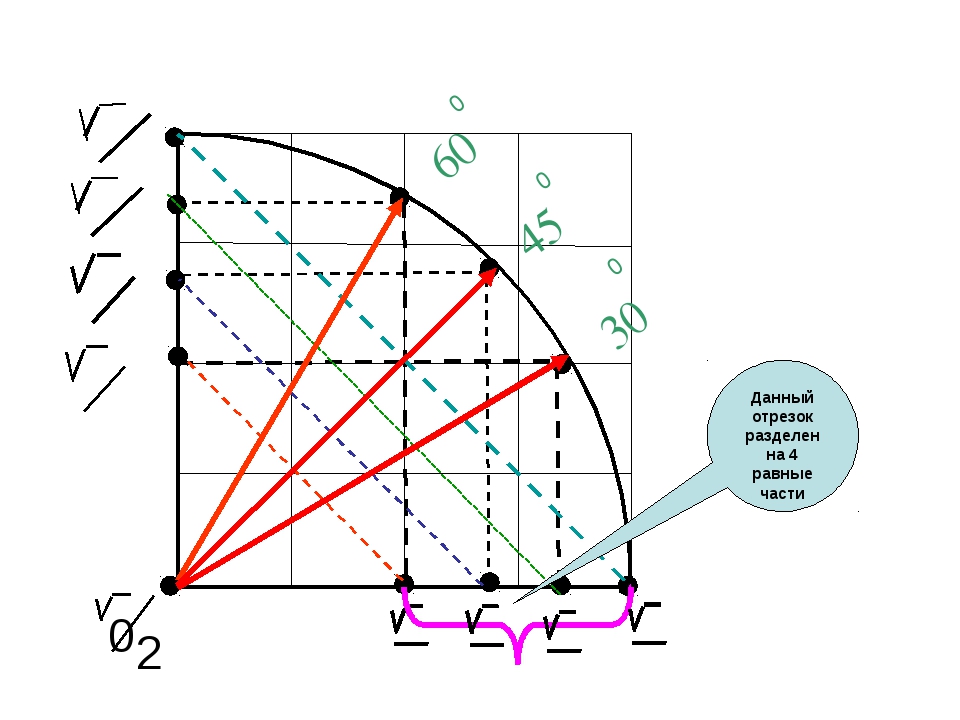 Было два варианта солнечных часов — напольные и настенные. Так вот, стрелки этих двух типов часов (тень на циферблате) двигались в противоположных направлениях — по часовой стрелке у напольных и против часовой стрелки у настенных. Можно предположить, что такого понятия, как «вращение по часовой стрелке» у древних математиков не существовало. А в том, что древние люди были очень умными, мы можем убедиться, рассмотрев загадку вавилонской таблички.
Было два варианта солнечных часов — напольные и настенные. Так вот, стрелки этих двух типов часов (тень на циферблате) двигались в противоположных направлениях — по часовой стрелке у напольных и против часовой стрелки у настенных. Можно предположить, что такого понятия, как «вращение по часовой стрелке» у древних математиков не существовало. А в том, что древние люди были очень умными, мы можем убедиться, рассмотрев загадку вавилонской таблички.
как рассчитать минимальный угол наклона крыши, малоуклонная и наклонная конструкции
Возведение кровли является одним из важных этапов строительства. Кровля защищает жилье и выполняет эстетическую функцию, делая дизайн здания завершенным. Выбор подходящего материала – не единственный значимый нюанс. Также необходимо правильно рассчитать уклон кровли. О том, как это сделать, расскажет данная статья.
Особенности
В современных проектах загородных особняков учитывается большое количество требований. Исполнители вынуждены не только соблюдать нормы, но и воплощать в жизнь пожелания и капризы заказчиков. Однако на первом плане все же находятся нормативные требования, ведь кровля, прежде всего, должна быть надежной. Поэтому часто архитектурные изыски уходят на второй план.
Исполнители вынуждены не только соблюдать нормы, но и воплощать в жизнь пожелания и капризы заказчиков. Однако на первом плане все же находятся нормативные требования, ведь кровля, прежде всего, должна быть надежной. Поэтому часто архитектурные изыски уходят на второй план.
Кровельное покрытие должно выполнять свое прямое назначение – защищать от влаги. В некоторых случаях требуется термо- и звукоизоляция. Это бывает необходимо для повышения функциональности помещений, находящихся под крышей. Поэтому проектирование кровли нельзя назвать простым делом. Эта работа требует чрезвычайной ответственности, особенно, если заказчик настаивает на сложной конфигурации. В различных ситуациях профессионалы применяют различные методики. Расчеты производятся с помощью соответствующего программного обеспечения.
Расчеты производятся с помощью соответствующего программного обеспечения.
Теория расчетов может быть интересна и владельцу дома. Например, такие знания дают возможность проверить, правильную ли методику применили профессионалы. Также они помогают грамотно представлять свои авторские идеи. Кроме того, рассчитанные параметры позволяют определить нужное количество строительных материалов и для стропильной системы, и для кровельного покрытия.
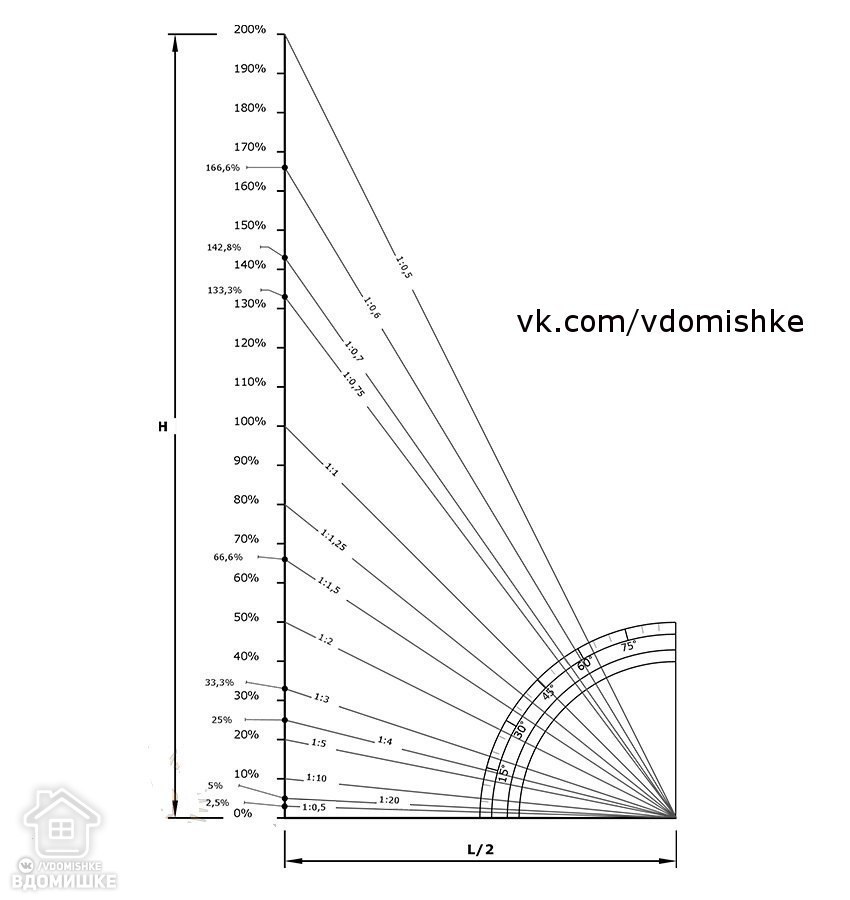
Особенности расчетов заключаются в том, что профессионалы пользуются разными величинами для измерений. Например, не все измеряют угол ската в градусах. В привычном обиходе некоторых мастеров встречаются такие понятия как процентное соотношение или относительное соотношение сторон.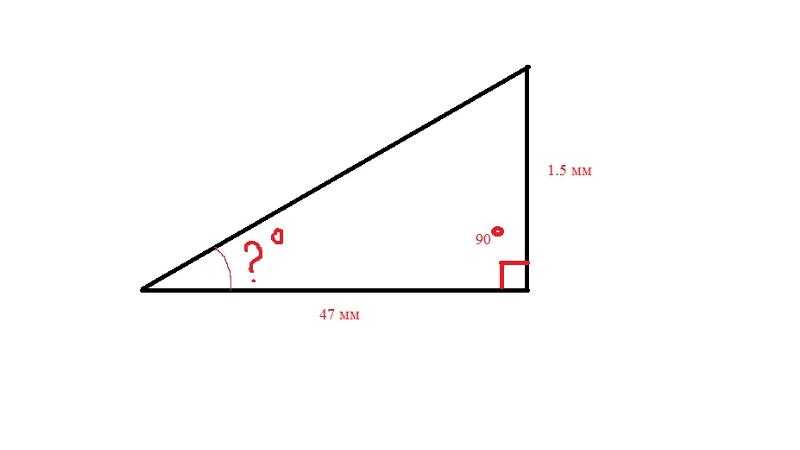 Также необходимо знать, что принимается за угол наклона крыши.
Также необходимо знать, что принимается за угол наклона крыши.
Угол наклона кровли образуется пересечением двух параметров:
- одна горизонтальная плоскость;
- одна плоскость ската кровли.
Этот параметр измеряется от верхнего края к основанию стропильной системы. При расчетах в учет берутся только острые углы, так как тупоугольных скатов не бывает по определению. Крутые скаты встречаются редко. Как правило, их применяют для декоративного оформления (например, когда строят башенки в готической стилистике).
Крутыми могут быть кровли мансардного вида. В этом случае нижние стропилы располагают под очень большим углом. На обычных кровлях монтируются скаты до 45 градусов.
Для лучшего представления, как это должно выглядеть, можно взять транспортир и посмотреть на деления с указанием градусов.
Величина наклонного угла рассчитывается как отношение параметров конька к половине ширины сооружения, помноженное на 100. Большинство профессиональных строителей пользуются так называемыми табличными графиками. В зависимости от показателей, кровли принято подразделять по видам.
Виды
Специалисты выделяют несколько основных видов крыш.
- Односкатная кровля. В этом случае крыша выглядит ровной плоскостью. Она имеет отличительные параметры по высоте.
- Двускатная кровля.
 Она представляет собой надежный, простой в монтаже вариант. Крыша включает в себя два ската, соединенные под прямым углом.
Она представляет собой надежный, простой в монтаже вариант. Крыша включает в себя два ската, соединенные под прямым углом.
- Вальмовая кровля. Она снабжается четырьмя скатами, два из которых – треугольники, а еще два – трапеции. Вершина такой кровли выглядит срезанной. Несмотря на сложность конструкции, такие кровли очень экономичны в плане расхода материала.
- Сводчатый тип кровли.
 Он встречается редко, так как предполагает ограниченный выбор материалов. Такие варианты возводят только из кирпича или камня. Редкость выбора в пользу таких крыш обусловлена и их тяжеловесностью. В мелком частном строительстве этот тип практически не используется.
Он встречается редко, так как предполагает ограниченный выбор материалов. Такие варианты возводят только из кирпича или камня. Редкость выбора в пользу таких крыш обусловлена и их тяжеловесностью. В мелком частном строительстве этот тип практически не используется.
- Многощипцовый тип кровли. Он сложен по конфигурации, но очень красив. Такую кровлю сложно укладывать из-за множества примыканий и перемычек.
Также специалисты выделяют виды кровли, которые можно впоследствии эксплуатировать, и варианты, которые не подлежат эксплуатации.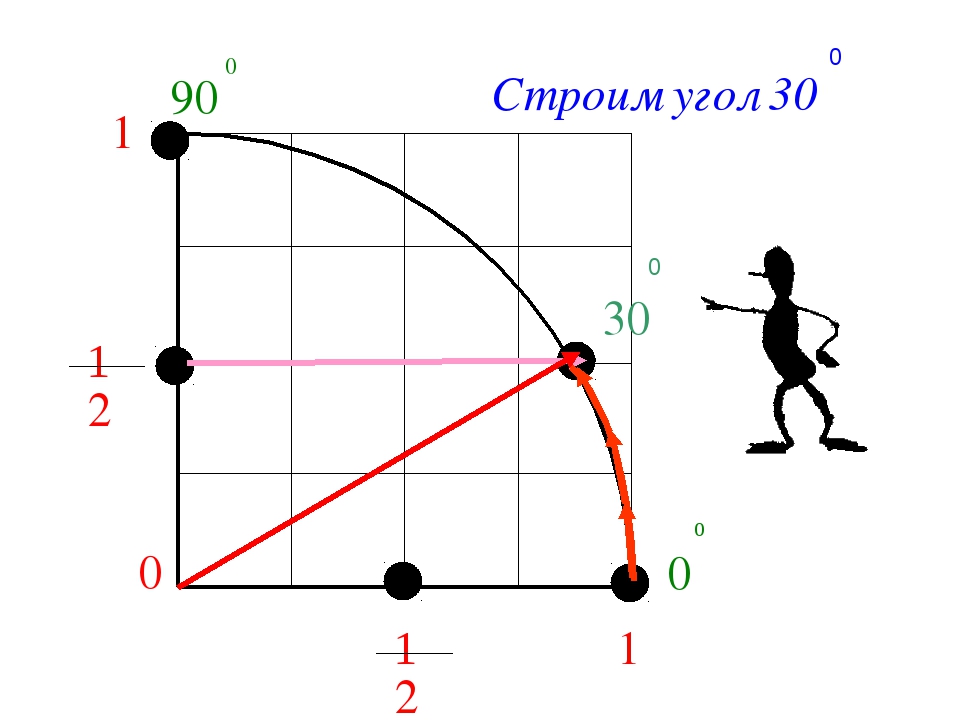 Если профессионалы причисляют кровлю к типу неэксплуатируемых, это значит, что между самой кровлей и верхним перекрытием практически нет пространства. Эту территорию можно использовать, но только как техническую. Например, такой бывает малоуклонная односкатная кровля.
Если профессионалы причисляют кровлю к типу неэксплуатируемых, это значит, что между самой кровлей и верхним перекрытием практически нет пространства. Эту территорию можно использовать, но только как техническую. Например, такой бывает малоуклонная односкатная кровля.
Односкатные кровли максимально выгодны для строительства. Они требуют минимум затрат на материалы, работу же можно выполнить самостоятельно. Если кровля отличается небольшим уклоном, то на ее поверхности можно реализовать место отдыха без сооружения сложной мансарды.
Пространство под крышей можно использовать, если тип кровли является скатным. Чердачная территория может использоваться для хозяйственных нужд. Также за счет нее можно расширить жилое пространство.
Чердачная территория может использоваться для хозяйственных нужд. Также за счет нее можно расширить жилое пространство.
Выбор того или иного типа кровли связан со многими нюансами. Одним из основных является климатический фактор.
Влияние климата
Часто специалисты связывают наклонный угол крыши с рекомендуемыми оптимальными показателями для того или иного региона. То есть, возможности выбора связаны с той местностью, где будут вестись строительные работы.
Например, огромная нагрузка на стропильную конструкцию может возникнуть из-за ветра. Даже незначительное увеличение наклонного угла увеличивает ветровую нагрузку. Например, если угол наклона кровли больше нормативных показателей на 30 градусов, ветровая нагрузка становится больше в пять раз. Поэтому даже незначительное увеличение показателей может сыграть с хозяином дома злую шутку при стихийном бедствии.
Даже незначительное увеличение наклонного угла увеличивает ветровую нагрузку. Например, если угол наклона кровли больше нормативных показателей на 30 градусов, ветровая нагрузка становится больше в пять раз. Поэтому даже незначительное увеличение показателей может сыграть с хозяином дома злую шутку при стихийном бедствии.
В регионах с сильными и частыми ветрами рекомендованы к установке скатные кровли с углом наклона 25-30 градусов. При небольшой ветровой нагрузке в регионе допустимы скатные кровли с наклоном 30-45 градусов.
Не менее разрушительно действуют на качество кровли атмосферные осадки. При этом грамотно подобранный чуть больший уклон позволит избежать накапливания снега на поверхности. Схода снега не будет вовсе при уклоне кровли 30 градусов. А при уклоне 45 градусов будут соблюдены нормативные показатели для снеговой нагрузки на крышу.
При этом грамотно подобранный чуть больший уклон позволит избежать накапливания снега на поверхности. Схода снега не будет вовсе при уклоне кровли 30 градусов. А при уклоне 45 градусов будут соблюдены нормативные показатели для снеговой нагрузки на крышу.
В северных странах (Швеции, Финляндии, Норвегии и др. ) принято делать очень высокие скатные кровли. Очевидно, что на высоких скатах снег не задерживается. Однако принято считать, что некоторый снеговой слой на крыше играет роль дополнительной теплоизоляции.
Для исключения риска пролома кровельного материала выполняется прочная стропильная система, ведь большой вес будет воздействовать на всю конструкцию.
Стоит помнить, что чем больше наклонный угол кровли, тем больше средств придется потратить на строительство. Также расходы связаны с выбором варианта покрытия кровли (на высокие скатные кровли можно укладывать не все материалы).
Для разных материалов
Перед выбором кровельного материала стоит внимательно рассмотреть технические особенности покрытия. Это поможет принять оптимальное решение и выбрать наиболее надежный вариант. Существуют правила, которые определяют связь угла наклона кровли с применяемой кровельной конструкцией.
Шиферное покрытие или черепицу можно укладывать на кровлю с минимальным уклоном 22 градуса. На кровлях с меньшим уклоном в местах стыковки частей будет скапливаться и просачиваться внутрь влага. Если кровля имеет скаты с меньшим градусом, можно применять рубероид и прочие битумные материалы, которые монтируются цельным полотном.
Производители профилированного листа заявляют, что данный материал можно укладывать при минимально допустимых углах 12 градусов. При этом если угол ската является минимальным, то стыки между листами нужно обязательно проклеить герметиком.
При этом если угол ската является минимальным, то стыки между листами нужно обязательно проклеить герметиком.
Для металлической черепицы минимально возможный уклон ската составляет 14 градусов. При этом существуют правила обустройства перекрытий. Например, если угол более 45 градусов, то место монтажа подконьковой доски меняется. Также изменяется и способ монтажа самого конька. При небольших значениях величины между планкой конька и черепицей прикрепляется аэроролик. Он не допускает проникновения снега под кровлю.
Для кровли, покрытой ондулином, минимально возможный уклон – 6 градусов. Для мягкой черепицы оптимальный уклон поверхности составляет 11 градусов. Хотя для этого материала допустим и больший уклон. При этом обрешетка должна быть обязательно сплошной.
Для мягкой черепицы оптимальный уклон поверхности составляет 11 градусов. Хотя для этого материала допустим и больший уклон. При этом обрешетка должна быть обязательно сплошной.
Большей универсальностью отличаются покрытия мембранного типа. ПВХ мембрана, ЭПДМ мембрана, ТПО мембрана – это современные материалы, подходящие для крыш любой формы. Универсальность материалов обуславливается отличными техническими характеристиками и продолжительным сроком службы.
При выборе того или иного материала покрытия следует учитывать не только особенности скатов, но и прочностные значения крыши.
Конструкции должны удерживать не только собственный вес, но и массу кровельного материала. Кроме того, вся кровельная система должна успешно противостоять внешним нагрузкам.
С наклоном скатов часто связывают не только выбор материалов, но и выбор типа обрешетки. Если угол ската имеет небольшое значение, то монтируется сплошная обрешетка. Также при монтаже плоской кровли обязательно устройство системы водоотведения. Для любых вариантов кровли существуют нормативные параметры. Их следует иметь в виду, даже если выбран простейший плоский вариант.
Нормативные значения
Обустройство плоской кровли – несложное мероприятие.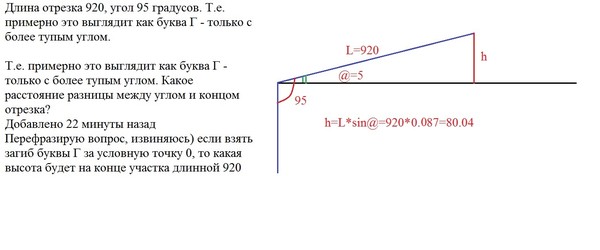 Главное – использовать правильно подобранный материал высокого качества. Немаловажное значение имеет и разуклонка плоской кровли.
Главное – использовать правильно подобранный материал высокого качества. Немаловажное значение имеет и разуклонка плоской кровли.
На самом деле плоская кровля не является полностью горизонтальной. На такой кровле сооружается разуклонка, равная 15 градусам. Уклоны обязательно должны присутствовать, так как только в этом случае вода будет стекать в водостоки. Если разуклонка не будет сделана в соответствии с установленными нормами, на поверхности крыши будет образовываться застой воды.
Для обустройства разуклонки на плоской кровле используются самые разные материалы.
Это может быть:
- теплоизоляция;
- легкий слой бетона;
- керамзит, гравий, шлак;
- плиты перекрытий;
- обычная стяжка.
При выборе тех или иных основ следует учитывать тип конструкции. Например, если перекрытия деревянные, то дополнительный вес для кровли противопоказан.
На сегодняшний день в продаже можно найти специальные плиты, отличающиеся высокими теплоизоляционными качествами. Такие плиты имеют клиновидную форму. Материал достаточно уложить на плоскую поверхность. Получится уклон, соответствующий нормативным показателям. Единственный недостаток материала – достаточно высокая стоимость.
Такие плиты имеют клиновидную форму. Материал достаточно уложить на плоскую поверхность. Получится уклон, соответствующий нормативным показателям. Единственный недостаток материала – достаточно высокая стоимость.
При использовании других материалов для начала нужно убедиться в том, что поверхность является абсолютно ровной. Затем на нее устанавливаются маячки. Уклон должен быть направлен в водостоки.
При создании разуклонки стоит учитывать площадь кровли. Для кровли гаража, например, стоит учесть один скат, который будет направлен в водосточную воронку. Разуклонка для стандартного дома размером 80 кв. м будет составлять 2-4 уклона. При этом все они должны направляться в водосточную систему, чтобы беспрепятственно доставлять в нее воду.
Разуклонка для стандартного дома размером 80 кв. м будет составлять 2-4 уклона. При этом все они должны направляться в водосточную систему, чтобы беспрепятственно доставлять в нее воду.
Как рассчитать?
Если с обустройством плоской кровли обычно сложностей не возникает, то для монтажа крыши с несколькими скатами необходимы инженерные расчеты. Проще всего посчитать и определить величины в градусах. Например, для обустройства кровли с уклонным углом 30 градусов можно воспользоваться математическим способом.
Для этого потребуются два замера.
- Вертикальная высота (H).
 Величина измеряется от верхней точки наклонной плоскости до низа стропильной системы (от конька до карниза).
Величина измеряется от верхней точки наклонной плоскости до низа стропильной системы (от конька до карниза). - Заложение (L). Это горизонтальная длина от середины нижней точки ската до карниза.
Математический расчет производится по формуле. Высчитать нужный параметр можно так: I=H: L. К примеру, длина заложения равна 5 м, а высота составляет 3м. В таком случае уклон будет равен 0,6 (при расчете I= 3: 5). Эту величину нужно умножить на 100. Получается 60 процентов.
Для перевода величины в градусы можно применить специальную таблицу соотношений. Ее можно найти в специализированных учебниках. Иногда такую таблицу можно встретить в продаже в строительных гипермаркетах. Переводить относительные величины необязательно. При значениях из приведенного примера угол наклона будет равен 30 градусам.
Специалисты в своих измерениях не всегда пользуются переводной таблицей. Коэффициент в процентах может применяться наравне с коэффициентом в градусах. Вообще, профессионалы применяют в расчетах специальные инструменты. Например, измерить параметр площади можно, используя специальный уклономер.
Коэффициент в процентах может применяться наравне с коэффициентом в градусах. Вообще, профессионалы применяют в расчетах специальные инструменты. Например, измерить параметр площади можно, используя специальный уклономер.
Инструмент представляет собой линейку с рейкой. Одна ось содержит привычную шкалу в сантиметрах, другая – маятник. Если рейка с делениями лежит горизонтально, то маятник будет показывать ноль. При замерах уклонного наклона рейка устанавливается перпендикулярно коньку. При этом шкала показывает результат для конкретного значения сразу в градусах.
В настоящее время на рынке можно встретить самые разные инструменты, которыми можно замерять уклоны. Уровни могут быть как приспособлениями капельного типа, так и электронными устройствами. В связи с этим математический способ замера нельзя считать актуальным. Современные приборы позволяют производить более точные расчеты.
Уровни могут быть как приспособлениями капельного типа, так и электронными устройствами. В связи с этим математический способ замера нельзя считать актуальным. Современные приборы позволяют производить более точные расчеты.
Советы
Если кровля дома преждевременно вышла из строя, это означает, что при монтаже были допущены ошибки. Причины выхода из строя скатной кровли могут быть разными. Например, неправильный проект стропильной системы может стать причиной обрушения конструкции.
Если были неверно выбраны теплоизоляционные материалы, то это может привести к образованию конденсата. Теплоизоляция в этом случае потеряет свои функциональные особенности. Ошибки при укладке гидроизоляции приведут к протеканию кровли. Поэтому при обустройстве крыши важно уделить внимание каждому элементу конструкции.
Теплоизоляция в этом случае потеряет свои функциональные особенности. Ошибки при укладке гидроизоляции приведут к протеканию кровли. Поэтому при обустройстве крыши важно уделить внимание каждому элементу конструкции.
Для того чтобы избежать крушения стропильной системы, ее нужно проектировать в соответствии со строительными нормами и требованиями. Если стропила будут опираться непосредственно на стену, крыша быстро придет в негодность. Нельзя в качестве подпорок использовать подставки из небрежно прикрепленных досок. Также стойки должны быть установлены в определенном порядке, а не хаотично.
При монтаже важно учитывать и температурно-влажностный режим, который обуславливается применением тех или иных строительных материалов. Теплоизоляция в кровельной конструкции будет способствовать энергоэффективности, только если материалы являются качественными и уложены правильно.
Теплоизоляция в кровельной конструкции будет способствовать энергоэффективности, только если материалы являются качественными и уложены правильно.
Некачественная пароизоляция приведет к попаданию влаги в утеплитель. В дальнейшем в нем образуется конденсат. Влажный утеплитель не только потеряет свои свойства, но и станет причиной образования плесени в помещениях.
Существует несколько основных правил грамотного устройства кровли.
- Утепление, как правило, устраивается между частями стропильной системы. Пароизоляция помещается с внутренней части утеплителя.
- Для скатных крыш не подходят слишком рыхлые материалы.
- При выборе тех или иных материалов обращайте внимание на рекомендации производителя.
- Учитывайте, что некоторые виды покрытий, например, мягкая черепица, являются сплошной непроницаемой изоляцией. Они не требуют дополнительных изоляционных элементов.
- Необходимость в изоляционных материалах возрастает пропорционально уменьшению уклона кровли.
- Изоляция обязательна для таких материалов как металлочерепица, профильное железо.
- Для изоляции выбирайте мембранные основы с перфорацией.
 Такие материалы более надежны. Их основа полностью непроницаема, поэтому исключает продувание ветром. Кроме того, пленки из нетканной основы впитывают образующуюся влагу.
Такие материалы более надежны. Их основа полностью непроницаема, поэтому исключает продувание ветром. Кроме того, пленки из нетканной основы впитывают образующуюся влагу. - Менять слои изоляции подкровельных материалов местами нельзя. Иначе температурно-влажностный режим чердачного пространства может нарушиться. Стропила будут впитывать влагу, а несущая деревянная система провиснет.
В некоторых случаях важное значение имеет обустройство системы вентиляции. Например, это становится актуальным, если чердак холодный. Также по несущим конструкциям иногда проходят системы центрального отопления. Щелевые продухи устраивают в карнизах. Их наличие ускоряет прогрев участков в период оттепелей. Кроме того, такая вентиляция отличается простотой обустройства, экономичностью и полностью соответствует нормативам.
Кроме того, такая вентиляция отличается простотой обустройства, экономичностью и полностью соответствует нормативам.
О том, как расчитать уклон и произвести монтаж крыши, смотрите в следующем видео.
Некоторые свойства прямоугольных треугольников
Вспомним,
что прямоугольным называют треугольник, который содержит прямой угол. Две стороны, образующие прямой угол, называют катетами, а противолежащую
сторону — гипотенузой прямоугольного треугольника.
Две стороны, образующие прямой угол, называют катетами, а противолежащую
сторону — гипотенузой прямоугольного треугольника.
Теорема:
Сумма углов треугольника равна 180 градусов.
Свойство:
Сумма двух острых углов прямоугольного треугольника равна 90 градусов.
Доказательство:
Пусть АВС — прямоугольный треугольник, у которого ∠С=90 градусов.
Так как сумма углов треугольника равна 180 градусов, то:
Что и требовалось доказать.
Свойство:
Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.
Пусть АВС — прямоугольный треугольник, у которого ∠С=90 градусов, а ∠А=30 градусов. А тогда по теореме о сумме углов треугольника ∠В=60 градусов. Докажем, что катет ВС равен половине гипотенузы АВ.
Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:
Получили,
что у треугольника АВD все углы равны по 60
градусов, то есть он является равносторонним.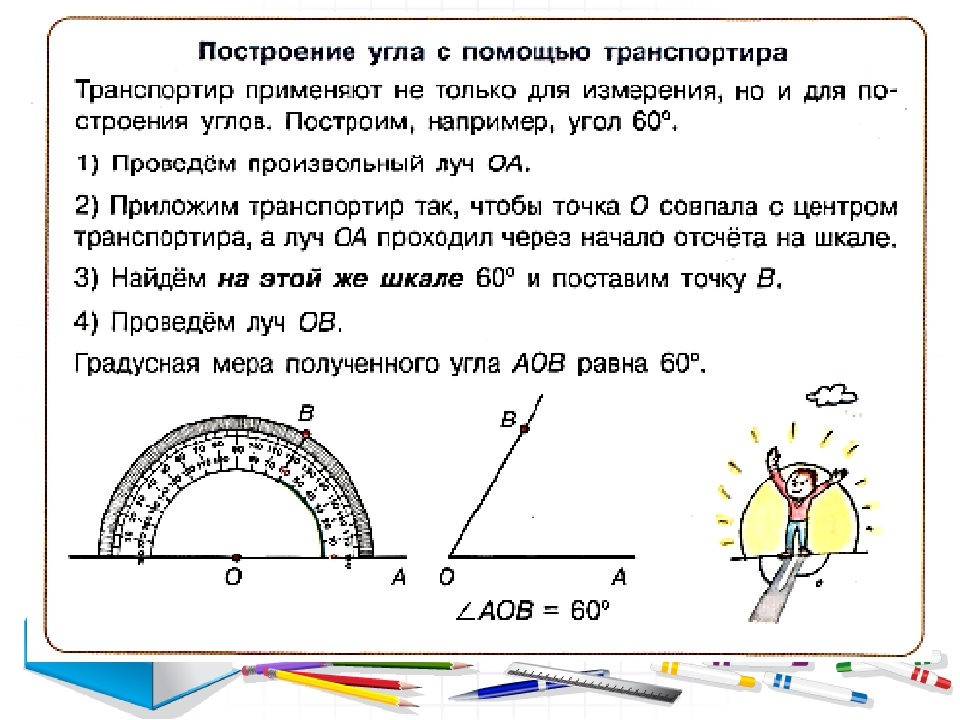 Получаем:
Получаем:
Что и требовалось доказать.
Свойство:
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов.
Доказательство:
Пусть АВС — прямоугольный треугольник, у которого катет ВС равен половине гипотенузы АВ. Докажем, что угол ВАС=30 градусов.
Приложим к треугольнику АВС равный ему треугольник АСD следующим образом:
Получили равносторонний треугольник АВD. Известно, что все углы равностороннего треугольника равны 60 градусам. Полуаем:
Что и требовалось доказать.
Пример.
Сумма гипотенузы и катета, лежащего против угла в 30 градусов, равна 15 сантиметров. Найти длину гипотенузы.
Пусть АВС — прямоугольный треугольник. ∠А=30 градусов. Получим:
Подставим это в предыдущее равенство и получаем:
Пример.
В прямоугольном треугольнике АВС, ∠С=90 градусов, а ∠ВАС=60 градусов. Найти длину катета ВС, если высота СD треугольника АСВ равна 5 сантиметров.
Рассмотрим прямоугольный треугольник АВС. ∠АСВ=90 градусов, ∠ВАС=60 градусов. А так как сумма острых углов прямоугольного треугольника равна 90 градусов, то ∠АВС=90-60=30 градусов.
Рассмотрим треугольник ВСD, который является прямоугольным, так как СD - высота и ∠СВD=30 градусов, то катет СD лежит против угла в 30 градусов. Следовательно, по выше доказанному свойству, гипотенуза ВС=2*5=10 см.
Пример.
Отрезок СD - высота прямоугольного треугольника АВС с прямым углом С, ВС=2*ВD. Доказать, что АВ=4*ВD.
Рассмотрим прямоугольный треугольник BCD:
У него ∠ВСD=30 градусов, так как по условию ВС=2*ВD.
По
условию задачи ∠АСВ=90 градусов, а ∠ВСD=30
градусов, значит, ∠АСD=60 градусов.
Так как СD - высота, то треугольник АСD - прямоугольный. ∠АСD=60 градусов. Следовательно, ∠САD=30 градусов.
Теперь рассмотрим треугольник АВС. У него ∠ВАС=30 градусов. Следовательно, гипотенуза АВ=2*ВС, так как катет ВС лежит против угла в 30 градусов. По условию задачи ВС=2*ВD.
Получаем, что АВ=4*ВD.
Измерение углов. Транспортир | Математика
Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус — это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °
, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор — транспортир:
У транспортира две шкалы — внутренняя и внешняя.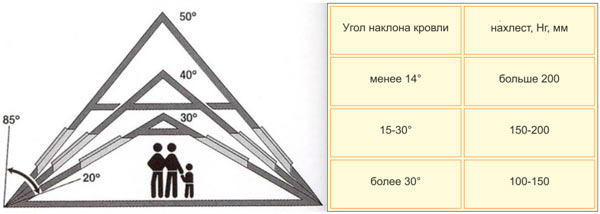 Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов
и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный
части градуса. Секунда — это угол, равный части минуты. Минуты обозначают знаком ‘
, a секунды — знаком »
. Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34‘19».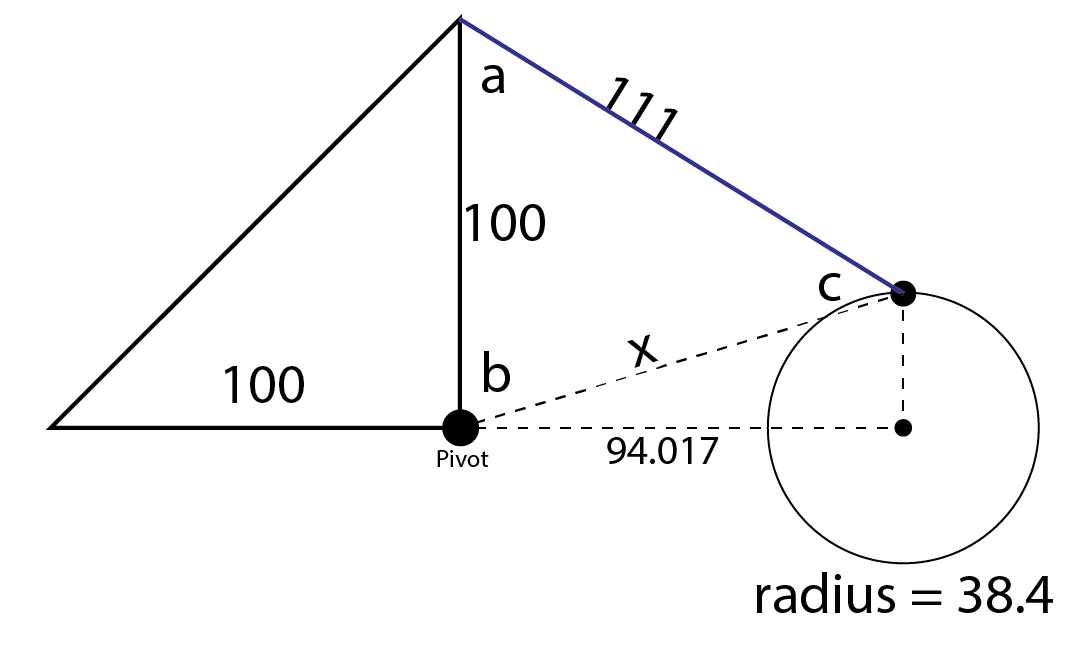
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Калькулятор прямоугольного треугольника
ΔABC — прямоугольный треугольник
Катеты a = BC, b = AC
Гипотенуза c = AB
Как пользоваться онлайн-калькулятором. В форме укажите известные параметры прямоугольного треугольника:
а) 2 катета,
б) катет и гипотенуза,
в) катет и противолежащий острый угол,
г) гипотенуза и острый угол.
Заполните поле «Текст с картинки». Нажмите «Решить».
Нажмите «Решить».
Калькулятор сторон и углов треугольника
При помощи калькулятора прямоугольного треугольника можно найти гипотенузу онлайн, а также катеты, величины острых и противолежащих углов прямоугольного треугольника.
В форме калькулятора гипотенузы указываются два параметра прямоугольного треугольника онлайн: две стороны или острый угол и сторона.
Для углов имеются два поля: для градусов и для минут.
Далее заполнить поле «Текст с картинки» и нажать «Решить». Компьютерная программа автоматически сделает расчет.
Приводятся ответы с подробными решениями, включая формулы. Для решения задач используется теорема Пифагора. Катеты и гипотенуза вычисляются через синус.
Примеры решения калькулятора прямоугольного треугольника:
1) как найти неизвестный катет или катеты, если известна гипотенуза, равная 2 см, и острый угол 20°. В поле для гипотенузы «c» указывается 2, в поле «Угол (градусов, °)» ставится 20, в поле «Угол (минут, ‘)» указывается 0. Ответ онлайн калькулятора прямоугольного треугольника: длина катетов a = 0,68 см; b = 1,88 см, острый угол B = 70°.
В поле для гипотенузы «c» указывается 2, в поле «Угол (градусов, °)» ставится 20, в поле «Угол (минут, ‘)» указывается 0. Ответ онлайн калькулятора прямоугольного треугольника: длина катетов a = 0,68 см; b = 1,88 см, острый угол B = 70°.
2) пример вычисления неизвестных сторон и острых углов прямоугольного треугольника по двум катетам или по гипотенузе и катету. Вопрос: как найти угол прямоугольного треугольника, зная его стороны, т.е. зная 2 катета или 2 стороны. Известна длина катетов a=11, b=60.
В полях для катетов «a» указывается 11, в поле «b» 60. Нажать «Решить». В ходе решения находим третью сторону – гипотенузу – и находим угол в прямоугольном треугольнике, уже зная все стороны.
Ответ калькулятора гипотенузы: гипотенуза c=61, значения углов A= 10°23′, B = 79°37′. Если даны катет и гипотенуза, то заполняются поля для катета «a» и для гипотенузы «c».
3) с помощью этого онлайн-калькулятора можно решить задачу, где требуется найти катет онлайн, или как найти гипотенузу, зная катет и угол. Например, a=3, противолежащий угол = 30°27′. В поле для катетов «a» указывается 3, в поле «Угол (градусов, °)» ставится 30, в поле «Угол (минут, ‘)» указывается 27. Ответ калькулятора углов прямоугольного треугольника: гипотенуза c = 5,92; катет b = 5,10; угол 59°33’.
Например, a=3, противолежащий угол = 30°27′. В поле для катетов «a» указывается 3, в поле «Угол (градусов, °)» ставится 30, в поле «Угол (минут, ‘)» указывается 27. Ответ калькулятора углов прямоугольного треугольника: гипотенуза c = 5,92; катет b = 5,10; угол 59°33’.
Калькулятор сторон прямоугольного треугольника может найти гипотенузу по катету и углу. Онлайн калькулятор гипотенузы находит катет по гипотенузе и углу.
Если стоит задача, как найти катет, если известна гипотенуза и угол, то можно использовать решение прямоугольного треугольника на этой странице. Гипотенузу прямоугольного треугольника, его угол быстро вычисляет компьютерная программа. Калькулятор теоремы Пифагора может найти катет по углу и катету.
Здесь предлагаются ответы на тесты, если требуется вычислить угол по двум катетам. Расчет гипотенузы выполняется онлайн.
Вычисление гипотенузы и углов прямоугольного треугольника при помощи калькулятора катетов дает ответы на следующие тестовые задания по теме «катет и гипотенуза«:
— как найти угол прямоугольного треугольника, зная его стороны,
— узнать гипотенузу, катет прямоугольного треугольника,
— определить гипотенузу по двум катетам,
— рассчитать третью сторону прямоугольного треугольника,
— вычислить катет, если известна гипотенуза и угол,
— найти решение прямоугольного треугольника,
— определить длину гипотенузы, зная 2 катета,
— посчитать угол в прямоугольном треугольнике,
— узнать гипотенузу по катетам,
— рассчитать величину угла в градусах и минутах по катетам,
— найти длину катета по катету и углу,
— вычислить угол или углы прямоугольного треугольника онлайн,
— решить прямоугольный треугольник,
— подсчитать угол по катетам,
— найти сторону прямоугольного треугольника,
— рассчитать прямоугольный треугольник онлайн.
Угол наклона крыши для металлочерепицы: как рассчитать оптимальный?
09.01.2020
Уклон кровли – это угол, который образуют кровельный скат и плоскость перекрытий. Угол наклона крыши из металлочерепицы зависит от многих параметров. К примеру, производитель Компания Металл Профиль прямо указывает в инструкции, какой именно уклон рекомендован для того или иного профиля черепицы. В целом диапазон, в котором может находиться угол кровельного ската из металлочерепицы, довольно велик – от 12 до 90 градусов. Однако специалисты по монтажу указывают 22 градуса, как оптимальный угол. Если по каким-то причинам вы хотите сделать кровлю более крутой или более пологой, примите во внимание некоторые особенности того и другого вариантов.
Малый уклон
- Слишком малый наклон кровли затруднит использование мансардного пространства.
- Чем меньше угол ската, тем хуже с неё стекает вода и тем больше снега скапливается на кровле.
- Более пологая кровля даёт больше нагрузки на стропильную систему.
 В таком случае целесообразно изготавливать её из более толстых пиломатериалов или же уменьшать шаг между элементами.
В таком случае целесообразно изготавливать её из более толстых пиломатериалов или же уменьшать шаг между элементами.
Большой уклон
- Слишком большой уклон затруднит выход на крышу, её обслуживание и ремонт.
- С повышением угла ската увеличится и его площадь, а, следовательно, количество необходимых стройматериалов: металлочерепицы, древесины для обрешётки, гидро- и теплоизоляции. Также вырастет вес кровельного пирога в целом и стоимость работ по монтажу кровли.
Вычислить лучший угол наклона кровли из металлочерепицы лучше всего на этапе проектирования дома, чтобы адекватно рассчитать нагрузку на фундамент. При этом необходимо учесть ряд критериев.
Снеговая нагрузка
Чем больше снега выпадает в вашем регионе, тем круче должен быть минимальный уклон крыши из металлочерепицы. Ошибка может стоить вам обрушения всей стропильной конструкции, не выдержавшей снеговую массу.
Ветровая нагрузка
И напротив, наклон крыши для металлочерепицы желательно сделать минимальным в том случае, если сильные ветра и ураганы в регионе не редкость.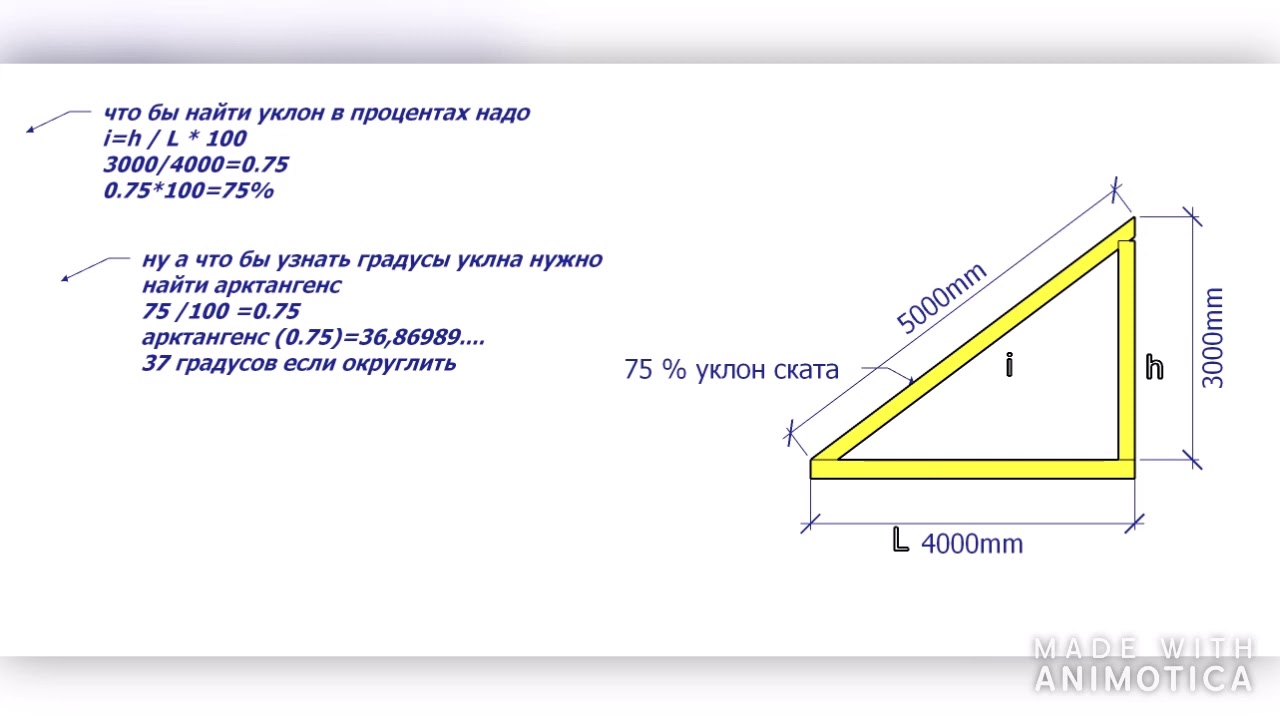 Такая структура уменьшит парусность крыши.
Такая структура уменьшит парусность крыши.
Тип кровли
На выбор угла ската влияет также тип будущей кровли. Односкатной крыше достаточно 20-30 градусов, двускатную можно сделать покруче, с углом 20-45 градусов.
Таким образом, мы видим, что нельзя однозначно ответить на вопрос: какой минимальный угол наклона крыши для металлочерепицы? Довольно много параметров нужно учесть, чтобы получить надёжную и практичную кровлю. Поэтому лучше решение этой задачи доверить профессионалам.
Как рассчитать углы: 9 шагов (с изображениями)
Поддержите образовательную миссию wikiHow
Каждый день в Wikihow, мы упорно работаем, чтобы дать вам доступ к инструкции и информацию, которые помогут вам жить лучше, то ли это держать вас безопасным, здоровым, или улучшение Вашего благосостояния. В условиях нынешнего кризиса общественного здравоохранения и экономического кризиса, когда мир резко меняется, и мы все учимся и приспосабливаемся к изменениям в повседневной жизни, людям нужна wikiHow больше, чем когда-либо. Ваша поддержка помогает wikiHow создавать более подробные иллюстрированные статьи и видеоролики и делиться нашим надежным брендом учебного контента с миллионами людей во всем мире. Пожалуйста, подумайте о том, чтобы внести свой вклад в wikiHow сегодня.
Ваша поддержка помогает wikiHow создавать более подробные иллюстрированные статьи и видеоролики и делиться нашим надежным брендом учебного контента с миллионами людей во всем мире. Пожалуйста, подумайте о том, чтобы внести свой вклад в wikiHow сегодня.
Об этой статье
Соавторы:
Доцент кафедры математики
Соавтором этой статьи является Mario Banuelos, Ph.Д. Марио Бануэлос — доцент математики Калифорнийского государственного университета во Фресно. Имея более восьми лет опыта преподавания, Марио специализируется на математической биологии, оптимизации, статистических моделях эволюции генома и науке о данных. Марио имеет степень бакалавра математики Калифорнийского государственного университета во Фресно и докторскую степень. Имеет степень доктора прикладной математики Калифорнийского университета в Мерседе. Марио преподавал как в средней школе, так и на уровне колледжа. Эта статья была просмотрена 356 027 раз (а).
Соавторы: 12
Информация обновлена: 9 февраля 2021 г.
Просмотры: 356,027
Резюме статьиXЧтобы вычислить углы в многоугольнике, сначала узнайте, к чему складываются ваши углы при суммировании, например, 180 градусов в треугольнике или 360 градусов в четырехугольнике. Как только вы узнаете, к чему складываются углы, сложите известные вам углы, а затем вычтите ответ из общих значений углов для вашей формы.Например, сложите 60 и 80, чтобы получить 140 для двух углов в треугольнике, затем вычтите 140 из 180, чтобы вычислить третий угол в треугольнике, который будет 40 градусов. Чтобы узнать, как рассчитать угол в прямоугольном треугольнике, читайте дальше!
- Печать
- Отправить письмо поклонника авторам
30 60 90 Правые треугольники
Треугольник особого вида
Прямоугольный треугольник 30-60-90 (буквально произносится как «тридцать шестьдесят девяносто») — это особый тип прямоугольного треугольника, в котором три угла составляют 30 градусов, 60 градусов и 90 градусов. Треугольник важен, потому что стороны существуют в легко запоминающемся соотношении: 1: \ (\ sqrt {3} \): 2. То есть гипотенуза в два раза длиннее более короткого отрезка, а более длинное отрезок представляет собой квадратный корень из 3-кратного более короткого отрезка. Вы также можете помнить это как «корни X, 2X и X из 3», как я это помню, но тогда вы должны помнить, что на самом деле самая длинная сторона — это 2X, а не X корней из 3.
Треугольник важен, потому что стороны существуют в легко запоминающемся соотношении: 1: \ (\ sqrt {3} \): 2. То есть гипотенуза в два раза длиннее более короткого отрезка, а более длинное отрезок представляет собой квадратный корень из 3-кратного более короткого отрезка. Вы также можете помнить это как «корни X, 2X и X из 3», как я это помню, но тогда вы должны помнить, что на самом деле самая длинная сторона — это 2X, а не X корней из 3.
Какая сторона какая? Сторона, противоположная углу 30 градусов, будет иметь наименьшую длину.Сторона, противоположная углу 60 градусов, будет в \ (\ sqrt {3} \) раз длиннее, а сторона, противоположная углу 90 градусов, будет вдвое длиннее. Треугольник ниже показывает эту взаимосвязь. Помните, что самая длинная сторона будет напротив самого большого угла, а самая короткая — напротив самого маленького угла.
Мы можем использовать соотношение между углами и сторонами треугольника 30-60-90, чтобы найти недостающие углы или длины сторон. Взгляните на этот пример:
Пример 1
Для треугольника 30-60-90 ниже найдите длины недостающих сторон:
Поскольку это прямоугольный треугольник 30-60-90, мы знаем, что стороны существуют в пропорции 1: \ (\ sqrt {3} \): 2. Самая короткая сторона, 1, находится напротив угла 30 градусов. Поскольку сторона X противоположна углу в 60 градусов, мы знаем, что он равен \ (1 * \ sqrt {3} \), или примерно 1,73. Наконец, сторона Y противоположна прямому углу, и это в два раза короче сторона, или 2.
Самая короткая сторона, 1, находится напротив угла 30 градусов. Поскольку сторона X противоположна углу в 60 градусов, мы знаем, что он равен \ (1 * \ sqrt {3} \), или примерно 1,73. Наконец, сторона Y противоположна прямому углу, и это в два раза короче сторона, или 2.
Откуда взялась формула?
Это еще одна выдуманная математическая формула? Нет! Это просто приложение базовой тригонометрии. В приведенном выше примере мы могли бы взять синус крайнего левого угла: sin (30) = 1/2.Поскольку синус дает нам отношение противоположности к гипотенузе, мы бы знали, что гипотенуза должна быть 2. По сути, вся причина, по которой треугольник 30-60-90 легко решить, заключается в том, что синус и косинус этих углов равны тоже очень просто.
Пример 2
Используйте те же принципы для поиска неизвестных переменных X и Y.
Известная сторона — 4, и это самая длинная сторона. Помните, как длинная сторона вдвое больше короткой стороны для треугольника 30-60-90? Это означает, что Y должно быть 2!
Теперь мы можем найти оставшуюся сторону. Поскольку сторона , противоположная углу в 60 градусов, равна умножению более короткой стороны на квадратный корень из 3 , мы можем вычислить, что X равно \ (2 * \ sqrt {3} \).
Поскольку сторона , противоположная углу в 60 градусов, равна умножению более короткой стороны на квадратный корень из 3 , мы можем вычислить, что X равно \ (2 * \ sqrt {3} \).
Сводка
Для прямоугольного треугольника с углами, равными 30, 60 и 90 градусов, стороны будут иметь длину в соотношении 1: \ (\ sqrt {3} \): 2, как показано на этой диаграмме:
Дополнительная справка
Как всегда, вы можете задать свои конкретные вопросы на нашей доске сообщений справки по математике, выполнить поиск в Google или пройти этот урок по 30-60-90 треугольникам или этот.Или, чтобы вычислить стороны и углы треугольника, используйте интерактивный инструмент ниже:
Специальные значения углов: 30-60-90 и 45-45-90 Треугольники
Purplemath
Есть несколько ( очень несколько) углов, которые имеют относительно «аккуратные» тригонометрические значения, включая, в худшем случае, один квадратный корень. Из-за их относительно простых значений, эти углы обычно используются в математических задачах (особенно в расчетах), и вы будете , как ожидается, запомнят значения этих углов.
Из-за их относительно простых значений, эти углы обычно используются в математических задачах (особенно в расчетах), и вы будете , как ожидается, запомнят значения этих углов.
Ожидается, что вы будете использовать эти значения для получения «точных» ответов при решении прямоугольных треугольников и нахождении значений различных тригонометрических соотношений.
Обычно в учебниках эти значения представлены в виде таблицы, которую вы должны запомнить.Но картинки часто легче вспомнить на тестах и т.д., по крайней мере, для некоторых из нас. Если эти таблицы не работают для вас, то этот урок покажет, как многие люди (включая меня!) на самом деле отслеживают эти значения.
MathHelp.com
Далее я использую градусы для измерения углов. Обычно так студентов знакомят с угловыми мерами. Однако, если вы работаете с радианами, я также отмечу эквиваленты радианов для измерения угла.
Обычно так студентов знакомят с угловыми мерами. Однако, если вы работаете с радианами, я также отмечу эквиваленты радианов для измерения угла.
Значения угла 45 ° (из треугольника 45-45-90)
Все треугольники 45-45-90 похожи; то есть все они имеют соотношения сторон. (Угол в 45 ° равен в радианах
π / 4.) Итак, давайте посмотрим на очень простой угол 45-45-90:Гипотенуза этого треугольника, обозначенного выше как 2, находится путем применения теоремы Пифагора к прямоугольному треугольнику со сторонами, имеющими длину
sqrt [2] .Базовый угол в нижнем левом углу обозначен символом «тета» (θ, THAY-tuh) и равен 45 °. Так как же нам помогает знание этого треугольника? Это помогает нам, потому что все треугольники 45-45-90 похожи. Следовательно, любой вопрос «оценки» или «решение треугольника», включающий треугольник 45-45-90 или просто угол 45 °, может быть выполнен с использованием этого треугольника. Эта картинка — все, что вам нужно.
Эта картинка — все, что вам нужно.
Значения углов 30 ° и 60 ° (из треугольника 30-60-90)
Когда нам нужно работать под углом 30 или 60 градусов, процесс аналогичен описанному выше, но настройка немного дольше.(Угол 30 ° эквивалентен углу
π / 6 радиан; угол 60 ° эквивалентен углу π / 3 радиан.)Для любого из углов это треугольник, с которого мы начинаем:
Это треугольник 60-60-60 (то есть равносторонний треугольник), длина сторон которого равна двум единицам.
Опускаем вертикальную биссектрису с верхнего угла вниз на нижнюю сторону:
Обратите внимание, что эта биссектриса также является высотой (высотой) треугольника.
Используя теорему Пифагора, мы получаем, что длина биссектрисы равна
sqrt [3]. И эта биссектриса образовала два треугольника 30-60-90.
И эта биссектриса образовала два треугольника 30-60-90.Когда мы работаем с углом 60 градусов, мы используем левый треугольник наверху, он стоит, с основным углом (слева), обозначенным «α» (AL-phuh, забавно выглядящим «a»). «):
Когда мы работаем с углом 30 градусов, мы используем правый треугольник, перевернутый влево, базовый угол (слева) обозначен «β» (BAY-tuh, забавно выглядящее «b» ):
Мы можем найти тригонометрические значения и соотношения для треугольников с 30 и 60 градусами точно так же, как и с треугольниками с 45 градусами.Все, что вам понадобится, — это изображения выше.
Вы можете найти одного из тех учителей, которые не хотят, чтобы вы рисовали эти картинки (потому что к этому моменту вы должны все запомнить). Вот почему у твоего карандаша есть ластик. Мой инструктор по исчислению II сказал, что если мы нарисуем картинки на наших тестах, вся задача будет засчитана неправильно. Я все равно рисовал картинки, но очень легко, и стер их все, прежде чем сдать тесты. Он так и не узнал, и я прошел курс.Делай то, что должен.
Я все равно рисовал картинки, но очень легко, и стер их все, прежде чем сдать тесты. Он так и не узнал, и я прошел курс.Делай то, что должен.
Использование стола
Рисунки выше — это то, что я всегда использовал, и многие находят их полезными. С другой стороны, некоторые люди предпочитают таблицы или другие методы. Если вам больше подходят столы, то настоятельно рекомендуется использовать этот стол, который прошел «полевые испытания» действующим инструктором:
Чтобы найти, скажем, синус угла в сорок пять градусов, вы должны провести поперек в строке «грех» и вниз по столбцу «45 °», взяв с собой символ квадратного корня и не забывая включите «деленное на 2» снизу, чтобы получить
sin (45 °) = sqrt (2) / 2.Аккуратный узор «1, 2, 3» в верхней строке и «3, 2, 1» в средней строке призван помочь вам запомнить значения таблицы.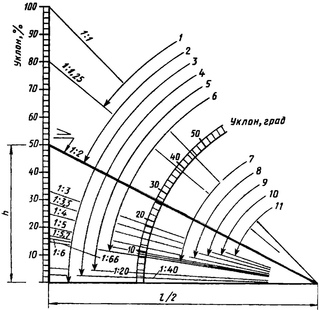 Имейте в виду, что квадратный корень из 1 равен 1, поэтому, например, cos (60 °) = sqrt (1) / 2 = 1/2. Чтобы найти тангенс, нужно разделить значение синуса на значение косинуса.
Имейте в виду, что квадратный корень из 1 равен 1, поэтому, например, cos (60 °) = sqrt (1) / 2 = 1/2. Чтобы найти тангенс, нужно разделить значение синуса на значение косинуса.Использование пальцев
Другой метод использует вашу левую руку, чтобы сделать то же самое. Повернув ладонь к себе, отсчитайте основные исходные углы, начиная с большого пальца: 0 °, 30 °, 45 °, 60 ° и 90 °.
Чтобы найти значение триггера, вы опустите палец, соответствующий этому углу, держа ладонь к себе. В качестве значения синуса вы возьмете квадратный корень из числа пальцев слева от опущенного пальца и разделите его на 2; для значения косинуса возьмите квадратный корень из числа пальцев справа от опущенного пальца и разделите его на 2; для касательной разделите квадратный корень из числа пальцев слева на квадратный корень из числа справа (и при необходимости рационализируйте).
Например, если вы хотите работать под углом в тридцать градусов, вы должны сориентировать руку следующим образом:
Синус — это квадратный корень из большого пальца (то есть квадратный корень из единицы) над двумя, что дает:
Косинус — это квадратный корень из трех ваших пальцев (то есть квадратный корень из трех) над двумя, что дает:
Филиал
С другой стороны, если вы хотите оценить sin (0 °), cos (0 °) и cot (0 °), вы должны сориентировать левую руку следующим образом:
Поскольку ваш большой палец сложен вниз, 0 пальцев слева и 4 пальца справа.Тогда значения синуса и косинуса находятся как:
sin (0 °) = sqrt [0] / 2 = 0
cos (0 °) = sqrt [4] / 2 = 1
Котангенс — это величина, обратная касательной. Каково значение тангенса?
Каково значение тангенса?
загар (0 °) = sqrt [0] / sqrt [4] = 0
Переворачивание вышеуказанного приведет к делению на ноль, что недопустимо.Таким образом, cot (0 °) не определено.
(Угол в 0 ° эквивалентен углу в 0 радиан. Угол в 90 ° эквивалентен углу в
π / 2 радиан.)URL: https://www.purplemath.com/modules/specang.htm
Простое руководство к треугольнику 30-60-90
Острый, тупой, равнобедренный, равносторонний… Когда дело доходит до треугольников, существует много различных разновидностей, но лишь немногие из них являются «особенными».«У этих особых треугольников есть стороны и углы, которые согласованы и предсказуемы, и их можно использовать, чтобы сократить путь к решению ваших геометрических или тригонометрических задач.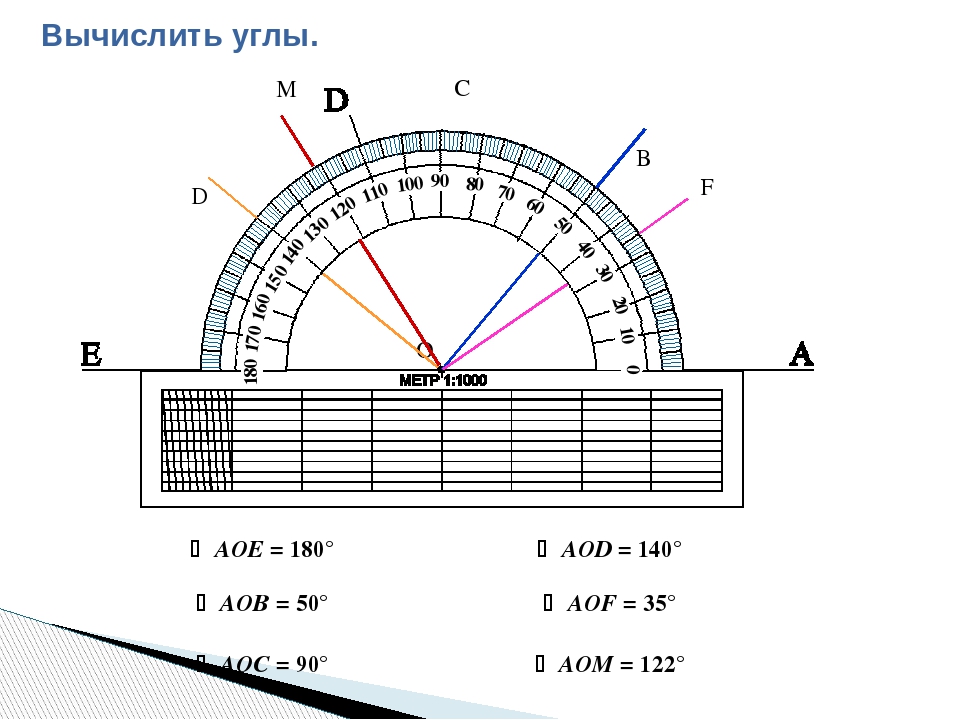 А треугольник 30-60-90 — произносится как« тридцать шестьдесят девяносто »- оказывается совершенно особенным действительно тип треугольника.
А треугольник 30-60-90 — произносится как« тридцать шестьдесят девяносто »- оказывается совершенно особенным действительно тип треугольника.
В этом руководстве мы расскажем, что такое треугольник 30-60-90, почему он работает и когда (и как) использовать свои знания о нем. Итак, приступим!
Что такое треугольник 30-60-90?
Треугольник 30-60-90 — это специальный прямоугольный треугольник (прямоугольный треугольник — это любой треугольник с углом 90 градусов), который всегда имеет углы 30, 60 и 90 градусов.Поскольку это особый треугольник, у него также есть значения длины стороны, которые всегда находятся в постоянном соотношении друг с другом.
Базовое соотношение треугольника 30-60-90:
Сторона, противоположная углу 30 °: $ x
Сторона, противоположная углу 60 °: $ x * √3 $
Сторона, противоположная углу 90 °: 2 доллара x
долларов СШАНапример, треугольник 30-60-90 градусов может иметь длину стороны:
2, 2√3, 4
7, 7√3, 14
√3, 3, 2√3
(Почему более длинная часть 3? В этом треугольнике самая короткая часть ($ x $) равна $ √3 $, поэтому для более длинной ветви $ x√3 = √3 * √3 = √9 = 3 $.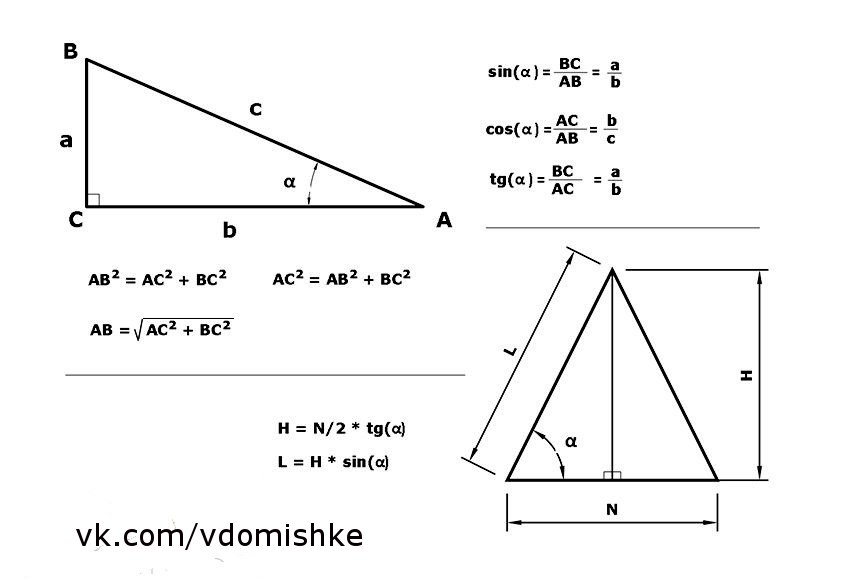 А гипотенуза — это 2 кратчайшего отрезка, или 2√3 $)
А гипотенуза — это 2 кратчайшего отрезка, или 2√3 $)
И так далее.
Сторона, противоположная углу 30 °, всегда является наименьшим , потому что 30 ° — наименьший угол. Сторона, противоположная углу 60 °, будет средней длиной , потому что 60 градусов — это средний угол в этом треугольнике. И, наконец, сторона, противоположная углу 90 °, всегда будет самой большой стороной (гипотенуза) , потому что 90 градусов — это наибольший угол.
Хотя он может выглядеть так же, как и другие типы прямоугольных треугольников, причина, по которой треугольник 30-60-90 настолько особенная, заключается в том, что вам нужно всего три части информации, чтобы найти любое другое измерение. Пока вы знаете значение двух угловых мер и длины одной стороны (неважно, с какой стороны), вы знаете все, что вам нужно знать о своем треугольнике.
Например, мы можем использовать формулу треугольника 30-60-90, чтобы заполнить все оставшиеся информационные поля треугольников ниже.
Пример 1
Мы видим, что это прямоугольный треугольник, в котором гипотенуза в два раза длиннее одного из катетов. Это означает, что это должен быть треугольник 30-60-90, а меньшая заданная сторона противоположна 30 °.
Следовательно, более длинная полка должна располагаться напротив угла 60 ° и иметь размер 6 * √3 $ или 6√3 $.
Пример 2
Мы видим, что это должен быть треугольник 30-60-90, потому что мы видим, что это прямоугольный треугольник с одним заданным размером 30 °.Тогда немаркированный угол должен составлять 60 °.
Поскольку 18 — это мера, противоположная углу 60 °, она должна быть равна $ x√3 $. Тогда самая короткая ветка должна иметь размер 18 долл. США / √3 долл. США.
(обратите внимание, что длина отрезка на самом деле будет $ 18 / {√3} * {√3} / {√3} = {18√3} / 3 = 6√3 $, потому что знаменатель не может содержать радикальный / квадратный корень) .
А гипотенуза будет 2 (18 / √3) $
(обратите внимание, что, опять же, у вас не может быть радикала в знаменателе, поэтому окончательный ответ будет в два раза больше длины ноги $ 6√3 $ => $ 12√3 $).
Пример 3
Опять же, нам даны два измерения угла (90 ° и 60 °), поэтому третье измерение будет 30 °. Поскольку это треугольник 30-60-90, а гипотенуза равна 30, самый короткий отрезок будет равен 15, а более длинный отрезок будет равен 15√3.
Не нужно обращаться к волшебному шару-восьмерке — эти правила работают всегда.
Почему это работает: 30-60-90 Доказательство теоремы о треугольнике
Но почему этот особый треугольник работает именно так? Как мы узнаем, что эти правила законны? Давайте подробно рассмотрим, как работает теорема о треугольнике 30-60-90, и докажем, почему эти длины сторон всегда будут согласованными.
Во-первых, давайте на секунду забудем о прямоугольных треугольниках и посмотрим на равносторонний треугольник .
Равносторонний треугольник — это треугольник, у которого все стороны и углы равны. Поскольку внутренние углы треугольника всегда составляют в сумме 180 ° и $ 180/3 = 60 $, равносторонний треугольник всегда будет иметь три угла по 60 °.
Теперь давайте опустим высоту от самого верхнего угла до основания треугольника.
Теперь мы создали два прямых угла и два равных (равных) треугольника.
Откуда мы знаем, что это равные треугольники? Поскольку мы опустили высоту равностороннего треугольника , мы разделили основание ровно пополам. Новые треугольники также имеют одну общую длину стороны (высоту), и каждый из них имеет одинаковую длину гипотенузы. Поскольку у них три общих длины стороны (SSS), это означает, что треугольники равны .
Примечание: два треугольника конгруэнтны на основе принципов длины стороны-стороны или SSS, но также основаны на измерениях стороны-угла-стороны (SAS), угла-угла-стороны (AAS) и угла -угловой (ASA).По сути? Они определенно совпадают.
Теперь, когда мы доказали конгруэнтность двух новых треугольников, мы можем видеть, что каждый из верхних углов должен быть равен 30 градусам (потому что каждый треугольник уже имеет углы 90 ° и 60 ° и в сумме должно составлять 180 °). . Это означает, что мы сделали два треугольника 30-60-90.
. Это означает, что мы сделали два треугольника 30-60-90.
И поскольку мы знаем, что мы разрезаем основание равностороннего треугольника пополам, мы можем видеть, что сторона, противоположная углу 30 ° (самая короткая сторона) каждого из наших треугольников 30-60-90, составляет ровно половину длины треугольника. гипотенуза.2} / 4
долларов США$ b = {√3x} / 2
$Итак, у нас осталось: x / 2, {x√3} / 2, x
Теперь давайте умножим каждую меру на 2, просто чтобы облегчить жизнь и избежать всех дробей. Таким образом, у нас осталось:
$ x $, $ x√3 $, 2x $
Таким образом, мы можем видеть, что треугольник 30-60-90 всегда будет иметь одинаковые длины сторон $ x $, $ x√3 $ и $ 2x $ (или $ x / 2 $, $ {√3x } / 2 $ и $ x $).
К счастью для нас, мы можем доказать, что правила треугольника 30-60-90 верны без всего…это.
Когда использовать правила треугольника 30-60-90
Знание правил треугольника 30-60-90 поможет вам сэкономить время и силы при решении множества различных математических задач, а именно, большого разнообразия задач по геометрии и тригонометрии.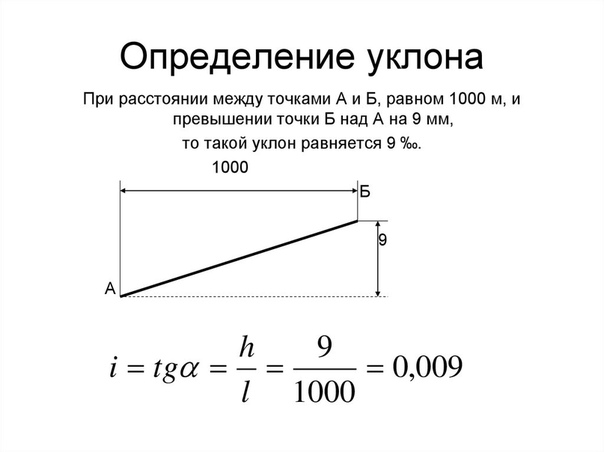
Геометрия
Правильное понимание треугольников 30-60-90 позволит вам решать вопросы геометрии, которые либо невозможно решить, не зная этих правил соотношения, либо, по крайней мере, потребуется значительное время и усилия для решения «долгого пути».«
С помощью специальных соотношений треугольников вы можете вычислить недостающие высоты или длины участков треугольника (без использования теоремы Пифагора), найти площадь треугольника, используя недостающую информацию о высоте или базовой длине, и быстро вычислить периметры.
Каждый раз, когда вам нужна скорость, чтобы ответить на вопрос, вам пригодятся такие ярлыки, как правила 30-60-90.
Тригонометрия
Запоминание и понимание соотношения треугольников 30-60-90 также позволит вам решать многие тригонометрические задачи без использования калькулятора или необходимости приближать ваши ответы в десятичной форме.
Треугольник 30-60-90 имеет довольно простые синусы, косинусы и тангенсы для каждого угла (и эти измерения всегда будут согласованы).
Синус 30 ° всегда будет $ 1/2 $.
Косинус 60 ° всегда будет $ 1/2 $.
Хотя другие синусы, косинусы и тангенсы довольно просты, их легче всего запомнить, и они, вероятно, обнаружатся на тестах. Таким образом, знание этих правил позволит вам как можно быстрее найти эти тригонометрические измерения.
Советы по запоминанию правил 30-60-90
Вы знаете, что эти правила соотношения 30-60-90 полезны, но как вы удерживаете информацию в своей голове? Чтобы помнить правила треугольника 30-60-90, нужно помнить о соотношении 1: √3: 2 и знать, что длина самой короткой стороны всегда противоположна самому короткому углу (30 °), а длина самой длинной стороны всегда противоположна наибольший угол (90 °).
Некоторые люди запоминают соотношение, думая: « $ \ bi x $, $ \ bo 2 \ bi x $, $ \ bi x \ bo √ \ bo3 $, », потому что последовательность «1, 2, 3» обычно легко запомнить. Единственная мера предосторожности при использовании этого метода — помнить, что самая длинная сторона на самом деле — это $ 2x $, , а не , $ x $, умноженное на $ √3 $.
Другой способ запомнить ваши отношения — это использовать мнемоническую игру слов на соотношении 1: корень 3: 2 в их правильном порядке. Например, «Джеки Митчелл выбил Лу Герига и« выиграл и Рути тоже »»: один, корень три, два. (И это, кстати, настоящий факт из истории бейсбола!)
Поиграйте со своими собственными мнемоническими устройствами, если они вам не нравятся — спойте отношение к песне, найдите свои собственные фразы «один, корень три, два» или придумайте стихотворение о соотношении.Вы даже можете просто запомнить, что треугольник 30-60-90 — это половина равносторонней стороны, и вычислить оттуда размеры, если вам не нравится их запоминать.
Тем не менее, для вас имеет смысл запомнить эти правила 30-60-90, держать их в уме для будущих вопросов по геометрии и тригонометрии.
Запоминание — ваш друг, но вы можете сделать это возможным.
Указывает ли ваша школа, что ваш средний балл является взвешенным или невзвешенным? Каким будет ваш средний балл, с учетом 4. Шкала 0, 5.0 или 6.0? Воспользуйтесь нашим инструментом, чтобы рассчитать свой невзвешенный и взвешенный средний балл успеваемости, чтобы выяснить, как вы соотноситесь с другими поступающими в колледж. Вы также получите наш собственный расчет среднего балла среднего балла колледжа и советы о том, где можно улучшить, чтобы стать лучшим поступающим в колледж.
Шкала 0, 5.0 или 6.0? Воспользуйтесь нашим инструментом, чтобы рассчитать свой невзвешенный и взвешенный средний балл успеваемости, чтобы выяснить, как вы соотноситесь с другими поступающими в колледж. Вы также получите наш собственный расчет среднего балла среднего балла колледжа и советы о том, где можно улучшить, чтобы стать лучшим поступающим в колледж.
Пример 30-60-90 Вопросы
Теперь, когда мы рассмотрели «как» и «почему» 30-60-90 треугольников, давайте поработаем над некоторыми практическими задачами.
Геометрия
Строитель прислоняет 40-футовую лестницу к стене здания под углом 30 градусов от земли.Земля ровная, а сторона здания перпендикулярна земле. Как далеко вверх по зданию до ближайшего подножия поднимается лестница?
Не зная наших специальных правил треугольника 30-60-90, нам пришлось бы использовать тригонометрию и калькулятор, чтобы найти решение этой проблемы, так как у нас есть только измерение одной стороны треугольника. Но поскольку мы знаем, что это особый треугольник , мы можем найти ответ за считанные секунды.
Но поскольку мы знаем, что это особый треугольник , мы можем найти ответ за считанные секунды.
Если здание и земля перпендикулярны друг другу, это должно означать, что здание и земля образуют прямой (90 °) угол.Также известно, что лестница встречается с землей под углом 30 °. Таким образом, мы видим, что оставшийся угол должен составлять 60 °, что составляет треугольник 30-60-90.
Теперь мы знаем, что гипотенуза (самая длинная сторона) этого 30-60-90 составляет 40 футов, что означает, что самая короткая сторона будет вдвое меньшей длины. (Помните, что самая длинная сторона всегда вдвое длиннее — $ 2x $ — самой короткой стороны.) Поскольку самая короткая сторона находится напротив угла 30 °, и этот угол является мерой лестницы от земли в градусах, это означает, что верхняя часть лестницы ударяется о здание на высоте 20 футов от земли.
Наш окончательный ответ — 20 футов.
Тригонометрия
Если в прямоугольном треугольнике sin Θ = $ 1/2 $, а длина самого короткого участка равна 8. Какова длина недостающей стороны, НЕ являющейся гипотенузой?
Какова длина недостающей стороны, НЕ являющейся гипотенузой?
Так как вы знаете свои правила 30-60-90, вы можете решить эту проблему без использования теоремы Пифагора или калькулятора.
Нам сказали, что это прямоугольный треугольник, и мы знаем из наших специальных правил прямоугольного треугольника, что синус 30 ° = $ 1/2 $.Следовательно, недостающий угол должен составлять 60 градусов, что делает треугольник 30-60-90.
И поскольку это треугольник 30-60-90, и нам сказали, что самая короткая сторона равна 8, гипотенуза должна быть равна 16, а недостающая сторона должна быть $ 8 * √3 $ или 8√3 $.
Наш окончательный ответ — 8√3.
Итоги
Запомнив правила для треугольников 30-60-90, вы сможете сократить свой путь через множество математических задач .Но имейте в виду, что, хотя знание этих правил — удобный инструмент, который нужно держать на поясе, вы все равно можете решить большинство проблем без них.
Следите за правилами $ x $, $ x√3 $, $ 2x $ и 30-60-90 любым понятным для вас образом и старайтесь придерживаться их, если можете, но не паникуйте, если вы ум исчезает, когда наступает время кризиса. В любом случае, у вас есть это.
И, если вам нужно больше практики, попробуйте эту викторину с треугольником 30-60-90. Удачной сдачи теста!
Калькулятор угла и гипотенузы прямоугольного треугольника
- Цель использования
- для использования в строительно-монтажных работах на стройплощадке
- Комментарий / запрос
- Я не могу найти угол скоса в регуляторе головки при орошении
[1] 2020/12/30 13:12 Мужчина / До 20 лет / Инженер / Очень /
- Цель использования
- Определите ширину экрана Iphone 8 Plus, поскольку я использую его для измерения ширины кусочка зубной нити, которым я измерял безымянный палец моей подруги без линейки, чтобы купить обручальное кольцо.
[2] 2020/10/14 17:58 Мужчина / Уровень 30 лет / Средняя школа / Университет / Аспирант / Полезно /
- Цель использования
- Для выработки угла крыши садовой постройки.
[3] 2020.09.11 18:57 Мужской / 50-летний уровень / Другое / Очень /
- Цель использования
- Необходим для определения оптимального размера телевизора, если рекомендуемый угол просмотра составляет 30 градусов от края до края телевизора при измерении из положения сидя.
[4] 2020/08/18 00:21 Мужчина / Уровень 40 лет / Другое / Полезно /
- Цель использования
- Направление направленной антенны на вышку сотовой связи на вершине горы
[5] 2020/07/29 05:31 — / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Убедитесь, что планировка машинного навеса будет квадратной и возведенной в соответствии с проектом.
[6] 2020/06/30 21:44 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Определение угла и длины гипотенузы для резки деревянной балки для каркаса А на крыше форта My Kids
[7] 2020.06.06 19:33 Мужчина / Уровень 40 лет / Инженер / Очень /
- Цель использования
- Кардиолог 67 лет.
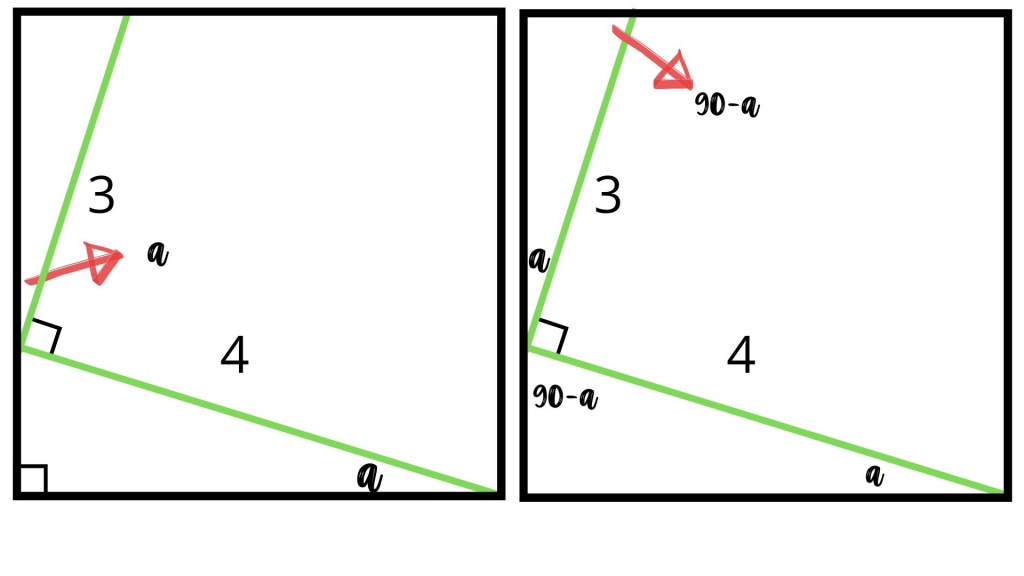 Расчет длин и углов для проекта изготовления металлических изделий Плюс, отличный обзор, отличный обзор тригонометрии!
Расчет длин и углов для проекта изготовления металлических изделий Плюс, отличный обзор, отличный обзор тригонометрии!
[8] 2020/06/01 20:35 Мужчина / 60 лет и старше / Самостоятельно занятые лица / Очень /
- Цель использования
- найдите угол прямоугольного треугольника с подъемом и спуском, известный как скат для инвалидных колясок.
[9] 2020/03/11 03:24 Мужчина / Уровень 40 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Не могу вспомнить противоположное по соседнему правилу для угла в прямоугольном треугольнике!
[10] 2019/11/08 23:57 Мужской / 50-летний уровень / Самозанятые / Полезные /
Треугольник 30 ° -60 ° -90 ° — объяснение и примеры
- Дом
- >
- Треугольник 30 ° -60 ° -90 ° — пояснения и примеры
Теперь, когда мы закончили с прямоугольным треугольником и другими специальными прямоугольными треугольниками, пора пройти через последний специальный треугольник, который представляет собой треугольник 30 ° -60 ° -90 °.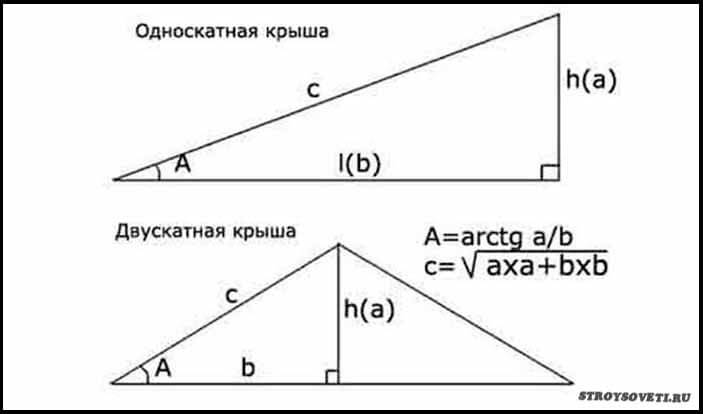
Он также имеет такое же значение, что и треугольник 45 ° -45 ° -90 ° из-за соотношения сторон. У него два острых угла и один прямой.
Что такое треугольник 30-60-90?
Треугольник 30-60-90 — это специальный прямоугольный треугольник, углы которого равны 30º, 60º и 90º. Треугольник особенный, потому что его стороны всегда находятся в соотношении 1: √3: 2.
Любой треугольник формы 30-60-90 можно решить без применения длинных шагов , таких как теорема Пифагора и тригонометрические функции.
Самый простой способ запомнить соотношение 1: √3: 2 — это запомнить числа; «1, 2, 3» . Одна из мер предосторожности при использовании этой мнемоники — помнить, что 3 находится под знаком квадратного корня.
Из иллюстрации выше мы можем сделать следующие наблюдения относительно треугольника 30-60-90:
- Более короткая ножка, противоположная 30-градусному углу, помечена как x.

- Гипотенуза, противоположная углу 90 градусов, в два раза длиннее более короткого отрезка (2x).
- Более длинная полка, противоположная углу в 60 градусов, равна произведению более короткой ветви и квадратного корня из трех (x√3).
Как решить треугольник 30-60-90?
Решая задачи с треугольниками 30-60-90, вы всегда знаете одну сторону, по которой можно определить другие стороны. Для этого вы можете умножить или разделить эту сторону на соответствующий коэффициент.
Вы можете резюмировать различные сценарии как:
- Если известна более короткая сторона, вы можете найти более длинную, умножив более короткую сторону на квадратный корень из 3.После этого вы можете применить теорему Пифагора, чтобы найти гипотенузу.
- Когда длинная сторона известна, вы можете найти более короткую, погружая большую сторону на квадратный корень из 3. После этого вы можете применить теорему Пифагора, чтобы найти гипотенузу.
- Когда известна более короткая сторона, вы можете найти гипотенузу, умножив более короткую сторону на 2.
 После этого вы можете применить теорему Пифагора, чтобы найти более длинную сторону.
После этого вы можете применить теорему Пифагора, чтобы найти более длинную сторону. - Если гипотенуза известна, вы можете найти более короткую сторону, разделив гипотенузу на 2.После этого вы можете применить теорему Пифагора, чтобы найти более длинную сторону.
Это означает, что более короткая сторона действует как шлюз между другими двумя сторонами прямоугольного треугольника . Вы можете найти более длинную сторону, когда задана гипотенуза, или наоборот, но вам всегда нужно сначала найти более короткую сторону.
Кроме того, для решения задачи , связанной с треугольниками 30-60-90 , вам необходимо знать следующие свойства треугольников:
- Сумма внутренних углов в любом треугольнике в сумме дает 180 °.Следовательно, если вы знаете величину двух углов, вы можете легко определить третий угол, вычтя величину этих двух углов из 180 градусов.
- Самая короткая и самая длинная стороны в любом треугольнике всегда противоположны наименьшему и наибольшему углу соответственно.
 Это правило также относится к треугольнику 30-60-90.
Это правило также относится к треугольнику 30-60-90. - Треугольники с одинаковыми углами похожи, и их стороны всегда будут иметь одинаковое отношение друг к другу. Таким образом, концепция подобия может использоваться для решения задач, связанных с треугольниками 30-60-90.
- Поскольку треугольник 30-60-90 является прямоугольным, то теорема Пифагора a 2 + b 2 = c 2 также применима к треугольнику. Например, мы можем доказать, что гипотенуза треугольника равна 2x, следующим образом:
⇒ c 2 = x 2 + (x√3) 2
⇒ c 2 = x 2 + (x√3) (x√3)
⇒ c 2 = x 2 + 3x 2
⇒ c 2 = 4x 2
Найдите квадратный корень из обеих частей.
√c 2 = √4x 2
с = 2х
Значит, доказано.
Давайте поработаем над некоторыми практическими задачами.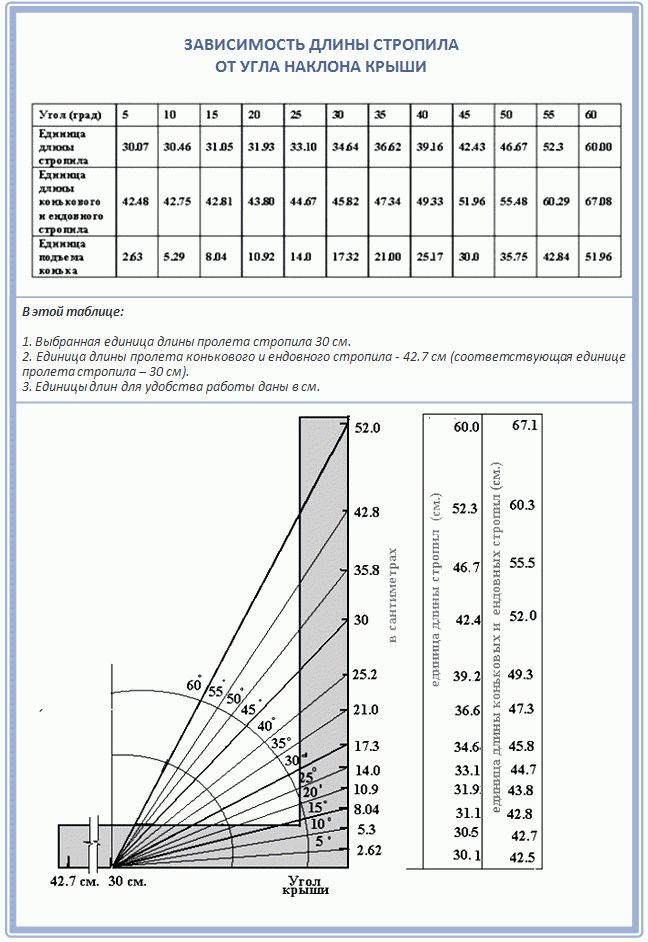
Пример 1
У прямоугольного треугольника с одним углом 60 градусов длинная сторона равна 8√3 см. Вычислите длину его более короткой стороны и гипотенузу.
Решение
Из отношения x: x√3: 2x длинная сторона равна x√3. Итак, у нас есть;
x√3 = 8√3 см
Возведите обе части уравнения в квадрат.
⇒ (x√3) 2 = (8√3) 2
⇒ 3x 2 = 64 * 3
⇒ x 2 = 64
Найдите квадрат обеих сторон.
√x 2 = √64
x = 8 см
Запасной.
2x = 2 * 8 = 16 см.
Следовательно, более короткая сторона равна 8 см, а гипотенуза — 16 см.
Пример 2
Лестница, прислоненная к стене, образует с землей угол 30 градусов.Если длина лестницы 9 м, найти;
а. Высота стены.
г. Вычислите длину между основанием лестницы и стеной.
Решение
Учитывая, что один угол равен 30 градусам, тогда это должен быть прямоугольный треугольник 60 ° — 60 ° — 90 °.
Соотношение = x: x√3: 2x.
⇒ 2x = 9
⇒ х = 9/2
= 4,5
Запасной.
а. Высота стены = 4,5 м
г. х√3 = 4.5√3 м
Пример 3
Диагональ прямоугольного треугольника равна 8 см. Найдите длины двух других сторон треугольника, учитывая, что один из его углов равен 30 градусам.
Решение
Это должен быть треугольник 30 ° -60 ° -90 °. Поэтому мы используем соотношение x: x√3: 2x.
Диагональ = гипотенуза = 8 см.
⇒2x = 8 см
⇒ x = 4 см
Запасной.
x√3 = 4√3 см
Более короткая сторона прямоугольного треугольника равна 4 см, а длинная — 4√3 см.
Пример 4
Найдите значения x и z на диаграмме ниже:
Решение
Длина 8 дюймов будет короче, потому что она противоположна углу в 30 градусов. Чтобы найти значение z (гипотенуза) и y (более длинный отрезок), мы действуем следующим образом;
Из соотношения x: x√3: 2x;
x = 8 дюймов.
Запасной.
⇒ x√3 = 8√3
⇒2x = 2 (8) = 16.
Следовательно, y = 8√3 дюйма и z = 16 дюймов.
Пример 5
Если один угол прямоугольного треугольника равен 30º, а длина самой короткой стороны равна 7 м, каковы размеры двух оставшихся сторон?
Решение
Это треугольник 30-60-90, в котором длины сторон находятся в соотношении x: x√3: 2x.
Заменим x = 7 м для более длинного отрезка и гипотенузы.
⇒ x √3 = 7√3
⇒ 2x = 2 (7) = 14
Следовательно, другие стороны 14 м и 7√3 м
Пример 6
В прямоугольном треугольнике гипотенуза равна 12 см, а меньший угол равен 30 градусам.Найдите длину длинной и короткой ноги.
Решение
Дано соотношение сторон = x: x√3: 2x.
2x = 12 см
x = 6 см
Для получения длинной и короткой ножки замените x = 6 см;
Короткая штанина = 6 см.
длинная ножка = 6√3 см
Пример 7
Две стороны треугольника 5√3 мм и 5 мм. Найдите длину его диагонали.
Решение
Проверьте соотношение длин сторон, если оно соответствует соотношению x: x√3: 2x.
5: 5√3 😕 = 1 (5): √3 (5) 😕
Следовательно, x = 5
Умножить 2 на 5.
2x = 2 * 5 = 10
Следовательно, гипотенуза равна 10 мм.
Пример 8
Пандус, образующий угол 30 градусов с землей, используется для разгрузки грузовика высотой 2 фута. Рассчитайте длину пандуса.
Решение
Это должен быть треугольник 30-60-90.
x = 2 фута.
2x = 4 фута
Следовательно, длина пандуса составляет 4 фута.
Пример 9
Найдите гипотенузу треугольника 30 ° — 60 ° — 90 °, длинная сторона которого 6 дюймов.
Решение
Соотношение = x: x√3: 2x.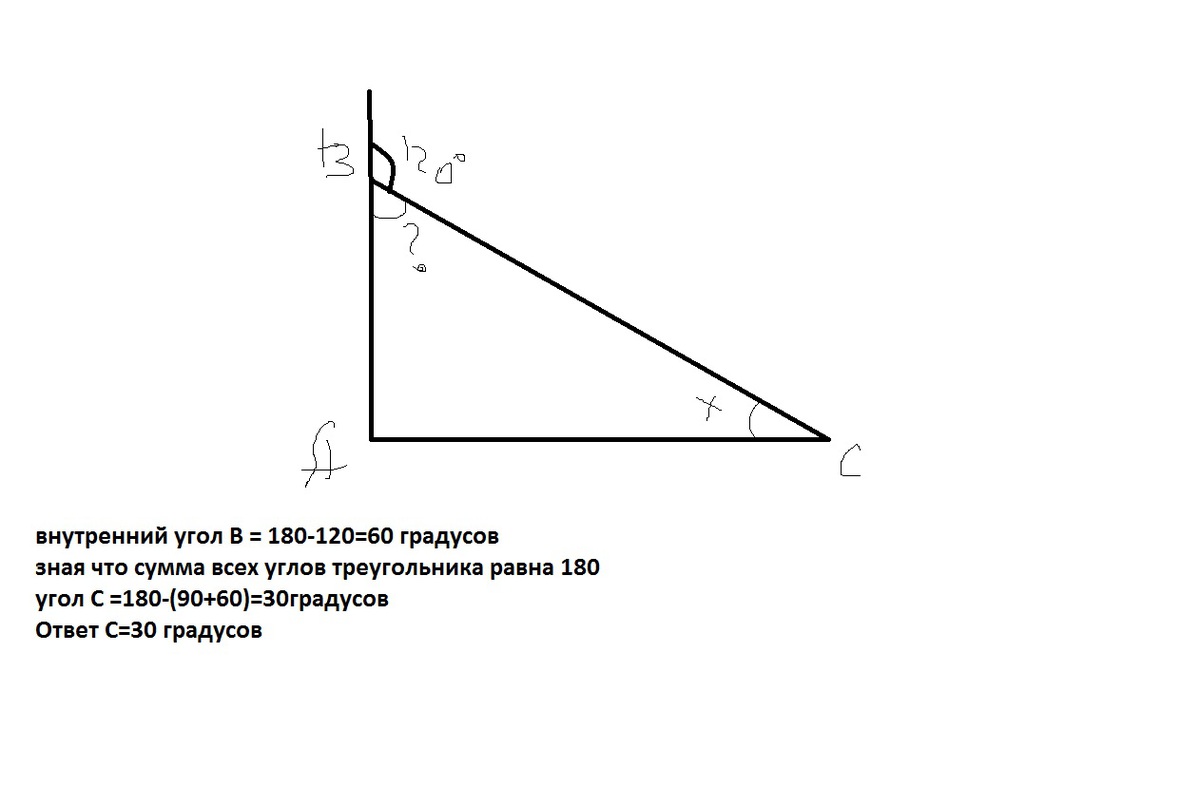
⇒ x√3 = 6 дюймов.
Квадрат с двух сторон
⇒ (x√3) 2 = 36
⇒ 3x 2 = 36
х 2 = 12
x = 2√3 дюйма.
Пример 10:
Какова длина гипотенузы прямоугольного треугольника, у которого две стороны 4 дюйма и 4√3 дюйма.
Решение:
Проверить, соответствует ли соотношение длин соотношению n: n√3: 2n
4: 4√3 😕 = п: п√3: 2n
Да, это треугольник 30-60-90 с n = 4
Теперь найдите длину третьей стороны.
2n = 2 × 4 = 8
Следовательно, длина гипотенузы составляет 8 дюймов.
Пример 11:
Гипотенуза и один угол прямоугольного треугольника составляют 8 дюймов и 30 °. соответственно. Найдите длины двух других сторон треугольника.
Решение:
Учитывая, что отношение сторон равно n: n√3: 2n,
Подставляем значения, чтобы получить,
2n = 8 ⇒ n = 4.
Длина двух сторон составляет 4 дюйма и 4√3 дюйма.
Практические проблемы
- В треугольнике 30 ° — 60 ° — 90 ° пусть сторона, лежащая напротив угла 60 °, равна 9√3.Найдите длину двух других сторон.
- Если гипотенуза треугольника 30 ° — 60 ° — 90 ° равна 26, найдите две другие стороны.
- Если длинная сторона треугольника 30 ° — 60 ° — 90 ° равна 12, какова сумма двух других сторон этого треугольника?
- Покажите, что длины треугольника 30 ° — 60 ° — 90 ° находятся в соотношении n: n√3: 2n,
- Найдите длину дорожного знака, имеющего форму равностороннего треугольника высотой 18√3 дюймов.
Предыдущий урок | Главная страница | Следующий урок
Измерение углов
Измерение угловПонятие угла
Понятие угла — одно из самых важных понятий в геометрии.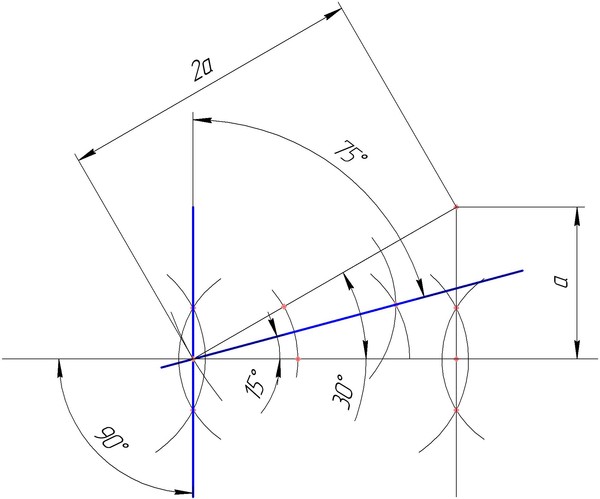 Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .
Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равняется π /180 радиани 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. |
Краткая записка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей работе Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e iθ = cos θ + i sin θгде θ — это то, что позже было названо радианами измерения угла. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается в виде отношения.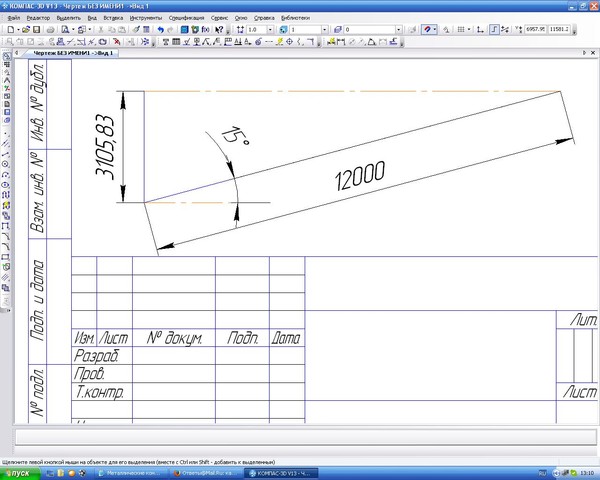 Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, то радианная мера равна 1.5.
Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, то радианная мера равна 1.5.Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает то же число, что и приведенное выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтому
Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерения в радианах даны как π . Конечно, его можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π .| Уголок | градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С. Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», , Пенсильванский университет, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», , Пенсильванский университет, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.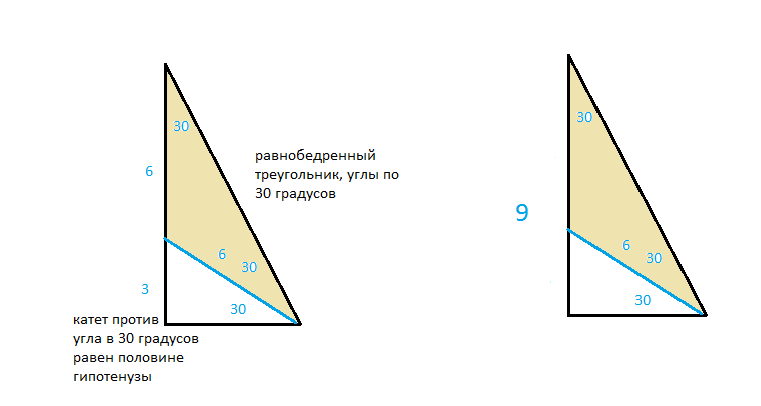
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину продолжающейся дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.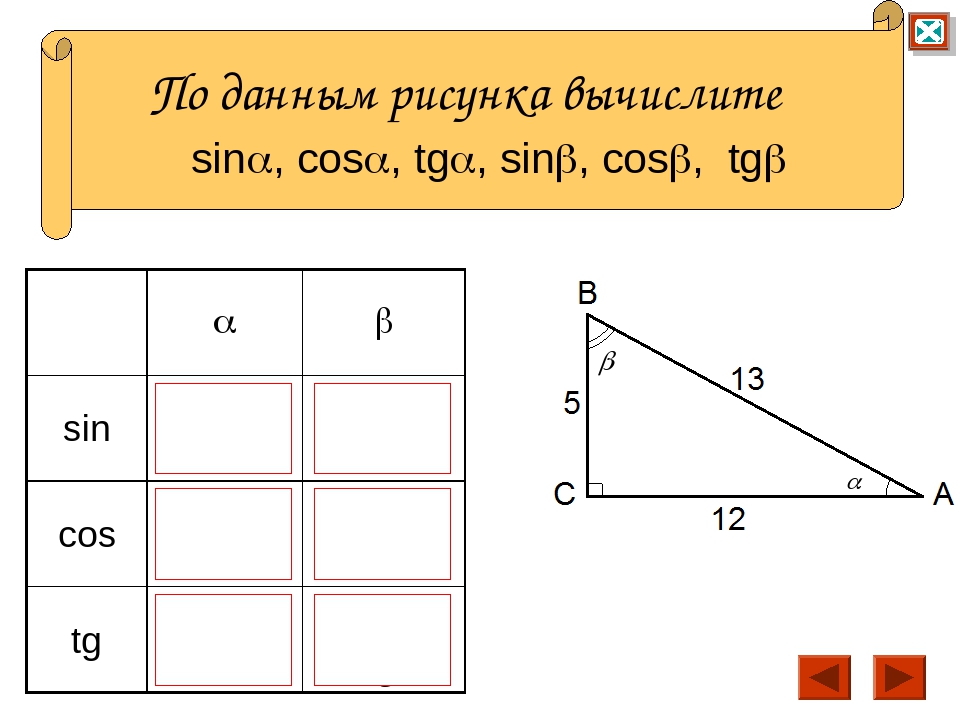
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Итак, 0,47623, разделенное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус.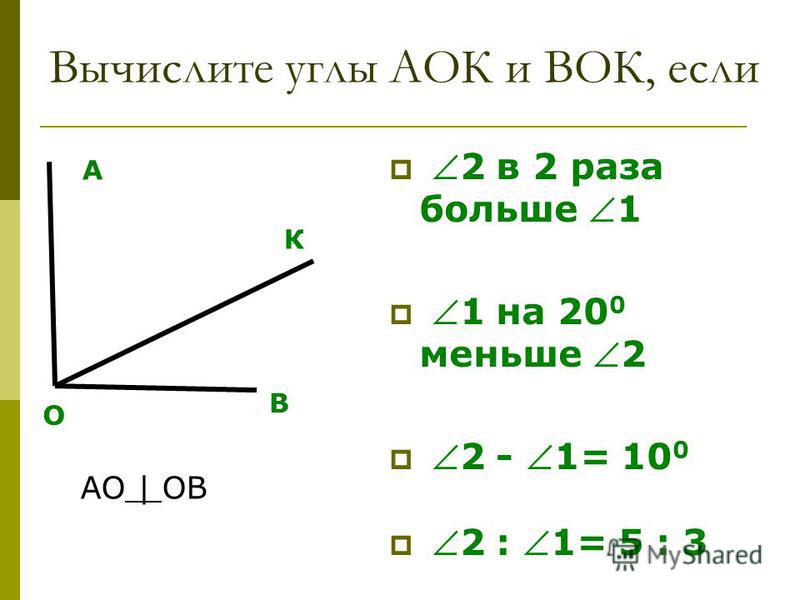 Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас получился круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы выяснить, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко.) Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935, с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим количеством цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.

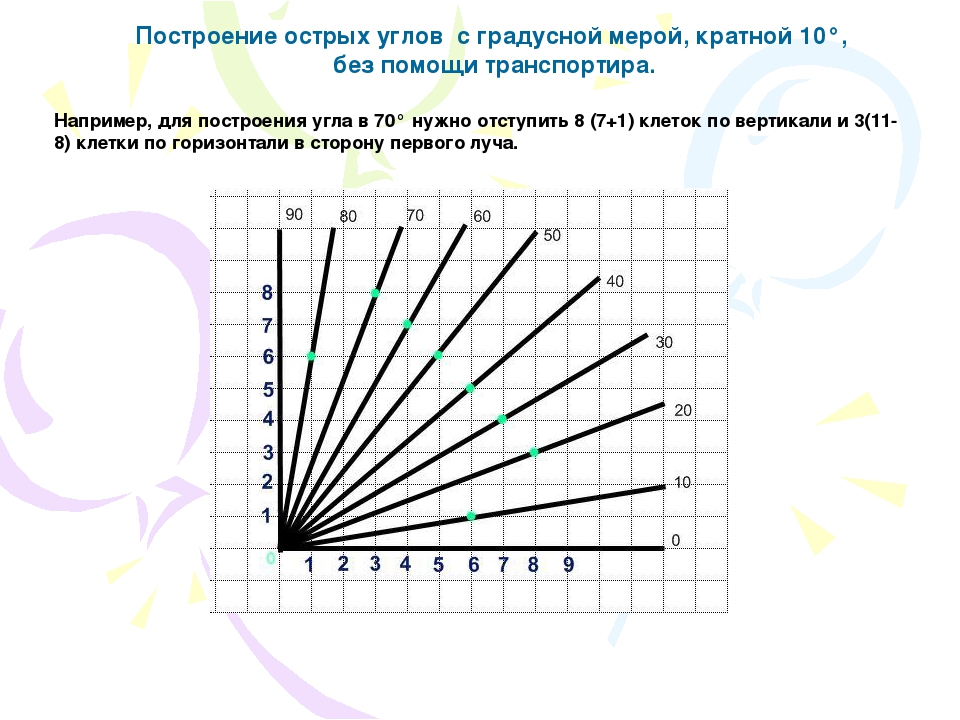

 Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.
Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.