Как измерять угол склона методом маятника
25 января 2016 | Анна Ханкевич
Советы и инструкции
фрирайд
Источник: Блог Анны Ханкевич
| Фрирайдер Анна Ханкевич пошагово объясняет, как определить угол склона и потенциальную лавиноопасность с помощью простых лыжных палок. |
|
Хочу рассказать про то, как измерять угол склона. У меня есть волшебный бипер PIEPS DSP Prо, у которого есть функция измерения наклона. Она включается нажатием кнопки Scan (сканирование) и работает в режиме передачи. Но он есть не у всех. Поэтому я хочу рассказать о методе маятника (который к своему стыду, узнала совсем недавно из методички Сергея Веденина). Многим известно, что приблизительно можно прикинуть угол склона по расстоянию от вытянутой руки стоящего человека до склона.
|
| Но этот способ подходит только для грубой оценки. Однако зачастую нам надо узнать угол более точно. Диапазон от 25 до 40 является самым лавиноопасным, и умение анализировать наклон важно. |
|
Также для скитура умение на взгляд точно определить угол склона крайне важно, ведь при углах выше 20-25 градусов мы начинаем проскальзывать при движении прямо вверх и нужно перейти к траверсам. Однако, нам надо определять угол со стороны, заранее. Поэтому рекомендую постоянно тренироваться, прикидывая угол на взгляд и потом проверяя свою оценку с помощью метода маятника. Также для передачи информации необходимо точно знать численные значения. |
|
Метод маятника позволяет определить угол склона с точностью до нескольких градусов и не требует никаких специальных приспособлений, кроме обычных палок, которые у лыжника всегда с собой=) Только палки должны быть одной длины. Шаг первыйНаходясь на склоне, положите палку вниз по линии падения воды ручкой вниз. Можно провести засечку на снегу у конца ручки. |
Шаг второйТеперь поднимайте эту палку вверх, оставляя острие палки на снегу. Подставьте вторую палку, соединив их рукоятками, при этом вторая палка должна прийти в вертикальное положение (можно представить вторую палку как отвес). |
|
Засеките расстояние от засечки на снегу до острия второй палки. Если острие выше по склону, чем засечка — то угол меньше 30 градусов. Если острие ниже по склону, чем засечка — то угол больше 30 градусов. Но я обещала точное количественное значение градусов. Для этого прикиньте расстояние между острием и засечкой в сантиметрах, каждые 10 см — это разница в три градуса. То есть если палка-отвес воткнулась ниже засечки на 20 см, то угол склона 36 градусов, если выше по склону на 10 см — то угол склона 27 градусов. Ну и хочу напомнить, что уклон в градусах и процентах — не одно и то же-) |
| Безопасного и интересного катания! |
комментарии к статье
Леонид
20.03.2016
30 градусов верно для любой длины палок, а вот дальше — 10см=3градуса — здесь от длины палок зависит
Владислав Рябиков
31. 01.2016
01.2016
Класс! Настолько очевидно, что непонятно как раньше не догадался.
Андрею
Читайте внимательней и смотрите картинку. Три одинаковых отрезка образуют равносторонний треугольник, углы в нём 60градусов, 90 минус 60 будет 30. Всё просто.
clips павел
Метод маятника позволяет определить угол склона с точностью до нескольких градусов и не требует никаких специальных приспособлений, кроме обычных палок, которые у лыжника всегда с собой=) Только палки должны быть одной длины.
от длины палок вообще ничего не зависит, главное чтоб одинаковые.:)
Андрей
29.01.2016
+/- 10 см = +/- 3 градуса — это очень грубое тождество. Палки-то у лыжников разного роста тоже могут быть очень разной длины.
Андрей
27. 01.2016
01.2016
попробовал на бумаге, не работает
Оставьте комментарий
* ваша оценка
(.jpg .png .gif), не больше 2Mb
Пожалуйста, дождитесь завершения отправки формы
Мы всегда открыты для обратной связи
Задайте вопрос
Помогите нам стать лучше, поделитесь своим мнением. Есть любые вопросы? Мы оперативно ответим на них.
Напишите нам
Подпишитесь на наши новости
Только полезные новости и не чаще 2 раз в неделю — статьи экспертов, обзоры снаряжения, спецпредложения.
Присоединяйтесь к нам в соцсетях
Следите за новостями горного outdoor и событиями АльпИндустрии и обсуждайте их с единомышленниками.
Болеем горами. Надеемся заразить вас!
Сергей Зон-Зам, бессменный лидер, взрослел в горах
Мы не продаем, мы советуем
Сергей Ковалев, МСМК, покоритель Эвереста и сложных вершин по всему миру
Ваша безопасность — наша работа
Иван Аленцев, инструктор по альпинизму
Расчет наклона крыши — сможет сделать каждый
В этом материале много технической информации.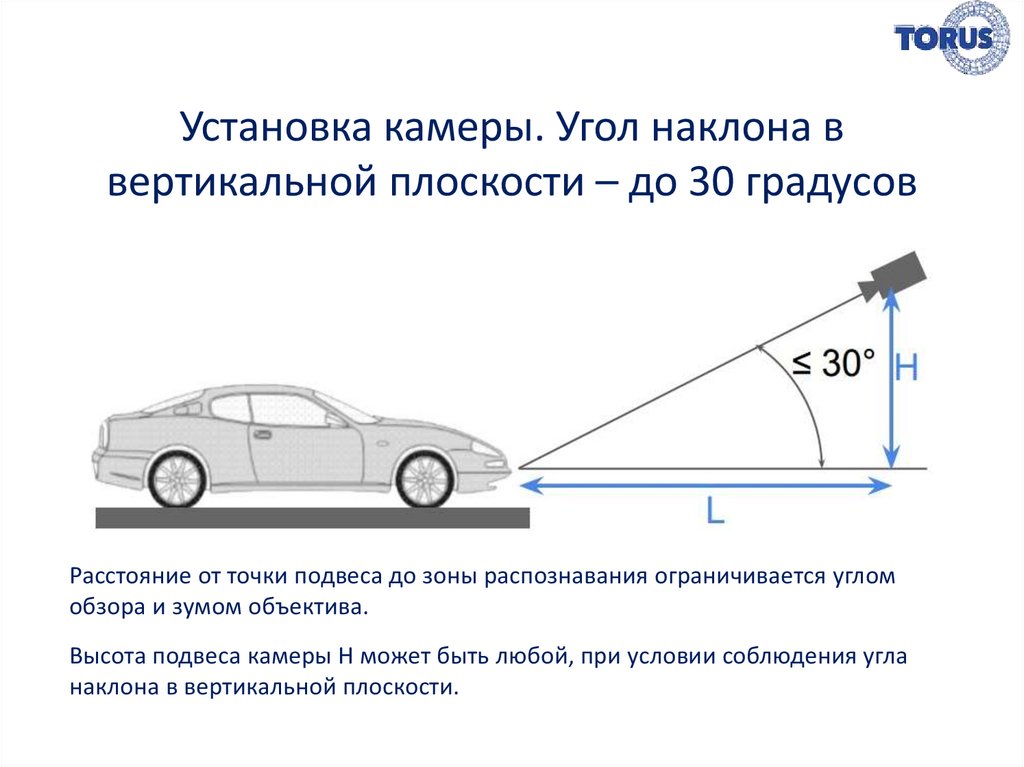 Если Вам нужно выполнить расчет наклона крыши, здесь находится все, чтобы понять, как это делается. Если Вы самостоятельно строите дом, найдите человека, который проверит Ваши расчеты. Отнеситесь ответственно к этому разделу, здесь собраны данные, которые помогут сделать крышу прочной и надежной.
Если Вам нужно выполнить расчет наклона крыши, здесь находится все, чтобы понять, как это делается. Если Вы самостоятельно строите дом, найдите человека, который проверит Ваши расчеты. Отнеситесь ответственно к этому разделу, здесь собраны данные, которые помогут сделать крышу прочной и надежной.
Если крыша, которую Вы проектируете, имеет сложную конфигурацию, без толковых инженеров не обойтись. Если конструкция крыши более простая, даже без строительного образования, следуя нашим инструкциям, можно выполнить расчет наклона крыши.
Помните, что расчет наклона крыши – это не единственный расчет, который необходимо провести, проектируя крышу. Возможно, Вам понадобиться сортамент уголков равнополочных, чтобы закрепить стропила.
В проектировании крыши также нужно учитывать снеговую и ветровую нагрузку, которая будет меняться в зависимости от места проживания. Здесь для получения данных необходимо знать угол наклона крыши.
Некоторые моменты специально упрощены, чтобы не усложнять Вам жизнь, однако то, что приведено в расчетах – обязательно нужно выполнить.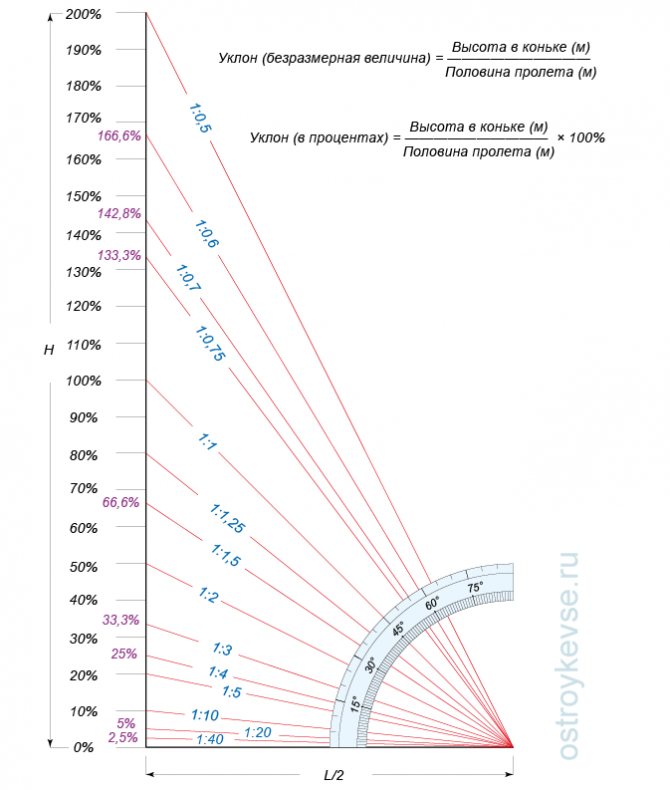 В результате Вы сможете предварительно узнать угол наклона крыши и все необходимые размеры для проектирования.
В результате Вы сможете предварительно узнать угол наклона крыши и все необходимые размеры для проектирования.
Величины измерения угла наклона крыши
Вы можете сказать, что здесь нет ничего сложного, ведь угол наклона измеряется в градусах, и будете правы, но всего лишь отчасти. В строительных нормативных документах, а иногда и в проектных чертежах угол наклона может измеряться в процентах или в соотношении сторон. Чтобы понимать все эти данные, сначала необходимо понять, что подразумевается, под углом наклона крыши.
Угол наклона кровли (α) – это угол, который образуют две плоскости: горизонтальная плоскость (L) и плоскость ската. Для определения угла наклона кровли нам понадобиться высота от пола чердака до конька (H). Эти данные часто меняются на стадии проектирования, если необходимо корректировать либо угол наклона кровли, либо высоту чердака.
Угол наклона крыши может быть исключительно острым, то есть в диапазоне от 0º до 90º. Тупой уголь в уклоне крыши не может быть по определению.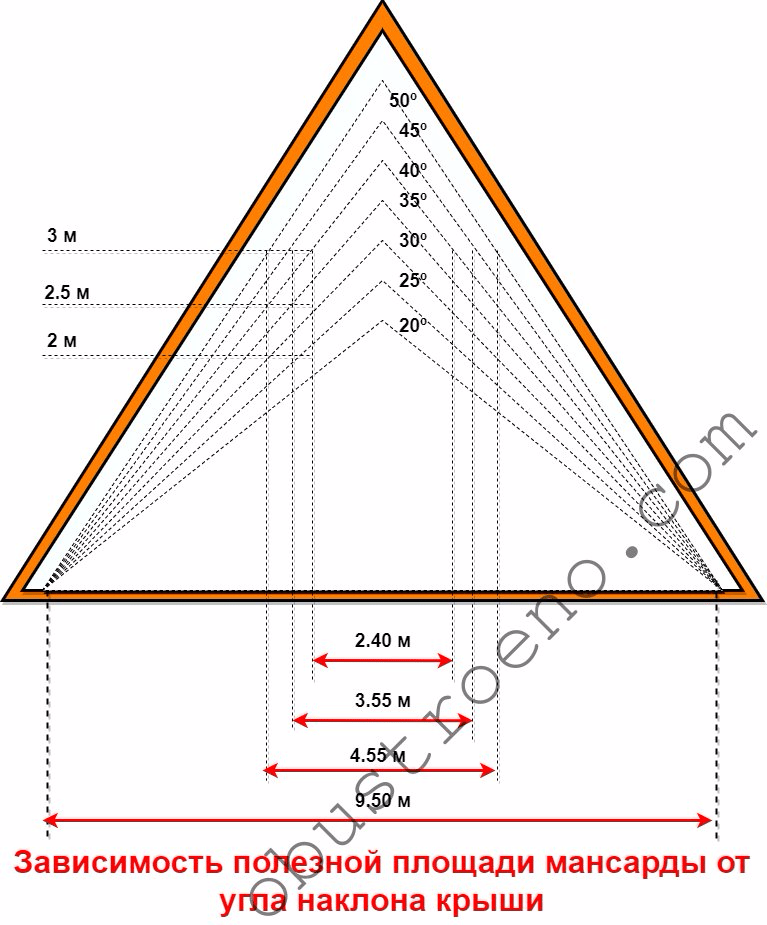 На практике уклоны больше 50º встречаются крайне редко. Такие уклоны могут быть на нижних стропилах крыши мансардного типа.
На практике уклоны больше 50º встречаются крайне редко. Такие уклоны могут быть на нижних стропилах крыши мансардного типа.
Если уклон показывается в виде соотношения, например 1 : 3, то эту надпись следует читать, как обычную дробь, которая означает соотношение высоты подъема ската (H) до проекции ската крыши на горизонтальную плоскость (L).
Сложность такого исчисления заключается в том, что соотношения иногда могут быть не простыми, например 3 : 13. Такую запись тяжело перенести на строительный объект, поэтому чаще всего используют обозначение уклона в процентах.
Определение уклона в процентах простое, берем наше сложное соотношение 3 : 13 и выполняем деление. Три поделить на тринадцать будет, примерно 0,23. Теперь данное число надо умножить на 100, и мы получим уклон крыши 23%.
3 : 13 х 100 = 23%
Достаточно легко уклон крыши можно перевести от процентов к градусам и наоборот. Для проведения таких расчетов важно запомнить, что уклон в 100% — это угол в 45º при условии, что высота ската (H) и длина его проекции на горизонтальную плоскость (L) равны между собой.
45º/100=0,45º=27′ – получается, что 1% уклона соответствует показателю в ноль градусов и 27 минут. А вот если
100/45º=2,22% – один градус уклона равняется показателю в 2,22%.
Основные данные по преобразованию углов наклона в разные единицы сведены в таблицу.
| Значение в градусах | Значение в процентах | Значение в градусах | Значение в процентах | Значение в градусах | Значение в процентах | ||
| 1° | 2,22% | 16° | 35,55% | 31° | 68,88% | ||
| 2° | 4,44% | 17° | 37,77% | 32° | 71,11% | ||
| 3° | 6,66% | 18° | 40,00% | 33° | 73,33% | ||
| 4° | 8,88% | 19° | 42,22% | 34° | 75,55% | ||
| 5° | 11,11% | 20° | 44,44% | 35° | 77,77% | ||
| 6° | 13,33% | 21° | 46,66% | 36° | 80,00% | ||
| 7° | 15,55% | 22° | 48,88% | 37° | 82,22% | ||
| 8° | 17,77% | 23° | 51,11% | 38° | 84,44% | ||
| 9° | 20,00% | 24° | 53,33% | 39° | 86,66% | ||
| 10° | 22,22% | 25° | 55,55% | 40° | |||
| 11° | 24,44% | 26° | 57,77% | 41° | 91,11% | ||
| 12° | 26,66% | 27° | 60,00% | 42° | 93,33% | ||
| 13° | 28,88% | 28° | 62,22% | 43° | 95,55% | ||
| 14° | 31,11% | 29° | 64,44% | 44° | 97,77% | ||
| 15° | 33,33% | 30° | 66,66% | 45° | 100,00% |
Кровельный материал для разного наклона крыши
Ниже представлен чертеж-схема, который наглядно показывает взаимосвязь всех уклонов.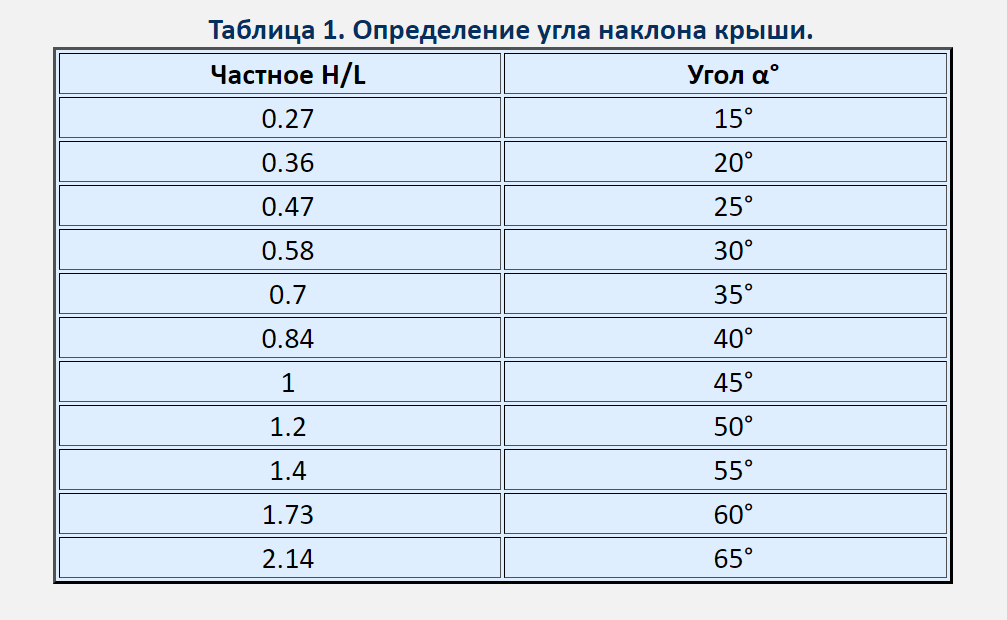 На картинке указаны цифры в кружочках – это рекомендуемые типы материалов для кровли с соответствующим уклоном. Детальная расшифровка находится под картинкой.
На картинке указаны цифры в кружочках – это рекомендуемые типы материалов для кровли с соответствующим уклоном. Детальная расшифровка находится под картинкой.
Здесь не учитывается материал стен, это может быть кирпич облицовочный одинарный или газобетон. Материал кровли зависит только от уклона и прочности несущих конструкций.
1 – редко используемые покрытия из дранки, натурального гонта и прочие подобные материалы.
2 – покрытия из черепицы, разные битумно-полимерные и сланцевые плитки.
3 – популярные рулонные материалы, мягкие кровли, которые укладываются в несколько слоев методом наплавления. Верхний слой таких материалов всегда имеет защитную посыпку. Для обеспечения надежности кровли используют не менее четырех слоев.
4 – все то же самое, что и в пункте «три», но с меньшим количеством слоев рулонного материала. Не меньше трех слоев.
5 – все то ж самое, что и в пунктах «три» и «четыре», но допускается использование без верхнего защитного слоя.
6 – мягкие кровли с рулонного материала в два слоя. В эту категорию также входит металлочерепица и профнастил.
7 – унифицированные асбестоцементные листы.
8 – глиняная черепица.
9 – асбестоцементные материалы с усилением.
10 – кровельная листовая сталь
11 — популярные в прошлом, асбестоцементные листы, он же шифер самого обычного и стандартного профиля
Диаграмма распределения крыш по крутизне ската
Как показывает диаграмма, крыши можно поделить на три типа. Это плоские крыши с уклоном до 5º, крыши с небольшим уклоном от 6º до 30º и крутоуклонные крыши с уклоном больше 30º. В зависимости от используемого материала, уклон для крыши допускается разный. Для того чтобы обеспечить надежность конструкций, необходимо провести расчет наклона крыши и только после этого выбирать подходящий материал для несущих стропил и покрытия кровли.
У каждого типа кровли есть свои положительные и негативные стороны. Крыши с большим уклоном обычно строят на территории, где зимой преобладает большое количество снежных масс. Крутой скат крыши обеспечивает быстрое сползание снега, который не будет задерживаться, превращаться в лед и добавлять большую нагрузку на стропильную систему. В то же время, такие крыши из-за своей конструкции воспринимают большое ветровое давление и это также необходимо учитывать.
Крутой скат крыши обеспечивает быстрое сползание снега, который не будет задерживаться, превращаться в лед и добавлять большую нагрузку на стропильную систему. В то же время, такие крыши из-за своей конструкции воспринимают большое ветровое давление и это также необходимо учитывать.
Расчет наклона крыши. Высота конька
Чтобы правильно выполнить расчет наклона крыши и определить соответствующую высоту конька, необходимо вспомнить геометрию. Исходные данные необходимо тщательно замерить, в качестве используемой величины надо узнать длину пролета, между стенами.
Задание на расчет наклона крыши сложное и здесь необходимо вспомнить не только геометрию, но обратиться к некоторым пособиям (часть из них приведена в таблицах в этой статье). Это задание на проектирование инженерных сетей имеет более вольную форму, а крыша требует ответственности и точности.
- H – высота конька;
- L – половина длины пролета, если крыша не двускатная, а односкатная, то L – это полная длина пролета;
- S – длина ската крыши;
- α – угол, который образуют две плоскости (S и L)
Как видно на картинке, рассматриваемые нами элементы крыши являются прямоугольным треугольником, для которого характерны следующие зависимости:
tg α = H/L =>>> H = L x tg α
sin α = H/S =>>> S = H/sin α
Если Вы хорошо усвоите эти две зависимости и вытекающие отсюда производные, Вы сможете решить практически любую задачу по расчету наклона крыши.
Высоту конька (H) и длину пролета (L), Вы найдете без труда, а вот значения tg α и sin α легко можно определить по таблице. Например, при H= 3,0 метра и L=4,5 метра, находим tg α:
tg α = H/L = 3,0/4,5 ≈ 0,66
Находим в таблице похожее значение. Это будет 0,67451 tg (34º). Итого, крыши при заданных параметрах будет установлена под углом 34º.
| Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса | |||
| tg(1°) | 0,01746 | tg(21°) | 0,38386 | tg(41°) | 0,86929 | tg(61°) | 1,80405 | |||
| tg(2°) | 0,03492 | tg(22°) | 0,40403 | tg(42°) | 0,9004 | tg(62°) | 1,88073 | |||
| tg(3°) | 0,05241 | tg(23°) | 0,42447 | tg(43°) | 0,93252 | tg(63°) | 1,96261 | |||
| tg(4°) | 0,06993 | tg(24°) | 0,44523 | tg(44°) | 0,96569 | tg(64°) | 2,0503 | |||
| tg(5°) | 0,08749 | tg(25°) | 0,46631 | tg(45°) | 1,0 | tg(65°) | 2,14451 | |||
| tg(6°) | 0,1051 | tg(26°) | 0,48773 | tg(46°) | 1,03553 | tg(66°) | 2,24604 | |||
| tg(7°) | 0,12278 | tg(27°) | 0,50953 | tg(47°) | 1,07237 | tg(67°) | 2,35585 | |||
| tg(8°) | 0,14054 | tg(28°) | 0,53171 | tg(48°) | 1,11061 | tg(68°) | 2,47509 | |||
| tg(9°) | 0,15838 | tg(29°) | 0,55431 | tg(49°) | 1,15037 | tg(69°) | 2,60509 | |||
| tg(10°) | 0,17633 | tg(30°) | 0,57735 | tg(50°) | 1,19175 | tg(70°) | 2,74748 | |||
| tg(11°) | 0,19438 | tg(31°) | 0,60086 | tg(51°) | 1,2349 | tg(71°) | 2,90421 | |||
| tg(12°) | 0,21256 | tg(32°) | 0,62487 | tg(52°) | 1,27994 | tg(72°) | 3,07768 | |||
| tg(13°) | 0,23087 | tg(33°) | 0,64941 | tg(53°) | 1,32704 | tg(73°) | 3,27085 | |||
| tg(14°) | 0,24933 | tg(34°) | 0,67451 | tg(54°) | 1,37638 | tg(74°) | 3,48741 | |||
| tg(15°) | 0,26795 | tg(35°) | 0,70021 | tg(55°) | 1,42815 | tg(75°) | 3,73205 | |||
| tg(16°) | 0,28675 | tg(36°) | 0,72654 | tg(56°) | 1,48256 | tg(76°) | 4,01078 | |||
| tg(17°) | 0,30573 | tg(37°) | 0,75355 | tg(57°) | 1,53986 | tg(77°) | 4,33148 | |||
| tg(18°) | 0,32492 | tg(38°) | 0,78129 | tg(58°) | 1,60033 | tg(78°) | 4,70463 | |||
| tg(19°) | 0,34433 | tg(39°) | 0,80978 | tg(59°) | 1,66428 | tg(79°) | 5,14455 | |||
| tg(20°) | 0,36397 | tg(40°) | 0,8391 | tg(60°) | 1,73205 | tg(80°) | 5,67128 |
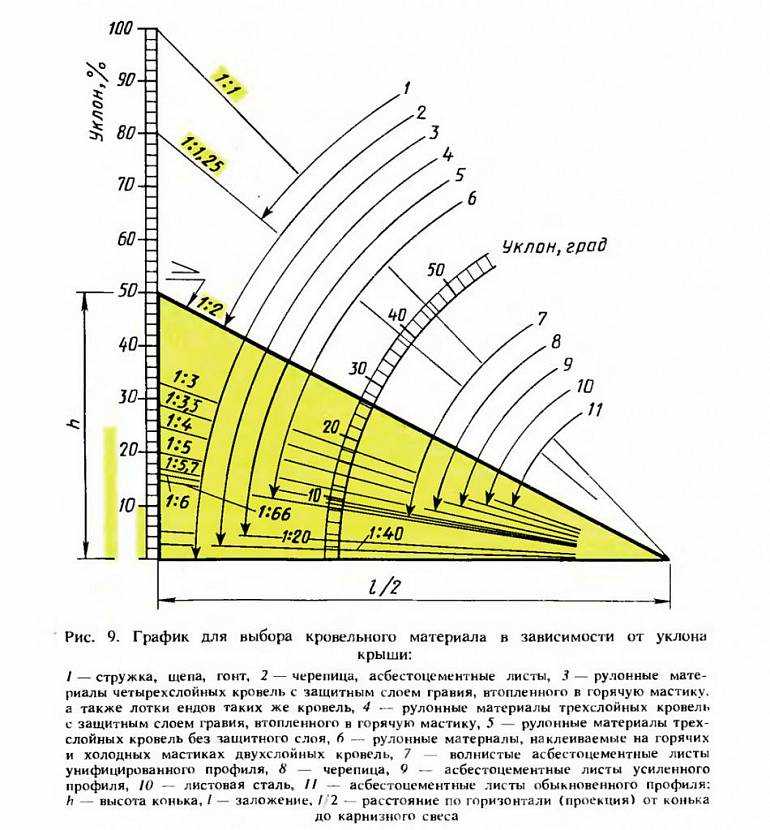
Для того чтобы посчитать длину наклонного стропила (S), можно обратиться к теореме Пифагора или же использовать уже найденный угол наклона крыши.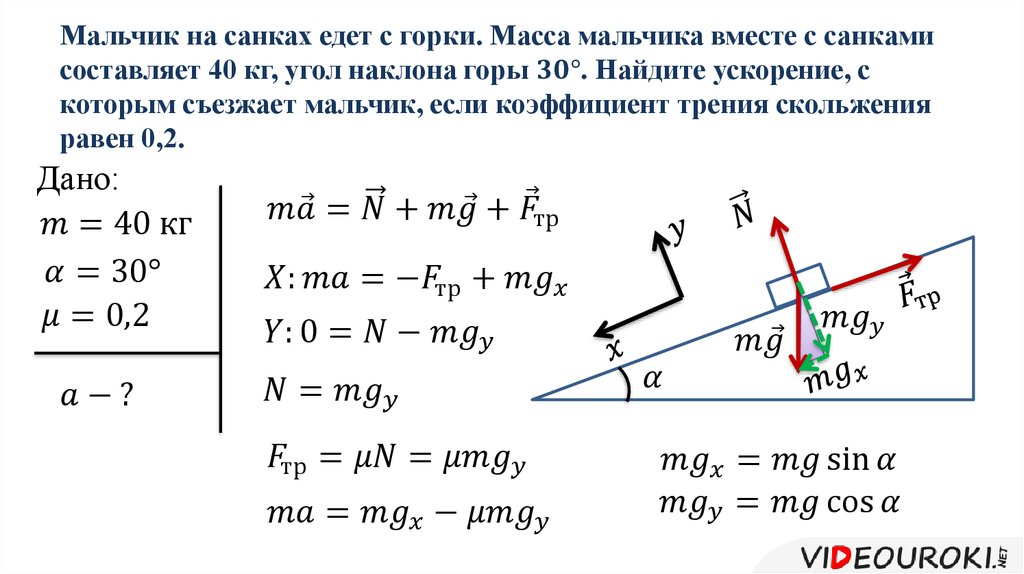
Учитывая уже имеющийся угол, который мы посчитали раньше, легче использовать вторую формулу. Если Вы хотите проверить себя, можете посчитать длину наклонного стропила по первой формуле и сравнить результаты. Значения sin α приведены в таблице ниже.
| Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса | |||
| sin(1°) | 0,017452 | sin(21°) | 0,358368 | sin(41°) | 0,656059 | sin(61°) | 0,87462 | |||
| sin(2°) | 0,034899 | sin(22°) | 0,374607 | sin(42°) | 0,669131 | sin(62°) | 0,882948 | |||
| sin(3°) | 0,052336 | sin(23°) | 0,90731 | sin(43°) | 0,681998 | sin(63°) | 0,891007 | |||
| sin(4°) | 0,069756 | sin(24°) | 0,406737 | sin(44°) | 0,694658 | sin(64°) | 0,898794 | |||
| sin(5°) | 0,087156 | sin(25°) | 0,422618 | sin(45°) | 0,707107 | sin(65°) | 0,906308 | |||
| sin(6°) | 0,104528 | sin(26°) | 0,438371 | sin(46°) | 0,71934 | sin(66°) | 0,913545 | |||
| sin(7°) | 0,121869 | sin(27°) | 0,45399 | sin(47°) | 0,731354 | sin(67°) | 0,920505 | |||
| sin(8°) | 0,139173 | sin(28°) | 0,469472 | sin(48°) | 0,743145 | sin(68°) | 0,927184 | |||
| sin(9°) | 0,156434 | sin(29°) | 0,48481 | sin(49°) | 0,75471 | sin(69°) | 0,93358 | |||
| sin(10°) | 0,173648 | sin(30°) | 0,5 | sin(50°) | 0,766044 | sin(70°) | 0,939693 | |||
| sin(11°) | 0,190809 | sin(31°) | 0,515038 | sin(51°) | 0,777146 | sin(71°) | 0,945519 | |||
| sin(12°) | 0,207912 | sin(32°) | 0,529919 | sin(52°) | 0,788011 | sin(72°) | 0,951057 | |||
| sin(13°) | 0,224951 | sin(33°) | 0,544639 | sin(53°) | 0,798636 | sin(73°) | 0,956305 | |||
| sin(14°) | 0,241922 | sin(34°) | 0,559193 | sin(54°) | 0,809017 | sin(74°) | 0,961262 | |||
| sin(15°) | 0,258819 | sin(35°) | 0,573576 | sin(55°) | 0,819152 | sin(75°) | 0,965926 | |||
| sin(16°) | 0,275637 | sin(36°) | 0,587785 | sin(56°) | 0,829038 | sin(76°) | 0,970296 | |||
| sin(17°) | 0,292372 | sin(37°) | 0,601815 | sin(57°) | 0,838671 | sin(77°) | 0,97437 | |||
| sin(18°) | 0,309017 | sin(38°) | 0,615661 | sin(58°) | 0,848048 | sin(78°) | 0,978148 | |||
| sin(19°) | 0,325568 | sin(39°) | 0,62932 | sin(59°) | 0,857167 | sin(79°) | 0,981627 | |||
| sin(20°) | 0,34202 | sin(40°) | 0,642788 | sin(60°) | 0,866025 | sin(80°) | 0,984808 |
Приведенные выше формулы можно применить для расчета наклона крыши вальмового типа. Здесь понадобиться немного пространственного воображения, чтобы разбить всю конструкцию крыши на простые треугольники. Ниже приводится наглядная схема, по которой делается расчет вальмовой крыши.
Здесь понадобиться немного пространственного воображения, чтобы разбить всю конструкцию крыши на простые треугольники. Ниже приводится наглядная схема, по которой делается расчет вальмовой крыши.
- α – угол наклона вальмы;
- β – угол наклона ската трапецевидной формы;
- СМ – высотка конька крыши;
- АС, ВС – диагональные стропила;
- Lдтс – длина торцевой стены дома;
- Lдс – длина стены дома;
- LAC, LBC – длина диагональных стропил;
- Lк – длина конька;
- Hк=Lптсх tg β;
- Lc= Hк/sin β;
- Lптс – половина длины торцевой стены дома;
- Нк – высота конька;
- tg β, sin β – тангенс и синус угла наклона ската трапецевидной формы;
- Lc – длина стропил скатов трапецевидной формы.
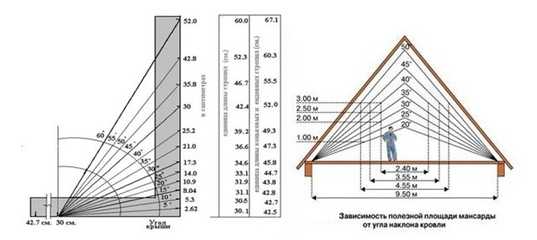
Габариты мансарды и угол наклона крыши
Если Вы планируете использовать чердачное помещение в качестве мансарды, то расчет наклона крыши имеет первостепенное значение, поскольку влияет на полезную площадь, которую можно будет использовать в помещении.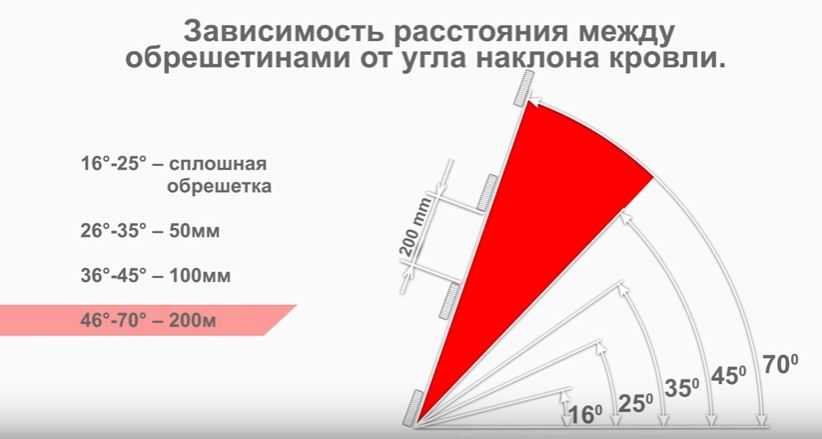 Схема проста: чем больше угол наклона крыши, тем больше внутри свободного пространства.
Схема проста: чем больше угол наклона крыши, тем больше внутри свободного пространства.
Более наглядно данную зависимость показывает схема, выполненная в масштабе. Обратите внимание, что высота потолка никак не может быть ниже 2,0 метра. Доказано многими застройками, что уменьшение этого размера делает помещение некомфортным и давящим на человека. В жилых помещениях используют высоту до потолка не ниже 2,5 метров.
Существуют стандартные размеры, которые применяются во многих застройках и вполне отвечают требованиям комфорта. В таблице приведены углы наклона крыши, высота конька, длина ската, полезная площадь мансарды и площадь кровельного покрытия.
| Угол ската крыши | Высота конька, м | Длина ската, м | Полезная площадь мансардного помещения на 1м длины здания (при высоте потолка 2м), м2 | Площадь кровельного покрытия на 1м длины здания, м2 |
| 20° | 1,82 | 5,32 | нет | 11,64 |
| 25° | 2,33 | 5,52 | 0,92 | 12,03 |
| 30° | 2,89 | 5,77 | 2,61 | 12,55 |
| 35° | 3,50 | 6,10 | 3,80 | 13,21 |
| 40° | 4,20 | 6,53 | 4,75 | 14,05 |
| 45° | 5,00 | 7,07 | 5,52 | 15,14 |
| 50° | 5,96 | 7,78 | 6,16 | 16,56 |
Вывод простой.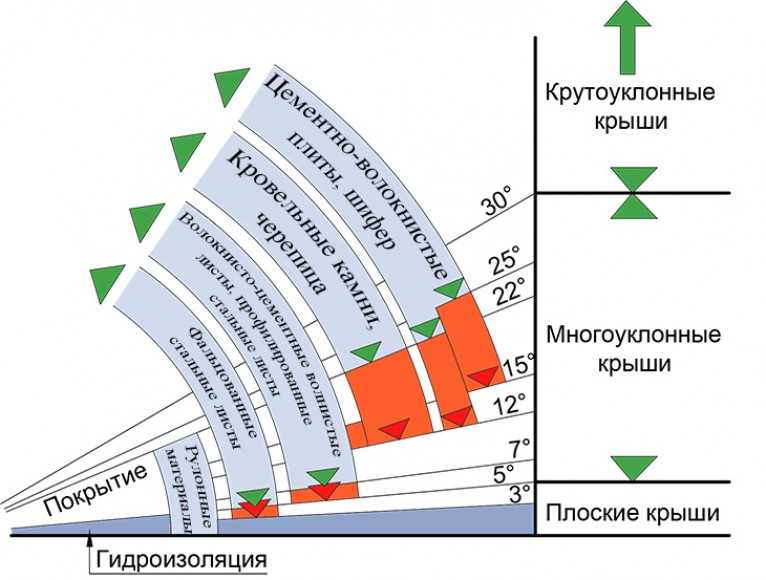 Чем больше уклон крыши, тем больше полезная площадь мансарды, длиннее наклонные стропила и больше площадь, которую нужно покрыть кровельным материалом. Связь пропорциональна.
Чем больше уклон крыши, тем больше полезная площадь мансарды, длиннее наклонные стропила и больше площадь, которую нужно покрыть кровельным материалом. Связь пропорциональна.
Также для правильного расчета наклона крыши необходимо учитывать соответствующие снеговые и ветровые нагрузки. Подбираются они в зависимости от расположения объекта согласно рекомендациям, которые изложены в ДБН В.1.2-2: 2006 «Нагрузки и воздействия». Это отдельная сложная тема, которую мы разберем в следующих статьях на нашем сайте.
© Статья является собственностью recenz.com.ua. Использование материала разрешается только с установлением активной обратной ссылки
Добавить комментарий
Угол наклона в задачах по физике
Автор: The Experts at Dummies и
Обновлено: 26 марта 2016 )
Физика I: 501 Практические задачи для чайников (+ Бесплатная онлайн-практика)
Исследовать книгу Купить на Amazon
В физике, если объект толкают вниз по склону, угол наклона склона влияет на ускорение объекта. Например, когда вы толкаете сани с покрытого льдом холма, вы можете рассчитать угол наклона холма, зная массу и ускорение саней.
Например, когда вы толкаете сани с покрытого льдом холма, вы можете рассчитать угол наклона холма, зная массу и ускорение саней.
Вес — гравитационная сила, с которой Земля воздействует на объект. У поверхности Земли вес равен массе, умноженной на 9,8 метра в секунду в квадрате. величина силы трения равна коэффициенту трения, умноженному на величину нормальной силы. Трение всегда препятствует относительному движению двух поверхностей.
Вот несколько практических вопросов, которые помогут проиллюстрировать эту концепцию.
Практические вопросы
25-килограммовые санки скользят по склону, покрытому ледяным снегом. Если сани движутся вниз по склону со скоростью 4,8 метра в секунду в квадрате, каков угол наклона холма по отношению к горизонту?
Предположим, что снег представляет собой поверхность без трения, и округлите ответ до ближайшего целого градуса.
Саманта толкает дочь, сидящую на санках, вниз по заснеженной горке с постоянным уклоном с силой 50 ньютонов.
 Сани разгоняются до 1,9метров в секунду в квадрате. Если общая масса ее дочери и санок равна 40 кг, каков угол наклона горки?
Сани разгоняются до 1,9метров в секунду в квадрате. Если общая масса ее дочери и санок равна 40 кг, каков угол наклона горки?Округлите ответ до ближайшего градуса.
Ответы
Ниже приведены ответы на практические вопросы:
29 градусов.
Сначала нарисуйте диаграмму свободного тела:
Только одна сила направлена вдоль оси движения
, так что это единственный вклад в чистое ускорение вдоль поверхности холма:
4 степени.
Три силы участвуют ( F N , Нормальная сила; F G , Сила из -за
666666666666666666666666666666666666 2 666666666666666666666 2 666666666666666666666 2 666666666166666666666666 2 666666666666666666666 2 . . сила толчка Саманты). Нарисуйте диаграмму свободного тела, показывающую векторы и любые необходимые компоненты, чтобы выровнять силы по двум перпендикулярным осям:
Сани движутся вдоль оси, параллельной поверхности холма, так что это направление ускорения вам нужно изучить.
 Суммируя силы в этом направлении:
Суммируя силы в этом направлении:(В этой установке в качестве положительного направления используется «вниз по склону».) По второму закону Ньютона
Об этой статье
Эта статья из книги:
- Физика I: 501 Практические задачи для чайников (+ Бесплатная онлайн-практика),
Об авторе книги:
Эту статью можно найти на категория:
- Физика,
Видео-вопрос: Нахождение угла наклона точки предельного равновесия лестницы, опирающейся на шероховатый пол и шероховатую стену
Стенограмма видео
Однородный стержень опирается одним концом
о шероховатую вертикальную стену, а коэффициент трения между стержнем и
стена составляет три десятых. Другой конец стержня сидит на
шероховатый горизонтальный пол, а коэффициент трения между стержнем и
этаж — треть. Рассчитать угол наклона
𝜃 между стержнем и полом, когда он находится в предельном равновесии, что дает
ответ с точностью до минуты.
Другой конец стержня сидит на
шероховатый горизонтальный пол, а коэффициент трения между стержнем и
этаж — треть. Рассчитать угол наклона
𝜃 между стержнем и полом, когда он находится в предельном равновесии, что дает
ответ с точностью до минуты.
Перед выполнением каких-либо вычислений здесь мы собираемся просто начать с рисования диаграммы свободного тела. Помните, это очень просто эскиз, который просто показывает все ключевые силы, которые нас интересуют. Вот жесткий стержень, наклоненный под угол 𝜃 градусов к горизонту. Мы собираемся назвать конец 𝐵 конец который сидит у стены и заканчивается 𝐴 концом, который сидит на полу. Нам также говорят, что стержень униформа. Это означает направленную вниз силу его вес будет действовать ровно посередине лестницы.
Для простоты давайте определим
длина лестницы два 𝑥 метра.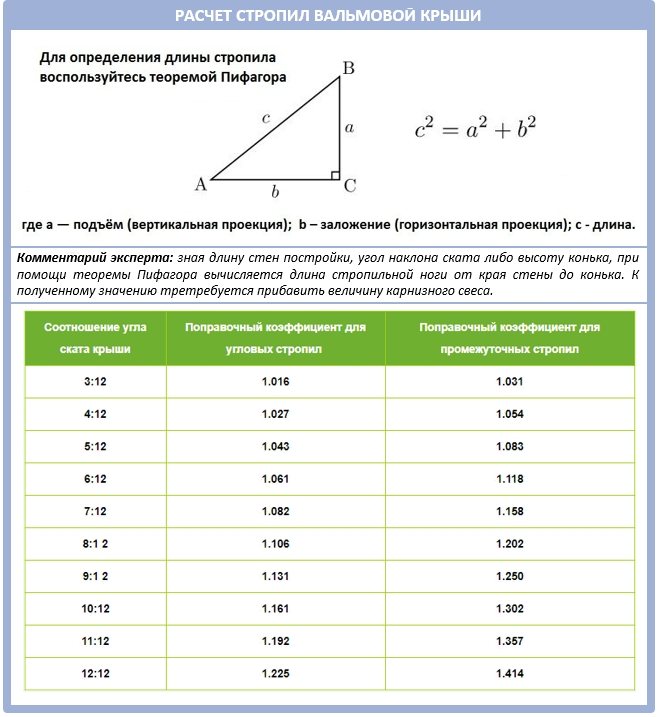 Итак, сила тяжести действует с
точка 𝑥 метров от точки 𝐴. Затем рассмотрим третий закон Ньютона.
закон движения. Это говорит нам о том, что если стержень
воздействует на стену и пол, стена и пол должны сами
на стержень действует нормальная сила реакции. Мы собираемся назвать нормальный
сила реакции пола на стержень 𝑅 переводника 𝐴 и нормальная сила реакции
стена на стержне 𝑅 саб 𝐵.
Итак, сила тяжести действует с
точка 𝑥 метров от точки 𝐴. Затем рассмотрим третий закон Ньютона.
закон движения. Это говорит нам о том, что если стержень
воздействует на стену и пол, стена и пол должны сами
на стержень действует нормальная сила реакции. Мы собираемся назвать нормальный
сила реакции пола на стержень 𝑅 переводника 𝐴 и нормальная сила реакции
стена на стержне 𝑅 саб 𝐵.
Затем есть еще две силы
что нас интересует. Нам говорят, что стена и
пол грубый. Это означает, что должно быть трение
действующие силы. Нам также говорят, что стержень находится в
предельное равновесие. значит дело в точке
скользящий. Помните, что сила трения будет
действовать против направления, в котором тело пытается двигаться. Итак, сила трения в точке 𝐴 будет
действуйте по направлению к стене, как показано на рисунке.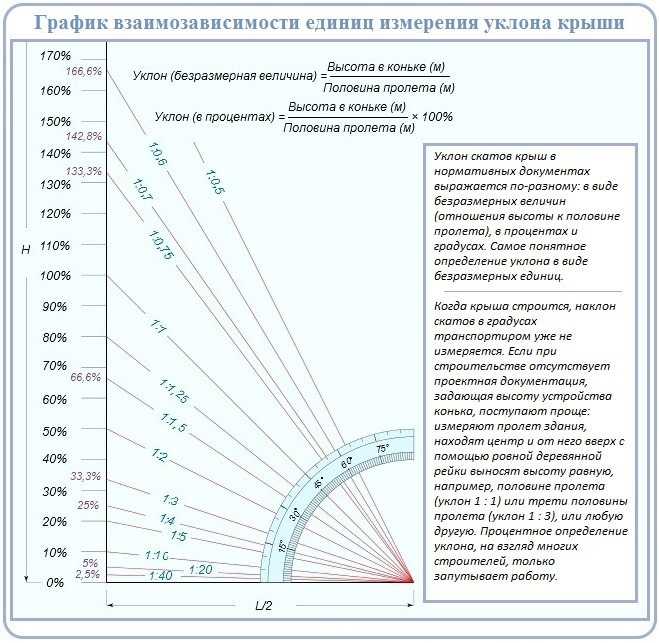 И сила трения при 𝐵,
назовем это Fr sub 𝐵, должно быть направлено вверх.
И сила трения при 𝐵,
назовем это Fr sub 𝐵, должно быть направлено вверх.
И в этот момент мы можем вспомнить Формула, которая поможет нам рассчитать трение. Трение равно 𝜇𝑅, где 𝜇 – коэффициент трения, а 𝑅 – нормальная сила реакции при этом точка. Нам говорят коэффициент трение между стержнем и полом, то есть в точке 𝐴, составляет одну треть. Итак, 𝜇𝑅 будет третий 𝑅 суб 𝐴. Точно так же коэффициент трение между стержнем и стенкой составляет три десятых. Итак, 𝜇𝑅 в точке 𝐵 должно быть три десятых раза 𝑅 саб 𝐵.
Теперь мы извлекли все
соответствующая информация нам нужна от этого вопроса. Итак, давайте расчистим место. Итак, раз у нас есть все силы
помечены, что делать дальше? Ну и напомним, что тело было
в предельном равновесии. Мы обсудили, что ограничивающая часть
имел в виду.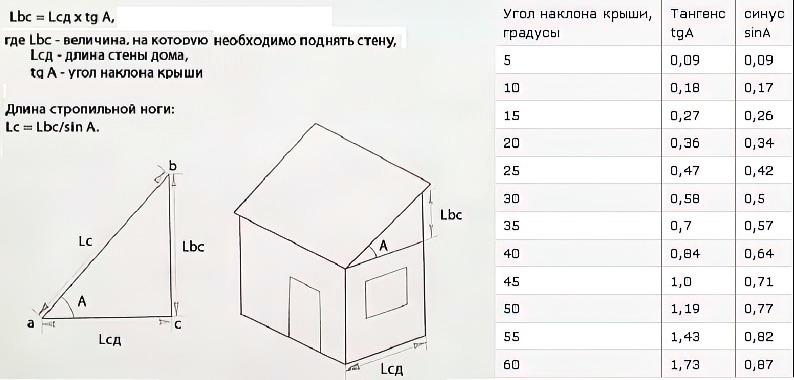 Это означало, что это на грани
скользящий. Но чтобы тело было в
равновесия, необходимо учитывать два условия. Во-первых, сумма всех сил
действующая на тело должна быть равна нулю. Мы склонны ломать их
по направлению и говорят, что сумма горизонтальных сил равна нулю, а сумма
вертикальные силы равны нулю.
Это означало, что это на грани
скользящий. Но чтобы тело было в
равновесия, необходимо учитывать два условия. Во-первых, сумма всех сил
действующая на тело должна быть равна нулю. Мы склонны ломать их
по направлению и говорят, что сумма горизонтальных сил равна нулю, а сумма
вертикальные силы равны нулю.
Мы также знаем, что сумма всех моменты, действующие на тело, также должны быть равны нулю, где момент равен 𝐹𝑑. 𝐹 — сила, а 𝑑 — сила перпендикулярное расстояние линии действия этой силы от точки о который тело пытается повернуть. И так, что мы собираемся делать здесь Начнем с разрешения сил на нашей диаграмме. Потом будем считать моменты.
Мы решим оба
горизонтально и вертикально. Начнем с решения
вертикально, и мы собираемся поднять вверх, чтобы быть положительным. Действуя вверх, имеем
сила реакции в точке 𝐴 и сила трения в точке 𝐵. И тогда, действуя вниз, мы имеем
вес тела. Сумма этих сил равна
естественно, равно нулю. Сейчас мы на самом деле собираемся
замените силу трения в 𝐵 выражением, которое мы разработали ранее,
три десятых 𝑅 под 𝐵.
И тогда, действуя вниз, мы имеем
вес тела. Сумма этих сил равна
естественно, равно нулю. Сейчас мы на самом деле собираемся
замените силу трения в 𝐵 выражением, которое мы разработали ранее,
три десятых 𝑅 под 𝐵.
Итак, получаем 𝑅 саб 𝐴 плюс три десятых 𝑅 меньше 𝐵 минус 𝑤 равно нулю. Затем мы добавляем 𝑤 к обеим сторонам. В итоге мы хотим получить избавьтесь от всех 𝑤 в нашем уравнении. Итак, мы получаем 𝑅 саб 𝐴 плюс три десятых 𝑅 меньше 𝐵 равно 𝑤.
Далее разрешаем по горизонтали. И мы собираемся взять
направление, в котором действует сила трения в точке 𝐴, положительно. В этом направлении у нас есть
сила трения 𝐴. А в другую сторону имеем
сила реакции в 𝐵. Итак, их сумма равна Fr sub 𝐴 минус 𝑅
sub 𝐵 и это, конечно же, равно нулю. Сейчас мы заменим
сила трения в 𝐴 с выражением, которое мы разработали ранее, третий 𝑅 sub
𝐴.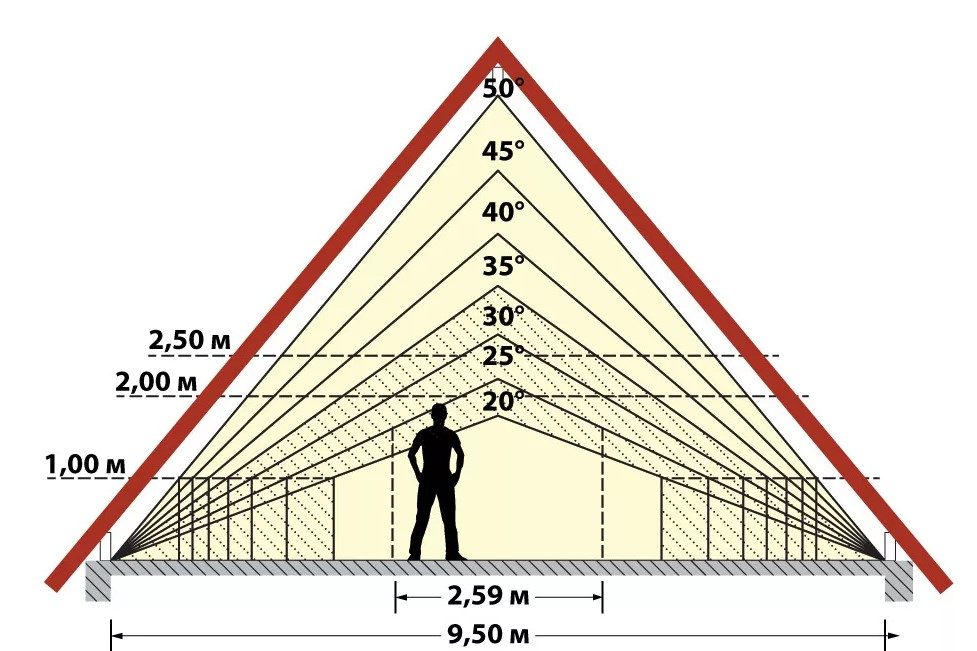
Получаем одну треть 𝑅 sub 𝐴 минус 𝑅 sub 𝐵 равно нулю. Мы собираемся сделать 𝑅 sub 𝐴 тема здесь. И в конце концов, что мы собираемся сделать нужно попытаться найти выражение исключительно с точки зрения 𝑅 sub 𝐵. Если мы добавим 𝑅 sub 𝐵 к обеим сторонам нашего уравнения, а затем умножаем на три, мы находим, что 𝑅 sub 𝐴 в три раза больше 𝑅 суб 𝐵. Теперь это действительно полезно, потому что теперь мы можем заменить этот 𝑅 sub 𝐴 в нашем предыдущем уравнении. Итак, обратите внимание, у нас есть уравнение только с точки зрения двух переменных сейчас. У нас есть 𝑤 равно трижды 𝑅 sub 𝐵 плюс три десятых 𝑅 sub 𝐵 или 𝑤 равно 33 на 10 𝑅 sub 𝐵.
Теперь мы собираемся вычислить
моменты. Начнем с того, что найдем точку о
которые мы хотим вычислить эти моменты. На самом деле не важно, какой
точку выбираем. Мы должны получить тот же ответ
так или иначе, но мы склонны выбирать нижнюю часть лестницы, так как там обычно больше
действующие здесь силы. Мы также собираемся определить
направление против часовой стрелки должно быть положительным. И так, начнем с веса
сила.
Мы должны получить тот же ответ
так или иначе, но мы склонны выбирать нижнюю часть лестницы, так как там обычно больше
действующие здесь силы. Мы также собираемся определить
направление против часовой стрелки должно быть положительным. И так, начнем с веса
сила.
Помните, когда мы вычисляем момент, мы хотим найти составляющую каждой силы, которая действует перпендикулярно тело. Добавляем прямоугольный треугольник, и нам нужно найти значение 𝑥. Теперь 𝑥 является компонентом интересующая нас сила веса. Это не то же самое, что длина лестница. Прилежащий угол здесь равен 𝜃, 𝑤 — гипотенуза, а 𝑥 — примыкающая. Таким образом, мы можем использовать отношение косинусов к найти какое-то выражение для 𝑥.
Когда мы это делаем, мы получаем потому что 𝜃 равно 𝑥
более 𝑤. И тогда, когда мы умножаем на 𝑤, мы
получить 𝑥 равно 𝑤 потому что 𝜃. Теперь, конечно, мы сказали, что 𝑤
тридцать три десятых 𝑅 sub 𝐵 Итак, у нас есть выражение для 𝑥 через 𝜃
и 𝑅 под 𝐵. Момент будет негативным
так как это пытается повернуть стержень по часовой стрелке. Сила умножить на расстояние
тридцать три десятых 𝑅 суб 𝐵 потому что 𝜃 раз 𝑥.
Теперь, конечно, мы сказали, что 𝑤
тридцать три десятых 𝑅 sub 𝐵 Итак, у нас есть выражение для 𝑥 через 𝜃
и 𝑅 под 𝐵. Момент будет негативным
так как это пытается повернуть стержень по часовой стрелке. Сила умножить на расстояние
тридцать три десятых 𝑅 суб 𝐵 потому что 𝜃 раз 𝑥.
Есть еще два момента, которые мы
нужно рассмотреть; это моменты, связанные с 𝑅 sub 𝐵 и фрикционным
сила в 𝐵. Еще раз, мы собираемся решить
𝑅 sub 𝐵 найти составляющую этой силы, действующую перпендикулярно
стержень. На этот раз 𝑅 саб 𝐵
гипотенуза, а мы пытаемся найти значение 𝑦, которое противоположно. Итак, мы собираемся использовать синус
соотношение. Когда мы это делаем, мы обнаруживаем, что грех 𝜃
𝑦 над 𝑅 под 𝐵. И мы можем умножить обе части
это уравнение с помощью 𝑅 sub 𝐵. Итак, 𝑦 это 𝑅 суб 𝐵 грех 𝜃.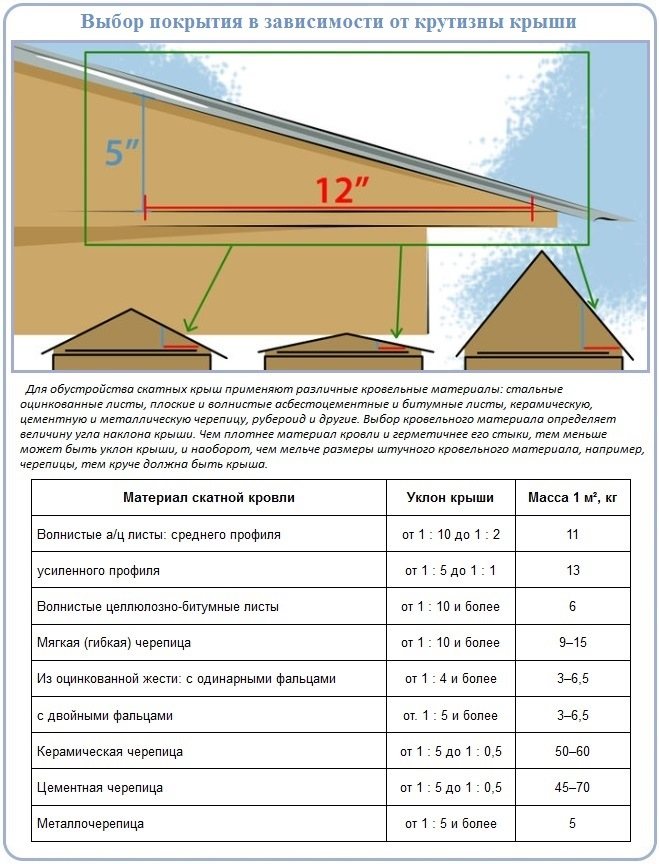 На этот раз этот момент будет
быть положительным, так как он действует в направлении против часовой стрелки. И сила, умноженная на расстояние, равна 𝑅 sub
𝐵 грех 𝜃 раз два 𝑥.
На этот раз этот момент будет
быть положительным, так как он действует в направлении против часовой стрелки. И сила, умноженная на расстояние, равна 𝑅 sub
𝐵 грех 𝜃 раз два 𝑥.
Есть еще одна сила, которую мы интересует, и это силы трения в 𝐵. Еще раз, мы можем добавить здесь прямоугольный треугольник. И мы пытаемся найти значение из 𝑧; это составляющая силы трения, перпендикулярная стержень. Немного сложнее найти интересующий нас здесь угол. На самом деле, однако, этот угол, т. угол при 𝐵 равен 90 минус 𝜃. Мы можем убедить себя, что это верно, потому что угол между 𝑅 под 𝐴 и силой трения в 𝐴 должен быть 90. Затем у нас есть пара соответствующие углы. Итак, этот угол здесь должен сама будет 𝜃, так как сумма углов в треугольнике равна 180.
Мы знаем гипотенузу и
смежные в этом треугольнике тогда. Итак, возвращаемся к формуле cos
𝜃 смежна по гипотенузе. Итак, cos 𝜃 равен 𝑧 над
сила трения в 𝐵. Мы умножаем обе части этого
уравнение силой трения в точке 𝐵. Но помните, у нас есть выражение
для этого; это три десятых 𝑅 саб 𝐵. И мы нашли компонент
сила трения в точке 𝐵 перпендикулярно стержню; это три десятых 𝑅 саб 𝐵
раз, потому что 𝜃. Итак, мы можем найти момент
эта сила. Еще раз, это положительно. Это три десятых 𝑅 саб 𝐵 потому что 𝜃
раз два 𝑥.
Итак, возвращаемся к формуле cos
𝜃 смежна по гипотенузе. Итак, cos 𝜃 равен 𝑧 над
сила трения в 𝐵. Мы умножаем обе части этого
уравнение силой трения в точке 𝐵. Но помните, у нас есть выражение
для этого; это три десятых 𝑅 саб 𝐵. И мы нашли компонент
сила трения в точке 𝐵 перпендикулярно стержню; это три десятых 𝑅 саб 𝐵
раз, потому что 𝜃. Итак, мы можем найти момент
эта сила. Еще раз, это положительно. Это три десятых 𝑅 саб 𝐵 потому что 𝜃
раз два 𝑥.
Тело находится в равновесии. Итак, мы устанавливаем это равным нулю. Теперь мы хотим найти 𝜃, но
у нас на самом деле есть три неизвестных здесь. У нас есть 𝑅 подписка 𝐵, 𝜃 и 𝑥. Однако мы определили два 𝑥 как
длина лестницы, поэтому 𝑥 было вдвое меньше. И никак 𝑥 не может быть равным
до нуля. Таким образом, мы можем разделить
через 𝑥. Точно так же мы знаем реакцию
сила в 𝐵 также не может быть равна нулю. Итак, делим на 𝑅 sub
𝐵. Итак, у нас осталось минус 33
более 10 cos 𝜃 плюс два sin 𝜃 плюс три пятых cos 𝜃 равно нулю.
Точно так же мы знаем реакцию
сила в 𝐵 также не может быть равна нулю. Итак, делим на 𝑅 sub
𝐵. Итак, у нас осталось минус 33
более 10 cos 𝜃 плюс два sin 𝜃 плюс три пятых cos 𝜃 равно нулю.
Заметьте, сейчас мы работаем только с
одна переменная. Мы собираемся собрать вместе
потому что 𝜃 первый. Итак, два греха 𝜃 минус 27 на 10, потому что
𝜃 равно нулю. И тогда мы собираемся вспомнить один
наших ключевых тригонометрических тождеств; то есть tan 𝜃 равен sin 𝜃 по cos
𝜃. Мы хотим, чтобы наше уравнение выглядело немного
так. Итак, мы собираемся добавить 27 к 10.
потому что 𝜃 в обе стороны. Далее мы собираемся разделить через
по причине 𝜃. Итак, два sin 𝜃 над cos 𝜃 равны
двадцать семь десятых. Но, конечно, мы можем заменить грех
𝜃 над cos 𝜃 с загаром 𝜃, и теперь мы собираемся разделить на два.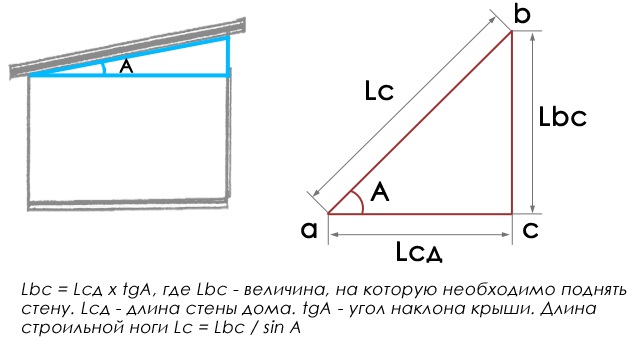


 Если расстояние равно нулю, то есть если острие вертикальной палки воткнулось точно в отметку — угол склона равен 30 градусам.
Если расстояние равно нулю, то есть если острие вертикальной палки воткнулось точно в отметку — угол склона равен 30 градусам.