- Соединение конденсаторов — Основы электроники
- Параллельное и последовательное соединение конденсаторов (формулы, законы для вычисления емкости и напряжения)
- электричества. Есть ли физическое объяснение тому, почему увеличение емкости конденсатора и сопротивления цепи снижает скорость разряда конденсатора?
- . Интуитивно понятно, почему последовательное соединение конденсаторов уменьшает эквивалентную емкость?
Соединение конденсаторов — Основы электроники
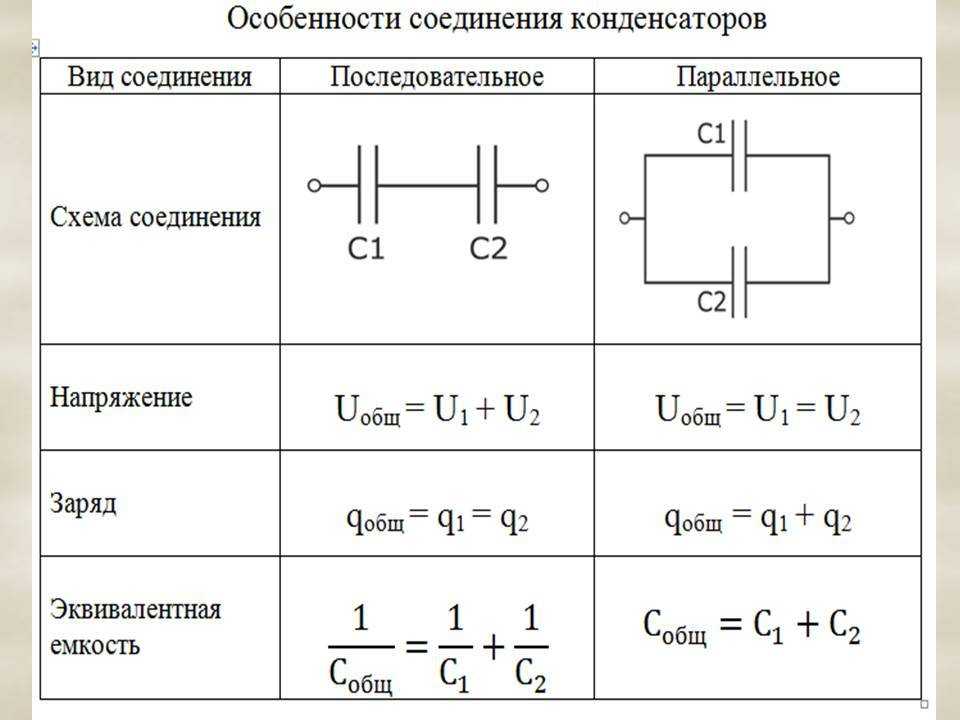
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.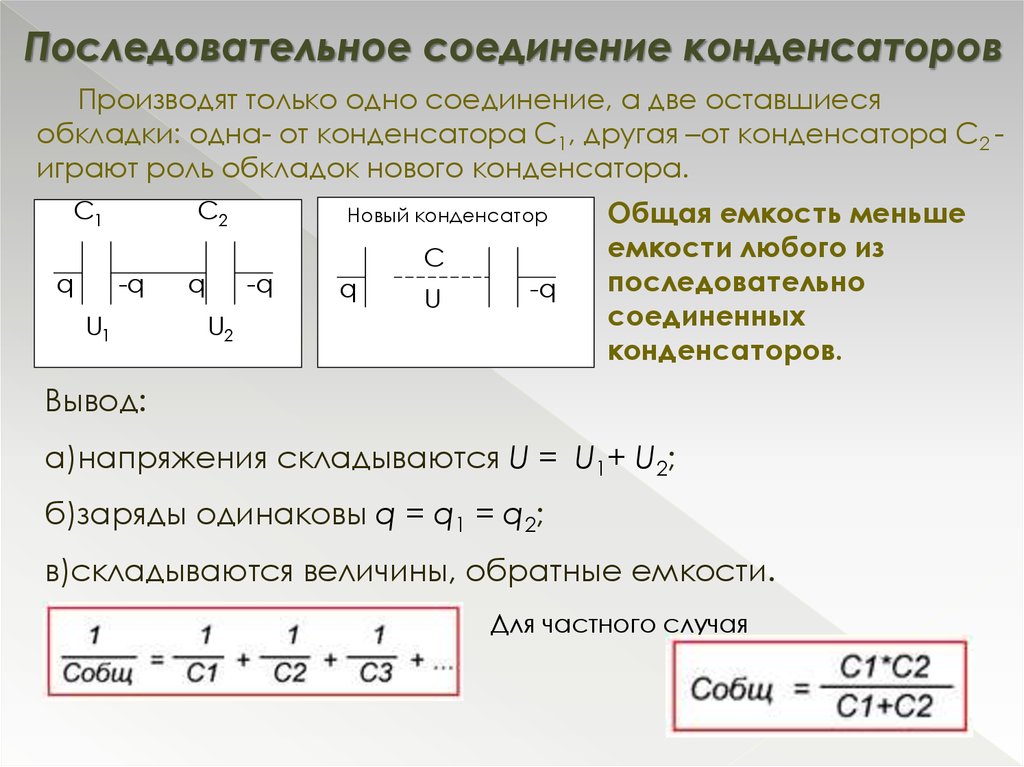
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.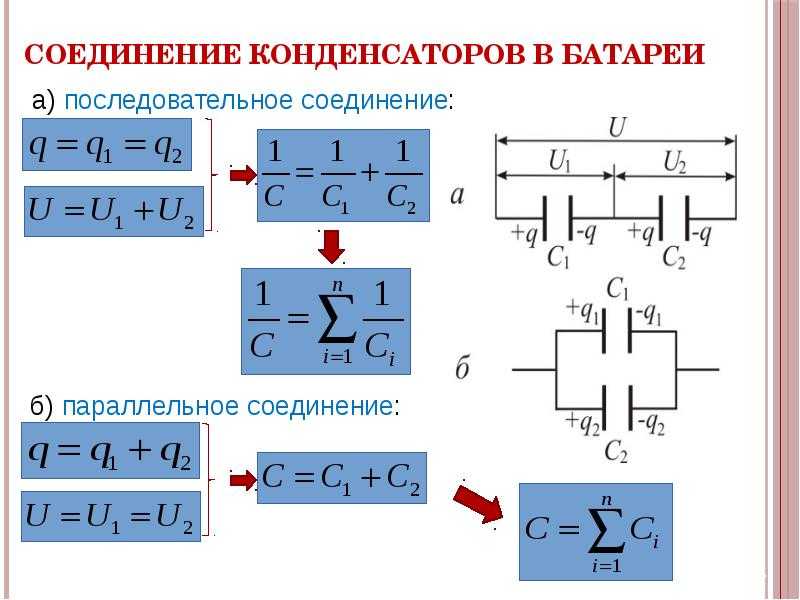
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Параллельное и последовательное соединение конденсаторов (формулы, законы для вычисления емкости и напряжения)
Содержание
- Отличия параллельного и последовательного соединения конденсаторов
- Смешанное подключение
- Общая емкость и распределение напряжений между элементами при разных типах включения
- Примеры подключений
Электрические схемы могут содержать элементы, основным параметром которых является емкость. Чаще всего это конденсаторы (также в этом качестве используются, например, варикапы, ионисторы и т.п.). Такие элементы можно соединять параллельно или последовательно и получать участки схемы с иными параметрами.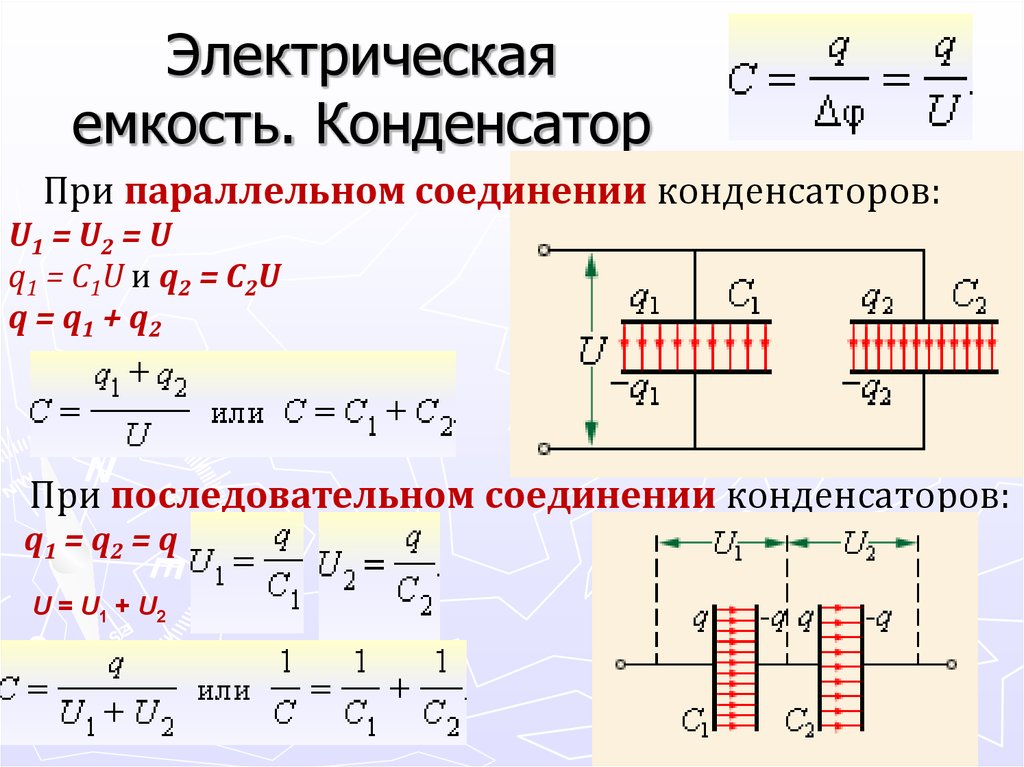
Отличия параллельного и последовательного соединения конденсаторов
При параллельном (parallel) подключении обкладки конденсаторов соединяются в одной точке, а противоположные – в другой. К этим точкам подключается источник напряжения. Наглядно продемонстрировать такую схему можно на примере полярных приборов (например, электролитических конденсаторов), когда все положительные электроды соединяются между собой и подключаются к плюсу питания.
Отрицательные обкладки также соединяются в один узел, на который подается минус питающего напряжения. У неполярных элементов нет разделения на положительные и отрицательные электроды, они соединяются произвольным образом, но по тому же принципу (в этом случае на батарею можно подавать и двухполярное напряжение). Каждый конденсатор подключен непосредственно к источнику питания, поэтому напряжение на каждой банке одинаково.
Параллельное включение элементов.При последовательном (serial) соединении одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.
Напряжение подается на свободные выводы крайних элементов.
Смешанное подключение
Также существует смешанное соединение элементов, когда часть ячеек включена параллельно, часть последовательно. Такие схемы несколько сложнее для анализа.
Батарея из смешанно соединенных конденсаторов.Общая емкость и распределение напряжений между элементами при разных типах включения
Емкость конденсаторов зависит, в том числе, и от площади обкладок. Если однотипные элементы соединить параллельно, это можно рассматривать как суммирование всех площадей обкладок, что означает сложение емкостей банок, входящих в батарею. Очевидно, что это же правило действует и для разнотипных элементов. Аналитическим путем к этому можно прийти в результате следующих рассуждений:
- очевидно, что при таком подключении на каждом элементе напряжения будут равны (U1=U2=U);
- запасенные заряды всех пластин суммируются (q=q1+q2);
- тогда общая емкость равна С=U*q=U*(q1+q2)=U*q1+U*q2=C1+C2.
Эта же формула действует при параллельном соединении n конденсаторов:
С=С1+С2+..+Cn.
Последовательное соединение емкостей.Если соединить в последовательную цепь, например, три конденсатора различной емкости и полностью их зарядить до напряжения U, то выяснится, что:
- заряды –q1 и q2, -q2 и q3 равны между собой, так как обкладки с этими зарядами электрически соединены;
- заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по абсолютной величине, но противоположны по знаку.
Конденсаторы в таком включении получают равный заряд q, но при разной емкости получится, что напряжения на каждом элементе равны:
- U1=q/ C1;
- U2=q/ C2;
- U3= q/ C3.
Напряжения распределяются пропорционально емкостям (при равных параметрах на каждой банке падает одинаковое сопротивление). А общая емкость равна С=q/(U1+U2+U3), отсюда 1/С=( U1+U2+U3)/q=1/С1+1/С2+1/С3.
А общая емкость равна С=q/(U1+U2+U3), отсюда 1/С=( U1+U2+U3)/q=1/С1+1/С2+1/С3.
Для n элементов, подключенных в последовательную цепь:
1/С=1/С1+1/С2+..+1/Сn.
Формула выглядит громоздко, но для цепи из двух элементов можно пользоваться приведенным видом С= С1* С2/( С1+ С2).
Для предварительного анализа схем, состоящих из емкостных элементов, подключенных различными способами, надо запомнить несколько законов:
- при параллельном соединении емкости складываются, суммарная емкость всегда больше, чем у элемента с самым большим значением емкости;
- напряжения при параллельном соединении одинаковы на каждом элементе цепи;
- при последовательном соединении итоговая емкость будет меньше наименьшего значения емкости любого элемента;
- напряжения на последовательно включенных звеньях распределяются пропорционально емкости.

Анализ и расчет схем со смешанным подключением элементов надо начинать с приведения цепи к единому виду, где конденсаторы будут включены либо только последовательно, либо только в параллель.
Преобразование к последовательному виду.Так, схема на рисунке содержит три элемента, два из которых включены в параллель, и один последовательно. Удобно С1 и С3 заменить одним эквивалентным звеном С – при этом останутся только последовательные звенья. Остается выполнить расчет схемы, а потом вернуться к изначальной цепи.
Преобразование к последовательному виду.Рекомендуем видео-урок по физике.
Примеры подключений
Параллельное соединение применяется в тех случаях, когда надо увеличить итоговую емкость. По экономическим или компоновочным причинам использование одного элемента с необходимыми параметрами может быть невозможно или нерационально. Поэтому собирают батарею из конденсаторов так, чтобы сумма емкостей давала необходимое значение. Такая схема применяется, например, для фильтров блоков питания в целях увеличения емкости сглаживающего фильтра.
По экономическим или компоновочным причинам использование одного элемента с необходимыми параметрами может быть невозможно или нерационально. Поэтому собирают батарею из конденсаторов так, чтобы сумма емкостей давала необходимое значение. Такая схема применяется, например, для фильтров блоков питания в целях увеличения емкости сглаживающего фильтра.
Другой вариант параллельного включения – когда емкость надо точно настраивать по месту, а подстроечного конденсатора с необходимыми пределами или нет в наличии, или не существует. Тогда параллельно конденсатору постоянной емкости включают подстроечный элемент. После монтажа устройства во время настройки устанавливается точное значение.
Параллельно включенный прибор с постоянными параметрами и подстроечник.Последовательное включение нескольких элементов дает увеличение рабочего напряжения цепочки, но уменьшает общую емкость. К тому же купить приборы на высокое напряжение (до нескольких киловольт) несложно, поэтому последовательные цепи в целях достижения необходимых параметров применяются нечасто. Обычно такое включение используется в емкостных делителях напряжения. В отличие от резистивных компонентов, через реактивные элементы не протекает активный ток, поэтому не надо решать задачу отвода тепла. Такие делители можно применять, к примеру, в индикаторах наличия высокого напряжения. Несколько киловольт на входе подбором номиналов банок делятся так, что напряжение на нижнем элементе безопасно для индикаторной лампы.
Обычно такое включение используется в емкостных делителях напряжения. В отличие от резистивных компонентов, через реактивные элементы не протекает активный ток, поэтому не надо решать задачу отвода тепла. Такие делители можно применять, к примеру, в индикаторах наличия высокого напряжения. Несколько киловольт на входе подбором номиналов банок делятся так, что напряжение на нижнем элементе безопасно для индикаторной лампы.
Также такой делитель можно найти в схемах импульсных источников питания с полумостовой схемой. Таким способом образуется средняя точка с потенциалом, равным половине питания.
Фрагмент схемы блока питания с фильтром-делителем и выравнивающими резисторами.
Еще один пример применения последовательного соединения элементов – в умножителях напряжения. В них нагрузочная способность источника питания зависит от емкости, поэтому в умножителях также применяются оксидные конденсаторы.
Последовательная батарея для умножителя.
Смешанное включение встречается гораздо реже. Один из примеров такой схемы – колебательный контур с переменной частотой настройки. Его резонанс зависит, в том числе, от емкости конденсатора, и перестройка по частоте зависит от пределов изменения емкости. Ряд конденсаторов переменной емкости, выпускаемый промышленностью, довольно ограничен, поэтому для достижения необходимых границ параллельно и последовательно с КПЕ включают «растягивающие» конденсаторы.
КПЕ с «растягивающими» элементами.Если имеется конденсатор с пределами изменения характеристик от 10 до 430 пФ, при подключении добавочных конденсаторов пределы изменения емкости получаются:
| С1, пФ | С2, пФ | Новые пределы изменения, пФ |
|---|---|---|
| 15 | 40 | 15..36 |
| 25 | 100 | 25..82 |
Знание свойств соединения емкостных элементов позволяет быстро анализировать процессы, происходящие в электрических схемах. Также понимание, как изменяются характеристики цепи при различных видах подключения, позволяет комбинировать имеющиеся элементы, создавая участки схем с новыми параметрами.
электричества. Есть ли физическое объяснение тому, почему увеличение емкости конденсатора и сопротивления цепи снижает скорость разряда конденсатора?
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 11 тысяч раз
$\begingroup$ 9{-t/RC}$$
Таким образом, увеличение сопротивления и емкости увеличивает время, необходимое для снижения начального напряжения, например, до 63% от исходного значения, что также означает, что экспоненциальный график затухания будет менее крутым при более высоком сопротивлении и емкости.
Но есть ли физическое объяснение этому явлению, особенно для емкости? Поскольку емкость параллельной пластины определяется выражением $C=q/V$, т. е. зарядом, накопленным в одной из пластин на единицу напряжения на пластине, как емкость влияет на скорость разряда или падение напряжения?
е. зарядом, накопленным в одной из пластин на единицу напряжения на пластине, как емкость влияет на скорость разряда или падение напряжения?
- электричество
- электрические цепи
- электрический ток
- емкость
$\endgroup$
$\begingroup$
Отвечу по аналогии, чтобы была яснее картина происходящего. В некотором смысле конденсатор подобен резервуару для хранения электронов. Это означает, что конденсатор с большей емкостью может хранить больше заряда, чем конденсатор с меньшей емкостью, при фиксированном напряжении на выводах конденсатора.
Напряжение на выводах конденсатора очень похоже на давление воды в трубе, так как более высокое напряжение приводит к более высокой скорости потока электронов (электрический ток) в проводе для заданного электрического сопротивления в соответствии с законом Ома.
Учитывая аналогию с резервуаром, если я увеличу диаметр резервуара с водой, но оставлю начальный уровень воды таким же, каким он был изначально, у меня будет больше воды в резервуаре.
Если я уменьшу размер отверстия (увеличим сопротивление потоку), постоянная времени для обоих резервуаров увеличится, но маленький резервуар всегда будет работать всухую первым, если оба резервуара начинаются с одного уровня.
Что касается названия этого запроса, скорость разрядки конденсатора обычно рассматривается как скорость, с которой заряд покидает пластины конденсатора. Это ток в соответствующей цепи. Насколько быстро уменьшается напряжение на обкладках конденсатора и насколько быстро уменьшается ток в соответствующей цепи, зависит от постоянной времени цепи, которая НЕ является током, протекающим в цепи.
$\endgroup$
4
$\begingroup$
Конденсатор большего размера хранит больше энергии при заданном напряжении, чем конденсатор меньшего размера. Добавление сопротивления к цепи уменьшает количество тока, протекающего через нее. Оба этих эффекта снижают скорость рассеивания накопленной энергии конденсатора, что увеличивает значение постоянной времени цепи.
$\endgroup$
$\begingroup$
Есть ли физическое объяснение тому, почему увеличение конденсатора емкость и сопротивление цепи уменьшают скорость конденсатора разряда?
Уравнение, которое вы даете в своем вопросе, описывает разрядку конденсатора от начального напряжения на $V_i$ до нуля, поэтому это будет контекст этого ответа. По физическим признакам имеем следующее:
По физическим признакам имеем следующее:
(1) Количество заряда $Q$, протекающего через резистор в процессе разряда, согласно основному уравнению конденсатора $Q = CV_i$
(2) Начальная скорость , с которой протекает заряд через резистор $\frac{dQ}{dt} = \frac{V_i}{R}$, который независим от емкости $C$, и это максимальная скорость .
То есть увеличивает $C$ увеличивает количество заряда $Q$, которое должно пройти через резистор во время разряда без изменения максимальная скорость, с которой течет заряд. Таким образом, по физическим причинам для разрядки конденсатора потребуется на
И наоборот, увеличивает $R$ уменьшает начальную (и максимальную) скорость прохождения заряда через резистор. Таким образом, по физическим причинам для разрядки конденсатора потребуется на больше времени, чем , при увеличении $R$.
$\endgroup$
1
$\begingroup$
.
..как емкость влияет на скорость разряда или падение напряжения?
При любом заданном уровне напряжения большой конденсатор хранит больше заряда, чем меньший конденсатор, поэтому при одинаковом токе разряда (который при любом заданном уровне напряжения определяется сопротивлением резистора) потребуется больше времени для разрядки. разрядить больший конденсатор, чем меньший.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
 Электромагнетизм
Электромагнетизм. Интуитивно понятно, почему последовательное соединение конденсаторов уменьшает эквивалентную емкость?
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 14 тысяч раз
$\begingroup$
Может кто-нибудь объяснить, интуитивно (без всякой формулы, я понимаю формулы), почему эквивалентная емкость последовательно соединенных конденсаторов меньше емкости любого отдельного конденсатора?
Возьмем простой случай. Скажем, у нас есть 2 конденсатора с емкостью 2 (без учета единиц), и мы размещаем их последовательно. В обоих возникает напряжение $V$, а на одной из их обкладок накапливается заряд $+Q$.
- электромагнетизм
- электрические цепи
- емкость
$\endgroup$
3
$\begingroup$
Может кто-нибудь объяснить, интуитивно (без всяких формул, я разберитесь в формулах), почему эквивалентная емкость конденсаторов последовательно меньше емкости любого отдельного конденсатора?
Я полагаю, вы знаете, что чем больше пластины конденсатора, тем больше его емкость при прочих равных условиях. Также я предполагаю, что вы знаете, чем больше расстояние между пластинами (чем толще диэлектрик между пластинами), тем меньше емкость при прочих равных условиях.
На верхнем рисунке слева показаны два конденсатора, включенных параллельно. Это эквивалентно диаграмме вверху справа. Если два или более конденсатора соединены параллельно, общий эффект будет таким же, как у одного (эквивалентного) конденсатора, имеющего общую площадь пластин, равную сумме площадей пластин отдельных конденсаторов. Таким образом, для параллельных конденсаторов эквивалентная емкость представляет собой сумму емкостей.
Нижняя средняя диаграмма показывает два последовательно соединенных конденсатора. Это эквивалентно диаграмме в правом нижнем углу. Если два или более конденсатора соединены последовательно, общий эффект будет таким же, как у одного (эквивалентного) конденсатора, имеющего сумму расстояний между пластинами отдельных конденсаторов. Таким образом, для последовательных конденсаторов эквивалентная емкость меньше, чем для отдельных конденсаторов. Если конденсаторы одинаковые и равны $C$, то эквивалентная емкость равна $C/2$
Для справки на диаграмме приведены соответствующие уравнения для емкости, основанные на физических параметрах ($A$, $d$, $e$) и электрических параметрах ($Q$, $V$).
Это начинает обретать смысл. Но не возражаете ли вы разработать тини немного больше о том, почему общая стоимость серийного кейса составляет $Q$, а не $2Q$?
Суммарный заряд эквивалентной последовательной емкости равен $Q/2$, а не $Q$. Заряд двух конденсаторов, соединенных последовательно через источник напряжения, меньше, чем если бы один из конденсаторов был подключен к тому же источнику напряжения. Это можно показать, рассматривая заряд каждого конденсатора из-за напряжения на каждом конденсаторе или рассматривая заряд эквивалентной последовательной емкости.
На нижнем левом рисунке показан один конденсатор емкостью $C$, подключенный к напряжению $V$. Заряд конденсатора равен $Q=CV$ после его полной зарядки, как показано на рисунке.
На нижнем среднем рисунке показаны два конденсатора одинаковой емкости $C$, подключенные последовательно к одному и тому же источнику напряжения. Напряжение на каждом равно $V/2$. Поскольку $Q=CV$, это означает, что заряд каждого будет $Q=C\frac{V}{2}$. Однако, как указал @Kaz, проводник и пластины между двумя конденсаторами не способствуют разделению зарядов. Иными словами, суммарный заряд пластин и проводника между конденсаторами равен нулю. Это приводит к заряду эквивалентной емкости, равному $Q=C\frac{V}{2}$, как показано на нижней правой диаграмме.
Однако, как указал @Kaz, проводник и пластины между двумя конденсаторами не способствуют разделению зарядов. Иными словами, суммарный заряд пластин и проводника между конденсаторами равен нулю. Это приводит к заряду эквивалентной емкости, равному $Q=C\frac{V}{2}$, как показано на нижней правой диаграмме.
К такому же выводу можно прийти, если учесть, что эквивалентная емкость двух одинаковых конденсаторов, соединенных последовательно, составляет половину емкости каждого, или $C_{equiv}=\frac{C}{2}$. Следовательно, заряд на эквивалентной последовательной емкости такой же, как заряд на каждом из последовательных конденсаторов, или $\frac{C}{2}V$, как показано на нижней правой диаграмме.
Надеюсь, это поможет
$\endgroup$
1
$\begingroup$
Один из способов взглянуть на это — хотя , возможно , больше с точки зрения электроники , чем с точки зрения физики — не думать о конденсаторе как о вещи , хранящей заряд . Поскольку весь компонент электрически нейтрален, если смотреть снаружи, общее количество заряда внутри него всегда одинаково; он просто перераспределяется способами, которые не должны касаться нас на более высоком уровне абстракции.
Поскольку весь компонент электрически нейтрален, если смотреть снаружи, общее количество заряда внутри него всегда одинаково; он просто перераспределяется способами, которые не должны касаться нас на более высоком уровне абстракции.
С этой точки зрения конденсатор является зависимым источником напряжения, где напряжение в любой момент времени пропорционально чистому количеству заряда, прошедшего через конденсатор за время его жизни.
Емкость измеряет, сколько заряда нам нужно протолкнуть через конденсатор, чтобы изменить его напряжение на заданную величину.
Если у нас есть два последовательно соединенных конденсатора, любой заряд, который мы пропустим через весь комплекс, пройдет через оба конденсатора одновременно, но напряжение, которое мы измерим на нем, будет .0063 сумма напряжений отдельных конденсаторов. Таким образом, для создания любого желаемого изменения общего напряжения требуется меньше заряда, то есть емкость меньше.
$\endgroup$
0
$\begingroup$
Вот объяснение того, как заряды перемещаются по цепи.
В случае одного конденсатора уравнение $Q = CV$ означает, что при приложении напряжения $V$ к системе конденсаторов с емкостью $C$ количество зарядов, перемещаемых из одного места в другое, составляет $Q$ . См. приведенную ниже диаграмму.
При подаче напряжения $V_1$ на конденсатор $C_1$ заряд $Q$ снимается с одной пластины и осаждается на противоположной пластине.
Теперь рассмотрим, что происходит с двумя последовательно соединенными конденсаторами:
Источник выдает напряжение $V_1 = V$ на конденсаторы $C_1$ и $C_2$. Наша цель — определить общее количество перемещенного заряда после того, как ток упадет до нуля после подключения источника напряжения.
Верхняя пластина конденсатора $C_1$ находится под напряжением $+V$, а нижняя пластина конденсатора $C_2$ – при напряжении $0$ (абсолютные значения не имеют значения, важны только их различия). Между ними нижняя пластина конденсатора $C_1$ должна находиться под тем же напряжением $V’$, что и верхняя пластина конденсатора $C_2$, так как они соединены проводом. Что это за напряжение? Это не может быть $V$, так как тогда не было бы разницы напряжений на $C_1$ и он не получил бы никакого заряда — как будто его и не было. Точно так же он не может быть равен нулю, поскольку тогда на $C_2$ не будет напряжения. В случае $C_1 = C_2 = C,$ можно сделать вывод, что $V’ = V/2$, так как одинаковые последовательно соединенные компоненты должны иметь одинаковые падения напряжения. Если подумать иначе, два конденсатора будут иметь одинаковый заряд после замыкания цепи, поскольку любой заряд, сходящий с $C_1$, должен попасть на $C_2$, и наоборот. Поскольку это идентичные конденсаторы с одинаковым зарядом, они должны иметь одинаковое падение напряжения на них.
Между ними нижняя пластина конденсатора $C_1$ должна находиться под тем же напряжением $V’$, что и верхняя пластина конденсатора $C_2$, так как они соединены проводом. Что это за напряжение? Это не может быть $V$, так как тогда не было бы разницы напряжений на $C_1$ и он не получил бы никакого заряда — как будто его и не было. Точно так же он не может быть равен нулю, поскольку тогда на $C_2$ не будет напряжения. В случае $C_1 = C_2 = C,$ можно сделать вывод, что $V’ = V/2$, так как одинаковые последовательно соединенные компоненты должны иметь одинаковые падения напряжения. Если подумать иначе, два конденсатора будут иметь одинаковый заряд после замыкания цепи, поскольку любой заряд, сходящий с $C_1$, должен попасть на $C_2$, и наоборот. Поскольку это идентичные конденсаторы с одинаковым зарядом, они должны иметь одинаковое падение напряжения на них.
Итак, сколько заряда находится на каждом конденсаторе, мы используем первое уравнение, чтобы найти, что $Q’ = CV/2$, так как теперь на конденсаторе находится половина напряжения. Два конденсатора идентичны, поэтому второй конденсатор получает одинаковый заряд $Q’ = CV/2.$
Два конденсатора идентичны, поэтому второй конденсатор получает одинаковый заряд $Q’ = CV/2.$
Наконец, сколько зарядов было перемещено? Заряд может передаваться только по проводам, поэтому, если верхняя пластина верхнего конденсатора получила заряд $Q/2$, этот заряд должен был исходить от нижней пластины нижнего конденсатора. Несмотря на то, что оба конденсатора получили заряд $Q/2$ (где $Q$ — заряд, перенесенный в первой цепи), заряды переместились с одного конденсатора на другой. Таким образом, общий перемещенный заряд составил Q/2.
Из всего этого мы находим, что емкость двух одинаковых конденсаторов, соединенных последовательно, вдвое меньше емкости одного конденсатора, потому что половина заряда перемещается при одном и том же напряжении.
$\endgroup$
$\begingroup$
Это просто (но не очевидно):
Предположим, параллельная пластина: $C = \epsilon A/d$
Предположим, что пластины бесконечно тонкие
Вставка бесконечно тонкой пластина посередине
Влияет ли C? Нет, потому что пластина отсоединена и диэлектрическая проницаемость ($\epsilon$) не изменяется.

Но: теперь у вас есть 2 конденсатора с расстоянием $d/2$, каждый с емкостью $2C$.
КЭД.
$\endgroup$
$\begingroup$
Разве мы не накапливаем в сумме заряд $2Q$ при разности потенциалов $2V$? Почему только $1Q$?
Итак, вот в чем суть вопроса. Соответствующий заряд здесь равен $Q$, а не $2Q$. Так почему же?
Это потому, что в последовательной цепи все компоненты видят весь заряд. (Эквивалентно, все компоненты видят весь ток.) Если я пропускаю 1 кулон заряда через всю цепь, это означает, что я пропускаю 1 кулон заряда через каждого конденсатора.
Это очень похоже на то, как если у меня есть пара из 2 дверей последовательно, и я посылаю через двери 100 человек, то через каждую дверь проходит 100 человек, а не 50.
$\endgroup$
$\begingroup$
Пожалуйста, взгляните на аналогию в области давления воды. Представим устройство, состоящее из поршня в трубке, соединенной с пружиной. Когда разница давлений увеличивается, поршень перемещается и тянет пружину до тех пор, пока силы, вызванные давлением и пружиной, не уравновесятся.
Представим устройство, состоящее из поршня в трубке, соединенной с пружиной. Когда разница давлений увеличивается, поршень перемещается и тянет пружину до тех пор, пока силы, вызванные давлением и пружиной, не уравновесятся.
Если рассматривать разницу давлений как аналогию напряжения, то объем воды, протекающей по трубе, будет электрическим зарядом, а их соотношение будет аналогией емкости.
Если соединить оба таких устройства параллельно, то количество воды, которое оно может «накапливать» при определенном давлении, будет суммироваться. Таким образом, емкость будет, очевидно, суммой.
Если мы соединим их последовательно, то количество воды, прошедшей через них, должно быть одинаковым во всех последовательно соединенных устройствах. Давление будет равномерно распределяться между двумя пружинами, что приведет к снижению тягового усилия и снижению Δx. В конце концов объем воды на давление будет ниже.
Возвращаясь к области электричества, стоит отметить, что электрический заряд в звене между конденсаторами никогда не изменится, потому что мы рассматриваем его как изолированное. Вместо этого электрический потенциал будет балансировать где-то между потенциалами источника напряжения.
Вместо этого электрический потенциал будет балансировать где-то между потенциалами источника напряжения.
$\endgroup$
$\begingroup$
Представьте себе два простых конденсатора, каждый из которых состоит из двух пластин, каждая из которых имеет площадь A, разделенных расстоянием D. Если они соединены последовательно, нижняя пластина верхнего конденсатора закорочена на верхнюю пластину нижнего конденсатора, создавая эквивалент одиночного конденсатора. пластина, которая на самом деле не связана ни с чем другим, поэтому ею можно пренебречь. В результате получается эквивалент одиночного конденсатора с площадью A и расстоянием между пластинами 2D.
Поскольку емкость обратно пропорциональна расстоянию между пластинами, емкость будет вдвое меньше, чем у одиночного конденсатора. Это можно обобщить на более чем два конденсатора. (примечание: формулы не используются)
$\endgroup$
3
$\begingroup$
почему эквивалентная емкость последовательно соединенных конденсаторов меньше емкость любого отдельного конденсатора?
Чтобы развить свою интуицию, поместите последовательно с другим конденсатором идеальный конденсатор с плоскими пластинами (для простоты вакуумный диэлектрик) с расстоянием между пластинами $d$. Теперь рассмотрим предел, когда расстояние $d$ стремится к нулю (предположим, что начальный заряд равен нулю).
Теперь рассмотрим предел, когда расстояние $d$ стремится к нулю (предположим, что начальный заряд равен нулю).
Интуитивно понятно, что емкость идеального конденсатора с параллельными пластинами неограниченно возрастает, и то, что остается в пределе, фактически представляет собой идеальное короткое замыкание, когда $d = 0$ (две пластины соприкасаются).
То есть последовательное соединение двух конденсаторов стало последовательно включенным конденсатором с идеальным КЗ. Ясно, что объединенная емкость — это просто емкость оставшегося конденсатора.
Теперь оставьте расстояние $d$ постоянным и вместо этого дайте площади пластины $A$ обнулиться. Интуитивно понятно, что емкость идеального пластинчатого конденсатора стремится к нулю, и то, что остается в пределе, фактически является идеальной разомкнутой цепью.
То есть последовательное соединение двух конденсаторов стало последовательно включенным конденсатором с идеальным разомкнутым контуром. Ясно, что суммарная емкость равна нулю.
Отсюда следует, что общая емкость двух последовательных конденсаторов с конечной емкостью равна меньше чем меньшая из двух емкостей
$\endgroup$
$\begingroup$
Емкость – это заряд на напряжение. Два последовательно соединенных конденсатора одинаковой емкости, содержащие одинаковый заряд, будут иметь такой же заряд, доступный на двух внешних обкладках конденсатора, как и один конденсатор, но напряжение будет удвоено. Таким образом, емкость составляет половину.
$\endgroup$
1 9* = \frac{U}{Q}$ вместо этого. (Действительно, это значение сегодня называется «эластичность». Спасибо Альфреду Центавру за ваш комментарий.)
Если бы они сделали это, «емкость» (которая была бы $\frac {U}{Q}$) конденсаторов последовательно будет увеличивать а не уменьшать!
По этой причине я сомневаюсь, что можно объяснить явление «интуитивно» без хотя бы обращения к формуле $C=\frac {Q}{U}$.
Я также хотел бы дать общий ответ, который также применим к «настоящим» конденсаторам без пластин…
… почему эквивалентная емкость последовательно соединенных конденсаторов меньше емкости любого отдельного конденсатора?
Сначала следует вспомнить, о чем вы говорите, если говорите о «емкости последовательного соединения»:
Вы — это , говоря о напряжении, измеренном на обоих концах последовательного соединения, и о заряде, который перетекал в один конец последовательного соединения.
Вы , а не и говорите о напряжениях, измеренных внутри последовательного соединения, и/или зарядах где-то внутри последовательного соединения.
Если некоторое количество электронов втекает в один конец конденсатора или один конец последовательного соединения, такое же количество электронов вытекает из конденсатора или последовательного соединения на другом конце. Это количество электронов и есть «заряд конденсатора» $Q$.
При последовательном соединении электроны, вытекающие из первого конденсатора, перетекают во второй конденсатор. Это означает, что если в один конец последовательного соединения потечет некоторый заряд $Q$, то все конденсаторы будут заряжены зарядом $Q$.
Поскольку мы определили заряд, перетекающий в один конец последовательного соединения, как «заряд последовательного соединения», «заряд последовательного соединения» составляет только $Q$, а не $N\x Q$, если есть $N$ конденсаторов, соединенных последовательно, каждый из которых имеет заряд $Q$.
С другой стороны, напряжение $U$ описывает энергию, необходимую для перемещения электрона из одной точки цепи в другую. Чтобы переместить некоторое количество электрона с одного конца последовательного соединения на другой конец, нам нужна энергия для переноса электрона с одного конца первого конденсатора на другой конец первого конденсатора. И нам нужна энергия, чтобы транспортировать ее от одного конца второго конденсатора к другому его концу. Это означает, что напряжение при последовательном соединении является суммой напряжений конденсаторов. 9{*}=\frac{U}{Q}$:
Это означает, что напряжение при последовательном соединении является суммой напряжений конденсаторов. 9{*}=\frac{U}{Q}$:
Поскольку напряжения суммируются, но заряд последовательного соединения равен заряду каждого отдельного конденсатора, емкость последовательного соединения составляет:
$\displaystyle {C = \frac{Q}{\sum U_\text{capacitor}}}$
Это означает, что числитель дроби $\frac{Q}{U}$ одинаков для одиночного конденсатора и ряда соединение, но знаменатель больше при последовательном соединении.
$\endgroup$
2 9`- эти две пластины и проводник не вносят вклад для разделения заряда.
Кроме того, внешние пластины в два раза дальше друг от друга, чем в одиночном конденсаторе. Увеличенное разделение уменьшает емкость вдвое.
$\endgroup$
$\begingroup$
Когда вы говорите «интуитивно», ответ зависит от того, что вы уже считаете интуитивным. Интуитивны ли для вас аналогичные правила для резисторов? (Последовательно соединенные резисторы имеют общее сопротивление, равное сумме двух отдельных сопротивлений). Считаете ли вы взаимосвязь между емкостью и импедансом интуитивно понятной? (Xc = 1/(2 * pi * f * c)).
Интуитивны ли для вас аналогичные правила для резисторов? (Последовательно соединенные резисторы имеют общее сопротивление, равное сумме двух отдельных сопротивлений). Считаете ли вы взаимосвязь между емкостью и импедансом интуитивно понятной? (Xc = 1/(2 * pi * f * c)).
Если да, то объяснение простое:
Конденсаторы ведут себя точно так же, как резисторы. Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных импедансов двух конденсаторов. Поскольку импеданс обратно пропорционален емкости, больший импеданс последовательной цепи означает меньшую емкость.
$\endgroup$
$\begingroup$
Изменение напряжения на конденсаторе или в любой области пространства является отрицательным интегралом пути от точки поля. Таким образом, если два конденсатора соединены последовательно, у вас будет вдвое большее расстояние для интеграла пути по сравнению с одним конденсатором отдельно. Теперь, поскольку расстояние удваивается, чтобы получить конечное напряжение, равное напряжению батареи, которая ее заряжает, электрическое поле должно составлять всего 1/2 электрического поля одиночного конденсатора. Поскольку электрическое поле пропорционально плотности заряда, вам нужна только 1/2 плотности заряда, которая была бы на одном конденсаторе, поэтому C = (Qsingle/2)/V.
Теперь, поскольку расстояние удваивается, чтобы получить конечное напряжение, равное напряжению батареи, которая ее заряжает, электрическое поле должно составлять всего 1/2 электрического поля одиночного конденсатора. Поскольку электрическое поле пропорционально плотности заряда, вам нужна только 1/2 плотности заряда, которая была бы на одном конденсаторе, поэтому C = (Qsingle/2)/V.
$\endgroup$
$\begingroup$
Чем больше зазор, тем меньше емкость. Последовательное соединение нескольких конденсаторов приводит к последовательному соединению нескольких зазоров, что увеличивает зазоры.
Другая интерпретация состоит в том, что это делитель напряжения, и поэтому индуцированный заряд соответствует только части напряжения.
$\endgroup$
$\begingroup$
Если у вас есть конденсатор и вы помещаете заряд на одну из пластин, на другой пластине за счет индукции собирается противоположный заряд; чтобы поддерживать эту конфигурацию, вы должны приложить определенные усилия (т.
