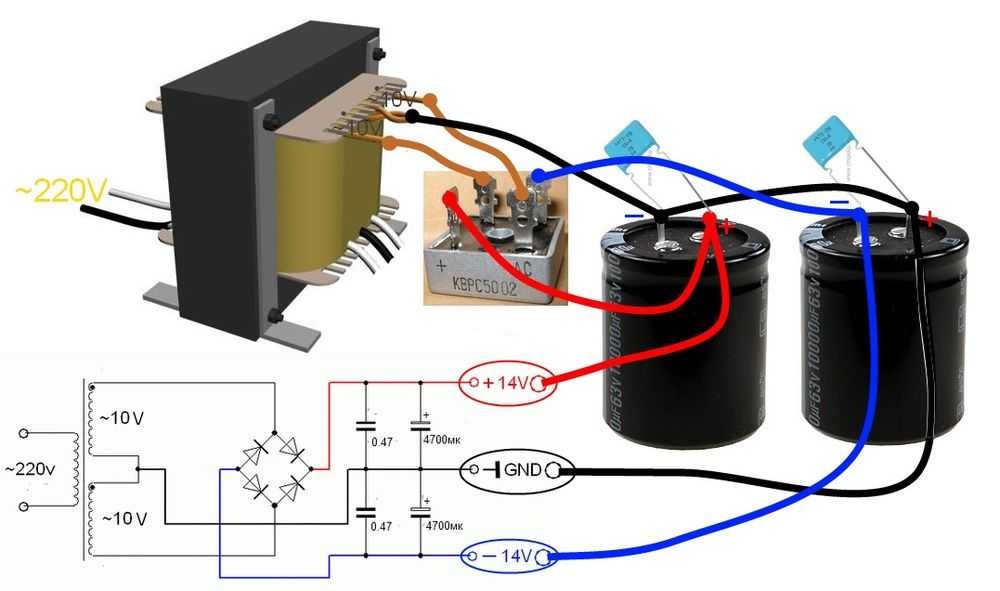
Последовательное и параллельное соединение.
Оцените материал
- 1
- 2
- 3
- 4
- 5
(17 голосов)
Иногда нужно увеличить ёмкость или сопротивление, а подходящих деталей на нужное сопротивление нет, или размеры конструкции не позволяют вставить один большой конденсатор на 3000 мкф.
В этом случае можно набрать необходимые ёмкость или сопротивление из нескольких деталей, а вместо конденсатора на 3000 микрофарад вставить 3 штуки по 1000 микрофарад.
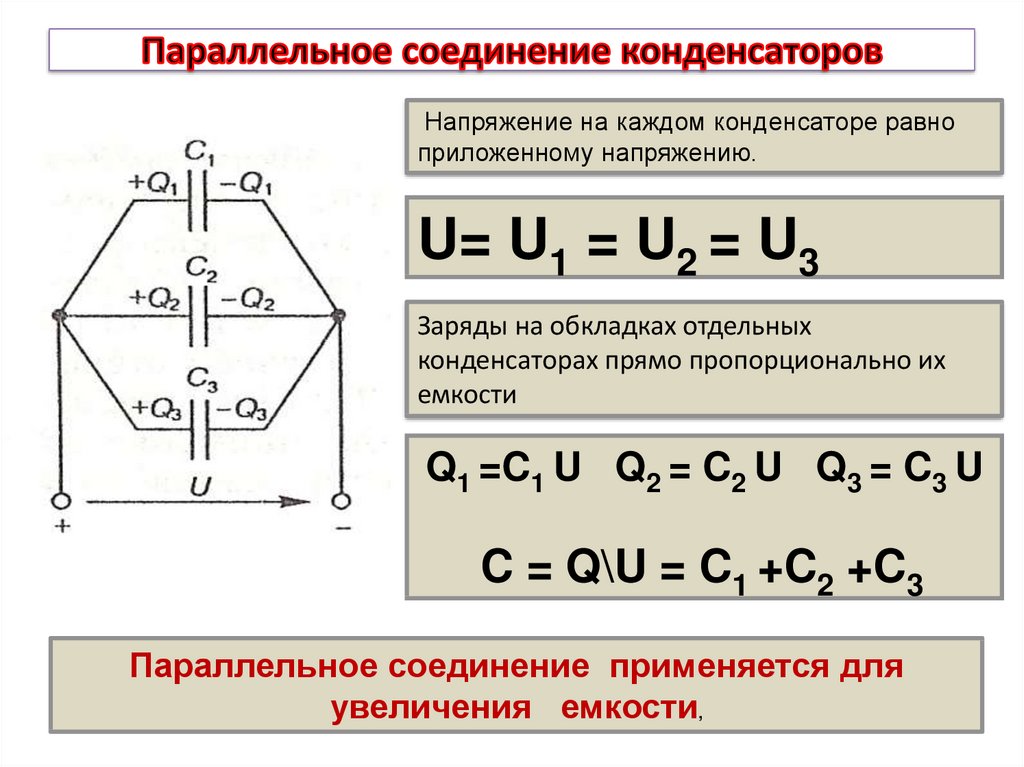
Для увеличения ёмкости конденсаторы соединяются параллельно.
Для увеличения сопротивления резисторы соединяются последовательно.
Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.
Последовательное соединение — когда детали стоят друг за дружкой, «в очереди», будто за колбасой, потому оно так и называется.
Не путайте эти соединения, для увеличения ёмкости конденсаторы соединяются параллельно, а резисторы для увеличения сопротивления последовательно !
Со сложением ёмкостей и сопротивлений всё легко.
С параллельным соединением резисторов и последовательным соединением конденсаторов слегка посложнее, но к нашему счастью конденсаторы довольно редко соединяют последовательно, а резисторы параллельно.
Последовательное соединение конденсаторов может понадобиться например в сборке гаусс-гана (электромагнитной стрелялки), когда под рукой конденсаторы только на 400 вольт, а нам нужен 800-вольтовый конденсатор, а их редко где найдёшь и они дорогие.
Параллельное соединение резисторов считается вот по какой формуле:
Через три трубы, в которых в каждой по валенку, вода лучше потечёт, чем через одну трубу с одним валенком. Или если в бочке проковырять три дырки, то вода быстрее выльется, чем если бы мы проковыряли одну дырку.
Последовательное соединение конденсаторов считается по той же формуле.
Если два одинаковых конденсатора по 680uF с максимальным напряжением 400В поставить последовательно, то получится конденсатор на 340 uF с напряжением 800 вольт.
Ёмкость уменьшается, зато вырастает максимальное допустимое напряжение, а запасаемая в обеих конденсаторах энергия остаётся та же самая.
Последнее от Антон
- Обзор нового варианта печатных плат SDR malamute
- Печатные платы V3 для SDR «Malamute»
- Raspberry Pi – компьютер с ARM архитектурой
- Отладочные платы Arduino Uno
- Трансивер «Маламут» NEW
Другие материалы в этой категории: « Делаем двухстороннюю плату Как оно работает!? »
Добавить комментарий
Наверх
Последовательное и параллельное соединение конденсаторов
ОТ КАТОДА ДО АНОДА
Поиск по сайту Новости Миниатюрные audio усилители от Diodes | ГЛАВНАЯ » КОНДЕНСАТОРЫ » Последовательное и параллельное соединение конденсаторов Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели.
А общее напряжение будет равняться сумме напряжений всех конденсаторов. При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора. C = C1 + C2 + C3 + C4 + … Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В. Соединение более двух конденсаторов последовательно редко встречается в реальных схемах. Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления. Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратны формулам вычисления сопротивления при последовательном и параллельном соединении резисторов. |
При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.
Как увеличить емкость?
Подсказка: Способность системы накапливать электрический заряд известна как емкость. Емкость конденсатора с плоскими пластинами зависит от величины площади пластин, расстояния между пластинами и среды между пластинами. Следовательно, чтобы увеличить емкость, можно изменить одно или несколько из этих условий.
Полный ответ:
Устройство, образованное двумя изолированными друг от друга проводниками, называется конденсатором. Емкость — это, по сути, способность системы накапливать заряд, и технически она определяется как отношение заряда на проводнике к с к разности потенциалов между проводниками, которая математически выражается как 9{-2}$
$A$ = площадь двух параллельных пластин
$d$ = расстояние между параллельными пластинами
Обычно в пространстве между пластинами нет ничего, кроме вакуума, поэтому мы берем диэлектрическую проницаемость свободного пространства в уравнении емкости.
Но, как мы знаем, этот вакуум неполяризуемый и, следовательно, переносит относительно меньше заряда. Следовательно, заменим все пространство между пластинами конденсатора поляризуемым диэлектрическим материалом, диэлектрическая проницаемость которого выражается как $\varepsilon$ . Следовательно, теперь емкость с диэлектрическим материалом выражается как
$C’=\dfrac{\varepsilon A}{d}$
Теперь отношение диэлектрической проницаемости диэлектрического материала к диэлектрической проницаемости вакуума определяется как диэлектрическая проницаемость среды, которая математически выражается как
$\ dfrac{\varepsilon }{{{\varepsilon }_{0}}}=K$
$\Rightarrow\varepsilon =K{{\varepsilon }_{0}}$
Мы можем подставить это значение в уравнение емкости as,
$C’=\dfrac{K{{\varepsilon}_{0}}A}{d}$
$\следовательно C’=KC$
Следовательно, емкость с диэлектрическим материалом составляет $K$ раз емкость со свободным пространством между пластинами. Экспериментально доказано, что значение $K$ всегда больше $1$.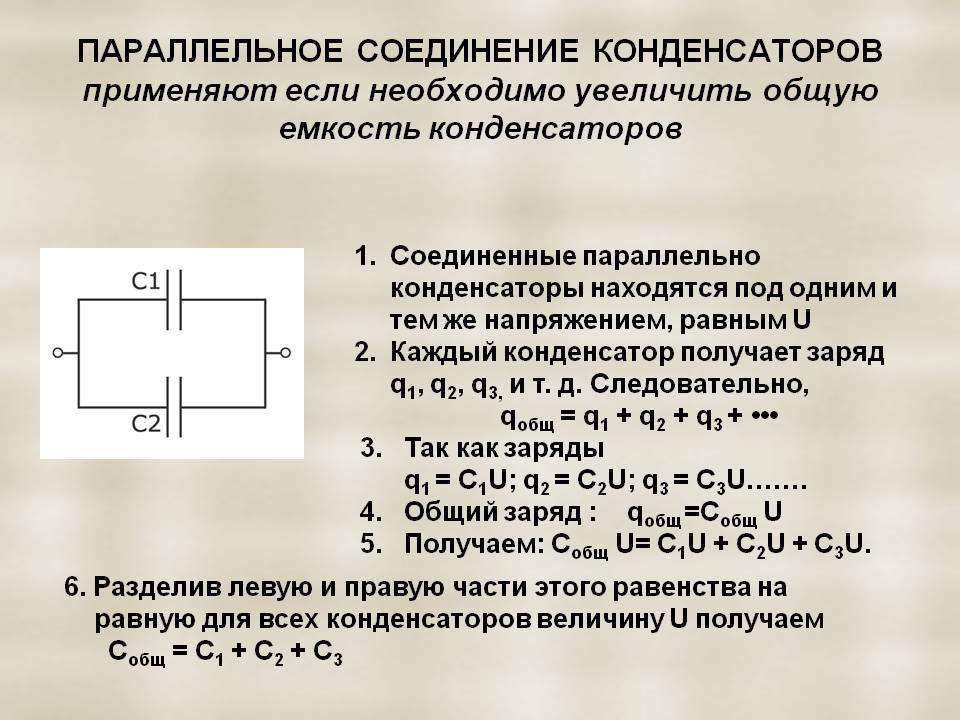
Следовательно, емкость с диэлектрическим материалом всегда будет больше, чем емкость со свободным пространством между пластинами.
Следовательно, мы можем увеличить емкость, вставив диэлектрический материал между пластинами.
Примечание: Из формулы емкости видно, что емкость также пропорциональна площади пластин и обратно пропорциональна расстоянию между пластинами. Следовательно, емкость также можно увеличить, либо увеличив площадь пластин, либо уменьшив расстояние между пластинами. Но из уравнения можно понять, что даже для увеличения емкости на $1\mu F$ площадь пластин нужно увеличить на несколько сотен метров или расстояние между пластинами уменьшить до нескольких микрометров. Оба условия практически невозможны. Следовательно, мы увеличиваем емкость только с использованием диэлектрического материала.
gif»> 
gif»>
