- Соединение конденсаторов.
- Как подключить конденсатор для увеличения емкости
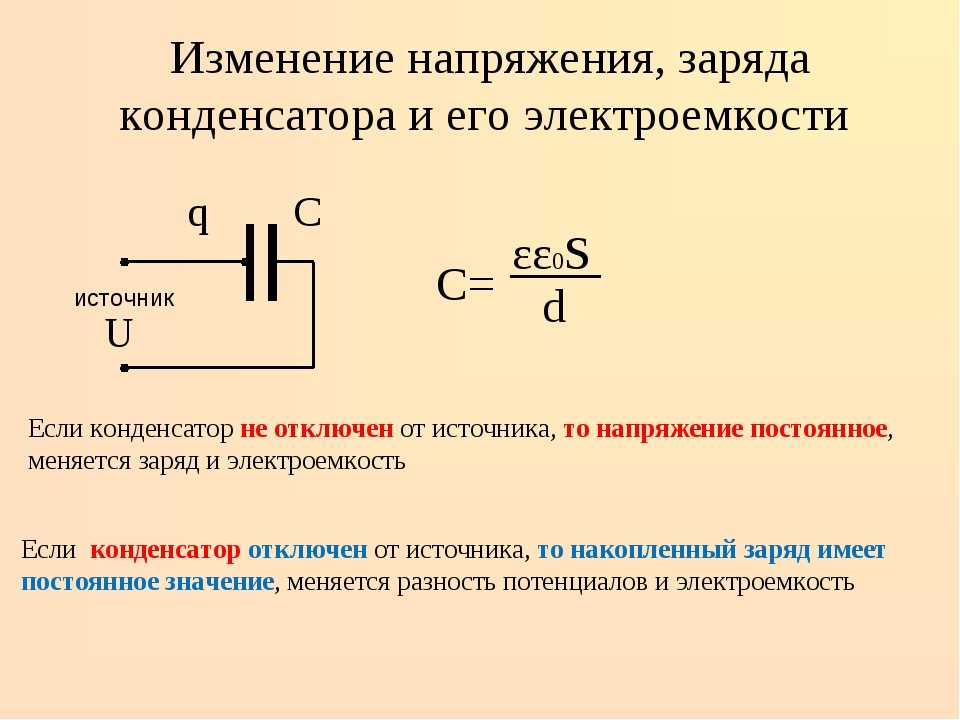
- Электрическая емкость
- Работа диодного моста
- Параллельное соединение
- Сравнение различных вариантов
- Последовательное включение конденсаторов
- Повышение напряжения в сети электропитания
- Смешанный способ
- Устройство увеличивающее напряжение в 2 раза! Всего 4 детали.
- Параллельное соединение
- «Узкие места» в конденсаторных установках, по факту влияющие на срок службы и интенсивность отказов
- Последовательное соединение
- Полупроводниковые выпрямители блоков питания, схемы, онлайн расчёт
- Смешанное подключение
- Защита от перепадов напряжения
- Как правильно соединять конденсаторы?
- Конденсаторы и установки повышения коэффициента мощности. Часть первая. Надёжность и долговечность
- Электрическая емкость. Конденсаторы. Емкость конденсатора.
- Как влияет тип диэлектрика на емкость конденсатора?
- Урок 28. электрическая ёмкость. конденсатор — Физика — 10 класс
- В каких случаях применяется параллельное соединение конденсаторов
- Молекулярные выражения: электричество и магнетизм
- Факторы, влияющие на емкость
- Вопросы или комментарии? Отправить нам письмо.
- © 1995-2022 автор Майкл В. Дэвидсон и Университет штата Флорида. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами.
- Этот веб-сайт поддерживается нашим
- Последнее изменение: среда, 7 июня 2017 г., 13:21
- Количество обращений с 3 апреля 1999 г.: 485222
- Конденсатор — Энергетическое образование
- Что можно сделать, чтобы увеличить емкость в цепи?
- Какими способами можно увеличить емкость плоского конденсатора?
- Что можно сделать, чтобы увеличить емкость в тесте схемы?
- Что вызывает увеличение емкости?
- Что происходит, когда вы увеличиваете емкость в цепи?
- Какова функция конденсатора в цепи?
- Какое свойство объектов лучше всего измеряется их емкостью?
- Как увеличить емкость конденсатора?
- Что из следующего увеличит емкость конденсатора?
- Где мы используем конденсатор?
- Зависит ли емкость от формы?
- Когда конденсатор подключен к аккумулятору?
- Почему в конденсаторе не используется вода?
- Как конденсаторы влияют на ток?
- Что произойдет, если использовать неправильный конденсатор?
- Вызывают ли конденсаторы падение напряжения?
- 19.5 Конденсаторы и диэлектрики – Колледж физики главы 1-17
- 18.
- Раздел Цели обучения
- Поддержка учителей
- Основные термины раздела
- Поддержка учителей
- Конденсаторы
- Поддержка учителей
- Смотреть физику
- Проверка захвата
- Виртуальная физика
- Проверка захвата
- Рабочий пример
- Стратегия ЗА (А)
- Стратегия ЗА (Б)
- Рабочий пример
- Стратегия
- Практические задачи
- Диэлектрики
- Поддержка учителей
- Поддержка учителей
- Поддержка учителей
- Рабочий пример
- Стратегия ЗА (А)
- Стратегия ЗА (Б)
- Практические задачи
- Проверьте свое понимание
- Заряд, разделение пластин и напряжение
Соединение конденсаторов.
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах.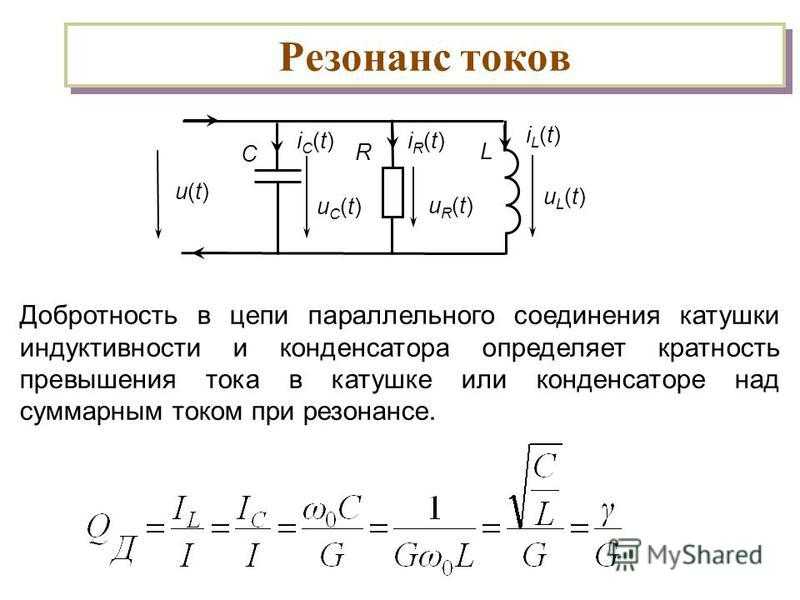 Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф. ),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Научись паять! Минимальный наборчик для пайки.
Научись паять! Подготовка и уход за паяльником.
«Мультирозетка». Собираем многофункциональную розетку.
Резистор. Параметры резисторов.
Как подключить конденсатор для увеличения емкости
Электрическая емкость
При соединении приборов для конденсации заряда, как правило, техника интересует электрическая емкость, которая получится в итоге.
Электроемкость показывает способность двухполюсника накапливать в себе заряд и измеряется в фарадах. Может показаться, что чем выше это значение, тем лучше, но на практике не существует возможности создать все возможные на свете емкости, более того, часто это и не нужно, так как во всех приборах, использующихся повседневно, применяются стандартные приборы для конденсации.
Можно соединить несколько приборов для конденсации в цепь, создав одну конденсирующую емкость, при этом значение характерной величины будет зависеть от типа подключения, и для его расчета есть давно известные формулы.
Работа диодного моста
Принцип работы диодного моста заключается в следующем. На его вход, обозначенный переменным значком, производится подача переменного тока с изменяющейся полярностью. Частота изменений, как правило, совпадает с частотой в электрической сети. На выходе, где расположены положительный и отрицательный выводы, получается ток исключительно с одной полярностью.
Однако, на выходящем токе будут наблюдаться пульсации с частотой, превышающей частоту переменного тока, подаваемого на вход. Такие пульсации являются нежелательными и препятствуют нормальной работе всей схемы. Для ликвидации таких пульсаций, применяются специальные фильтры. Для самых простых фильтров используются электролитические конденсаторы с большой емкостью. Таким образом, во всех блоках питания устанавливается диодный мост, схема с конденсатором которого позволяет эффективно сглаживать все пульсации выходящего тока.
Чтобы повысить производительность выпрямляющих устройств, в их конструкции применяется схема диодной сборки. В ее состав входят четыре диода с одинаковыми параметрами, объединенные в одном общем корпусе. Для их соединения используется схема мостового выпрямителя. Такая сборка очень компактная, для всех диодов соблюдается одинаковый тепловой режим. Стоимость общей конструкции значительно ниже, чем у четырех отдельных диодов. Однако, существенным недостатком является необходимость замены всего диодного моста, при выходе из строя хотя-бы одного диода.
В ее состав входят четыре диода с одинаковыми параметрами, объединенные в одном общем корпусе. Для их соединения используется схема мостового выпрямителя. Такая сборка очень компактная, для всех диодов соблюдается одинаковый тепловой режим. Стоимость общей конструкции значительно ниже, чем у четырех отдельных диодов. Однако, существенным недостатком является необходимость замены всего диодного моста, при выходе из строя хотя-бы одного диода.
Параллельное соединение
Существует два типа подключения приборов в цепь: последовательное и параллельное. Каждый из них обладает своими свойствами, но, как правило, используется параллельное соединение конденсаторов.
Параллельное соединение обладает такими свойствами:
Соединить конденсаторы для увеличения емкости, как показывают свойства, лучше этим способом. Для этого нужно соединить выводы с каждого двухполюсника по группам: у каждого из них два вывода. Нужно создать две группы: в одну соединить все конденсаторы с одного вывода, а во вторую с оставшегося.
При таком соединении приборы для конденсации образуют одну емкость, поэтому верна такая формула: С=С1+С2+…СN, где N — количество конденсаторов в цепи.
Например, если имеются номинальные значения 50мкф, 100мкф и 150мкф, то при последовательном подключении общее значение в цепи будет 300мкф.
В жизни это подключение используют довольно часто, например, если при расчетах оказалось, что требуется такой двухполюсник, которого в продаже точно не найти. С помощью этого способа можно варьировать емкость конденсатора так, как это потребуется, при этом не изменяя напряжение в сети.
Сравнение различных вариантов
| Емкость | Напряжение | |
| Параллельное | Увеличивается | Не изменяется |
| Последовательное | Уменьшается | Увеличивается |
| Смешанное | Изменяется | Увеличивается |
Для выбора соединения можно воспользоваться такой таблицей.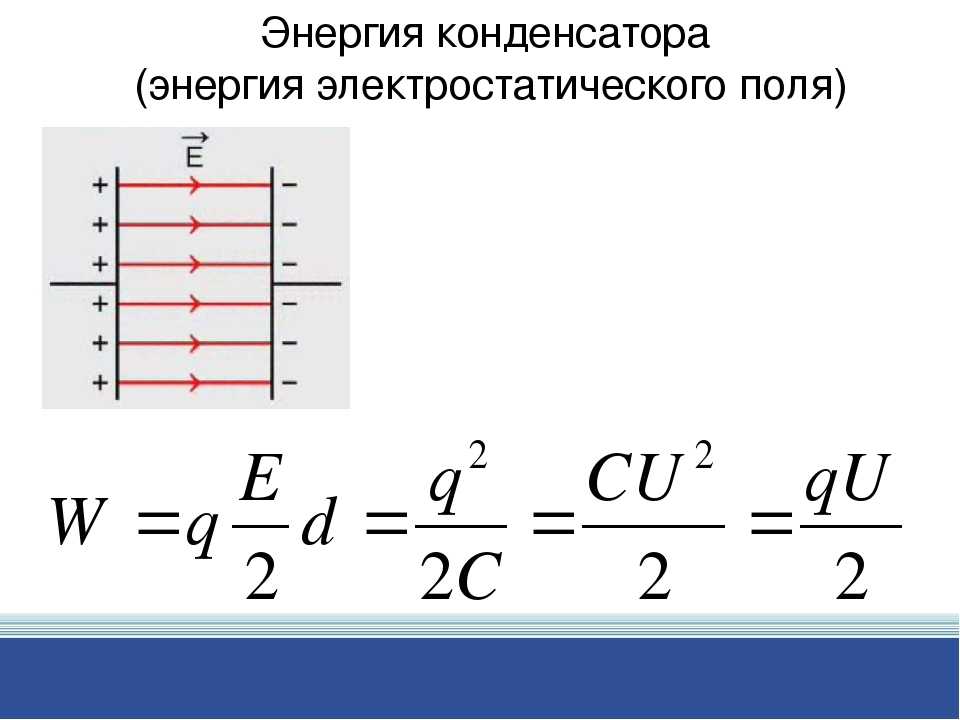 Слева тип соединения приборов, сверху свойства прибора для конденсации заряда.
Слева тип соединения приборов, сверху свойства прибора для конденсации заряда.
Если требуется увеличить емкость, то нужно использовать параллельное соединение, а если увеличить напряжение — то последовательное. Если же требуется и то, и то, то нужно будет рассчитывать смешанное подключение конденсаторов в цепь.
Последовательное включение конденсаторов
Свойства последовательного включения конденсаторов:
Для такого подключения нужно просто соединять выводы двухполюсников один с другим, образуя цепочку: вывод первого будет соединен с выводом второго, оставшийся вывод второго с выводом третьего и так далее.
Формула подключения: 1/(1/С1+1/С2+…+1/СN), где N — это количество приборов в соединении.
Например, есть три конденсатора по 100мкф. 1/100+1/100+1/100=0,03мкф. 1/0,03=33мкф.
Заряды распределятся с чередующимся знаком, а емкостное значение будет ограничено только им же для самого слабого звена в цепи.
Как только он получит свой заряд, передача тока в цепи прекратится.
Для чего тогда нужен подобный способ подключения? Такая цепь более устойчива и может выдержать большее напряжение при подключении в схему при меньшем емкостном номинале конденсатора. Однако в продаже имеются приборы, которые и без того обладают нужными свойствами, поэтому-то такое подключение в жизни практически не используется, а если используется, то для специфических задач.
READ Как подключить внешнюю антенну к usb модему huawei
Повышение напряжения в сети электропитания
Если же низкое напряжение у всех в округе – нужно думать, как повысить напряжение в сети у себя. Но не пугайтесь сразу же больших затрат на чудеса современной электроники. Они нужны, о них речь пойдет ниже. Но чаще всего проблему можно решить быстро и без хлопот подручными средствами. Причем – технически грамотно и совершенно безопасно.
При стабильно низком напряжении в сети выручит самый обыкновенный понижающий трансформатор на 12 – 36 В. Да, да, именно понижающий. И большой его мощности не потребуется. 100-ваттный потянет нагрузку в 500 Вт, а киловаттный – в 5 кВт. И увеличить напряжение в сети можно до допустимых пределов.
Да, да, именно понижающий. И большой его мощности не потребуется. 100-ваттный потянет нагрузку в 500 Вт, а киловаттный – в 5 кВт. И увеличить напряжение в сети можно до допустимых пределов.
Никаких чудес, никакой паранауки – достаточно такой трансформатор использовать как повышающий автотрансформатор, добавив напряжение понижающей обмотки к линейному. Тогда при 175 В в розетке на выходе будет при 12 В добавочных 187 В. Маловато, но бытовая техника работать будет. Если вдруг напряжение повысится до нормы, автотрансформатор выдаст 232 В; это еще в норме. При 36 В добавочных 175 В вытягиваем до 211 В – норма! Но вдруг и в розетке норма окажется, получим 256 В, а это уже нехорошо для электроприборов. Поэтому лучше всего – 24 В добавочных.
А как же мощность? Дело в том, что в сетевой обмотке автотрансформатора течет РАЗНОСТНЫЙ ток, и если повышать напряжение на небольшую долю от исходного, он окажется совсем незначительным. Правда, в дополнительной обмотке пойдет суммарный ток, но она в понижающих трансформаторах выполняется из толстого провода и при мощности исходного трансформатора в 100 Вт выдержит ток в 3-5 А, а это более 500 Вт при 220 В.
Нужно только правильно сфазировать обмотки. Для этого включаем трансформатор, как показано на схеме, БЕЗ НАГРУЗКИ. К гнездам «Прибор» подключаем любой вольтметр переменного тока на 300 В и более, хотя бы тестер. Показывает меньше, чем в розетке? Меняем местами концы любой из обмоток. Стало больше, чем в розетке? Все, можно пользоваться. Потребителей включаем вместо измерительного прибора.
Нужно только поставить в цепь сети предохранитель – вдруг в розетке «зашкалит» (это может случиться, если на старой и плохо обслуживаемой подстанции испортится зануление), так пусть он сгорит, а не техника.
Подходящий трансформатор можно найти на «железном» или радиорынке, а то и у себя в кладовке. Не спутайте только с гасящим устройством для низковольтных электропаяльников – они выполнены на конденсаторах, и от них толку не будет, а будет авария.
Смешанный способ
Сочетает в себе параллельное и последовательное подключения.
При этом для участков с последовательным соединением характерны свойства последовательного соединения, а для участков с параллельным — свойства параллельного.
Оно используется, когда ни электроемкость, ни номинальное напряжение приборов, имеющихся в продаже, не подходят для задачи. Обычно такая проблема возникает в радиотехнике.
Чтобы определить общее значение электроемкости, нужно будет сначала определить это же значение для параллельно соединенных двухполюсников, а потом для их последовательного соединения.
Устройство увеличивающее напряжение в 2 раза! Всего 4 детали.
Довольно часто случается такое, что для питания какого либо самодельного устройства требуется постоянное напряжение нестандартной величины, например 30В, а под рукой у вас только сетевой трансформатор с выходным напряжением 12В и током 1А (или на другое напряжение).
Так как же нам получить из 12В переменного напряжения — 30В постоянного, при этом использовав минимум деталей?
Опытные электронщики наверняка уже догадались о каком устройстве пойдет речь далее!
Для сборки устройства нам понадобится всего лишь 4 детали, которые с легкостью можно купить в любом радиомагазине или достать из ненужной техники. Стоимость устройства обойдется вам в копейки!
Стоимость устройства обойдется вам в копейки!
Перечень необходимых элементов
- Конденсатор 16В-2600мкФ — 2 шт.
- Диод 4007 — 2 шт.
Схема устройства
Два диода соединяются последовательно. Два конденсатора так же соединяются последовательно. Диоды и конденсаторы соединяются параллельно.
Проверка работоспособности
Подключим собранное устройство к нашему трансформатору и замерим выходное напряжение.
Для начала замерим напряжение на вторичной обмотке трансформатора, что бы убедиться что там около 12В.
Теперь можно замерить и на выходе умножителя напряжения!
На выходе получилось чуть больше 30В! То есть напряжение увеличилось почти в 3 раза!
Вот так вот просто, используя всего лишь 4 детали, удалось значительно увеличить напряжение! Но выходной ток при этом уменьшился во столько же раз, плюс потери на преобразование.
Если нравится электроника и запах канифоли, подписывайся на канал!
Источник
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи.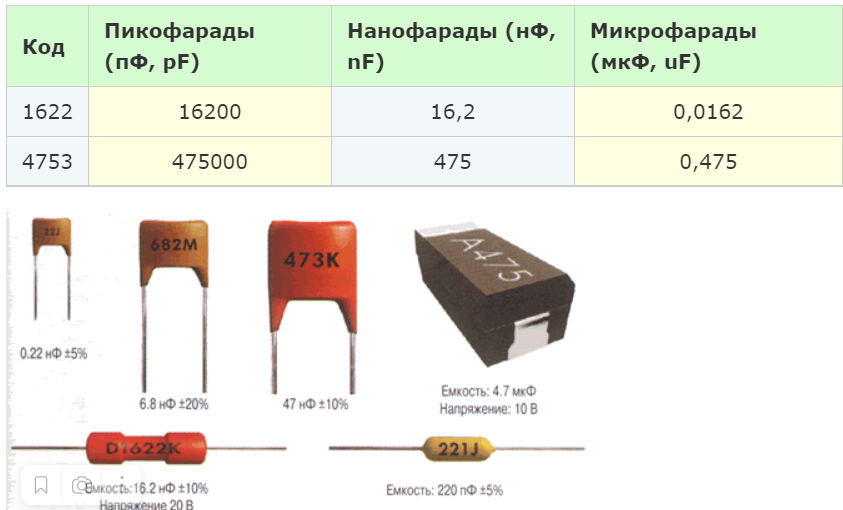 В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Схема параллельного крепления
Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
Схема — напряжение на накопителях
В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
«Узкие места» в конденсаторных установках, по факту влияющие на срок службы и интенсивность отказов
Наиболее проблемными электрическими/электронными компонентами любой установки, от которых напрямую зависит срок службы и интенсивность отказов, можно признать:
- конденсаторы в батареях-ступенях, выход из строя которых влечет за собой остановку УКРМ на ремонт;
- коммутационные устройства — контакторы, тиристорные свитчи, частота и ресурс коммутации которых определяет возможности УКРМ и время до ремонта;
- регуляторы-контроллеры со своим ресурсом коммутации и возможностями, в том числе мониторингом температуры внутри шкафа, управлением принудительной вентиляцией для поддержания оптимального температурного режима, выбором ступени для подключения с исключением рисков частой коммутации и т.
 д.
д.
Имеет значение для ресурса эксплуатации и снижения интенсивности отказов конструктивные особенности компоновки компонентов внутри шкафа УКРМ — расстояние между конденсаторами, которое согласно п. 5.3.4.2 ГОСТ Р 56744-2015 должно быть не менее 50 мм, наличие или отсутствие управляемого принудительного охлаждения, индуктивности для демпфирования набросов тока при включении и токов гармоник, достаточная строительная длина, сечение кабелей с исключающим внутренние напряжения радиусом изгиба и т. д.
Источник
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Схема — схема последовательного соединения
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = ic1 = ic2 = ic3 = ic4, то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
Видео: как соединять конденсаторы параллельным и последовательным методом
Полупроводниковые выпрямители блоков питания, схемы, онлайн расчёт
Классификация, свойства, схемы, онлайн калькулятор. Расчёт ёмкости сглаживающего конденсатора.
«- Почему пульт не работает? — Я, конечно, не электрик, но, по-моему, пульт не работает, потому что телевизора нет».
— А для чего нам ещё «нахрен не упал» профессиональный электрик? — Для чего? Да много для чего! Например, для того, чтобы быть в курсе, что без источника питания, а точнее без преобразователя сетевого переменного напряжения в постоянное, не обходится ни одно электронное устройство. — А электрик? — Электрик, электрик… Что электрик?… «Электрик Сидоров упал со столба и вежливо выругался…»
Итак, приступим. Выпрямитель — это электротехническое устройство, предназначенное для преобразования переменного напряжения в постоянное. Выпрямитель содержит трансформатор, необходимый для преобразования напряжения сети Uc до величины U2, определяемой требованиями нагрузки; вентильную группу (в нашем случае диодную), которая обеспечивает одностороннее протекание тока в цепи нагрузки; фильтр, передающий на выход схемы постоянную составляющую напряжения и сглаживающий пульсации напряжения.
Расчёт трансформатора — штука громоздкая, в рамках этой статьи рассматриваться не будет, поэтому сразу перейдём к основным и наиболее распространённым схемам выпрямителей блоков питания радиоэлектронной аппаратуры. В процессе повествования давайте сделаем допущение, что под величинами переменных напряжений и токов в цепях выпрямителей мы будем подразумевать их действующие (эффективные) значения: Uдейств = Uампл/√2 и Iдейств = Iампл/√2. Именно такие значения приводятся в паспортных характеристиках обмоток трансформаторов, да и большинство измерительных приборов отображают — не что иное, как аккурат эффективные значения сигналов переменного тока.
В процессе повествования давайте сделаем допущение, что под величинами переменных напряжений и токов в цепях выпрямителей мы будем подразумевать их действующие (эффективные) значения: Uдейств = Uампл/√2 и Iдейств = Iампл/√2. Именно такие значения приводятся в паспортных характеристиках обмоток трансформаторов, да и большинство измерительных приборов отображают — не что иное, как аккурат эффективные значения сигналов переменного тока.
Однополупериодный выпрямитель.
На Рис.1 приведена однофазная однополупериодная схема выпрямления, а также осциллограммы напряжений в различных точках (чёрным цветом — напряжение на нагрузке при отсутствии сглаживающего конденсатора С1, красным — с конденсатором). В данном типе выпрямителя напряжение с вторичной обмотки трансформатора поступает в нагрузку через диод только в положительные полупериоды переменного напряжения. В отрицательные полупериоды полупроводник закрыт, и напряжение в нагрузку подаётся только с заряженного в предыдущий полупериод конденсатора. Однополупериодная схема выпрямителя применяется крайне редко и только для питания цепей с низким током потребления ввиду высокого уровня пульсаций выпрямленного напряжения, низкого КПД, и неэффективного использования габаритной мощности трансформатора.
Однополупериодная схема выпрямителя применяется крайне редко и только для питания цепей с низким током потребления ввиду высокого уровня пульсаций выпрямленного напряжения, низкого КПД, и неэффективного использования габаритной мощности трансформатора.
Здесь обмотка трансформатора должна обеспечивать величину тока, равную удвоенному значению максимального тока в нагрузке Iобм = 2×Iнагр и напряжение холостого хода
U2 ≈ 0,75×Uн. При выборе диода D1 для данного типа схем, следует придерживаться следующих его параметров: Uобр > 3,14×Uн и Iмакс > 3,14×Iн.
Едем дальше. Двухполупериодный выпрямитель с нулевой точкой.
Схема, приведённая на Рис.2, является объединением двух противофазных однополупериодных выпрямителей, подключённых к общей нагрузке. В одном полупериоде переменного напряжения ток в нагрузку поступает с верхней половины вторичной обмотки через открытый диод D1, в другом полупериоде — с нижней, через второй открытый диод D2. Как и любая двухполупериодная, эта схема выпрямителя имеет в 2 раза меньший уровень пульсации по сравнению с однополупериодной схемой. К недостаткам следует отнести более сложную конструкцию трансформатора и такое же, как в однополупериодной схеме — нерациональное использование трансформаторной меди и стали.
Как и любая двухполупериодная, эта схема выпрямителя имеет в 2 раза меньший уровень пульсации по сравнению с однополупериодной схемой. К недостаткам следует отнести более сложную конструкцию трансформатора и такое же, как в однополупериодной схеме — нерациональное использование трансформаторной меди и стали.
Каждая из обмоток трансформатора должна обеспечивать величину тока, равную значению максимального тока в нагрузке Iобм = Iнагр и напряжение холостого хода
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов
READ Как программно подключить сетевой диск
Существует также смешанное соединение двух и более конденсаторов.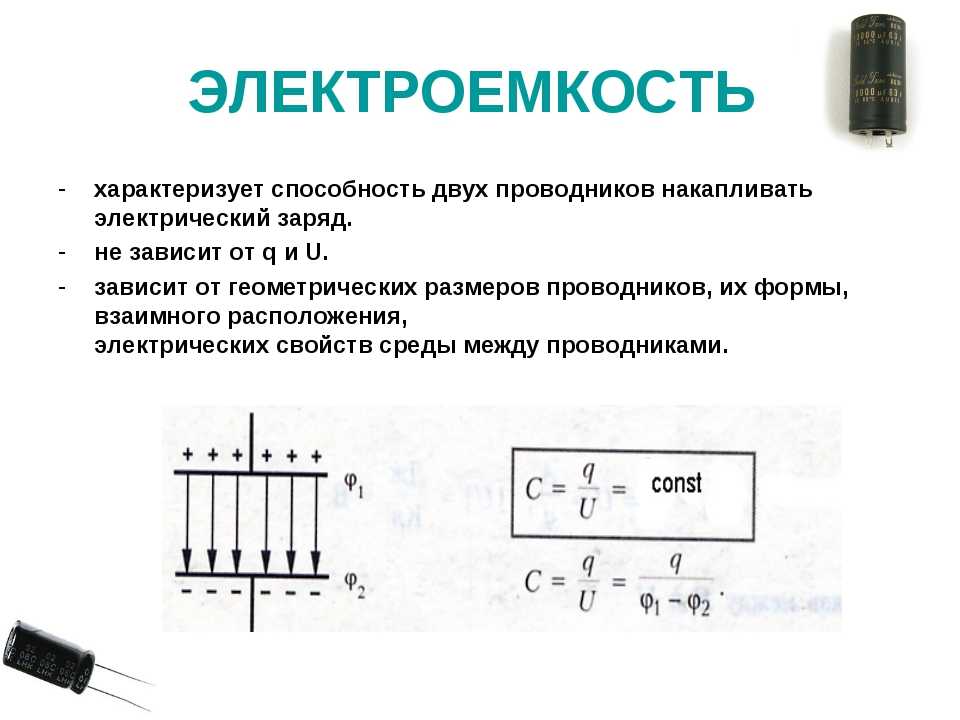 Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
Источник
Защита от перепадов напряжения
В городских условиях напряжение в сети, как правило, держится, но актуальной становится защита квартиры от перепадов напряжения. Вот тут пора вспомнить о чудесах электроники, поскольку «железно – проволочная» электротехника эффективных, простых и дешевых способов их сглаживания не знает.
Поспрашивайте в электро- и радиомагазинах автомат защиты от перепадов напряжения; их еще называют «барьер защитный». Как примерно такой выглядит, видно на иллюстрации. Современные устройства такого типа сравнительно недороги, компактны, их легко подключить и обслуживания в процессе эксплуатации они не требуют.
Простой защитный барьер для домашней электросети
Но не вспоминайте об автотрансформаторе на даче – защитный барьер лишь устраняет броски напряжения; все время держать напряжение в розетке при стабильно пониженном он не может. В качестве накопителей энергии в таких устройствах используются суперконденсаторы, а они хоть и «супер», но все же не электрогенераторы.
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад.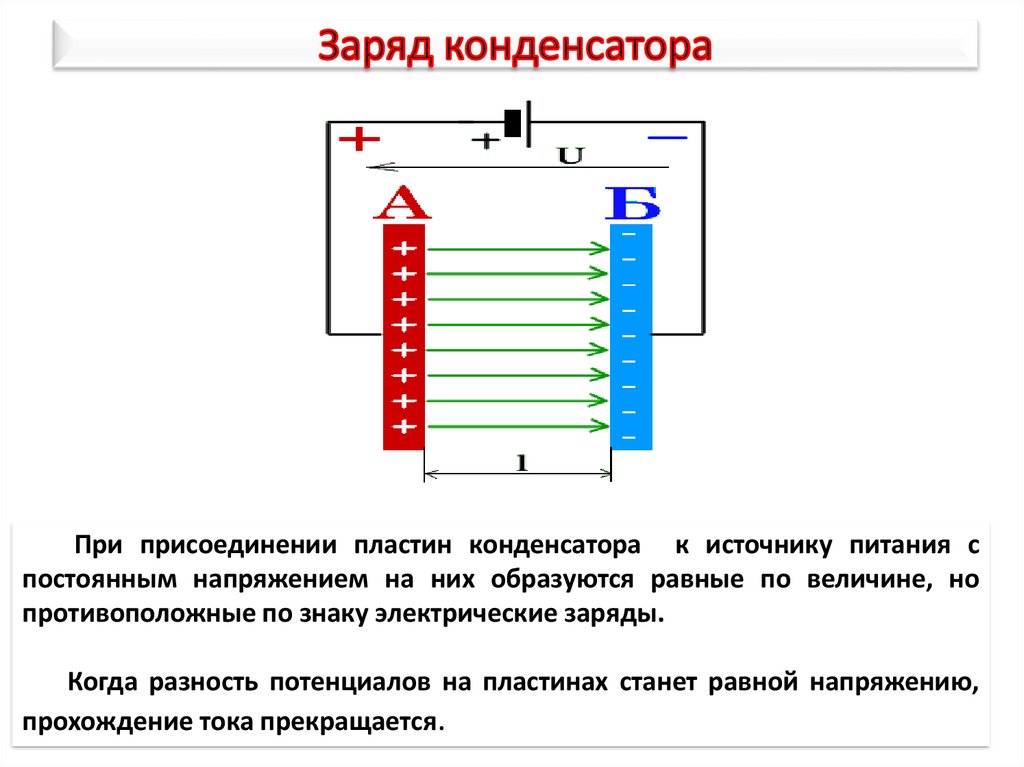 Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение Принципиальная схема параллельного соединения Последовательное соединение Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается
.
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
READ Как подключить ноутбук по локальной сети к роутеру
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.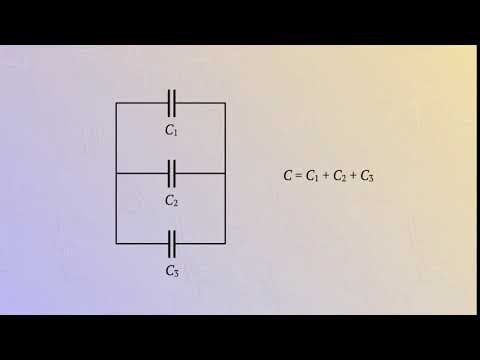
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.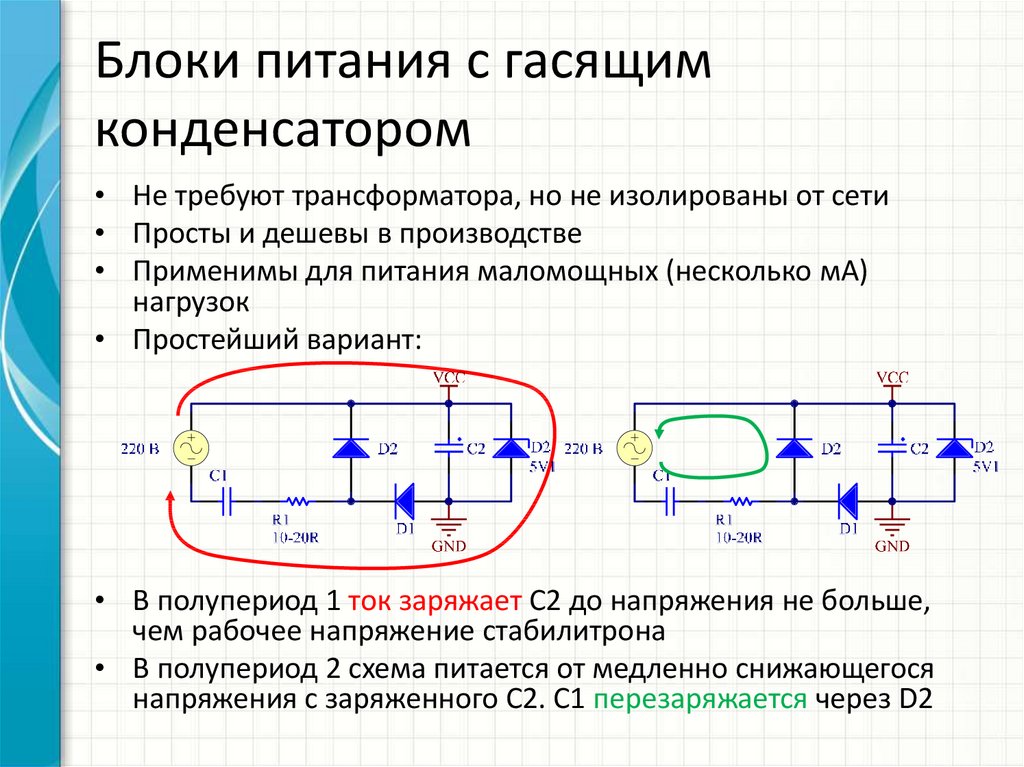
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Конденсаторы и установки повышения коэффициента мощности. Часть первая. Надёжность и долговечность
Завод конденсаторных установок «МИРКОН» предлагает к ознакомлению цикл статей, посвящённых конденсаторам и установкам повышения коэффициента мощности. Первая публикация этой тематики затрагивает вопросы надёжности оборудования, включая требования действующих стандартов в отношении УКРМ, а также обзор «узких мест» в конденсаторных установках, влияющих на срок службы изделий и интенсивность отказов.
В экономическом и технологическом аспектах в пакет критериев, определяющих выбор конденсаторных установок, входит их реальный срок службы и надежность, которая по факту формализована в международных стандартах и СТО 34. 01-3.2.11-012-2017 ПАО «Россети», как интенсивность отказов. Это вполне понятно, ведь выход из строя любой УКРМ влечет за собой, как затраты на ремонт, реновацию или замену, так и остановку или нарушения производственно-технологического процесса из-за снижения качества электроэнергии в силовой сети.
01-3.2.11-012-2017 ПАО «Россети», как интенсивность отказов. Это вполне понятно, ведь выход из строя любой УКРМ влечет за собой, как затраты на ремонт, реновацию или замену, так и остановку или нарушения производственно-технологического процесса из-за снижения качества электроэнергии в силовой сети.
Вместе с тем, именно срок службы и интенсивность отказов УКРМ, реализуемых на рынке, остаются наиболее «непрозрачными» характеристиками, а действующие ГОСТ IEC 61921-2013, ГОСТ Р 56744-2015 и ГОСТ Р 51321.1-2007 (на НКУ — низковольтные комплектные устройства) этому способствуют, поскольку не ввели эти параметры ни в маркировку, ни в перечни типовых испытаний.
Условным исключением из правил стали ГОСТ IEC15 и ГОСТ IEC 60931-1-2013, определяющие методики испытаний на долговечность конденсаторов, которая условно оценивается по изменению емкости, увеличению тангенса угла потерь, электрической прочности. Однако вывода реального срока службы и интенсивности отказов в стандартах также нет.
Электрическая емкость. Конденсаторы. Емкость конденсатора.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Электрическая емкость. Конденсаторы. Емкость…
Электрическая емкость. Конденсаторы. | |
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: , где эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. |
|
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: . | |
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. | Емкость шара в СИ: — |
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. | 1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф |
Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.). |
|
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. | |
На рисунке — плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального — все). Усферического — все поле сосредоточено между обкладками. |
|
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: . | |
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. |
|
Емкость плоского конденсатора. , т. | |
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора. | |
Виды конденсаторов | |
При подключении электролитического конденсатора необходимо соблюдать полярность. | |
Назначение конденсаторов
|
|
Теги:
конспект
Как влияет тип диэлектрика на емкость конденсатора?
Плоские конденсаторы, будь то вакуумные или воздушные, т.е. имеющие вакуум или воздух между обкладками, обычно имеют небольшую емкость. Её можно увеличить, манипулируя размером конденсатора, например, увеличивая площадь поверхности обкладок или уменьшая расстояние между ними. Однако оба решения не очень эффективны, поскольку, например, слишком большой размер ограничивает применимость конденсатора на практике, а уменьшение расстояния между обкладками может привести к пробою.
Существует еще один способ увеличения емкости конденсатора: между его обкладками можно поместить материал с диэлектрическими свойствами. Таким образом, в зависимости от используемого диэлектрика, емкость конденсатора может быть увеличена от нескольких до десятков раз.
Диэлектрики – это материалы, которые не проводят электричество. Во внешнем электрическом поле напряженностью E0 молекулы диэлектрика поляризуются.
Во внешнем электрическом поле напряженностью E0 молекулы диэлектрика поляризуются.
Эта поляризация создает внутреннее электрическое поле в диэлектрике Ep. Это поле направлено противоположно внешнему полю. В результате напряженность результирующего электрического поля внутри диэлектрика: E = E0 + Ep , имеет меньшее значение, чем внешнее поле (рис. 1): E = E0 – Ep .
Рис. 1. Линии электрического поля внутри плоского вакуумного конденсатора (слева) и конденсатора с диэлектриком между обкладками (справа)Из-за поляризации внутри диэлектрика, заполняющего конденсатор, плотность линий электрического поля, а следовательно, и его напряженность, меньше, чем в вакуумном конденсаторе.
Отношение E0 к E зависит от свойств диэлектрика и называется относительной диэлектрической проницаемостью: E0 / E = εr .
Заметим, что константа εr безразмерна (не имеет определенных единиц) и ее значение удовлетворяет условию: εr ≥ 1 , где εr = 1 характеризует вакуум.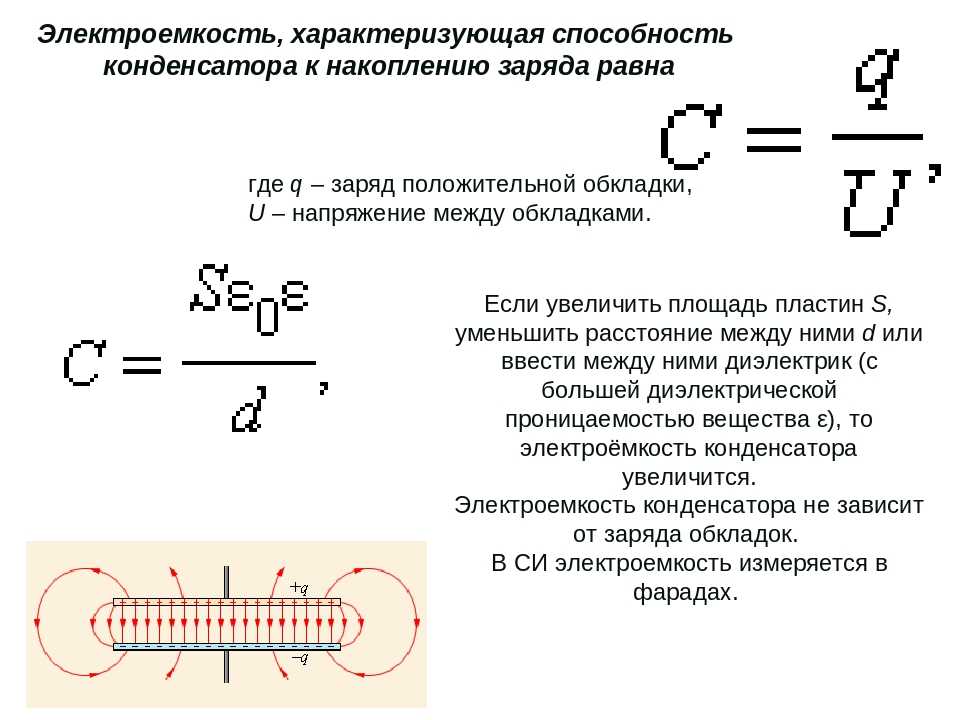
Заметим также, что если напряженность электрического поля внутри диэлектрика уменьшается в εr раз, то разность потенциалов (т.е. напряжение U) внутри диэлектрика также должна уменьшиться в εr раз: U0 / U = εr [5].
Что же произойдет, если мы заполним пространство между обкладками конденсатора диэлектриком? Это уменьшит значение разности потенциалов U, сохраняя заряд на обкладках неизменным. Итак, давайте рассмотрим, как это повлияет на емкость данного конденсатора.
Емкость вакуумного конденсатора, т.е. конденсатора, между обкладками которого имеется вакуум, определяется по формуле:
С0 = Q / U0
Таким образом, после введения диэлектрика емкость составит: C = Q / U = Q / ( U0 / εr ) = εr * Q / U0 = εr * C0 .
Это означает, что если между обкладками конденсатора поместить диэлектрик, то его емкость увеличится в εr раз: C = εr * C0 .
В таблице 1. приведены примеры значений относительной диэлектрической проницаемости выбранных диэлектриков при комнатной температуре.
| Материал | Относительная диэлектрическая проницаемость |
| Вакуум | 1,0000 |
| Воздух | 1,0005 |
| Тефлон | 2,1 |
| Полиэтилен | 2,3 |
| Бумага | 3,5 |
| Стекло | 4,5 |
| Фарфор | 6,5 |
| Вода | 78 |
Как измерить значение относительной диэлектрической проницаемости?
Мы не измеряем эту величину напрямую, а определяем ее. Один из способов определения этой величины, который можно использовать, например, на уроках физики, заключается в измерении разности потенциалов между обкладками плоского конденсатора.
Вам понадобятся: диэлектрическая пластина (например, кусок стекла или пластика), демонстрационный конденсатор (или две металлические пластины, которые можно расположить параллельно друг другу), электроскоп и электростатическая (индукционная) машина.
Мы раздвигаем обкладки конденсатора (или металлические пластины) так, чтобы диэлектрик заполнил пространство между ними (около 1-2 см). С помощью электростатической машины мы заряжаем одну из обкладок конденсатора. Вторую обкладку можно прикрепить к штативу или просто держать в руке – если ее заземлить, она выработает тот же заряд, что и первая. Считайте показания электроскопа (рис. 2.). Затем вставьте диэлектрик между крышками и снова считайте показания электроскопа.
Рис. 2. Исследование с помощью электроскопа напряжения между обкладками плоского конденсатора: а) с воздухом, б) с диэлектриком между обкладкамиКогда диэлектрик вставляется между обкладками конденсатора, напряжение между обкладками уменьшается, что заставляет створки электроскопа опускаться вниз.
Электроскоп измеряет напряжение между обкладками конденсатора. Подставив полученные результаты в формулу (5), определим относительную диэлектрическую проницаемость материала. Обратите внимание, что не имеет значения, в каких единицах мы измеряем напряжение – параметр εr является безразмерным.
Урок 28. электрическая ёмкость. конденсатор — Физика — 10 класс
Физика, 10 класс
Урок 28. Электрическая ёмкость. Конденсатор
Перечень вопросов, рассматриваемых на уроке:
- Электрическая ёмкость
- Плоский конденсатор
- Энергия конденсатора
Глоссарий по теме:
Конденсатор – устройство для накопления электрического заряда.
Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Под зарядом конденсатора понимают модуль заряда одной из его обкладок.
Последовательное соединение – электрическая цепь не имеет разветвлений. Все элементы цепи включают поочередно друг за другом. При параллельном соединении концы каждого элемента присоединены к одной и той же паре точек.
Смешанное соединение — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Энергия конденсатора прямо пропорциональна квадрату напряжённости электрического поля внутри его:
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения.
Основная и дополнительная литература по теме:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 97-100.
Теоретический материал для самостоятельного изучения
Конденсатор при переводе с латиницы означает, то что уплотняет, сгущает – устройство, предназначенное для накопления зарядов энергии электрического поля. Конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга. Главной характеристикой этого прибора, является его электроёмкость, которая зависит от площади его пластин, расстояния между ними и свойств диэлектрика.
Заряд конденсатора определяется – модулем заряда на любой одной из её обкладок. Заряд конденсатора прямо пропорционален напряжению между обкладками конденсатора. Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора.
Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Чем больше площадь проводников и чем меньше пространство заполняющего диэлектриком, тем больше увеличивается ёмкость обкладок конденсатора.
Измеряется электрическая ёмкость в Международной системе СИ в Фарадах. Эта единица имеет своё название в честь английского физика экспериментатора Майкла Фарадея который внёс большой вклад в развитие теории электромагнетизма. Один Фарад равен ёмкости такого конденсатора, между пластинами которого возникает напряжение, равное одному Вольту, при сообщении заряда в один Кулон.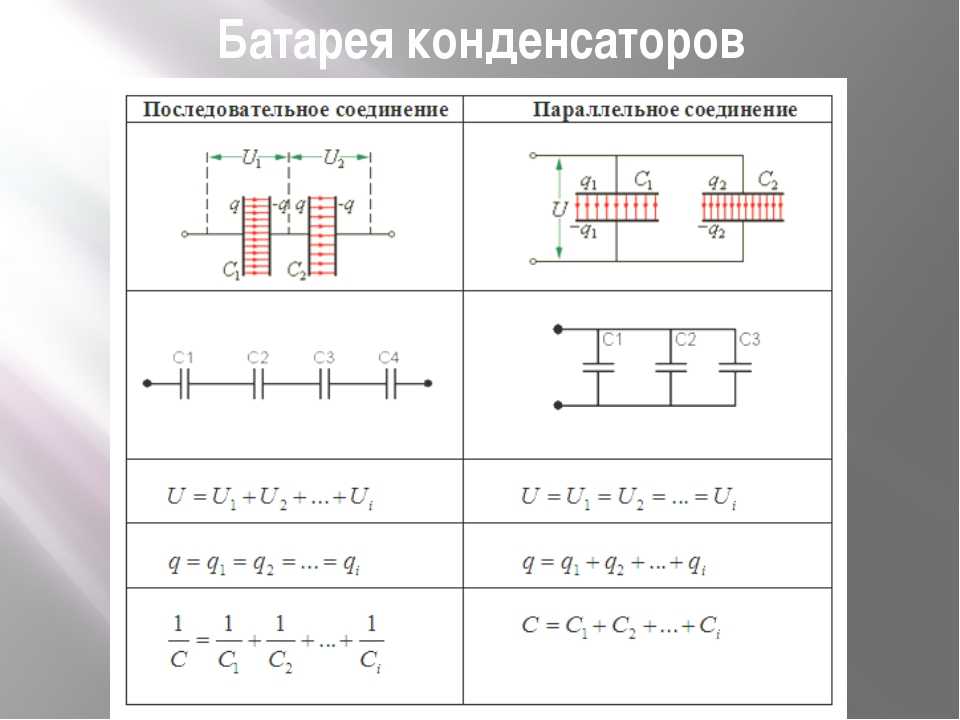
Электрическая ёмкость конденсаторов определяется их конструкцией, самыми простыми из них являются плоские конденсаторы.
Чем больше площадь взаимного перекрытия обкладок и чем меньше расстояние между ними, тем значительнее будет увеличение ёмкости обкладок конденсатора. При заполнении в пространство между обкладками стеклянной пластины, электрическая ёмкость конденсатора значительно увеличивается, получается, что она зависит от свойств используемого диэлектрика.
Электрическая ёмкость плоского конденсатора зависит от площади его обкладок, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками и определяется по формуле:
где – электрическая постоянная.
Для того чтобы получить необходимую определённую ёмкость, берут несколько конденсаторов и собирают их в батарею применяя при этом параллельное, последовательное или смешанное соединения.
Параллельное соединение:
q = q1 + q2 + q3
u = u1 = u2 = u3
с = с1+с2+с3
с = n∙с
Последовательное соединение:
q = q1 = q2 = q3
u = u1 + u2 + u3
Энергия конденсатора равна половине произведения заряда конденсатора напряжённости поля и расстояния между пластинами конденсатора: u = Еd
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин, это поле совершает положительную работу. При этом энергия электрического поля уменьшается:
При этом энергия электрического поля уменьшается:
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения:
Примеры и разбор решения заданий:
1. Плоский конденсатор, расстояние между пластинами которого равно 3 мм, заряжен до напряжения 150 В и отключен от источника питания. Разность потенциалов между пластинами возросла до 300 В.
- Во сколько раз увеличилась разность потенциалов между пластинами?
- Какое расстояние между пластинами конденсатора стало после того, как пластины были раздвинуты?
- Во сколько раз изменилось расстояние между пластинами.
Решение:
Электрическая ёмкость конденсатора определяется по формуле:
1.По условию разность потенциалов увеличилось в два раза. U1 = 150В→ U2 = 300В.
2.По условию d = 3 мм, если разность потенциалов увеличилось в два раза, по формуле соответственно и расстояние между пластинами увеличилось в два раза, и d =2·3 мм = 6 мм.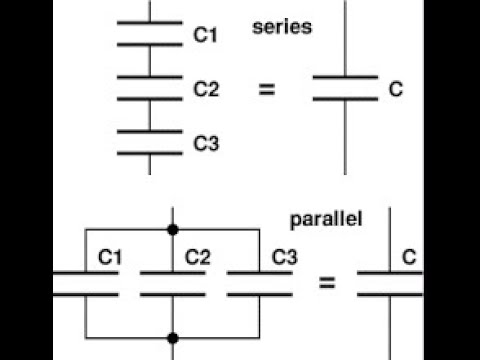
3.Расстояние между пластинами увеличилось в два раза.
Ответ:
1. 2
2. 6мм
3. 2
2. Конденсатор электроёмкостью 20 мкФ имеет заряд 4 мкКл. Чему равна энергия заряженного конденсатора?
Дано: С = 20 мкФ = 20 · 10-6 Ф, q = 4 мкКл = 4·10-6 Кл.
Найти: W.
Решение:
Энергия заряженного конденсатора W через заряд q и электрическую ёмкость С определяется по формуле:
Ответ: W = 0,4 мкДж.
В каких случаях применяется параллельное соединение конденсаторов
При параллельном соединении конденсаторов к каждому конденсатору приложено одинаковое напряжениеU, а величина заряда на обкладках каждого конденсатора Q пропорциональна его емкости (рис. 2).
Общий заряд Q всех конденсаторов
Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.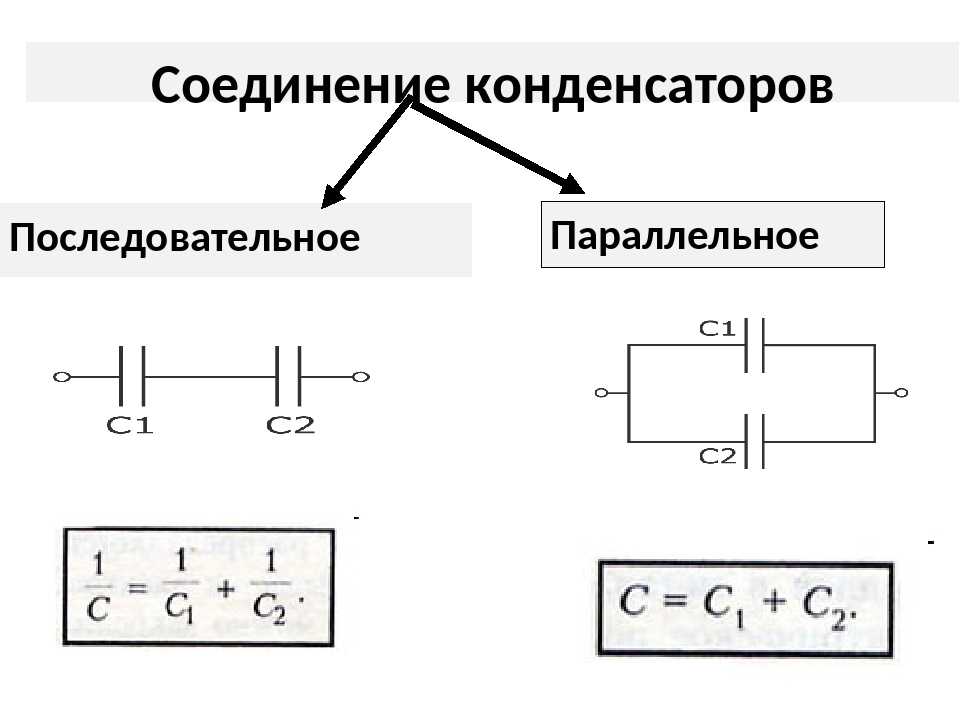
Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.
4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением
Последовательное соединение конденсаторов
На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.
Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:
Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.
При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:
Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:
Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
На практике может оказаться , что допустимое рабочее напряжение Up конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего Up. Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения Up.
Смешанное соединение конденсаторов
Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.
где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U.
Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.
15.Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)
Рисунок 5- Схема электрическая
Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.
На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.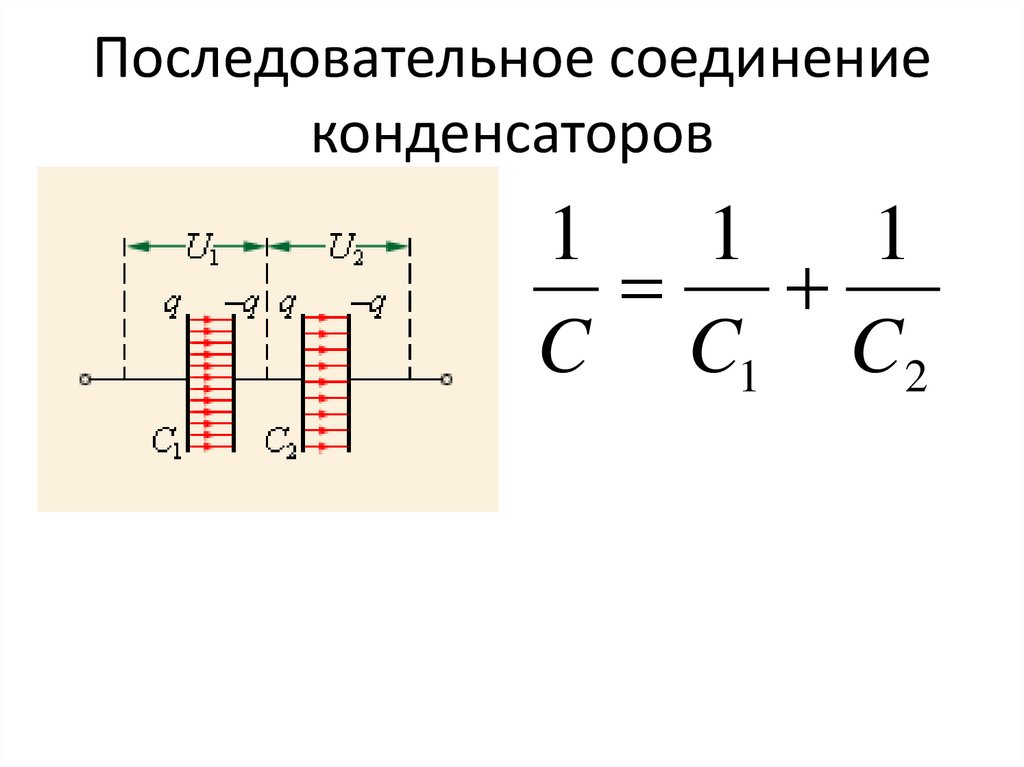
1.Схемы замещения элементов электрических цепей
На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).
Приr= 0 внутреннее падение напряженияUо = 0, поэтому
напряжение на зажимах источника при любом токе равно
В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияIK, а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg=1/r.
Возможность такой замены можно доказать, разделив равенство (3.1) на r:
где U/r = Io—некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E/r = IK — ток короткого замыкания источника;
Вводя новые обозначения, получим равенство IK= Io + I, которому удовлетворяет эквивалентная схема рис.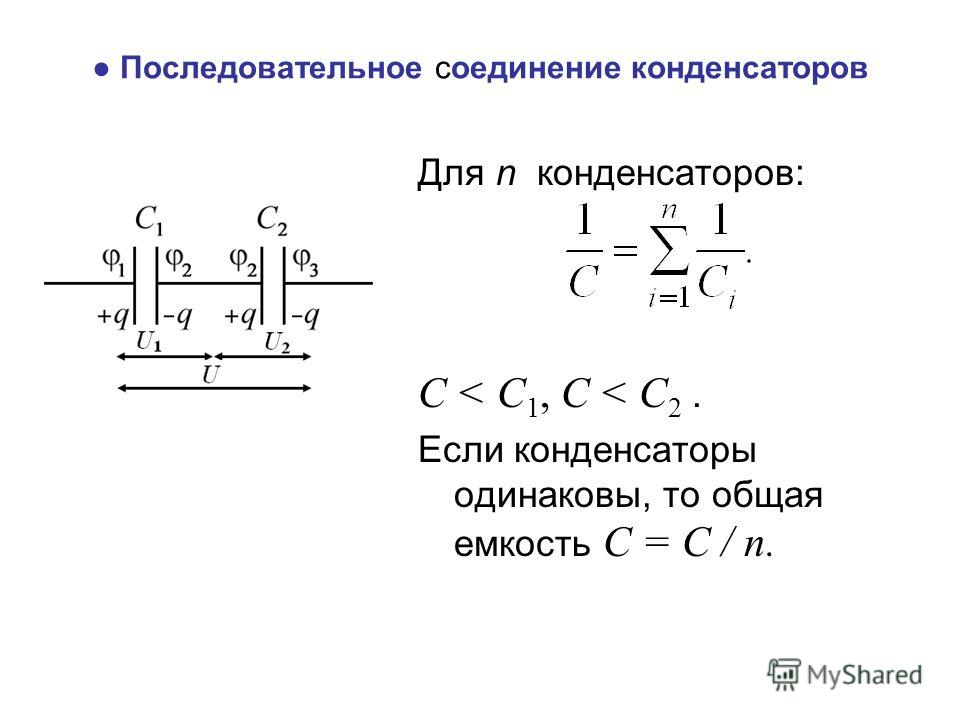 3.14,а.
3.14,а.
В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):
Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.
Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад.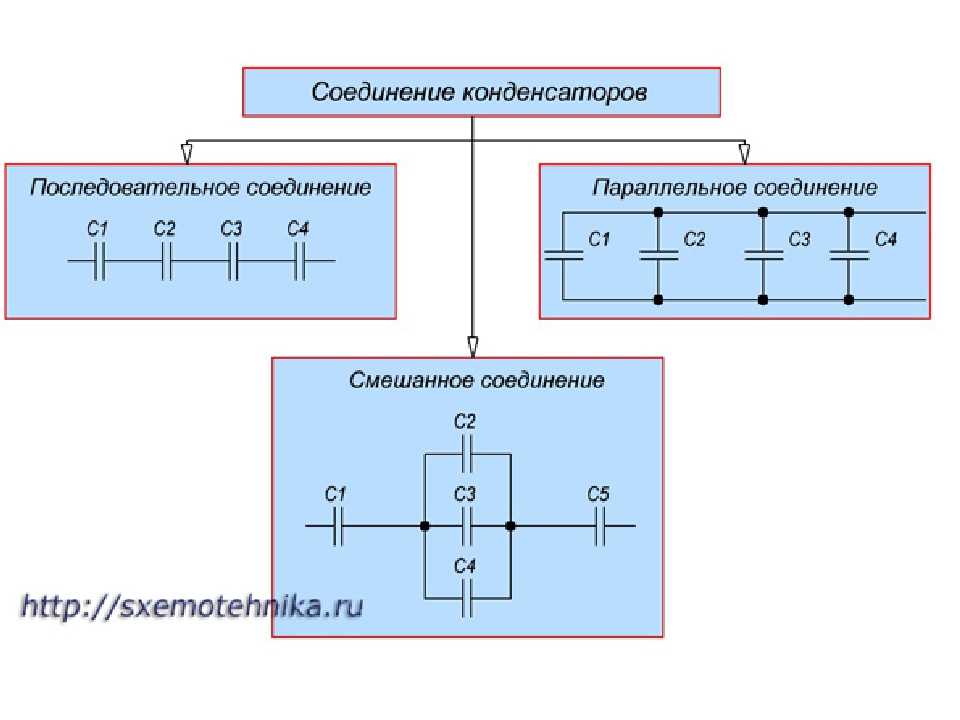 Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.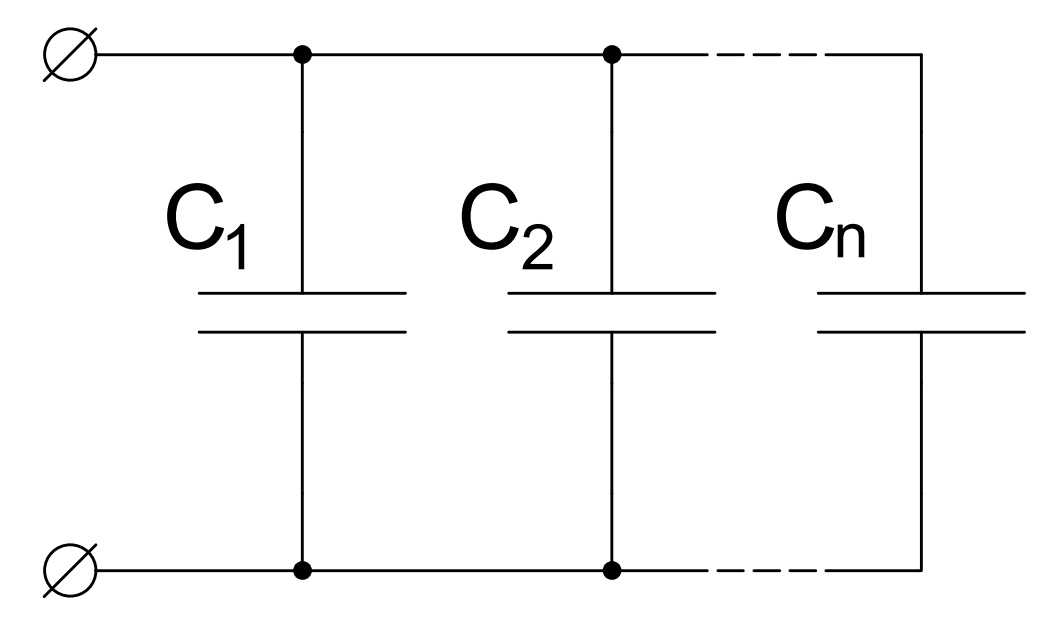
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.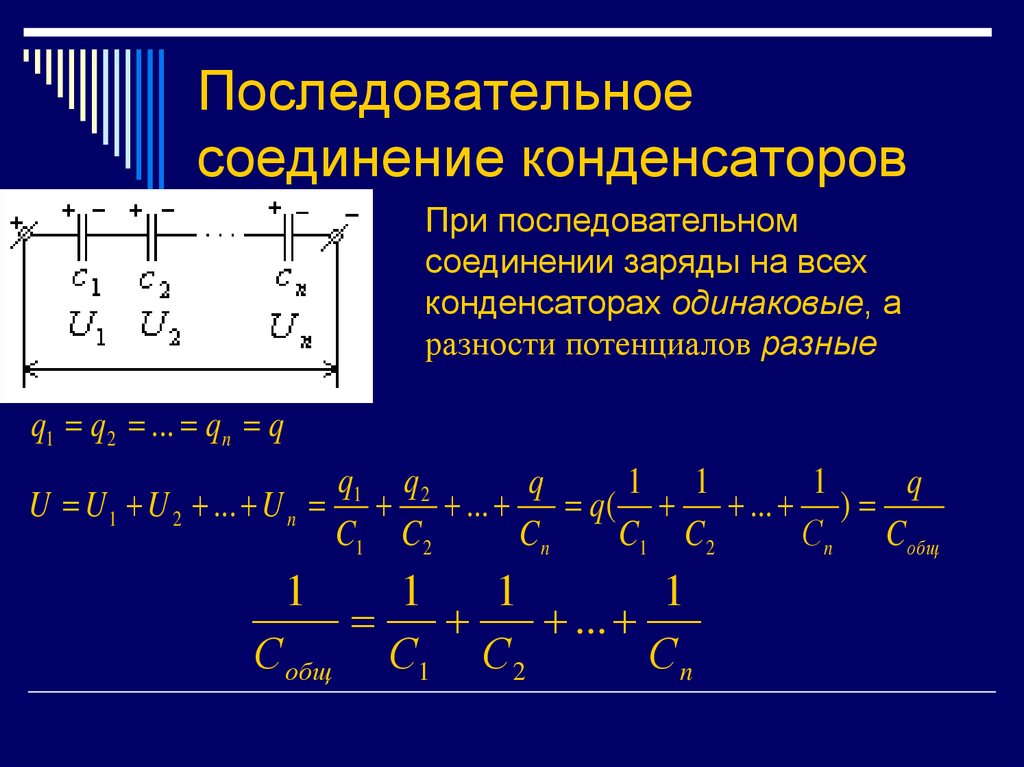
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Учимся ремонтировать кинескопные, LED и ЖК телевизоры вместе.

25.04.2016 Lega95 0 Комментариев
Всем привет. Этот маленький пост посвящу теме соединения конденсаторов.
На практике, часто бывает так, что в наличии нет конденсатора нужного номинала для установки, а технику нужно срочно отремонтировать. Как раз для таких случаев нам необходимы знания о правилах соединения конденсаторов.
Способов соединения конденсаторов существуют всего два. Это последовательное и параллельное соединение. Сейчас более детально рассмотрим оба способа.
Параллельное соединение конденсаторов.
Это наиболее частый вид соединения конденсаторов. При подключении параллельно, емкость конденсатора увеличивается, а напряжение остается прежним.
Формула параллельного соединения конденсаторов: С= С1+С2+С3…
Рассмотрим на примере. Предположим, что необходим конденсатор 100 мкф 50в, а у Вас в наличии только 47мкф на 50в. Если соединить эти конденсаторы параллельно (плюс к плюсу а минус к минусу) то общая емкость получившегося конденсатора будет ровняться около 94 мкф на 50в. Это допустимое отклонение, так что можно свободно устанавливать в технику.
Это допустимое отклонение, так что можно свободно устанавливать в технику.
Параллельное соединение конденсаторов
Последовательное соединение конденсаторов.
При подключении, таким образом, общая емкость уменьшается, а напряжение работы конденсатора растёт.
Рассчитывается последовательное подключение конденсаторов по такой формуле:
Формула расчета последовательного соединения конденсаторов
Для примера подключим 3 конденсатора номиналом 100мкф на 100в последовательно. Согласно формуле, делим единицу, на емкость конденсаторов. Потом суммируем . Далее единицу делим на результат.
(1:100)+(1:100)+(1:100) = 0,01 + 0,01 + 0,01 = 0,03 далее 1 : 0,03 = 33 мкф на 300вольт (напряжение суммируем 100+100+100 = 300в). Итого 33мкф на 300в.
В работе, последовательное соединение использую редко, но иногда бывает.
Рекомендую ознакомиться со статей о ESR конденсаторов.
| Факторы, влияющие на емкость Конденсатор представляет собой электрическое устройство, предназначенное для накопления электрического заряда, обычно состоящее из двух параллельных проводящих пластин, разделенных изолирующим слоем, называемым диэлектриком. Нажмите на стрелки, чтобы выбрать различные комбинации диэлектриков, площадей пластин и расстояний. На емкость конденсатора влияет площадь пластин, расстояние между пластинами и способность диэлектрика выдерживать электростатические силы. В этом руководстве показано, как изменение этих параметров влияет на емкость конденсатора. Пластины большего размера обеспечивают большую емкость для накопления электрического заряда. Следовательно, с увеличением площади пластин увеличивается емкость. Емкость прямо пропорциональна электростатическому силовому полю между пластинами. Это поле сильнее, когда пластины расположены ближе друг к другу. Следовательно, при уменьшении расстояния между пластинами емкость увеличивается. Диэлектрические материалы оцениваются на основе их способности выдерживать электростатические силы с точки зрения числа, называемого диэлектрической проницаемостью. Чем выше диэлектрическая проницаемость, тем больше способность диэлектрика выдерживать электростатические силы. ВЕРНУТЬСЯ К РУКОВОДСТВУ ПО ЭЛЕКТРИЧЕСТВУ И МАГНИТИЗМУ Вопросы или комментарии? Отправить нам письмо.© 1995-2022 автор Майкл В. Дэвидсон и Университет штата Флорида. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами.Этот веб-сайт поддерживается нашимГруппа графического и веб-программирования в сотрудничестве с Optical Microscopy в Национальной лаборатории сильного магнитного поля. Последнее изменение: среда, 7 июня 2017 г., 13:21Количество обращений с 3 апреля 1999 г.: 485222 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Конденсатор — Энергетическое образование
Energy EducationМеню навигации
ИСТОЧНИКИ ЭНЕРГИИ
ИСПОЛЬЗОВАНИЕ ЭНЕРГИИ
ЭНЕРГЕТИЧЕСКОЕ ВОЗДЕЙСТВИЕ
Поиск
Рис.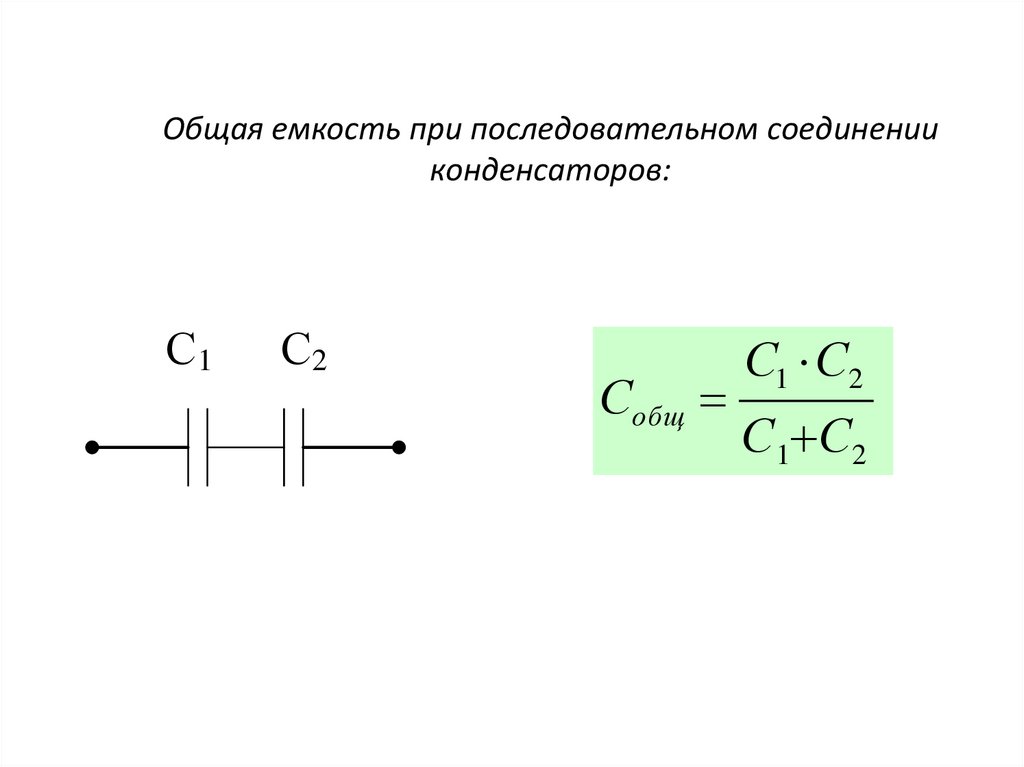 1. Схема конденсатора, включающего две параллельные пластины с площадью поверхности A и расстоянием между ними d. Хотя не все конденсаторы имеют такую форму, их часто считают таковыми, поскольку это самая простая геометрия.
1. Схема конденсатора, включающего две параллельные пластины с площадью поверхности A и расстоянием между ними d. Хотя не все конденсаторы имеют такую форму, их часто считают таковыми, поскольку это самая простая геометрия.
Рис. 2. Анимация из имитации PhET батареи, заряжающей конденсатор до тех пор, пока ток не перестанет течь по цепи. [1]
Конденсатор — это электронное устройство, накапливающее заряд и энергию. Конденсаторы могут отдавать энергию намного быстрее, чем батареи, что приводит к гораздо более высокой плотности мощности, чем батареи с таким же количеством энергии. Исследования конденсаторов продолжаются, чтобы выяснить, можно ли их использовать для хранения электроэнергии для электрической сети. В то время как конденсаторы — это старая технология, суперконденсаторы — это новый поворот в этой технологии.
Конденсаторы — это простые устройства, состоящие из двух проводников с одинаковыми, но противоположными зарядами. Простой конденсатор с плоскими пластинами состоит из двух металлических пластин одинакового размера, известных как электроды, разделенных изолятором, известным как диэлектрик, которые удерживаются параллельно друг другу. Затем конденсатор включается в электрическую цепь. В простой цепи постоянного тока каждая пластина конденсатора со временем становится противоположно заряженной из-за прохождения электрического тока по цепи. Аккумулятор направляет заряд в одном направлении, так что одна пластина становится положительно заряженной, а другая — отрицательной. Это создает электрическое поле из-за накопления одинаковых и противоположных зарядов, что приводит к разности потенциалов или напряжению между пластинами. Поскольку емкость пластин постоянна, напряжение между пластинами пропорционально увеличивается. По мере увеличения заряда на каждой пластине напряжение между пластинами равняется напряжению батареи, после чего ток больше не будет течь по цепи. [2] Этот эффект зарядки и разрядки можно увидеть на рис. 2. Ток может возобновиться, если открыть альтернативный путь, чтобы конденсаторы могли разряжаться самостоятельно, или с помощью переменного тока, чтобы конденсатор периодически заряжался и разряжался.
Затем конденсатор включается в электрическую цепь. В простой цепи постоянного тока каждая пластина конденсатора со временем становится противоположно заряженной из-за прохождения электрического тока по цепи. Аккумулятор направляет заряд в одном направлении, так что одна пластина становится положительно заряженной, а другая — отрицательной. Это создает электрическое поле из-за накопления одинаковых и противоположных зарядов, что приводит к разности потенциалов или напряжению между пластинами. Поскольку емкость пластин постоянна, напряжение между пластинами пропорционально увеличивается. По мере увеличения заряда на каждой пластине напряжение между пластинами равняется напряжению батареи, после чего ток больше не будет течь по цепи. [2] Этот эффект зарядки и разрядки можно увидеть на рис. 2. Ток может возобновиться, если открыть альтернативный путь, чтобы конденсаторы могли разряжаться самостоятельно, или с помощью переменного тока, чтобы конденсатор периодически заряжался и разряжался.
Важным параметром конденсатора является емкость, мера способности объекта накапливать заряд. Есть два основных способа расчета емкости, используя либо физическую площадь пластин, либо напряжение, приложенное к пластинам. 92} {2}[/math]
- [math]\Delta V[/math] — напряжение между пластинами, измеренное в вольтах (В)
- [math]C[/math] — емкость конденсатора, измеренная в фарадах (Ф)
- [math]E[/math] энергия, запасенная в конденсаторе, измеренная в джоулях (Дж) .
В качестве альтернативы в конденсатор можно добавить диэлектрик. Диэлектрик представляет собой изолятор, помещенный между электродами. Это увеличивает емкость конденсатора без необходимости изменения его размеров. Это позволяет конденсатору хранить больше энергии, оставаясь при этом небольшим. Степень увеличения зависит от материала, используемого для диэлектрика. [3]
Использование
Конденсаторы не обладают такой высокой плотностью энергии, как батареи, а это означает, что конденсатор не может хранить столько же энергии, сколько батарея сравнимого размера.
 Тем не менее, более высокая мощность конденсаторов означает, что они хороши для приложений, требующих хранения небольшого количества энергии, а затем очень быстрого ее высвобождения. 9Гоночные автомобили 0450 Le Mans Prototype используют конденсаторы для питания электродвигателей передних колес. Эти конденсаторы заряжаются за счет рекуперативного торможения и обеспечивают полный привод и дополнительную мощность при выходе из поворотов. [4]
Тем не менее, более высокая мощность конденсаторов означает, что они хороши для приложений, требующих хранения небольшого количества энергии, а затем очень быстрого ее высвобождения. 9Гоночные автомобили 0450 Le Mans Prototype используют конденсаторы для питания электродвигателей передних колес. Эти конденсаторы заряжаются за счет рекуперативного торможения и обеспечивают полный привод и дополнительную мощность при выходе из поворотов. [4] Конденсаторы также используются во многих электронных устройствах, для которых требуется батарея. Этот конденсатор накапливает энергию, чтобы предотвратить потерю памяти при замене батареи. Распространенный (хотя и не обязательно широко известный) пример — зарядка вспышки фотокамеры. Вот почему нельзя сделать два снимка со вспышкой в быстрой последовательности; конденсатор должен накапливать энергию от батареи. [5]
Кроме того, конденсаторы играют ключевую роль во многих практических цепях, прежде всего в качестве стабилизаторов тока и компонентов, помогающих преобразовать переменный ток в постоянный в адаптерах переменного тока.
 Их можно использовать таким образом из-за того, что конденсаторы устойчивы к внезапным изменениям напряжения, а это означает, что они могут действовать как буфер для хранения и отвода электроэнергии для поддержания стабильного выходного тока. [6] Таким образом, конденсатор способен стабилизировать переменный ток благодаря своей способности удерживать и отдавать электрическую энергию в разное время.
Их можно использовать таким образом из-за того, что конденсаторы устойчивы к внезапным изменениям напряжения, а это означает, что они могут действовать как буфер для хранения и отвода электроэнергии для поддержания стабильного выходного тока. [6] Таким образом, конденсатор способен стабилизировать переменный ток благодаря своей способности удерживать и отдавать электрическую энергию в разное время.Поскольку конденсаторы хранят энергию в электрических полях, некоторые исследователи работают над созданием суперконденсаторов, чтобы помочь с хранением энергии. Это может оказаться полезным при транспортировке энергии или для хранения и высвобождения энергии из непостоянных источников, таких как энергия ветра и солнца.
Моделирование Phet
Университет Колорадо любезно разрешил нам использовать следующее моделирование Phet. Исследуйте эту симуляцию, чтобы увидеть, как потенциальная энергия гравитации и потенциальная энергия пружины перемещаются вперед и назад и создают изменяющееся количество кинетической энергии (подсказка: нажмите показать энергию до подвешивания массы):
Ссылки
- ↑ Университет Колорадо.
 (25 апреля 2015 г.). Набор для сборки схем [Онлайн]. Доступно: http://phet.colorado.edu/sims/circuit-construction-kit/circuit-construction-kit-ac_en.jnlp
(25 апреля 2015 г.). Набор для сборки схем [Онлайн]. Доступно: http://phet.colorado.edu/sims/circuit-construction-kit/circuit-construction-kit-ac_en.jnlp - ↑ Гиперфизика. (25 апреля 2015 г.). Конденсаторы [Онлайн]. Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capac.html
- ↑ Р. Д. Найт, «Потенциал и поле», в Физика для ученых и инженеров: стратегический подход, 2-е изд. Сан-Франциско: Пирсон Аддисон-Уэсли, 2008 г., гл. 30, с. 5, стр. 922-932.
- ↑ «Суперконденсаторы берут верх в Германии», Филип Болл, бюллетень MRS, том 37, выпуск 09, 2012 г., стр. 802–803.
- ↑ (2014, 27 июня). Как работают вспышки камеры [Онлайн]. Доступно: http://electronics.howstuffworks.com/camera-flash.htm
- ↑ Искра. (25 апреля 2015 г.). Конденсаторы [Онлайн]. Доступно: https://learn.sparkfun.com/tutorials/capacitors
Что можно сделать, чтобы увеличить емкость в цепи?
Если вы хотите увеличить емкость параллельного пластинчатого конденсатора, увеличьте площадь поверхности, уменьшите расстояние между пластинами и используйте материал с более высокой прочностью на пробой .

Какими способами можно увеличить емкость плоского конденсатора?
- A. Использование пластин меньшего размера.
- B. Замена диэлектрического материала между пластинами на материал с меньшей диэлектрической проницаемостью.
- C. Снижение напряжения между пластинами.
- D. Увеличение напряжения между пластинами.
- E. Сближение пластин.
Что можно сделать, чтобы увеличить емкость в тесте схемы?
Увеличение полярности диполей в диэлектрике делает его более сильным диэлектриком . Для данного заряда это уменьшает электрическое поле между пластинами и, следовательно, напряжение на конденсаторе. Это увеличивает емкость.
Что вызывает увеличение емкости?
На емкость влияют три фактора: размер проводников , размер зазора между ними и материал между ними (диэлектрик). Чем больше проводники, тем больше емкость. Чем меньше зазор, тем больше емкость.
Что происходит, когда вы увеличиваете емкость в цепи?
В емкостной цепи, когда емкость увеличивается, емкостное реактивное сопротивление X C уменьшается, что приводит к увеличению тока цепи и наоборот .
 … При увеличении сопротивления ток в цепи уменьшается и наоборот.
… При увеличении сопротивления ток в цепи уменьшается и наоборот.Какова функция конденсатора в цепи?
Конденсатор — это электронный компонент, который накапливает и выдает электричество в цепи . Он также пропускает переменный ток, не пропуская постоянный ток.
Какое свойство объектов лучше всего измеряется их емкостью?
Известно, что конденсатор накапливает заряд. Следовательно, свойство объектов, которое лучше всего измеряется их емкостью, равно возможность хранения заряда . Правильный вариант — в. способность накапливать заряд.
Как увеличить емкость конденсатора?
Если вы хотите увеличить емкость параллельного пластинчатого конденсатора, увеличьте площадь поверхности, уменьшите расстояние между пластинами и используйте диэлектрический материал между пластинами , который имеет более высокую диэлектрическую прочность на пробой.
Что из следующего увеличит емкость конденсатора?
Увеличение площади пластин увеличивает емкость плоского конденсатора.
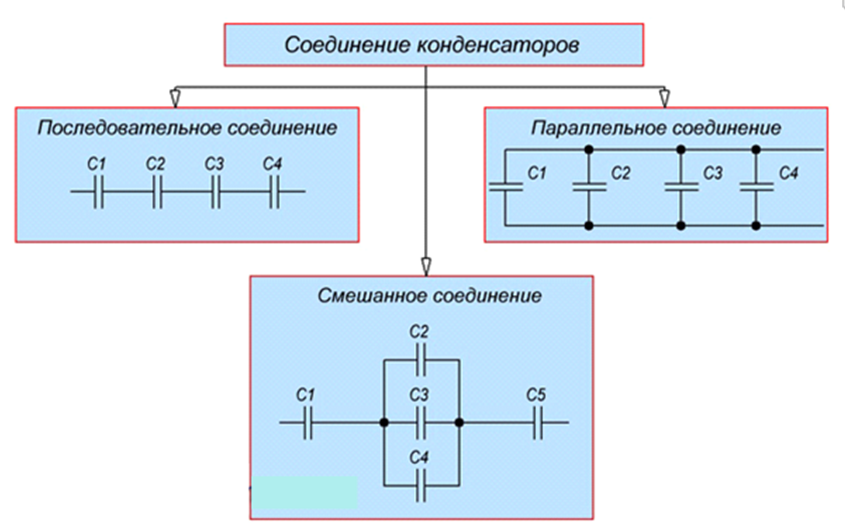 Уменьшение площади пластин увеличивает емкость плоского конденсатора. Уменьшение расстояния между пластинами увеличивает емкость плоского конденсатора.
Уменьшение площади пластин увеличивает емкость плоского конденсатора. Уменьшение расстояния между пластинами увеличивает емкость плоского конденсатора.Где мы используем конденсатор?
Чаще всего конденсаторы используются для хранения энергии . Дополнительные области применения включают преобразование мощности, соединение или развязку сигналов, электронную фильтрацию шума и дистанционное зондирование. Благодаря своему разнообразному применению конденсаторы используются в самых разных отраслях промышленности и стали жизненно важной частью повседневной жизни.
Зависит ли емкость от формы?
Емкость конденсатора не зависит от (от формы пластин (б) размера пластин в) зарядов на пластинах (г) расстояния между пластинами.
Когда конденсатор подключен к аккумулятору?
Если незаряженный конденсатор C подключить к батарее с потенциалом V, то при зарядке пластин конденсатора будет протекать переходный ток. Поток тока от батареи прекращается, как только заряд Q на положительной пластине достигает значения Q = C × V .

Почему в конденсаторе не используется вода?
Вода не используется в качестве диэлектрика между пластинами конденсатора, так как имеет очень низкую диэлектрическую прочность и высокую диэлектрическую проницаемость . Он выступает в роли проводника.
Как конденсаторы влияют на ток?
По сути, ток «видит» конденсатор как разомкнутую цепь . Если эта же цепь имеет источник переменного напряжения, лампа загорится, указывая на то, что через цепь протекает переменный ток. … Таким образом, конденсатор пропускает больший ток по мере увеличения частоты источника напряжения.
Что произойдет, если использовать неправильный конденсатор?
Если установлен неправильный рабочий конденсатор, двигатель не будет иметь равномерного магнитного поля . Это заставит ротор колебаться в тех местах, которые неровны. Это колебание приведет к тому, что двигатель станет шумным, увеличит потребление энергии, приведет к падению производительности и вызовет перегрев двигателя.

Вызывают ли конденсаторы падение напряжения?
Конденсаторы в серии Резюме
Поскольку заряд ( Q ) равен и постоянен, Падение напряжения на конденсаторе определяется емкостью конденсатора только как V = Q ÷ C . Небольшое значение емкости приведет к большему напряжению, а большое значение емкости приведет к меньшему падению напряжения.
19.5 Конденсаторы и диэлектрики – Колледж физики главы 1-17
19 Электрический потенциал и электрическое поле
Резюме
- Опишите действие конденсатора и определите емкость.
- Объясните конденсаторы с плоскими пластинами и их емкости.
- Обсудите процесс увеличения емкости диэлектрика.
- Определить емкость при данных заряде и напряжении.
Конденсатор — это устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах.
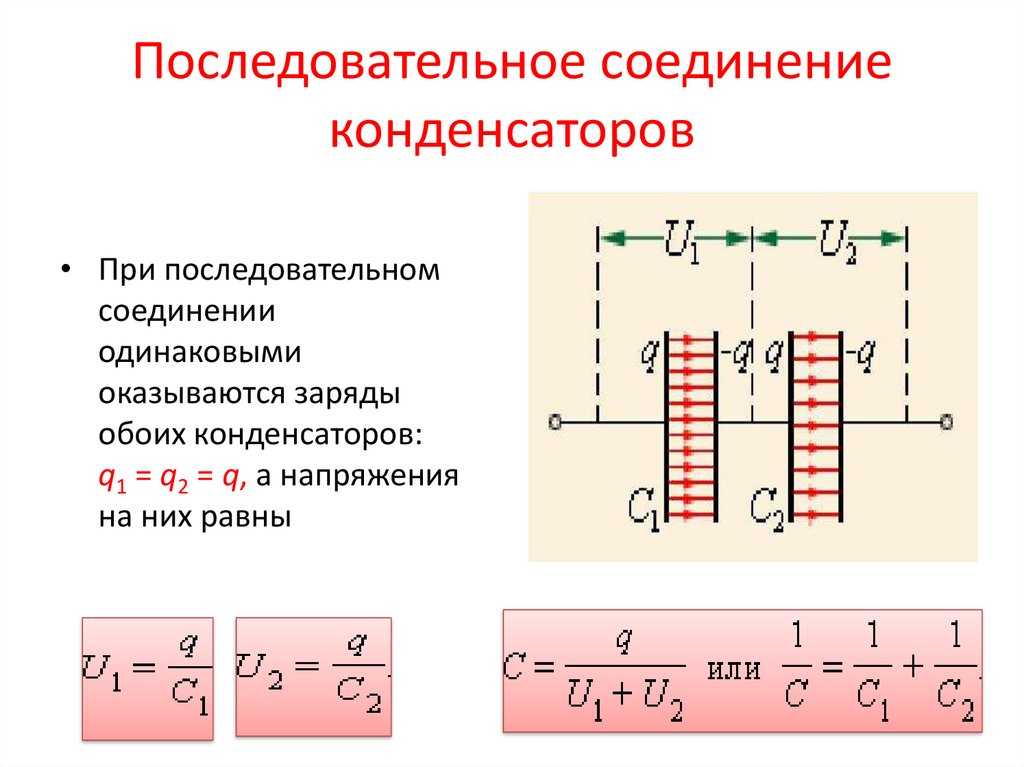 Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]\boldsymbol{+Q}[/латекс] и [латекс]\boldsymbol{-Q}[/латекс], разделены на его две тарелки. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]\boldsymbol{Q}[/латекс].
Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]\boldsymbol{+Q}[/латекс] и [латекс]\boldsymbol{-Q}[/латекс], разделены на его две тарелки. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]\boldsymbol{Q}[/латекс].Конденсатор
Конденсатор — это устройство, используемое для накопления электрического заряда.
Рис. 1. Оба показанных здесь конденсатора были изначально разряжены перед подключением к батарее. Теперь у них есть отдельные заряды + Q и – Q на две половины. а) Конденсатор с плоскими пластинами. (b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.
(b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.Сумма заряда [латекс]\boldsymbol{Q}[/латекс] a , который может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Количество заряда
Q Конденсатор может хранитьКоличество заряда [латекс]\boldsymbol{Q}[/latex] конденсатора зависит от двух основных факторов: приложенного напряжения и емкости конденсатора. физические характеристики, например размер.
Система, состоящая из двух одинаковых параллельных проводящих пластин, разделенных расстоянием, как показано на рис. 2, называется конденсатором с параллельными пластинами. Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше.
Рисунок 2. Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна [латексной ]\boldsymbol{Q}[/латекс]
линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна [латексной ]\boldsymbol{Q}[/латекс]Поле пропорционально заряду:
[латекс]\boldsymbol{E \propto Q},[/латекс]
, где символ [латекс]\жирныйсимвол{\пропто}[/латекс] означает «пропорционально». Из обсуждения в главе 19.2 Электрический потенциал в однородном электрическом поле, мы знаем, что напряжение на параллельных пластинах равно [латекс]\boldsymbol{V = Ed}[/латекс].
 Таким образом,
Таким образом,[латекс]\boldsymbol{V \propto E}.[/латекс]
Отсюда следует, что [латекс]\boldsymbol{V \propto Q}[/латекс], и наоборот,
[латекс]\boldsymbol{Q \propto V}.[/латекс]
В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больший заряд в нем хранится.
Различные конденсаторы сохраняют различное количество заряда при одном и том же приложенном напряжении в зависимости от их физических характеристик. Мы определяем их емкость [латекс]\boldsymbol{C}[/latex] так, чтобы заряд [латекс]\boldsymbol{Q}[/латекс], хранящийся в конденсаторе, был пропорционален [латекс]\boldsymbol{C}[ /латекс]. Заряд, хранящийся в конденсаторе, равен 9.0347
[латекс]\boldsymbol{Q = CV}.[/латекс]
Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора, [латекс]\boldsymbol{C}[/латекс], и напряжение, ВВ . Преобразовав уравнение, мы видим, что емкость [латекс]\boldsymbol{C}[/latex] – это количество накопленного заряда на вольт, или
.
[латекс]\boldsymbol{C =}[/латекс] [латекс]\boldsymbol{\frac{Q}{V}}.[/латекс]
Емкость
Емкость [латекс]\boldsymbol{C}[/латекс] — это количество заряда, хранящегося на вольт, или
[латекс]\жирный символ{С =}[/латекс] [латекс]\жирныйсимвол{\фракция {Q}{V}}.[/латекс]
Единицей измерения емкости является фарад (Ф), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или
.[латекс]\boldsymbol{1 \;\textbf{F} =}[/latex] [латекс]\boldsymbol{\frac{1 \;\textbf{C}}{1 \;\textbf{V}}} .[/латекс] 9{-3} \;\textbf{F})}[/latex].
На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.
Рисунок 3. Некоторые типовые конденсаторы. Размер и значение емкости не обязательно связаны. (кредит: Уинделл Оскей)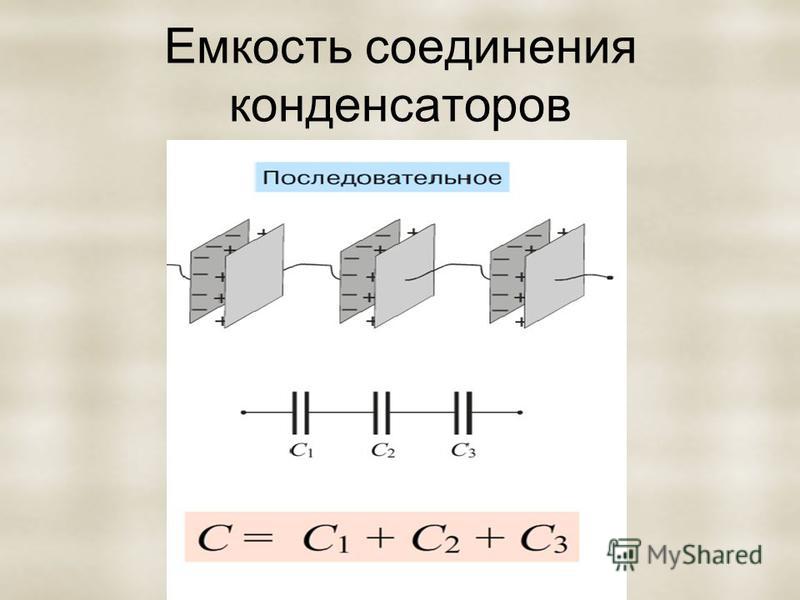
Конденсатор с плоскими пластинами, показанный на рисунке 4, имеет две одинаковые проводящие пластины, каждая из которых имеет площадь поверхности [латекс]\boldsymbol{A}[/latex], разделенную расстоянием [латекс]\boldsymbol{d}[/латекс] ( без материала между пластинами). Когда к конденсатору прикладывается напряжение [latex]\boldsymbol{V}[/latex], он накапливает заряд [latex]\boldsymbol{Q}[/latex], как показано на рисунке. Мы можем увидеть, как его емкость зависит от [латекс]\boldsymbol{A}[/латекс] и [латекс]\boldsymbol{d}[/латекс], рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом, [латекс]\boldsymbol{C}[/latex] должен быть больше для больших [латекс]\boldsymbol{A}[/латекс].
Рис. 4. Конденсатор с параллельными пластинами, пластины которых разнесены на расстояние d . Каждая пластина имеет площадь A . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Так что [латекс]\boldsymbol{C}[/латекс] должен быть больше для меньшего [латекс]\жирныйсимвол{d}[/латекс].
Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Так что [латекс]\boldsymbol{C}[/латекс] должен быть больше для меньшего [латекс]\жирныйсимвол{d}[/латекс].Можно показать, что для конденсатора с плоскими пластинами есть только два фактора ([латекс]\boldsymbol{A}[/латекс] и [латекс]\жирныйсимвол{d}[/латекс]), которые влияют на его емкость [латекс] \boldsymbol{C}[/латекс]. Емкость конденсатора с плоскими пластинами в виде уравнения определяется как
.[латекс]\boldsymbol{C = {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}.[/latex]
Емкость плоскопараллельного конденсатора
[латекс]\boldsymbol{C = {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}.[/latex]
[латекс]\boldsymbol{A}[/латекс] — площадь одной пластины в квадратных метрах, а [латекс]\жирный символ{d}[/латекс] — расстояние между пластинами в метрах.
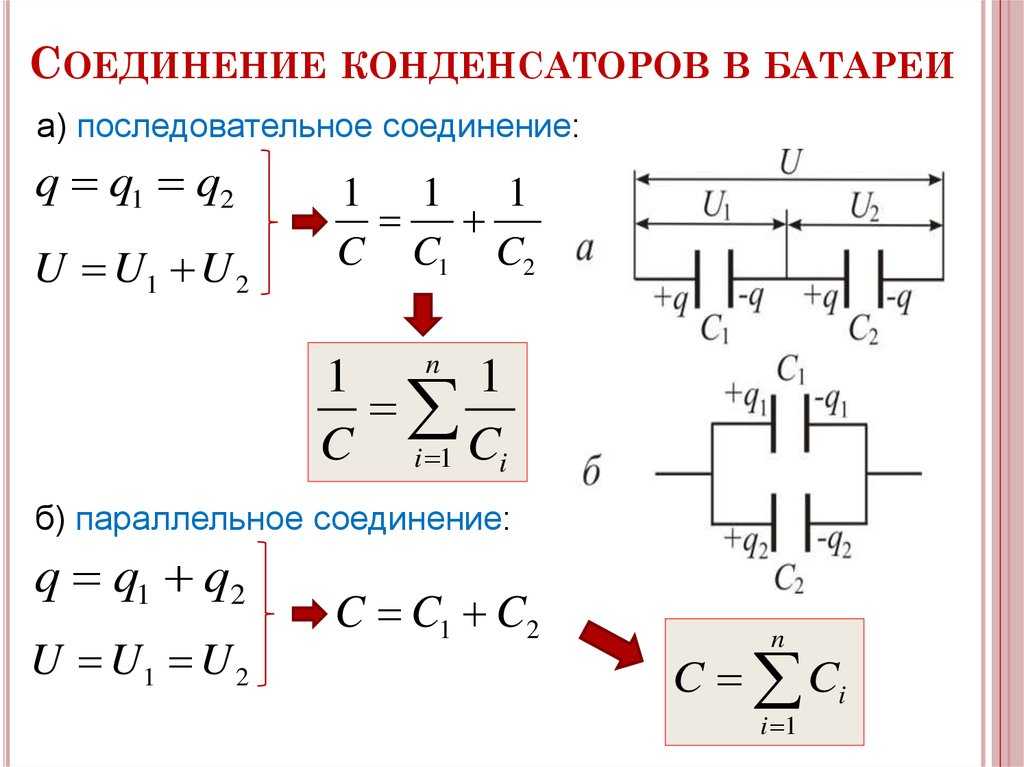 2}[/latex]. Небольшое числовое значение [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] связано с большим размером фарады. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.) 93 \;\textbf{V}}[/latex] применяется к нему?
2}[/latex]. Небольшое числовое значение [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] связано с большим размером фарады. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.) 93 \;\textbf{V}}[/latex] применяется к нему?Стратегия
Нахождение емкости [латекс]\boldsymbol{C}[/latex] является прямым применением уравнения [латекс]\boldsymbol{C = {\varepsilon}_0 A/d}[/latex] . Как только [латекс]\boldsymbol{C}[/латекс] найден, накопленный заряд можно найти с помощью уравнения [латекс]\жирныйсимвол{Q = CV}[/латекс].
Решение для (a)
Ввод данных значений в уравнение для емкости плоского конденсатора дает 9{-9} \;\textbf{F} = 8,85 \;\textbf{nF}}. \end{array}[/latex]
Обсуждение для (a)
Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью.
 Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.
Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.Решение для (b)
Заряд, хранящийся в любом конденсаторе, определяется уравнением [латекс]\boldsymbol{Q = CV}[/латекс]. Ввод известных значений в это уравнение дает 96 \;\textbf{V} / \textbf{m}}[/latex], на этом конденсаторе нельзя накопить больше заряда за счет увеличения напряжения.
Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. На мембране существует разность потенциалов около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 96 \;\textbf{V} / \textbf{m}}.[/latex]
Этого электрического поля достаточно, чтобы вызвать пробой воздуха.
В предыдущем примере подчеркивается сложность сохранения большого количества заряда в конденсаторах.
 Если [латекс]\boldsymbol{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]\жирныйсимвол{E = V/d}[/латекс ]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и позволить [латексу]\boldsymbol{d}[/латексу] быть как можно меньше. Мало того, что меньший [латекс]\boldsymbol{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.
Если [латекс]\boldsymbol{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]\жирныйсимвол{E = V/d}[/латекс ]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и позволить [латексу]\boldsymbol{d}[/латексу] быть как можно меньше. Мало того, что меньший [латекс]\boldsymbol{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.Существует еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем указанная уравнением [латекс]\boldsymbol{C = {\varepsilon}_0 \frac{A}{d}}[/latex], на коэффициент [латекс]\boldsymbol {\kappa}[/latex] , называемая диэлектрической проницаемостью . Емкость плоского конденсатора с диэлектриком между пластинами равна
.
[латекс]\boldsymbol{C = \kappa {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}[/latex] [латекс]\boldsymbol{(\textbf{ плоскопараллельный конденсатор с диэлектриком})}.[/latex]
Значения диэлектрической проницаемости [латекс]\boldsymbol{\kappa}[/латекс] для различных материалов приведены в таблице 1. Обратите внимание, что [латекс]\жирныйсимвол{\каппа}[/латекс] для вакуума ровно 1, а поэтому приведенное выше уравнение справедливо и в этом случае. Если используется диэлектрик, возможно, путем помещения тефлона между пластинами конденсатора в примере 1, то емкость будет больше в [латекс]\жирныйсимвол{\каппа}[/латекс], что для тефлона составляет 2,1.
Самостоятельный эксперимент: создание конденсатора
Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой.
Материал Диэлектрическая проницаемость [латекс]\boldsymbol{\kappa}[/латекс] Диэлектрическая прочность (В/м) Пылесос 1.  6}[/латекс] 96}[/латекс]
6}[/латекс] 96}[/латекс]Вода 80 — Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC Также обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится слишком большой . (Напомним, что [латекс]\boldsymbol{E = V/d}[/латекс] для конденсатора с плоскими пластинами.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые диэлектрической прочностью, для нескольких материалов. Это поля, выше которых материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного разделения пластин.
 4 \;\textbf{V})} \\[1em] & \boldsymbol{ 1.1 \;\textbf{mC}.} \end{массив}[/latex]
4 \;\textbf{V})} \\[1em] & \boldsymbol{ 1.1 \;\textbf{mC}.} \end{массив}[/latex]Это в 42 раза больше заряда того же воздушного конденсатора.
Диэлектрическая прочность
Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
Каким образом диэлектрик увеличивает емкость под микроскопом? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость [латекс]\boldsymbol{\kappa}[/латекс]. Вода, например, является полярной молекулой, потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рис. 5 схематично показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора.
Рис. 5. (а) Молекулы изоляционного материала между пластинами конденсатора поляризуются заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (b) Диэлектрик уменьшает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.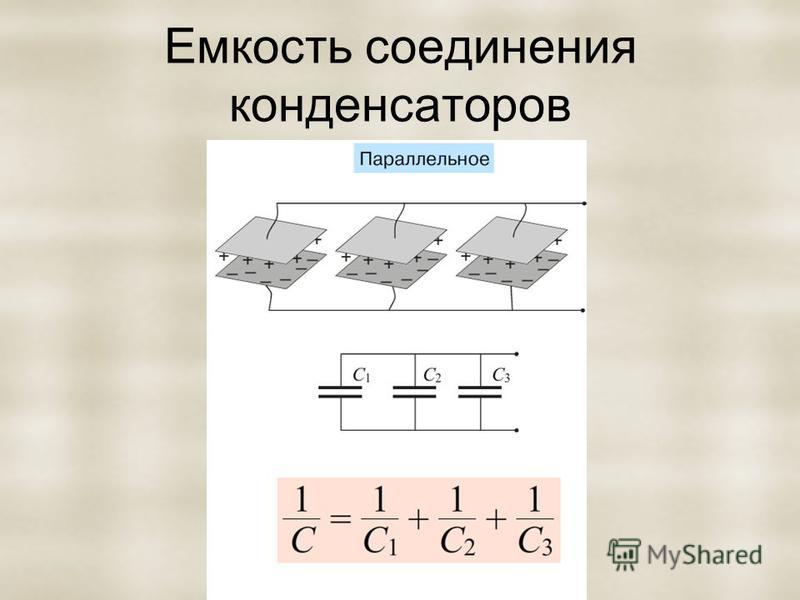 Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]\boldsymbol{d}[/латекс].
Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]\boldsymbol{d}[/латекс].Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком.
 Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]\boldsymbol{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]\boldsymbol{V}[/латекс] для того же заряда [латекс]\boldsymbol{Q}[/латекс]; поскольку [латекс]\boldsymbol{C = Q/V}[/латекс], емкость [латекс]\boldsymbol{C}[/латекс] больше.
Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]\boldsymbol{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]\boldsymbol{V}[/латекс] для того же заряда [латекс]\boldsymbol{Q}[/латекс]; поскольку [латекс]\boldsymbol{C = Q/V}[/латекс], емкость [латекс]\boldsymbol{C}[/латекс] больше.Диэлектрическая проницаемость обычно определяется как [латекс]\boldsymbol{\kappa = E_0/E}[/латекс] или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале и тесно связано с поляризуемость материала.
Вещи большие и малые
Субмикроскопическое происхождение поляризации
Поляризация — это разделение зарядов внутри атома или молекулы.
 Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0347 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0347 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.В главе 30 «Атомная физика» мы найдем, что орбиты электронов правильнее рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и траекторий планет в их орбиты вокруг Солнца).
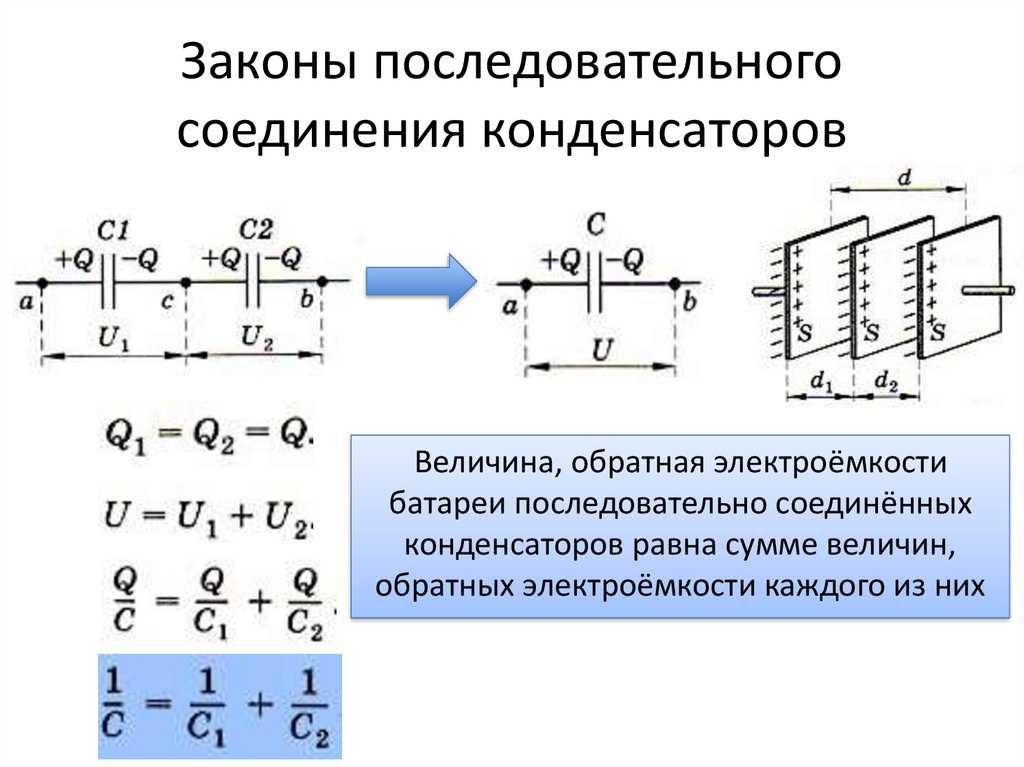 Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. На рис. 7 показано разделение заряда в молекуле воды, имеющей два атома водорода и один атом кислорода [латекс]\boldsymbol{\textbf{H}_2 \textbf{O}}[/latex]. Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость.
Рисунок 7. Представление художника о молекуле воды. Существует неотъемлемое разделение зарядов, поэтому вода является полярной молекулой. Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда вблизи двух ядер водорода. (Обратите внимание, что схема справа представляет собой грубую иллюстрацию распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.) Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.PhET Explorations: Capacitor Lab
Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.
Рис. 8. Конденсаторная лаборатория Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.- Конденсатор — это устройство, используемое для накопления заряда.
- Количество заряда [латекс]\boldsymbol{Q}[/латекс], которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
- Емкость [латекс]\boldsymbol{C}[/латекс] представляет собой количество заряда, накопленного на вольт , или
[латекс]\boldsymbol{C} =[/латекс] [латекс]\boldsymbol{\frac{Q}{V}}. [\латекс]
- Емкость конденсатора с параллельными пластинами равна [латекс]\boldsymbol{C = {\varepsilon}_0 \;\frac{A}{d}}}[/латекс], когда пластины разделены воздухом или свободным пространством. [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] называется диэлектрической проницаемостью свободного пространства.
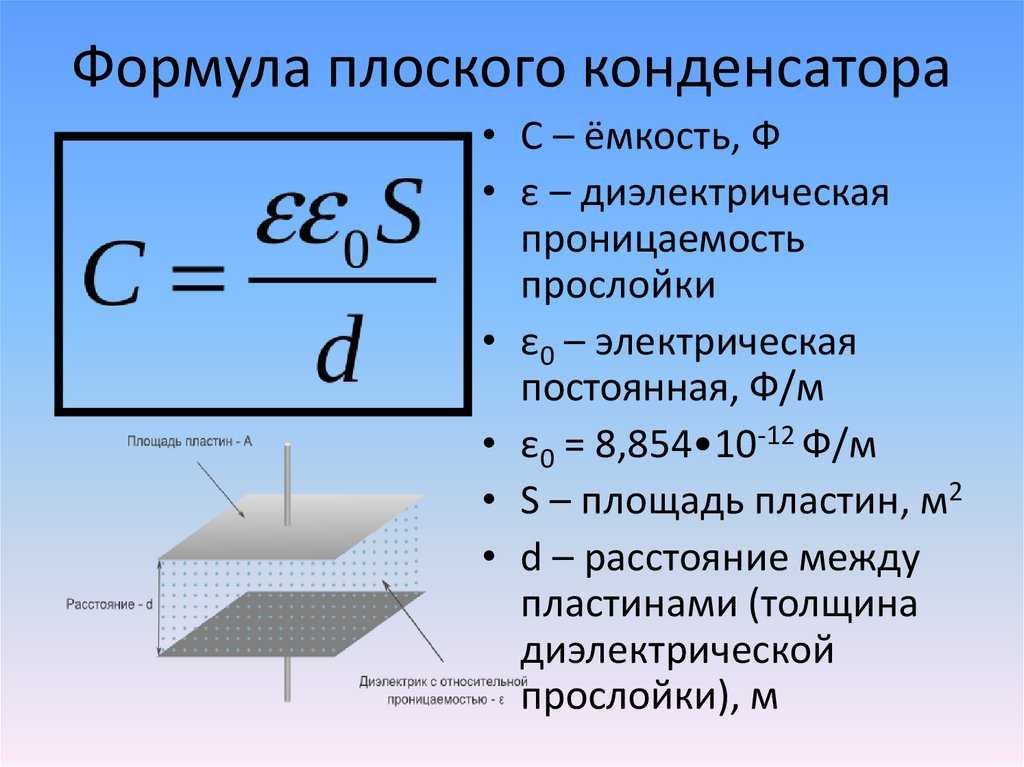
- Емкость плоского конденсатора с диэлектриком между пластинами определяется выражением
[латекс]\boldsymbol{C = \kappa {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}},[/latex]
, где [латекс]\boldsymbol{\kappa}[/латекс] — диэлектрическая проницаемость материала.
- Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
- конденсатор
- устройство, накапливающее электрический заряд
- емкость
- количество накопленного заряда на единицу вольта
- диэлектрик
- изоляционный материал
- диэлектрическая прочность
- максимальное электрическое поле, при превышении которого изоляционный материал начинает разрушаться и проводить
- Плоский конденсатор
- две одинаковые проводящие пластины, разделенные расстоянием
- полярная молекула
- молекула с присущим разделением зарядов
18.
 5 Конденсаторы и диэлектрики. Физика
5 Конденсаторы и диэлектрики. ФизикаРаздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Вычислять энергию, запасенную в заряженном конденсаторе, и емкость конденсатора
- Объясните свойства конденсаторов и диэлектриков
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
- (Ф) спроектировать и рассчитать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.
Кроме того, руководство по физике для средней школы обращается к содержанию этого раздела лабораторной работы под названием «Электрический заряд», а также к следующим стандартам:
- (5) Учащийся знает природу сил в физическом мире.
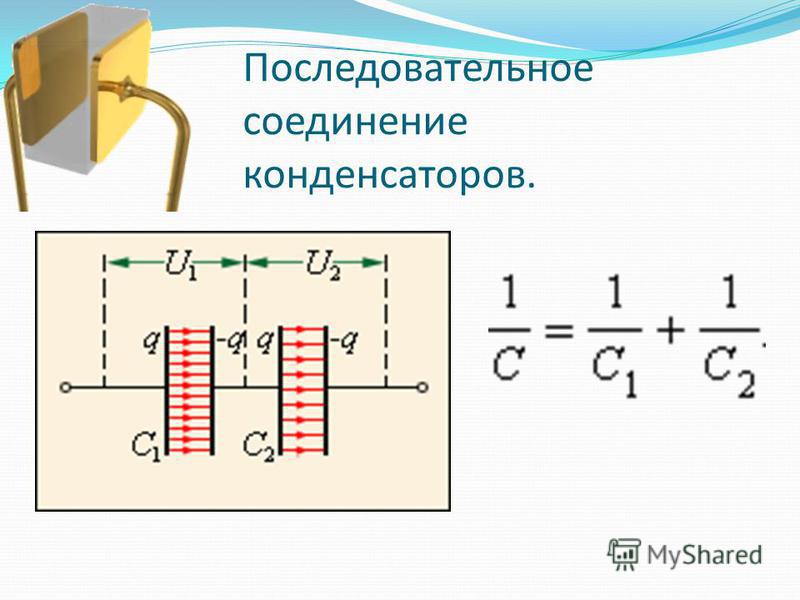 Ожидается, что студент:
Ожидается, что студент:- (Ф) спроектировать и рассчитать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.
Основные термины раздела
конденсатор диэлектрик Поддержка учителей
Поддержка учителей
Чтобы представить конденсаторы, в этом разделе подчеркивается их способность накапливать энергию. Диэлектрики введены как способ увеличить количество энергии, которое может храниться в конденсаторе. Чтобы представить идею хранения энергии, обсудите с учащимися другие механизмы хранения энергии, такие как плотины или батареи. Спросите, у кого больше мощность.
Конденсаторы
Поддержка учителей
Поддержка учителей
Объясните, что электрические конденсаторы являются жизненно важными частями всех электрических цепей.
 На самом деле, все электрические устройства имеют емкость, даже если конденсатор явно не встроен в устройство.
На самом деле, все электрические устройства имеют емкость, даже если конденсатор явно не встроен в устройство.[BL]Попросите учащихся определить, как слово емкость используется в повседневной жизни. Предложите им найти определение в словаре. Сравните и сопоставьте обыденное значение со значением термина в физике.
[OL]Спросите учащихся, слышали ли они слово конденсатор , используемый вместе с электричеством, например, на электростанциях или в электрических цепях. Попросите их описать, как используется это слово.
[AL]Обсудите, как пружина способна накапливать механическую энергию. Обсудите, какие свойства пружины увеличивают ее способность накапливать энергию. Укажите, что эти свойства присущи пружине.
Снова рассмотрим рентгеновскую трубку, рассмотренную в предыдущем примере задачи. Как создать однородное электрическое поле? Один положительный заряд создает электрическое поле, направленное от него, как показано на рис.
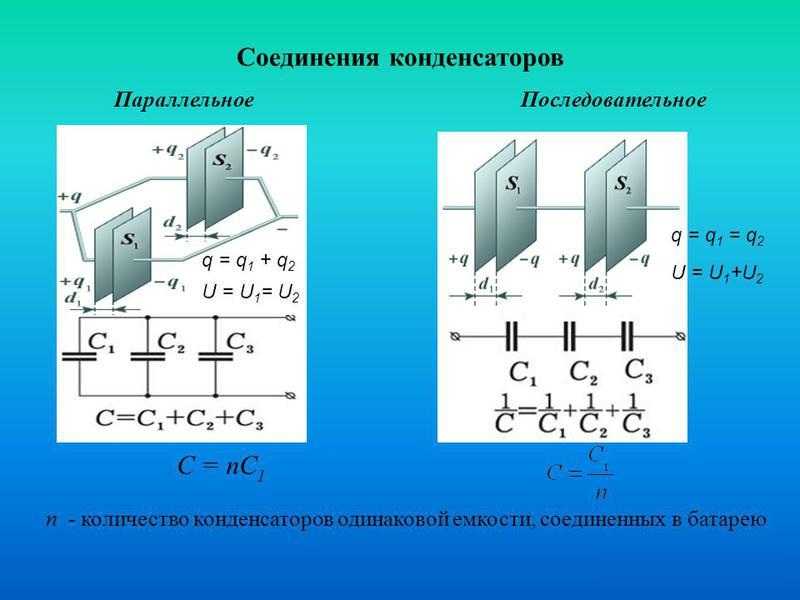 18.17. Это поле неоднородно, так как расстояние между линиями увеличивается по мере удаления от заряда. Однако, если мы объединим положительный и отрицательный заряды, мы получим электрическое поле, показанное на рис. 18.19.(а). Обратите внимание, что между зарядами силовые линии электрического поля расположены более равномерно.
18.17. Это поле неоднородно, так как расстояние между линиями увеличивается по мере удаления от заряда. Однако, если мы объединим положительный и отрицательный заряды, мы получим электрическое поле, показанное на рис. 18.19.(а). Обратите внимание, что между зарядами силовые линии электрического поля расположены более равномерно.Что произойдет, если мы поместим, скажем, пять положительных зарядов в линию напротив пяти отрицательных зарядов, как показано на рис. 18.27? Теперь область между линиями заряда содержит довольно однородное электрическое поле.
Рисунок 18.27 Красные точки — положительные заряды, синие — отрицательные. Направление электрического поля показано красными стрелками. Обратите внимание, что электрическое поле между положительными и отрицательными точками довольно однородно.
Мы можем распространить эту идею еще дальше и на два измерения, поместив две металлические пластины лицом к лицу и зарядив одну положительным зарядом, а другую равной по величине отрицательной зарядкой.
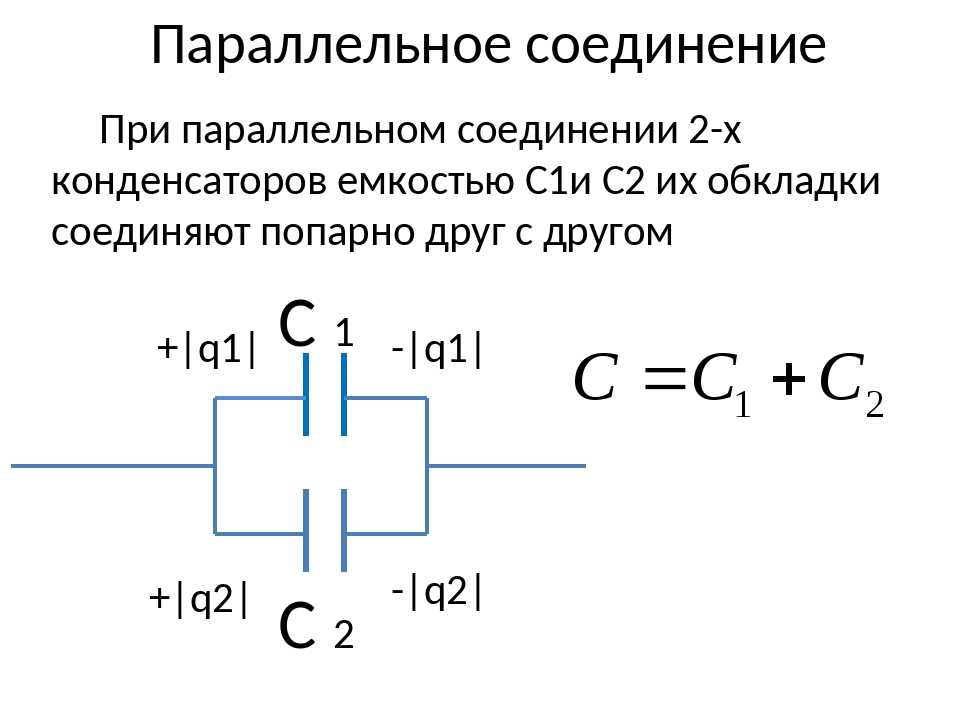 Это можно сделать, подключив одну пластину к положительной клемме батареи, а другую пластину к отрицательной клемме, как показано на рис. 18.28. Электрическое поле между этими заряженными пластинами будет чрезвычайно однородным.
Это можно сделать, подключив одну пластину к положительной клемме батареи, а другую пластину к отрицательной клемме, как показано на рис. 18.28. Электрическое поле между этими заряженными пластинами будет чрезвычайно однородным.Рисунок 18.28 Две параллельные металлические пластины заряжаются противоположным зарядом, соединяя пластины с противоположными клеммами батареи. Величина заряда на каждой пластине одинакова.
Давайте подумаем о работе, необходимой для зарядки этих пластин. До того, как пластины подключены к батарее, они нейтральны, то есть имеют нулевой суммарный заряд. Размещение первого положительного заряда на левой пластине и первого отрицательного заряда на правой пластине требует очень мало работы, потому что пластины нейтральны, поэтому противоположные заряды отсутствуют. Теперь рассмотрите возможность размещения второго положительного заряда на левой пластине и второго отрицательного заряда на правой пластине. Поскольку первые два заряда отталкивают вновь прибывших, к двум новым зарядам нужно приложить силу на расстоянии, чтобы они оказались на пластинах.
 Это определение работы, которое означает, что по сравнению с первой парой требуется больше работы, чтобы положить вторую пару зарядов на пластины. Чтобы разместить третий положительный и отрицательный заряды на пластинах, требуется еще больше работы, и так далее. Откуда эта работа? Батарея! Его химическая потенциальная энергия преобразуется в работу, необходимую для разделения положительных и отрицательных зарядов.
Это определение работы, которое означает, что по сравнению с первой парой требуется больше работы, чтобы положить вторую пару зарядов на пластины. Чтобы разместить третий положительный и отрицательный заряды на пластинах, требуется еще больше работы, и так далее. Откуда эта работа? Батарея! Его химическая потенциальная энергия преобразуется в работу, необходимую для разделения положительных и отрицательных зарядов.Несмотря на то, что батарея работает, эта работа остается в рамках системы аккумуляторной пластины. Следовательно, закон сохранения энергии говорит нам, что если потенциальная энергия батареи уменьшится до отдельных зарядов, энергия другой части системы должна увеличиться на ту же величину. По сути, энергия батареи запасается в электрическом поле между пластинами. Эта идея аналогична рассмотрению того, что потенциальная энергия поднятого молота хранится в гравитационном поле Земли. Если бы гравитационное поле исчезло, у молота не было бы потенциальной энергии. Точно так же, если бы между пластинами не существовало электрического поля, между ними не накапливалась бы энергия.

Если мы сейчас отсоединим пластины от батареи, они будут удерживать энергию. Мы могли бы, например, подключить пластины к лампочке, и лампочка будет гореть до тех пор, пока эта энергия не будет израсходована. Таким образом, эти пластины обладают способностью накапливать энергию. По этой причине устройство, подобное этому, называется конденсатором. Конденсатор — это совокупность объектов, которые в силу своей геометрии могут накапливать энергию электрического поля.
Различные реальные конденсаторы показаны на рис. 18.29.. Обычно они изготавливаются из проводящих пластин или листов, разделенных изоляционным материалом. Они могут быть плоскими или свернутыми или иметь другую геометрию.
Рисунок 18.29 Некоторые типовые конденсаторы. (кредит: Уинделл Оскей)
Емкость конденсатора определяется его емкостью C , которая определяется как
С=QV,C=QV,
18,35
, где Q — величина заряда на каждой пластине конденсатора, а В — это разность потенциалов при переходе от отрицательной пластины к положительной.
 Это означает, что и Q , и V всегда положительны, поэтому емкость всегда положительна. Из уравнения для емкости видно, что единицами измерения емкости являются C/V, которые называются фарадами (F) в честь английского физика девятнадцатого века Майкла Фарадея.
Это означает, что и Q , и V всегда положительны, поэтому емкость всегда положительна. Из уравнения для емкости видно, что единицами измерения емкости являются C/V, которые называются фарадами (F) в честь английского физика девятнадцатого века Майкла Фарадея.Уравнение C=Q/VC=Q/V имеет смысл: конденсатор с плоскими пластинами (подобный показанному на рис. 18.28) размером с футбольное поле может удерживать большой заряд, не требуя слишком большой работы на единицу заряда для втолкнуть заряд в конденсатор. Таким образом, Q будет большим, а V будет маленьким, поэтому емкость C будет очень большой. Вдавливание того же заряда в конденсатор размером с ноготь потребовало бы гораздо больше работы, поэтому V было бы очень большим, а емкость была бы намного меньше.
Хотя из уравнения C=Q/VC=Q/V кажется, что емкость зависит от напряжения, на самом деле это не так.
 Для данного конденсатора отношение запасенного в конденсаторе заряда к разности напряжений между обкладками конденсатора всегда остается одним и тем же. Емкость определяется геометрией конденсатора и материалами, из которых он изготовлен. Для плоского конденсатора, между пластинами которого ничего нет, емкость равна
Для данного конденсатора отношение запасенного в конденсаторе заряда к разности напряжений между обкладками конденсатора всегда остается одним и тем же. Емкость определяется геометрией конденсатора и материалами, из которых он изготовлен. Для плоского конденсатора, между пластинами которого ничего нет, емкость равнаC0=ε0Ad,C0=ε0Ad,
18,36
где А площадь пластин конденсатора и d их расстояние между собой. Мы используем C0C0 вместо C , потому что между пластинами конденсатора ничего нет (в следующем разделе мы увидим, что происходит, когда это не так). Константа ε0,ε0, равная эпсилон ноль , называется диэлектрической проницаемостью свободного пространства, и ее значение равно
.ε0=8,85×10−12 Ф/мε0=8,85×10−12 Ф/м
18.37
Возвращаясь к энергии, запасенной в конденсаторе, мы можем спросить, сколько именно энергии запасает конденсатор.
. Если конденсатор зарядить, подав на него напряжение В , например, подключив его к батарее с напряжением В , то электрическая потенциальная энергия, запасенная в конденсаторе, равна
Если конденсатор зарядить, подав на него напряжение В , например, подключив его к батарее с напряжением В , то электрическая потенциальная энергия, запасенная в конденсаторе, равнаUE=12CV2.UE=12CV2.
18,38
Обратите внимание, что форма этого уравнения аналогична форме для кинетической энергии, K=12mv2K=12mv2 .
Смотреть физику
Откуда взялась емкость?
В этом видео показано, как определяется емкость и почему она зависит только от геометрических свойств конденсатора, а не от напряжения или накопленного заряда. При этом он дает хороший обзор понятий работы и электрического потенциала.
Проверка захвата
Если увеличить расстояние между пластинами конденсатора, как изменится его емкость?
- Удвоение расстояния между пластинами конденсатора уменьшит емкость в четыре раза.

- Удвоение расстояния между пластинами конденсатора уменьшит емкость в два раза.
- Удвоение расстояния между пластинами конденсатора увеличивает емкость в два раза.
- Удвоение расстояния между пластинами конденсатора увеличит емкость в четыре раза.
Виртуальная физика
Зарядите конденсатор
В этой симуляции вам предлагается конденсатор с плоскими пластинами, подключенный к батарее переменного напряжения. Аккумулятор изначально находится при нулевом напряжении, поэтому конденсатор не заряжен. Сдвиньте ползунок батареи вверх и вниз, чтобы изменить напряжение батареи, и наблюдайте за зарядами, которые накапливаются на пластинах. Отображение емкости, заряда верхней пластины и накопленной энергии при изменении напряжения батареи. Вы также можете отобразить линии электрического поля в конденсаторе. Наконец, проверьте напряжение между различными точками этой цепи с помощью вольтметра.
Проверка захвата
Верно или неверно — в конденсаторе накопленная энергия всегда положительна, независимо от того, заряжена ли верхняя пластина отрицательным или положительным зарядом.
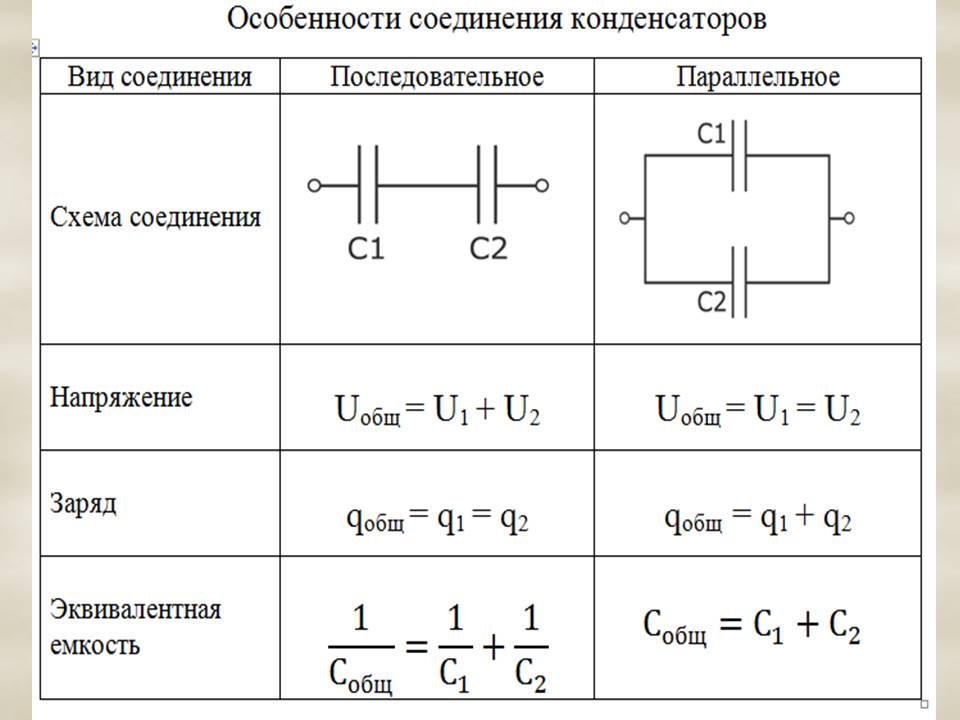
- ложный
- правда
Рабочий пример
Емкость и заряд, хранящиеся в конденсаторе с параллельными пластинами
(a) Какова емкость плоского конденсатора с металлическими пластинами площадью 1,00 м 2 , каждая из которых расположена на расстоянии 0,0010 м? б) Какой заряд сохраняется в этом конденсаторе, если напряжение 3,00·10 3 В на него подается?
Стратегия ЗА (А)
Используйте уравнение C0=ε0AdC0=ε0Ad .
Решение для (a)
Ввод данных значений в это уравнение для емкости плоского конденсатора дает 9 F=8,9 нФ.C=ε0Ad=(8,85×10-12 Ф/м)1,00 м20,0010 м=8,9×10-9 Ф=8,9 нФ.
18,39
Обсуждение для (a)
Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу, или использование диэлектрика (будет обсуждаться ниже).

Стратегия ЗА (Б)
Зная C , найдите накопленный заряд, решив уравнение C=Q/VC=Q/V для заряда Q .
Решение для (b)
Заряд Q на конденсаторе равен
Q=CV=(8,9×10-9F)(3,00×103В)=2,7×10-5C.Q=CV=(8,9×10 -9F)(3,00×103В)=2,7×10-5C.
18,40
Обсуждение для (b)
Этот заряд лишь немного превышает типичный заряд статического электричества. Больше заряда можно сохранить, используя диэлектрик между обкладками конденсатора.
Рабочий пример
Какая батарея нужна для зарядки конденсатора?
Ваш друг дает вам конденсатор емкостью 10 мкФ10 мкФ. Чтобы хранить 120 мкКл120 мкКл на этом конденсаторе, аккумулятор какого напряжения нужно купить?
Стратегия
Используйте уравнение C=Q/VC=Q/V, чтобы найти напряжение, необходимое для зарядки конденсатора.

Решение
Решение C=Q/VC=Q/V для напряжения дает V=Q/CV=Q/C . Вставка C=10 мкФ=10×10-6FC=10 мкФ=10×10-6F и Q=120 мкC=120×10-6CQ=120 мкC=120×10-6C дает
V=QC=120×10−6C10×10−6F=12VV=QC=120×10−6C10×10−6F=12V
18.41
Обсуждение
Такую батарею должно быть легко достать. Остается вопрос, содержит ли аккумулятор достаточно энергии для обеспечения нужного заряда. Уравнение UE=12CV2UE=12CV2 позволяет рассчитать требуемую энергию.
UE=12CV2=12(10×10−6F)(12В)2=72мJUE=12CV2=12(10×10−6F)(12В)2=72мДж
18,42
Обычный коммерческий аккумулятор может легко обеспечить это много энергии.
Практические задачи
23.
Какое напряжение на 35 мкФ при заряде 25 нКл?
- 8,75 × 10 −13 В
- 0,71 × 10 −3 В
- 1,4 × 10 −3 В
- 1,4 × 10 3 В
24.

Какое напряжение находится на конденсаторе емкостью 100 мкФ, хранящем 10 Дж энергии?
- −4,5 × 10 2 В
- 4,5 × 10 2 В
- ±4,5 × 10 2 В
- ±9 × 10 2 В
Диэлектрики
Поддержка учителей
Поддержка учителей
Объясните, что диэлектрик является сокращением от диэлектрический материал , который имеет особые электрические свойства, которые будут обсуждаться в этом разделе. Слово диэлектрик используется для обозначения способности материала накапливать энергию. Напомните учащимся, что изолятор используется для обозначения способности материала препятствовать прохождению электрического заряда.
[BL][OL]Обратите внимание, что префикс к означает два или два.
 В сочетании со словом электрический это означает, что диэлектрик может иметь два электрических заряда.
В сочетании со словом электрический это означает, что диэлектрик может иметь два электрических заряда.[AL]Спросите учащихся, знают ли они другие слова, которые используют префикс di в науке (двухатомный, двуокись углерода, диполь, …).
Прежде чем приступить к решению некоторых примеров задач, давайте посмотрим, что произойдет, если мы поместим изоляционный материал между пластинами заряженного конденсатора, а затем отсоединим его от заряжаемой батареи, как показано на рис. 18.30. Поскольку материал является изолирующим, заряд не может перемещаться через него с одной пластины на другую, поэтому заряд Q на конденсатор не меняется. Между пластинами заряженного конденсатора существует электрическое поле, поэтому изолирующий материал поляризуется, как показано в нижней части рисунка. Электроизоляционный материал, который поляризуется в электрическом поле, называется диэлектриком.

На рис. 18.30 показано, что отрицательный заряд молекул материала смещается влево, в сторону положительного заряда конденсатора. Этот сдвиг происходит из-за электрического поля, которое действует слева на электроны в молекулах диэлектрика. Правые стороны молекул теперь лишены небольшого количества отрицательного заряда, поэтому их суммарный заряд положительный.
Рисунок 18.30 Верхний и нижний конденсаторы несут одинаковый заряд Q . Верхний конденсатор не имеет диэлектрика между пластинами. Нижний конденсатор имеет диэлектрик между пластинами. Молекулы в диэлектрике поляризуются электрическим полем конденсатора.
Поддержка учителей
Поддержка учителей
Укажите положительный и отрицательный поверхностный заряд на каждой стороне диэлектрика. Обсудите со студентами, что линии электрического поля нарисованы так, что они касаются поверхностных зарядов, потому что линии электрического поля всегда начинаются или заканчиваются на заряде.
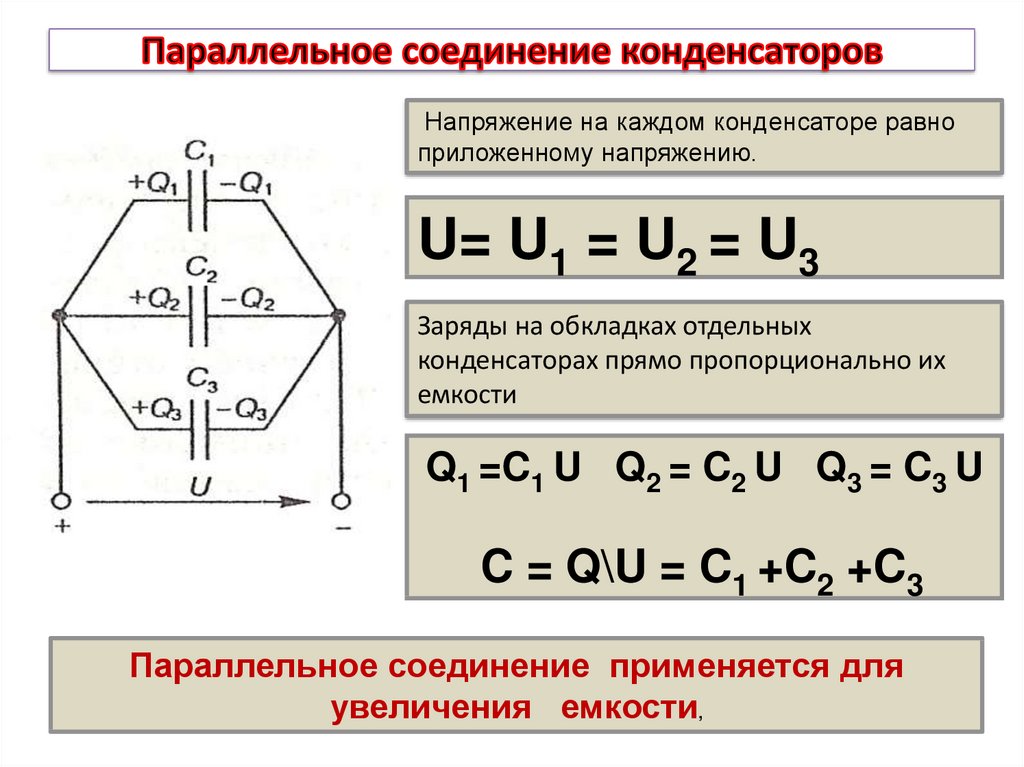 Таким образом, через диэлектрик проходит меньше линий электрического поля, а это означает, что электрическое поле внутри диэлектрика слабее.
Таким образом, через диэлектрик проходит меньше линий электрического поля, а это означает, что электрическое поле внутри диэлектрика слабее.Все электроизоляционные материалы являются диэлектриками, но некоторые из них являются лучшими диэлектриками, чем другие. Хорошим диэлектриком является тот, молекулы которого позволяют своим электронам сильно смещаться в электрическом поле. Другими словами, электрическое поле немного оттягивает их электроны от их атома, но они не убегают полностью от своего атома (именно поэтому они являются изоляторами).
На рис. 18.31 показано макроскопическое изображение диэлектрика в заряженном конденсаторе. Обратите внимание, что линии электрического поля в конденсаторе с диэлектриком разнесены дальше, чем линии электрического поля в конденсаторе без диэлектрика. Это означает, что электрическое поле в диэлектрике слабее, поэтому оно хранит меньше электрической потенциальной энергии, чем электрическое поле в конденсаторе без диэлектрика.

Куда делась эта энергия? На самом деле молекулы в диэлектрике действуют как крошечные пружинки, и энергия электрического поля идет на то, чтобы растянуть эти пружинки. При ослаблении электрического поля разница напряжений между двумя сторонами конденсатора меньше, поэтому становится легче зарядить конденсатор. Таким образом, помещение диэлектрика в конденсатор перед его зарядкой позволяет накопить в конденсаторе больше заряда и потенциальной энергии. Параллельная пластина с диэлектриком имеет емкость
C=κε0Ad=κC0,C=κε0Ad=κC0,
18,43
где κκ ( каппа ) — безразмерная постоянная, называемая диэлектрической проницаемостью . Поскольку κκ больше 1 для диэлектриков, емкость увеличивается, когда диэлектрик помещается между пластинами конденсатора. Диэлектрическая проницаемость некоторых материалов показана в таблице 18.1.
Материал Диэлектрическая проницаемость (κκ) Пылесос 1.  00000
00000Воздух 1.00059 Плавленый кварц 3,78 Неопреновый каучук 6,7 Нейлон 3,4 Бумага 3,7 Полистирол 2,56 Стекло пирекс 5,6 Силиконовое масло 2,5 Титанат стронция 233 Тефлон 2.1 Вода 80 Стол 18.1 Диэлектрические постоянные для различных материалов при 20 °C
Рисунок 18.31 Верхний и нижний конденсаторы несут одинаковый заряд Q. Между пластинами верхнего конденсатора нет диэлектрика. Нижний конденсатор имеет диэлектрик между пластинами. Поскольку некоторые линии электрического поля заканчиваются и начинаются на поляризационных зарядах в диэлектрике, электрическое поле в конденсаторе менее сильное.
 Таким образом, при том же заряде конденсатор запасает меньше энергии, если он содержит диэлектрик.
Таким образом, при том же заряде конденсатор запасает меньше энергии, если он содержит диэлектрик.Поддержка учителей
Поддержка учителей
Подчеркнем, что линии электрического поля в диэлектрике менее плотные, чем в конденсаторе без диэлектрика, что показывает, что электрическое поле в диэлектрике слабее.
Рабочий пример
Конденсатор для вспышки камеры
Типичная вспышка для компактной камеры использует конденсатор емкостью около 200 мкФ 200 мкФ. а) Если разность потенциалов между обкладками конденсатора составляет 100 В, то есть 100 В подается «на конденсатор», сколько энергии хранится в конденсаторе? б) Если бы диэлектриком, используемым в конденсаторе, был лист нейлона толщиной 0,010 мм, какова была бы площадь поверхности пластин конденсатора?
Стратегия ЗА (А)
Учитывая, что V=100VV=100V и C=200×10-6FC=200×10-6F, мы можем использовать уравнение UE=12CV2UE=12CV2, чтобы найти электрическую потенциальную энергию, запасенную в конденсаторе.

Решение для (a)
Подстановка заданных величин в UE=12CV2UE=12CV2 дает −6F)(100 В)2=1,0 Дж.
18,44
Обсуждение для (a)
Этой энергии достаточно, чтобы поднять 1-килограммовый мяч примерно на 1 м над землей. Вспышка длится примерно 0,001 с, поэтому мощность, отдаваемая конденсатором за это короткое время, равна P=UEt=1,0J0,001с=1kWP=UEt=1,0J0,001с=1кВт. Учитывая, что автомобильный двигатель выдает около 100 кВт мощности, для маленького конденсатора это неплохо!
Стратегия ЗА (Б)
Поскольку обкладки конденсатора находятся в контакте с диэлектриком, мы знаем, что расстояние между обкладками конденсатора составляет d=0,010 мм=1,0×10-5md=0,010 мм=1,0×10-5м. Из предыдущей таблицы диэлектрическая проницаемость нейлона составляет κ=3,4 κ=3,4. Теперь мы можем использовать уравнение C=κε0AdC=κε0Ad, чтобы найти площадь A конденсатора.
Решение (b)
Решение уравнения площади A и подстановка известных величин дает
C=κε0AdA=Cdκε0=(200×10−6F)(1,0×10−5м)(3,4)(8,85×10−12F/м)=66м2.
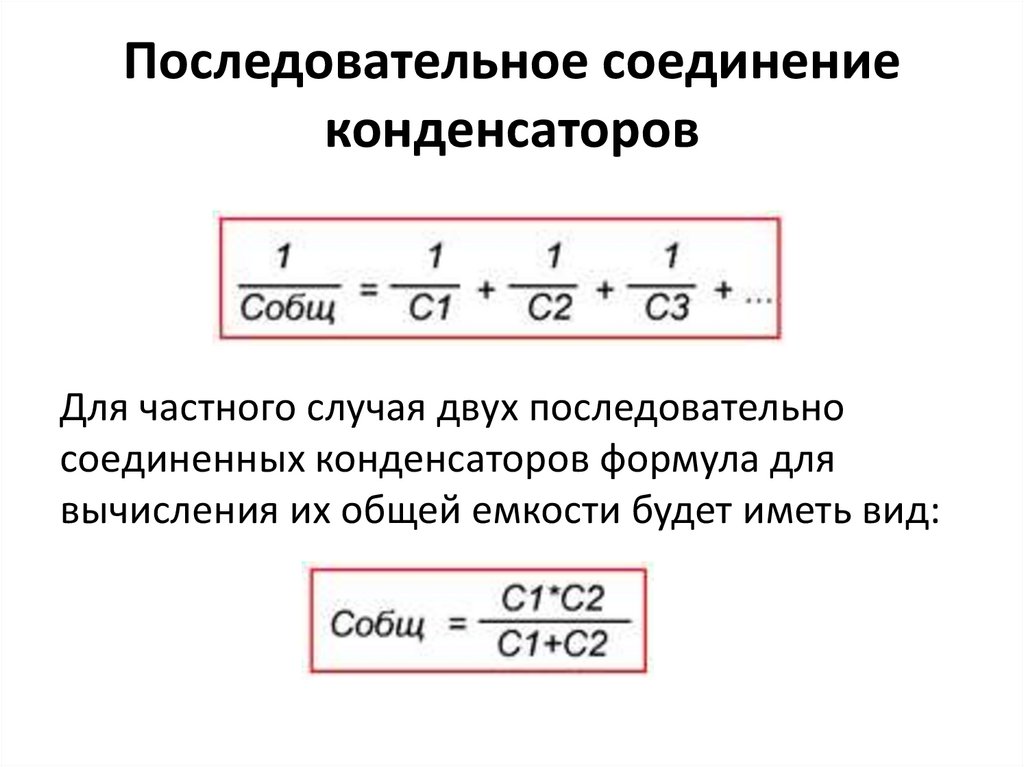 C=κε0AdA=Cdκε0=(200×10−6F )(1,0×10-5м)(3,4)(8,85×10-12 Ф/м)=66м2.
C=κε0AdA=Cdκε0=(200×10−6F )(1,0×10-5м)(3,4)(8,85×10-12 Ф/м)=66м2.18,45
Обсуждение для (b)
Это слишком большая площадь, чтобы свернуть ее в конденсатор, достаточно маленький, чтобы поместиться в переносную камеру. Вот почему в этих конденсаторах используются не простые диэлектрики, а более продвинутая технология для получения высокой емкости.
Практические задачи
25.
При напряжении 12 В на конденсаторе он принимает заряд 10 мКл. Какова его емкость?
- 0,83 мк F
- 83 μ F
- 120 μ F
- 830 μ F
26.
Пластинчатый конденсатор имеет площадь 10 см 2 и расстояние между пластинами 100 мк м . Какова его емкость, если между пластинами конденсатора находится бумага?
- 3,3 × 10 −10 F
- 3,3 × 10 −8 F
- 3,3 × 10 −6 Ф
- 3,3 × 10 −4 F
Проверьте свое понимание
27.

Если площадь плоского конденсатора удвоится, как изменится его емкость?
Емкость останется прежней.
Емкость удвоится.
Емкость увеличится в четыре раза.
Емкость увеличится в восемь раз.
28.
Если удвоить площадь пластинчатого конденсатора и уменьшить расстояние между пластинами в четыре раза, как изменится емкость?
Увеличится в два раза.

Увеличится в четыре раза.
Увеличится в шесть раз.
Увеличится в восемь раз.
Заряд, разделение пластин и напряжение
Дорожка динамики
Наклонная плоскость
ИмпульсКонденсатор
Пластинчатый сеп.
Пластинчатый сеп./вольт
ДиэлектрикиЦепи
Закон Ома
Последовательно/параллельноРесивер Wave
Частота/Длина волны
Двухточечный Интерф.
Оптическая скамья
Преломление
Фокусное расстояниеКонденсатор с параллельными пластинами
Заряд конденсатора, разделение пластин и напряжение
Конденсатор используется для накопления электрического заряда. Чем большее напряжение (электрическое давление) вы прикладываете к конденсатору, тем больше заряда попадает в конденсатор. Кроме того, чем большей емкостью обладает конденсатор, тем больше заряда будет вызвано данным напряжением. Это соотношение описывается формулой q=CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение.
Глядя на эту формулу, можно задаться вопросом, что произошло бы, если бы заряд оставался постоянным, а емкость изменялась. Ответ, конечно же, что напряжение изменится! Это то, что вы будете делать в этой лаборатории.
Лабораторный конденсатор
Конденсатор с плоскими пластинами — это прибор, используемый для изучения конденсаторов.
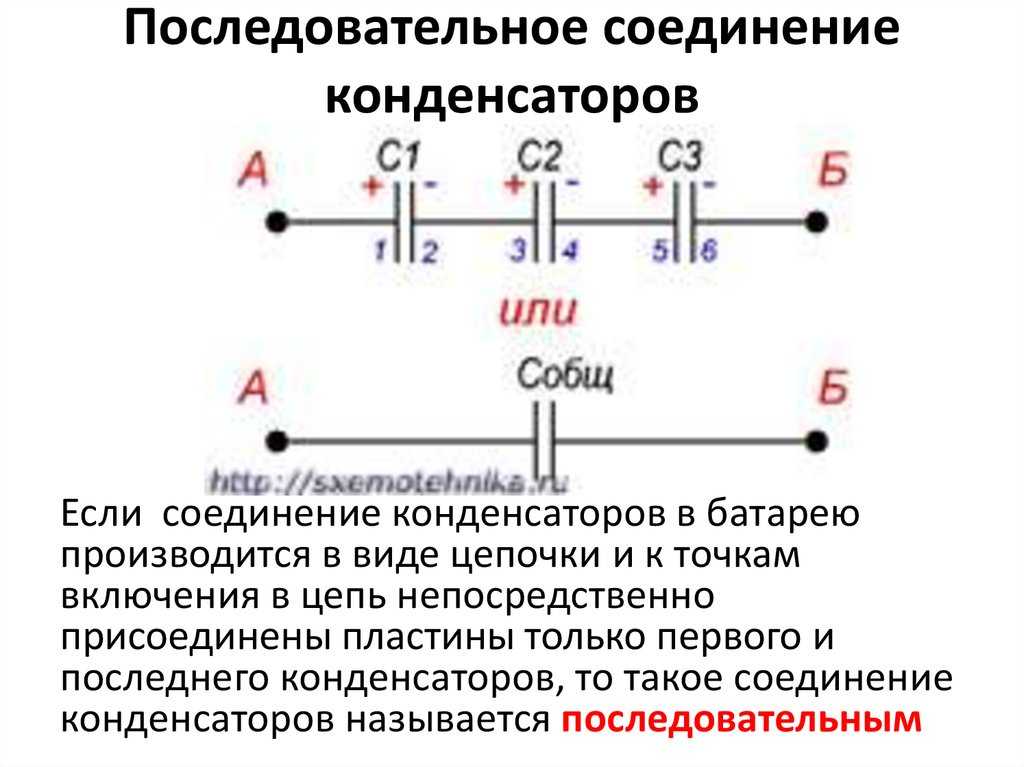 Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно свернуты в спирали в небольших упаковках, поэтому конденсатор с плоскими пластинами значительно упрощает привязку функции к устройству.
Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно свернуты в спирали в небольших упаковках, поэтому конденсатор с плоскими пластинами значительно упрощает привязку функции к устройству.Этот конденсатор работает путем создания противоположных зарядов на параллельных пластинах, когда напряжение подается с одной пластины на другую. Количество заряда, перемещающегося на пластины, зависит от емкости и приложенного напряжения по формуле Q=CV, где Q — заряд в кулонах, C — емкость в фарадах, а V — разность потенциалов между пластинами в вольт.
Конденсаторы для хранения энергии
Если на конденсатор подается напряжение, а затем он отключается, заряд, хранящийся в конденсаторе, сохраняется до тех пор, пока конденсатор не разрядится каким-либо образом. Тогда между пластинами возникает электрическое поле, которое позволяет конденсатору накапливать энергию. Это один из полезных аспектов конденсаторов, способность накапливать энергию в электрическом поле, чтобы ее можно было использовать позже.

От чего зависит емкость?
Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними. Чем больше пластины и чем ближе они расположены друг к другу, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами. Заряд, сохраняемый на приложенный вольт, представляет собой емкость, измеряемую в фарадах.
Может ли изменение емкости заряженного конденсатора изменить его напряжение?
Лабораторный конденсатор можно регулировать, поэтому мы можем провести интересный эксперимент с изменением емкости и напряжения. Если конденсатор имеет постоянный заряд, изменение емкости должно привести к изменению напряжения. Раздвигание пластин уменьшит емкость, поэтому напряжение должно увеличиться.
Как математически определить емкость нашего конденсатора?
Для плоского конденсатора емкость определяется по следующей формуле:С = ε 0A/d
Где C — емкость в фарадах, ε 0 — константа диэлектрической проницаемости свободного пространства (8,85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах.

Фарад — это очень большая величина емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6 Ф, или в пикофарадах (пФ), что составляет 1,0×10 -12 Ф. 1,0Ф = 1 000 000 мкФ = 1 000 000 000 000 пФ! Будьте очень осторожны с расчетами!
Этот расчет даст вам приблизительное значение емкости лабораторного конденсатора. Однако есть и другие факторы, которые вносят ошибки в реальное измерение емкости и напряжения. Вы должны быть осторожны, чтобы принять во внимание эти факторы.
Лабораторное оборудование:
Чтобы получить хорошие результаты, эта лабораторная работа требует специального оборудования. Вам нужен хороший регулируемый источник питания, чтобы напряжение, подаваемое на конденсатор, было одинаковым в каждом испытании.
Вам также нужен очень точный способ измерения напряжения между пластинами без приложения резистивной нагрузки к конденсатору.
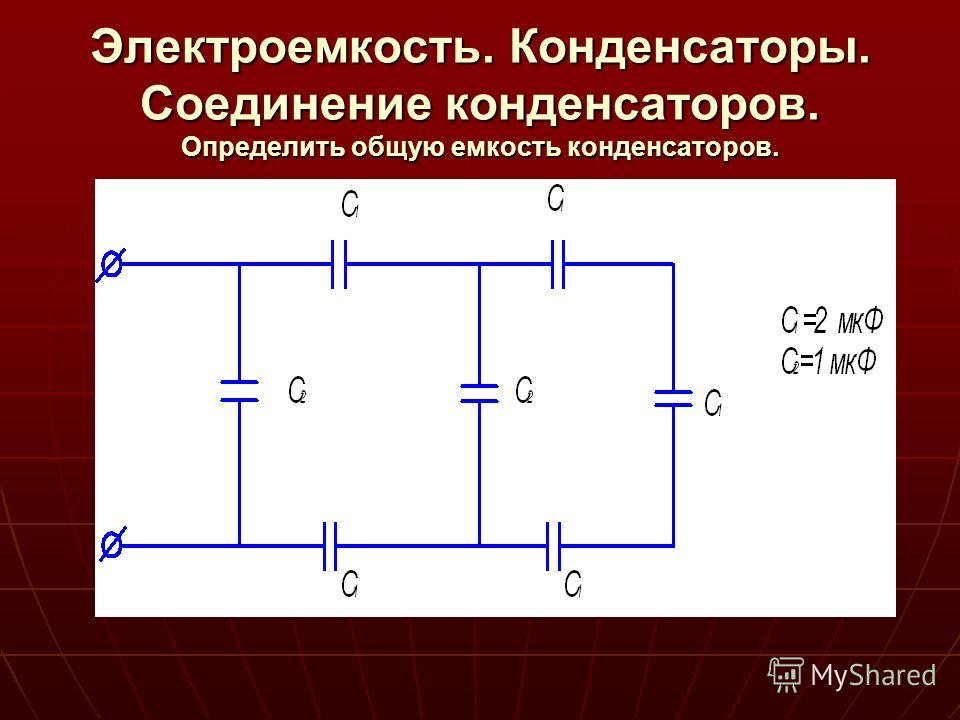 Количество сохраняемого заряда очень мало, поэтому обычный вольтметр не подойдет. Небольшой заряд, накопившийся в конденсаторе, просто разрядился бы через измеритель, сделав любое измерение бесполезным. Вы будете использовать специальное устройство для измерения напряжения, называемое электрометром, которое измеряет напряжение без разрядки конденсатора.
Количество сохраняемого заряда очень мало, поэтому обычный вольтметр не подойдет. Небольшой заряд, накопившийся в конденсаторе, просто разрядился бы через измеритель, сделав любое измерение бесполезным. Вы будете использовать специальное устройство для измерения напряжения, называемое электрометром, которое измеряет напряжение без разрядки конденсатора.Одна проблема с электрометром заключается в том, что он имеет некоторую собственную емкость. Поскольку эта емкость параллельна емкости конденсатора, встроенная емкость выводов должна быть добавлена к емкости конденсатора.
Назначение:
Целью этой лабораторной работы является исследование взаимосвязи между расстоянием между пластинами и напряжением в конденсаторе с параллельными пластинами, поддерживаемом при постоянном заряде.
Оборудование:
- Переменный конденсатор
- Электрометр
- Регулируемый блок питания
- Перемычки
- Провода электрометра
Меры предосторожности:
Это хрупкое оборудование.
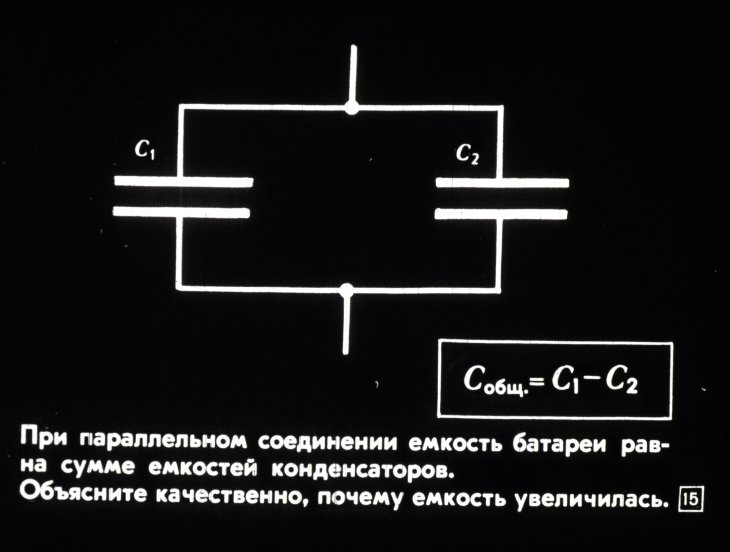 Все должно сочетаться с самыми легкими прикосновениями. Ничего не форсировать!
Все должно сочетаться с самыми легкими прикосновениями. Ничего не форсировать!Ваша первая задача — предсказать, что произойдет с напряжением конденсатора, когда вы зарядите его источником 10 В, а затем раздвинете пластины (что уменьшит емкость). Вы сделаете это в следующем разделе.
Теоретические расчеты:
Сначала необходимо рассчитать теоретическую емкость для каждого расстояния между пластинами. Мы сделаем первое, а потом вы сможете сделать все остальное! Самое сложное в этом — правильно подобрать единицы измерения. Самый простой способ продолжить — перевести все в метры для расчетов:
- Измерьте диаметр пластин конденсатора в сантиметрах. Ваше измерение должно быть около 17,8 см
- Разделите диаметр на 100, чтобы получить значение в метрах. Результат 0,178м. Разделите это на два, чтобы получить радиус: 0,089 м
- Площадь пластины определяется по общей формуле A=πr 2.
 Подставьте числа, чтобы получить A = π(0,089) 2 = 0,0249 м 2
Подставьте числа, чтобы получить A = π(0,089) 2 = 0,0249 м 2 - Преобразуйте расстояние между пластинами (1 мм) в метры, разделив на 1000. 1/1000 = 0,001 м.
- Используйте эти числа в формуле C = ε 0A/d для определения расчетной емкости следующим образом: C = 8,85×10 -12(0,0249)/0,001 = 2,20×10 -10. Это равно 220×10 -12F или 220pF
- Добавьте встроенную емкость электрометра (50 пФ) к теоретической емкости, чтобы получить 270 пФ.
- Запишите этот результат (270 пФ) в столбце «Расчетная емкость» и в строке 1 мм.
- Повторите этот процесс для других расстояний между пластинами. Обратите внимание, что площадь пластины одинакова для всех, поэтому все, что вам нужно сделать, это повторить шаги 5, 6 и 7, вставляя правильные значения интервала в каждом случае.
- Теперь вы рассчитаете теоретическое напряжение для каждого интервала. Мы примем напряжение 10 В для расстояния 1,0 мм, поэтому вы можете просто ввести это значение непосредственно в таблицу.
 Во-первых, вы определяете количество заряда в конденсаторе при этом расстоянии и напряжении. Используйте формулу Q=CV, чтобы определить заряд таким образом: Q=270×10-12F(10V)=2700×10-12C. Этот заряд остается одинаковым при любом расстоянии между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец «Расчетный заряд»! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V=Q/C, таким образом: V=2700×10 -12C/94,0×10-12F=28,7В. Введите это значение в столбец Расчетное напряжение в строке 5 мм.
Во-первых, вы определяете количество заряда в конденсаторе при этом расстоянии и напряжении. Используйте формулу Q=CV, чтобы определить заряд таким образом: Q=270×10-12F(10V)=2700×10-12C. Этот заряд остается одинаковым при любом расстоянии между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец «Расчетный заряд»! Теперь используйте это значение заряда, чтобы определить расчетное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V=Q/C, таким образом: V=2700×10 -12C/94,0×10-12F=28,7В. Введите это значение в столбец Расчетное напряжение в строке 5 мм. - Повторите тот же расчет напряжения для остальных промежутков между пластинами. Используйте расчетную емкость и постоянный заряд для каждого интервала и введите значение напряжения в столбец Расчетное напряжение таблицы.
- Поздравляем! Вы закончили предварительные расчеты! Все, что вам нужно сделать сейчас, это сделать фактические измерения!
В следующих разделах вы проведете реальный эксперимент, чтобы проверить (или, возможно, не подтвердить!) свои теоретические расчеты.

Процедура настройки переменного конденсатора (если лаборатория уже настроена, переходите к следующему разделу!)
- Поместите переменный конденсатор в центр лабораторного стола так, чтобы отметка 0 см находилась слева от вас. Не ставьте конденсатор слишком близко к краю стола!
- Поместите блок питания за переменным конденсатором. Подключите блок питания, но не включайте его.
- Подсоедините красный и черный провода перемычки к красной и черной клеммам источника питания. Просто прикрепите зажим типа «крокодил» к отверстию и оставьте другой конец провода свободным.
- Поместите электрометр слева от конденсатора.
- Прикрепите лепестковые выводы проводов электрометра к клеммам на задней стороне каждой пластины конденсатора. Красный провод идет к правой пластине, черный провод идет к левой пластине.
- Вставьте разъем BNC в электрометр.

- Установите пластины на расстоянии не менее 1 мм. Белые бамперы препятствуют тому, чтобы пластины располагались ближе друг к другу. Если пластины не параллельны друг другу, используйте регулировочные ручки в середине правой опоры, чтобы выровнять пластины. Левый край пластикового язычка, обращенный к шкале, должен быть совмещен с отметкой 1 мм.
Сбор экспериментальных данных
- Убедитесь, что установка оборудования завершена и выполнена правильно.
- Полностью поверните все четыре регулятора на блоке питания против часовой стрелки.
- Поверните крайнюю левую ручку (Fine Current) в положение «12 часов» (прямо вверх!)
- Включите источник питания. Дисплеи должны загореться.
- Используйте ручки Fine и Coarse Voltage (две самые правые ручки), чтобы установить напряжение на 10,0 В.
- Установите пластины на минимум
- Установите электрометр на шкалу 30 В.

- Нажмите кнопку питания на электрометре. Должен загореться светодиод 30 В.
- Нажмите кнопку нуля на электрометре. Это обнуляет счетчик и гарантирует, что пластины находятся при нулевом напряжении относительно друг друга.
- На мгновение прикоснитесь проводами от источника питания к пластинам, черным к левой пластине и красным к правой пластине.
- В этот момент электрометр должен показывать 12 В (12 В – это первая маленькая отметка над «1» на нижней шкале. Если он не проверит настройку, попробуйте еще раз. Иногда приходится несколько раз прикасаться проводами к пластинам. чтобы получить правильное значение 12 В.
- С этого момента вы должны быть осторожны, чтобы не касаться пластин. Если вы дотронетесь до них, вы измените заряд пластин и испортите данные!
- Следите за электрометром, чтобы убедиться, что заряд удерживается. Если вы видите падение более чем на вольт за 30 секунд, остановитесь и выясните, что не так, прежде чем продолжить.

- Переключите электрометр на настройку 100 В. Счетчик должен по-прежнему показывать 12 В, но по шкале 100 В.
- Осторожно раздвиньте пластины на расстояние 5 мм.
- Снимите показания электрометра и запишите их в таблицу в столбце «Измеренное напряжение».
- Повторите предыдущие два шага для других расстояний между пластинами и запишите соответствующие данные.
Разделение пластин
(мм)
Расчетная емкость
(пФ)Расчетный расход
(ПК)
Расчетное напряжение
(В)
Измеренное напряжение
(В)
1
г. 
5
10
15
20
г. 25
30
35
40
г. 
Анализ данных:
- На миллиметровой бумаге отобразите расчетную емкость по оси x (горизонтальной) в зависимости от напряжения по оси y (вертикальной). Нанесите расчетное значение и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различить две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначьте оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»).
- Изучите свой график и ответьте на следующие вопросы:
- Подтверждают ли ваши измеренные данные измеренные значения?
- ↑ Университет Колорадо.

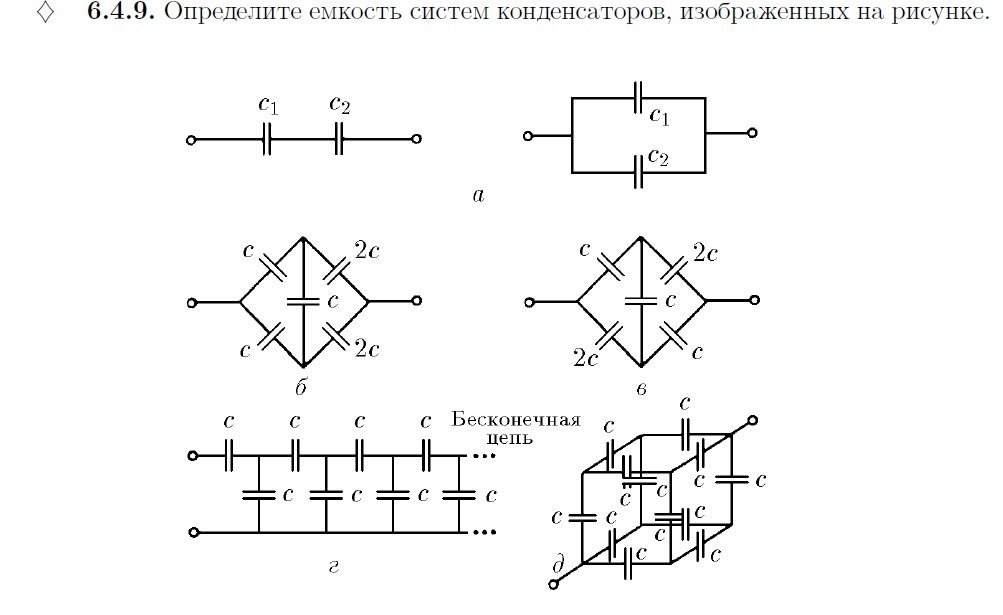
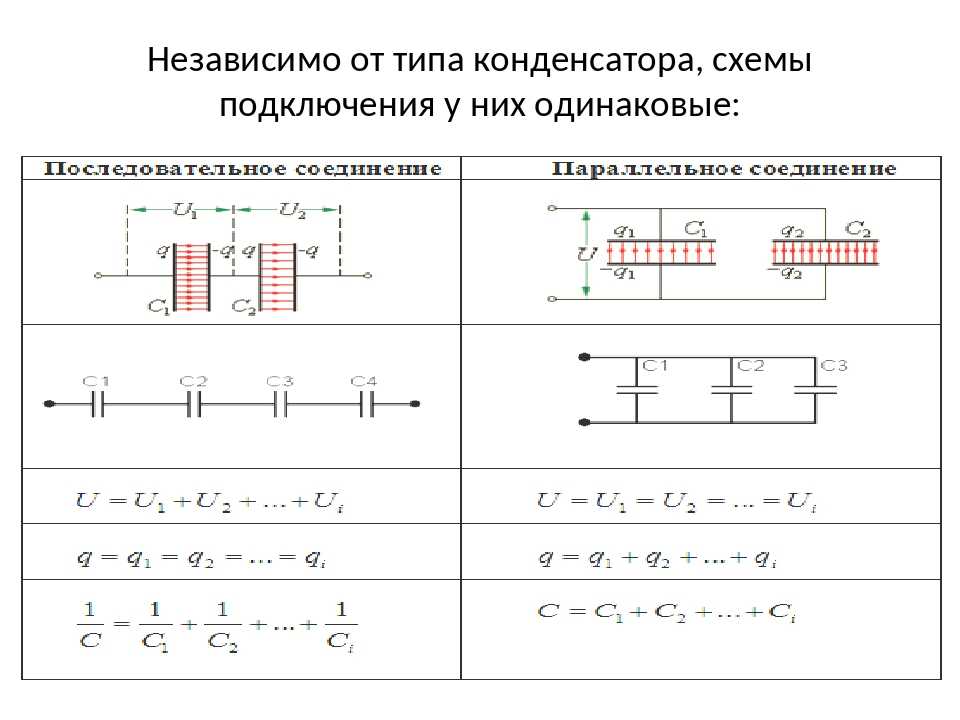 Этот вывод справедлив для проводника любой формы.
Этот вывод справедлив для проводника любой формы.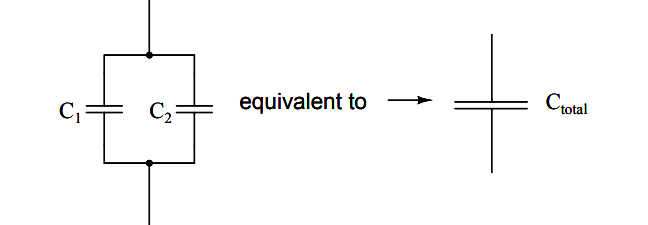

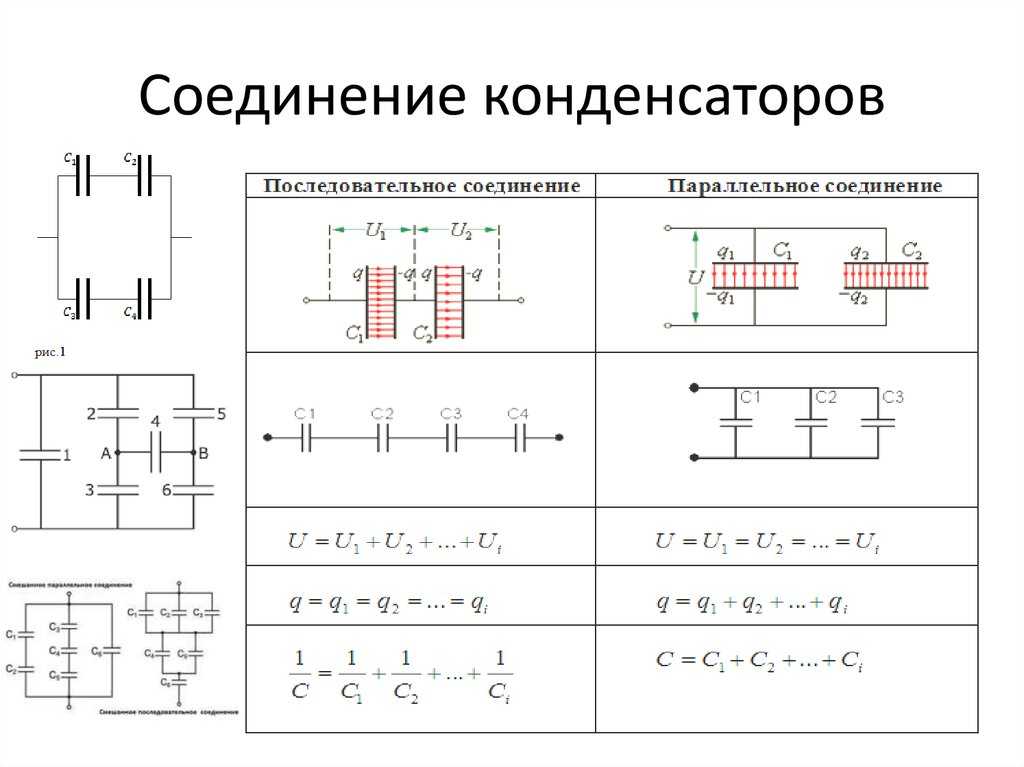 о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.

 Следовательно, с увеличением диэлектрической проницаемости увеличивается емкость.
Следовательно, с увеличением диэлектрической проницаемости увеличивается емкость.