Как проверить т: как проверить слово кажется букву т

Парные согласные в словах — как проверить? Правила и примеры

Научим писать без ошибок и интересно рассказывать

Начать учиться

109.6K

Парные буквы и звуки могут обманывать нас. Бывают случаи, когда в корне слова стоит буква, которая чаще обозначает звонкий звук, но при этом она звучит глухо, и наоборот. Именно такие случаи мы и рассмотрим в этой статье. После нее вы будете разбираться в правописании парных согласных в корне и легко сможете подбирать проверочные слова. Как обычно, в конце вас будут ждать задания для самопроверки.

Что такое парные и непарные согласные

Всего в русском языке существует 36 согласных звуков — они могут быть глухими или звонкими. Например, в слове «кот» буква т звучит глухо — обратите внимание на то, как мало вы вкладываете голоса в этот звук. Теперь возьмем другое слово — «коды». Буква д в конце звучит звонко, в произнесении этого звука участвует голос. В этом и есть отличие между звонкими и глухими звуками.

Звуки [л], [м], [н], [р], [й`] бывают только звонкими, а [ч], [щ], [ц], [х] — только глухими. Остальные образуют между собой пары по глухости-звонкости. Увидеть их все можно в таблице ниже.

Звонкие	[б]	[в]	[г]	[д]	[ж]	[з]
Глухие	[п]	[ф]	[к]	[т]	[ш]	[с]

Запоминаем!

Звуки, у которых есть пара по глухости-звонкости или твердости-мягкости, называются парными. Те, у которых такой пары нет, — непарными.

В этой статье мы разберем правописание парных звонких и глухих согласных. Подробнее о том, как они могут звучать в корне слова, поговорим дальше.

Демоурок по русскому языку

Пройдите тест на вводном занятии и узнайте, какие темы отделяют вас от «пятёрки» по русскому.

Оглушение парных согласных в корне слова

Запоминаем!

Парные по глухости-звонкости согласные б, в, г, д, ж, з в конце слова или перед глухими согласными в середине звучат глухо. Это называется

оглушением.

Чтобы стало понятнее, как это работает, разберемся на примерах:

• пруд — [прут],

• ложка — [лошка],

• лошадь — [лошат`],

• узкий — [уск`ий`].

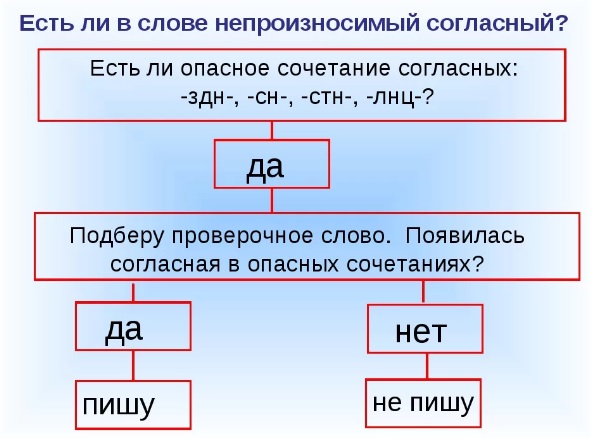
Из этих примеров видно, что мы не всегда можем быть уверены, какая согласная стоит в корне — глухая или звонкая. Это орфограммы, и в таких случаях нужно проверять их написание. Как именно — разберемся чуть позже.

Проверьте себя

Прочтите слова и выберите те из них, которые можно отнести к примерам оглушения парной согласной: нагрузка, вошь, картошка, лаз, салазки, магазин, копоть, приказ, провод.

Озвончение парных согласных звуков в корне слова

Запоминаем!

Парные по глухости-звонкости согласные к, т, п, с, ф, ш звучат звонко, когда стоят перед звонкими звуками. Это называется озвончением.

Примеры:

• просьба — [проз`ба],

• сдаваться — [здавац:а],

• вокзал — [вагзал].

Проверьте себя

Прочтите слова и выберите те из них, которые можно отнести к примерам оглушения парной согласной: футбол, мороз, все, мешок, рюкзак, блузка, тогда, парашют, общий.

2 способа проверить слова с парными согласными в корне

Теперь, когда мы знаем все ловушки парных согласных в корне слова, научимся их обходить на примерах. Для этого поставим звук, который хотим проверить, в сильную позицию. Сделать это помогут 2 способа. Рассмотрим их дальше.

1. Подставляем к слову «нет»

Этот способ хорошо работает в случаях, когда интересующая нас согласная находится в конце существительного. Например:

2. Проверяем с помощью уменьшительно-ласкательного слова

Этот способ эффективен тогда, когда парная согласная стоит в середине или в конце слова:

• ложка — ложечка,

• лодка — лодочка,

• узкий — узенький,

• клюв — клювик.

То есть в обоих случаях мы просто меняем форму слова так, чтобы после парной согласной шла гласная или сонорная согласная, то есть л, м, н, р, й. Это универсальный способ, который помогает проверить согласные в середине или конце любого слова.

Вот еще несколько примеров с разными согласными.

В этих примерах мы видим обратную картину: на письме парная согласная в корне слова глухая, но мы произносим ее звонко. Такие случаи тоже нужно проверять, чтобы не ошибиться.

[б] — [п]:

• гриб — грибы;

• пробка — пробочный;

• лоб — лобный.

[в] — [ф]:

• пристав — приставной;

• устав — уставной;

• любовь — любовный;

• уловка — уловить;

• булавка — булавочный.

[д] — [т]:

• ягодка — ягодный;

• лодка — лодочный;

• площадка — площадочный;

• тетрадка — тетрадный.

[ж] — [ш]:

• нож — ножик;

• ножка — ноженька;

• дорожка — дорожный;

• ложь — ложный.

[з] — [с]:

• повязка — повязать;

• сказка — сказочный;

• указка — указать;

• просьба — просить;

• вязка — вязать.

Запоминаем!

Буквы, написание которых можно проверить через однокоренное слово, называются проверяемыми. Слова с теми, что проверить нельзя, — непроверяемые — это словарные слова, их придется просто запомнить. Например: космонавт, вокзал, анекдот, рикша, зигзаг, вокзал, Евфрат.

Проверьте себя

Давайте проверим, хорошо ли вы усвоили новую тему парных согласных в конце и середине слов. Выполните задания ниже, чтобы отработать навыки, которые вы получили из этой статьи.

Задание №1

Прочтите предложения ниже, расставьте пропущенные буквы в словах и напишите проверочное слово к каждому из них.

1. Садово__ посадил молодые саженцы.

2. Геоло__ открыл новое месторождение руды.

3. Рыболо__ шел довольный уловом.

4. Лесору__ повалил огромное дерево.

5. Сне__ укутал верхушки деревьев.

6. На ветках бере__ появились сережки.

7. Сугро__ закрыл выход из избы.

Задание №2

Прочтите слова ниже и измените их так, чтобы они оканчивались на согласную букву.

Уловы, шефы, львы, брови, глаза, клювы, морозы, арбузы, алмазы, посевы, коллективы, берега, рекорды, серпы, молоты, отряды, заводы, лошади, рукава, луга, сторожа.

Задание №3

Вставьте пропущенные слова так, чтобы предложения обрели смысл. Определите, какие парные согласные пишутся во вставленных словах и подбери к ним проверочные слова.

1. Собака — друг человека, а волк — ___.

2. Железо тяжелое, а пух ___.

3. Река широкая, а ручей ___.

4. Чеснок горький, а яблоко ___.

5. Кисель густой, а суп ___.

6. Дом высокий, а сарай ___.

7. Дождь частый, а гром ___.

Слова, которые нужно использовать: легкий, низкий, враг, редкий, сладкое, узкий, жидкий.

Если вы хотите, чтобы ребенок лучше усвоил правила о парных согласных и другие темы за 2 класс, в этом помогут дополнительные занятия. На курсе русского языка в онлайн-школе Skysmart преподаватели объяснят простыми словами даже самую трудную тему, а интерактивные задания помогут закрепить ее на практике. Начните с вводного занятия — это бесплатно!

Шпаргалки для родителей по русскому

Все формулы по русскому языку под рукой и бесплатно

Алёна Федотова

Автор Skysmart

К предыдущей статье

Непроизносимые согласные в корне слова

К следующей статье

274. 2K

Н и НН в разных частях речи

Получите план развития речи и письма на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

t-критерий Стьюдента для проверки гипотезы о средней и расчета доверительного интервала в Excel

Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).

Распределение Стьюдента

Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ². Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией

Тогда случайная величина

имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.

Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:

где

Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96s_x̅. Другими словами, являются ли распределения случайных величин

и

эквивалентными.

Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.

Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.

Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.

Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:

Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.

Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.

Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.

Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.

Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».

У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина

зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.

Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:

1. средняя X̅ и выборочная дисперсия s² являются независимыми величинами;

2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ²(хи-квадрат) с таким же количеством степеней свободы, т.е.

где k – количество степеней свободы (на английском degrees of freedom (d.f.))

Вернемся к распределению средней. Разделим числитель и знаменатель выражения

на σ_X̅. Получим

Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.

Тогда исходное выражение примет вид

Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.

Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.

Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин

где ξ распределена по стандартному нормальному закону, а χ²_k подчиняется распределению χ² c k степенями свободы.

Таким образом, формула критерия Стьюдента для средней арифметической

есть частный случай стьюдентова отношения

Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.

При k > 30 t-критерий практически не отличается от стандартного нормального распределения.

В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.

Условия применения t-критерия Стьюдента

Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.

Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.

Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.

Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.

Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel

В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.

СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.

СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).

СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.

СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.

СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058

СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.

ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.

Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.

Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.

Краткое условие в обще принятых обозначениях выглядит так.

H₀: μ = 50 кг

H_a: μ ≠ 50 кг

Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.

Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:

Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).

По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.

Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H₀ о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.

Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.

Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.

Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.

Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.

P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.

Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.

Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.

Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.

Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Скачать файл с примером.

Всего доброго, будьте здоровы.

Поделиться в социальных сетях:

Т-тест | Введение в статистику

Что такое тест

t-?

Тест t (также известный как тест t Стьюдента) представляет собой инструмент для оценки средних значений одной или двух совокупностей с использованием проверки гипотез. Стьюдентный тест можно использовать для оценки того, отличается ли отдельная группа от известного значения (одновыборочный t-критерий), отличаются ли две группы друг от друга (независимый двухвыборочный t-критерий) или существует ли значительная разница в парных измерениях (парный или зависимый t-критерий выборки).

Как используются тесты

t ?

Сначала вы определяете гипотезу, которую собираетесь проверить, и указываете допустимый риск ошибочного вывода. Например, при сравнении двух совокупностей вы можете предположить, что их средние значения одинаковы, и принять решение о приемлемой вероятности вывода о существовании различия, когда это не так. Затем вы вычисляете тестовую статистику на основе своих данных и сравниваете ее с теоретическим значением из распределения t-. В зависимости от результата вы либо отвергаете, либо не можете отвергнуть свою нулевую гипотезу.

Что делать, если у меня более двух групп?

Вы не можете использовать тест t . Используйте метод множественного сравнения. Примерами являются дисперсионный анализ (ANOVA ) , попарное сравнение Тьюки-Крамера, сравнение Даннета с контролем и анализ средних значений (ANOM).

t -тестовые допущения

В то время как t -тесты относительно устойчивы к отклонениям от предположений, t -тесты действительно предполагают, что:

• Данные непрерывны.
• Данные выборки были взяты случайным образом из населения.
• Имеется однородность дисперсии (т. е. вариабельность данных в каждой группе аналогична).
• Распределение примерно нормальное.

Для двухвыборочных t -испытаний у нас должны быть независимые выборки. Если выборки не являются независимыми, то может быть уместным парный тест t .

Типы

т -тесты

Есть три т -тесты для сравнения означают: одновыборочный t -тест, двухвыборочный t -тест и парный t -тест. В таблице ниже приведены характеристики каждого из них и приведены рекомендации по выбору правильного теста. Посетите отдельные страницы для каждого типа теста t , чтобы увидеть примеры, а также подробную информацию о предположениях и расчетах.

	Однопробный t- тест	Двухвыборочный t- тест	Парные T — Тест
Синонимы	Студент T -Тест	Независимые группы T -Test Независимые выборки . STARIST 9004.STARINES 9004.STARINES 9004SERSE 9004.STARINES 9004SENTERSE 9004.STARISTARSE 9004.STARINES 9004.STERSE 9004.STERSE 9004.STERSE 9004. Объединенные t -тест Неравные дисперсии t -тест	Парные группы t- 30009 0 зависимые образцы0004 -test
Number of variables	One	Two	Two
Type of variable	Continuous measurement	Continuous measurement Categorical or Nominal to define groups	Непрерывное измерение Категориальный или Номинальный для определения спаривания внутри группы
Цель теста	Решите, равно ли среднее значение генеральной совокупности определенному значению или нет	Определите, равны ли средние значения генеральной совокупности для двух разных групп	Определите, равна ли разница между парными измерениями для генеральной совокупности нулю или нет
Пример: проверить, если. ..	Средняя частота сердечных сокращений группы людей равна 65 или нет	Средняя частота сердечных сокращений для двух групп людей одинакова или различна	группа людей до и после тренировки равна нулю или нет
Оценка среднего значения совокупности	Среднее значение выборки	Среднее значение выборки для каждой группы	Среднее значение выборки различий в парных измерениях стандартные отклонения для каждой группы	Неизвестно, используйте выборочное стандартное отклонение различий в парных измерениях
Степени свободы	Количество наблюдений в выборке минус 1, или: n–1	Сумма наблюдений в каждой выборке минус 2, или: n 1 + n 2 – 2	Количество парных наблюдений в выборке минус 1, или: n–1

В приведенной выше таблице показаны только t -тесты для средних значений населения. Другой распространенный тест t предназначен для коэффициентов корреляции. Вы используете этот тест t , чтобы решить, значительно ли коэффициент корреляции отличается от нуля.

Сравнение односторонних и двусторонних тестов

Когда вы определяете гипотезу, вы также определяете, какой у вас критерий: односторонний или двусторонний. Вы должны принять это решение перед сбором данных или выполнением каких-либо расчетов. Вы принимаете это решение для всех трех из t -тестов на средства.

Чтобы объяснить, давайте воспользуемся одновыборочным t -критерием. Предположим, у нас есть случайная выборка протеиновых батончиков, и на этикетке батончиков указано, что в каждом батончике содержится 20 граммов белка. Нулевая гипотеза состоит в том, что неизвестное среднее значение совокупности равно 20. Предположим, мы просто хотим знать, показывают ли данные, что у нас другое среднее значение совокупности. В этой ситуации наши гипотезы таковы:

$ \mathrm H_o: \mu = 20 $

$ \mathrm H_a: \mu \neq 20 $

Здесь у нас есть двусторонний тест. Мы будем использовать данные, чтобы увидеть, достаточно ли среднее значение выборки отличается от 20 — выше или ниже — чтобы сделать вывод, что неизвестное среднее значение генеральной совокупности отличается от 20.

Вместо этого предположим, что мы хотим узнать, верна ли реклама на этикетке. . Подтверждают ли данные идею о том, что неизвестная популяция означает не менее 20 человек? Или нет? В этой ситуации наши гипотезы таковы:

$ \mathrm H_o: \mu >= 20 $

$ \mathrm H_a: \mu < 20 $

Здесь у нас есть односторонний тест. Мы будем использовать данные, чтобы увидеть, достаточно ли среднее значение выборки меньше 20, чтобы отвергнуть гипотезу о том, что неизвестное среднее значение генеральной совокупности равно 20 или выше.

См. раздел «хвосты для тестов гипотез» на странице распространения t , где представлены изображения, иллюстрирующие концепции односторонних и двусторонних тестов.

Как выполнить

t -тест

Для всех тестов t , включающих средние значения, вы выполняете одни и те же шаги анализа:

1. Определите свою нулевую ($ \mathrm H_o $) и альтернативную ($ \mathrm H_a $) гипотезы перед сбором данных.
2. Определите значение альфа (или значение α). Это включает в себя определение риска, на который вы готовы пойти, сделав неверный вывод. Например, предположим, что вы установили α=0,05 при сравнении двух независимых групп. Здесь вы выбрали 5%-й риск сделать вывод, что неизвестные средние значения населения различны, когда это не так.
3. Проверьте данные на наличие ошибок.
4. Проверьте предположения для теста.
5. Проведите тест и сделайте вывод. Все t -тесты на средства включают вычисление тестовой статистики. Вы сравниваете тестовую статистику с теоретическим значением из распределения t-. Теоретическое значение включает в себя как значение α, так и степени свободы для ваших данных. Для получения более подробной информации посетите страницы для однообразного t -теста, двухобразного t -теста и парного т — тест.

Что такое несколько формул и когда их использовать

Что такое Т-тест?

Стьюдент-критерий — это выводная статистика, используемая для определения того, существует ли значительная разница между средними значениями двух групп и тем, как они связаны. T-тесты используются, когда наборы данных следуют нормальному распределению и имеют неизвестные отклонения, например, набор данных, записанный при 100-кратном подбрасывании монеты.

Стьюдентный тест – это тест, используемый для проверки гипотез в статистике. Он использует t-статистику, значения t-распределения и степени свободы для определения статистической значимости.

Ключевые выводы

• Стьюдент-критерий — это статистический вывод, используемый для определения наличия статистически значимой разницы между средними значениями двух переменных.
• Стьюдентный критерий — это критерий, используемый для проверки гипотез в статистике.
• Для расчета t-критерия требуются три основных значения данных, включая разницу между средними значениями из каждого набора данных, стандартное отклонение каждой группы и количество значений данных.
• Т-тесты могут быть зависимыми или независимыми.

Т-тест

Понимание Т-теста

Стьюдентный тест сравнивает средние значения двух наборов данных и определяет, получены ли они из одной и той же совокупности. В приведенных выше примерах выборка учащихся из класса A и выборка учащихся из класса B, скорее всего, не будут иметь одинаковое среднее значение и стандартное отклонение. Точно так же образцы, взятые из контрольной группы, получавшей плацебо, и образцы, взятые из группы, которой прописали лекарство, должны иметь несколько разные среднее значение и стандартное отклонение.

Математически t-критерий берет выборку из каждого из двух наборов и устанавливает постановку задачи. Он предполагает нулевую гипотезу о том, что два средних равны.

С помощью формул рассчитываются значения и сравниваются со стандартными значениями. Предполагаемая нулевая гипотеза соответственно принимается или отвергается. Если нулевая гипотеза может быть отвергнута, это указывает на то, что показания данных сильны и, вероятно, не случайны.

Стьюдент-тест — это лишь один из многих тестов, используемых для этой цели. Статистики используют дополнительные тесты, кроме t-критерия, для изучения большего количества переменных и больших размеров выборки. Для выборки большого размера статистики используют z-критерий. Другие варианты тестирования включают тест хи-квадрат и f-тест.

Использование Т-теста

Предположим, что производитель лекарств тестирует новое лекарство. Следуя стандартной процедуре, препарат дается одной группе пациентов, а плацебо — другой группе, называемой контрольной группой. Плацебо — это вещество, не имеющее терапевтической ценности, и служит эталоном для измерения того, как реагирует другая группа, получающая реальное лекарство.

После испытания препарата члены контрольной группы, получавшей плацебо, сообщили об увеличении средней продолжительности жизни на три года, в то время как члены группы, которым прописали новый препарат, сообщили об увеличении средней продолжительности жизни на четыре года.

Начальное наблюдение указывает на то, что препарат работает. Однако также возможно, что наблюдение может быть обусловлено случайностью. Стьюдентный тест можно использовать, чтобы определить, являются ли результаты правильными и применимыми ко всей популяции.

При использовании t-теста делаются четыре предположения. Собранные данные должны соответствовать непрерывной или порядковой шкале, такой как баллы для теста IQ, данные собираются из случайно выбранной части всего населения, данные будут иметь нормальное распределение в виде колоколообразной кривой, и равная или гомогенная дисперсия существует, когда стандартные вариации равны.

Формула Т-теста

Для расчета t-критерия требуются три значения фундаментальных данных. Они включают разницу между средними значениями из каждого набора данных или среднюю разницу, стандартное отклонение каждой группы и количество значений данных в каждой группе.

Это сравнение помогает определить влияние случайности на разницу, а также определить, находится ли разница за пределами этого диапазона вероятности. Стьюдентный тест ставит вопрос о том, представляет ли разница между группами истинную разницу в исследовании или просто случайную разницу.

На выходе t-критерий выдает два значения: t-значение и степени свободы. Значение t или t-оценка представляет собой отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок.

Значение числителя представляет собой разницу между средним значением двух наборов выборок. Знаменатель представляет собой вариацию, существующую в наборах выборок, и является мерой дисперсии или изменчивости.

Это рассчитанное t-значение затем сравнивается со значением, полученным из таблицы критических значений, называемой таблицей T-распределения. Более высокие значения t-показателя указывают на большую разницу между двумя наборами выборок. Чем меньше t-значение, тем больше сходства существует между двумя наборами выборок.

T-Score

Большой t-показатель или t-значение указывает на то, что группы различаются, а маленький t-показатель указывает на то, что группы похожи.

Степени свободы относятся к значениям в исследовании, которые могут варьироваться и необходимы для оценки важности и достоверности нулевой гипотезы. Вычисление этих значений обычно зависит от количества записей данных, доступных в выборке.

Т-тест для парных образцов

Коррелированный t-критерий, или парный t-критерий, является зависимым типом теста и выполняется, когда выборки состоят из согласованных пар одинаковых единиц или когда есть случаи повторных измерений. Например, могут быть случаи, когда одни и те же пациенты повторно тестируются до и после получения конкретного лечения. Каждый пациент используется в качестве контрольного образца против себя.

Этот метод также применим к случаям, когда образцы связаны или имеют совпадающие характеристики, например, сравнительный анализ с участием детей, родителей или братьев и сестер.

Формула для вычисления t-значения и степеней свободы для парного t-теста:

Т «=» иметь в виду 1 − иметь в виду 2 с ( разница ) ( н ) где: иметь в виду 1 и иметь в виду 2 «=» Средние значения каждого из выборочных наборов с ( разница ) «=» Стандартное отклонение разностей парных значений данных н «=» Размер выборки (количество парных различий) н − 1 «=» Степени свободы \begin{align}&T=\frac{\textit{mean}1 — \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\& \textbf{где:}\\&\textit{mean}1\text{ и }\textit{mean}2=\text{Средние значения каждого из выборочных наборов}\\&s(\text{diff}) =\text{Стандартное отклонение разностей парных значений данных}\\&n=\text{Размер выборки (количество парных разностей)}\\&n-1=\text{Степени свободы}\end {выровнено} ​T=(n)​s(diff)​mean1−mean2​где:mean1 и mean2=средние значения каждого набора выборокss(diff)=стандартное отклонение разностей парных значений данныхn=размер выборки (количество парных различий)n−1=степени свободы​

Равная дисперсия или объединенный T-критерий

Стьюдентный критерий равной дисперсии является независимым t-тестом и используется, когда количество выборок в каждой группе одинаково или дисперсия двух наборов данных аналогична. 2 }{ n1 + n2 — 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{ Средние значения каждого} \\&\text{выборочных наборов}\\&var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов}\\&n1 \text{ и } n2 = \text{ Количество записей в каждом наборе образцов} \end{aligned} T-значение=n1+n2−2(n1−1)×var12+(n2−1)×var22×n11+n21среднее1−среднее2, где:среднее1 и среднее2=средние значения каждого из выборочных наборовvar1 и var2 = дисперсия каждого набора образцов n1 и n2 = количество записей в каждом наборе образцов​

и,

Степени свободы «=» н 1 + н 2 − 2 где: н 1 и н 2 «=» Количество записей в каждом наборе образцов \begin{align} &\text{Степени свободы} = n1 + n2 — 2 \\ &\textbf{где:}\\ &n1 \text{ и } n2 = \text{Количество записей в каждом наборе образцов} \ \ \ конец {выровнено} ​Степени свободы=n1+n2−2, где: n1 и n2=количество записей в каждом наборе образцов​

Т-тест с неравной дисперсией

Стьюдентный критерий неравной дисперсии является независимым t-тестом и используется, когда количество выборок в каждой группе различно, и дисперсия двух наборов данных также различна. Этот тест также называют t-критерием Уэлча.

Формула, используемая для расчета t-значения и степеней свободы для t-критерия неравной дисперсии:

Т-значение «=» м е а н 1 − м е а н 2 ( в а р 1 н 1 + в а р 2 н 2 ) где: м е а н 1 и м е а н 2 «=» Средние значения каждого наборов образцов в а р 1 и в а р 2 «=» Дисперсия каждого из наборов образцов н 1 и н 2 «=» Количество записей в каждом наборе образцов \begin{align}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)} }}\\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{Средние значения каждого} \\&\text{набора образцов} \\&var1 \text{ и } var2 = \text{Дисперсия каждого набора образцов} \\&n1 \text{ и } n2 = \text{Количество записей в каждом наборе образцов} \end{выравнивание} ​T-значение=(n1var1​+n2var2​)​mean1-mean2​где:mean1 и mean2=Средние значения каждого из выборочных наборов var1 и var2=дисперсия каждого из выборочных наборов n1 и n2=количество записей в каждом выборочном наборе​ 92 }{ n2 — 1}} \\ &\textbf{где:}\\ &var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов} \\ &n1 \text{ и } n2 = \text {Количество записей в каждом наборе образцов} \\ \end{aligned} ​Степени свободы=n1−1(n1var12​)2​+n2−1(n2var22​)2​(n1var12​+n2var22​)2​, где: var1 и var2 = дисперсия каждого набора выборки n1 и n2 = число записей в каждом наборе образцов​

Какой Т-тест использовать?

Следующая блок-схема может быть использована для определения того, какой t-критерий использовать, исходя из характеристик наборов выборок. Ключевые элементы, которые следует учитывать, включают сходство записей выборки, количество записей данных в каждой выборке и дисперсию каждой выборки.

Изображение Джули Банг © Investopedia 2019

Пример T-критерия неравной дисперсии

Предположим, что берется диагональный размер картин, полученных в художественной галерее. В одну группу образцов входит 10 картин, в другую – 20 картин. Наборы данных с соответствующими средними значениями и значениями дисперсии следующие:

	Набор 1	Набор 2
	19,7	28,3
	20,4	26,7
	19,6	20,1
	17,8	23,3
	18,5	25,2
	18,9	22,1
	18,3	17,7
	18,9	27,6
	19,5	20,6
	21,95	13,7
		23,2
		17,5
		20,6
		18
		23,9
		21,6
		24,3
		20,4
		23,9
		13,3
Среднее	19,4	21,6
Разница	1,4	17,1

Хотя среднее значение набора 2 выше, чем у набора 1, мы не можем заключить, что совокупность, соответствующая набору 2, имеет более высокое среднее значение, чем население, соответствующее набору 1.

Является ли разница между 19,4 и 21,6 исключительно случайной, или существуют различия в общей совокупности всех картин, полученных в художественной галерее? Мы устанавливаем проблему, принимая нулевую гипотезу о том, что среднее значение одинаково для двух наборов выборок, и проводим t-тест, чтобы проверить, правдоподобна ли гипотеза.

Поскольку количество записей данных различно (n1 = 10 и n2 = 20) и дисперсия также различна, значение t и степени свободы вычисляются для вышеуказанного набора данных с использованием формулы, упомянутой в Т-критерии неравной дисперсии. раздел.

Значение t равно -2,24787. Поскольку знак минус можно игнорировать при сравнении двух t-значений, вычисленное значение равно 2,24787.

Значение степени свободы равно 24,38 и уменьшено до 24 из-за определения формулы, требующей округления значения до наименьшего возможного целого числа.

Можно указать уровень вероятности (альфа-уровень, уровень значимости, p ) в качестве критерия приемлемости. В большинстве случаев можно принять значение 5%.

Используя значение степени свободы, равное 24, и уровень значимости 5%, просмотр таблицы распределения t-значения дает значение 2,064. Сравнение этого значения с вычисленным значением 2,247 показывает, что рассчитанное значение t больше табличного значения при уровне значимости 5%. Следовательно, можно с уверенностью отвергнуть нулевую гипотезу об отсутствии разницы между средними значениями. Набор населения имеет внутренние различия, и они не случайны.

Как используется таблица Т-распределения?

Таблица Т-распределения доступна в одностороннем и двустороннем форматах. Первый используется для оценки случаев, которые имеют фиксированное значение или диапазон с четким направлением, положительным или отрицательным. Например, какова вероятность того, что выходное значение останется ниже -3 или будет больше семи при броске пары игральных костей? Последний используется для анализа с привязкой к диапазону, например, чтобы узнать, находятся ли координаты в диапазоне от -2 до +2.