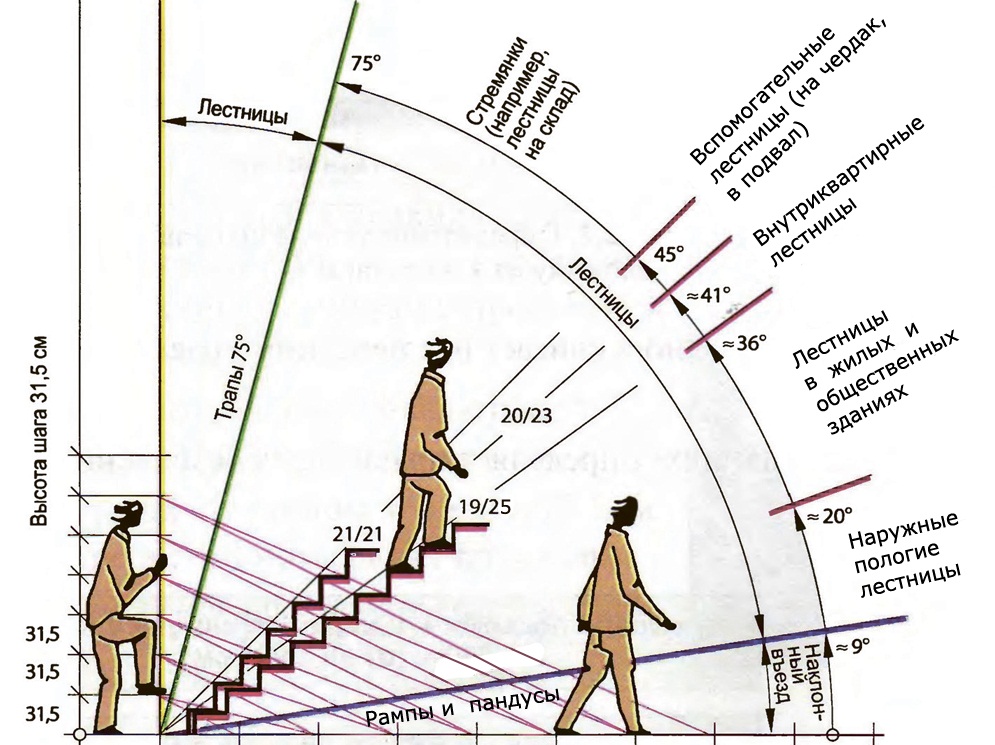
- Оптимальный угол наклона кровли: как определить и рассчитать
- Учимся правильно определять угол наклона крыши
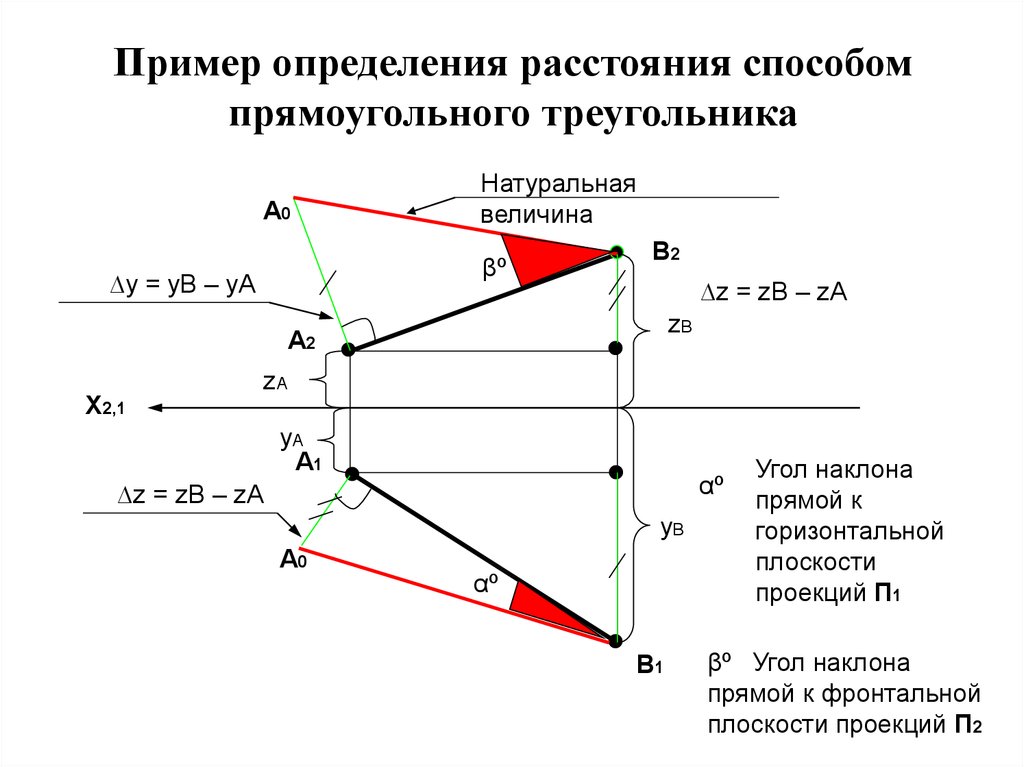
- Угол наклона и наклон линии
- 4.3 Наклон линии | Аналитическая геометрия
Оптимальный угол наклона кровли: как определить и рассчитать
Содержание
Возведение крыши — завершающий этап строительства дома. Этот этап не менее важен, чем закладка фундамента и несущих стен, ведь кровля призвана выполнять сразу несколько функций: защищать здание от осадков, ветра и холода, предотвращать теплопотери, делать экстерьер эстетически привлекательным и завешенным. Из-за особенностей климата в нашей стране принято строить дома со скатными крышами, главной характеристикой которых является угол кровли.
От того, насколько правильно рассчитана величина уклона кровли, будет зависеть не только внешний вид дома, но и прочность и долговечность крыши. Нередки случаи, когда люди, сделавшие крышу «на глаз», были вынуждены среди зимы переделывать все перекрытие, так как оно просело под весом снега или было сорвано сильным ветром. Ниже в статье подробно рассказано, на какие факторы нужно ориентироваться, определяя оптимальный угол уклона будущей крыши, а также показано, как с точностью до 1 градуса рассчитать эту величину.
Типы крыш в зависимости от угла наклона
Все крыши жилых и нежилых помещений делятся на две общие категории: плоские и скатные. В странах с умеренным и континентальным климатом плоские кровли делают только для многоэтажек, а частные дома покрывают крышей с тем или иным углом уклона. И в зависимости от величины наклона, все скатные кровли делятся на три группы:
- С пологим скатом — угол составляет от 10 до 30°;
- Со скатом средней величины — градусы крыши находятся в пределах 30-45°;
- С высоким скатом — угол между коньком и скатом находится в диапазоне 45-60°.
Если скат крыши расположен под углом менее 10°, она также будет считаться плоской. Величину наклона кровельного перекрытия определяют и рассчитывают заранее, при разработке проекта стропильной системы. Помимо угла уклона, на этом этапе также определяется тип крыши в зависимости от количества скатов. Исходя из этой характеристики, кровля может быть:
- Односкатная — самая простая в реализации крыша, представляющая собой одну плоскость, лежащую на стенах разной высоты;
- Двускатная — кровля с двумя равными или разными по величине и углу наклона скатами;
- Шатровая — красивое и экономичное перекрытие, состоящее из нескольких треугольных плоскостей, замыкающихся вершинами в одной точке;
- Вальмовая — крыша с 4 скатами трапециевидной и треугольной формы;
- Многощипцовая — кровля с неограниченным количеством скатов, которые располагаются под разными углами и составляют красивую сложную архитектурную форму.
Углы наклона разных скатов одной крыши могут существенно отличаться. Главное, учитывать при составлении проекта стропильной системы особенности эксплуатации кровельных материалов и следить, чтобы фактическая величина ни одного уклона не получилась меньше установленного ГОСТ минимума.
Факторы, влияющие на величину угла наклона кровли
При разработке проекта стропильной системы нужно учитывать целый ряд факторов, главными из которых являются экономичность, особенности климата, тип кровельного перекрытия и планируемая эксплуатация чердака. Исходя из этих факторов, можно будет определить оптимальный угол уклона и рассчитать точное количество материалов, которые понадобятся на строительство крыши.
Экономичность
Для большинства людей, мечтающих о собственном частном доме, финансовый вопрос выходит на первый план. Выбирая тип крыши, они в первую очередь обращают внимание на то, сколько материалов понадобится для возведения той или иной конструкции и насколько сложным и длительным (а значит — и дорогостоящим) будет строительство крыши.
Относительно расхода бруса и кровельных материалов, а также сложности сооружения, самыми экономичными и быстро возводимыми являются плоские крыши. Но ни в средней полосе России, ни на юге и тем более, на севере страны, такой тип кровли не рекомендуется сооружать из-за неподходящих погодных условий.
Крыши с одним и двумя скатами, имеющими пологий и средний угол уклона, также являются достаточно экономичными и простыми в сооружении. Они способны выдерживать ветровые нагрузки, а снег и дождевая вода быстро стекают из перекрытия такой формы, не успевая создать высокую нагрузку на кровлю и стать причиной проседания и протечек.
Сооружение сложных архитектурных форм с 3-4 и более скатами в большинстве случаев требует не больше, а порою — и меньше кровельных материалов, чем классические 2-скатные крыши. Но рассчитать углы наклона такой кровли, продумать расположение всех скатов относительно друг друга и создать проект стропильной системы под силу только опытному архитектору.
Погодные условия
В большинстве регионов России, а также в соседних странах традиционно строят дома с 2-скатным перекрытием со средним углом наклона.
А вот в некоторых южных районах России можно увидеть дома, подобные традиционным жилищам жителей теплых и сухих стран Азии. Эти домики отличаются плоским перекрытием или крышей с очень малым углом уклона. Причина такой огромной разницы между архитектурными традициями кроется вовсе не в разнице вкусов северных и южных народов, а в том, как климатические условия влияют на эксплуатацию кровель зданий. Самыми важными погодными условиями, определяющими угол наклона кровли, являются:
- Сила ветра. Крыши с крутыми уклонами имеют высокую парусность, из-за чего они беззащитны перед сильными ветровыми нагрузками. Сильные порывы ветра могут повредить и даже полностью сорвать кровлю с углом более 45°.
- Количество дождей. Чем больше дождей выпадает в регионе, тем больше должно быть градусов крыши, ведь из кровель с крутыми скатами вода быстро стекает, не задерживаясь и не протекая под перекрытие.
- Снеговая нагрузка. В северных широтах, где выпадает много снега зимой, строят домики с крутыми крышами, чтобы снег сползал вниз, а на накапливался на перекрытии. В противном случае кровельные материалы и стропила могут не выдержать большой постоянной нагрузки и рухнуть.
Кратко подытожив особенности влияния погодных факторов на прочность и долговечность кровли, можно сделать вывод, что в областях, где часто дуют ветра, нужно сооружать плоские или пологие перекрытия, а там, где много снега — кровли с большой высотой конька и крутыми уклонами. Но во многих регионах России осенью и весной стоит ветреная погода, а зимой выпадает много снега, поэтому нужны компромиссные варианты. Опытные отечественные архитекторы дают такие рекомендации по определению угла уклона крыши исходя из погодных условий в регионе:
- в южных районах, где снега практически нет, а климат сухой и ветреный, оптимальным будет угол уклона скатов 10-15°;
- если в регионе зимы снежные, а ветра дуют редко, лучше всего возводить крыши с углом от 30 до 45°;
- в областях со средним уровнем осадков и сильными ветрами оптимальной величиной угла между высотой конька и скатом будет 15-25°.
В регионах, где из года в год дуют сильные ветра одного направления (восточные или северные), отличным вариантом обустройства кровельного перекрытия здания будет крыша с 2 и более скатами с разными углами наклона. Скат с ветреной стороны должен быть более пологим, а с безветренной — более крутым. Благодаря такому решению, кровля будет максимально устойчивой к ветровой нагрузке. На ней также не будут скапливаться грязь и снег, так как с более высокого склона они попросту сразу же осыпятся вниз, а с более пологого их сдует ветром.
Кровельные материалы
Разные кровельные покрытия отличаются разной надежностью и степенью устойчивости к погодным условиям, статическим и динамическим нагрузкам. По этой причине минимальный уклон кровли невозможно определить прежде, чем будет выбран материал для покрытия крыши.
Минимальный угол уклона напрямую зависит от прочности, твердости, веса и способа фиксации покрытия и строго прописан в ГОСТ для каждого кровельного материала.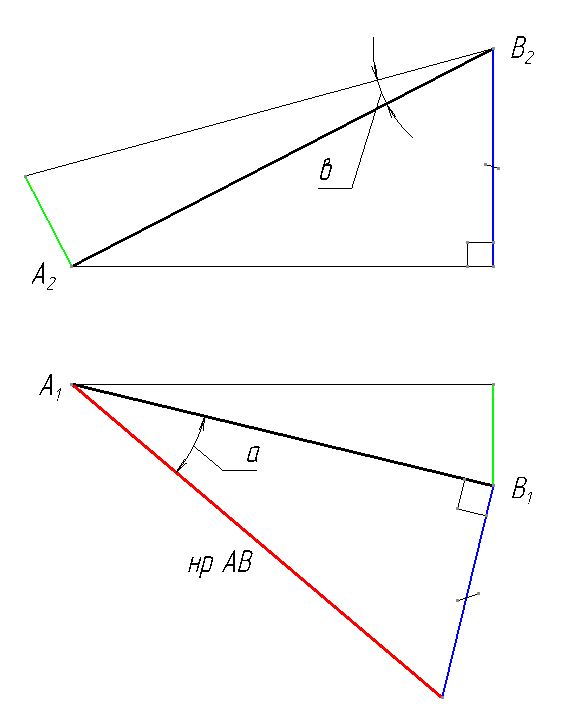 Точные минимальные величины для самых распространенных в нашей стране материалов можно узнать из приведенной ниже таблицы.
Точные минимальные величины для самых распространенных в нашей стране материалов можно узнать из приведенной ниже таблицы.
Вид кровли | Минимальный угол уклона |
2 слоя рулонных битумных материалов | 0-10° |
3-4 слоя рулонных битумных материалов | 0-15° |
Фальцевое покрытие | 4-8° |
Ондулин | 5-6° |
Шифер | 15-20° |
Черепица из битума | 11-20° |
Черепица из керамики | 11-20° |
Металлочерепица | |
Черепица из цементно-песчаного раствора | 34° |
Профнастил | 12° |
Дерево | 39° |
Игнорировать приведенные в таблице минимальные и максимальные величины нельзя, так как в противном случае кровля вряд ли прослужит долго.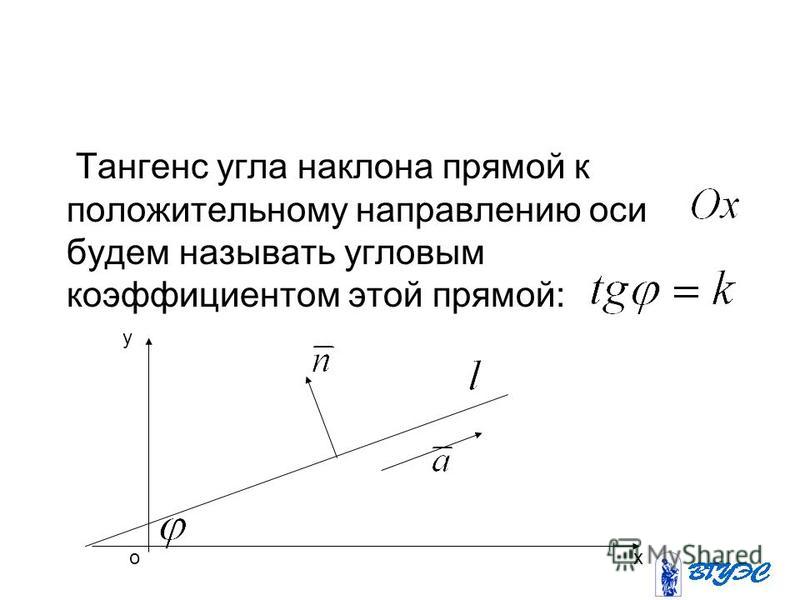 К примеру, рулонные материалы нельзя использовать на на кровле с уклоном более 15 градусов, так как они неизбежно будут сползать. Черепица, наоборот, не может использоваться как покрытие для плоских кровель и скатов с малым уклоном, так как под нее проникнет влага. А популярный в нашей стране шифер не подойдет для крутых крыш, ведь в противном случае его листы сорвет даже не очень сильный ветер.
К примеру, рулонные материалы нельзя использовать на на кровле с уклоном более 15 градусов, так как они неизбежно будут сползать. Черепица, наоборот, не может использоваться как покрытие для плоских кровель и скатов с малым уклоном, так как под нее проникнет влага. А популярный в нашей стране шифер не подойдет для крутых крыш, ведь в противном случае его листы сорвет даже не очень сильный ветер.
Обустройство мансардного этажа
Дома с мансардным этажом с разной шириной намного более экономичные, чем двухэтажные сооружения. Но если планируется обустройство на чердаке мансарды, важно подобрать и оптимальный угол наклона кровли, и кровельное покрытие. Уклон в этом случае не должен быть ни слишком крутым, ни пологим, так как в первом случае возникнут сложности с оформлением интерьера и эксплуатацией помещения, а во втором — нахождение на мансарде будет не комфортным из-за низкой крыши.
По расчетам архитектором, специализирующихся на проектировании частных домиков с мансардным этажом, оптимальный уклон кровли в них 25-30 градусов. Такая величина угла даст возможность обустроить на чердаке полноценную жилую комнату, в которой будет комфортно человеку любого роста. В отдельных случаях, если площадь дома (и мансарды) большая, допускается немного меньший наклон — от 20 до 25°. При расчете оптимального угла уклона важно не забыть учесть толщину будущей внутренней теплоизоляции кровли.
Такая величина угла даст возможность обустроить на чердаке полноценную жилую комнату, в которой будет комфортно человеку любого роста. В отдельных случаях, если площадь дома (и мансарды) большая, допускается немного меньший наклон — от 20 до 25°. При расчете оптимального угла уклона важно не забыть учесть толщину будущей внутренней теплоизоляции кровли.
Минимальный и оптимальный угол ската
В ГОСТах, технической документации и учебниках по проектированию жилых помещений указаны минимальные углы наклона для разных типов кровельных покрытий. Но следует понимать, что минимальные значения в большинстве случаев не являются оптимальными. А вот для определения оптимального угла наклона кровли нужно не только посмотреть табличку с нормами ГОСТ, но и учесть следующие параметры:
- ветровые нагрузки на крышу;
- количество атмосферных осадков;
- планы касательно эксплуатации чердачного помещения;
- климат в регионе.
Так как при возведении здания планируется, что оно будет служить долгие годы, важно ориентироваться на максимальные значения нагрузок, которые могут влиять на перекрытия. К примеру, даже если в регионе сильные ветра дуют редко, нельзя упускать их из внимания и сооружать крышу со скатами круче 30-35°.
К примеру, даже если в регионе сильные ветра дуют редко, нельзя упускать их из внимания и сооружать крышу со скатами круче 30-35°.
В областях с большим количеством осадков архитекторы не рекомендуют строить дома с плоским или пологим перекрытием, так как оно попросту не справится с отводом стоков. Оптимальным углом уклона крыши в таких регионах будет 20-25 градусов. Если же дизайн дома предполагает пологую, а не угловую кровлю, нужно уделить особое внимание ее гидроизоляции и обустройству системы отвода стоков.
От угла уклона перекрытия также зависит способность крыши удерживать тепло. В домах из плоскими крышами теплопотери выше, чем в помещениях с кровлей с средним уклоном скатов. Поэтому нет смысла стелить плоскую крышу в целях экономии кровельных материалов — ее теплоизоляция в будущем обойдется в разы дороже.
Формула для вычисления угла наклона крыши
Чтобы рассчитать значение угла наклона кровли, достаточно использовать простую математическую формулу и знать две величины: высоту конька и длину заложения.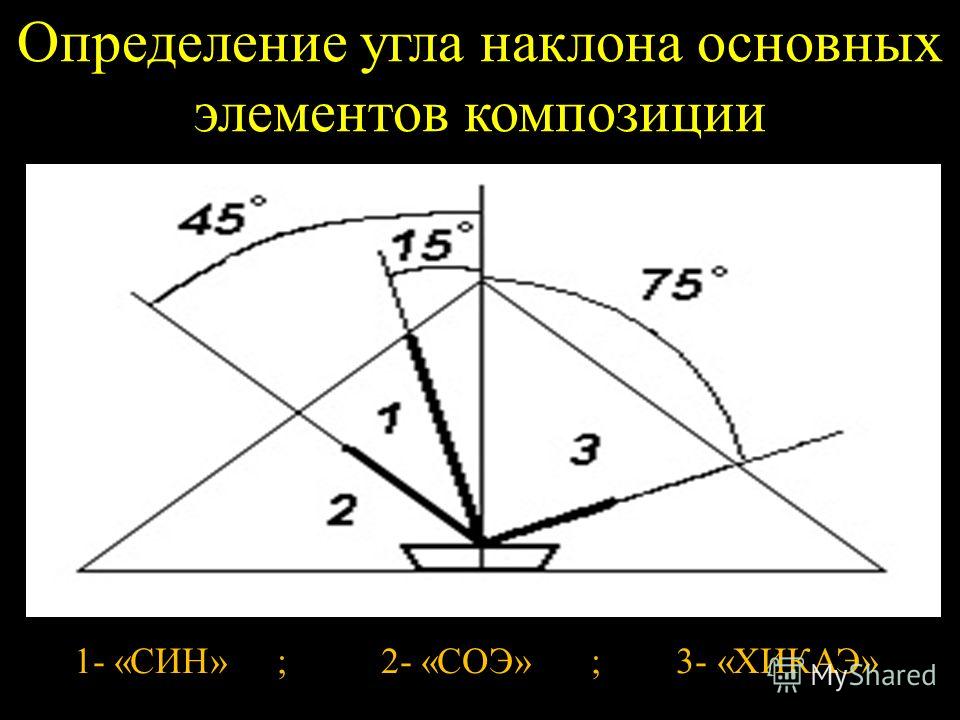 Высота конька — это расстояние от верхней точки ската до нижней, а заложение — расстояние между нижней точной ската и стеной. Сама формула выглядит следующим образом:
Высота конька — это расстояние от верхней точки ската до нижней, а заложение — расстояние между нижней точной ската и стеной. Сама формула выглядит следующим образом:
Угол = Высота конька : Длина заложения * 100%.
К примеру, если высота кровли равна 2 метра, а длина заложения — 4 метра, угол будет: 2:4*100% = 50%. По формуле получена требуемая величина в процентах. Для того, чтобы определить, сколько градусов в процентах, нужно лишь посмотреть данные в следующей таблице.
Исходя из данных в таблице, уклон угла в случае высоты крыши 2 метра и заложения 4 метра равняется 50% или 26.5 градусов.
Если по проекту будущей крыши планируется сооружение стропильной системы таким образом, что конек будет не строго посередине, углы наклонных скатов будут разными, и их нужно рассчитывать отдельно. Полученные значение необходимо учесть при выборе тех или иных кровельных материалов, ведь допускать, чтобы хотя бы один угол оказался меньше минимального по ГОСТ, не рекомендуется.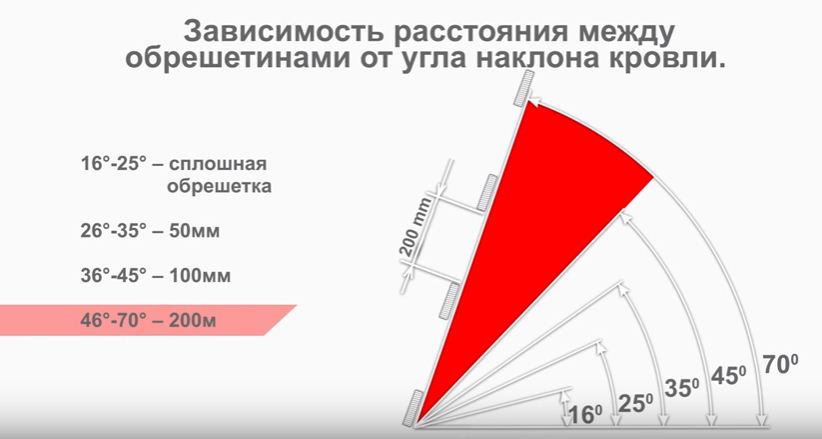
Перед тем, как закреплять стропила, важно перемерять получившиеся углы специальным прибором — уклономером или электронными геодезическими уровнями. Это не займет много времени, но будет полезным — позволит удостовериться, что размеры соответствуют предварительным расчетам, и крыша будет надежной и долговечной.
Учимся правильно определять угол наклона крыши
Угол наклона крыши зависит от многих показателей, но самый главный из них – это конструкция кровельного покрытия и его материал. Так, у плоских крыш угол наклона небольшой, а вот кровли, выполненные с использованием стропильных конструкций, – это отдельная тема. Здесь особенно важно правильно вычислить требуемый угол наклона, поскольку от этого зависит степень удаления осадков с кровли. Обычно данный показатель выражается в градусах, процентах или соотношении катетов. В нашей статье мы научимся определять требуемый угол наклона крыши.
Градусная мера наклона крыши показывает нам угол, образующийся кровлей по отношению к горизонту.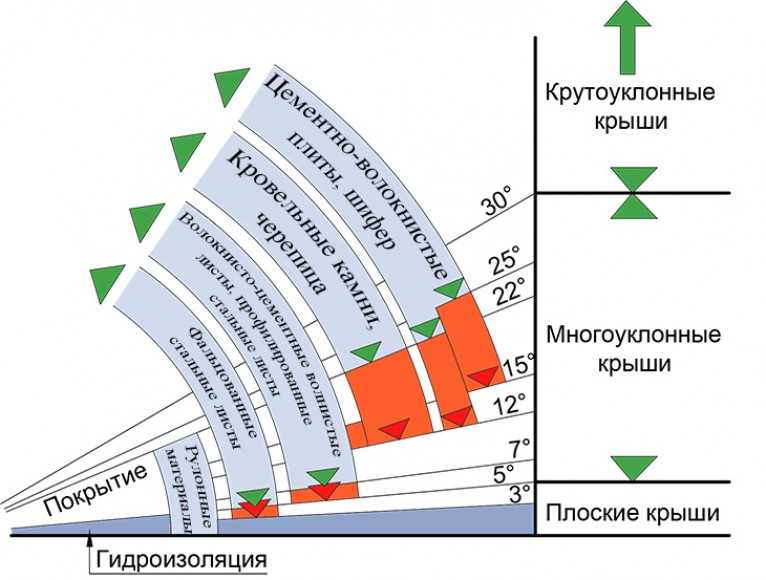 Крыши с большим углом наклона называются крутыми, с маленьким – пологими.
Крыши с большим углом наклона называются крутыми, с маленьким – пологими.
Определение угла наклона в разных величинах измерения
Как вы уже поняли, для определения угла наклона крыши, нужно точно знать, какое кровельное покрытие будет использоваться.
Как правило, в качестве покрытия скатных крыш могут использоваться следующие материалы:
- шифер;
- гибкие рулонные кровельные материалы
- металлочерепица;
- рубероид;
- натуральная черепица;
- профнастил и др.
Если представить прямоугольный треугольник, то можно понять, что его гипотенуза будет в любом случае больше катетов, поэтому оптимальным углом наклона той или иной крыши будем считать наименьший допустимый показатель. Как же определить угол наклона крыши? Прежде всего, этот показатель зависит от плотности кровельного покрытия и герметичности всей конструкции кровли в целом. Это связано с тем, что крыши с большим углом наклона имеют большую парусность, поэтому требуется хорошая герметичность.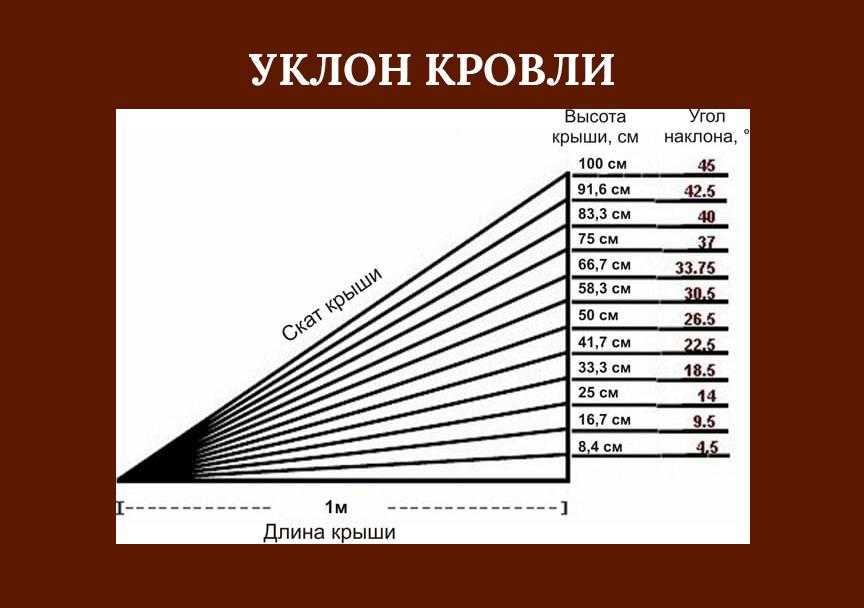 А на крышах с небольшим углом скатов будут задерживаться осадки, тем самым создавая повышенные нагрузки на покрытие.
А на крышах с небольшим углом скатов будут задерживаться осадки, тем самым создавая повышенные нагрузки на покрытие.
На представленной ниже таблице вы видите график, помогающий определить угол наклона крыши в процентах и соотношении катетов. Также можно связать данные показатели с градусным определением меры угла. Чтобы понять, как пользоваться графиком взгляните на угол наклона в 50%. При этом видно, что высота конька (Н) укладывается два раза в катет в основании треугольника (L/2), отсюда получается соотношение 1:2.
Самым удобным способом исчисления угла наклона кровли является безразмерный показатель (соотношение катетов). Например, показатель угла ската в виде соотношения 1/3 говорит о том, что для определения высоты конька нужно найти среднюю точку пролёта и отложить вверх третью часть его длины.
Тип кровельного покрытия и угол наклона кровли
Чтобы вы имели представление о верхних и нижних допустимых пределах угла наклона крыши с использованием того или иного кровельного покрытия, мы разработали специальную таблицу.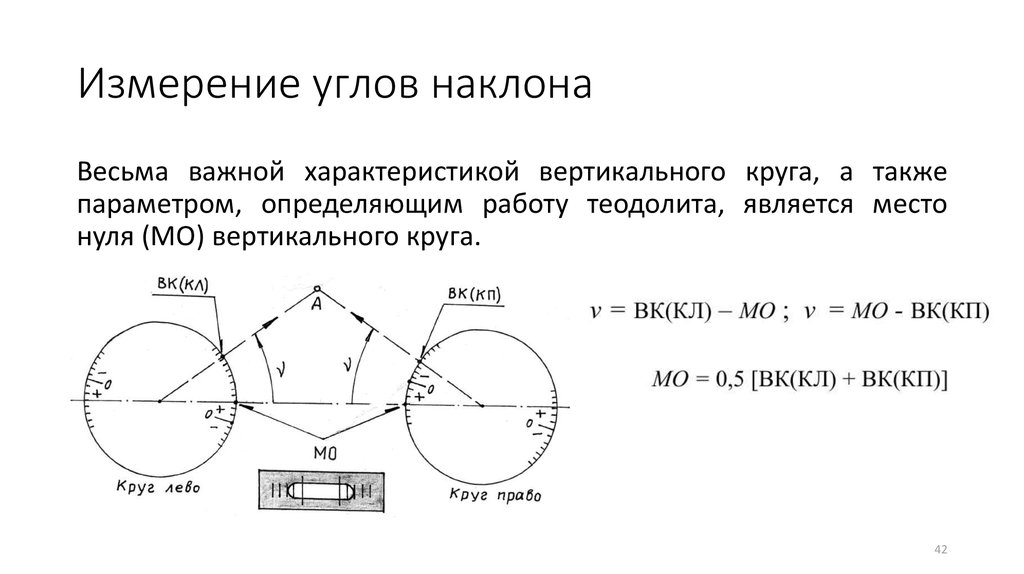 Изучение различных нормативных документов, а также наблюдения в ходе строительных работ позволили нам сделать выводы об условиях использования различных кровельных материалов.
Изучение различных нормативных документов, а также наблюдения в ходе строительных работ позволили нам сделать выводы об условиях использования различных кровельных материалов.
Однако стоит помнить, что строительный рынок стремительно наполняется новыми материалами, а эксплуатационные качества уже существующих кровельных покрытий могут улучшаться в ходе развития современных технологий. Поэтому с течением времени прочность некоторых материалов может увеличиваться, как следствие угол наклона крыши может меняться.
Нижний предел угла наклона крыши
| Вид кровельного покрытия | Вес 1 м.кв,кг | Безразмерный уклон крыши | Процентная мера уклона | Величина уклона в градусах |
| Шифер (среднего профиля/усиленного профиля) | 11/13 | 1:10 / 1:5 | 10% / 20% | 6° / 11,5° |
| Целлюлозно-битумные листы | 6 | 1:10 | 10% | 6° |
| Профнастил (однофальцевый) | 3-6,5 | 1:4 | 25% | 14° |
| Мягкая рулонная кровля | 9-15 | 1:10 | 10% | 6° |
| Профнастил (двухфальцевый) | 3-6,5 | 1:5 | 20% | 11,5° |
| Металлочерепица | 5 | 1:5 | 20% | 11,5° |
| Керамическая черепица | 50-60 | 1:5 | 20% | 11,5° |
| Цементная черепица | 45-70 | 1:5 | 20% | 11,5° |
Что же касается максимального угла наклона крыши, то для таких лёгких кровельных материалов, как целлюлозно-битумные покрытия, мягкая кровля, металлочерепица и профнастил, он может быть даже больше чем 1:1.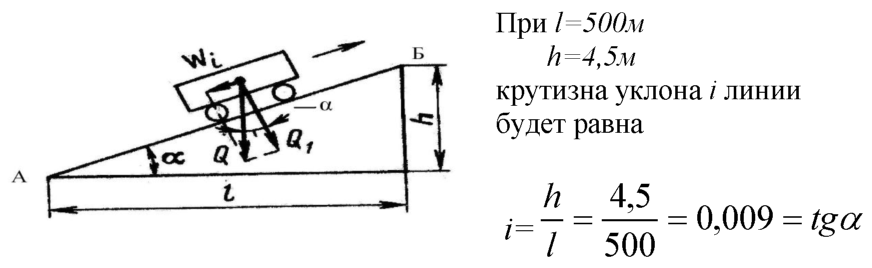 Максимальный уклон всех остальных кровельных покрытий вы можете посмотреть в ниже предложенной таблице.
Максимальный уклон всех остальных кровельных покрытий вы можете посмотреть в ниже предложенной таблице.
Верхний предел угла наклона крыши
| Вид кровельного покрытия | Вес 1 м.кв,кг | Безразмерный уклон крыши | Процентная мера уклона | Величина уклона в градусах |
| Шифер (среднего профиля/усиленного профиля) | 11/13 | 1:2 / 1:1 | 50% / 100% | 27° / 45° |
| Керамическая черепица | 50-60 | 1:0,5 | 200% | 64° |
| Цементная черепица | 45-70 | 1:0,5 | 200% | 11,5° |
Чтобы вы могли легко и быстро перевести градусную меру угла в процентное соотношение, можете воспользоваться предложенной таблицей.
| Градус | Процент |
| 1 | 1,8 |
| 2 | 3,4 |
| 3 | 5,2 |
| 4 | 7,0 |
| 5 | 8,8 |
| 6 | 10,5 |
| 7 | 12,3 |
| 8 | 14,1 |
| 9 | 15,8 |
| 10 | 17,6 |
| 11 | 19,4 |
| 12 | 21,2 |
| 13 | 23,0 |
| 14 | 24,9 |
| 15 | 26,8 |
| 16 | 28,7 |
| 17 | 30,5 |
| 18 | 32,5 |
| 19 | 34,4 |
| 20 | 36,4 |
| 21 | 38,4 |
| 22 | 40,4 |
| 23 | 42,4 |
| 24 | 44,5 |
| 25 | 46,6 |
| 26 | 48,7 |
| 27 | 50,9 |
| 28 | 53,1 |
| 29 | 55,4 |
| 30 | 57,7 |
| 31 | 60,0 |
| 32 | 62,4 |
| 33 | 64,9 |
| 34 | 67,4 |
| 35 | 70,0 |
| 36 | 72,6 |
| 37 | 75,4 |
| 38 | 78,9 |
| 39 | 80,9 |
| 40 | 83,9 |
| 41 | 86,0 |
| 42 | 90,0 |
| 43 | 93,0 |
| 44 | 96,5 |
| 45 | 100,0 |
Определение высоты конька
Зная угол наклона крыши, вы легко сможете высчитать высоту стояния конька. Для облегчения данного вычисления вы можете воспользоваться предложенной ниже таблицей, где каждому углу кровли в градусах соответствует определённая относительная величина, которая и поможет высчитать высоту конькового бруса. Для этого нужно ½ длины пролёта крыши умножить на показатель из крайней правой колонки таблицы.
Для облегчения данного вычисления вы можете воспользоваться предложенной ниже таблицей, где каждому углу кровли в градусах соответствует определённая относительная величина, которая и поможет высчитать высоту конькового бруса. Для этого нужно ½ длины пролёта крыши умножить на показатель из крайней правой колонки таблицы.
| Угол наклона кровли, град | Относительная величина |
| 5 | 0,8 |
| 10 | 0,17 |
| 15 | 0,26 |
| 20 | 0,36 |
| 25 | 0,47 |
| 30 | 0,59 |
| 35 | 0,79 |
| 40 | 0,86 |
| 45 | 1,0 |
| 50 | 1,22 |
| 55 | 1,45 |
| 60 | 1,78 |
Например, длина пролёта в вашем здании составляет 16 метров, а проектируемый угол наклона ската равен 30 градусам.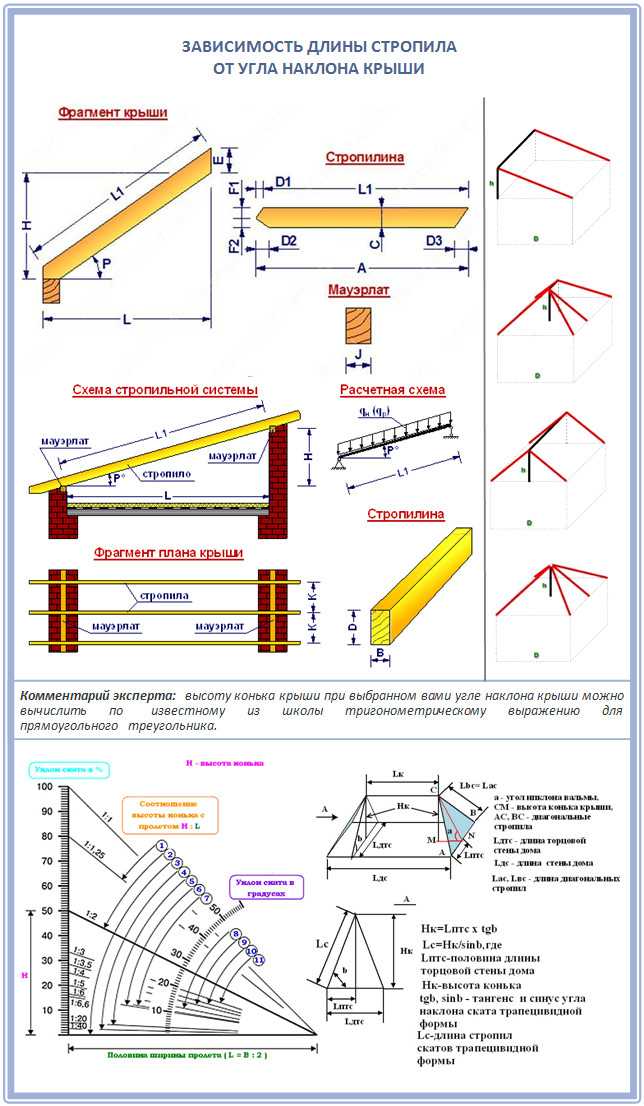 Находим высоту конька следующим образом: 16:2х0,59=4,72. В данном случае число 0,59 взято из таблицы из учёта, что угол наклона кровли составляет 30 градусов.
Находим высоту конька следующим образом: 16:2х0,59=4,72. В данном случае число 0,59 взято из таблицы из учёта, что угол наклона кровли составляет 30 градусов.
Теперь вы знаете, как правильно находить угол наклона крыши, от каких показателей зависит эта величина. Надеемся, что наши таблицы помогут вам без труда ориентироваться в значениях уклона ската кровли.
Угол наклона и наклон линии
Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный в направлении против часовой стрелки, называется углом наклона прямая л.
На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.
(i) 0° ≤ θ ≤ 180°
(ii) Для горизонтальных линий θ = 0° или 180° и для вертикальных линий θ = 90°
(iii) Если прямая линия первоначально лежит вдоль оси x и начинает вращаться вокруг неподвижной точки A на оси x против часовой стрелки и, наконец, совпадает с осью x, то угол наклона прямой линии в начальном положении равно 0°, а линии в конечном положении равно 0°.
(iv) Линии, перпендикулярные оси x, называются вертикальными линиями.
(v) Линии, перпендикулярные оси Y, называются горизонтальными линиями.
(vi) Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.
Угол наклона и наклон линии – приложение
Основное применение угла наклона прямой линии – определение уклона.
Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».
Следовательно, наклон прямой равен
м = tan θ
для 0° ≤ θ ≤ 180°
Найдем наклон прямой по приведенной выше формуле
(i) Для горизонтальных линий угол наклона равен 0° или 180°.
То есть
θ = 0° или 180°
Следовательно, наклон прямой линии равен
м = tan0° или tan 180° = 0
(ii) Для вертикальных линий угол наклона равен 90°.
То есть
θ = 90°
Следовательно, наклон прямой равен
м = tan90° = Не определено
(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.
Если же θ тупой, то наклон отрицательный.
Наклон линии — положительный или отрицательный, нулевой или неопределенный
Когда мы смотрим на прямую линию визуально, мы можем легко узнать знак наклона.
Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.
Это иллюстрируют приведенные ниже рисунки.
Решенные задачи
Задача 1 :
Найдите угол наклона прямой, наклон которой равен 1/√3.
Решение:
Пусть θ — угол наклона линии.
Тогда, наклон линии составляет
M = TANθ
Дано: наклон = 1/√3
Затем,
1/√3 = tanθ
θ = 30 °
Таким наклон 30°.
Задача 2 :
Если угол наклона прямой равен 45°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Тогда, наклон линии,
M = TANθ
Дано: θ = 45 °
Затем,
M = TAN 45 °
M = 1
Итак, склон — 1.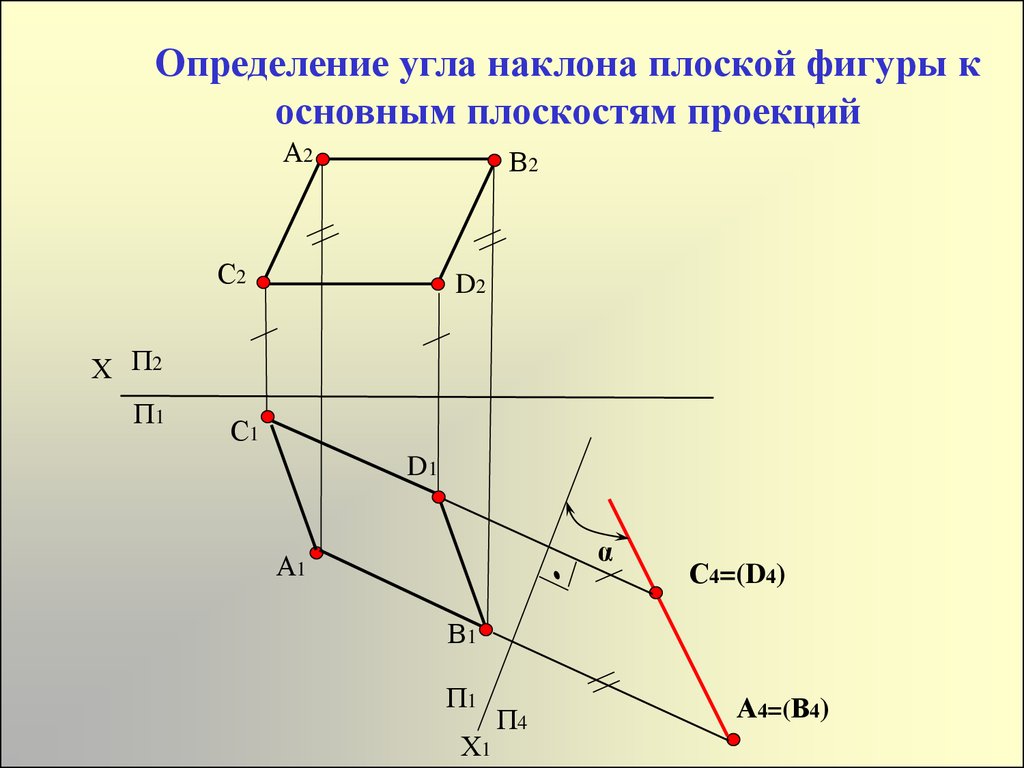
Задача 3 :
Если угол наклона прямой равен 30°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: θ = 30°
Тогда
м = tan30°
м = 1/√3
Итак, уклон равен √3
.
Задача 4 :
Найдите угол наклона прямой, наклон которой равен √3.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: Уклон = √3
Тогда,
√3 = tanθ
θ = 60°
Итак, угол наклона равен 60°.
Задача 5 :
Найдите угол наклона прямой, уравнение которой y = x + 32.
Решение :
Пусть θ — угол наклона линии.
Данное уравнение находится в форме пересечения наклона.
То есть
y = mx + b
Сравнивая
y = x + 32
и
y = mx + b,
получаем наклон 1. m = 9.0004
Мы знаем, что наклон линии равен
м = tanθ
Тогда
1 = tanθ
θ = 45°
Итак, угол наклона равен 45°.
Пожалуйста, отправьте свой отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
4.3 Наклон линии | Аналитическая геометрия
4.3 Наклон линии (EMBGD)
На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется угол наклона прямой.
Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения \(y\)-направление на изменение \(x\)-направления:
\[m=\frac{\Delta y}{\Delta x}\]Из тригонометрии мы знаем, что функция тангенса определяется как отношение:
\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]
А из схемы мы видим, что
\начать{выровнять*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \конец{выравнивание*}
Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и
положительное направление оси \(х\).
Вертикальные линии
- \(\тета = \текст{90}\текст{°}\)
- Градиент не определен, так как значения \(x\) не изменились (\(\Delta x = 0\)).
- Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta = \text{90}\text{°}\)).
Горизонтальные линии
- \(\тета = \текст{0}\текст{°}\)
- Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
- Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через происхождение \((\text{0}\text{°};0))\).
Линии с отрицательным уклоном
Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный
между прямой и положительным направлением оси \(х\) тупая.
Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в второй квадрант:
Если нам дана прямая с градиентом \(m = -\text{0,7}\), то мы можем определить угол наклон с помощью калькулятора: 9{-1}(-\текст{0,7}) \\ &= -\текст{35,0}\текст{°} \конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой угол во втором квадранте:
\начать{выровнять*} \тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\ &= \текст{145}\текст{°} \конец{выравнивание*}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\)
дает градиент \(m = -\text{0,7}\).
Угол наклона
Учебник Упражнение 4.5
\(\text{60}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{60}\text{°} \\ \поэтому m &= \text{1,7} \end{align*}
\(\text{135}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -\text{1} \end{выравнивание*}
\(\text{0}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{0}\текст{°} \\ \поэтому m &= \text{0} \end{align*}
\(\text{54}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{54}\text{°} \\ \поэтому m &= \text{1,4} \end{выравнивание*}
\(\text{90}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{90}\текст{°} \\ \поэтому m & \text{ не определено} \end{align*}
\(\text{45}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{45}\text{°} \\ \поэтому m &= \text{1} \end{выравнивание*}
\(\text{140}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{140}\text{°} \\ \поэтому m &= -\text{0,8} \end{align*}
\(\text{180}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{180}\text{°} \\ \поэтому m &= \text{0} \end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\ \поэтому \тета &= \text{36,8}\text{°} \end{align*}
\(2y — x = 6\)
\begin{align*} 2у — х&=6\ 2у &= х + 6 \\ y &= \frac{1}{2}x + 3 \\ \загар \тета &= м \\ &= \фракция{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \поэтому \тета &= \текст{26,6}\текст{°} \end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\ \поэтому \тета &= \text{45}\text{°} \end{align*}
\(y=4\)
Горизонтальная линия
\(x = 3y + \frac{1}{2}\)
\begin{align*} х &= 3y + \frac{1}{2} \\ x — \frac{1}{2} &= 3y \\ \frac{1}{3}x — \frac{1}{6} &= y \\ \поэтому m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \поэтому \тета &= \text{18,4}\text{°} \end{выравнивание*} 9{-1} \влево( \text{0,577} \вправо) \\ \поэтому \тета &= \текст{30}\текст{°} \конец{выравнивание*}
Рабочий пример 8: Наклон прямой линии
Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии
проходящей через точки \((2;1)\) и \((-3;-9)\).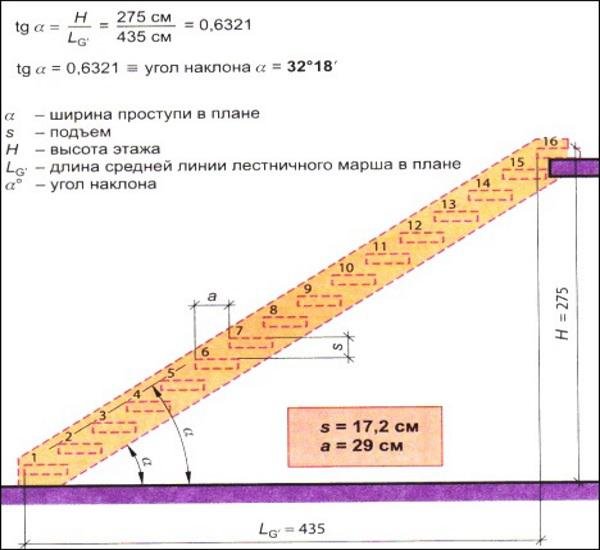 {-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
{-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).
Напишите окончательный ответ
Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).
temp textРабочий пример 9: Наклон прямой линии
Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом наклон \(\text{135}\text{°}\).
Используйте угол наклона для определения градиента линии
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -1 \конец{выравнивание*}
Запишите уравнение прямой линии в форме точки градиента. x — x_1)\]
Подставить заданную точку \((3;1)\)
\begin{выравнивание*} у — 1 & = -(х — 3) \\ у&=-х+3+1\ &= -х + 4 \конец{выравнивание*}
Напишите окончательный ответ
Уравнение прямой линии \(y = -x + 4\).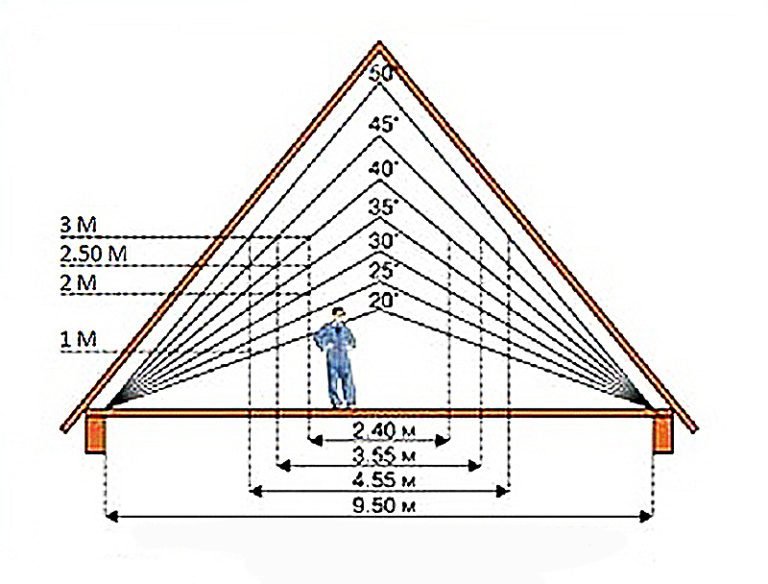
Рабочий пример 10: Наклон прямой линии
Определить острый угол (с точностью до \(\text{1}\) десятичного знака) между прямой, проходящей через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = — \frac{3}{2}x + 4\).
Нарисуйте эскиз
Проведите прямую через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямую \(y = — \ дробь{3}{2}x + 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона две строки. Обозначьте \(\theta\) острый угол между двумя прямыми.
Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.
\[\begin{массив}{rll}
\hat{B}_1 &= \text{180}\text{°} — \beta & (\angle \text{на строке}) \\
\text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle =
\text{ сумма внутр.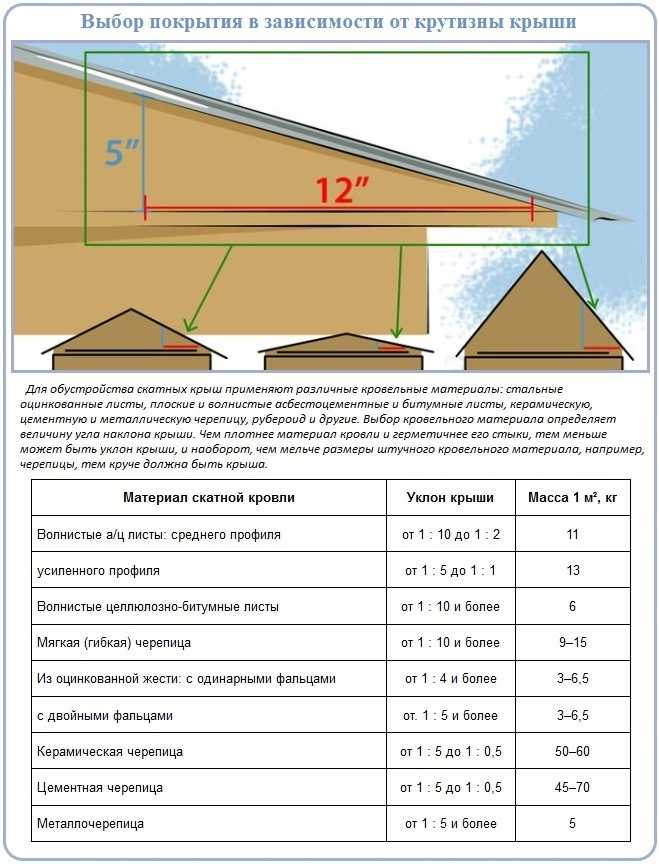 опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен тупой угол лежит во второй четверти, поэтому
\начать{выравнивать*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \текст{123,7}\текст{°} \конец{выравнивание*}
Определить градиент и угол наклона линии через \(M\) и \(N\)
Определение градиента \начать{выравнивать*} m & = \frac{y_2 — y_1}{x_2 — x_1} \\ & = \dfrac{3 — \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \фракция{1}{4} \end{align*}
Определить угол наклона \начать{выравнивать*} \загар \альфа & = м\\ & = \фракция{1}{4} \\ \поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \текст{14,0}\текст{°} \end{выравнивание*}
Напишите окончательный ответ
\begin{align*} \тета & = \текст{180}\текст{°} + \альфа — \бета\\ & = \text{180}\text{°} + \text{14,0}\text{°} — \text{123,7}\text{°} \\ & = \текст{70,3}\текст{°} \end{align*}
Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\). {-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
{-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)
\begin{выравнивание*} m &= \frac{y_2 -y_1}{x_2 — x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\ \поэтому m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \поэтому \тета &= \text{45}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\ \поэтому \тета &= -\текст{18,4}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} — \text{18,4}\text{°} \\ \поэтому \тета &= \текст{161,6}\текст{°} \end{align*}
Градиент undefined
Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\)
и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\). {-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
{-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).
Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя строки будут \(\тета\):
\начать{выравнивать*}
у &= — х + 3 \\
\поэтому m &= — 1 \\
\alpha &= \tan^{-1} \left(-1\right) \\
\поэтому \alpha &= -\text{45}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{45}\text{°} \\
\поэтому \alpha &= \text{135}\text{°} \\
х &= у + \ гидроразрыва {1} {2} \\
х — \фракция{1}{2} &= у \\
\поэтому m &= 1 \\
\beta &= \tan^{-1} \left(1 \right) \\
\поэтому \бета &= \text{45}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext.