- Конденсатор в цепи переменного тока
- Однофазные цепи переменного тока (страница 2)
- 8.3: Конденсаторы последовательно и параллельно
- 8.2 Конденсаторы последовательно и параллельно — University Physics Volume 2
Конденсатор в цепи переменного тока
Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.
Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).
Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.
В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.
Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.
С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.
Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.
Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.
В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.
Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока.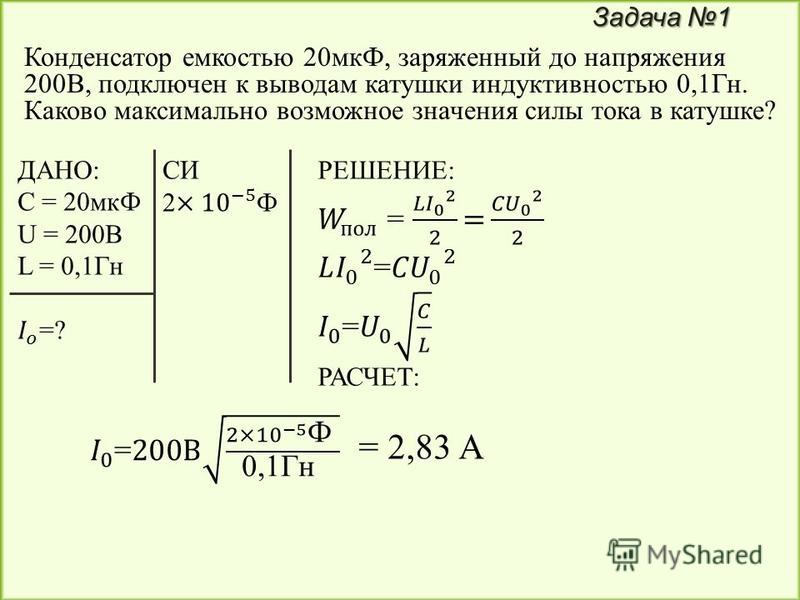 Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны
Емкостное сопротивление конденсатора
Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.
Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.
Величина емкостного сопротивления определяется по следующей формуле:
где Хс — емкостное сопротивление конденсатора в ом;
f—частота переменного тока в гц;
ω — угловая частота переменного тока;
С — емкость конденсатора в ф.
При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.
Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.
Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.
Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.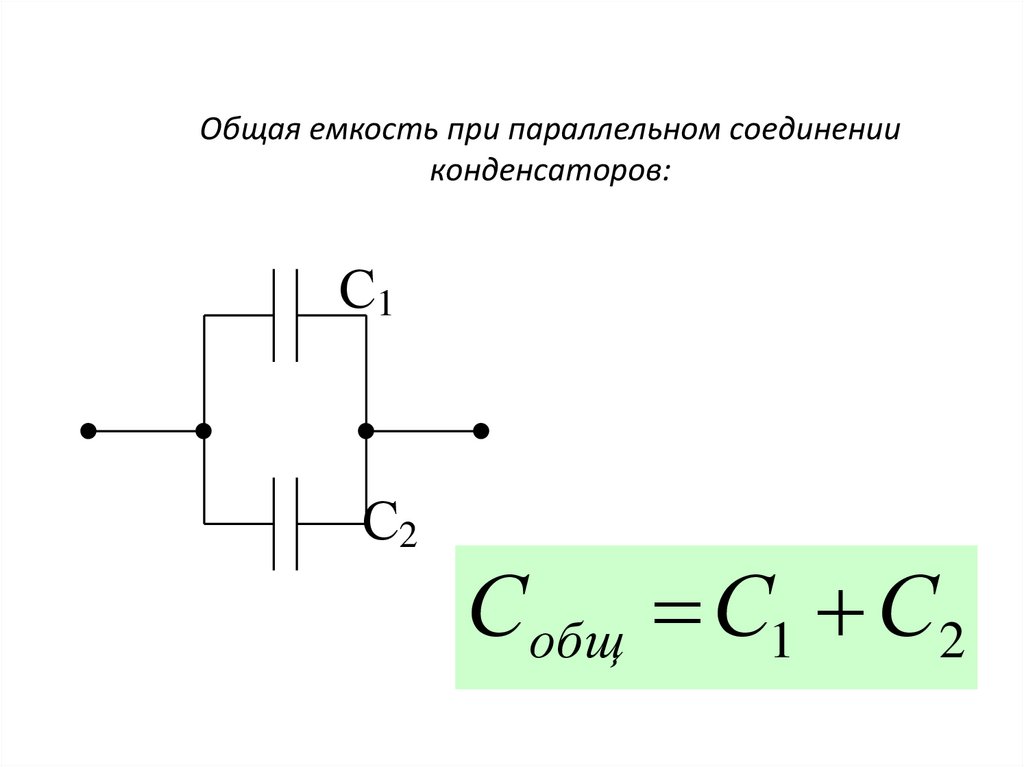
Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.
Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.
Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.
Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.
Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.
В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.
В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.
Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.
Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.
Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.
Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.
И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.
При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.
А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Однофазные цепи переменного тока (страница 2)
12. Конденсатор емкостью С = 8,36 мкФ включен на синусоидальное напряжение U=380 В частотой f=50 Гц.
Определить ток в цепи конденсатора.
Решение:
Емкостное сопротивление
Ток в цепи конденсатора при синусоидальном напряжении 380 В
Для получения больших токов требуются при данной частоте большие значения емкости.
13. При включении конденсатора на синусоидальное напряжение U=220 В частотой f=50 Гц в цепи установился ток I=0,5 А.
Какую емкость имеет конденсатор?
Решение:
На основании закона Ома емкостное сопротивление
Из формулы емкостного сопротивления
емкость
Метод определения емкости конденсатора, рассмотренный в данной задаче, является наименее точным, но он прост и не требует больших затрат для применения на практике.
14. При включении разомкнутого на конце кабеля на напряжение U=6600 В частотой f=50 Гц в цепи установился ток I=2 А.
Пренебрегая электрическим сопротивлением кабеля, определить приближенно емкость кабеля на 1 км его длины, если длина кабеля 10 км.
Решение:
Изолированные друг от друга жилы кабеля представляют собой конденсатор. Если пренебречь сопротивлением жил кабеля, то ток холостой работы кабеля, т. е. ток в кабеле, разомкнутом на конце, можно считать чисто емкостным. В этом случае действительно соотношение
где
— емкостная проводимость.
Отсюда
При частоте f=50 Гц угловая частота
, следовательно,
Емкость кабеля на 1 км его длины
Описанный способ определения емкости кабеля на 1 км его длины является очень приближенным (в нем пренебрегают активным сопротивлением жил кабеля и активной проводимостью утечки от жилы к жиле вследствие несовершенства изоляции; допускается равномерное распределение емкости по длине кабеля).
15. Какая емкость батареи конденсаторов требуется для получения реактивной (емкостной) мощности 152 ВАР при напряжении U=127 В и частоте f=50 Гц.
Решение:
При частоте f=50 Гц угловая частота
. Так как ток батареи считается чисто
реактивным (опережающим по фазе напряжение на 1/4 периода), то реактивная мощность равна произведению напряжения и тока:
откуда
Емкостный ток равен произведению напряжения на емкостную проводимость, поэтому
Емкость батареи конденсаторов
Реактивную (емкостную) мощность можно представить в виде
, выразив ток через напряжение и емкостную проводимость; отсюда следует, что при данном напряжении и частоте реактивная (емкостная) мощность пропорциональна емкости. Если изоляция пластин батареи конденсаторов допускает повышение напряжения (например, в раз), то реактивная (емкостная) мощность увеличится пропорционально квадрату напряжения (т. е. в 3 раза). Таким образом, в рассматриваемом случае важное значение имеет отношение напряжения от номинального.
е. в 3 раза). Таким образом, в рассматриваемом случае важное значение имеет отношение напряжения от номинального.
16. В катушке (см. задачу 10), включенной на переменное напряжение U=12 В частотой f=50 Гц установился ток 1,2 А.
Определить индуктивность катушки.
Решение:
Отношение переменного напряжения, приложенного к катушке, к току, устанавливающемуся в ней, называется полным сопротивлением z катушки;
В задаче 10 было определено, что активное сопротивление катушки r=2,8 Ом. Сопротивление катушки при перееденном токе больше сопротивления г при постоянном токе вследствие наличия э. д. с. самоиндукции, препятствующей изменению переменного тока. Это равносильно появлению в катушке сопротивления, называемого индуктивным:
где L — индуктивность, Гн
f — частота, Гц.
Связь между полным сопротивлением z, индуктивным сопротивлением
и активным сопротивлением r такая же, как между гипотенузой и катетами в прямоугольном треугольнике:
откуда индуктивное сопротивление
Индуктивность катушки
В рассматриваемой катушке ток отстает по фазе от напряжения, причем тангенс угла сдвига фаз
. Из таблиц тригонометрических величин .
Из таблиц тригонометрических величин .
17. В схеме (рис. 23) вольтметр показывает 123 В, амперметр 3 А и ваттметр 81 Вт, частота сети 50 Гц.
Oпределить параметры катушки.
Решение:
Отношение напряжения к току равно полному сопротивлению катушки:
Ваттметр измеряет активную мощность цепи, которая в данной задаче является потерей мощности в сопротивлении r, поэтому сопротивление катушки
Полное сопротивление z, активное сопротивление r и индуктивное сопротивление
катушки связаны между собой таким же соотношением, как гипотенуза и катеты в прямоугольном треугольнике.
Следовательно,
При частоте f=50 Гц угловая частота
Индуктивное сопротивление
равно произведению угловой частоты ω и индуктивности L; следовательно,
Коэффициент мощности катушки
. Из таблиц тригонометрических величин .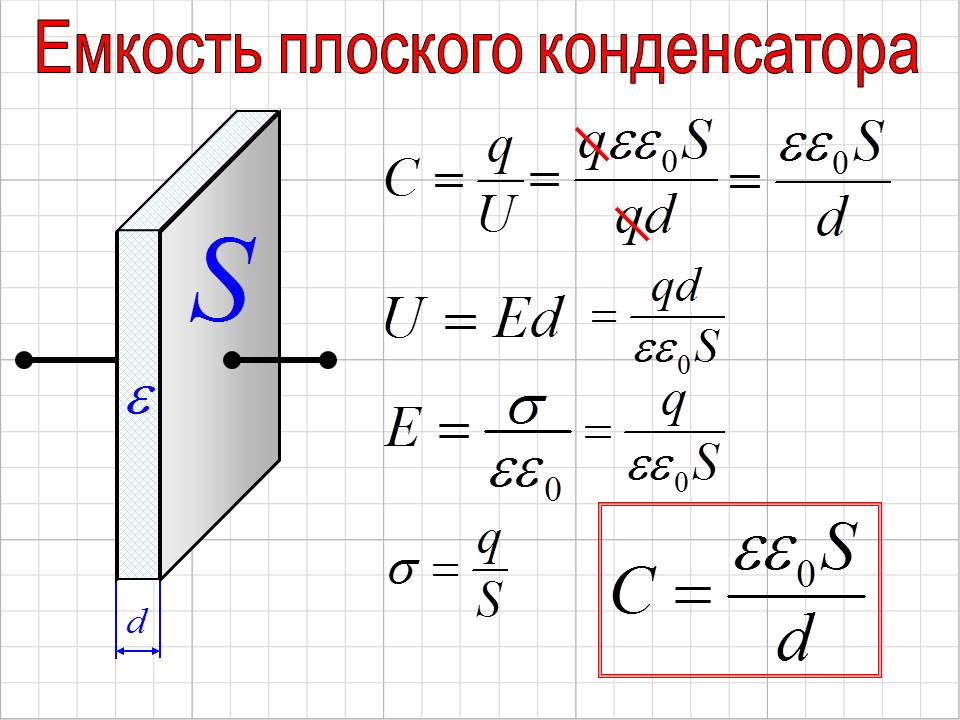
18. Катушка без стального сердечника включена на постоянное напряжение 2,1 В, ток которой равен 0,3 А. При включении этой же катушки на синусоидальное напряжение частотой 50 Гц с действующим значением 50 В ток имеет действующее значение 2 А.
Определить параметры катушки, активную и полную мощности.
Решение:
Отношение постоянного напряжения к постоянному току в катушке практически равно (если пренебречь увеличением сопротивления из-за вытеснения переменного тока на поверхность провода) активному сопротивлению:
Это один из параметров катушки. Отношение этих же величин при переменном токе в катушке равно полному сопротивлению:
Индуктивное сопротивление:
Индуктивность катушки — второй ее параметр:
Коэффициент мощности катушки:
Из таблиц тригонометрических величин
.
Активная мощность
Полная мощность
Коэффициент мощности
В задачах 17 и 18 рассмотрены два различных способа определения параметров катушки.
19. Батарея конденсаторов емкостью С=50 мкФ соединена последовательно с реостатом сопротивлением r=29,1 Ом.
Определить напряжения на батарее конденсаторов и реостате, а также ток в цепи и мощность, если приложенное напряжение U=210 В и частота сети f=50 Гц.
Решение:
Частоте 50 Гц и емкости 50 мкФ соответствует емкостное сопротивление, в 50 раз меньшее, чем емкости в 1 мкФ. Следовательно,
Здесь 3185 Ом — сопротивление конденсатора емкостью 1 мкФ.
По условию, сопротивление реостата r=29,1 Ом. Полное сопротивление цепи связано с активным и емкостным сопротивлениями таким же соотношением, как гипотенуза и катет прямоугольного треугольника:
На основании закона Ома ток в цепи
Напряжение на реостате
Напряжение на батарее конденсаторов
В силу последовательного соединения большее напряжение оказалось на элементе цепи, имеющем большее сопротивление.
Коэффициент мощности
Из таблиц тригонометрических величин угол сдвига фаз
.
Активная мощность цепи
Полная мощность цепи равна произведению действующих значений напряжения и тока:
Полная мощность намного больше активной мощности, так как коэффициент мощности мал, т. е. полное сопротивление цепи во много раз превышает активное сопротивление.
20. Электрическую лампу мощностью Р=60 Вт при напряжении
необходимо подсоединить к сети с переменным напряжением U=220 В и частотой 50 Гц. Для компенсации части этого напряжения последовательно с лампой включается конденсатор.
Какой емкости необходимо взять конденсатор?
Решение:
Напряжение на лампе будет активной составляющей приложенного напряжения сети, а напряжение на конденсаторе — его реактивной (емкостной) составляющей. Эти напряжения связаны соотношением
Напряжение на конденсаторе
Ток в конденсаторе тот же, что и в лампе, т. е.
На основании закона Ома емкостное сопротивление
Так как при частоте f=50 Гц емкости С=1 мкФ соответствует емкостное сопротивление
, то емкость рассматриваемого конденсатора приблизительно равна 8,7 мкФ.
Избыточное напряжение можно было бы скомпенсировать и путем последовательного включения реостата с лампой. Так как реостат, как и электрическая лампа, представляет чисто активное сопротивление, то напряжения на этих элементах цепи совпадают по фазе с общим током, а следовательно, и между собой. В этом случае будет действительно соотношение
где
— напряжение на реостате, равное
При токе лампы 0,5 А сопротивление реостата должно составлять
В реостате будет расходоваться энергия, переходящая в тепло, причем потери мощности в реостате
В случае включения емкости «погашение» напряжения происходит без потерь энергии.
21. В случае электрической сварки дугой тонких листов при переменном токе в ней развивается мощность
при токе I=20 A. Напряжение источника U=120 В, частота сети f=50 Гц (рис. 24). Чтобы иметь необходимое напряжение на дуге, последовательно с ней включили индуктивную катушку, сопротивление которой r=1 Ом.
Определить индуктивность катушки; сопротивление реостата, который можно было бы включить вместо катушки; к.п.д. схемы при наличии в ней катушки и реостата.
Решение:
Полное сопротивление схемы
Полная мощность на входе схемы
Потери мощности в обмотке катушки
Активная мощность схемы
Коэффициент мощности схемы
Из таблиц тригонометрических величин
.
Активное сопротивление схемы
сопротивление дуги
Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:
Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )
Искомая индуктивность катушки
Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:
откуда
Потери мощности в катушке
Потери мощности в реостате
Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
к. п. д. при наличии реостата
Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере
при наличии катушки и при наличии реостата).
22. Последовательно с катушкой, параметры которой
и L=15,92 мГн, включен реостат сопротивлением, . Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.
Решение:
Индуктивное сопротивление катушки
Полное сопротивление катушки
Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,
Полное сопротивление цепи
На основании закона Ома ток в цепи
Напряжение на катушке
Напряжение на реостате
Арифметическая сумма
много больше приложенного напряжения U=130 В.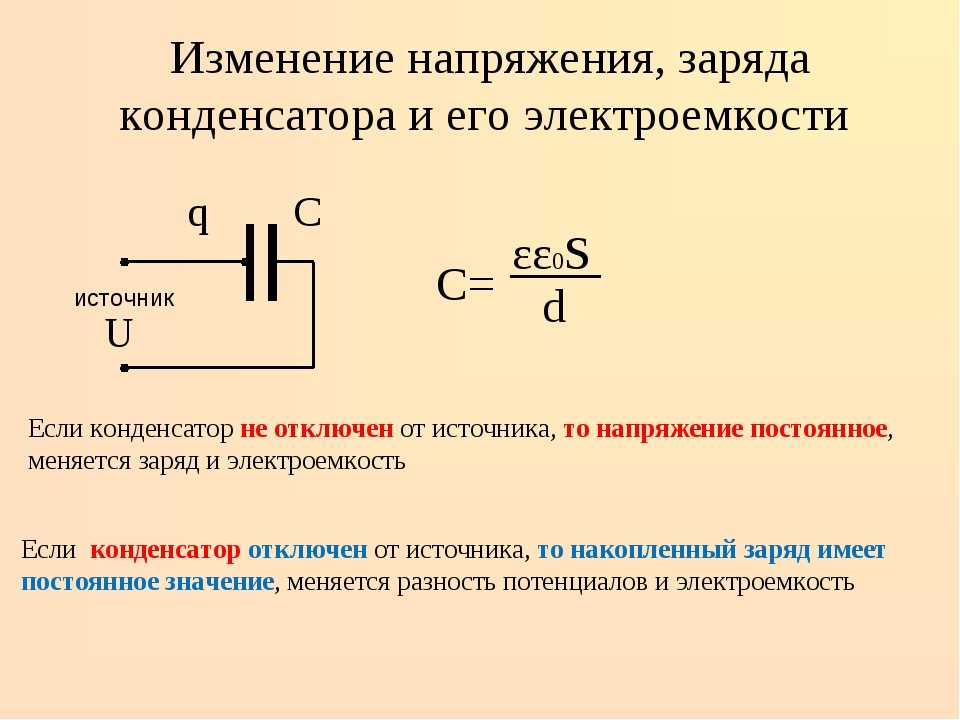 Коэффициент мощности цепи
Коэффициент мощности цепи
Коэффициент мощности катушки
Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки
активная мощность реостата
Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора в сторону опережения вектора тока I, под углом в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке . Векторы построены так с целью сложения по правилу многоугольника.
23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность
и сопротивление , у второй катушки индуктивность и сопротивление .
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.
Решение:
Индуктивное сопротивление первой катушки
т. е. оно численно равно активному сопротивлению
, что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз
Индуктивное сопротивление второй катушки
Так как ее активное сопротивление
то тангенс угла сдвига фаз
Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений
. Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .
Полное сопротивление
первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление , и под прямым углом к нему вверх — отрезок, изображающий сопротивление . Гипотенуза се прямоугольного треугольника означает полное сопротивление второй катушки.
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. . Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (, отрезок аf) и индуктивные (, отрезок ef) сопротивления катушек.
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:
Ток в цепи определяется по закону Ома:
Напряжение на первой катушке
Напряжение на второй катушке
Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока
; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения ; при этом вектор напряжения будет иметь длину 55,2 мм, вектор напряжения — длину 71 мм, а вектор приложенного напряжения — длину 126 мм.
Начало вектора совмещено с концом вектора для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).
8.3: Конденсаторы последовательно и параллельно
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4394
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснить, как определить эквивалентную емкость конденсаторов при последовательном и параллельном соединении
- Вычислить разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определить чистую емкость сети конденсаторов
Несколько конденсаторов можно соединить вместе для использования в различных приложениях.
Последовательная комбинация конденсаторов
На рисунке \(\PageIndex{1}\) показана последовательная комбинация трех конденсаторов, расположенных в ряд в цепи. Как и для любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:
\[ C=\dfrac{Q}{V}.\]
При подключении этой последовательной комбинации к аккумулятору с напряжением В каждый из конденсаторов приобретает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \(+Q\), а заряд на пластине, подключенной к отрицательной клемме, равен \(-Q\). Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала \(V_1 = Q/C_1\) на одном конденсаторе может отличаться от падения потенциала \(V_2 = Q/C_2\) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентная емкость ) меньше, чем наименьшая из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как и заряд любого конденсатора в последовательном соединении: То есть все конденсаторы последовательного соединения имеют одинаковый заряд .
Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \(+Q\), а заряд на пластине, подключенной к отрицательной клемме, равен \(-Q\). Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала \(V_1 = Q/C_1\) на одном конденсаторе может отличаться от падения потенциала \(V_2 = Q/C_2\) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентная емкость ) меньше, чем наименьшая из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как и заряд любого конденсатора в последовательном соединении: То есть все конденсаторы последовательного соединения имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с обкладки первого конденсатора (обозначим его как \(-Q\)), он должен быть помещен на пластину второго конденсатора (обозначим его как \( +Q\)) и так далее.
Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с обкладки первого конденсатора (обозначим его как \(-Q\)), он должен быть помещен на пластину второго конденсатора (обозначим его как \( +Q\)) и так далее.
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 соответственно равны \(V_1 = Q/C_1\), \(V_2 = Q/C_2\) и \(V_3 = Q/C_3\). Эти потенциалы должны суммироваться с напряжением батареи, что дает следующий баланс потенциалов:
\[V = V_1 + V_2 + V_3.\]
Потенциал \(V\) измеряется на эквивалентном конденсаторе, который удерживает заряд \(Q\) и имеет эквивалентную емкость \(C_S\). Подставляя выражения для \(V_1\), \(V_2\) и \(V_3\), получаем
Подставляя выражения для \(V_1\), \(V_2\) и \(V_3\), получаем
\[\dfrac{Q}{C_S} = \dfrac{Q}{C_1} + \dfrac{ Q}{C_2} + \dfrac{Q}{C_3}.\]
Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \(C_S\) трех последовательно соединенных конденсаторов:
\[\dfrac{1}{C_S} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3}.\]
Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.
Комбинация последовательностей
Для последовательно соединенных конденсаторов обратная величина эквивалентной емкости представляет собой сумму обратных величин отдельных емкостей:
\[\dfrac{1}{C_S} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} + \dots \label{capseries}\]
Пример \(\PageIndex{1}\): эквивалентная емкость последовательной сети
Найти общая емкость для трех конденсаторов, соединенных последовательно, при условии, что их отдельные емкости равны \(1,000 мкФ), \(5,000 мкФ\) и \(8,000 мкФ\).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ref{capseries} с тремя членами.
Решение
Вводим данные емкости в уравнение \ref{capseries}:
\[ \begin{align*} \dfrac{1}{C_S} &= \dfrac{1}{C_1} + \ dfrac{1}{C_2} + \dfrac{1}{C_3} \\[4pt] &= \dfrac{1}{1,000 мкм F} + \dfrac{1}{5,000 мкм F} + \dfrac{ 1}{8.000 \мкФ} \\[4pt] &= \dfrac{1.325}{\мкФ}.\end{align*} \]
Теперь инвертируем этот результат и получаем
\[ \begin{align*} C_S &= \dfrac{\mu F}{1.325} \\[4pt] &= 0.755 \mu F.\end{align*} \номер\]
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше, чем наименьшая отдельная емкость в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, в которой одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \(\PageIndex{2a} \). Так как конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на пластинах . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость \(C_p\) параллельной сети, заметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:
Так как конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на пластинах . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость \(C_p\) параллельной сети, заметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:
\[Q = Q_1 + Q_2 + Q_3.\ ]
В левой части этого уравнения мы используем соотношение \(Q = C_pV\), которое справедливо для всей сети. В правой части уравнения мы используем отношения \(Q_1 = C_1 V\), \(Q_2 = C_2V\) и \(Q_3 = C_3V\) для трех конденсаторов в сети. Таким образом, мы получаем
\[C_pV = C_1V + C_2V + C_3V.\]
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
\[C_p = C_1 + C_2 + C_3.\ ]
Это выражение легко обобщается на любое количество конденсаторов, соединенных параллельно в сети.
Параллельное соединение
Для конденсаторов, соединенных параллельно, эквивалентная (чистая) емкость представляет собой сумму всех отдельных емкостей в сети,
\[C_p = C_1 + C_2 + C_3 + . .. \label{capparallel}\]
.. \label{capparallel}\]
Пример \(\PageIndex{2}\): эквивалентная емкость параллельной сети
Найдите чистую емкость трех конденсаторов, соединенных параллельно, если их индивидуальные емкости равны F\) и \(8,0 мкF\).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ref{capparallel} с тремя членами.
Решение
Ввод данных емкостей в уравнение \ref{capparallel} дает
\[\begin{align*} C_p &= C_1 + C_2 + C_3 \\[4pt] &= 1.0 \мкФ + 5.0 \mu F + 8.0 \mu F \\[4pt] &= 14.0 \mu F. \end{align*}\]
Значимость
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.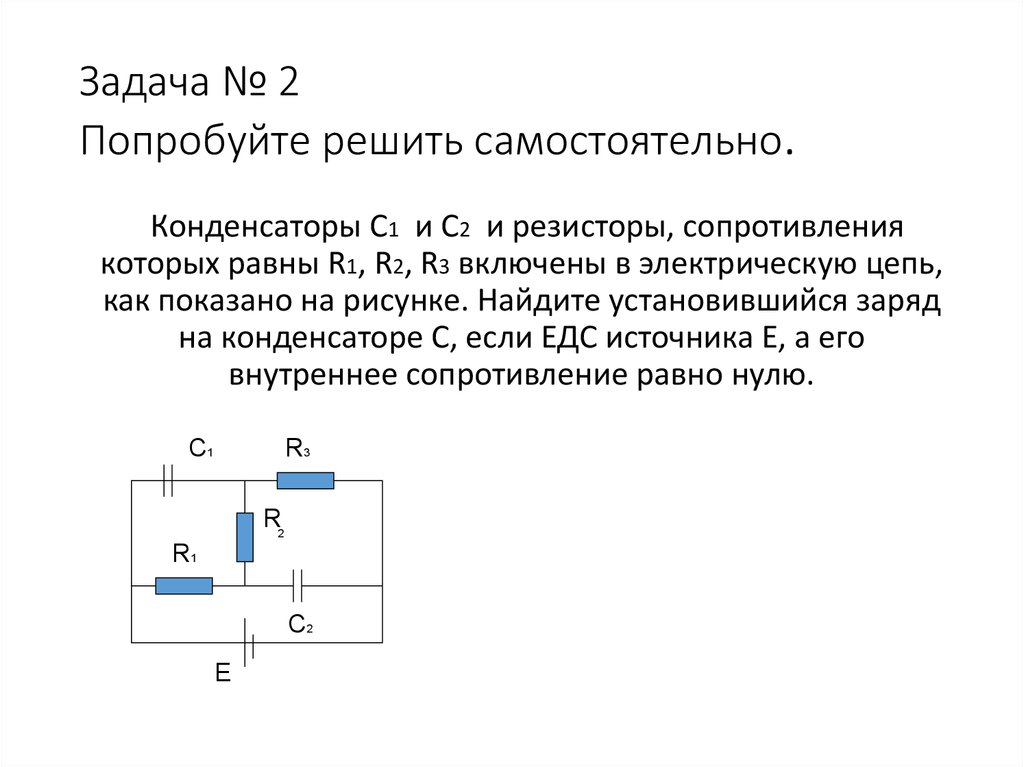
Сети конденсаторов обычно представляют собой некоторую комбинацию последовательных и параллельных соединений, как показано на рисунке \(\PageIndex{3}\). Чтобы найти чистую емкость таких комбинаций, мы идентифицируем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Рисунок \(\PageIndex{3}\): (a) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. (b) \(C_1\) и \(C_2\) последовательно; их эквивалентная емкость равна \(C_S\) c) Эквивалентная емкость \(C_S\) подключена параллельно \(C_3\). Таким образом, эквивалентная емкость всей сети представляет собой сумму \(C_S\) и \(C_3\).Пример \(\PageIndex{3}\): эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рисунке \(\PageIndex{3}\). Предположим, что емкости известны с точностью до трех знаков после запятой (\(C_1 = 1,000 мкФ, C_2 = 5,000 мкФ, C_3 = 8,000 мкФ\)). Округлите ответ до трех знаков после запятой.
Округлите ответ до трех знаков после запятой.
Стратегия
Сначала мы определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы \(C_1\) и \(C_2\) включены последовательно. Их комбинация, обозначенная \(C_S\), параллельна \(C_3\).
Решение
Поскольку \(C_1\) и \(C_2\) соединены последовательно, их эквивалентная емкость \(C_S\) получается с помощью уравнения \ref{capseries}:
\[\begin{align* } \dfrac{1}{C_S} &= \dfrac{1}{C_1} + \dfrac{1}{C_2} \\[4pt] &= \dfrac{1}{1,000 мкм F} + \dfrac{ 1}{5.000 \мкФ} \\[4pt] &= \dfrac{1.200}{\мкФ} \end{align*}\]
Таким образом,
\[ C_S = 0,833 \mu F. \nonnumber\]
Емкость \(C_S\) подключена параллельно с третьей емкостью \(C_3\), поэтому используем уравнение \ref{capparallel} найти эквивалентная емкость C всей сети:
\[\begin{align*} C &= C_S + C_3 \\[4pt] &= 0,833 мкФ + 8,000 мкФ \\[4pt] &= 8,833 мкФ. \end{align*}\]
\end{align*}\]
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \(\PageIndex{4}\), когда емкости равны \(C_1 = 12,0 мкФ, C_2 = 2,0 мкФ\) и \(C_3 = 4,0 мкФ\). Когда на комбинации сохраняется разность потенциалов 12,0 В, найти заряд и напряжение на каждом конденсаторе.
Рисунок \(\PageIndex{4}\): (a) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.Стратегия Сначала мы вычисляем чистую емкость \(C_{23}\) параллельного соединения \(C_2\) и \(C_3\). Тогда C — чистая емкость последовательного соединения \(C_1\) и \(C_{23}\). Мы используем соотношение \(C = Q/V\), чтобы найти заряды \(Q_1, Q_2\) и \(Q_3\), а также напряжения \(V_1, V_2\) и \(V_3\) на конденсаторы 1, 2 и 3 соответственно.
Решение Эквивалентная емкость для \(C_2\) и \(C_3\) равна
\[C_{23} = C_2 + C_3 = 2,0 мкФ + 4,0 мкФ = 6,0 мкФ.\]
Вся комбинация из трех конденсаторов эквивалентна двум конденсаторам, включенным последовательно,
\[ \dfrac{1}{C} = \dfrac{1}{12,0 мкм F} + \dfrac{1}{6,0 мкм F} = \dfrac{1}{4,0 мкм F} \Rightarrow C = 4,0 \ mu F. \]
\]
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \(\PageIndex{2b}\). Поскольку конденсаторы соединены последовательно, они имеют одинаковый заряд \(Q_1 = Q_{23}\). Кроме того, конденсаторы имеют общую разность потенциалов 12,0 В, поэтому
\[12,0 В = V_1 + V_{23} = \dfrac{Q_1}{C_1} + \dfrac{Q_{23}}{C_{23}} = \dfrac{Q_1}{12,0 мкм F} + \dfrac{Q_1}{6,0 мкФ} \Rightarrow Q_1 = 48,0 мкКл\]
Теперь разность потенциалов на конденсаторе 1 равна
\[V_1 = \dfrac{Q_1}{C_1} = \dfrac{ 48,0 мкКл}{12,0 мкФ} = 4,0 В.\]
Поскольку конденсаторы 2 и 3 соединены параллельно, они имеют одинаковую разность потенциалов:
\[V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В.\]
Следовательно, заряды на этих двух конденсаторах соответственно равны
\[Q_2 = C_2V_2 = (2,0 мкм F)(8,0 В) = 16,0 мкм C,\]
\[Q_3 = C_3V_3 = (4,0 мкм F)(8,0 В) = 32,0 мкм C. \]
Значимость Как и ожидалось, чистый заряд при параллельной комбинации \(C_2\) и \(C_3\) равен \(Q_{23} = Q_2 + Q_3 = 48,0 мкКл\)
Упражнение \ (\PageIndex{1}\)
Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \(C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ\) и \(C_4 = 5,0 пФ\). Найдите заряд каждого конденсатора, предполагая, что в каждой сети существует разность потенциалов 12,0 В.
Предположим, что \(C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ\) и \(C_4 = 5,0 пФ\). Найдите заряд каждого конденсатора, предполагая, что в каждой сети существует разность потенциалов 12,0 В.
- Ответить
\(C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл\)
- Ответ б
\(C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл\)
- Ответ c
\(C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл\)
Эта страница под названием 8.3: Конденсаторы последовательно и параллельно распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- конденсаторы параллельно конденсаторы
- серии
- параллельная комбинация Комбинация серии
- источник@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
8.2 Конденсаторы последовательно и параллельно — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как определить эквивалентную емкость конденсаторов при последовательном и параллельном соединении
- Вычислите разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определите чистую емкость сети конденсаторов
Несколько конденсаторов можно соединить вместе для использования в различных приложениях. Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как  Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серийная комбинация конденсаторов
На рис. 8.11 показано последовательное соединение трех конденсаторов, расположенных в ряд внутри цепи. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 8.1. При подключении этой последовательной комбинации к батарее с напряжением V каждый из конденсаторов приобретает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен +Q+Q, а заряд на пластине, подключенной к отрицательной клемме, равен -Q-Q. Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1=Q/C1V1=Q/C1 на одном конденсаторе может отличаться от падения потенциала V2=Q/C2V2=Q/C2 на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разные емкости.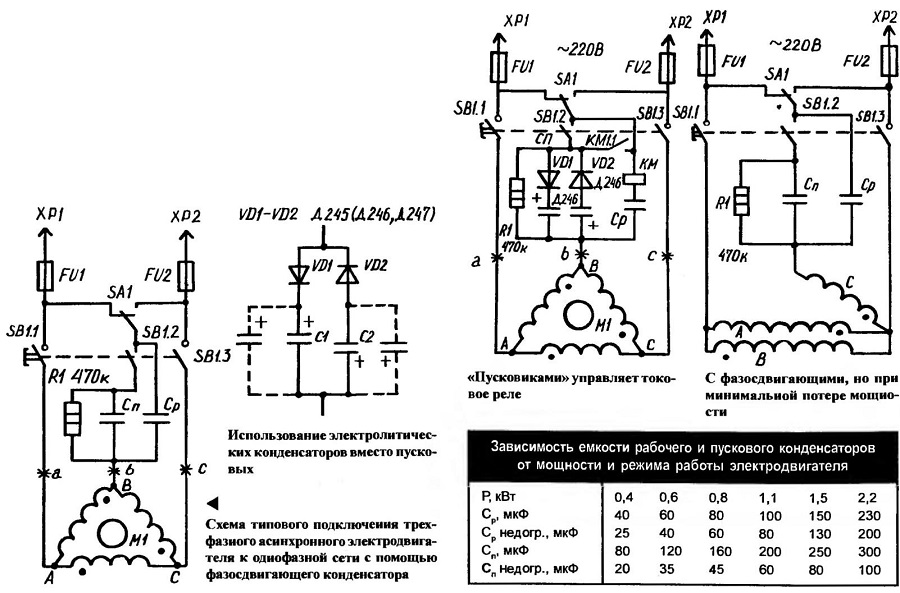
Рисунок
8.11
а) Три конденсатора соединены последовательно. Величина заряда на каждой пластине Å . (b) Цепочка конденсаторов в (а) эквивалентна одному конденсатору, емкость которого меньше, чем у любой из отдельных емкостей в (а), а заряд на его пластинах равен Å .
(b) Цепочка конденсаторов в (а) эквивалентна одному конденсатору, емкость которого меньше, чем у любой из отдельных емкостей в (а), а заряд на его пластинах равен Å .
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны соответственно V1=Q/C1V1=Q/C1, V2=Q/C2V2=Q/C2 и V3=Q/C3V3=Q/C3. Эти потенциалы должны суммироваться с напряжением батареи, что дает следующий баланс потенциалов:
В=В1+В2+В3.В=В1+В2+В3.
Потенциал В измеряется на эквивалентном конденсаторе, удерживающем заряд Q и имеющем эквивалентную емкость CSCS. Вводя выражения для V1V1, V2V2 и V3V3, получаем
QCS=QC1+QC2+QC3.QCS=QC1+QC2+QC3.
Отменяя заряд Q , получаем выражение, содержащее эквивалентную емкость CSCS трех последовательно соединенных конденсаторов:
1CS=1C1+1C2+1C3. 1CS=1C1+1C2+1C3.
1CS=1C1+1C2+1C3.
Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.
Комбинация серий
Для последовательно соединенных конденсаторов обратная величина эквивалентной емкости представляет собой сумму обратных величин отдельных емкостей:
1CS=1C1+1C2+1C3+⋯.1CS=1C1+1C2+1C3+⋯.
8,7
Пример 8.4
Эквивалентная емкость последовательной сети
Найдите общую емкость трех последовательно соединенных конденсаторов, если их отдельные емкости равны 1000 мкФ, 1000 мкФ, 5000 мкФ, 5000 мкФ и 8000 мкФ, 8000 мкФ.
Стратегия
Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.7 с тремя членами.
Раствор
Мы вводим данные емкости в уравнение 8.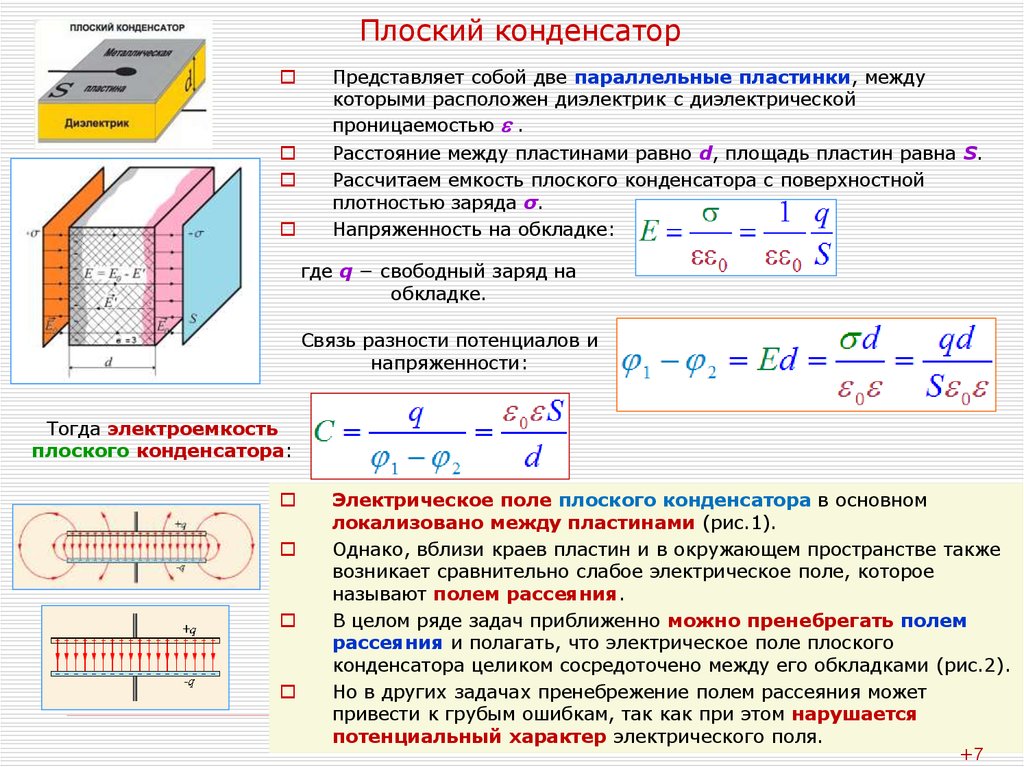
.
Теперь инвертируем этот результат и получаем CS=мкФ1,325=0,755мкФ.CS=мкФ1,325=0,755мкФ.
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация из трех конденсаторов, в которой одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рис. 8.12 (а). Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих обкладках . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость CPCP параллельной сети, заметим, что общий заряд
Q=Q1+Q2+Q3.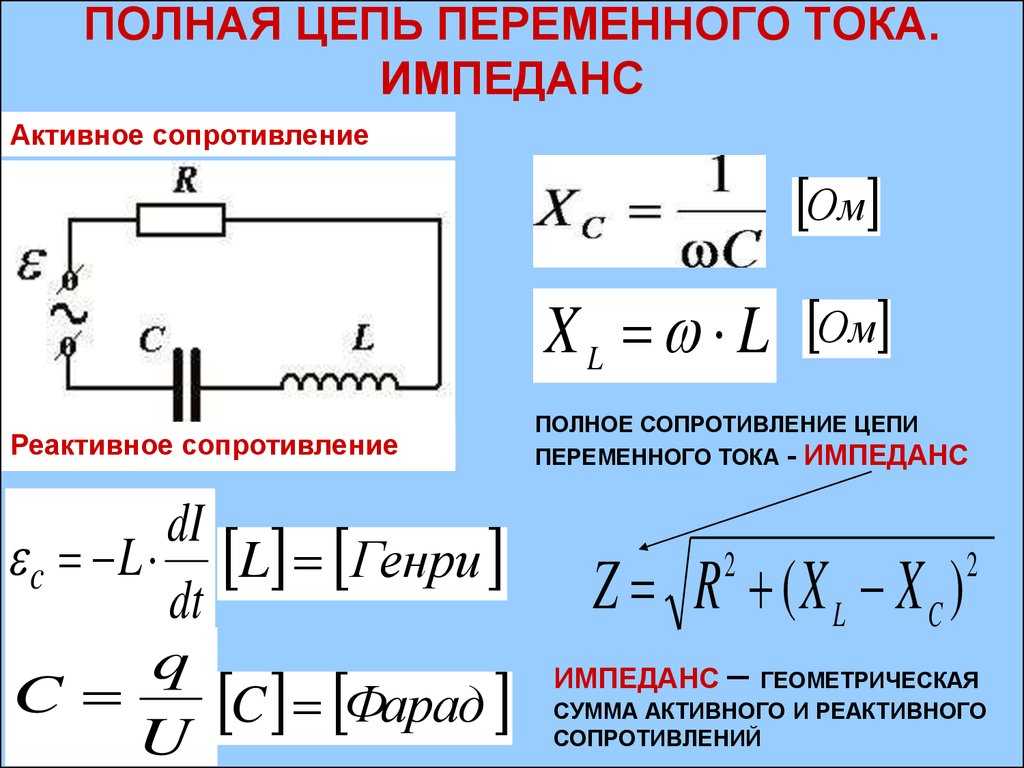 Q=Q1+Q2+Q3.
Q=Q1+Q2+Q3.
В левой части этого уравнения мы используем соотношение Q=CPVQ=CPV, которое верно для всей сети. В правой части уравнения мы используем соотношения Q1=C1V, Q2=C2V, Q1=C1V, Q2=C2V и Q3=C3VQ3=C3V для трех конденсаторов в сети. Таким образом, мы получаем
CPV=C1V+C2V+C3V.CPV=C1V+C2V+C3V.
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
СР=С1+С2+С3. СР=С1+С2+С3.
Это выражение легко обобщается на любое количество конденсаторов, соединенных параллельно в сети.
Параллельная комбинация
Для конденсаторов, соединенных параллельно, эквивалентная (чистая) емкость представляет собой сумму всех отдельных емкостей в сети,
CP=C1+C2+C3+⋯.CP=C1+C2+C3+⋯.
8,8
Рисунок
8.12
а) Три конденсатора соединены параллельно. Каждый конденсатор подключен непосредственно к аккумулятору. б) Заряд эквивалентного конденсатора равен сумме зарядов отдельных конденсаторов.
б) Заряд эквивалентного конденсатора равен сумме зарядов отдельных конденсаторов.
Пример 8,5
Эквивалентная емкость параллельной сети
Найдите общую емкость для трех конденсаторов, соединенных параллельно, учитывая, что их отдельные емкости составляют 1,0 мкФ, 5,0 мкФ и 8,0 мкФ, 1,0 мкФ, 5,0 мкФ и 8,0 мкФ.
Стратегия
Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.8 с тремя членами.
Раствор
Ввод данных емкостей в уравнение 8.8 дает
CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ. CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ.
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.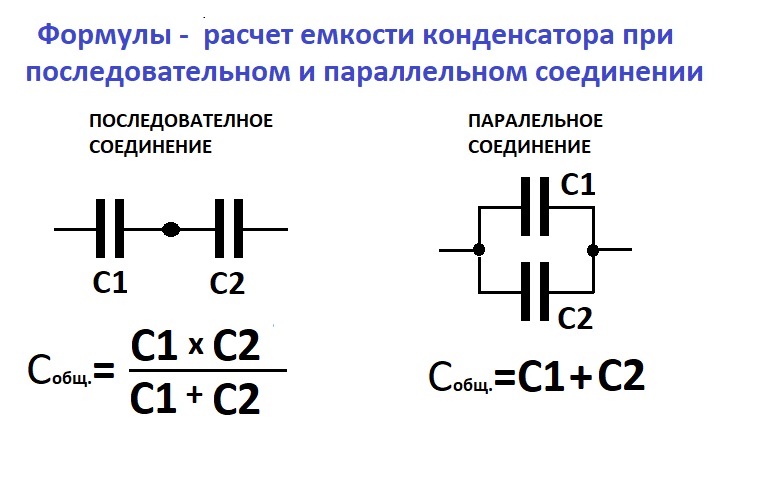
Сети конденсаторов обычно представляют собой некоторую комбинацию последовательных и параллельных соединений, как показано на рис. 8.13. Чтобы найти чистую емкость таких комбинаций, мы идентифицируем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Рисунок 8.13 а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. (б) C1C1 и C2C2 соединены последовательно; их эквивалентная емкость CS.CS. (c) Эквивалентная емкость CSCS подключена параллельно C3.C3. Таким образом, эквивалентная емкость всей сети представляет собой сумму CSCS и C3.C3.
Пример 8,6
Эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рис. 8.13.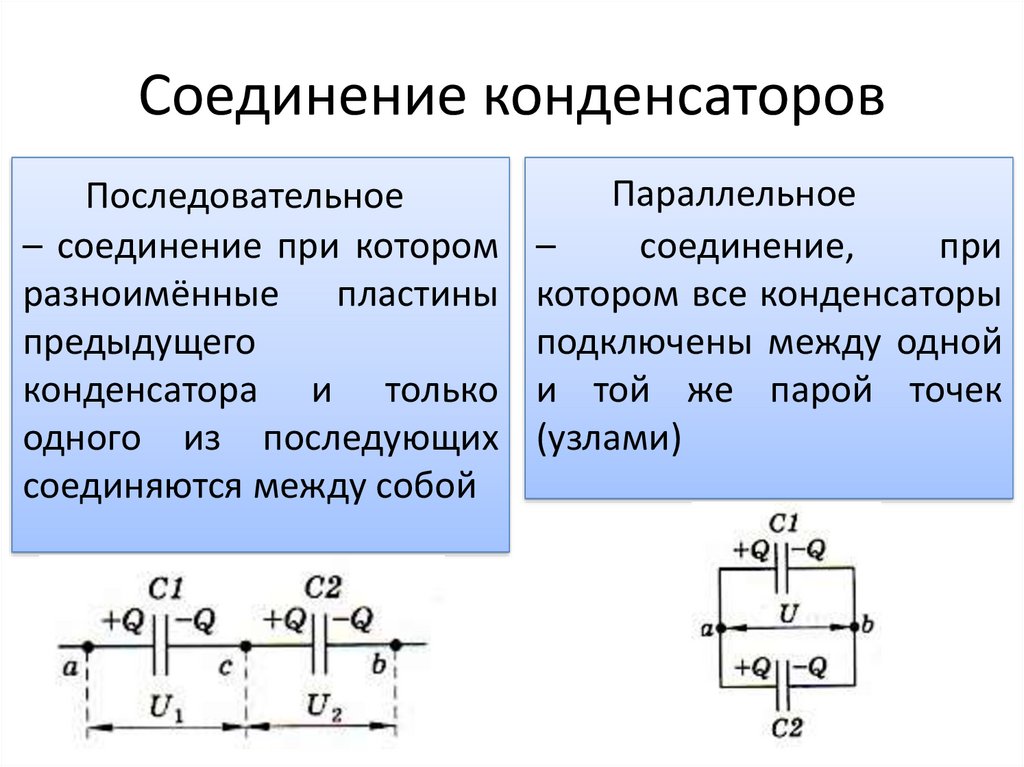 Предположим, что емкости известны с точностью до трех знаков после запятой (C1=1,000 мкФ, C2=5,000 мкФ, (C1=1,000 мкФ, C2=5,000 мкФ, C3=8,000 мкФ).C3=8,000 мкФ). Округлите ответ до трех знаков после запятой.
Предположим, что емкости известны с точностью до трех знаков после запятой (C1=1,000 мкФ, C2=5,000 мкФ, (C1=1,000 мкФ, C2=5,000 мкФ, C3=8,000 мкФ).C3=8,000 мкФ). Округлите ответ до трех знаков после запятой.
Стратегия
Сначала мы определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы C1C1 и C2C2 включены последовательно. Их комбинация, обозначенная CS,CS, параллельна C3.C3.
Решение
Поскольку C1 и C2, C1 и C2 включены последовательно, их эквивалентная емкость CSCS получается с помощью уравнения 8.7:
1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.
Емкость CSCS подключена параллельно с третьей емкостью C3C3, поэтому мы используем уравнение 8.8, чтобы найти эквивалентную емкость C всей сети:
C=CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.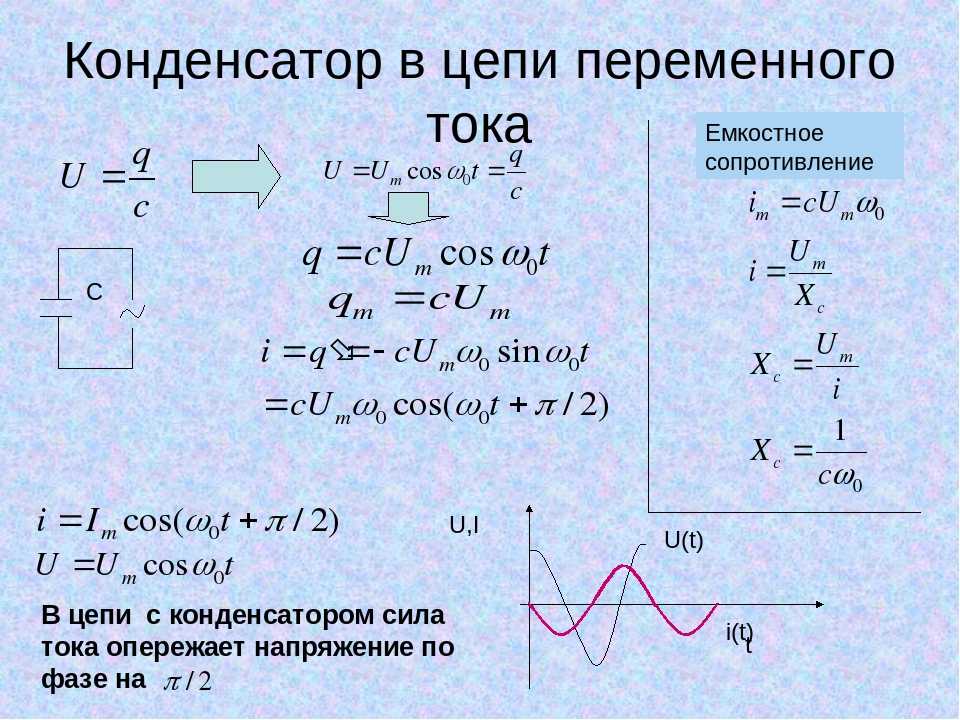 =CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.
=CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.
Пример 8,7
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рис. 8.14, при следующих значениях емкости: C1=12,0 мкФ, C2=2,0 мкФ, C1=12,0 мкФ, C2=2,0 мкФ и C3=4,0 мкФ3=4,0 мкФ. Когда на комбинации сохраняется разность потенциалов 12,0 В, найти заряд и напряжение на каждом конденсаторе.
Рисунок 8.14 а) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.
Стратегия
Сначала мы вычисляем чистую емкость C23C23 параллельного соединения C2C2 и C3C3. Тогда C — это чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C=Q/VC=Q/V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.
Раствор
Эквивалентная емкость для C2C2 и C3C3 равна
C23=C2+C3=2,0 мкФ+4,0 мкФ=6,0 мкФ.C23=C2+C3=2,0 мкФ+4,0 мкФ=6,0 мкФ.
Вся комбинация из трех конденсаторов эквивалентна двум конденсаторам, включенным последовательно,
1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 8.14(b). Поскольку конденсаторы соединены последовательно, они имеют одинаковый заряд Q1=Q23Q1=Q23. Кроме того, конденсаторы имеют разность потенциалов 12,0 В, поэтому
12,0 В=V1+V23=Q1C1+Q23C23=Q112,0 мкФ+Q16,0 мкФ⇒Q1=48,0 мкКл.12,0 В=V1+V23=Q1C1+Q23C23= Q112,0 мкФ+Q16,0 мкФ⇒Q1=48,0 мкКл.
Теперь разность потенциалов на конденсаторе 1 равна
V1=Q1C1=48,0 мкC12,0 мкФ=4,0 В. V1=Q1C1=48,0 мкC12,0 мкФ=4,0 В.
Поскольку конденсаторы 2 и 3 соединены параллельно, они имеют одинаковую разность потенциалов:
V2=V3=12,0 В−4,0 В=8,0 В.
