Динамическое давление жидкости: Как объяснить понятие динамическое давление жидкости

Динамическое давление жидкости Калькулятор | Вычислить Динамическое давление жидкости

✖Плотность жидкости – это масса на единицу объема жидкости.ⓘ Плотность жидкости [LD]		сантиграмм / литрдециграмм/ литрдекаграмм / литрПлотность Землифемтограмм/ литрЗерно на кубический футЗерно на галлон (Великобритания)Зерно на галлон (США)Грамм на кубический сантиметрГрамм на кубический метрГрамм на кубический миллиметрГрамм на литрГрамм на миллилитргектограмм / литрКилограмм на кубический сантиметрКилограмм на кубический дециметрКилограмм на кубический метрКилограмм на литрмегаграмм / литрмикрограмм / литрМиллиграмм на кубический сантиметрМиллиграмм на кубический метрМиллиграмм на кубический миллиметрМиллиграмм на литрнанограмм / литрУнция на кубический футУнция на кубический дюймУнция на галлон (Великобритания)Унция на галлон (США)пикограмм / литрПланковская плотностьФунт на кубический футФунт на кубический дюймФунт на кубический ярдФунт на галлон (Великобритания)Фунт на галлон (США)Слаг на кубический футСлаг на кубический дюймСлаг на кубический ярдТонна (длинная) на кубический ярдТонна (короткая) на кубический ярд	+10% -10%
✖Скорость жидкости – это объем жидкости, протекающей в данном сосуде на единицу площади поперечного сечения. ⓘ Скорость жидкости [uFluid]		Сантиметр в часСантиметр в минутуСантиметр в секундуКосмическая скорость прежде всегоКосмическая скорость СекундаКосмическая скорость третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометры / часКилометр в минутуКилометры / секМорской узелУзел (Великобритания)МахаМаха (стандарт СИ)Метр в часМетр в минутуметр в секундумили / часмили / минутумили / секМиллиметр / часМиллиметр в минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек	+10% -10%

✖Динамическое давление — это просто удобное название для величины, которая представляет снижение давления из-за скорости жидкости.ⓘ Динамическое давление жидкости [Pdynamic]

Атмосфера ТехническийАттопаскальБармикробарСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)сантипаскальдекапаскальдесятипаскальДина на квадратный сантиметрэкса паскаль Фемто паскаль Морская вода для ног (15 °C)Вода для ног (4 °C)Вода для ног (60 ° F)ГигапаскальГрамм-сила на квадратный сантиметргектопаскальДюйм ртутного столба (32 ° F)Дюйм ртутного столба (60 ° F)Дюйм водяного столба (4 °C)Дюйм воды (60 ° F)кгс / кв. смКилограмм-сила на квадратный метрКилограмм-сила / кв. миллиметрКилоньютон на квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыМетр воды (4 °C)МикробармикропаскальМиллибарМиллиметр ртутного столба (0 °C)Миллиметр воды (4 ° C)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футФунт-сила на квадратный футФунт-сила на квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТонна-сила (длинная) на квадратный футТон-сила (длинный) / квадратный дюймТонна-сила (короткая) на квадратный футТонна-сила (короткая) на квадратный дюймторр

⎘ копия

👎

Формула

сбросить

👍

Динамическое давление жидкости Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. (2))/2

Что такое динамическое давление?

Динамическое давление определяется как давление на поверхность, на которой текущая жидкость останавливается, превышающее давление на нее, когда жидкость не течет.

Share

Copied!

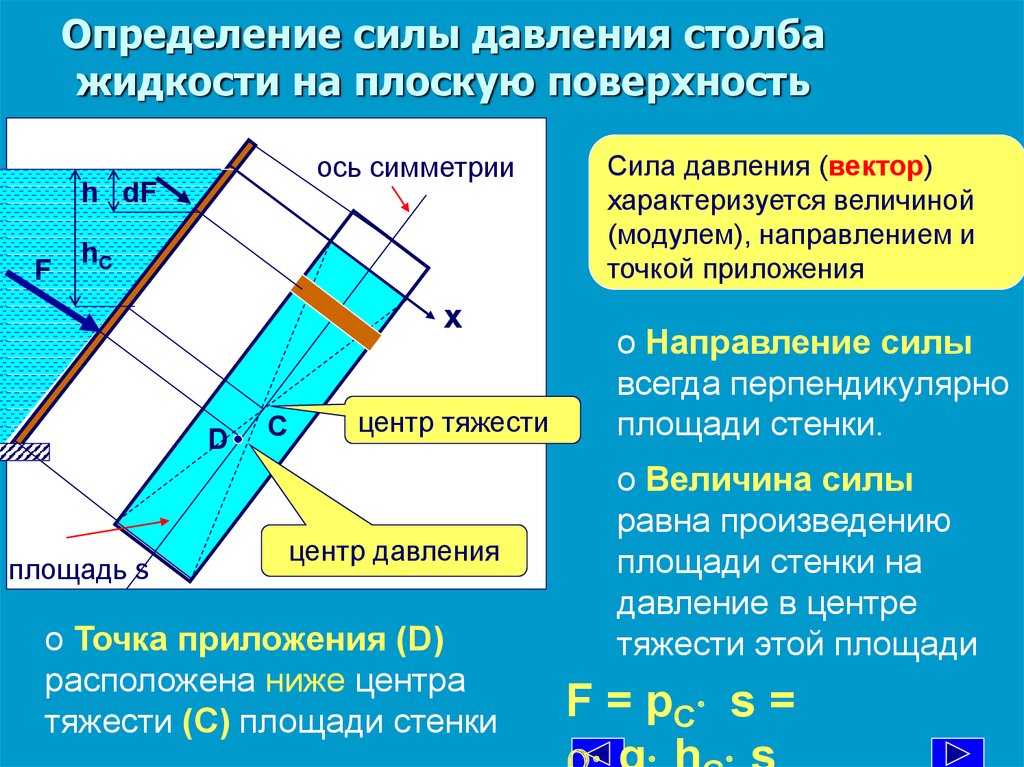
6.2.3. Измерение давления в текущей жидкости

В предыдущем параграфе мы выяснили, что давление в жидкости связано с величиной скорости течения. Введение в жидкость прибора для измерения давления нарушает характер движения жидкости, а следовательно, может изменить и величину измеряемого давления. Поместим в жидкость изогнутую манометрическую трубку с входным отверстием, обращенным навстречу потоку (рис. 6.12). Такую трубку называют

трубкой Пито.

Рис. 6.12. Измерение давления в текущей

жидкости с помощью трубки Пито

Рассмотрим линию тока, упирающуюся своим концом в центр отверстия трубки. Скорость вдоль рассматриваемой линии тока будет изменяться от значения для невозмущенного потока (на больших расстояниях от трубки) до нуля непосредственно перед отверстием. Напишем уравнение Бернулли для точек 1 и 2 упирающейся в отверстие линии тока с учетом, что

Здесь равно давлению в невозмущенном потоке, равно давлению, измеренному манометром. Следовательно, манометр, соединенный с трубкой Пито, покажет давление, равное

=. (6.16)

Слагаемое называют динамическим давлением. Давление в невозмущенном потоке называют статическим. Давление , равное сумме статического и динамического давлений, называют полным давлением. Таким образом, с помощью трубки Пито, можно измерить полное давление (6.16).

Если в тонкой изогнутой трубке сделать боковые отверстия, то скорость (а, следовательно, и давление) вблизи таких отверстий будет мало отличаться от скорости (и давления) невозмущенного потока (рис. 6.13). Поэтому манометр, присоединенный к такой трубке, называемой зондом, покажет статическое давление в жидкости р.

Рис. 6.13. Зонд для измерения статического давления

Зная полное и статическое давления, можно найти динамическое давление, а, следовательно, и скорость течения жидкости (плотность жидкости предполагается известной).

Если трубку Пито и зонд смонтировать вместе, как показано на рис. 6.14, и подсоединить к разным коленам дифференциальный манометр (т.е. манометр, измеряющий разность давлений), то показания манометра будут непосредственно давать динамическое давление.

Рис. 6.14. Трубка для измерения динамического давления

Проградуировав манометр в значениях скорости , можно получить прибор для измерения скорости течения жидкости.

импульса

К жидкостям и газам, как и к другим телам, применим закон сохранения импульса.

Используем этот закон для решения некоторых задач.

Реакция текущей жидкости на стенки изогнутой трубы

Предположим, что в изогнутой трубе установился стационарный поток несжимаемой жидкости (рис. 6.15). Возьмем трубу постоянного сечения . Тогда в силу неразрывности струи скорость в каждом сечении будет одинакова по величине и равна .

Рис. 6.15. Струя жидкости, вытекающая из трубы,

уносит с собой импульс, этот импульс сообщается

вытекающей жидкости сосудом

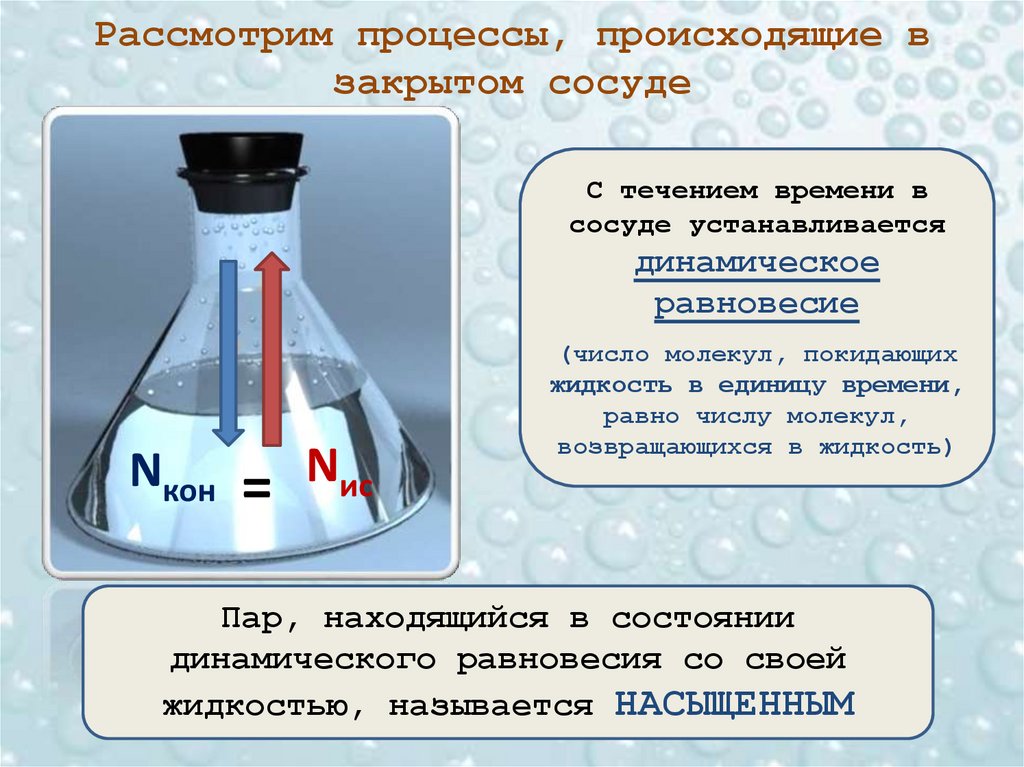
Рассмотрим объем изогнутого участка трубы, ограниченного сечениями и . За время ∆t в этот объем будет втекать через сечение количество жидкости , обладающее импульсом , где — вектор скорости жидкости, протекающей через сечение . Одновременно из этого объема будет вытекать через сечение такое же количество жидкости, обладающее импульсом .

Таким образом, стенки изогнутого участка трубы сообщают за время текущей мимо них жидкости изменение импульса . Пусть сечение трубы постоянно, т.е. ==, тогда и для изменения импульса получим:

=.

Как мы знаем, изменение импульса тела за единицу времени равно действующей на тело силе. Следовательно, стенки трубы действуют на жидкость с силами, равнодействующая которых равна:

.

По третьему закону Ньютона текущая жидкость действует на стенки трубы с силами, равнодействующая которых равна:

. (6.17)

Силу называют реакцией текущей жидкости на стенки трубы – реакция вытекающей струи.

Таким образом, жидкость, текущая по изогнутой трубе, действует на трубу с силой реакции , направленной в сторону, противоположную, направлению изгиба трубы.

Струя жидкости, вытекающая из отверстия в сосуде (рис. 6.16), уносит с собой за время ∆t импульс ( − плотность жидкости, — площадь отверстия, − скорость истечения струи). Этот импульс сообщается вытекающей жидкости сосудом.

Рис. 6.16. Сосуд поставили на тележку,

под действием силы реакции тележка двигается

в направлении противоположном направлению струи

По третьему закону Ньютона сосуд получает от вытекающей жидкости за время

∆t импульс, т.е. испытывает действие силы реакции.

Если сосуд поставить на тележку, то под действием силы он придет в движение в направлении, противоположном направлению струи.

Найдем величину силы , воспользовавшись выражением для скорости истечения жидкости из отверстия – формула Торричелли (6.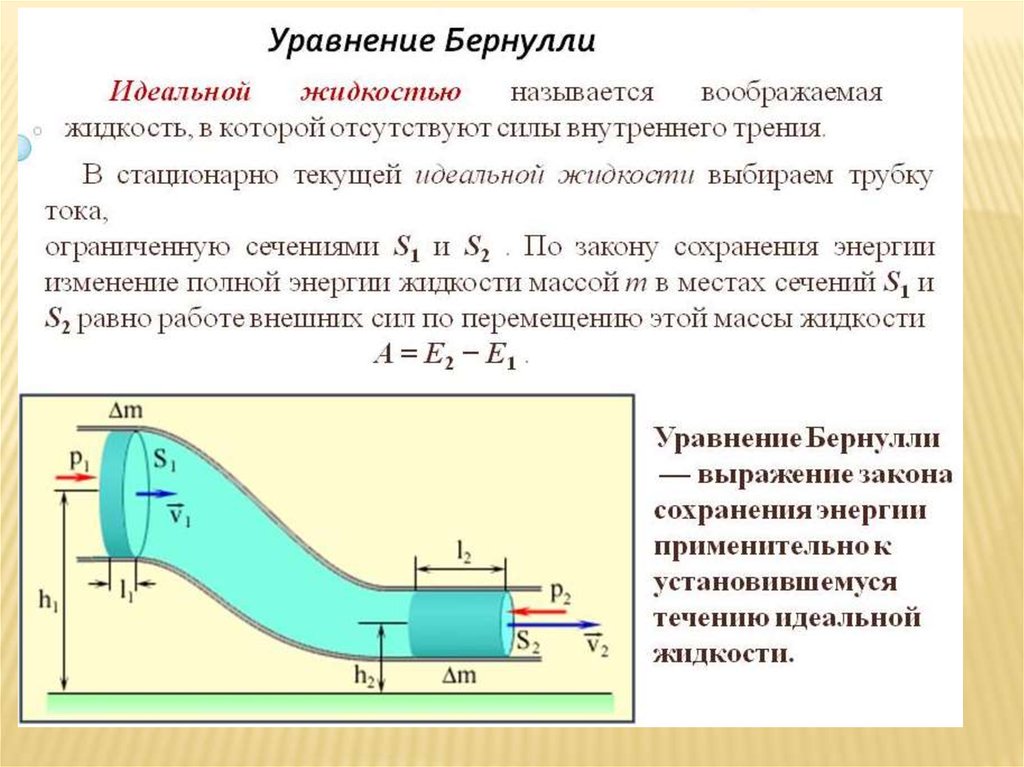 15):

. (6.18)

Если бы, как это может показаться на первый взгляд, сила совпадала по величине с силой гидростатического давления, которое жидкость оказывала бы на пробку, закрывающую отверстие, то была бы равна .

На самом деле сила оказывается в два раза большей. Это объясняется тем, что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.

На реакции вытекающей струи газа основано действие реактивных двигателей и ракет. Реактивное движение, не нуждаясь для своего осуществления в наличии атмосферы, используется для полетов в космическое пространство.

Основоположником теории межпланетных сообщений является выдающийся русский ученый и изобретатель К. Э. Циолковский (1857—1935). Он дал теорию полета ракеты и обосновал возможность применения реактивных аппаратов для межпланетных сообщений. В частности, Циолковским была разработана теория движения составных ракет, в которых каждая последующая ступень вступает в действие после того, как предыдущая ступень, израсходовав полностью топливо, отделится от ракеты. Идеи Циолковского получили дальнейшее развитие и были осуществлены советскими учеными и инженерами, обеспечившими ведущую роль России в освоении и изучении космического пространства.

11.3: Уравнение Бернулли — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14503

• Безграничный
• Безграничный

задачи обучения

• Адаптировать уравнение Бернулли для нестационарных или сжимаемых течений

Применение уравнения Бернулли

Связь между давлением и скоростью в идеальных жидкостях количественно описывается уравнением Бернулли, названным в честь его первооткрывателя, швейцарского ученого Даниэля Бернулли (1700–1782). Уравнение Бернулли утверждает, что для несжимаемой и невязкой жидкости полная механическая энергия жидкости постоянна. (Невязкая жидкость считается идеальной жидкостью без вязкости.)

Принцип Бернулли : Краткое введение в принцип Бернулли для студентов, изучающих жидкости.

Полная механическая энергия жидкости существует в двух формах: потенциальной и кинетической. Кинетическая энергия жидкости хранится в виде статического давления, psps, и динамического давления, 12ρV212ρV2, где \rho — плотность жидкости в (единица СИ: кг/м ³ ), а V — скорость жидкости (единица СИ: м /с). Единицей статического и динамического давления в системе СИ является паскаль.

Перекачка : Перекачка жидкости между двумя резервуарами. Выходной расход можно определить, проведя линию тока из точки (А) в точку (С).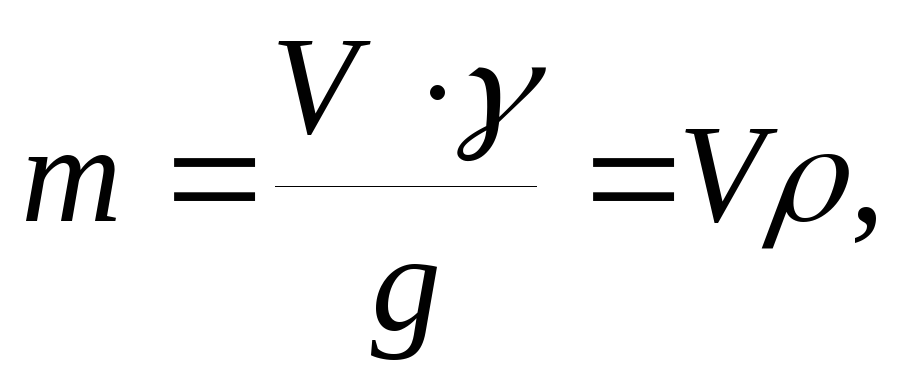

Статическое давление — это просто давление в данной точке жидкости, динамическое давление — это кинетическая энергия на единицу объема жидкой частицы. Таким образом, жидкость не будет иметь динамического давления, если она не движется. Поэтому, если потенциальная энергия вдоль линии тока не изменяется, уравнение Бернулли подразумевает, что полная энергия вдоль этой линии тока постоянна и представляет собой баланс между статическим и динамическим давлением. Математически из предыдущего утверждения следует: 92+ρgΔh=constant.}\]

Вывод уравнения Бернулли

Уравнение Бернулли можно получить, интегрируя 2-й закон Ньютона вдоль линии тока с силами гравитации и давления как единственными силами, действующими на жидкий элемент. Учитывая, что любой обмен энергией является результатом консервативных сил, полная энергия вдоль линии тока постоянна и просто обменивается между потенциальной и кинетической.

Применение уравнения Бернулли

Уравнение Бернулли можно применять при перекачивании жидкости между двумя резервуарами. Еще одним полезным применением уравнения Бернулли является вывод закона Торричелли для потока из отверстия с острыми краями в резервуаре. Линия тока может быть проведена от верхней части резервуара, где известна полная энергия, до точки выхода, где известны статическое давление и потенциальная энергия, но неизвестно динамическое давление (скорость исходящего потока).

Адаптация уравнения Бернулли

Уравнение Бернулли можно адаптировать к нестационарным и сжимаемым потокам. Однако предположение о невязком течении сохраняется как в нестационарной, так и в сжимаемой версиях уравнения. Эффекты сжимаемости зависят от скорости потока относительно скорости звука в жидкости. Это определяется безразмерной величиной, известной как число Маха. Число Маха представляет собой отношение скорости объекта, движущегося в среде, к скорости звука в среде.

Закон Торричелли

Закон Торричелли – это теорема об отношении скорости выхода жидкости из отверстия в резервуаре к высоте жидкости над отверстием.

цели обучения

• Выведите скорость на выходе из уравнения Бернулли

Закон Торричелли — это теорема гидродинамики об отношении скорости выхода жидкости из отверстия с острыми краями в резервуаре к высоте жидкости над этим отверстием. Это соотношение справедливо для «идеальной» жидкости (невязкой и несжимаемой) и является результатом обмена потенциальной энергией 92}\]

Это можно решить для выходной скорости, в результате чего

\[\mathrm{v_e=\sqrt{2gh_t}}\]

, где снова h _t — разница высот между вершиной резервуара и выходного отверстия. Из-за предположения об идеальной жидкости все силы, действующие на жидкость, консервативны, и, таким образом, происходит обмен между потенциальной и кинетической энергией. В результате скорость, приобретаемая жидкостью, такая же, какую приобрело бы тело, просто брошенное с высоты h _т ^.

Простой эксперимент для проверки закона Торричелли включает в себя наполнение бутылки из-под газировки водой и прокалывание дна небольшим отверстием (около 1 см в диаметре).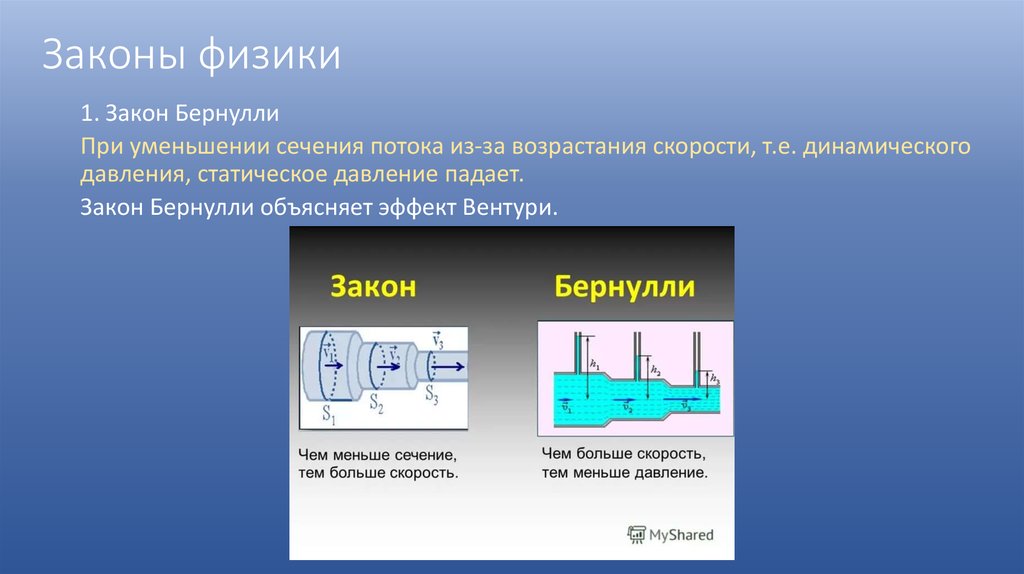 По мере уменьшения высоты в резервуаре скорость на выходе также будет уменьшаться. Скорость на выходе можно увеличить, закрыв верхнюю часть резервуара и создав в нем давление.

Закон Торичелли : Скорость на выходе зависит от высоты жидкости над выходным отверстием. 9

Поверхностное натяжение молекулы.

цели обучения

• Обобщить причины различного поверхностного натяжения на поверхности жидкости

Поверхностное натяжение – это тенденция поверхности жидкости сопротивляться приложенным к ней силам. Этот эффект является результатом сцепления молекул жидкости, в результате чего поверхность жидкости сжимается до минимально возможной площади. Этот эффект виден в природе у водомерок, которые могут ходить по воде. Кроме того, скрепка или булавка могут поддерживаться за счет поверхностного натяжения на границе раздела вода-воздух.

Поверхностное натяжение FBD : Диаграммы сил, показывающие направление сил воды, удерживающих ногу водомерки (насекомого) и булавку.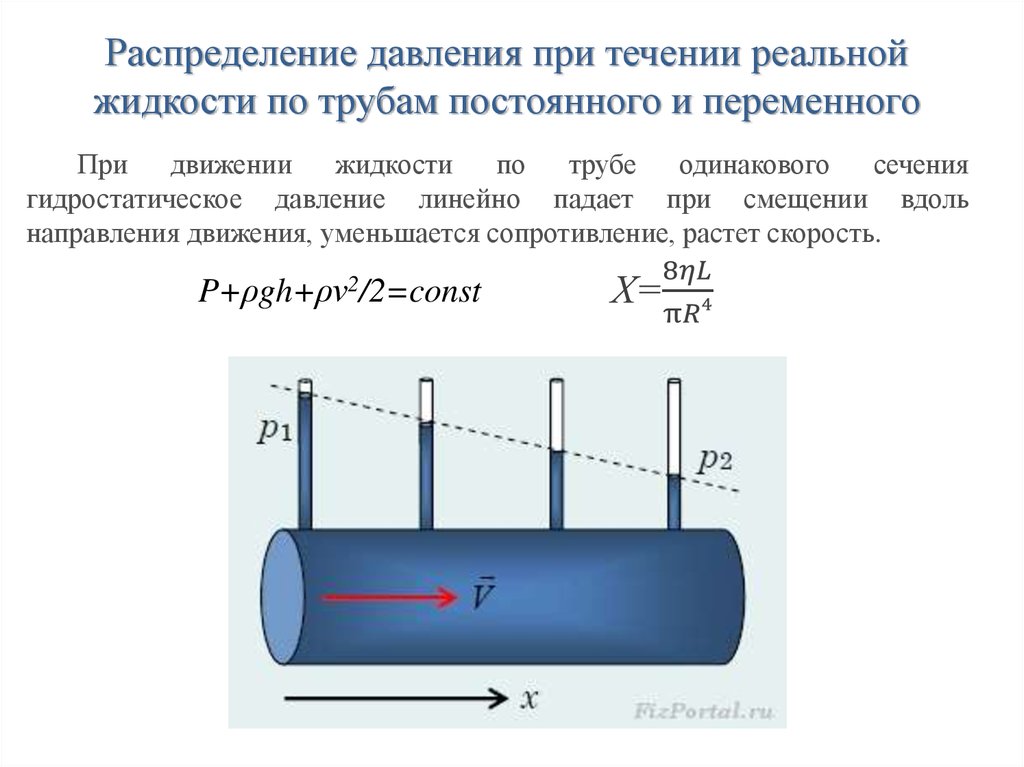 В обоих случаях вертикальной составляющей поверхностного натяжения достаточно, чтобы выдержать вес объекта.

В объеме жидкости молекулы одинаково тянутся во всех направлениях. Молекулы на поверхности испытывают большую силу притяжения к объемному материалу, чем материал поверхности раздела.

Поверхность жидкости – это поверхность раздела между другой жидкостью, твердым телом или тем и другим. Следовательно, поверхностное натяжение будет свойством границы раздела, а не просто жидкости. Адгезия описывает силу притяжения между молекулами разных типов. Поверхность жидкости в сосуде представляет собой границу между жидкостью, воздухом и сосудом. Там, где встречаются поверхности, силы должны находиться в равновесии. Это приводит к контактному углу на границе раздела. Контактный угол измеряется в жидкости и зависит от относительной силы сил сцепления в жидкости и сил сцепления между жидкостью и материалами раздела. Если молекулы жидкости сильно притягиваются к молекулам твердой поверхности (силы сцепления > силы сцепления), капля будет стремиться расплыться, и краевой угол будет близок к нулю градусов. Если когезионные силы больше, чем силы сцепления, результирующие краевые углы будут большими, и капля будет более круглой.

Капля воды на листе : Когда капля воды образуется на листе, силы сцепления между молекулами воды превышают силы сцепления между водой и поверхностью листа. Лист представляет собой гидрофобную поверхность.

Контактный угол : Контактный угол — это угол, измеренный в жидкости, который возникает, когда граница раздела жидкость-газ встречается с твердой поверхностью.

Когда жидкость представляет собой воду, поверхность с малым контактным углом называется гидрофильной. Большие краевые углы присутствуют на гидрофобных поверхностях. Контактный угол определяет смачиваемость поверхности.

Ключевые моменты

• Простейшая форма уравнения Бернулли (стационарное и несжимаемое течение) утверждает, что сумма механической энергии, потенциальной энергии и кинетической энергии вдоль линии тока постоянна. Следовательно, любое увеличение одной формы приводит к уменьшению другой.
• Уравнение Бернулли учитывает только силы давления и гравитации, действующие на частицы жидкости. Следовательно, если вдоль линии тока нет изменения высоты, уравнение Бернулли становится балансом между статическим давлением и скоростью.
• Стационарное уравнение Бернулли для несжимаемой жидкости может быть получено путем интегрирования 2-го закона Ньютона вдоль линии тока.
• Закон Торричелли применим к невязкой, несжимаемой жидкости («идеальной» жидкости).
• Вы можете получить результаты, применяя уравнение Бернулли между верхней частью резервуара и выходным отверстием.
• Связь возникает из-за обмена потенциальной энергии в верхней части резервуара на кинетическую энергию на выходе.
• Конечная кинетическая энергия эквивалентна той, которую приобрело бы твердое тело при падении с высоты h.
• Поверхностное натяжение является результатом сцепления между молекулами жидкости. Молекулы на поверхности жидкости ощущают силу притяжения, притягивающую их к объему жидкости больше, чем твердое тело или жидкость на границе раздела.
• Когда встречается граница раздела жидкость-твердое тело-газ, контактный угол представляет собой меру относительной силы адгезионных и когезионных сил.
• Контактный угол определяет смачиваемость поверхности.

Ключевые термины

• вязкость : Величина, выражающая величину внутреннего трения в жидкости, измеряемая силой на единицу площади, препятствующей равномерному потоку.
• Ideal Fluid : Невязкая и несжимаемая жидкость
• несжимаемый : Невозможно сжать или сжать.
• невязкий : Жидкость с нулевой вязкостью (внутреннее трение). В действительности вязкость присутствует всегда. Однако она часто очень мала по сравнению с другими силами (например, силой тяжести, давлением), и для обычных жидкостей (воды и воздуха) жидкость можно приблизительно представить как имеющую нулевую вязкость.
• когезия : Различные межмолекулярные силы, удерживающие твердые тела и жидкости вместе.
• смачиваемость : Способность твердой поверхности уменьшать поверхностное натяжение жидкости, находящейся с ней в контакте, так что она растекается по поверхности и смачивает ее.
• адгезия : Способность вещества прилипать к другому веществу.

ЛИЦЕНЗИИ И ОТНОШЕНИЯ

CC ЛИЦЕНЗИОННЫЙ КОНТЕНТ, РАСПРОСТРАНЯЕМЫЙ РАНЕЕ

• Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ​​КОНКРЕТНОЕ АВТОРСТВО

• Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/ideal-fluid . Лицензия : CC BY-SA: Attribution-ShareAlike
• несжимаемый. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/incompressible . Лицензия : CC BY-SA: Attribution-ShareAlike
Вязкость
• . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/viscosity . Лицензия : CC BY-SA: Attribution-ShareAlike
• Сифонирование2. Предоставлено : Wikimedia. Расположен по адресу : commons.wikimedia.org/wiki/File:Syphoning2.svg . Лицензия : Общественное достояние: Нет данных Copyright
• Принцип Бернулли. Расположен по адресу : http://www.youtube.com/watch?v=57OB21-I2lQ . Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
• Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/inviscid . Лицензия : CC BY-SA: Attribution-ShareAlike
• Сифонирование2. Предоставлено : Wikimedia. Расположен по адресу : commons.wikimedia.org/wiki/File:Syphoning2.svg . Лицензия : Общественное достояние: Нет данных Copyright
• Принцип Бернулли. Расположен по адресу : http://www.youtube.com/watch?v=57OB21-I2lQ . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
• Предоставлено : Wikimedia. Расположен по адресу : http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5b/TorricelliLaw.svg/200px-TorricelliLaw.svg.png . Лицензия : Общественное достояние: Нет данных Copyright
• Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/5106d670e4b010f3dd6d22de/ideal.png . Лицензия : Общественное достояние: Нет данных Copyright
• Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/5106d406e4b010f3dd6d22c1/peke.png . Лицензия : Общественное достояние: Нет данных Copyright
• Принцип Торричелли. Расположен по адресу : http://www.youtube.com/watch?v=57OB21-I2lQ . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
• Поверхностное натяжение. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Surface_tension%23Effects_of_surface_tension . Лицензия : CC BY-SA: Attribution-ShareAlike
Адгезия
• . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/adhesion . Лицензия : CC BY-SA: Attribution-ShareAlike
• сплоченность. Предоставлено : Викисловарь. Расположен по адресу : en. wiktionary.org/wiki/cohesion . Лицензия : CC BY-SA: Attribution-ShareAlike
• смачиваемость. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/wettability . Лицензия : CC BY-SA: Attribution-ShareAlike
• Сифонирование2. Предоставлено : Wikimedia. Расположен по адресу : commons.wikimedia.org/wiki/File:Syphoning2.svg . Лицензия : Общественное достояние: Нет данных Copyright
• Принцип Бернулли. Расположен по адресу : http://www.youtube.com/watch?v=57OB21-I2lQ . Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
• Предоставлено : Wikimedia. Расположен по адресу : http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5b/TorricelliLaw.svg/200px-TorricelliLaw.svg.png . Лицензия : Общественное достояние: Нет данных Copyright
• Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/5106d670e4b010f3dd6d22de/ideal.png . Лицензия : Общественное достояние: Нет данных Copyright
• Безграничный. Предоставлено : Amazon Web Services. Расположен по адресу : s3.amazonaws.com/figures.boundless.com/5106d406e4b010f3dd6d22c1/peke.png . Лицензия : Общественное достояние: Нет данных Copyright
• Принцип Торричелли. Расположен по адресу : http://www.youtube.com/watch?v=57OB21-I2lQ . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
• Эрик Кристенсен, Колледж физики II. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42197/latest/?collection=col11458/1.2 . Лицензия : CC BY: Attribution
• SurfTensionContactAngle. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:SurfTensionContactAngle.png . Лицензия : Общественное достояние: Нет данных Copyright
• Роса 2. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Dew_2.jpg . Лицензия : Общественное достояние: Нет данных Copyright

---

Эта страница под названием 11.3: Уравнение Бернулли распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Безграничный

   Показать оглавление

   нет

2. Теги

   1. адгезия
   2. Уравнение Бернулли
   3. сплоченность
   4. идеальная жидкость
   5. несжимаемый
   6. невязкий
   вязкость
   8. смачиваемость

Учет динамического давления (напора) при выходе жидкости из трубы в системе Pipe Flow Expert

Давления: статическое давление в сравнении с давлением застоя
(с учетом динамического давления из-за скорости жидкости)

1. Статическое давление — это давление, которое жидкость оказывала бы на окружающую среду, если бы она не двигалась.
2. Динамическое давление, также известное как скоростное давление, представляет собой давление, вызванное скоростью жидкости.
3. Давление застоя — это общее давление, которое представляет собой статическое давление плюс динамическое давление.

В Pipe Flow Expert резервуар действует как бесконечный резервуар с жидкостью, который считается покоящимся с нулевой скоростью жидкости. Когда жидкость находится в состоянии покоя, полное давление (давление застоя) и статическое давление равны, поскольку динамическое давление отсутствует, поскольку скорость жидкости равна нулю.

Когда жидкость начинает двигаться по трубе со скоростью, часть давления преобразуется в динамическое (скоростное) давление и, следовательно, статическое давление в трубе уменьшается (на скоростное давление).

В Pipe Flow Expert условия граничного давления, определенные параметрами Резервуары или Конечные давления, представляют собой статические давления, которые не включают динамическое давление из-за скорости жидкости. Для учета скоростного давления в точке нагнетания необходимо предусмотреть «выходной» фитинг, чтобы обеспечить потерю давления, эквивалентную скоростному давлению. Точка непосредственно перед выходным фитингом представляет общее давление, включая скоростной напор (статическое давление нагнетания + динамическое давление из-за скорости жидкости). 92/2g, что является динамическим скоростным давлением в напоре жидкости.

Разность давлений от давления в точке вверх по течению до общего давления в точке нагнетания определяет расход, который будет иметь место, поэтому необходимо включать выходной фитинг, чтобы получить общее давление, включая скорость голову в точке непосредственно перед выгрузкой.

Если мы возьмем, например, выброс в атмосферу, мы можем использовать узел конечного давления в Pipe Flow Expert и установить его на 0 бар изб. Здесь статическое атмосферное давление равно 0 бар изб., однако жидкость вытекает из конца трубы с некоторой скоростью (динамическое давление), и поэтому мы также включаем выходной фитинг с коэффициентом k, равным 1, для учета этого давления скорости, что делает точка перед выходным фитингом равна общему давлению, включая скоростное давление.

В модель включен выходной фитинг с коэффициентом k, равным 1 (как поясняется в техническом документе Crane 410). Потери через этот фитинг, по существу, представляют собой динамическое давление протекающей жидкости.

, то есть вы можете думать об этом как о программном обеспечении, использующем выходной фитинг для «расчета» того, какое давление застоя (общее давление) будет непосредственно перед выходным фитингом, поскольку это статическое давление плюс динамическое давление жидкости.

Если вы хотите указать статическое давление для сброса, как в случае сброса в атмосферу или в какой-либо контейнер, вам необходимо включить выпускной фитинг для учета скоростного напора, как описано в примечаниях выше.

Примечание: При рассмотрении общей работы трубопроводной системы разница между полным и статическим давлением может быть незначительной. Для большинства жидких применений скорости жидкости, как правило, относительно низки, чтобы свести к минимуму потери на трение, и это приводит лишь к небольшому количеству динамической энергии жидкости, что означает разницу между полным и статическим давлением, хотя часто и незначительную, при измерении их на многих промышленные манометры.