Аксонометрия
Аксонометрия — особый отдел в черчении, в нем изучается то, как получить наглядное изображение предметов на плоскости. Аксонометрическая проекция выглядит как точный рисунок предмета. Аксонометрия, расшифровывается как измерение по осям.
Проекции в аксонометрии разделяют на несколько видов:
1) Прямоугольная — это когда проецируемые прямые, перпендикулярные к плоскости акс.проекции. Так же в этот вод входят — диметрическая и изометрическая.
2) Косоугольная — этом когда прямые идут не под углом 900 относительно акс. проекции. Так же в этот вид входит проекция фронтальная диметрическая.
Во время выполнения переноса предмета на проекцию, возможно искажение осей.
Помощь в ознакомлении с учебником или с любой книгой по которой учатся предоставляет сайт — учебник pdf (http://ruscopybook.com/). Публикация изданий позволяет учителям ознакомиться с существующими учебно-методическими комплектами и выбрать подходящий для преподавания.
Чаще всего используются в работе, косоугольная фронтальная диметрическая и изометрическая проекции, потому что они являются наиболее простыми. Их мы и разберем. По другим предметам поможет разобраться сайт учебник pdf (http://ruscopybook.com/).
— Косоугольная фронтальная диметрическая проекция.
для данной проекции искажение на оси у — 0,5, на оси х и z = 0. Это означает что высота и длина отмеряются в натуральные, а ширина отмеряется с уменьшением в два раза.
— Прямоугольная изометрическая проекция
Данная проекция обладает преимуществом так как данные не искажаются на всех осях. То есть имеет одинаковое измерение по всем осям, соответственно и размеры предмета, на осях откладываются натуральные.
Для того что бы получить аксонометрическую проекцию, нужно расположить предмет в системе координатных осей, перед акс.плоскостью. Дать проецируемое направление и провести через все точки мысленно, лучи до пересечения с плоскостью.
— Изометрическая Прямоугольная
Перемещаем предмет в угол координат и ставим его так что бы наклон сторон был равным к акс. плоскости. Проводим невидимые лучи через точки, под углом девяносто градусов, до пересечения с плоскостью.
— Косоугольная фронтальная диметрическая проекция.
Рядом с P-плоскостью ставим предмет, чтобы передняя сторона находилась фронтально к плоскости. Проводим лучи параллельные, относительно плоскости под острым углом. Получаем координатные оси и проекцию предмета косоугольную фронтальную диметрическую.
Для чего нужно уметь правильно переносить плоские фигуры на проекцию?
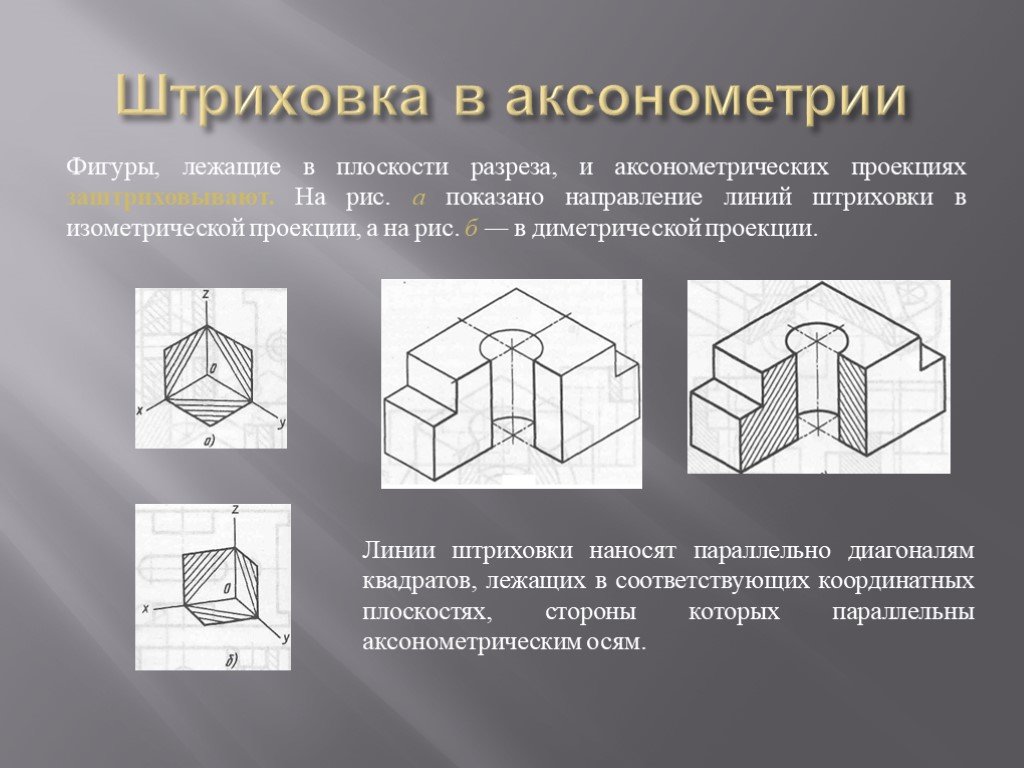
Разрез в аксонометрических проекциях.
При выполнении аксонометрических изображений сложных деталей, имеющие внутренние полости, применяют разрезы для выявления внутренних форм деталей. Их осуществляют двумя или тремя плоскостями, каждую из которых располагают параллельно координатной плоскости. Чаще всего секущие плоскости совпадают с плоскостями симметрии детали и соответствуют плоскостям разрезов, выполненных на чертеже детали. На аксонометрических проекциях не рекомендуется выполнять полный разрез, так как при этом теряется наглядность изображения. Обычно вырезают одну четвертую часть детали. Угол, образованный секущими плоскостями, всегда должен быть видимым.
Для определения
наклона линии штриховки в каждой
плоскости сечений поступают следующим
образом.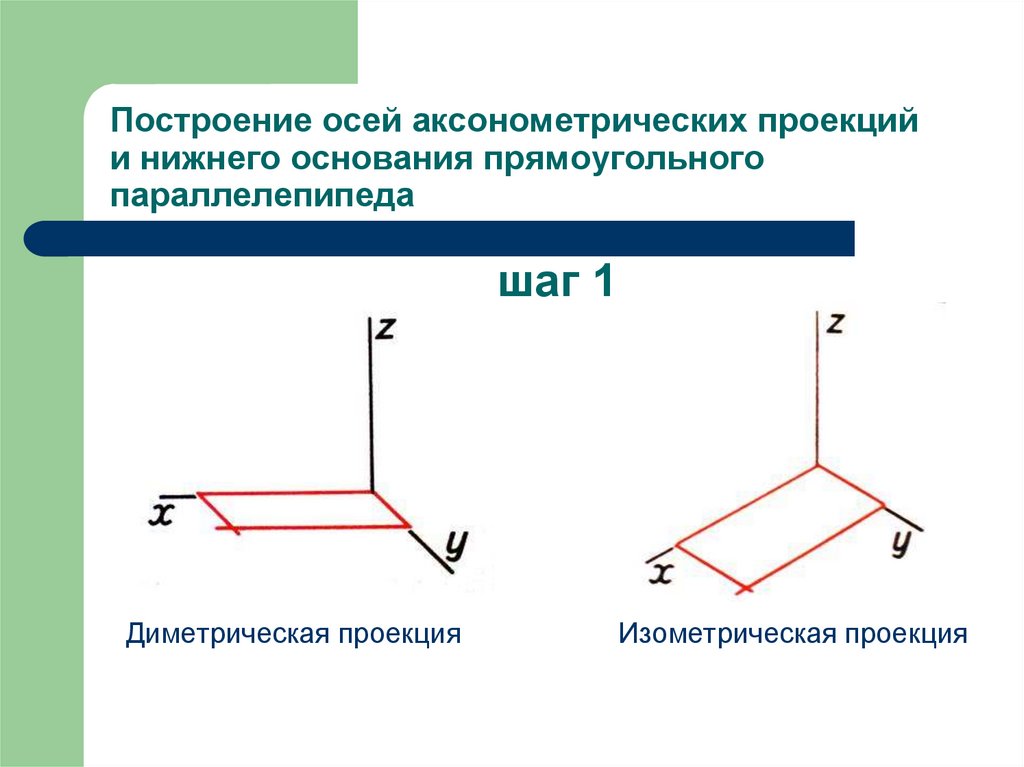
Строят аксонометрические
проекции квадратов, лежащих в координатных
плоскостях XOY,
XOZ,YOZ, причем стороны
квадратов параллельны и лежат на
координатных осях X,
Y,
Z.
Линии штриховки наносят параллельно
диагоналям квадратов (рисунок
11.21, 11.22).
Рисунок 11.21 Рисунок 11.22
На рисунках 11.23, 11.24 показано направление штриховки прямоугольной изометрической проекции, на рисунках 11.25, 11.26 – в прямоугольной диметрической проекции.
Пример штриховки в четверти выреза детали показаны на рисунках 11.23, 11.24, 11.25, 11.26.
Рисунок 11.23
Рисунок 11.24
Рисунок 11.25
Рисунок 11.26
Если секущая плоскость
проходит через ребра жесткости, сплошные
выступы или тонкие стенки, то сечения
этих элементов деталей всегда покрывают
штриховкой, то есть изображают разрезанными
(рисунок 11.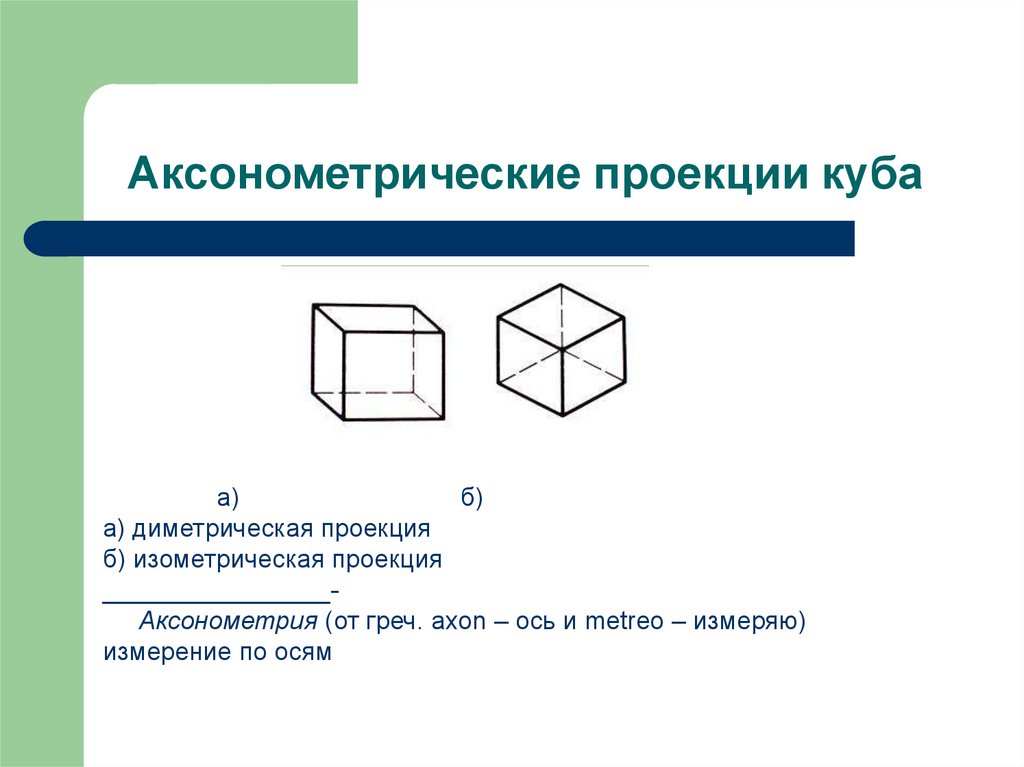
27).
Рисунок 11.27
Для построения аксонометрических проекций применяют способы координат, вторичных проекций, сечений, вписанных сфер, проекционной связи и др..
Способы координат.
Часто приходится, пользуясь ортогональными проекциями, строить аксонометрические изображения по координатам. При построении необходимо откладывать по осям в аксонометрии соответствующие размеры, взятые с ортогонального чертежа.
Плоские и пространственные кривые строят по координатам отдельных точек. Приступая к вычерчиванию деталей в аксонометрии, следует прежде всего решить, вдоль какой оси будет направлен тот или иной их размер. Обычно длину откладывают вдоль оси OX, ширину – вдоль оси OY и высоту – вдоль оси OZ.
Аксонометрические
координаты, откладываемые параллельно
соответствующим осям, равны натуральным
координатам X, Y, Z, измеренными по
ортогональным проекциям и умноженным
на соответствующий показатель искажения
(рисунок 11.
Рисунок 11.28
На рисунке 11.29 показано выполнение аксонометрии детали с четвертью выреза
Рисунок 11.29
Способы сечений.
По данному комплексному чертежу предмета сначала строят аксонометрические проекции фигур сечения, затем дочерчивают части изображения предмета, расположенные за секущими плоскостями. Второй способ упрощает построение, освобождает чертеж от лишних линий (рисунок 11.30).
Рисунок 11.30
При
выборе вида аксонометрического
изображения необходимо учитывать
следующее: если тело имеет квадратную
форму или отдельная часть предмета
квадратная, то следует выполнять
прямоугольную диметрическую проекцию
этого тела, так как в прямоугольной
изометрии ухудшается наглядность
изображения.
Другие способы построения аксонометрических проекций подробно рассмотрены в учебнике «Строительные черчение» авторы Будасов Б.В., Каменский В.П. (Стройиздат 1995г. с изменениями).
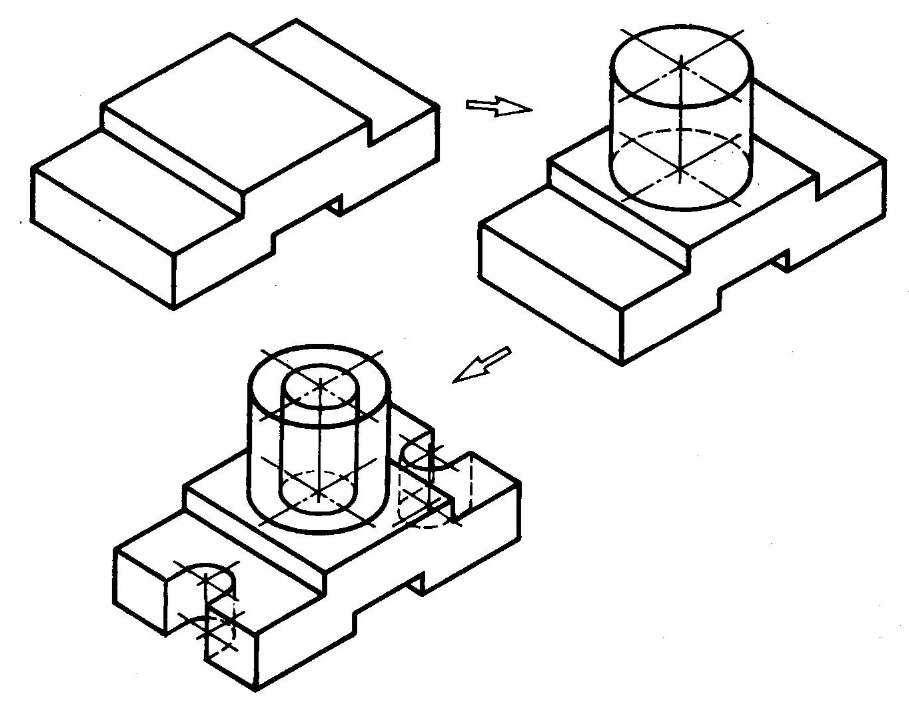
Пересечение тел в аксонометрии. Пересечение цилиндрических поверхностей.
Для построения изометрической проекции пересекающихся цилиндров необходимо построить линию пересечения этих тел (глава 8 п.8.3;п.8.4) на комплексном чертеже (рисунок 11.31).
Рисунок 11.31
Построение
прямоугольной изометрической проекции
пересекающихся цилиндров начинают с
построения изометрии вертикального
цилиндра. Далее через точку о´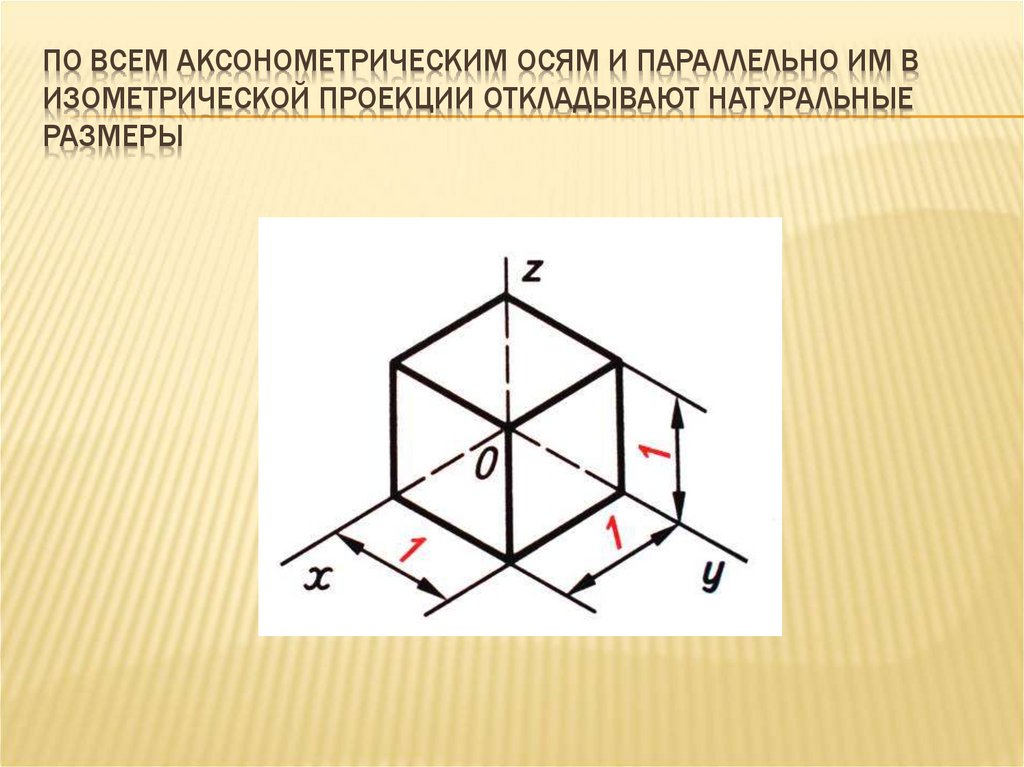
32). откладывая от точки
о´1 по оси горизонтального цилиндра отрезок
l, получим точку о´ – центр основания
горизонтального цилиндра.
Рисунок 11.32
Изометрия линии пересечения строится по точкам при помощи трех координат, как это было показано на рисунке 2. однако в данном примере искомые точки можно построить несколько иначе.
Так,
например, изометрию точек 3´ и 2´ строят
следующим образом. От центра 0´2 (рис.11.32) вверх по прямой, параллельной
оси о´z´, откладывают отрезки m и n, взятые
с комплексного чертежа. Через концы
этих отрезков проводят прямые, параллельные
оси о´у´, до пересечения с эллипсом или
овалом (основанием горизонтального
цилиндра) в точках 3´ 1 и 2´1 . Затем из точек 3´1 и 2´1 проводят прямые, параллельные оси о´х´,
и на них откладывают отрезки, равные
расстоянию от основания горизонтального
цилиндра до линии пересечения, взяты с
фронтальной или горизонтальной проекции
комплексного чертеже, например, отрезок
3´1 3´ = 31 3.
Конечные точки этих отрезков будут
принадлежать изометрии линий пересечений.
Через эти точки проводят по лекалу
кривую, выделяя ее видимы и невидимые
часть.
Пересечение поверхностей призм и пирамид.
В приемах построения проекции линии пересечения двух прямых призм много общего с построением линий пересечения двух цилиндров. Если ребра двух призм взаимно перпендикулярны (рисунок 11.33) линия пересечения призм строится следующим образом.
Рисунок 11.33
В данном случае горизонтальная и профильная проекции линии пересечения совпадаю соответственно с горизонтальной проекцией пятиугольника (основание одной призмы) и с профильной проекцией части четырехугольника (основание другой призмы). Фронтальную проекцию ломанной линии пересечения строят по точкам пересечения ребер одной призмы с гранями другой.
Например,
взяв горизонтальную 11 и профильную 12 проекции точки 11 пересечение ребра пятигранной призмы
с гранью четырехгранной и пользуясь
известным приемом построения, с помощью
линии связи можно легко найти и фронтальную
проекцию 12 точки 11,
принадлежащей линии пересечения призмы.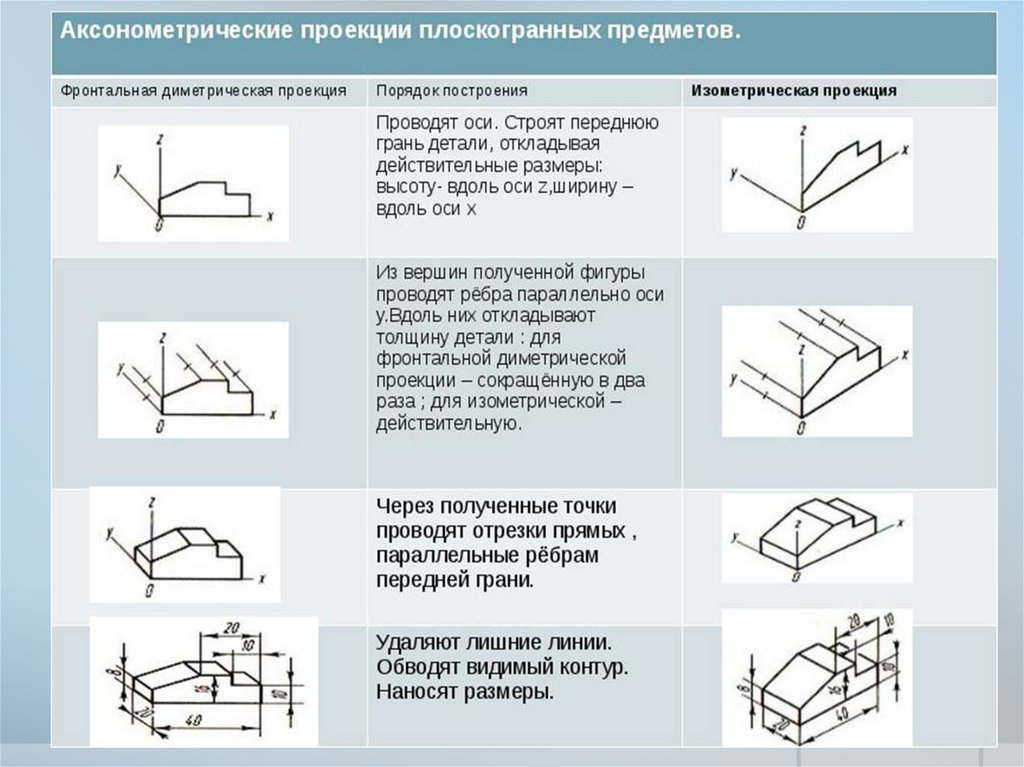
Изометрическая проекция линии пересечения двух призм может быть построена по координатам точек этой линии.
Рисунок 11.34
Например, изометрию двух точек 5´ и 5´1, симметрично расположенных на левой грани пятигранной призмы, строят так. Принимая для удобства построений за начало координат точку о´, лежащую на верхнем основании пятигранной призмы, откладываем в лево от о´ по направлению, параллельному изометрической оси о´х´, отрезок о´Е´, равной координате х5, взятой с комплексного чертежа на фронтальной или горизонтальной проекции. Далее из точки Е´ вниз параллельно оси o´z´ откладываем отрезок Е´F´, равный второй координате z5 = a, и, наконец, от точки F´ влево и вправо параллельно оси о´y´ откладываем отрезки F´5´ и F´5´1, равные третьей координате у5 = .
Далее от точки F´
параллельно оси о´x´ откладываем отрезок
n, взятый с комплексного чертежа.
Через
его конец проводим прямую, параллельную
оси о´y´, и откладываем на них отрезок,
равный с. Вниз параллельно оси о´z´
откладываем отрезок, равный b, и параллельно
о´y´ — отрезок, равные к. В результате
получаем изометрию основания четырехгранной
призмы.
Точки 1´ и 4´ на ребрах пятигранной призмы можно построит используя только одну координату z.
Руководство дизайнера по изометрической проекции | Александр | Gravit Designer
Термин «изометрический» — одно из самых неправильно используемых слов в индустрии дизайна. Мы склонны называть любой неперспективный трехмерный рисунок «изометрическим».
Одним из недавних примеров псевдоизометрических работ является старый логотип Medium, использовавшийся с 2015 по 2017 год. Он был спроектирован на параллельной (аксонометрической) сетке, но совсем не изометрической.
Старый логотип Medium был разработан на триметрической сетке. В этой статье я объясню различия между изометрическими и другими типами проекций.
Графические рисунки
Способность визуализировать трехмерные формы — это навык, которым должен овладеть каждый дизайнер и инженер. Это особенно важно в 3D-моделировании. Однако есть явная разница между рисованием вида, который выглядит как трехмерный, и созданием настоящей 3D-модели.
Реальные 3D-модели можно поворачивать на экране для просмотра под любым углом. Компьютер вычисляет точки, углы и поверхности объекта в пространстве. Затем он отображает результат на плоском экране в виде так называемых графических рисунков.
Слово pictorial означает «как картинка». Это относится к любому реалистичному типу рисунка, изображающему высоту, ширину и глубину объекта. Графические рисунки чрезвычайно полезны, когда нам нужно сообщить проекты людям, которые не имеют технической подготовки в интерпретации многоракурсных проекций.
Пикториал с многоракурсными рисунками. Источник изображения site.google.com/site/multiviewdrawings/home.Несколько форм графических проекций используются в дизайне и технических чертежах:
- Перспектива — самые реалистичные рисунки.
Наши глаза видят объекты в перспективе. Существует три вида перспективных проекций: одно-, двух- и трехточечная перспектива.
Наши глаза видят объекты в перспективе. Существует три вида перспективных проекций: одно-, двух- и трехточечная перспектива.- Косой — наименее реалистичный. Только одна или две грани в косых проекциях имеют истинную форму и размеры. Косые проекции бывают трех видов: кабинетная, кавалерская и генеральная.
- Аксонометрические проекции более реалистичны, чем косые. Горизонтальные ребра объекта в аксонометрических проекциях параллельны друг другу и наклонены к плоскости. Различают три типа аксонометрических проекций: изометрические , диметрические и триметрические.
Аксонометрические проекции
Аксонометрические проекции являются наиболее распространенным способом изображения трехмерных объектов без использования перспективы.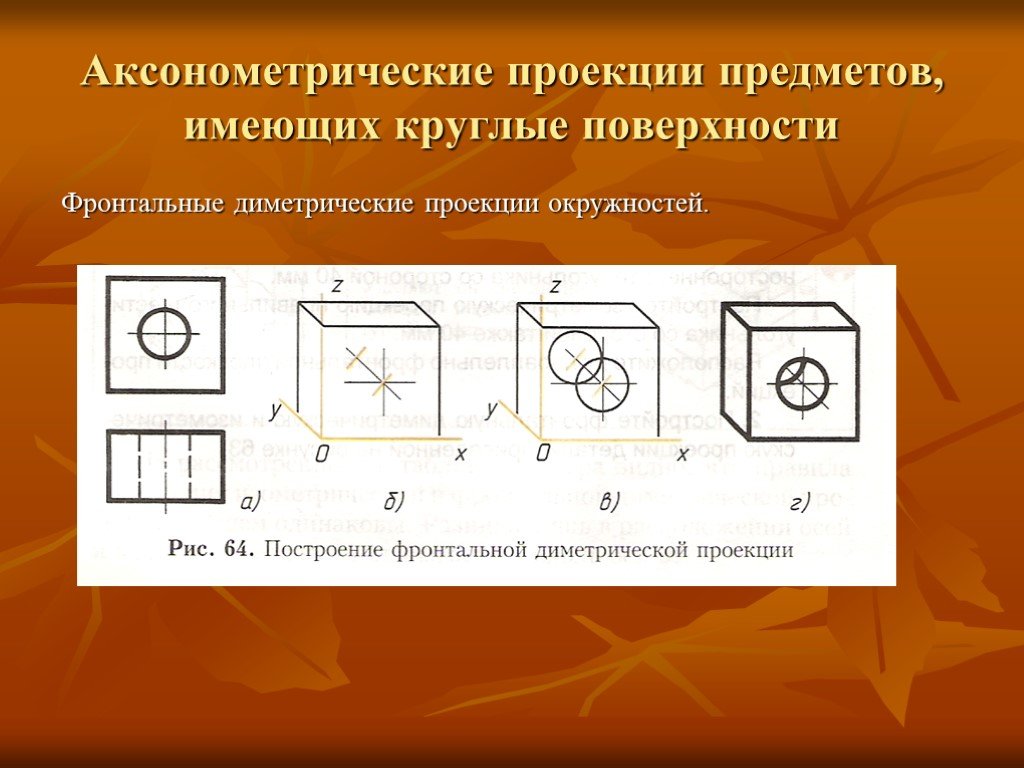
В отличие от чертежей в перспективе, все оси в аксонометрических проекциях не сходятся и всегда остаются параллельными.
Ни точек схода, ни линии горизонта. Объект не становится меньше с расстоянием. Это было очень важно для игровой индустрии между 1980 и 1990 годами, потому что компьютеры той эпохи с ограниченными ресурсами должны были отображать объект только один раз.
Основная цель аксонометрических проекций — показать форму и размер объекта. Они спроектированы таким образом, что прямо с этих проекций можно производить измерения объектов.
Все три типа аксонометрических проекций строятся на сетке, где оси X и Z наклонены к горизонтальной плоскости. Ось Y всегда остается перпендикулярной горизонтальной плоскости.
Оси X и Z наклонены к горизонтальной плоскости. Источник изображения: vitorials.net. Угол между «горизонтальными» осями X и Z и горизонтальной плоскостью определяет тип аксонометрической проекции.
Изометрическая проекция
Изометрическая (означает «равная мера») тип параллельной (аксонометрической) проекции, в которой оси X и Z наклонены к горизонтальной плоскости под углом 30⁰. Угол между аксонометрическими осями равен 120⁰.
30/120/30 также называют истинной изометрической сеткой.Идеальный куб в изометрической проекции выглядел бы как идеальный шестиугольник.
В Gravit Designer вы можете построить истинную изометрическую сетку прямо из коробки.
Вы можете настроить размер изометрической сетки по умолчанию в Gravit Designer.Поскольку все края изометрического объекта наклонены под одним и тем же углом, они одинаково укорочены. Это позволяет вам измерять каждую сторону объекта, используя один и тот же масштаб.
Изометрическая длина и истинная длина. Источник изображения: ed-zon.blogspot.com/2013/05/isometric-projection-and-isometric.html. Большинство дизайнеров игнорируют ракурс на этапе эскиза и строят изометрические виды объекта с фактической длиной.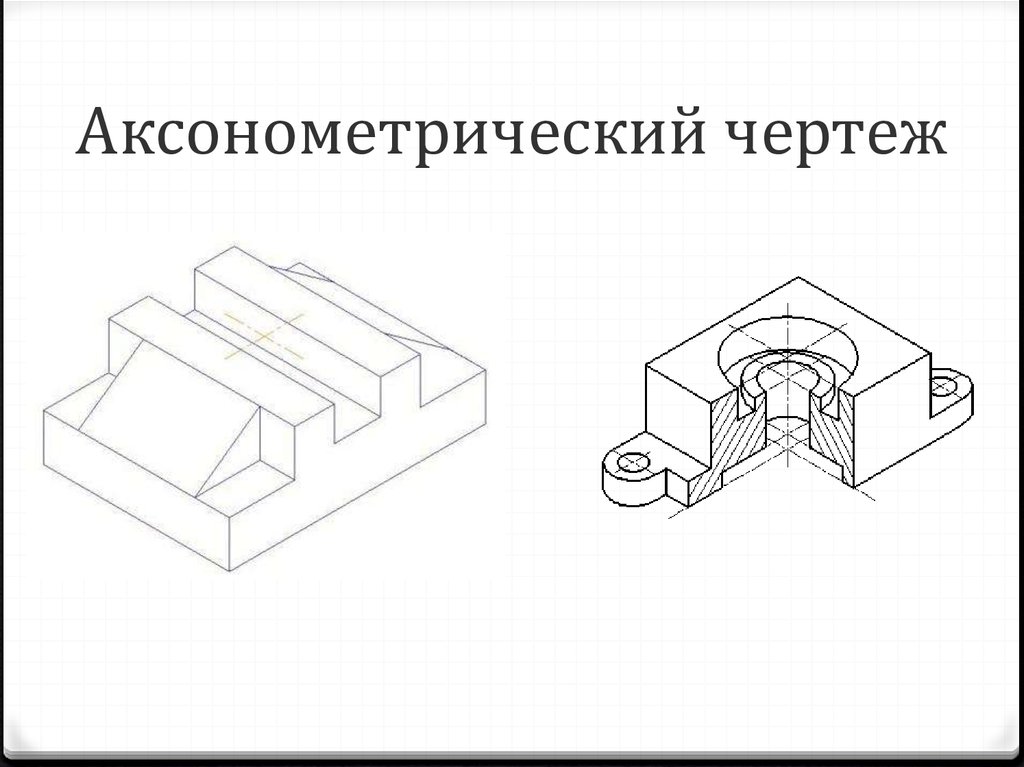
Конечным результатом будет изометрический эскиз, а не проекция.
Как строить изометрические изображения без сетки
Использование изометрической сетки — не единственный способ рисования изометрических изображений в Gravit Designer.
Их можно построить прямо из мультиракурсных проекций (сверху, спереди, сбоку и т.д.). Наиболее распространенными и простыми являются SR45⁰ и SSR30⁰ .
Это очень удобные методы, когда вам нужно создать анизометрический макет вашего дизайна в несколько кликов:
Создание изометрического актива с использованием метода SSR в Gravit Designer.SR45⁰ техника
«SR45⁰» обозначает масштабирование и поворот на угол 45⁰. Масштабное отношение составляет 0,577 или более ценно загар(30⁰) .
Вы можете создать изометрические прогнозы с помощью SR45⁰, используя панель Transform Designer Gravit в двух простых шагах
Шаг 1: Вращение объекта 45⁰
Шаг 2: Scale Abyt
SSR30⁰ Technique
«SSR3016
популярный и гибкий метод создания изометрических произведений искусства.
С помощью SSR30⁰ вы можете быстро создавать изометрические виды сверху, слева и справа.SSR30⁰ означает масштаб, наклон и поворот на 30⁰.
Использование метода SSR в Gravit Designer. Источник изображения: vitorials.net.Создание других аксонометрических проекций с помощью Gravit Designer
В диметрических проекциях только две стороны имеют одинаковый ракурс. Оси X и Z по-прежнему находятся под одним и тем же углом к горизонтальной плоскости, но не под углом 30°. Углы между осями не равны.
Общая диметрическая сетка 15⁰ в Gravit Designer.Триметрические проекции
Все углы триметрических проекций различны, поэтому все стороны (ребра) и оси укорачиваются неодинаково.
Вы можете настроить триметрическую сетку в Gravit Designer за несколько секунд.Вы можете использовать широкий спектр углов для создания триметрических и диметрических изображений, но обязательно избегайте маленьких. На мой взгляд, это делает проекцию слишком плоской:
Маленькие углы делают вашу работу слишком плоской.
Анатомия логотипа Medium
Оригинальный логотип Medium был разработан на неизометрической сетке, где оси X и Y наклонены к горизонтальной плоскости под углом -27⁰ и 60⁰ соответственно. Итак, логотип Medium построен на триметрической сетке.
Средний предыдущий логотип был трехметровымЕсли вы дошли до этого места, поздравляем! Я надеюсь, что все эти GIF и JPG не сделали ваш браузер (или даже вас 😉 ) излишним. Я также надеюсь, что вы получили некоторую ценность для себя и некоторые новые инструменты для использования в ваших изометрических рисунках.
Веб-сайт | Facebook | Твиттер | Форум
Напишите нам и получите до 100 €
Мы хотим пригласить вас, наш дорогой читатель, написать для нас. Это не только сохраняет актуальность блога, но и предоставляет новые…
medium.com
Аксонометрическая проекция — Вопросы и ответы по техническому чертежу
Зачем мне учиться решать вопросы и ответы по техническому чертежу в разделе «Аксонометрическая проекция»?
Изучите и попрактикуйтесь в решении раздела вопросов и ответов по техническому чертежу в разделе «Аксонометрическая проекция», чтобы улучшить свои навыки, чтобы вы могли пройти собеседования, конкурсные экзамены и различные вступительные тесты (CAT, GATE, GRE, MAT, банковские экзамены, железнодорожные экзамены, д.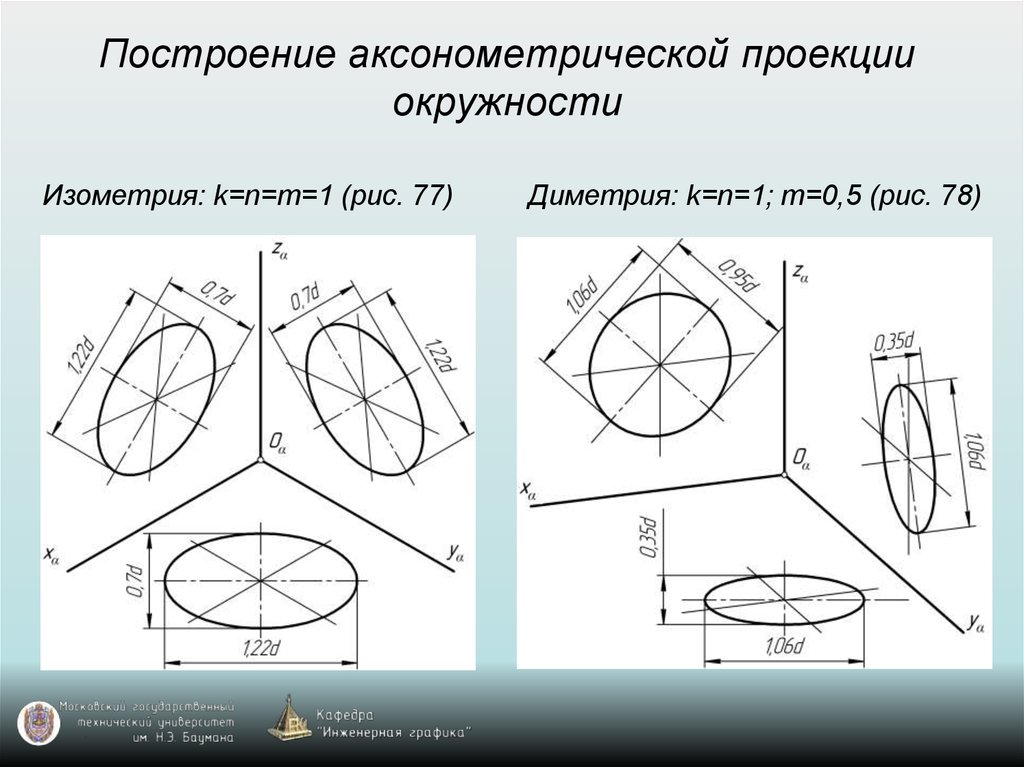
), с полной уверенностью.
Где я могу получить раздел вопросов и ответов по техническому чертежу «Аксонометрическая проекция»?
IndiaBIX предоставляет вам многочисленные вопросы и ответы по техническим чертежам, основанные на «аксонометрической проекции», а также полностью решенные примеры и подробные объяснения, которые будут просты для понимания.
Где я могу получить раздел «Технический рисунок» по вопросам и ответам типа MCQ «Аксонометрическая проекция» для собеседования (объективный тип, множественный выбор)?
Здесь вы можете найти вопросы и ответы по техническому чертежу с несколькими вариантами ответов, основанные на «Аксонометрической проекции», для собеседований при приеме на работу и конкурсных экзаменов. Также даны вопросы объективного типа и типа «истина или ложь».
Как загрузить раздел вопросов и ответов по техническому чертежу «Аксонометрическая проекция» в формате PDF?
Вы можете загрузить раздел вопросов и ответов викторины по техническому рисованию «Аксонометрическая проекция» в виде файлов PDF или электронных книг.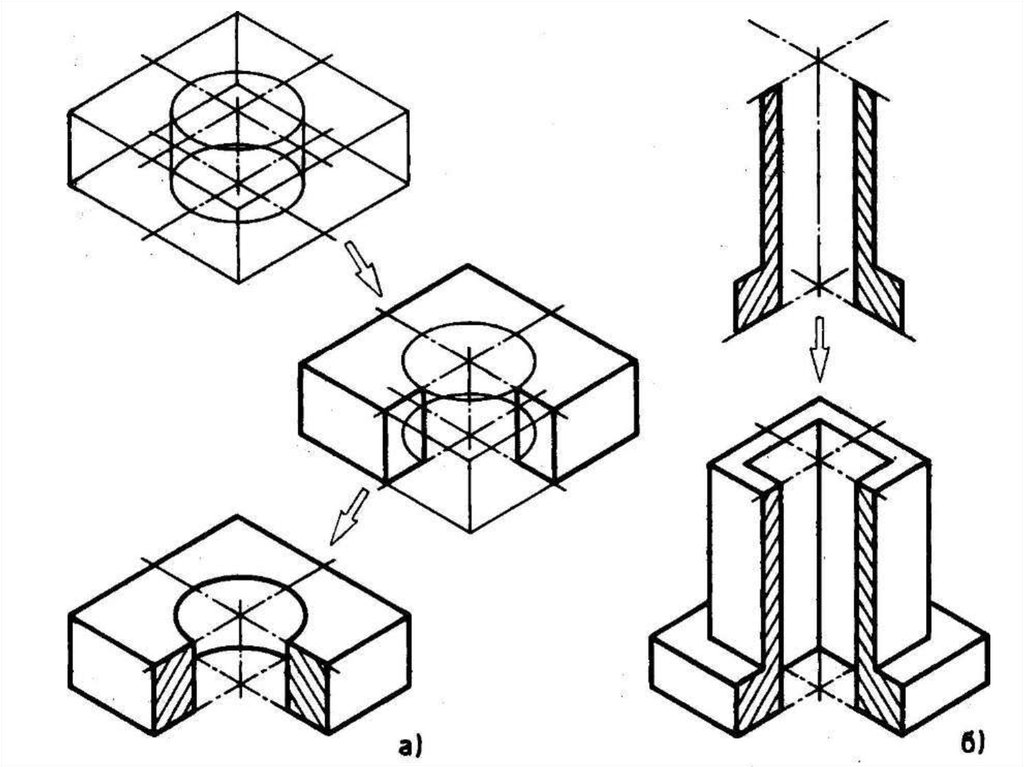
Как решить задачи викторины по техническому рисованию на основе «Аксонометрической проекции»?
Вы можете легко решать задачи викторины по техническому рисованию, основанные на «Аксонометрической проекции», выполняя данные упражнения, включая сокращения и приемы.
Упражнение: Аксонометрическая проекция. Общие вопросы
1.
В изометрической проекции все расстояния составляют примерно такой процент от их истинного размера: Опция
Объяснение:
Описание ответа отсутствует. Давайте обсудим.
2.
Углы проецируют истинный размер только тогда, когда плоскость, содержащая угол, и плоскость проекции:
Смежный
Выровненный
Перпендикулярный
Параллельный
Ответ: Вариант
Объяснение:
Описание ответа отсутствует. Давайте обсудим.
3.
В этом типе проекции каждая из осей имеет различные соотношения ракурсов:
Изометрическая
Диметрическая
Триметрическая
Параллельная
Ответ: Вариант
0003
Объяснение:
Описание ответа отсутствует.