Объем полого цилиндра формула: Объем полого цилиндра Калькулятор | Вычислить Объем полого цилиндра

Объем полого цилиндра Калькулятор | Вычислить Объем полого цилиндра

✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо.ⓘ Высота [h]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Радиус 2 — это радиальная линия от фокуса до любой точки кривой для 2-го радиуса. ⓘ Радиус 2 [r2]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Радиус 1 — это радиальная линия от фокуса до любой точки кривой для 1-го радиуса. ⓘ Радиус 1 [r1]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%

✖Объем — это количество пространства, которое занимает вещество или объект или которое заключено в контейнере. ⓘ Объем полого цилиндра [VT]

Акр-футАкр-фут (исследование США)Акко-дюймовыйБочка (масло)Бочка (UK)Ствол (США)Ванна (библейский)Совет для ногКабина (библейский)СантилитрКентум кубический футКор (библейский)шнурКубический Ангстремкубический сантиметркубический дециметркубический футкубический дюймКилометры CubicКубический метрКубический Mileкубический миллиметркубический ярдКубок (метрический)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДестистерДекастерДесертная ложка (Великобритания)Десертная ложка (США)драхмаКапляFemtoliterЖидкость Унция (Великобритания)Жидкость Унция (США)Галлон (Великобритания)Галлона (США)гигалитрГилл (Великобритания)Гилл (США)ГектолитрHin (библейский)хогсхедГомер (библейский)Сто кубический футкилолитрЛитрLog (библейский)мегалитрМикролитрМиллилитрMinim (Великобритания)Minim (США)нанолитрPetaliterпиколитрПинта (Великобритания)Пинта (США)Кварта (Великобритания)Quart (США)StereСтоловая ложка (метрическая)Столовая ложка (Великобритания)Столовая ложка (США)Таза (испанский)Чайная ложка (метрическая)Чайная ложка (Великобритания)Чайная ложка (США)тералитрTon РегистрацияТунОбъем Земли

⎘ копия

👎

Формула

сбросить

👍

Объем полого цилиндра Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. 2)

Что означает цилиндр?

Поверхность, очерченная прямой линией, движущейся параллельно фиксированной прямой и пересекающей фиксированную плоскую замкнутую кривую. Твердое тело или поверхность, ограниченная цилиндром и двумя параллельными плоскостями, особенно разрезающими все его элементы.

Share

Copied!

Объём стенки цилиндра — онлайн калькулятор

Чтобы посчитать объём стенки цилиндра, то есть объём полого цилиндра, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Найти чему равен объём полого цилиндра (V_ст) можно зная (либо-либо):

• Высоту цилиндра h, внешний радиус r₁ и внутренний радиус r₂
• Высоту цилиндра h, внешний диаметр d₁ и внутренний диаметр d₂
• Высоту цилиндра h, внешний радиус r₁ и толщину стенки δ
• Высоту цилиндра h, внутренний радиус r₂ и толщину стенки δ
• Высоту цилиндра h, внешний диаметр d₁ и толщину стенки δ
• Высоту цилиндра h, внутренний диаметр d₂ и толщину стенки δ

Зная оба радиуса (диаметра)

Чему равен объём стенки цилиндра V_ст если:

Внешний радиус r1диаметр d1 =
Внутренний радиус r2диаметр d2 =
Высота цилиндра h =
Ответ: V_ст =

Зная толщину стенки

Чему равен объём стенки цилиндра V_ст если:

Внешний радиус r1 Внутренний радиус r2 Внешний диаметр d1 Внутренний диаметр d2 =
Толщина стенки δ =
Высота цилиндра h =
Ответ: V_ст =

Теория

Чему равен объём полого цилиндра V_ст если:

Формулы

Через радиусы или диаметры цилиндра

V_ст = π ⋅ (r₁² — r₂²) ⋅ h , где r₁ — внешний радиус, r₂ — внутренний радиус , а h — высота

V_ст = π ⋅ ((^d₁/₂)² — (^d₂/₂)²) ⋅ h , где d₁ — внешний диаметр, d₂ — внутренний диаметр, а h — высота

Через толщину стенки цилиндра

V_ст = π ⋅ (d₂ ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d₂ — внутренний диаметр, а h — высота

V_ст = π ⋅ ((d₁ — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d₁ — внешний диаметр, а h — высота

V_ст = π ⋅ (2 ⋅ r₂ ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r₂ — внутренний радиус, а h — высота

V_ст = π ⋅ ((2 ⋅ r₁ — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r₁ — внешний радиус, а h — высота

Пример №1

К примеру, посчитаем каков объём металла в трубе, если её длинна 3 метра, внешний диаметр d₁=5 см, а внутренний d₂=4. 5 см?

V_ст = 3.14 ⋅ ((⁵/₂)² — (^4.5/₂)²) ⋅ 300 = 3.14 ⋅ (6.25 — 5.0625) ⋅ 300 ≈ 1119 см³

Пример №2

Теперь посчитаем объём металла в этой же 3-х метровой трубе, но возьмём внутренний радиус r₂ = 2.25 см и толщину стенки δ = 0.25 см (при этом у нас должен получится тот же ответ, что и в предыдущем примере):

V_ст = 3.14 ⋅ (2 ⋅ 2.25 ⋅ 0.25 + 0.25²) ⋅ 300 = 3.14 ⋅ 1.1875 ⋅ 300 ≈ 1119 см³

См. также

Объем полого цилиндра

Объем полого цилиндра определяется как заключенное в нем трехмерное пространство. Например, объем стекла говорит нам о доступном пространстве внутри него. Другими словами, объем говорит о максимальном пространстве, которое может быть занято водой, если воду налить в стакан.

Полый цилиндр — это цилиндр, пустой изнутри и имеющий некоторую разницу между внутренним и внешним радиусом. Другими словами, это пустой изнутри цилиндр, имеющий некоторую толщину на периферии. Форма, образующаяся на дне полого цилиндра, называется кольцевым кольцом, т. е. представляет собой область, ограниченную двумя концентрическими окружностями. В этом разделе мы обсудим объем полого цилиндра вместе с решенными примерами.

1.	Объем полого цилиндра Формула
2.	Расчет объема полого цилиндра
3.	Как найти объем полого цилиндра?
4.	Часто задаваемые вопросы по объему полого цилиндра

Объем полого цилиндра Формула

Цилиндр представляет собой трехмерную форму с круглым основанием. Цилиндр можно рассматривать как набор круглых дисков, уложенных друг на друга. В то время как полый цилиндр определяется как цилиндр, пустой изнутри и имеющий некоторую разницу между внутренним и внешним радиусом.

Объем данного полого цилиндра с известным внешним и внутренним радиусом можно определить по формуле:

Объем полого цилиндра, V = π (R ² — r ² ) h кубических единиц
Где

• R = внешний радиус
• r = внутренний радиус
• h = высота полого цилиндра

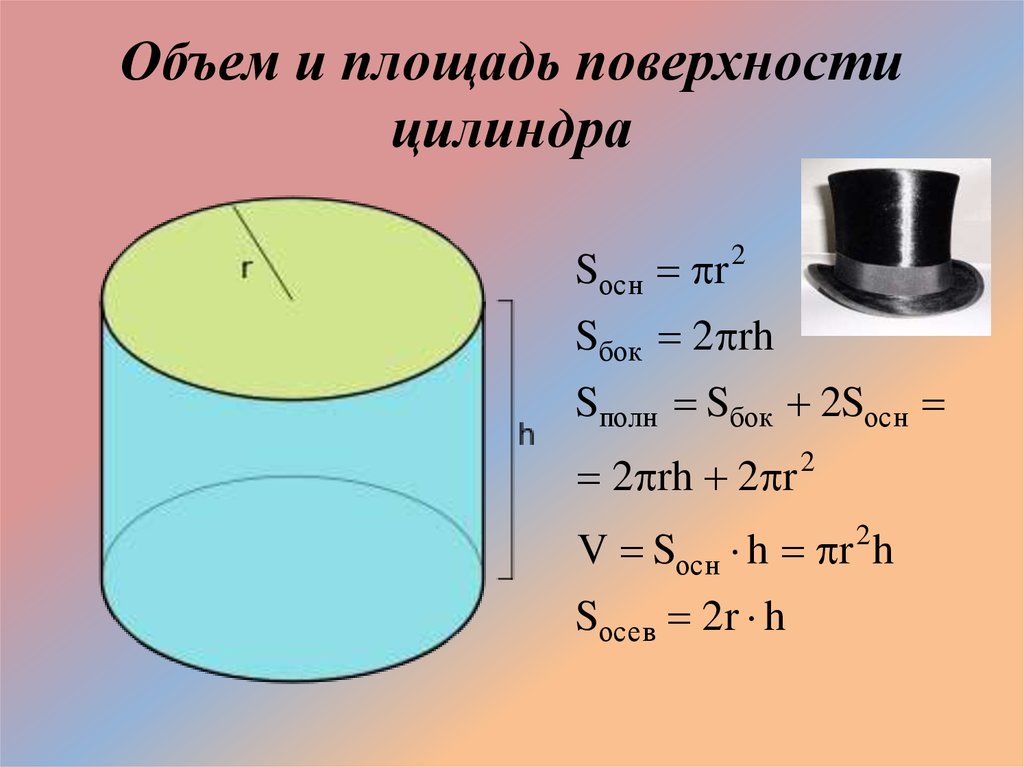
Расчет объема полого цилиндра

Формула для расчета объема цилиндра имеет следующий вид:

Объем цилиндра = Площадь основания × Высота = (π R ² ) × h кубических единиц

Где

• R = радиус цилиндра
• h = высота цилиндра

Объем полого цилиндра, имеющего внешний радиус R и внутренний радиус r, может быть записан как объем сплошного цилиндра с радиусом R и высотой h минус объем твердого тела цилиндр радиусом ‘r’ и высотой ‘h’,

Следовательно, объем полого цилиндра = объем внешнего цилиндра — объем внутреннего цилиндра
⇒ Объем полого цилиндра = π R ² h — π r ² h = π (R ² — r ² ) h кубических единиц

где,

• R = внешний радиус,
• r = внутренний радиус, а,
• h = высота полого цилиндра

Как найти объем полого цилиндра?

Чтобы рассчитать объем полого цилиндра с заданными внешним радиусом R, внутренним радиусом R и высотой H, мы можем выполнить следующие действия:

• Шаг 1: Запишите известные размеры полого цилиндра и убедитесь, что они должны иметь одинаковые единицы измерения.
• Шаг 2: Примените формулу для расчета объема полого цилиндра Объем полого цилиндра = π (R ² — r ² ) ч
• Шаг 3: Представьте ответ в единицах.

Пример: Как найти объем полого цилиндра, имеющего внутренний радиус = 20 единиц, внешний радиус = 30 единиц и высоту = 21 единицу? (Используйте π = 22/7)

Решение: Объем данного полого цилиндра = π (R ² — r ² ) h = (22/7)(30 ² — 20 ² )(21) = 66(30 — 20)(30 + 20) = 33 000 кубических единиц.

Теперь, когда мы поняли формулу и метод нахождения объема полого цилиндра, давайте взглянем на несколько решенных примеров в следующем разделе.

 

Примеры объема полого цилиндра

1. Пример 1: Найдите объем полого цилиндра, имеющего внутренний радиус = 6 см, внешний радиус = 8 см и высоту = 7 см. (Используйте π = 22/7)

   Решение:

   Дано:
   Внутренний радиус полого цилиндра (r) = 6 см
   Внешний радиус полого цилиндра (R) = 8 см
   Высота полого цилиндра (h) = 7 см

   Объем данного полого цилиндра = π (R ² — r ² ) h = (22/7)(8 ² — 6 ² ) (7) = 22(64 — 36) = 616 см ³

   Ответ: Объем данного полого цилиндра = 616 см ³

2. Пример 2: Объем полого цилиндра 440 см ³ . Если внешний радиус = 14 см, а внутренний радиус = 12 см. Найдите высоту цилиндра.

   Решение:

   Дано:
   Внутренний радиус полого цилиндра (r) = 6 см
   Внешний радиус полого цилиндра (R) = 8 см
   Объем полого цилиндра (V) = 440 см ³

   Пусть h высота полого цилиндра.
   Объем полого цилиндра = 440 = π (R ² — r ² ) h = (22/7)(14 ² — 12 ² ) h = (22/7) 52 × h

   ⇒ h = (440/1144) × 7 = 2,692 см ≈ 2,7 см

   Ответ: Высота данного полого цилиндра = 2,7 см

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по объему полого цилиндра

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об объеме полого цилиндра

Каков объем полого цилиндра?

Объем полого цилиндра определяется как пространство, ограниченное формой в трехмерной плоскости. Полый цилиндр — это тот, который пуст изнутри и имеет некоторую разницу между внутренним и внешним радиусом. Другими словами, это пустой изнутри цилиндр, имеющий некоторую толщину на периферии.

Какая формула используется для расчета объема полого цилиндра?

Формула для расчета объема полого цилиндра выглядит следующим образом: Объем полого цилиндра = π (R ² — r ² ) ч кубических единиц, где ‘R’ – внешний радиус, ‘r’ — внутренний радиус, а «h» — высота полого цилиндра.

Как найти объем полого цилиндра в литрах?

Чтобы найти объем полого цилиндра в литрах, мы можем преобразовать значение в литрах, используя приведенное ниже преобразование, то есть
1 литр = 1000 кубических см или см ³
Например: Цилиндрическая трубка объемом 1000 см ³ эквивалентна емкости 1 л.

Какая единица используется для выражения объема полого цилиндра?

При измерении объем полого цилиндра выражается в кубических единицах, таких как м ³ , см ³ , футы ³ , дюймы ³ , ярды ³ и т. д. Другие распространенные единицы измерения: литры (л) и миллиметры (мл).

Как изменится объем полого цилиндра при удвоении высоты?

Объем полого цилиндра прямо пропорционален высоте полого цилиндра. Следовательно, объем удваивается, когда высота полого цилиндра удваивается.

Как найти объем полого цилиндра, если известны только площадь основания и высота?

Объем цилиндра — это общая вместимость цилиндра, означающая количество любого материала, которое может быть погружено в него, или количество любого материала, который он может удержать. Из определения объем цилиндра = площадь основания × высота

Что такое кольцевое кольцо полого цилиндра?

Двумерная форма, образованная на дне полого цилиндра, называется кольцевым кольцом, т. е. представляет собой область, ограниченную двумя концентрическими окружностями. Площадь основания полого цилиндра – это площадь кольцевого кольца цилиндра.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по объему цилиндров

Калькулятор объема полого цилиндра

Создано Давиде Борчиа

Отзыв Комала Рафая

Последнее обновление: 23 сентября 2022 г.

Содержание:

• Что такое полый цилиндр?
• Как рассчитать объем полого цилиндра (с толщиной и без)
• Примеры применения формулы объема полого цилиндра
• Часто задаваемые вопросы

Привнесите немного математики в свою геометрию с помощью нашего калькулятора объема полого цилиндра: в этом простой инструмент, вы научитесь рассчитывать разность цилиндров и не только! Продолжайте читать, чтобы найти:

• Что такое полый цилиндр ?
• Как найти объем полого цилиндра;
• Формула объема полого цилиндра толщиной ; и
• Примерные расчеты объема такого твердого тела.

Что такое полый цилиндр?

Полый цилиндр представляет собой интересную трехмерную форму, полученную путем вычитания двух цилиндров , которые имеют общую ось .

Полые цилиндры можно найти во многих местах! Трубки, бутылки, толстые банки и так далее.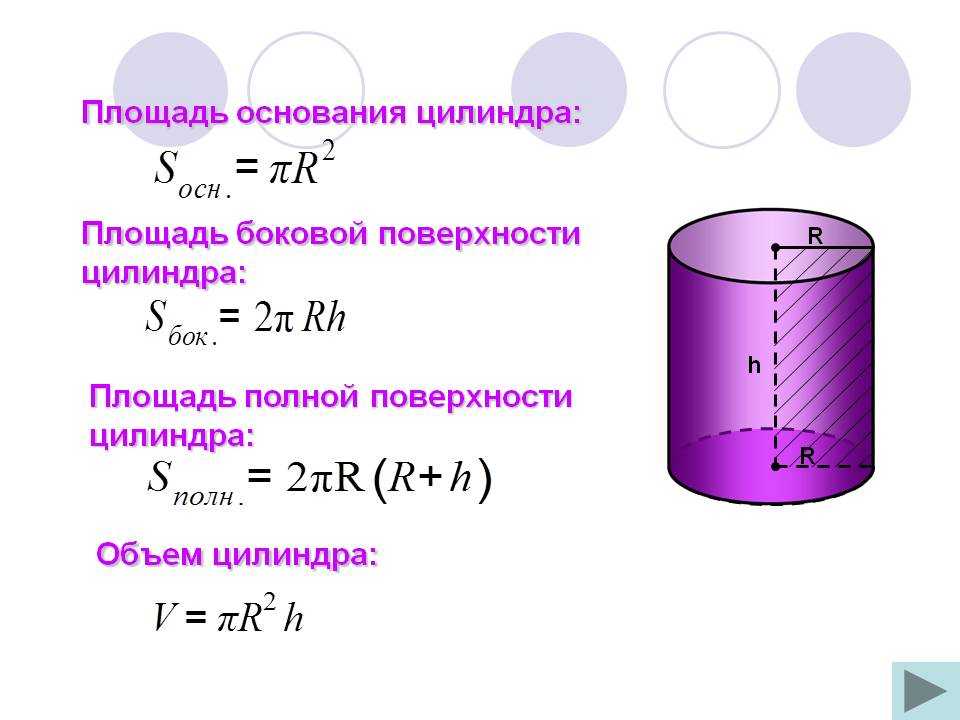 В большинстве случаев полые цилиндры, которые мы встречаем, изогнуты или гибки: в этом случае выпрямите их, прежде чем вычислять их объем!

Как рассчитать объем полого цилиндра (с толщиной и без)

Для расчета объема полого цилиндра можно использовать грубую, но эффективную формулу и вычесть объем двух правых цилиндров:

VH= VC1−VC2V _ {\ text {H}} = V _ {\ text {C} _1} — V _ {\ text {C} _2} VH ​= VC1 – VC2​

Где:

• VHV _{\text{H}}VH​ — объем полого цилиндра ;
• VC1V _{\text{C}_1}VC1 – объем большего внешнего цилиндра ; и
• VC2V _{\text{C}_2}VC2 – это объем меньшего внутреннего цилиндра .

Однако, если расширить формулу для объема цилиндра, формула для объема полого цилиндра примет вид:

VH=VC1−VC2=((π⋅R2) ⁣⋅ ⁣h) ⁣− ⁣( (π⋅r2) ⁣⋅ ⁣h) = π⋅(R2−r2)⋅h\begin{align*} V _ {\ text {H}} & = V _ {\ text {C} _1} -V _ {\ text {C} _2} \\ &=\left(\left(\pi\cdot R^2\right)\!\cdot\! h \right)\!-\!\left(\left(\pi\cdot r^2\right)\ !\cdot\!h \справа)\\ &=\pi\cdot\left(R^2-r^2\right)\cdot h \end{align*}VH​=VC1​−VC2​=((π⋅R2)⋅h)−((π⋅r2)⋅h)=π⋅(R2−r2)⋅h​

Где:

• hhh высота обоих цилиндров ;
• RRR — радиус большего цилиндра ; и
• rrr — радиус внутреннего цилиндра . 2R2-r2 с R-rR-rR-r. 92-2\!\cdot\! т\!\cdot\! r\right)\cdot hVH​=π⋅(t2−2⋅t⋅r)⋅h

  Как видите, в уравнении для объема полого цилиндра с толщиной нужно еще указать внутренний радиус : оглядываясь назад, это имеет смысл!

  Если вы хотите рассчитать внутренний объем полого цилиндра , а не его оболочки, посетите наш калькулятор объема трубы: не волнуйтесь, математика аналогична!

  Для других калькуляторов цилиндров посетите калькулятор радиуса цилиндра, калькулятор высоты цилиндра или калькулятор площади поверхности цилиндра

  Примеры применения формулы объема полого цилиндра

  Артур Кларк написал целую книгу о полом цилиндре: Встреча с Рамой . В романе группа астронавтов встречает гигантский инопланетный космический корабль в форме почти невыразительного полого цилиндра. Космический корабль Рама имеет длину 50 км50\ \text{км}50 км и внешний диаметр 16 км16\ \text{км}16 км ( мегаструктур играют важную роль в научной фантастике). Толщина космического корабля составляет 2 км2\ \text{км}2 км. Каков объем «скорлупы» Рамы?

  Вы знаете, как рассчитать объем полого цилиндра: примените формулу объема полого цилиндра с толщиной после расчета внутреннего диаметра :

  r=R−t=(8−2) km=6 kmr = R-t=(8-2)\ \text{км}=6\ \text{км}r=R−t=(8-2) км=6 км.

  Теперь у вас есть все величины, необходимые для расчета объема:

  VH=π⋅(t2−2 ⁣⋅ ⁣t ⁣⋅ ⁣r)⋅h=(π⋅(22−2 ⁣⋅ ⁣2 ⁣⋅  ⋅ 6)⋅50) км3=2, ⁣356,193 \end{align*}VH​=π⋅(t2−2⋅t⋅r)⋅h=(π⋅(22−2⋅2⋅6)⋅50) км3=2 356,19 км3​

  Объем Рамы оболочка огромная : в этом пространстве можно разместить более двух миллионов Эмпайр Стейтс Билдинг. Неудивительно, что футуристические проекты межзвездных кораблей предполагают такие конструкции, что в таких объемах может поместиться много людей!

  Наш калькулятор объема полого цилиндра упрощает ваши задачи: вам нужно только ввести данные. Толщина, внутренний и внешний диаметр уже связаны в нашем инструменте: если вы дадите нам два из них, мы рассчитаем третий!

  Часто задаваемые вопросы

  Как рассчитать объем полого цилиндра?

  Чтобы вычислить объем полого цилиндра, вы можете либо вычесть объемы двух цилиндров, образующих форму, либо использовать следующую формулу:
  VH = V₁-V₂ = π × (R² - r²) × h
  Где:

  • VH – объем полого цилиндра, а V₁ и V₂ – объемы цилиндров;
  • Р и Р радиусы цилиндров; и
  • h их высота.

  Каков объем полого цилиндра с D = 8, d = 4 и h = 12?

  Объем 452,5 см³ . Чтобы найти объем полого цилиндра с диаметрами D = 8 см и d=4 см и высотой h = 12 см , выполните следующие действия:

  1. Вычислите радиусы: R = D/2 = 4 см и r = d/2 = 2 см ;
  2. Рассчитайте объем «короны» при таких измерениях: π × (R² - r²) = π × (4² -2²) = 37,7 см² ;
  3. Умножьте это количество на высоту цилиндров, чтобы найти объем: VH = 37,7 × 12 = 452,4 см³

  Как рассчитать толщину полого цилиндра?

  Чтобы рассчитать толщину полого цилиндра, вычтите радиусы внутреннего и внешнего цилиндра, r и R : толщина твердого тела:
  t = R - r
  Вы можете рассчитать объем полый цилиндр с использованием толщины по формуле:
  VH = π × (t² + 2tr²) × h

  Можно ли рассчитать объем несимметричного полого цилиндра?

  Да! Поскольку объем цилиндрической оболочки равен разнице между объемами двух цилиндров, из которых мы строим само тело, не имеет значения, выровнены эти два цилиндра или нет, пока они не имеют одинаковую высоту и угол.

  No related posts.