4 простых шага для определения размера газовой трубы
Вы приступили к реализации проекта по добыче природного газа? Вы испытываете проблемы с расходом или давлением в вашей газовой установке?
Любой из этих сценариев требует определения размера газовой трубы. Знание размера газовой трубы может помочь устранить низкое давление, неэффективную скорость потока и потери энергии.
Существует базовая формула для определения размера газовой трубы, обеспечивающая эффективность и надежность вашей установки независимо от того, используете ли вы ее в домашних или коммерческих условиях.
В этой статье я объясню, как выбрать размер газовых труб, а также важные факторы, которые следует учитывать в процессе, чтобы обеспечить подачу газа для всех подключенных приборов в достаточном количестве для потребления.
Итак, вперед!
Содержание
- Важность правильного определения размера газа
- Переменные размера газовой трубы
- Пошаговое руководство по определению размера газовой трубы
- Расчет диаметра трубы с использованием требований к объемному расходу
- Резюме: Как определить размер газовой трубы
Важность правильного определения размера газа
В системе газоснабжения можно использовать не любую трубу.
Использование трубы правильного размера обеспечивает безопасность и эффективность всего применения.
Размер трубы определяет, сколько газа может пройти по трубе и достичь принимающего устройства. Более длинные трубы могут показаться идеальными, но чрезмерная длина может привести к снижению объемного расхода газа, измеряемого в британских тепловых единицах (БТЕ) в час. Информация о размерах газовых труб, включая диаметр и длину, поможет вам понять, сколько газа может проходить по системе трубопроводов.
Как правило, для эффективной работы газопроводной системы потеря давления не должна превышать разницу между начальным давлением на газовом счетчике и давлением на приборе.
Переменные размеры газовой трубы
При определении размера газовой трубы играют роль несколько факторов. Базовое понимание этих переменных поможет рассчитать и определить правильный размер трубы для вашей газовой установки.
Номинальный размер Номинальный размер газовой трубы относится к внешнему размеру, который обычно служит ориентиром при выборе размера трубы для газовых систем.
Внутренний размер трубы обычно меньше. Например, труба с номинальным размером 2 дюйма будет иметь внутренний размер чуть меньше одного дюйма.
Длина трубы играет большую роль в определении того, сколько газа проходит через трубу. Чем длиннее труба, тем ниже давление газа. Но вы также должны учитывать номинальный размер трубы. Труба меньшего номинального размера может ограничивать напорный поток. Большая труба обеспечивает более высокое давление, но это вызывает опасения по поводу экономической эффективности.
Приложение Как правило, газовая труба имеет номинальный размер около четырех дюймов, но в некоторых газовых системах обычно используются трубы диаметром 8 дюймов. Точный размер газовой трубы будет варьироваться от одного приложения к другому. Небольшим газовым системам может потребоваться труба меньшего номинального размера, чтобы по трубе можно было транспортировать газ непосредственно к конкретному прибору.
Этот канал также, вероятно, будет короче из-за размера используемого приложения. Для более крупных газовых систем, обеспечивающих несколько применений, потребуются более длинные трубы немного большего номинального размера, чтобы обеспечить желаемое давление в точке установки.
Материал трубы сильно влияет на количество БТЕ, которое газопроводная система может подать к устройству.
Тип используемой трубы зависит от строительных норм и правил, но наиболее распространены медные и стальные трубы. Полиэтиленовые и поливинилхлоридные трубы могут применяться в наружных и подземных газопроводах. В зависимости от применения вы также можете использовать трубы из других материалов, таких как железо, желтая латунь и алюминий.
Пошаговое руководство по выбору размера газовой трубы
Теперь, когда мы изучили основные переменные, влияющие на размер газовой трубы и эффективность газовой системы, давайте посмотрим, как выбрать размер трубы для обеспечения безопасности и эффективности.
При настройке системы природного газа вы должны учитывать количество приборов, которые вы включите в систему для получения газа. Количество обслуживаемых приборов будет влиять на длину трубы и номинальный размер.
Например, будет ли газовая система обслуживать только котел или установка будет включать в себя дополнительные приборы, такие как плита и система охлаждения и отопления? Эти соображения будут влиять на размер трубы.
Шаг 2: Определите механические требования к приборамПомимо эффективности и экономичности, безопасность должна быть вашим приоритетом при выборе правильного размера трубы для установки вашей газовой системы.
Соответствие размера и типа трубы механическим и техническим требованиям устройства может помочь обеспечить безопасность и целостность газовой системы.
Что касается технических и механических требований, наиболее важными деталями, на которые следует обратить внимание, являются давление на входе каждого прибора и скорость потока.
Шаг 3: Определите размер трубыСовет для профессионалов: Начертите систему трубопроводов, чтобы визуализировать процесс установки и определить необходимое количество труб и фитингов. Планировка должна начинаться от точки газового счетчика и включать все приборы, требующие газа.
Самая длинная длина является наиболее распространенным методом определения размера трубы. Метод включает в себя определение наибольшей длины трубы от точки подачи, регулятора или газового счетчика до самого дальнего устройства в системе. Эта длина известна как длина индекса.
При определении длины указателя следует учитывать возможную потерю давления из-за фитингов и изгибов. Основная формула для учета потери давления состоит в том, чтобы добавить к этому показателю 20 % исходной длины индекса.
Например, если длина от газового счетчика до самого дальнего прибора в системе составляет 35 м, расчетная длина индекса после прибавления 20 % будет равна 42 м, т.
е. 35+ (35×0,2).
Получите широко используемую таблицу размеров, которая поможет вам определить правильный размер трубы (с точки зрения номинального диаметра), который вам потребуется, исходя из BTU (расхода) и трубы. длина.
Используйте длину указателя в качестве контрольной точки и комбинированные БТЕ устройств в системе. Затем используйте таблицу, чтобы определить длину трубы, равную или превышающую индексную длину.
Затем просмотрите требования к расходу (BTU) каждого устройства. В таблице указано значение BTU, равное или превышающее значение BTU для каждого устройства. Затем проверьте соответствующий размер трубы.
При использовании метода наибольшей длины для определения размера газовой трубы необходимо учитывать некоторые факторы, такие как высота здания, различные требования к давлению и тип приборов.
Дополнительная высота повлияет на такие переменные, как длина трубы и требования к давлению, если вы прокладываете газопровод в очень высоком здании.
Приборы в вашей газовой системе могут иметь разные требования к давлению. Это обычное дело и не о чем беспокоиться. Но при выборе размера газовой трубы используйте в своих расчетах самые высокие требования к давлению.
Наконец, даже если в вашей газопроводной системе есть несколько приборов, они не будут работать одновременно. Таким образом, нет необходимости обеспечивать 100-процентный спрос.
Расчет диаметра трубы с использованием требований к объемному расходу
Как правило, инженеры-технологи рекомендуют скорость 90-100 футов в секунду газа, протекающего через трубу. Вы можете использовать этот стандарт, чтобы определить правильный размер диаметра трубы.
Чтобы завершить расчет, вы должны выяснить требования к общему объемному расходу каждого прибора в системе газопровода. Эта информация обычно указывается на приборе.
Допустим, требуемый объемный расход составляет 110 000 кубических футов в час при давлении 190 фунтов на квадратный дюйм (фунтов на квадратный дюйм).
Для определения диаметра трубы используйте рекомендуемую в отрасли скорость и объемный расход. Рекомендуемая скорость газа через трубу 90-100 футов в секунду, поэтому давайте возьмем в среднем 95 футов в секунду.
Сначала переведите рекомендуемую скорость из футов в секунду в футы в час. Для этого умножьте рекомендуемую скорость 95 на 3600 секунд (эквивалентно одному часу). В результате получается 342 000 футов в час.
Затем найдите номинальный диаметр трубы, разделив требуемый объемный расход оборудования (110 000 кубических футов в час) на скорость, т. е. 110 000 разделить на 342 000. Результат 0,29квадратных футов, что является диаметром трубы.
Резюме: Как определить размер газовой трубы
Определение правильного размера газовой трубы является первым шагом в обеспечении эффективной, экономичной, безопасной установки системы природного газа. Метод наибольшей длины чаще всего используется при определении размера газовой трубы для системы с более чем одним устройством.
С помощью одного устройства вы можете рассчитать номинальный диаметр, используя рекомендованное в отрасли значение скорости и объемный расход устройства для простых систем.
Ресурсы:
https://www.edcgov.us/Government/building/documents/Gas%20Pipe%20Sizing%20%28Natural%29.pdf
https://fire-boulder.com/wp-content /uploads/2014/08/PipeSizing.pdf
https://www.engineeringtoolbox.com/natural-gas-pipe-sizing-d_826.html
Теплопроводность | Инженерная библиотека
На этой странице представлена глава о кондуктивной теплопередаче из «Справочника DOE по основам термодинамики, теплопередачи и потока жидкости», DOE-HDBK-1012/2-9.2, Министерство энергетики США, июнь 1992 г.
Другие связанные главы из «Справочника по основам Министерства энергетики: термодинамика, теплопередача и поток жидкости» можно увидеть справа.
Кондуктивный теплообмен — это передача тепловой энергии за счет взаимодействий между соседними атомами и молекулами твердого тела.
Проводка
Теплопроводность включает передачу тепла за счет взаимодействия между соседними молекулами материала. Теплопередача за счет теплопроводности зависит от движущей «силы» разницы температур и сопротивления теплопередаче. Сопротивление теплопередаче зависит от природы и размеров теплоносителя. Все проблемы теплообмена связаны с разностью температур, геометрией и физическими свойствами изучаемого объекта.
В задачах о кондуктивном теплообмене объектом исследования обычно является твердое тело. Проблемы конвекции связаны с жидкой средой. Проблемы теплопередачи излучением связаны с твердыми или жидкими поверхностями, разделенными газом, паром или вакуумом. Существует несколько способов соотнести геометрию, физические свойства и разность температур объекта со скоростью теплопередачи через объект. В кондуктивной теплопередаче наиболее распространенным средством корреляции является закон проводимости Фурье. Закон в форме уравнения чаще всего используется в прямоугольной или цилиндрической форме (трубы и цилиндры), обе из которых представлены ниже.
| Прямоугольный | $$ \dot{Q} = k ~A \left({ \Delta T \over \Delta x }\right) $$ |
(2-4)
| Цилиндрический | $$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$ |
(2-5)
куда:
| \( \ точка {Q} \) | = | скорость теплопередачи (БТЕ/час) |
| А | = | площадь поперечного сечения теплопередачи (фут 2 ) |
| Δx | = | толщина плиты (футы) |
| Δr | = | толщина цилиндрической стенки (футы) |
| ΔТ | = | разница температур (°F) |
| к | = | теплопроводность плиты (БТЕ/фут-час-°F) |
Использование уравнений 2-4 и 2-5 для определения количества тепла, передаваемого теплопроводностью, продемонстрировано в следующих примерах.
Прямоугольные координаты проводимости
Пример:
1000 БТЕ/час проходит через участок изоляционного материала, показанный на рисунке 1, площадь поперечного сечения которого составляет 1 фут 
2 }
\end{эквнаррай}
$$ 92) \номер\\
&=& 28 800 ~{\text{Btu} \over \text{hr}}
\end{эквнаррай}
$$
Метод эквивалентного сопротивления
Теплопередачу можно сравнить с протеканием тока в электрических цепях. Скорость теплопередачи можно рассматривать как ток, а комбинацию теплопроводности, толщины материала и площади как сопротивление этому потоку. Разность температур представляет собой потенциальную или движущую функцию для теплового потока, в результате чего уравнение Фурье записывается в форме, аналогичной закону Ома теории электрических цепей. Если член теплового сопротивления Δx/k записать как член сопротивления, где сопротивление является обратной величиной теплопроводности, деленной на толщину материала, результатом будет уравнение проводимости, аналогичное электрическим системам или сетям. Электрическая аналогия может использоваться для решения сложных задач, связанных как с последовательными, так и с параллельными тепловыми сопротивлениями. Ученик обращается к рисунку 2, на котором показана схема эквивалентного сопротивления.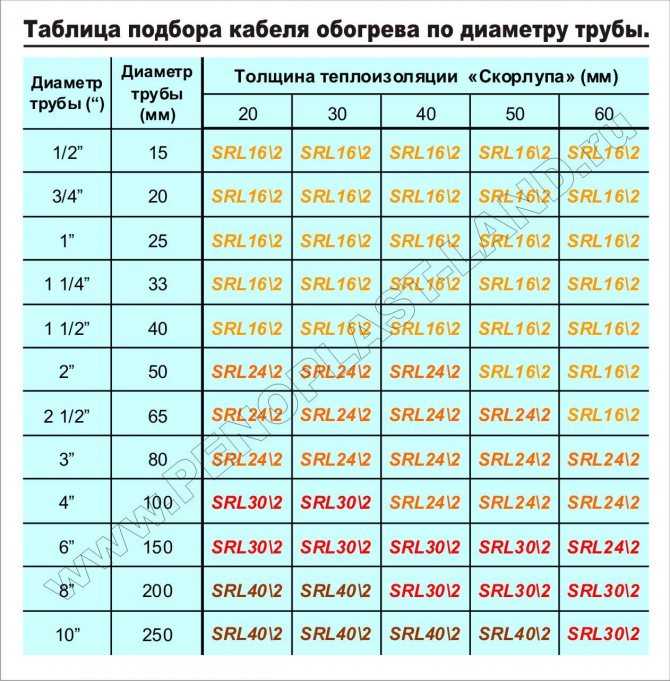
$$ \dot{Q}» = { \Delta T \over R_{th} } $$
(2-6)
куда:
| \(\точка{Q}»\) | = | Тепловой поток (\( \dot{Q}/A \)) (Btu/hr-ft 2 ) |
| ΔТ | = | Разница температур (°F) |
| Р й | = | Термическое сопротивление (Δx/k) (час-фут 2 -°F/Btu) |
Электрическая аналогия
Пример:
Композитная защитная стена состоит из медной пластины толщиной 1 дюйм, слоя асбеста толщиной 1/8 дюйма и слоя стекловолокна толщиной 2 дюйма. Теплопроводность материалов в единицах БТЕ/час-фут-°F следующая: k Cu = 240, k asb = 0,048 и k fib = 0,022.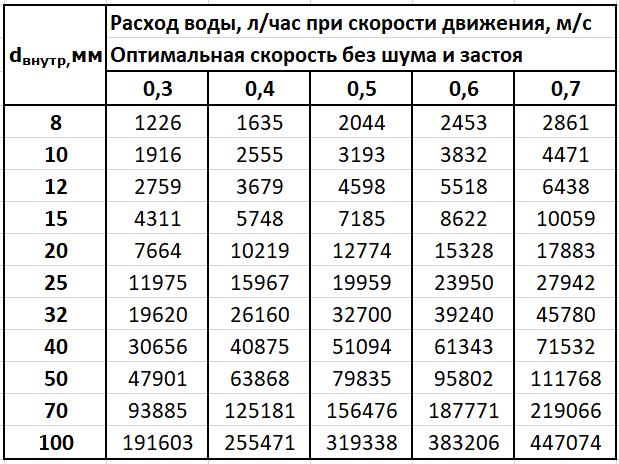
Общая разница температур по всей стене составляет 500°F. Рассчитайте термическое сопротивление каждого слоя стены и скорость теплопередачи на единицу площади (тепловой поток) через композитную конструкцию.
92}
\end{эквнаррай}
$$
Кондуктивно-цилиндрические координаты
Теплопередача через прямоугольное твердое тело является наиболее прямым применением закона Фурье. Теплопередачу через трубу или стенку трубы теплообменника оценить сложнее. Через цилиндрическую стенку площадь поверхности теплопередачи постоянно увеличивается или уменьшается. Фиг.3 представляет собой сечение трубы, изготовленной из однородного материала.
Рисунок 3: Площадь поперечного сечения цилиндрической трубыПлощадь поверхности (A) для передачи тепла по трубе (без учета концов трубы) прямо пропорциональна радиусу (r) трубы и длине (L) трубы.
А = 2πrL
По мере увеличения радиуса от внутренней стенки к внешней увеличивается площадь теплообмена.
Разработка уравнения, оценивающего теплопередачу через объект цилиндрической геометрии, начинается с закона Фурье (уравнение 2-5).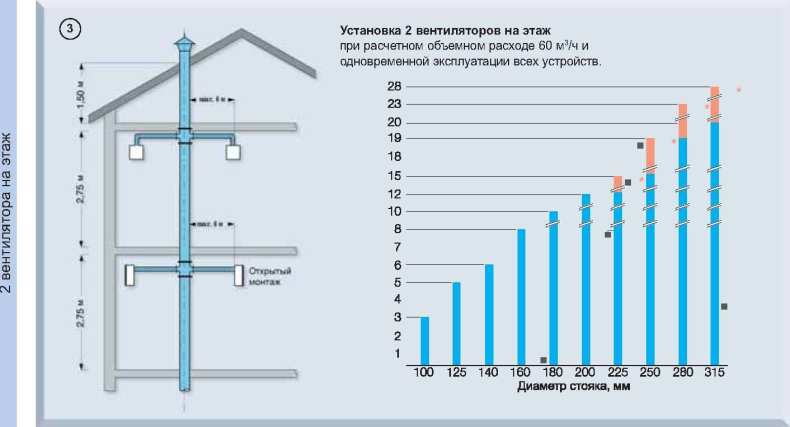
$$ \dot{Q} = k ~A \left({ \Delta T \over \Delta r }\right) $$
Из приведенного выше обсуждения видно, что никакое простое выражение для площади не является точным. Ни площадь внутренней поверхности, ни площадь внешней поверхности сами по себе не могут использоваться в уравнении. Для задачи с цилиндрической геометрией необходимо определить среднелогарифмическую площадь поперечного сечения (A
$$ A_{lm} = { A_{внешний} — A_{внутренний} \over \ln \left({ A_{внешний} \over A_{внутренний} }\right) } $$
(2-7)
Подстановка выражения 2πrL для площади в уравнении 2-7 позволяет вычислить среднелогарифмическую площадь по внутреннему и внешнему радиусу без предварительного вычисления внутренней и внешней площади.
$$ \begin{выравнивание} A_{lm} &=& { 2 \pi ~r_{внешняя} L — 2 \pi ~r_{внутренняя} L \over \ln \left({ 2 \pi ~r_{внешняя} L \over 2 \pi ~ r_{внутренний} L }\right) } \nonumber \\ &=& 2 \pi ~L \left({ r_{внешний} — r_{внутренний} \over \ln{ r_{внешний} \over r_{внутренний} } }\right) \end{эквнаррай} $$
Это выражение для логарифмической средней площади можно подставить в уравнение 2-5, что позволит нам рассчитать скорость теплопередачи для цилиндрических геометрий.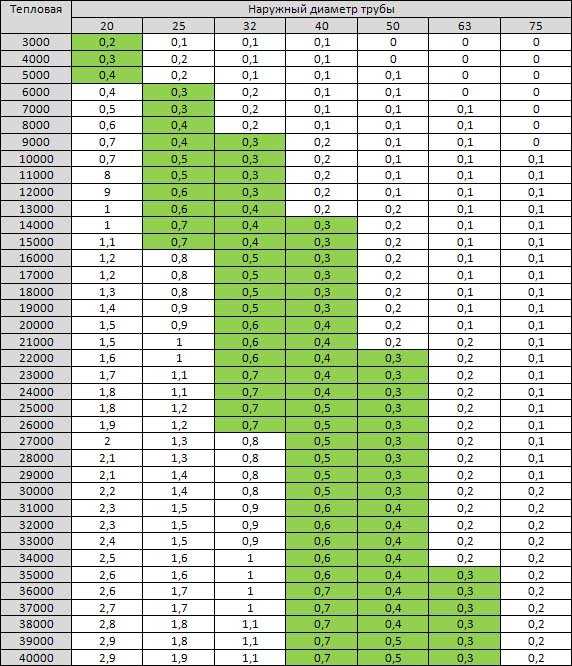
$$ \begin{выравнивание} \dot{Q} &=& k ~A_{lm} \left({ \Delta T \over \Delta r }\right) \nonumber \\ &=& k \left[ 2 \pi ~L \left({ r_o — r_i \over \ln{ r_o \over r_i } }\right) \right] \left({ T_o — T_i \over r_o — r_i }\ справа) \номер\\ \dot{Q} &=& { 2 \pi ~k ~L ~(\Delta T) \over \ln (r_o / r_i) } \end{эквнаррай} $$
(2-8)
куда:
| Л | = | длина трубы (фут) |
| р и | = | внутренний радиус трубы (футы) |
| р или | = | внешний радиус трубы (футы) |
Пример:
Труба из нержавеющей стали длиной 35 футов имеет внутренний диаметр 0,92 фута и внешний диаметр 1,08 фута. Температура внутренней поверхности трубы составляет 122°F, а температура внешней поверхности составляет 118°F. Теплопроводность нержавеющей стали составляет 108 БТЕ/час-фут-°F. 92 } \end{эквнаррай} $$
Пример:
Труба длиной 10 футов с внутренним радиусом 1 дюйм и внешним радиусом 1,25 дюйма имеет температуру внешней поверхности 250°F.