Как выставить диагональ крыши: Как правильно выставить диагональ крыши. Как выровнять обрешетку на крыше

Как правильно выставить диагональ крыши. Как выровнять обрешетку на крыше

Зачастую работу по замерам стремятся заказать в кровельных компаниях из опасения совершить какую-либо оплошность. Однако если знать несколько нехитрых правил, сделать грамотно и точно замеры кровли вы сможете самостоятельно.

Чертим схему в плоскости

В первую очередь, вам нужно начертить схему вашей кровли в плоскости. «Довольно часто клиенты пытаются рисовать всевозможные 3D-проекции, однако на самом деле, чтобы грамотно рассчитать количество материала, необходим самый элементарный чертеж , представляющий вид сверху, – комментирует Андрей Опук, генеральный директор ООО «Первая Кровельная». – Такой чертеж даже необязательно выполнять в масштабе.

Когда вы приедете в офис компании для итогового расчета, менеджер просто задаст вам уточняющие вопросы из серии «Правильно ли понимаю, что здесь у вас есть примыкание?» и пр. Вы просто дадите необходимые комментарии.

Даже компьютерная программа, которая автоматически осуществляет расчет материала, делит кровлю на сегменты, представляющие собой треугольники, трапеции и прочие элементарные фигуры».

Приступаем к замерам

Чтобы легче и быстрее измерить кровлю, лучше всего делать это вдвоем. Никаких специальных приспособлений типа лазерного дальномера вам не потребуется.

Как показала практика, достаточно длинномерной рулетки , которая продается в любом строительном супермаркете. С ее помощью вам необходимо зафиксировать размеры всех ребер.

Обычно замеры происходят следующим образом: один человек подходит ближе к краю кровли и фиксирует конец рулетки на том месте, где заканчивается стропильная нога, а если крыша старая и предстоит ее демонтаж – где заканчивается кровельное покрытие.

Второй человек фиксирует рулетку на верхней части крыши (на коньке).

Есть одно правило, которого следует обязательно придерживаться: помимо ребер, необходимо произвести замеры всех скатов . Дело в том, что зачастую размеры скатов не совпадают идеально. Могут быть небольшие смещения, которые незаметны невооруженным глазом. Ничего фатального в этом нет, однако их стоит учитывать при расчетах, а потому замерьте каждый скат отдельно.

Ни в коем случае не нужно делать все измерения со стороны чердака , изнутри. В противном случае вы получите очень приблизительные размеры.

Илья Быков, менеджер по работе с ключевыми клиентами ООО «Первая Кровельная»:

Во-первых, замеры кровли лучше всего производить уже после того, когда будет готова обрешетка . Имея только стропильную систему, замеры также возможны, но с использованием обрешетки они, однозначно, будут точнее.

Во-вторых, нужно обязательно померить периметр крыши , где потом предполагается карнизная планка. Этот размер также необходим, чтобы сосчитать количество листов металлочерепицы (или профнастила).

В-третьих, не забывайте, что металлочерепица не заканчивается стропильной ногой. Как правило, делается выпуск 5-10 см для того, чтобы кровля имела достойный вид. Когда вам будут делать итоговый расчет, обязательно озвучьте менеджеру свои пожелания по выпуску.

В-четвертых, следует обмерить периметр выходов труб с внешней стороны . Это необходимо, чтобы заказать планки примыкания, которые нужны для защиты от протечек.

Если планируются мансардные или слуховые окна, также измерьте их и укажите их расположение на чертеже. Это позволит сэкономить несколько метров черепицы.

Если же расчет будет осуществлен без учета мансардных окон, никаких проблем не возникнет: монтажники подрежут материал в размер. В случае примыкания к вашему дому каких-либо построек, также следует отразить это в чертеже.

Металлочерепица из наличия или в размер?

Иногда люди предпочитают заказывать большие листы металлочерепицы, к примеру, шириной 6 или 7 м, чтобы не монтировать их с нахлестами. Отметим особо, что нахлесты не являются причиной протечек, так как это невозможно конструктивно.

Что касается экономии в этом случае, отметим следующее.

Во-первых, «борясь» за размер, вы получаете довольно долгие сроки производства (в сезон до двух недель). Естественно, это не проблема, если вы никуда не торопитесь.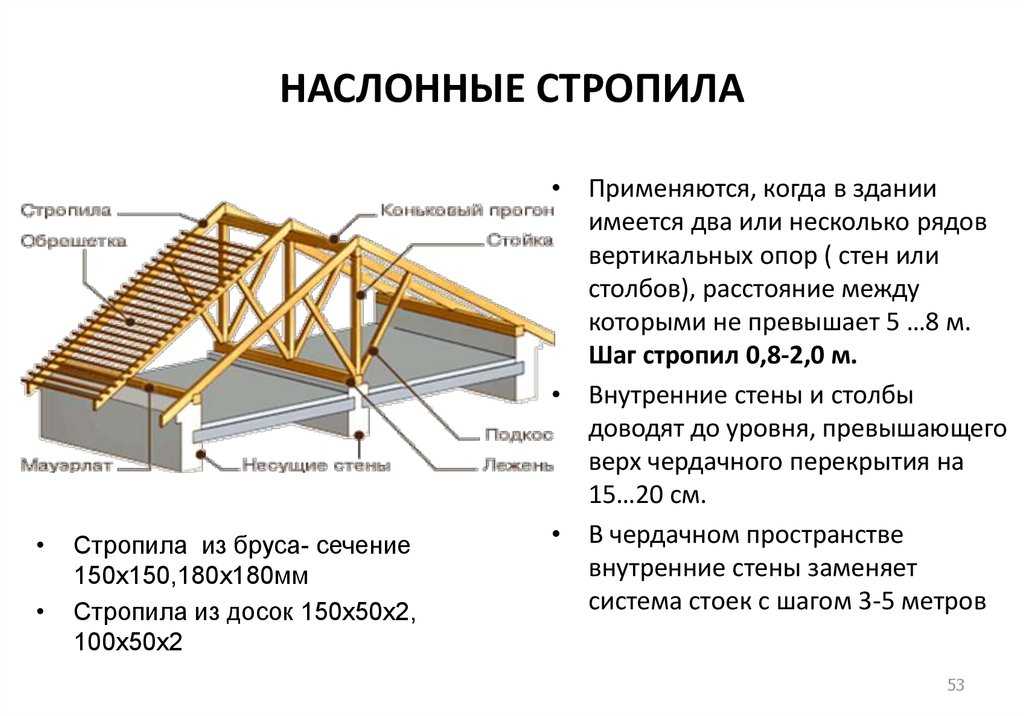

Во-вторых, если площадь вашей кровли составляет порядка 200 кв.м., то экономия за счет больших листов может составить максимум 4-5 квадратных метров, однако эта выгода, скорее всего, сойдет на нет , когда вам посчитают стоимость доставки и упаковки. Для доставки металлочерепицы длиной, к примеру, 7 или 6 метров газель уже не подойдет.

Кроме того, заводы-производители в обязательном порядке поставляют кровельные материалы в упаковке, а она продается погонными метрами. Получается, что доставка и упаковка стандартных размеров может стоить дешевле .

Отметим также, что при заказе больших листов металлочерепицы, процесс монтажа может усложниться. Поднимать вдвоем на высоту двух-, трехэтажного дома лист шириной 7 метров, довольно непросто. Кроме того, есть риск повредить полимерное покрытие, шоркнув лист металлочерепицы об лестницу или стропила.

Статья подготовлена экспертами «Первой Кровельной».

Чтоб правильно рассчитать и выставить диагональ фундамента или опалубки фундамента — очень хорошо нанять спецов. Но если вы уже несколько раз видели передачу «квадратный метр», несколько раз слышали разговор о том как надо строить, а еще кучу анекдотов о строительстве? — другое дело. Это и дает нам «полное право» предполагать, что мы сами справимся с таким простым делом, как углы и диагонали опалубки фундамента. Именно такого высокого мнения о себе каждый, кто планирует строить баню своими руками (Ха-ха!)

О начале разметки и проектирования фундамента и опалубки я писал в статье . На момент вбивания кольев и установки внешних досок опалубки я уже проверял длину диагонали. Все сходилось до миллиметра. Это самое главное условия получения прямых углов сруба бани. Но после первой разметки были манипуляции с установкой дна ростверка, монтаж внутренних щитов опалубки, доделывание опалубки столбиков от уровня земли до дна будущего фундамента. Конечно же, я очень старался чтоб ничего не сдвинуть, и колья вбивал глубоко.

Но как и во всякой стройке, случился перекосяк. Это не так страшно, как если бы я этого не заметил или я об этом не знал.

Поэтому я перед укладкой арматуры решил опять проверить диагонали. Разница получилась в 2 см. Вот и хорошо, что обнаружилось до заливки бетона.

Как вывести диагональ опалубки?

Для упрощения постройки правильной опалубки я делал длину стенок абсолютно равной. Поэтому перекос может получиться только в виде ромба. На рисунке умышлено увеличена степень перекоса опалубки для наглядности.
Для исправления ситуации поступили так:

Такое комбинированное перемещение одной из сторон опалубки (северной на рисунке) не было слишком трудном, поскольку колья и первоначальное расположение опалубки соответствовали правильному положению. Поэтому смещение диагонали было минимальным и усилия по «корректировке» положения щитов не вызывали механического напряжения и усилий.

Способ установки углов по равным диагоналям можно использовать только при условии равенства сторон. Равенства диагоналей будет достаточно!

Для сторон опалубки с большим размером возможно применить правило «золотого» треугольника.

Если такой треугольник, согласно теореме Пифагора, имеет стороны 3, 4, то гипотенуза равна 5 единицам. Таким образом, достаточно отмерить на сторонах опалубки части кратные 3 и 4 у вершины прямого угла и тогда расстояние между контрольными точками будет 5 частей! Это и будет гарантией прямых углов и равенства диагоналей!

Для осуществления правильного планирования монтажа опалубки очень рекомендую использовать метод обноски, который позволяет в любое время монтажных работ производить сверку углов, снимать и повторно устанавливать шнуры периметра фундамента.

Перед заливкой фундамента не поленитесь еще раз проверить диагонали. Это лишним не будет! Бетон невозможно легко и быстро поправить. Ошибки исправлять очень дорого и долго. Фундамент для сруба имеет больше требований к качеству чем фундамент для каменного дома. Раствором уже ничего не выровнять!

Не забудьте перед заливкой для ее легкого демонтажа!

При существующем многообразии кровельных материалов монтаж крыши, как правило, происходит по одной и той же схеме, объединенной несколькими основными правилами.

После установки лежня приступают к креплению стоек, которые должны иметь одинаковый размер по высоте и быть закреплены строго по отвесу в поперечном и продольном направлениях, после чего в них должен быть уложен прогон. После этого можно приступить к , которые должны быть установлены между прогоном и лежнем ветровых подкосов.

Установка стропил и обрешетки

Для устройства стропил и обрешетки понадобятся некоторые материалы и набор инструментов.

Необходимые материалы:

• стропильный брус;
• доска для мауэрлата, лежня;
• дюймовая доска или брус для обрешетки;
• утеплитель;
• паро- и гидроизоляция;
• скобы, гвозди;
• антисептик для обработки дерева, кисть, валик.

Схема монтажа стропильной системы: А – узел крепления стропил к мауэрлату, крепления кобылок; Б – общий вид правильно выполненных стропил; В – растяжка и подкос; Г – правильное крепление конька; Д – крепление к подкосу; Е – стропила в сборке.

Необходимые инструменты:

• рулетка;
• уровень, отвес, шнур, угольник;
• ножовка, электрическая пила, лобзик;
• молоток, гвоздодер, топор, кусачки;
• страховочный пояс и веревка.

Стропила должны быть установлены на одинаковом расстоянии друг от друга, оно называется шагом, а рассчитывается путем деления длины дома на их количество. Например, при длине стены 8 метров и через м их понадобится 9 штук на каждую сторону. Крайние стропила кровли устанавливаются по водяному уровню по отношению друг к другу, а те, которые находятся между ними по натянутому шнуру.

Собирать треугольную схему с лучше внизу на земле, потому что такую конструкцию тяжело собрать в вертикальном положении, их лучше устанавливать в собранном виде. Благодаря одинаково собранной форме стропильных ферм, выставленным по отвесу и точно установленным прокладкам, строго по уровню, горизонтальное положение конструкции получается без особых усилий.

Обрешетка кровли может быть сплошной, выполненной из дюймовой доски или бруса сечением 50х50 мм, который устанавливается в местах стыка кровельного материала. В зависимости от его длины, рассчитывается необходимое количество бруса между стыками. Лишнюю, торчащую по торцам дома обрешетку обрезают на одинаковом расстоянии от крайних стропил, оставляя края выступать по 10 см за них, образуя свободный свес для кровельных материалов. По сплошной обрешетке можно разложить рулоны рубероида или паронепроницаемой пленки.

Расчет и укладка кровельного материала

Расчет необходимого количества того или иного вида материала для устройства кровли производится путем замера и вычисления площади скатов, например, при длине 8 м и ширине 3 м площадь ската составит 24 м. Таким образом, учитывая нахлест, можно установить точное количество листов, необходимых для покрытия крыши дома. Если накрывать крышу профлистом длиной 3 м и шириной 1 м 15 см, то понадобится 8 таких листов.

Вне зависимости от того, какой кровельный материал выбран, порядок его укладки начинается снизу вверх, как бы навстречу потокам воды, в одну сторону нанесенной на нем маркировки. При укладке асбестоцементного шифера на стыке четырех его углов необходимо два нижних накрываемых угла откусить, это делается для того, чтобы зимой снег не скапливался на чердаке и весной не заливало талой водой верхний этаж. В основном кровельные материалы крепятся с помощью гвоздей или саморезов, часто они красятся под цвет покрытия и имеют уплотнительную резинку.

После окончания этих работ устанавливается конек и делаются примыкания вокруг труб или смотрового окна, если оно предусмотрено конструкцией кровли. обычно отделываются сайдингом или другим выбранным материалом. При проведении работ не стоит забывать о безопасности, необходимо использовать монтажный пояс и специальную проверенную веревку, можно сбить ходовой трап, по которому легко передвигаться.

С учетом всех технологических особенностей прослужит без затрат на ее ремонт и эксплуатацию на протяжении многих лет. Работы по ее устройству лучше всего доверить профессионалам, знающим все тонкости.

При всем разнообразии материалов кровельного покрытия устройство кровель мало чем отличается друг от друга. Их объединяют общие правила.
Правило 1. Скаты двухскатных крыш должны иметь форму правильного прямоугольника, скаты вальмовых крыш — форму равнобедренных трапеций и равнобедренных треугольников.
Это требование вызвано тем, что практически все штучные элементы кровельных покрытий имеют прямоугольную форму. При настилании их на скат, не имеющий прямых углов, например, имеющий ромбовидные очертания, неизбежно получится незакрытый клин. Закрыть такой клин можно только путем резания и подгонки штучных кровельных материалов, что создает дополнительные трудности, увеличивает расход материалов, снижает скорость строительства и, наконец, просто портит внешний вид здания. Но самое главное — многократно повышает возможность протечки кровли.
Равнобедренные скаты вальмовых крыш дают возможность резать кровельные материалы по одному-двум шаблонам, а половинки некоторых кровельных материалов использовать на противоположных сторонах ската. Например, асбестоцементный волнистый лист, разрезанный наискосок, можно использовать с двух сторон ската. Если по проекту или в результате небрежности скаты кровли имеют различные углы наклона, резку штучных элементов ведут индивидуально. В итоге — значительно снижается скорость работ, ни о какой экономии стройматериалов не возникает и речи.
Для получения правильных форм скатов нужно перво-наперво произвести промер длины, ширины, диагоналей и высот отстроенного остова здания. Здесь для застройщика может открыться масса неожиданных сюрпризов. Здание в плане может принять форму ромба или трапеции. Перепады по высоте на противоположных стенах могут достигать нескольких сантиметров. Такие погрешности образуются не только из-за небрежно выполненных работ по устройству стен. Они могли возникнуть из-за того, что на разных углах при рубке деревянных или кладке кирпичных стен стояли несработавшиеся каменщики или плотники. Например, двое несработавшихся каменщиков, постоянно стоящих на противоположных углах кладки, могут дать погрешность по 1 см на 1 м высоты лишь только потому, что у одного шов кладки на 1 мм толще, и это при том, что оба — хорошие каменщики. Что же тогда говорить о дилетантах, у которых погрешности будут не только по высоте, но и по линейным размерам из-за завалов углов наружу и внутрь. После проведения промеров нужно по возможности устранить выявленные дефекты стен. Для того чтобы конек кровли был строго горизонтален, а скат кровли лежал в одной плоскости с горизонтом, выполняют ряд мероприятий по устройству стропильной системы. Мауэрлат и лежень для наслонных стропил и подкладки для висячих стропил устанавливают по водяному уровню (рис. 1 ), тем самым добиваясь их горизонтальности.

Затем измеряют расстояние между мауэрлатом и лежнем (оно должно быть одинаковым) (рис. 2 ) и проверяют диагонали. При необходимости конструкцию поправляют. Подкладки под висячие стропила проверяют точно так же — измеряют расстояние между ними и по диагонали.

Этот подготовительный этап занимает иногда много времени, но чем тщательнее он будет выполнен, тем легче будет построить крышу . Лежень может быть изготовлен выше или ниже мауэрлатных балок, это не играет никакой роли, главное, чтобы он был горизонтальным. Мауэрлат должен лежать на одной высоте по всему периметру здания, подкладки так же. После установки лежня на него крепят стойки. Их готовят одинаковой проектной высоты и устанавливают по отвесу, причем вертикальность установки стоек проверяют как в продольном, так и в поперечном направлениях. Затем на стойки укладывают прогон. Так как лежень был выставлен горизонтально, а стойки одинаковы по высоте и выставлены вертикально, то, значит, и прогон ляжет горизонтально. После установки между лежнем и прогоном ветровых подкосов можно крепить стропильные ноги.
Стропила устанавливают на определенном расстоянии друг от друга. Это расстояние называют шагом установки стропил и определяют расчетным путем. Правильность установки стропил определяют путем закладывания на 3-4 стропильные ноги ровной доски. Если между доской и стропильной ногой есть видимый зазор, стропило переставляют. Если зазоров нет, значит, стропила выставлены верно, т. е. в одной плоскости. Окончательный контроль проводят визуально — стропильную систему просматривают от края до края. При креплении стропил следует избегать установки крученых и горбатых досок, так как их придется подтесывать под устройство обрешетки, а значит, уменьшать расчетное сечение. Доски, имеющие большое количество сучков, а также доски со сквозными сучками, направленными поперек волокон, ставить категорически запрещено — они могут сломаться.
Треугольные схемы висячих стропил трудно собрать в вертикальном положении, поэтому их собирают на земле или на жестком перекрытии и затем устанавливают в готовом виде. При их установке следят, чтобы коньковый узел был строго над осевой линией здания. Так как стропильные фермы имеют одинаковые габариты, а подкладки выставлены по уровню, их горизонтальность получается автоматически. Фермы выставляют по отвесу и закрепляют ветровыми связями.
Прямоугольность скатов кровли обеспечивается обрешеткой. Перед ее установкой желательно уже иметь в наличии кровельный материал. Обладая данными о физико-механических характеристиках и размерах материала, можно рассчитать величину бокового выноса обрешетки за стены и длину кобылок, т. е. определить реальные размеры ската кровли. При устройстве обрешетки вынос ее за стены делают несколько больший, чем требуется. Ширину ската при устройстве кровли рассчитывают с учетом нахлеста смежных листов штучного кровельного материала. Лучше всего этот расчет сделать в реальных условиях, т. е. разложить один ряд кровельных элементов непосредственно на крыше или на земле, а затем измерить рулеткой. Это как раз та ситуация, когда нужно семь раз отмерить, а один раз отрезать. Полученное в результате измерения или в результате расчета расстояние отмеряют на коньке крыши, от крайних точек откладывают прямые углы и лишнюю обрешетку отпиливают. Таким же образом высчитывают длину кобылок, обеспечивающих их карнизный свес. При расчете карнизного свеса нужно не забывать о свободном свесе кровельных элементов на 2-10 см. Свободный свес выполняют для того, чтобы срываемые ветром дождевые капли не смачивали нижнюю доску обрешетки. После всех этих не очень сложных подсчетов на скате кровли будет целое число элементов как в вертикальном, так и в горизонтальном рядах. А так как углы прямые, то никаких хлопот с настилкой кровли не будет. Получится изящная и ровная кровля . Прямой угол откладывают с помощью деревянного угольника (рис. 3 ) со сторонами 3, 4, 5 м или с меньшими сторонами, кратными этим цифрам.

На вальмовых кровлях, как уже говорилось выше, надо постараться сделать одинаковые углы наклона скатов, что возможно только при правильной установке мауэрлатов и лежней.
Правило 2. Перед устройством покрытия из основного кровельного материала разжелобки, ендовы, примыкания труб к кровле и примыкания слуховых окон покрывают по сплошной обрешетке оцинкованной кровельной сталью (рис. 4 и 5 ). Для покрытия примыкания труб и слуховых окон делают заготовку и устанавливают вместе с основным покрытием.

Правило 3. Нижний брусок обрешетки должен быть выше, чем все последующие бруски, на толщину укладываемого кровельного материала. Чтобы понять, для чего это нужно, достаточно взглянуть на рис. 6.

Будь этот брусок таким же, как и все другие, карнизный элемент кровли «клюнет носом».
Правило 4. Все кровли кроют снизу вверх, навстречу дождевому потоку. Некоторые кровли, например волнистые листы, укладывают навстречу преобладающим ветрам слева направо или, наоборот, справа налево.
Очень многие кровельные материалы уже имеют в своей конструкции отверстия для гвоздей или проволочных скруток, либо их выполняют на самоклеящейся основе, либо в комплекте имеются специальные клеи и герметичные прокладки. Устройство кровли из таких материалов не представляет трудности, так как оно полностью продумано.
Кровельные материалы нужно только собрать на крыше, как детский конструктор. К кровельным материалам, не имеющим крепежных отверстий (цементно-волокнистые волнистые листы, металлочерепица, профилированный настил), в комплекте поставляют кровельные гвозди под цвет покрытия. Эти гвозди крепят в гребень штучного элемента с резиновой уплотнительной шайбой.
Кроме крепежных деталей в комплектах современных кровельных материалов поставляют коньковый и карнизные элементы, разделки к трубам и многое другое.
Правило 5. Под кровли мансардных крыш укладывают дополнительный гидроизоляционный слой из полиэтиленовой пленки, толя или рубероида. Под «холодные» кровли дополнительная гидроизоляция желательна, но необязательна. На всех последующих рисунках дополнительная гидроизоляция будет показана, но это не значит, что она обязательна к исполнению.
Правило 6. При устройстве теплых крыш нельзя забывать о воздушном продухе между утеплителем и обрешеткой, который должен составлять от 2 до 5 см, иначе утеплитель потеряет свои свойства вследствие насыщения влагой.
Правило 7. При устройстве кровель нужно не забывать привязывать себя к коньку , а при укладке последнего конькового элемента продумать способ эвакуации с крыши. Очень часто приходится спускаться по веревке, перекинутой через конек крыши и привязанной за что-нибудь тяжелое, лежащее на земле с другой стороны, или веревку привязывают к коньку крыши и пропускают под верхний кровельный элемент, затем после спуска веревку выдергивают и кровлю поправляют изнутри. Конечно, такой спуск требует определенной физической подготовки. Почему упоминается такой каскадерский способ спуска, когда можно сделать ходовой трап и навечно оставить его на крыше? Потому что, как правило, крыши сплошь и рядом выполняют без трапа.
И последнее, если человек испытывает хотя бы малейшее головокружение при подъеме на высоту, то на крыше ему делать нечего, пусть ее делают другие — не все же рождены космонавтами.

Кафтанчиково — село в Томском районе Томской области, административный центр Заречного сельского поселения. Население 1323 человека. Село расположено на левом берегу Томи, в 15 км от Томска, рядом с селом проходит автодорога M53. В 16 веке на реке «Томь» жили несколько групп татар во главе с князем Тояном. Князь Тоян подал челобитную царю Борису Годунову, в которой от имени «томских жителей» просил построить в низовьях реки «Томь» крепость и принять томских татар в русское подданство. На что Борис Годунов дал свое согласие и в 1604 году был сформирован отряд для строительства русской крепости. Летом 1604 года крепость была построена. В последствии население Томска росло. Здесь селились русские крестьяне-промысловики. В 1626 году проживало уже 531 семья. Жителей надо было снабжать хлебом, в 1605 году появились первые посевы зерновых, люди занялись сельским хозяйством. Селения Заречного сельского поселения являются одними из старейших в устье реки «Томь», которые возникли в период 1627 по 1630 года. Место для деревень было выбрано удачно: близост…

Как выровнять диагональ крыши

Главная » Разное » Как выровнять диагональ крыши

Как выставить диагональ крыши. Возведение крыши дома своими руками

Завершающий этап строительства дома включает в себя окончательный выбор кровельного покрытия и его установку. Чаще всего возведение крыши доверяют специалистам, поскольку этот вид работы наиболее ответственен и небезопасен. На сегодняшний день металлочерепица стала популярным в частном домостроении видом кровли. Простота ее монтажа позволяет самостоятельно покрыть крышу, что значительно экономит средства.

Металлочерепица для простой конструкции крыши

Покрывать металлочерепицей лучше всего крыши со скатом, когда уклон наклона не меньше 14 градусов. Предпочтительно, чтобы крыша была геометрически простой, так как не придется разрезать сам материал и не останется невостребованных обрезков.

Зачем лишние траты, когда делаем крышу сами и для себя?

Приобретая нужное количество металлочерепицы, необходимо:

• точно измерить крышу;
• важно, чтобы лист был на4 смдлиннее крыши, чтобы его конец перекрыл карниз; подобное расположение позволит создать вентилируемое пространство на коньке;
• необходимо тщательно замерить параметры будущей крыши, в том числе – и по диагонали;
• до того, как начать крыть крышу, полезно убедиться, что она не имеет неровностей;
• если они есть, а выровнять не представляется возможным, можно уложить черепицу так, чтобы нижний край самой обрешетки совпадал полностью с линией свеса листа.

Устанавливать крышу своими руками невозможно без специального инструмента:

• ножниц по металлу,
• электродрели,
• болгарки,
• ножовки.

Начинать надо с установки стропильной системы. Стропила представляют собой балки и служат каркасом для будущей крыши. По установленному стандарту, стропильная система обеспечивает давление в200 кгна квадратный метр.

Совет. Независимо от характеристики самого кровельного материала это требование обязательно, чтобы крыша смогла выдерживать напор ветра, вес выпавшего снега.

1. Перед началом монтажа стропильной системы производится стяжка несущих стен.
2. Потом укладывается гидроизоляция, продольный брус и лежень.
3. Из подкосов, прогонов и стоек собирается подстропильная опорная система.
4. Дальше идет установка самих стропил, начиная с крайних, заканчивая промежуточными.

Хорошим подспорьем может служить видео как сделать крышу своими руками. На голый стропильный «скелет» никакая кровля не укладывается: необходима обрешетка.

Ее делают из различных материалов, чаще всего – из дерева. Деревянные доски гвоздями крепятся к стропилам. Параметры досок обрешетки зависят от материала, который будет использоваться для кровли.

Для требуется основа из доски сотки. Толщина рассчитывается индивидуально, но крайние длинные доски, обычно толще на 10 мм.

Исходя из значения поперечного шага профиля (350-400 мм) рассчитывают расстояние меж досками. Доска, выходящая за карниз, а также следующая за ней, располагают с шагом меньшей величины (300-350 мм).

Особенности обкладки двускатной крыши

К обрешетке крепятся листы металлочерепицы.

Совет. При обкладке двускатной крыши, следует начинать с торца, а в случае шатровой крыши, начинают с самой высшей точки, постепенно спускаясь вниз.

1. Металлочерепица всегда укладывается внахлест, предыдущий лист покрывается другим листом сверху.
2. Между собой листы металлочерепицы скрепляются с помощью саморезов, потом — к коньку при помощи шурупов.
3. Торцевые планки устанавливаются снизу вверх по фронтальным поверхностям крыши, а концы листов металлочерепицы накрываются.
4. Торцевые планки крепятся саморезами, которые прикручиваются к обрешетке и волнам (крайним) листа черепицы.
5. Когда будут установлены торцевые планки, устанавливают коньковые, которые крепят в верхней части каждой второй волны металлочерепицы. Они отвечают за фасад дома. Эти элементы так же привинчиваются шурупами.
6. После того, как планки установлены по длине, нахлест по ширине составляет примерно10 см.
7. В местах примыкания скатов осуществляется монтаж ендовы. Их – два экземпляра, нижняя ставится сверху планки карниза, прямо на обрешетку, а та, что сверху – поверх волны листа черепицы.
8. Далее проводится монтаж труб и сливов желобов.

Кто интересуется, как сделать крышу дома своими руками – видео демонстрирует схему, предложенную производителями. Нужно помнить, что крюки для монтажа системы необходимо прикреплять к обрешетке еще до начала монтажа металлочерепицы.

При желании можно установить громоотвод.

Крыша из обычного шифера

Для тех, кто хочет разобраться в том, как крыть крышу, не менее интересна более привычная технология – укладка шифера. Ее охотно используют, когда нужна построенная крыша массандра своими руками.

Заранее покрывается акриловой краской специально для окраски шифера. Без этого он будет активно впитывать влагу и со временем разрушится. В чистом виде шифер может держаться 15-20 лет. Покрашенный шифер в 3-5 раз прочнее и долговечнее.

Почему? Когда намокший шифер подмерзнет, то вода в микротрещинах расширит их и постепенно разрушит структуру шифера. Покрашенный материал защищён от воды в микротрещинах (они заполнены краской). Осматривать крышу из шифера достаточно раз в два-три года, по мере необходимости подкрашивая.

Для этих целей нужно позаботиться о безопасном доступе на крышу, необходим так называемый трап для крыши.

В современном доме каждый скат покрывают тремя рядками шифера. Средний ряд начинается от края не с целого, а в пол-листа шифера (разрезанного по длине).

Если стыковать другим способом, то 4 листа шифера ложатся углами друг на друга. Собравшись в одну точку, они образуют видимые щели и создадут непрочное соединение.

Не ищите инструкции как сделать крышу своими руками — видео демонстрирует как рассчитать количество шифера на дом и сколько из них необходимо разрезать. Режут шифер болгаркой, эта работа занимает час времени.

Один лист разрезается пополам – из расчета по 4 волны в половинке (шифер восьмиволновой). Два листа разрезаются так, чтобы образовались части из 5 волн и 3 волн. У частей с 5 волнами по краю должна присутствовать маленькая волна.

У заводского шифера последняя волна меньше, чем остальные – она предназначена специально для стыковки. Когда имеет место совмещенная крыша, то также шифер стелют таким образом, что маленькая волна остается присоединении под большой последующего листа (маленькая+маленькая не годится).

После разрезания получится 6 частей шифера: два 5-ти волновых (с них начинают покрывать средние ряды), два в четыре волны (они заканчивают покрытие средних рядов) и два в три волны (запасные).

Прикрепляется шифер кровельными саморезами поверх волны (если прикрепить внизу волны, вода станет затекать под крышу). Саморез входит в центр (или чуть выше) доски обрешётки. Победитовым сверлом Д 6-7 ммпросверливается отверстие в шифере под вкручиваемый саморез. Строители могут пробивать шифер гвоздём, чт

диагоналей прямоугольника с калькулятором

диагоналей прямоугольника с калькулятором — Math Open Reference

Попробуй это Перетащите любую вершину прямоугольника ниже. Он останется прямоугольником, и будет рассчитана длина диагонали.

Прямоугольник имеет две диагонали. Каждый из них отрезок нарисованный между противоположным вершины (углы) прямоугольника. Диагонали обладают следующими свойствами:

• Две диагонали конгруэнтные (одинаковой длины).На рисунке выше нажмите «показать обе диагонали», затем перетащите оранжевую точку в любую вершину прямоугольника и убедитесь, что это так.
• Каждая диагональ делит пополам другой. Другими словами, точка, где диагонали пересечь (крест), делит каждую диагональ на две равные части
• Каждая диагональ делит прямоугольник на две части. конгруэнтные прямоугольные треугольники. Поскольку треугольники конгруэнтны, они имеют одинаковую площадь, а каждый треугольник имеет половину площади прямоугольника
.

Длина по диагонали

На рисунке выше нажмите «Сброс».Как видите, диагональ прямоугольника делит его на две части. прямоугольные треугольники, BCD и DAB. Диагональ прямоугольника — это гипотенуза этих треугольников. Мы можем использовать Теорема Пифагора чтобы найти длину диагонали, если мы знаем ширину и высоту прямоугольника.

В виде формулы: где:
w — ширина прямоугольника
h — высота прямоугольника

Калькулятор

Воспользуйтесь калькулятором выше, чтобы вычислить свойства прямоугольника.

Введите длину двух сторон, и оставшаяся часть будет рассчитана. Например, введите длину двух сторон. Будут найдены площадь, периметр и длина диагонали.

Что попробовать

1. На рисунке вверху страницы нажмите «сбросить» и «скрыть детали». Затем перетащите углы, чтобы создать произвольный прямоугольник. Рассчитайте длину диагоналей. Нажмите «показать подробности», чтобы проверить свой ответ.
2. Прямоугольник имеет высоту 12 и диагональ 31.Найдите ширину прямоугольника и используйте анимацию или калькулятор выше, чтобы проверить свой ответ.

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

css — 3 блока подряд — не удается выровнять крайний правый

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя

.

диагоналей правильного восьмиугольника в геометрии GRE

Студенты любят пропустить основы, задавая такие вопросы, как: Сколько вершин у восьмиугольника? Сколько диагоналей у восьмиугольника? В чем разница между правильным восьмиугольником и ну восьмиугольником? И геометрия GRE действительно углубляется в сложную математику полигонов.

Но прежде чем мы перейдем к этому, я начну с двух сложных математических задач GRE.

GRE Геометрия: задачи многоугольников

1) Правильный пятиугольник P имеет все пять диагоналей.Каков угол между двумя этими диагоналями в точке пересечения их в вершине пятиугольника?

(A) 12 °

(B) 36 °

(C) 54 °

(D) 60 °

(E) 72 °

2) Сколько диагоналей дает правильная 20-гранная многоугольник есть?

(A) 60

(B) 120

(C) 170

(D) 240

(E) 400

Объяснения этих практических проблем появятся в конце этой статьи блога.Забегайте вперед, нажав здесь.

Полигоны

Во-первых, некоторые основные термины, чтобы начать это обсуждение. Многоугольник — это любая геометрическая фигура, все стороны которой являются прямыми отрезками. Любой треугольник — многоугольник. Любой четырехугольник (включая трапеции, параллелограммы, ромбы, прямоугольники и квадраты) является многоугольником. Пятиугольник — это 5-сторонний многоугольник. Шестигранник — это 6-сторонний многоугольник. Восьмиугольник — это восьмиугольный многоугольник.Круг, парабола или что-нибудь с изогнутой стороной — это , а не многоугольник.

Точка пересечения двух сторон многоугольника называется вершиной . Количество вершин многоугольника всегда равно количеству его сторон.

Еще один важный факт о многоугольнике касается суммы углов. Возможно, вы знаете, что сумма трех углов в любом треугольнике равна 180 °. Возможно, вы даже знаете, что сумма четырех углов в любом четырехугольнике равна 360 °. Этот образец является обобщающим. Сумма всех n углов в любом n-стороннем многоугольнике составляет:

сумма углов = (n — 2) * 180 °

Таким образом, любой пятиугольник (n = 5) будет иметь углы, которые в сумме составляют 3 * 180 = 540 °. У любого шестиугольника (n = 6) углы в сумме составляют 4 * 180 = 720 °. Любой восьмиугольник (n = 8) будет иметь углы в сумме 6 * 180 = 1080 °. (См. Блог о геометрических формулах GRE)

Наконец, есть это парадоксальное слово « обычный ». На обыденном языке «обычный» означает «обычный, ничем не примечательный, банальный».«В геометрии это означает прямо противоположное! Форма является правильной тогда и только тогда, когда она одновременно и равносторонняя, и равноугольная, то есть тогда и только тогда, когда все стороны имеют одинаковую длину и все углы равны. «Обычная» версия любого многоугольника — это самая элитная, наиболее симметричная версия этого многоугольника. «Правильный треугольник» — это то, что мы называем равносторонним треугольником. «Правильный четырехугольник» — это квадрат. Для более высоких полигонов вы, скорее всего, увидите обычную версию на GRE, потому что тест (как и все математики) любит симметрию.

Диагонали многоугольника

Теперь мы можем поговорить о диагоналях. Диагональ — это любая линия, проходящая внутри многоугольника, которая соединяет две несмежные вершины. Что это значит? Во-первых, начиная с любой вершины, смежная вершина — это либо вершина, соединенная с начальной вершиной одной стороной многоугольника.

Рассмотрим неправильный четырехугольник:

Начнем с вершины A. Начиная с вершины A, мы соединяемся сторонами этого четырехугольника как с B, так и с D; вершины B и D — это те, которые смежны с вершиной A.Единственная вершина, не соединенная с A стороной четырехугольника, — это C. C — единственная несмежная вершина A, а A — это C. Таким образом, одна диагональ идет от A к C. Нетрудно заметить, что другая идет от B к D. Любой четырехугольник имеет только две диагонали.

Обратите внимание, что треугольника НИКОГДА не имеют диагоналей : если мы начнем с любой вершины треугольника, две другие вершины будут смежными. В треугольнике просто нет несмежных вершин, поэтому диагонали невозможны.Среди четырехугольников существуют особые правила для диагоналей параллелограмма и категорий внутри параллелограммов:

Диагонали параллелограмма делят друг друга пополам: то есть точка пересечения двух диагоналей является средней точкой каждой из них. .

Ромб — это параллелограмм с четырьмя равными сторонами. Диагонали ромба пересекают друг друга и перпендикулярны.

Прямоугольник — это параллелограмм с четырьмя углами 90 °. Прямоугольники ромба делят друг друга пополам и имеют одинаковую длину.Это связано со старинной уловкой плотников. Когда плотник отрезает две пары одинаковой длины, чтобы сделать стороны дверной или оконной рамы, он знает, что у него есть параллелограмм из-за одинаковой длины, но как он узнает, есть ли у него прямоугольник? Без точного оборудования очень трудно измерить разницу, скажем, между углом 89 ° или 90 °. Что ж, все, что нужно сделать плотнику, — это измерить две диагонали: если эти две легко измеряемые длины равны, то гарантировано, что у него четыре прямых угла!

Квадрат — это параллелограмм, прямоугольник и ромб.Это правильный четырехугольник с четырьмя равными сторонами и четырьмя углами 90 °. Диагонали квадрата делят друг друга пополам, имеют одинаковую длину и перпендикулярны.

Диагонали правильного пятиугольника

Пятиугольник — это любой пятисторонний многоугольник, сумма углов которого составляет 540 °, как мы видели выше. Единственный пятиугольник, который вы можете встретить на GRE, — это самый симметричный, правильный пятиугольник. Поскольку углы равны, мы можем разделить сумму углов на пять.

540 ° / 5 = 108 °

Это угол каждого из пяти углов пятиугольника.

Вот правильный пятиугольник с пятью диагоналями.

Сколько диагоналей у пятиугольника? У любого пятиугольника ровно пять диагоналей. Эти диагонали повторяют форму классической пятиконечной звезды, например, звезды на флаге Соединенных Штатов Америки. Длина и деления этой звезды тесно связаны с этим магическим и мистическим числом, золотым сечением; Сакральная геометрия призвана дать представление о смысле жизни, но вам не нужно знать ничего из этого для GRE!

Как мы можем найти углы в этой форме? Ну, мы знаем, что каждый большой угол пятиугольника составляет 108 °.Взгляните, например, на треугольник ABC. Этот треугольник является равнобедренным, потому что AB = BC, и мы знаем, что угол ABC = 108 °. Два других угла должны быть равны: назовите их x.

108 ° + x + x = 180 *

2x = 180 ° — 108 ° = 72 °

x = 36 °

Это означает, что угол BAC = угол BCA = 36 °, как и многие другие симметрично связанные углы вокруг формы. Мы могли бы вычесть (угол BAC) из (угла BAE), чтобы получить (угол CAE)

угол CAE = (угол BAE) — (угол BAC) = 108 ° — 36 ° = 72 °

Из этого мы могли бы найти много другие углы внутри формы.Мы могли бы использовать аналогичные средства, чтобы найти углы, включающие диагонали любого более высокого многоугольника.

Диагонали правильного шестиугольника

Шестигранник — это любой шестигранный многоугольник, сумма углов которого равна 720 °, как мы видели выше. В правильном шестиугольнике

каждый угол = 720 ° / 6 = 120 °

Сколько диагоналей у шестиугольника? Начиная с одной вершины, две другие вершины являются смежными, поэтому 3 вершины не являются смежными, что делает возможными три диагонали из одной вершины.Из A мы можем провести диагонали к C, D и E.

От каждой вершины есть три диагонали. Поскольку существует шесть вершин, вы можете подумать, что всего будет 3 * 6 = 18 диагоналей, но этот метод подсчета учитывает все дважды. Видите ли, диагональ от A до C будет считаться один раз как диагональ от A, а затем как диагональ от C до A. Таким образом, количество диагоналей в шестиугольнике равно 18/2 = 9. Это могут быть группы по две. виды. Шесть более коротких диагоналей вместе образуют шестигранную звезду, Маген Давид.Три более длинные диагонали образуют всего три симметрично пересекающихся сегмента, то, что в математике называется «вырожденной шестиконечной звездой».

На этих двух диаграммах показаны девять диагоналей правильного шестиугольника. Конечно, шестиконечная звезда просто состоит из двух перекрывающихся равносторонних треугольников, направленных в противоположных направлениях. (Этот геометрический факт привел к обширным мистическим рассуждениям о Звезде Давида в Каббале, но опять же, вам не нужно понимать никакой мистики для GRE!)

Диагонали правильного семиугольника

семиугольник — это любой семигранный многоугольник (n = 7).Иногда его называют «септагон», но математическое название предпочтительнее «семиугольник». Сумма его углов будет

(n — 2) * 180 ° = 5 * 180 ° = 900 °

Это означает, что каждый из семи углов в правильном семиугольнике будет иметь размер

, каждый угол = 900 ° / 7 = 128,5714286… °

Угловые размеры не целые! Вот почему GRE вряд ли спросит вас о правильном семиугольнике, и именно поэтому вы, вероятно, никогда особо не говорили о правильных семиугольниках в школьной геометрии. Вот почему большинство людей даже не знают, как назвать этого зверя! Их нецелочисленная угловая мера делает их первой «белой вороной» в семействе обычных многоугольников! Я не буду больше ничего говорить о них, потому что они почти никогда не появляются на GRE, но я покажу вам две возможные семиконечные звезды по их диагоналям: эти звезды навязчиво красивы из-за их особой симметрии.

Диагонали правильного восьмиугольника

Восьмиугольник — это любой восьмиугольный многоугольник, сумма углов которого равна 1080 °, как мы видели выше.В правильном восьмиугольнике

каждый угол = 1080 ° / 8 = 135 °

Этот угол является дополнением к углу 45 °. Правильный восьмиугольник — типичная форма знака остановки во многих частях мира.

Сколько диагоналей у восьмиугольника? Сколько вершин у восьмиугольника?

Начиная с одной вершины, две другие вершины являются смежными, поэтому пять вершин не являются смежными, что делает возможными пять диагоналей из одной вершины. От A, B и H — симметричные вершины, поэтому мы можем провести диагонали к C, D, E, F и G.

Логика аналогична шестиугольнику: пять в каждой вершине, восемь вершин, но при этом каждая диагональ считается дважды, поэтому общее число равно 5 * 8/2 = 20. AC и AG — это то, что мы могли бы назвать «3 вершины». диагонали »: их восемь, которые образуют звезду. AF и AD, каждая из которых параллельна двум сторонам, — это то, что мы могли бы назвать «четырьмя диагоналями вершин»: восемь из них образуют другую звезду. Наконец, AE подобен диаметру всего восьмиугольника, пересекающему его центр: таких линий четыре, и они образуют вырожденную восьмиконечную звезду.

Подобно тому, как шестиконечная звезда состоит из двух перекрывающихся равносторонних треугольников, первая восьмиконечная звезда слева состоит из двух отдельных перекрывающихся квадратов: квадратного ACEG и квадратного BDFG. (Названия этих квадратов напоминают линии на W. 4th Street!) Между этими тремя звездами (считая вырожденный объект справа как «звезду») у нас есть все 20 диагоналей правильного восьмиугольника.

Сводка

Вперед и вперед! Методы, обсуждаемые в этом блоге, могут быть расширены для применения к шестиугольнику (n = 9), десятиугольнику (n = 10) или любому более высокому многоугольнику.Вооружившись этой информацией, вы сможете ответить на все, что вас спросит GRE о диагонали многоугольника! Если при чтении этого блога у вас были моменты «ага», возможно, вы захотите еще раз взглянуть на практические задачи в верхней части, прежде чем читать пояснения ниже.

Объяснение практических задач

1) Давайте посмотрим на пятиугольник с его пятью диагоналями.

Примером угла между двумя диагоналями в вершине может быть угол EBD, где диагонали BD и BE пересекаются в вершине B.

Мы будем следовать логике, изложенной выше.

Треугольник BCD равнобедренный, BC = CD, угол BCD = 108 °. Два других угла равны: назовите их каждый x.

108 ° + x + x = 180 *

2x = 180 ° — 108 ° = 72 °

x = 36 °

Итак, угол CBD = 36 °. Итак, треугольник ABE во всех отношениях равен треугольнику BCD, поэтому угол ABE также должен быть равен 36 °. Таким образом, мы можем вычесть из большого угла в вершине B.

(угол EBD) = (угол ABC) — (угол CBD) — (угол ABE)

(угол EBD) = 108 ° — 36 ° — 36 ° = 36 °

Ответ = (B)

2) Если мы начнем с одной вершины 20-стороннего многоугольника, то с каждой стороны будет смежная вершина.Не считая этих трех вершин, было бы 17 несмежных вершин, поэтому из любой вершины можно было бы провести 17 возможных диагоналей. Двадцать вершин, 17 диагоналей из каждой вершины, но этот метод учитывает диагонали дважды, как указано выше.

# диагоналей = (17 * 20) / 2 = 17 * 10 = 170

Ответ = (C)

Примечание редактора: этот пост был первоначально опубликован в январе 2014 года и был обновлен за свежесть, точность и полноту.

П.С. Готовы улучшить свой GRE? Начни сегодня.

Самые популярные ресурсы

.

Диагоналей многоугольника — Math Open Reference

Многоугольник диагоналей — Math Open Reference

Попробуйте это Отрегулируйте количество сторон многоугольника ниже или перетащите вершину чтобы отметить поведение диагоналей.

Диагональ многоугольника — это отрезок прямой соединение двух вершин. От любой данной вершины нет диагонали к вершине по обе стороны от нее, так как это будет лежать на стороне. Кроме того, очевидно, что нет диагонали от вершины к самой себе.Это означает, что диагоналей на три меньше, чем вершин. (диагонали к себе и по одной в обе стороны не учитываются).

Формула числа диагоналей

Как описано выше, количество диагоналей от одной вершины на три меньше, чем количество вершин или сторон, или (n-3).

Есть N вершин, что дает нам n (n-3) диагоналей.

Но у каждой диагонали два конца, так что каждый будет учитываться дважды. Итак, в качестве последнего шага мы разделим на 2 для окончательной формулы: где
n — количество сторон (или вершин)

Вогнутые полигоны

Одна из характеристик вогнутого многоугольника заключается в том, что некоторые диагонали будут лежать за пределами многоугольника.На рисунке выше снимите флажок «Обычный». Перетащите одну из вершин к центру многоугольника. Вы увидите белые области. Многоугольник закрашен желтым цветом, поэтому вы видите диагональ, лежащую за пределами вогнутого многоугольника.

Простая ошибка

Приведенная выше формула дает нам количество различных диагоналей, то есть количество фактических отрезков линии. Легко неправильно рассчитать диагонали многоугольника, делая это на глаз.

Если вы быстро взглянете на пятиугольник справа, у вас может возникнуть соблазн говорят, что диагоналей 10. Ведь в каждой вершине по две, а вершин 5. Некоторые люди видят, как они образуют три треугольника по 6 диагоналей. Но диагоналей всего 5. Тщательно пересчитайте их.

Другие темы в круге

Общие

Уравнения окружности

Углы по окружности

Дуги

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

---

Смотрите также

• Как построить трехскатную крышу
• Как утеплять крышу из металлочерепицы
• Как покрыть двухскатную крышу ондулином своими руками
• Как правильно крепить софиты на крыше
• Как правильно крышу ондулином
• Как залатать крышу из железа
• Как сделать крышу дома
• Как сделать крышу бани своими руками
• Как битумом залить крышу
• Как стыковать крышу пристройки к основному дому
• Как вырезать эллипс под проход в крыше 45 градусов

Диагональные распорки критически важны для устойчивости конструкции

В. Я столкнулся с некоторыми строительными проектами. Одна высокая колода, другой обрамляет садовый сарай, а потом мне нужно помочь другу с комнатой добавление. Меня интересует диагональная растяжка. Я не понимаю этого и нужно чтобы знать, почему это важно. Есть ли короткий путь? Можете ли вы дать мне исполнительную резюме, чтобы у меня не было проблем на этих работах?

A. Вы получите Резюме, хорошо. О диагональных связях написаны книги. Поговорите с любым инженером-строителем, и я уверен, что он расскажет вам, что весь колледж курсы предлагаются по теме. Это очень сложная тема, но я постараюсь чтобы дать вам основы, чтобы у вас не было провала ни в одном из ваших проектов.

Диагональные связи являются конструктивным элементом практически любого здания. Это обеспечивает боковую устойчивость, предотвращая обрушение стен, настилов, крыш и многие другие конструктивные элементы.

Давайте поговорим о том, что происходит со структурой, когда у вас нет диагонали распорка на месте. Представьте, что вы строите стену высотой 8 футов, используя 2 на 4 16 дюймов. по центру. Если вы поднимете стену и прибьете нижнюю пластину к полу, чтобы держите только это на месте, стена может показаться достаточно прочной, чтобы вы могли поставить вес сверху.

А вот и страшное испытание. Встаньте на стремянку на одном конце стены. Толкать на конце верхней пластины в движении, параллельном стене. Вы быстро обнаружите, что вы можете разрушить стену с минимальными усилиями закрыть дверь гармошкой. За считанные секунды вы можете сложить стену высотой 8 футов. на себя и всего в нескольких дюймах от пола.

ГОТОВ К СБОРУ

Теперь представьте, что произойдет, если вы построили дом без диагональных распорок или с плохими диагональными связями, и сильный ураган ударил по дому. Или представьте себе сильную тряску из стороны в сторону, которая происходит когда поперечные волны землетрясения обрушиваются на дом. Ты видишь, как дом может легко рухнуть? Когда профессиональные плотники строят дом, они устанавливают различные виды крепления. Одной из них может быть металлическая диагональная распорка снизу. угол стены до верхней пластины.

Фанера или ориентированно-стружечная плита, правильно прибитые гвоздями, также обеспечивают отличное диагональное крепление. Обычно вам нужно положить только один полный лист фанера на каждом углу стены для обеспечения необходимой устойчивости.

Недостаточное диагональное крепление приводит к обрушению многих настилов. я видел колоды чья внешняя опорная балка просто опирается на деревянные стойки. Если группа людей на колода начинает танцевать и создается гармоническое движение, вся колода может рухнуть, когда дека начнет сдвигаться вбок. Диагональные связи предотвращают это. движение из стороны в сторону.

Существует множество способов установки диагональных связей для настила. В одну сторону заключается в установке диагональных раскосов, которые соединяют балки настила с вертикальными стойками. Эти брекеты обычно вырезаются под углом 45 градусов. Очень важно закрепите их, а не полагайтесь на гвозди.

Вы также можете установить плоскую плиту 2 на 6 или 2 на 8 на нижней стороне пола. балки, чтобы дать настилу большую диагональную поддержку. Водите не менее двух 16d оцинкованные гвозди через скобу на каждой балке пола. Убедитесь, что ногти правильное покрытие, соответствующее обработанной древесине, которую вы используете, чтобы предотвратить коррозия.

Диагональные связи очень важны, если вы работаете с фермами крыши. что предстоящее дополнение комнаты. Многие плотники были убиты или серьезно получают травмы, когда стропильные фермы внезапно рушатся во время возведения. Ветер может легко толкните их, если у них нет крепления.

Крыши с большими фермами часто поставляются с подробными чертежами, показывающими крепления, которые должны быть установлены в стенках ферм. Всегда обязательно ссылайтесь какие-либо чертежи или поговорите с инженером ферменной компании, если у вас есть вопросов.

Если вы приобретете продукт или зарегистрируете учетную запись по одной из ссылок на нашем сайте, мы можем получить компенсацию.

Диагональные стены

Архивы — Башенные кирпичные конструкции

Введение

Сколькими способами можно прикрепить кирпич 1×6 к опорной плите? Как вы можете себе представить, их довольно много, но каждый раз шпильки кирпича должны совпадать с шпильками опорной плиты под ним. Именно так работает LEGO. Шпильки на опорной плите расположены в виде правильной квадратной сетки, поэтому вы можете размещать кирпичи 1×6 только так, чтобы они были параллельны одной из сторон опорной плиты. Предположим, вы строите замок из LEGO, и одна из ваших стен должна быть под углом 45 градусов, вам не повезло?

Помните обычную квадратную сетку, о которой я упоминал ранее? Если вы возьмете любую шпильку на опорной плите, она будет находиться на одинаковом расстоянии от каждого из своих соседей со всех 4 сторон, и это расстояние составит 0,8 см (или «шпилька», которая также основная единица измерения в LEGO). . Но шпильки в 4 углах находятся дальше (расстояние составляет √2 x 0,8 см = 1,414 x 0,8 см = 1,13 см, если быть точным). Это потому, что в квадрате 4 стороны имеют одинаковую длину, но расстояние между любыми двумя противоположными углами немного больше. Точно так же расстояние между любыми двумя стойками, измеренное под любым углом, отличным от 0 или 90 градусов не обязательно будет целым числом шпилек.

Итак, как мы можем повернуть наш кирпич 1×6 под другим углом, чтобы он по-прежнему был надежно прикреплен к опорной плите?

Основы для угловых стен

Давайте проведем небольшой эксперимент — поместите две пластины 1×1, как показано на рисунке ниже. Теперь, если вы поместите кирпич 1 × 6 по диагонали, соединив эти две пластины 1 × 1, это сработает! Шпильки на двух концах кирпича 1×6 совпадают с шпильками на двух пластинах 1×1. Это позволяет кирпичу 1×6 иметь хорошее соединение с опорной плитой (по крайней мере, на двух концах). Оставшиеся 4 стойки на кирпиче 1×6 по-прежнему не совпадают с нижними стойками (теперь понятно, почему нам пришлось использовать пластины 1×1 в качестве прокладок, чтобы поднять кирпич 1×6). Итак, что именно здесь происходит?

Если вы вспомните школьную математику (если вы еще не освоили ее, вам просто придется поверить мне на слово), уравнение a ²  + b ² = c ² может показаться смутно знакомым. Это теорема Пифагора, которая определяет соотношение между сторонами прямоугольного треугольника.

Давайте внимательнее посмотрим, где две пластины 1×1 были размещены на опорной плите. Если мы посчитаем вдоль двух сторон опорной плиты, начиная с угла, мы увидим, что пластины 1 × 1 находятся на расстоянии 3 и 4 стержня от углового стержня и составляют две стороны прямоугольного треугольника. Наш кирпич 1×6 расположен вдоль третьей (самой длинной) стороны, также известной как гипотенуза. Созданный нами треугольник удовлетворяет теореме Пифагора, потому что 3 ²  + 4 ² = 9 + 16 = 25, что равно 5 ² . Тогда имеет ли смысл использовать кирпич 1×6 для самой длинной стороны? Да, потому что три стороны прямоугольного треугольника пересекаются на стойках, а расстояние, которое действительно имеет значение, — это расстояние между стойками на двух концах кирпича 1 × 6, которое равно 5 стойкам.

Суть в том, что для того, чтобы любой кирпич или плиту можно было положить под углом, отличным от 0 или 90 градусов, нужно убедиться, что получившийся треугольник удовлетворяет теореме Пифагора. Любой набор из 3 чисел, удовлетворяющий этой теореме, называется тройкой Пифагора, а (3, 4, 5) — наименьший такой набор, состоящий из целых чисел. Какие еще есть пифагорейские тройки? Ниже перечислены все пифагорейские тройки с числами, меньшими или равными 25. Как видите, в сборках LEGO не так много из них имеют практическое применение.

3,	4,	5
5,	12,	13
6,
6,
6,
.	25
8,	15,	17
9,	12,	15
12,	16,	20

Angled walls с помощью шарнирных элементов

Если бы мы использовали метод, описанный ранее, для построения угловых стен, то просто не было бы хорошего способа избежать зазоров в углах, где сегменты наклонной стены встречаются с сегментами обычной стены, размещенными вдоль сетки LEGO. Альтернативой является использование шарнирных элементов.

Существует множество различных типов шарнирных элементов LEGO, но для угловых стен нам нужны поворотные, в частности шарнирная пластина 1×4, состоящая из поворотного основания 1×2 и поворотной верхней части 1×2.

Пластины 1×2, составляющие каждую из двух половин шарнирной пластины, соединены в своих углах шарниром, который позволяет изменять угол между пластинами от 0 до 180 градусов. Если вы разместите две шарнирные пластины 1 × 4, как показано ниже, вы можете соединить их пластиной 1 × 5 (да, LEGO делает одну сейчас!), прикрепленной сверху.

Мы по-прежнему создаем тот же прямоугольный треугольник (3, 4, 5), что и раньше, но на этот раз гипотенуза (согнутая сторона) имеет 5 выступов вместо 6. Это потому, что стороны прямоугольного треугольника теперь пересекаются в углы пластин, а не шпильки.

Примером официального набора LEGO, в котором широко используется тройка (3,4,5), является набор «Бутик-отель» (10297). Здесь вы можете найти не один, а 6 отдельных (3,4,5) треугольников, используемых для создания наклонных стен, которые придают зданию уникальную треугольную форму. Более подробную информацию можно найти здесь.

Наклонные стены с использованием поворотных столов

Поворотный стол LEGO состоит из основания (2×2 или 4×4), которое можно прикрепить как обычную пластину, и верхней части, которая может свободно поворачиваться на 360 градусов. Для основания 2×2 требуется соответствующий верхний элемент, в то время как основание 4×4 может вмещать множество совместимых элементов, включая круглую пластину 4×4.

Поворотные столы дают нам еще один способ создания наклонных стен, и этот метод использовался во многих официальных наборах LEGO. Примером может служить набор «Весенний фестиваль фонарей» (80107), в котором поворотные столы 4 × 4 используются для крепления арочного пешеходного моста под углом над прудом с карпами.

Даже когда мы используем поворотные столы для создания наклонной стены (или конструкции, прикрепленной под углом, как в этом примере), мы, по сути, создаем прямоугольный треугольник, удовлетворяющий теореме Пифагора. Стороны этого треугольника пересекаются на осях вращения поворотных кругов (в центрах верхних пластин). В данном случае используется пифагорейская тройка (6,8,10).

Near Triples (Когда достаточно близко)

Наклонная стена, которую мы построили ранее, вероятно, может сойти за стену под углом 45 градусов, но если вы присмотритесь к ней, меньший угол больше похож на 37 градусов. Прямоугольный треугольник с углом 45 градусов называется особым прямоугольным треугольником, потому что третий угол также равен 45 градусам (в сумме три угла треугольника должны составлять 180 градусов). Это также означает, что две стороны, составляющие прямой угол, должны быть одинаковой длины. Ни в одной из пифагорейских троек, которые мы видели, нет двух равных меньших чисел. Так действительно ли можно построить стену под углом 45 градусов с помощью LEGO?

К счастью, то немногое, что есть у шарнирных пластин, позволяет нам использовать числа, достаточно близкие к пифагорейским тройкам. Рассмотрим, например, (5,5,7) и (7,7,10), которые являются «почти тройками», которые позволяют вам строить стены LEGO под углом 45 градусов, как показано ниже.

(12, 12, 17) и (17, 17, 24) еще несколько. Есть также «почти тройки», такие как (4, 7, 8) и (4, 8, 9), которые не дают вам угол 45 градусов, но, тем не менее, полезны.

Официальные наборы также использовали «почти тройки», такие как набор «Угловой гараж» (10264), в котором используются (12,12,17) для создания части главного фасада, расположенной под углом 45 градусов. Вы можете найти более подробную информацию здесь.

Использование перемычек для еще большего количества вариантов

Тройки Пифагора (или «почти тройки») также работают, когда вы умножаете все числа в тройке на целое число, например 2, или делите их пополам. Например, возьмите тройку (3, 4, 5) и умножьте все числа на 2, и вы получите еще одну тройку (6, 8, 10). Точно так же, если взять «почти тройку» (7, 7, 10) и разделить все числа пополам, есть основания полагать, что (3,5, 3,5, 5) сработает. Но как создать треугольник со сторонами длиной 3,5 стержня? С помощью перемычек, конечно же!

Комбинация «почти тройных» с шагом в половину стойки дает вам больше возможностей для возведения стен под углом 45 градусов. Одна комбинация, которую я нашел особенно полезной, это (8,5, 8,5, 12), которая составляет половину «почти тройки» (17, 17, 24).

Наклонные стены – Hearst Tower

Hearst Tower в Нью-Йорке – прекрасный пример небоскреба, сочетающего в себе старый и новый архитектурные стили. Он сохраняет фасад оригинального 6-этажного здания в стиле ар-деко в качестве основания и добавляет современную стеклянную башню на вершине. Два угла основания скошены, и мне нужно было построить стены под углом 45 градусов для этих двух углов. Основываясь на масштабе, который я использовал, мне нужно было, чтобы угловая секция стены имела ширину около 7 стержней. Это было идеальное приложение для «почти тройки» (5,5,7).

Наклонные стены – Тадж-Махал

Одно из современных чудес света, Тадж-Махал в Агре, Индия, вероятно, является одним из самых известных шедевров исламской архитектуры. Главное сооружение Тадж-Махала — мавзолей, стоящий на возвышении. Мавзолей имеет форму куба с четырьмя усеченными углами, образующими неравный восьмиугольник. Чтобы создать скошенные углы в моей модели LEGO, я использовал еще одну «почти тройку» (7, 7, 10).

Наклонные стены — Башня Трибьюн

Один из самых красивых небоскребов в мире — Башня Трибьюн в Чикаго — вдохновлен неоготической архитектурой. Его богато украшенная корона с контрфорсами была спроектирована по образцу Масляной башни Руанского собора во Франции. Моя модель LEGO этого здания требовала не одного, а нескольких различных типов наклонных стен. Для скошенных углов главной башни я использовал «ближнюю тройку» (5,5,7). На двух уровнях восьмиугольной короны использовались две ближние тройки – (8.5, 8.5,12) и (7,7,10), а аркбутаны крепились к основанию венца с помощью еще одной ближней тройки (4,7,8). .

Наклонные стены – другие методы

Эта статья была бы неполной без упоминания хотя бы нескольких других способов строительства наклонных стен с помощью LEGO. Методы, которые мы видели до сих пор, создают наклонные стены, размещая элементы вдоль гипотенузы (наклонной стороны) прямоугольного треугольника. Но чтобы это работало, длина гипотенузы должна быть целым числом стержней, и это ограничивает наши возможности пифагорейскими тройками и почти тройками.

Есть несколько других методов, в которых мы фактически не размещаем никакие элементы вдоль гипотенузы и поэтому можем игнорировать ее длину. Это открывает немало других возможностей…

Техника «зеркальной гипотенузы»

Начнем с произвольного прямоугольного треугольника – скажем, стороны, составляющие прямой угол, имеют длину 6 стержней и 2 стержня. Длина гипотенузы (сторона под углом) будет равна √(6 ² + 2 ² ) = 6,32 гвоздика, что не является целым числом. Невозможно разместить элемент LEGO вдоль этой стороны, но если мы отразим прямоугольный треугольник вдоль гипотенузы, мы можем создать наклонную стену, разместив элементы LEGO вдоль двух других сторон второго треугольника. Нам нужно будет использовать шарнирные пластины, чтобы соединить два зеркальных прямоугольных треугольника вместе.

В более распространенном применении метода зеркальной гипотенузы используются клиновидные пластины для создания двух зеркальных треугольников. Клиновые пластины 6×3 создают треугольники, эквивалентные треугольникам из моего предыдущего примера (в конце концов, числа, которые я выбрал, не были такими уж произвольными). Эта техника используется для создания наклонных сторон в секциях пола и крыши набора «Бутик-отель» (10297). Вы можете найти более подробную информацию здесь.

Эту технику также можно распространить на неравные треугольники, где гипотенуза одного треугольника является одной из сторон, образующих прямой угол второго треугольника. Полученный четырехугольник (форма с четырьмя сторонами) должен удовлетворять уравнению для пифагорейской четверки, которая представляет собой ² + б ² + в ² = д ² . Простейшая пифагорейская четверка — это (1,2,2,3). Умножьте все числа на 2, и вы получите (2,4,4,6), что также является четверкой Пифагора.

Преимущество четверок Пифагора в том, что их можно использовать для размещения элементов под углом не только в 2-х, но и в 3-х измерениях. Идея принадлежит hafhead на Flickr.

Метод «переключаемых диагоналей»

Расстояние по диагонали между двумя шипами на пластине не может быть целым числом шипов. Но если взять прямоугольную пластину, то расстояния между двумя парами шпилек в противоположных углах (1, 3 и 2, 4) будут совершенно одинаковыми. Таким образом, вы можете повернуть пластину и прикрепить ее так, чтобы ее углы 2 и 4 совпадали с обычными углами 1 и 3. Вам снова нужно будет использовать пластины 1×1 в качестве прокладок.

Если вы думаете о 1-3 и 2-4 как о самых длинных сторонах двух идентичных прямоугольных треугольников, которые зеркально отражены, все, что вы делаете, это поворачиваете один из треугольников так, чтобы самые длинные стороны выровнялись. Угол поворота, очевидно, будет зависеть от размера прямоугольного треугольника (количество выступов на двух сторонах, составляющих прямой угол). Оказывается, ближе всего к 45-градусному повороту можно использовать пластину 4×8.

Этот метод также можно расширить, включив в него шарнирные элементы. Это выглядит немного по-другому, потому что на этот раз переключаемые диагонали доходят до углов пластин.

Заключение

Я уверен, что есть несколько других способов создания наклонных стен, которые я не смог описать здесь.